2. 清华大学深圳国际研究生院, 广东 深圳 518055;
3. 清华大学自动化系, 北京 100084
2. Tsinghua Shenzhen International Graduate School, Shenzhen 518055, China;
3. Department of Automation, Tsinghua University, Beijing 100084, China
空间机器人及其遥操作是航天工程与机器人学科相结合的产物,是空间作业中协助地面人员或替代宇航员执行危险或长期太空任务的重要手段,增强了人类探索空间环境的能力,在空间维护和修理、空间加工装配等在轨任务中发挥着重要作用。随着航空、航天等技术领域的飞速发展,狭小工作空间下的任务需求越来越多,如卫星太阳能故障帆板展开、飞行器狭小空间故障探测、维修等。传统关节式刚性机械臂的体积大、灵巧度低,不能很好地完成任务,而体型纤细、结构紧凑、运动灵活的绳驱超冗余柔性机械臂更适合完成上述任务[1]。受机构、控制、人工智能和传感技术水平的限制,在非结构化环境下实现智能空间机械臂的全自主式工作是当前乃至今后相当长时间内难以达到的。遥操作技术将是空间机械臂在自主能力受限情况下不可或缺的操控手段之一。德国建立了第一个可在地面进行遥操作的舱内空间机器人系统ROTEX[2],其后日本、加拿大等国家在空间机器人遥操作方面进行了大量研究,也建立了相应的遥操作系统[3-5]。国内多家单位,如哈尔滨工业大学、西北工业大学、中国科学院力学所和清华大学等也对空间机器人及其遥操作系统进行了大量的研究和实验[6-7]。
绳驱超冗余柔性机械臂在执行在轨任务时,应具备的能力有:(1) 速度快:大范围工作空间或无障碍情况下运动速度快;(2) 精度高:在狭小空间内或执行接触操作时控制精度高;(3) 交互性好:人机交互方式友好自然,可同时控制末端和臂形[8]。在传统的遥操作人机交互技术中,手控器[9]、骨骼式机械装置[10]、仿机器人外形的控制器[11]等接触式的机械设备经常被用作操作员和机器人之间交互的工具。这类控制器的最大缺点是需要操作员进行非常不直观的手臂动作对机器人进行控制,这就需要操作员具备一定的操作经验才能有效地对机器人进行准确控制。本文针对超冗余柔性机械臂构形特点和任务需求,提出了多种交互方式组合的遥操作人机交互系统,研究了适用于遥操作系统的自由度动态组合和末端—臂形同步规划的遥操作方法,从而使其高效率、高质量地完成在轨任务。
2 超冗余空间柔性机械臂遥操作系统设计(The teleoperation system design for hyper-redundant space flexible manipulator)柔性机械臂的主要任务包括辅助监视、狭小空间故障检测维修等。在执行复杂操作任务时,星上控制器计算能力有限,不能进行复杂算法计算。而且柔性机械臂自由度多、臂杆长,面对复杂工作环境避障难、精细操作控制难。因此,在空间柔性机械臂自主能力受限的情况下,为保证成功完成任务,将人的智能加入到控制闭环中,构建柔性机械臂天地闭环协同遥操作系统,该系统主要包括操作员、遥操作系统、天地通信链路、柔性机械臂。
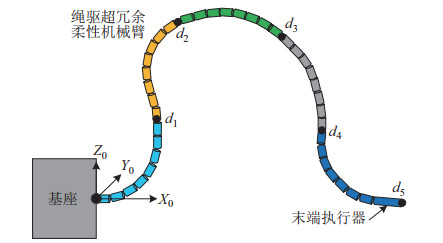
2.1 超冗余柔性机械臂超冗余柔性机械臂基于绳索驱动并采用主被动驱动分段联动的结构,每个关节段为全约束的主被动驱动结构,即其整体上由驱动绳进行主动驱动,而段内的多个小节则由联动绳进行被动驱动,实现等角度运动,具有体型纤细、分段联动、机电分离的特点。对于空间任务,它具有灵活的曲线跟踪能力和狭小空间作业的能力。如图 1所示,超冗余柔性机械臂包含5个独立运动的主动联动关节段,每段由3根主动驱动绳驱动,共15根驱动绳。每个大段内有8个依次串联的采用联动绳索约束的被动万向节小节,并以等角度方式运动。每个小节均具有2个方向的弯曲运动能力(2DOF)。因此,整个超冗余柔性机械臂共80个自由度。柔性臂单个小节长100 mm,其参数如表 1所示。在机械臂末端装有用来监视测量的视觉相机等工具。
|
图 1 绳驱超冗余柔性机械臂示意图 Fig.1 The schematic of cable-driven and hyper-redundant flexible manipulator |
|
|
表 1 单个柔性模块关节参数 Tab. 1 Joint parameters of a single flexible module |
柔性机械臂遥操作人机交互系统主要功能是将人的操作意图转化为柔性机械臂控制指令,实时生成、发送主从操作命令序列,控制柔性机械臂完成指定的遥操作任务。
柔性机械臂遥操作人机交互系统由人机交互单元、信息管理单元组成,如图 2所示。人机交互单元通过交互输入模块采集操作者的操作意图信息并将其转化为计算机指令;通过平滑滤波等算法对指令数据进行处理,提高指令数据的安全稳定性;利用柔性机械臂运动学算法及柔性机械臂控制输入信息,得到柔性机械臂控制指令;场景显示模块利用图形预测仿真技术给操作者实时提供可视化的操作场景,使操作者能快速准确地完成操作任务。信息管理单元将经过处理和安全检测的柔性机械臂控制指令发送给遥操作支持平台。遥操作支持平台作为地面遥操作系统和空间机械臂通信的桥梁,负责遥控和遥测信息的加工、转发。

|
图 2 遥操作系统组成图 Fig.2 The composition diagram of the teleoperation system |
(1) 人机交互单元在遥操作系统中主要承担将操作者的意图转化为柔性机械臂控制指令的功能,由交互输入模块、数据优化模块、数据解算模块、场景显示模块组成。一方面操作者通过人机交互设备产生自然高效的控制指令,另一方面,人机交互单元给操作者提供充分的远端环境临场感信息。
(2) 信息管理单元在遥操作系统中主要承担数据的接收、转发、存储,指令的安全检测,系统配置管理等功能,由配置管理模块、数据存储模块、数据管理模块、信息显示模块、安全检测模块、网络通信模块组成。信息管理单元是遥操作系统与外界的连接中枢。
2.3 人机交互方式人机交互设备是遥操作系统中不可或缺的模块,该模块是连接人与计算机的桥梁。人机交互设备将操作者的操作意识转化为数字信号发送给计算机,同时可将操作对象与环境的作用力反馈传递给操作者。为提高遥操作效率,遥操作系统人机交互方式应符合操作对象的运动学特性,针对柔性机械臂,不但要能控制末端位置、姿态,还应具备控制机械臂整体臂形的能力。
常用的遥操作设备——力反馈手控器,具有精度高、力反馈准确的优点。然而,由于手控器的操作空间有限,在涉及大范围工作空间交互操作任务时,需要进行多次重复复位,会导致操作效率降低。另外操作对象为多自由度超冗余柔性机械臂时,只能控制末端,不能控制臂形,无法控制机械臂完成避障等复杂任务[12]。为此,本文提出了针对多自由度超冗余柔性机械臂的多种交互方式组合的人机交互系统。当柔性机械臂臂杆周围有障碍、需要大范围工作空间运动时,采用虚拟现实(virtual reality,VR)手柄进行控制,可快速给出机械臂运动趋势指令并控制臂形;当柔性机械臂在狭小空间碰到危险需要精确操作或需接触操作时,采用力反馈手控器控制。采用多种交互方式组合能解决只采用手控器单一交互方式使得控制对象受限的问题,如表 2所示。
|
|
表 2 人机交互设备 Tab. 2 Human-machine interaction equipments |
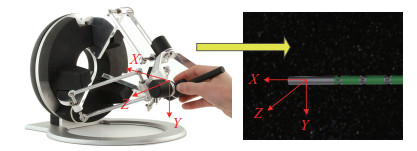
力反馈手控器的结构设计简洁合理、力反馈大、感知明显、控制精度高,适合狭小空间或目标接触操作。在力反馈手控器控制方式下,将手控器手柄处的位置姿态映射到柔性机械臂的末端位置姿态,通过柔性机械臂逆解算法计算出关节角和绳长控制数据,完成对柔性机械臂的实时控制,坐标映射关系如图 3所示。当末端需接触目标操作时,基于柔性机械臂的动力学模型,根据电机角度与绳索电流值计算出末端接触力大小,通过手控器反馈给操作者,完成力反馈控制。力反馈设备采用瑞士Force Dimension公司的Omega.6,它是基于Delta机构的并行运动学设计的高端力反馈设备。
|
图 3 手控器控制示意图 Fig.3 The schematic of the hand controller |
VR手柄的优点是人机交互直观自然、操作空间大、速度快,属于非接触式的人机交互设备,整个操作方式是非浸入式的,对操作员的干扰大大减小,应用于需要避障操作或大范围工作空间运动的工作场景[13-14]。操作员使用2个手柄,一个手柄控制柔性机械臂末端位姿,另一个手柄控制柔性机械臂中间臂形控制点,如图 4所示。对于长度达4 m的柔性机械臂只需一个操作者即可同时控制柔性臂的臂形与末端。VR设备采用Oculus VR公司推出的Oculus Rift头戴式虚拟现实设备,包括Oculus CV1眼镜、VR Touch手柄和定位器。

|
图 4 VR手柄控制柔性机械臂示意图 Fig.4 The schematic of flexible manipulator controlled by VR handle |
绳索驱动超冗余柔性机械臂采用分段联动结构,包括5个大的关节段,段内的多个小节利用联动绳索进行被动驱动,实现等曲率控制。每个关节段由8个模块化子关节组成,共包括40个子关节,每个关节可实现俯仰和偏航2个自由度的运动,实际上共包括80个自由度。按照一般建模方法,此时柔性机械臂雅可比矩阵为
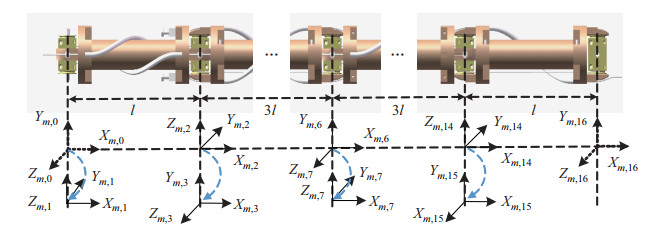
采用经典的D-H(Denavit-Hartenberg)法建立单个关节段的D-H坐标系[15],如图 5所示。根据建立的坐标系,可以得到其对应的D-H参数表,如表 3所示。柔性机械臂关节段的模块化子关节之间采用联动的运动方式,在任何构形下各个旋转轴之间具有等角度的约束关系。因此对于任意关节段
| $ \begin{align} {\mathit{\boldsymbol{T}}}_{m} &= {}^{1}{\mathit{\boldsymbol{T}}}_{m, 2} {}^{2}{\mathit{\boldsymbol{T}}}_{m, 3} {}^{3}{\mathit{\boldsymbol{T}}}_{m, 4} {}^{4}{\mathit{\boldsymbol{T}}}_{m, 5} \cdots{}^{14}{\mathit{\boldsymbol{T}}}_{m, 15} {}^{15}{\mathit{\boldsymbol{T}}}_{m, 16}\\ &=\mathit{\boldsymbol{f}}(\theta_{2m-1}, \theta_{2{m}}) \end{align} $ | (1) |
|
图 5 单个关节段自由度配置 Fig.5 Freedom configuration of a single joint segment |
|
|
表 3 单个关节段D-H参数表 Tab. 3 D-H parameters of single joint segment |
超冗余柔性机械臂共由5个联动关节段依次串联而成,从机械臂基座依次连乘相应的关节段可以得到其正运动学,其简化的参数化运动学方程为
| $ \begin{align} {}^{0}{\mathit{\boldsymbol{T}}}_{\rm{end}} =\prod\limits_{m=1}^5 {{\mathit{\boldsymbol{T}}}_{m}} =\mathit{\boldsymbol{f}}({\theta_{1}, \theta_{2}, \cdots, \theta_{10}}) \end{align} $ | (2) |
在单个关节段中,其子关节的个数为8个,自由度为16个,因此其末端的速度和角速度按传统的方法可以求解为
| $ \begin{align} \begin{bmatrix} {\mathit{\boldsymbol{v}}_{m}} \\ {\mathit{\boldsymbol{w}}_{m}} \end{bmatrix}=\:&\begin{bmatrix} {\mathit{\boldsymbol{e}}_{m, 1} \times \mathit{\boldsymbol{r}}_{m, 1}} & \cdots & {\mathit{\boldsymbol{e}}_{m, 16} \times \mathit{\boldsymbol{r}}_{m, 16}}\\ { \mathit{\boldsymbol{e}}_{m, 1}} & { \cdots} & { \mathit{\boldsymbol{e}}_{m, 16}} \end{bmatrix}\\ &\underbrace{[{\dot{\theta}_{2m-1}} \; \; {\dot{\theta}_{2m}} \; \; {\dot{\theta}_{2m}} \; \; \cdots \; \; {\dot{\theta}_{2m}} \; \; {\dot{\theta}_{2m}} \; \; {\dot{\theta}_{{2m-1}}}]^{\rm T}}_{16\dot{\theta}}\\ =\:&\mathit{\boldsymbol{J}}_{m} \dot{\mathit{\boldsymbol{\theta}}}_{m} \end{align} $ | (3) |
其中
雅可比矩阵可以表示为
| $ \begin{align} \mathit{\boldsymbol{J}}_{m} =\begin{bmatrix} {\mathit{\boldsymbol{e}}_{m, 1} \times \mathit{\boldsymbol{r}}_{m, 1}} & \cdots & {\mathit{\boldsymbol{e}}_{m, 16} \times \mathit{\boldsymbol{r}}_{m, 16}} \\ { \mathit{\boldsymbol{e}}_{m, 1}} & { \cdots} & { \mathit{\boldsymbol{e}}_{m, 16}} \end{bmatrix}^{6\times 16} \end{align} $ | (4) |
由此可知,关节段
由式(3) 可得,柔性机械臂关节段
| $ \begin{align} {{\mathit{\boldsymbol{v}}}}_{m} &={{\mathit{\boldsymbol{e}}}}_{m, 1} \times {{\mathit{\boldsymbol{r}}}}_{m, 1} \cdot \dot{\theta}_{2\:m-1} +{{\mathit{\boldsymbol{e}}}}_{m, 2} \times {{\mathit{\boldsymbol{r}}}}_{m, 2} \cdot \dot{\theta}_{{2m}} +\cdots +\\ &\quad\; {{\mathit{\boldsymbol{e}}}}_{m, 15} \times {{\mathit{\boldsymbol{r}}}}_{m, 15} \cdot \dot{\theta}_{{2m}} +{{\mathit{\boldsymbol{e}}}}_{m, 16} \times {{\mathit{\boldsymbol{r}}}}_{m, 16} \cdot \dot{\theta}_{2m-1} \\ &=[{{{\mathit{\boldsymbol{v}}}}_{m, 1}} \; \; {{{\mathit{\boldsymbol{v}}}}_{m, 2}}]\begin{bmatrix} {\dot{\theta}_{2m-1}} \\ {\dot{\theta}_{2m}} \end{bmatrix} \end{align} $ | (5) |
其中
| $ \begin{align} \begin{cases} {{\mathit{\boldsymbol{v}}}}_{m, 1} ={{\mathit{\boldsymbol{e}}}}_{m, 1} \times {{\mathit{\boldsymbol{r}}}}_{m, 1} +{{\mathit{\boldsymbol{e}}}}_{m, 4} \times {{\mathit{\boldsymbol{r}}}}_{m, 4} +{{\mathit{\boldsymbol{e}}}}_{m, 5} \times {{\mathit{\boldsymbol{r}}}}_{m, 5} +\\ \qquad\; \; \; {{\mathit{\boldsymbol{e}}}}_{m, 8} \!\times\! {{\mathit{\boldsymbol{r}}}}_{m, 8} \!+\! {{\mathit{\boldsymbol{e}}}}_{m, 9} \!\times\! {{\mathit{\boldsymbol{r}}}}_{m, 9} \!+\! {{\mathit{\boldsymbol{e}}}}_{m, 12} \!\times\! {{\mathit{\boldsymbol{r}}}}_{m, 12}+\\ \qquad\; \; \; {{\mathit{\boldsymbol{e}}}}_{m, 13} \times {{\mathit{\boldsymbol{r}}}}_{m, 13} +{{\mathit{\boldsymbol{e}}}}_{m, 16} \times {{\mathit{\boldsymbol{r}}}}_{m, 16}\\ {{\mathit{\boldsymbol{v}}}}_{m, 2} ={{\mathit{\boldsymbol{e}}}}_{m, 2} \!\times\! {{\mathit{\boldsymbol{r}}}}_{m, 2} \!+\! {{\mathit{\boldsymbol{e}}}}_{m, 3} \!\times\! {{\mathit{\boldsymbol{r}}}}_{m, 3} \!+\! {{\mathit{\boldsymbol{e}}}}_{m, 6} \!\times\! {{\mathit{\boldsymbol{r}}}}_{m, 6} +\\ \qquad\; \; \; {{\mathit{\boldsymbol{e}}}}_{m, 7} \!\times\! {{\mathit{\boldsymbol{r}}}}_{m, 7} \!+\! {{\mathit{\boldsymbol{e}}}}_{m, 10} \!\times\! {{\mathit{\boldsymbol{r}}}}_{m, 10} \!+\! {{\mathit{\boldsymbol{e}}}}_{m, 11} \!\times\! {{\mathit{\boldsymbol{r}}}}_{m, 11} + \\ \qquad\; \; \; {{\mathit{\boldsymbol{e}}}}_{m, 14} \times {{\mathit{\boldsymbol{r}}}}_{m, 14} +{{\mathit{\boldsymbol{e}}}}_{m, 15} \times {{\mathit{\boldsymbol{r}}}}_{m, 15} \end{cases}\!\!\!\!\!\! \end{align} $ | (6) |
同样地,其关节段末端的角速度也可以表示为
| $ \begin{align} \mathit{\boldsymbol{w}}_{m} =\;&\mathit{\boldsymbol{e}}_{m, 1} \cdot \dot{\theta}_{2m-1} +\mathit{\boldsymbol{e}}_{m, 2} \cdot \dot{\theta}_{\rm{2m}} +\cdots +\mathit{\boldsymbol{e}}_{m, 15} \cdot \dot{\theta}_{\rm{2m}} +\\ &\mathit{\boldsymbol{e}}_{m, 16} \cdot \dot{\theta}_{2m-1} \\ =\;&[{\mathit{\boldsymbol{w}}_{m, 1}}\; \; {\mathit{\boldsymbol{w}}_{m, 2}}] \begin{bmatrix} {\dot{\theta}_{2m-1}} \\[-3pt] {\dot{\theta}_{2m}} \end{bmatrix} \end{align} $ | (7) |
| $ \begin{align} \begin{cases} \mathit{\boldsymbol{w}}_{m, 1} =\mathit{\boldsymbol{e}}_{m, 1} +\mathit{\boldsymbol{e}}_{m, 4} +\mathit{\boldsymbol{e}}_{m, 5} +\mathit{\boldsymbol{e}}_{m, 8}+\\ \phantom{\mathit{\boldsymbol{w}}_{m, 1} =\; } \mathit{\boldsymbol{e}}_{m, 9} +\mathit{\boldsymbol{e}}_{m, 12} +\mathit{\boldsymbol{e}}_{m, 13} +\mathit{\boldsymbol{e}}_{m, 16} \\ \mathit{\boldsymbol{w}}_{m, 2} =\mathit{\boldsymbol{e}}_{m, 2} +\mathit{\boldsymbol{e}}_{m, 3} +\mathit{\boldsymbol{e}}_{m, 6} +\mathit{\boldsymbol{e}}_{m, 7}+\\ \phantom{\mathit{\boldsymbol{w}}_{m, 1} =\; } \mathit{\boldsymbol{e}}_{m, 10} +\mathit{\boldsymbol{e}}_{m, 11} +\mathit{\boldsymbol{e}}_{m, 14} +\mathit{\boldsymbol{e}}_{m, 15} \end{cases} \end{align} $ | (8) |
进一步地可以得到:
| $ \begin{align} \mathit{\boldsymbol{J}}_{m} \mathit{\boldsymbol{\dot{\theta}}}_{m} =\begin{bmatrix} {\mathit{\boldsymbol{v}}_{m}} \\[-3pt] {\mathit{\boldsymbol{w}}_{m}} \end{bmatrix}\mathit{\boldsymbol{\dot{\theta}}}_{m} =\begin{bmatrix} {\mathit{\boldsymbol{v}}_{m, 1}} & {\mathit{\boldsymbol{v}}_{m, 2}} \\[-3pt] {\mathit{\boldsymbol{w}}_{m, 1}} & {\mathit{\boldsymbol{w}}_{m, 2}} \end{bmatrix}\begin{bmatrix} {\dot{\theta}_{2m-1}} \\[-3pt] {\dot{\theta}_{2m}} \end{bmatrix} \end{align} $ | (9) |
再结合式(3) 可以得到简化后的雅可比矩阵:
| $ \begin{align} \mathit{\boldsymbol{J}}_{m} =\begin{bmatrix} {\mathit{\boldsymbol{v}}_{m, 1}} & {\mathit{\boldsymbol{v}}_{m, 2}} \\[-3pt] {\mathit{\boldsymbol{w}}_{m, 1}} & {\mathit{\boldsymbol{w}}_{m, 2}} \end{bmatrix} \end{align} $ | (10) |
整个柔性机械臂的雅可比矩阵的推导与单个关节段的类似,最后得到末端线速度和角速度与各个轴的关系:
| $ \begin{align} \mathit{\boldsymbol{J}}\mathit{\boldsymbol{\dot{\theta}}} =\begin{bmatrix} {\mathit{\boldsymbol{v}}_{1, 1}} & {\mathit{\boldsymbol{v}}_{1, 2}} & \cdots & {\mathit{\boldsymbol{v}}_{5, 2}} \\[-3pt] {\mathit{\boldsymbol{w}}_{1, 1}} & {\mathit{\boldsymbol{w}}_{1, 2}} & \cdots & {\mathit{\boldsymbol{w}}_{5, 2}} \end{bmatrix} [{\dot{\theta}_{1}} \; \; {\dot{\theta}_{2}} \; \; \cdots \; \; {\dot{\theta}_{10}} ]^{\rm T} \end{align} $ | (11) |
即超冗余柔性机械臂的雅可比矩阵为
| $ \begin{align} \mathit{\boldsymbol{J}} =\begin{bmatrix} {\mathit{\boldsymbol{v}}_{1, 1}} & {\mathit{\boldsymbol{v}}_{1, 2}} & \cdots & {\mathit{\boldsymbol{v}}_{5, 2}} \\ {\mathit{\boldsymbol{w}}_{1, 1}} & {\mathit{\boldsymbol{w}}_{1, 2}} & \cdots & {\mathit{\boldsymbol{w}}_{5, 2}} \end{bmatrix}^{6\times 10} \end{align} $ | (12) |
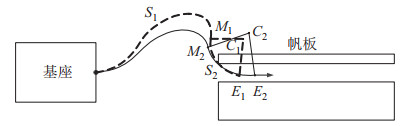
针对狭小空间作业的需求,提出基于自由度动态组合的规划方法。柔性机械臂在维修太阳帆板压紧杆的任务中,其最为困难的地方在于实现臂本体在帆板狭缝中穿越。基于此,柔性臂处于帆板狭缝之间的部分需要进行平面规划,并保持构形不变,而处于帆板外面的部分则需要进行空间规划。因此,可以将柔性机械臂划分为帆板外
|
图 6 自由度动态组合规划方法示意图 Fig.6 The planning method based on DOF dynamic combination |
| $ \begin{align} {}^{\rm 0}{{\mathit{\boldsymbol{T}}}}_{\rm M} ={}^{\rm 0}{{\mathit{\boldsymbol{T}}}}_{\rm end} {{\mathit{\boldsymbol{f}}}}_{S_{2}}^{-1} (\mathit{\boldsymbol{\theta}}_{S_{2}}) \end{align} $ | (13) |
式(13) 中解出了柔性臂段
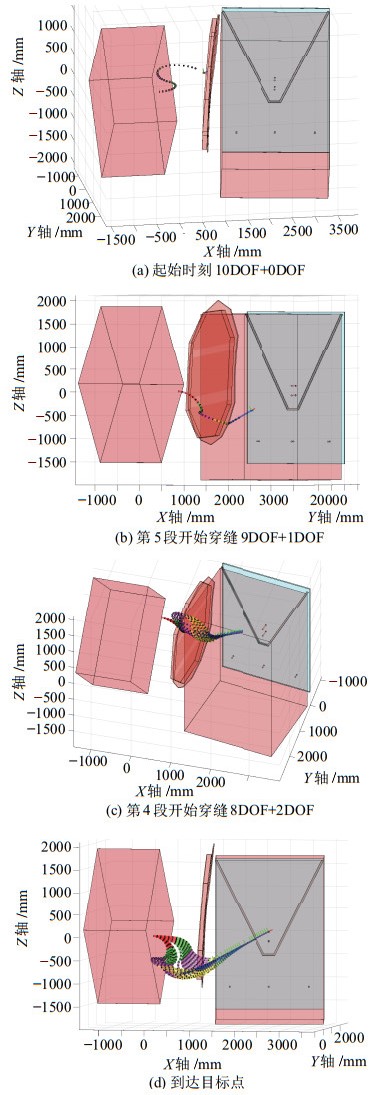
根据自由度的变化情况,柔性机械臂穿越帆板狭缝的规划过程可以分为3个子过程,帆板外采用10DOF
|
图 7 自由度动态组合规划仿真 Fig.7 Simulation of the planning method based on DOF dynamic combination |
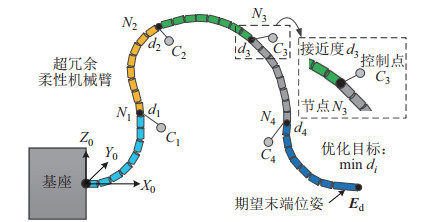
当超冗余柔性机械臂需要完成避障规划时,需要对末端位姿和臂形进行整体规划[16]。针对这一问题,提出将超冗余柔性机械臂段与段之间的控制点作为控制对象来调整机械臂臂形的方法,该方法在满足末端位姿到达的前提下,通过优化超冗余柔性机械臂所有自由度的方式,使中间臂形逼近控制点要求的整体臂形,因此,该方法满足了“整臂臂形—末端轨迹”同步规划的需求。
在末端轨迹与期望轨迹一致的基础上,在空间设置
|
图 8 末端—臂形同步规划示意图 Fig.8 Synchronous planning of the end and the arm configuration |
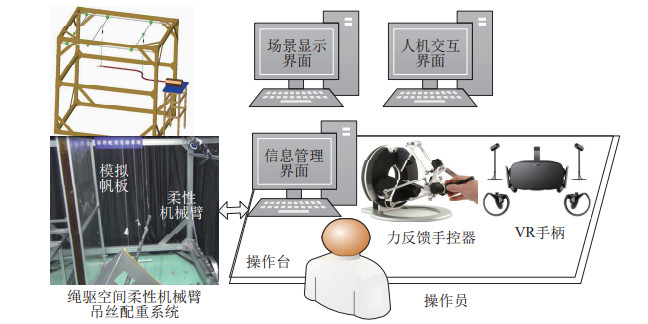
针对第2节系统设计内容建立超冗余空间柔性机械臂的遥操作人机交互系统,布局如图 9所示。遥操作系统由3个操作界面组成,其中场景显示界面实时显示柔性机械臂工作状态的预测仿真结果,完成空间机械臂任务场景的本地再现,刷新频率不低于25 Hz;人机交互界面负责将手控器或VR手柄采集的操作员操作数据转换为柔性机械臂控制数据,数据采集频率不低于50 Hz;信息管理界面负责发送、接收、存储和显示遥控指令和遥测数据,存储时间不低于24 h。吊丝配重实验系统采用重力补偿方法模拟空间柔性机械臂的真实工作状态,并用作空间机械臂地面遥操作实验中的操作对象。
|
图 9 遥操作人机交互系统布局图 Fig.9 The schematic of teleoperation human-machine interaction system |
卫星太阳帆板无法展开是一类典型的卫星故障。为了使卫星帆板能够顺利展开,需要拆除帆板压紧机构。帆板折叠时与卫星本体之间的缝隙很小,一般在10 cm以内,且压紧杆在帆板中间位置。刚性机械臂的臂杆和关节尺寸太大,无法通过狭小空间到达压紧杆位置。绳索驱动的柔性机械臂的电机处于臂的根部,柔性机械臂臂杆可以通过狭小空间且臂杆运动灵活,可以越过狭窄空间。但是执行在轨任务时,目标处于未知状态,柔性机械臂无法自主完成任务。现通过遥操作方式控制柔性机械臂穿越狭小空间完成预定任务,并针对此任务开展实验研究。
4.2.1 实验条件基于Unity 3D软件开发了空间柔性机械臂操作场景,场景中包括机械臂驱动控制箱、柔性机械臂臂杆、模拟太阳帆板、模拟障碍物等。基于自由度动态组合和末端—臂形同步规划遥操作方法配合手控器和VR手柄进行操作,完成柔性机械臂穿越太阳帆板狭缝到达压紧杆位置的实验。
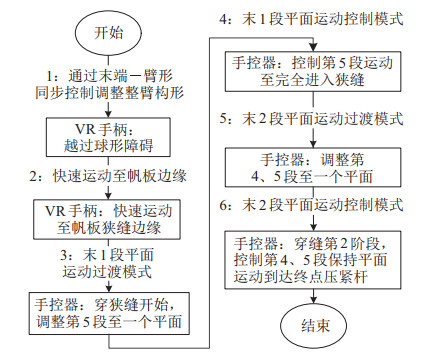
实验步骤如图 10所示,主要包括6个步骤。首先在离帆板较远且有障碍时,通过VR手柄调整臂形同时控制末端快速到达帆板边缘;然后通过自由度动态组合方法将末1段、末2段分别规划至平面运动;在保持末1段或末2段在一个平面的情况下,利用手控器精细控制柔性机械臂末端到达压紧杆。实验过程中可通过柔性机械臂末端视觉相机实时观察狭缝中目标的情况,调整操作策略。
|
图 10 实验步骤流程图 Fig.10 Flow chart of experimental steps |
在实验的初始位置,柔性臂的关节角度为(
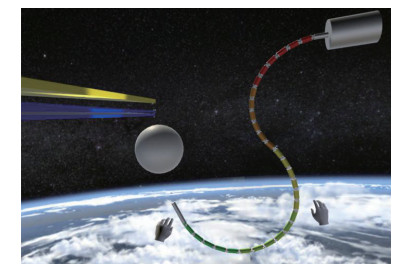
|
图 11 柔性机械臂穿越帆板的准备臂形 Fig.11 The prepared arm configuration of flexible manipulator crossing through the solar panels |
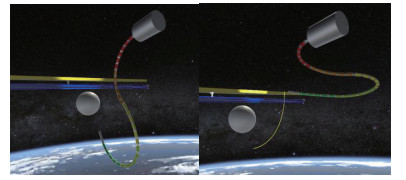
|
图 12 机械臂通过末端—臂形同步控制运动至帆板边缘 Fig.12 The manipulator moving to the edge of the solar panel by synchronous control of the end and the arm configuration |
到达帆板边缘后,为了防止臂杆和帆板发生碰撞及臂杆与帆板接触力过大,采用手控器对机械臂进行精细控制。首先,柔性机械臂第5段完成平面运动过渡,使最后一段俯仰方向角度
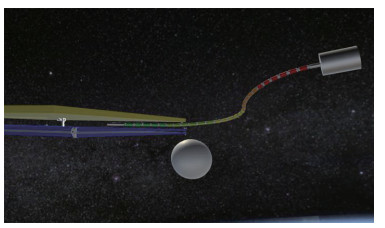
|
图 13 第5段保持平面运动进入狭缝 Fig.13 The 5th segment keeps the plane moving into the slit |
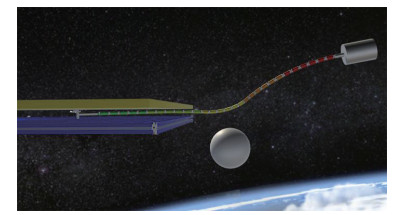
|
图 14 第4、5段保持平面进入狭缝 Fig.14 The 4th and 5th segment keep the plane moving into the slit |

|
图 15 吊丝配重系统下机械臂实物图 Fig.15 Physical diagram of the manipulator under the suspension system |
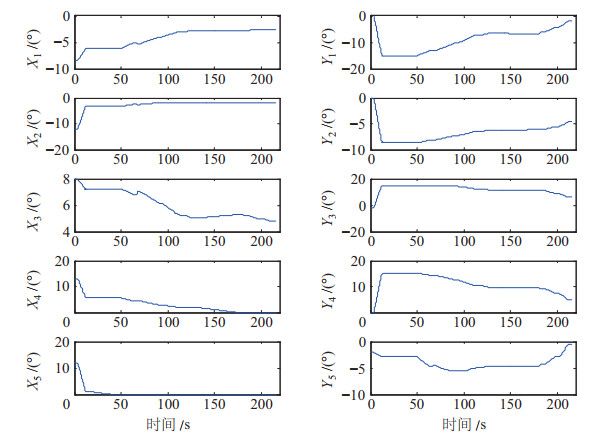
柔性机械臂5大段10个关节角的运动曲线如图 16所示,通过曲线可知在进入狭缝时,先是第5段俯仰角度
|
图 16 关节角度曲线 Fig.16 The curve of joint angles |
针对绳驱超冗余空间柔性机械臂的运动特点和在轨任务需求,提出并建立了基于力反馈手控器和VR手柄组合的遥操作人机交互系统,该系统可实现空间柔性机械臂在大范围工作空间内的快速运动,还可在狭小空间内在存在障碍和发生触碰等复杂工况下完成精细的在轨操作任务。提出了自由度动态组合和末端—臂形同步规划遥操作方法,并完成了太阳帆板狭缝穿越典型实验。实验验证了算法的可行性和遥操作人机交互系统的工程实用性。未来将继续研究优化适用于遥操作控制的超冗余柔性机械臂规划方法,并在绳驱柔性机械臂力反馈控制方面开展进一步研究。
| [1] |
刘天亮. 面向狭小空间作业的绳索驱动超冗余机械臂的研究[D]. 深圳: 哈尔滨工业大学, 2016. Liu T L. A study on the cable-driven and hyper redundant manipulator for the narrow space operations[D]. Shenzhen: Harbin Institute of Technology, 2016. |
| [2] |
Hirzinger G, Brunner B, Dietrich J, et al. Sensor-based space robotics-ROTEX and its telerobotic features[J]. IEEE Transaction on Robotics and Automation, 1993, 9(5): 649-663. DOI:10.1109/70.258056 |
| [3] |
Oda M, DoiT. Teleoperation system of ETS-ⅤⅡ robot experiment satellite[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, USA: IEEE, 1997: 1644-1650.
|
| [4] |
Ma O, Wang J, Misra S, et al. On the validation of SPDM task verification facility[J]. Journal of Robotic Systems, 2004, 21(5): 219-235. DOI:10.1002/rob.20011 |
| [5] |
Artigas J, Balachandran R, de Stefano M, et al. Teleoperation for on-orbit servicing missions through the ASTRA geostationary satellite[C]//IEEE Aerospace Conference. Piscataway, USA: IEEE, 2016. DOI: 10.1109/AERO.2016.7500785.
|
| [6] |
王学谦, 徐文福, 梁斌, 等. 空间机器人遥操作系统设计及研制[J]. 哈尔滨工业大学学报, 2010, 42(3): 337-342. Wang X Q, Xu W F, Liang B, et al. Design and development of teleoperation system for space robot[J]. Journal of Harbin Institute of Technology, 2010, 42(3): 337-342. |
| [7] |
张涛, 陈章, 王学谦, 等. 空间机器人遥操作关键技术综述与展望[J]. 空间控制技术与应用, 2014, 40(6): 1-9, 30. Zhang T, Chen Z, Wang X Q, et al. Overview and prospect of key technologies of teleoperation of space robot[J]. Aerospace Control and Application, 2014, 40(6): 1-9, 30. DOI:10.3969/j.issn.1674-1579.2014.06.001 |
| [8] |
Martín-Barrio A, Roldán J J, Terrile S, et al. Application of immersive technologies and natural language to hyper-redundant robot teleoperation[J]. Virtual Reality, 2020, 24(3): 541-555. DOI:10.1007/s10055-019-00414-9 |
| [9] |
Zhu C C, Song A G. Design of a 3-DOF parallel handcontroller[J]. Journal of Sensors, 2017. DOI:10.1155/2017/8162512 |
| [10] |
李家霖, 杨洋, 杨铁, 等. 外骨骼式遥操作主手设计及主从异构映射算法研究[J]. 机器人, 2020, 42(6): 651-660. Li J L, Yang Y, Yang T, et al. Design of exoskeletal teleoperation master device and research on master-slave isomerism mapping algorithm[J]. Robot, 2020, 42(6): 651-660. |
| [11] |
Singh J, Srinivasan A R, Neumann G, et al. Haptic-guided teleoperation of a 7-DoF collaborative robot arm with an identical twin master[J]. IEEE Transactions on Haptics, 2020, 13(1): 246-252. DOI:10.1109/TOH.2020.2971485 |
| [12] |
Qin L, Huang F, Chen Z, et al. Teleoperation control design with virtual force feedback for the cable-driven hyper-redundant continuum manipulator[J]. Applied Sciences, 2020, 10(22). DOI:10.3390/app10228031 |
| [13] |
Wang Q Y, Jiao W H, Yu R, et al. Modeling of human welders' operations in virtual reality human-robot interaction[J]. IEEE Robotics and Automation Letters, 2019, 4(3): 2958-2964. DOI:10.1109/LRA.2019.2921928 |
| [14] |
Wang H Y, Mecham R, Zhang B. A method targeting repair in space: Tele-operating a collaborative robot with virtual reality[C]//IEEE 7th Annual International Conference on CYBER Technology in Automation, Control, and Intelligent Systems. Piscataway, USA: IEEE, 2017: 1068-1071.
|
| [15] |
Liu T L, Xu W F, Yang T W, et al. A hybrid active and passive cable-driven segmented redundant manipulator: Design, kinematics, and planning[J]. IEEE/ASME Transactions on Mechatronics, 2021, 26(2): 930-942. |
| [16] |
Mu Z G, Yuan H, Xu W F, et al. A segmented geometry method for kinematics and configuration planning of spatial hyper-redundant manipulators[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2020, 50(5): 1746-1756. |
 2022, Vol. 44
2022, Vol. 44


