Approach for Scheduling Automatic Guided Vehicles Considering Equipment Failure and Power Management
https://doi.org/10.1007/s11804-023-00357-3
-
Abstract
Intermediate charging and sudden failure of automatic guided vehicles (AGVs) interrupt and severely affect the stability and efficiency of scheduling. Therefore, an AGV scheduling approach considering equipment failure and power management is proposed for outfitting warehouses. First, a power consumption model is established for AGVs performing transportation tasks. The powers for departure and task consumption are used to calculate the AGV charging and return times. Second, an optimization model for AGV scheduling is established to minimize the total transportation time. Different conditions are defined for the overhaul and minor repair of AGVs, and a scheduling strategy for responding to sudden failure is proposed. Finally, an algorithm is developed to solve the optimization model for a case study. The method can be used to plan the charging time and perform rescheduling under sudden failure to improve the robustness and dynamic response capability of AGVs.-
Keywords:
- Automatic guided vehicle ·
- Scheduling ·
- Outfitting warehouse ·
- Power consumption ·
- Equipment failure
Article Highlights• A power consumption model is established for calculating the AGV charging and return times.• A scheduling strategy for responding to the overhaul and minor repair is proposed.• An optimization algorithm considering equipment failure and power management is developed for outfitting vehicle scheduling. -
1 Introduction
Scheduling of automatic guided vehicles in outfitting warehouses is an important part of outfitting transportation and allocation and affects the efficiency of ship manufacturing. Scheduling determines the time sequence and optimal path for an AGV to perform a transportation task (Custodio and Machado, 2020). The scheduling plan must ensure that a vehicle is in good condition and has sufficient power to perform individual tasks, improve efficiency, and circumvent unexpected events (Umar et al., 2015).
AGVs in a fleet must have independent decision-making ability and be able to operate safely and autonomously in complex environments (Zacharia and Xidias, 2020). The inability to promptly handle AGV failure during transportation will lead to task failure, which can have catastrophic consequences. When an AGV fails, the type of failure and whether brief maintenance can return the AGV to operation must be determined. A scheduling strategy is developed according to the fault type to reduce deviations from conducting the transportation task and minimize the impact on the original scheduling plan. If the AGV work status cannot be recovered, then rescheduling is needed.
AGV scheduling is classified into static scheduling, dynamic scheduling, or simultaneous scheduling with other resources. The static scheduling problem of multi-AGV transportation for static tasks mainly involves assigning vehicles to tasks and determining the task sequence (Fu et al., 2020). Zou et al. (2022) performed static scheduling by considering the number of AGVs, energy consumption, and customer satisfaction as objectives and developed a novel energy-efficient scheduling approach for AGVs with release time. Li et al. (2010) integrated a product model, an operation model, a factory model, and a knowledge database of piping production to automate production scheduling. Giglio (2014) proposed an optimization method based on three consecutive stages for scheduling AGV activities in warehouses. The proposed method can be used to determine the number of AGVs, the assignment of AGVs to trucks, and the sequence of assigned tasks. Zhen et al. (2020) created a decision framework to design and schedule AGV routing plans under time-varying traffic conditions. Although researchers have solved path, task-sequence, and time-window problems in multi-AGV scheduling, existing research frameworks are not suitable for considering dynamic factors, such as predictive power management and fault-driven rescheduling.
Among the dynamic factors involved in scheduling workshops, charging is a key issue that is difficult to avoid. Dang et al. (2021) studied the scheduling of heterogeneous multiload AGVs with battery constraints. AGV batteries can be partially recharged using a critical battery threshold. Decisions must be made regarding assigning transport and charging requests for AGVs. Wang et al. (2021) constructed a path optimization model for multi-AGVs in an unmanned storage environment according to the charging utilization rate. The shortest path and highest charging utilization rate are considered dual goals in the model. However, some dynamic factors in transportation are often not considered in static scheduling. Mousavi et al. (2017) considered the AGV battery charge to establish a schedule model for minimizing the make-span and number of AGVs. Wu et al. (2022) proposed a hybrid dynamic path planning algorithm for forklift AGVs to circumvent obstacles that are suddenly encountered during driving. The rolling window method is used in the algorithm for local path planning to circumvent unknown static and dynamic obstacles that may suddenly appear. Current research on battery issues is mainly focused on issues such as power shortage alerts, battery maintenance, and backup vehicles. To date, no studies have been conducted on electricity forecasting for the static scheduling stage. Prediction of task power consumption can be used to prevent AGV power shortages from interrupting the scheduling at the early planning stage.
AGV failures are also critical factors in dynamic scheduling that directly affect the smooth completion of scheduling plans. Dynamic scheduling considers uncertain situations, such as emergency order insertion and equipment failure, to improve the stability of a scheduling system. Yan et al. (2022) considered the fault problem for multiload AGVs and used colored Petri nets to develop a mathematical model for determining the performance of a multiload AGV system under various scenarios. Periodic maintenance was combined with backup AGVs to replace onsite maintenance in the study. Yan et al. (2017) analyzed the reliability of an AGV system via fault tree analysis and failure mode construction. The reliability and acceptability of the failure of the vehicle mission were analyzed. Fazlollahtabar et al. (2015) integrated Markovian analysis with a back-propagation neural network to determine the reliability of multiple AGVs. Chiu and shih (2012) integrated preventive maintenance and rush orders in a two-machine flow shop. Witczak et al. (2020) and Majdzik et al. (2022) studied fault diagnosis and fault-tolerant control. A mathematical description of multi-AGVs was developed, and an algorithm was proposed to generate an optimal sequence. Current research on AGV failures is mainly focused on equipment online maintenance, reliability evaluation, and backup vehicle configuration. Event-driven rescheduling strategies have not been investigated.
Dynamic scheduling does not provide an immediate response to dynamic conditions but creates a specific predictive response mechanism. Although rescheduling in the event of emergencies is essential for manufacturing, insufficient research has been conducted on the integration of uncertain and regular factors into this process.
A literature review reveals research gaps in integrating predictive power management and dynamic scheduling in response to sudden failures. Given that a scheduling plan is assigned to an AGV, the inability to predict the power consumed by subsequent tasks makes it difficult to determine whether the AGV can complete the plan. No scheduling plan for multi-AGVs should be developed under the assumption that an AGV has sufficient power for task completion. If the real-time power signal displayed on a vehicle is used to determine whether the vehicle needs to be returned for charging, then the charging event will turn into an emergency during transportation. The response time needed to handle an emergency can trigger rescheduling and considerably interfere with the original scheduling plan.
Therefore, this study improves upon research on the scheduling of AGVs, as detailed below.
1) The power state for individual periods, including power consumption and residual power, is accurately calculated and integrated into multi-AGV scheduling, which can be used to determine whether an AGV can complete the scheduling plan at the beginning of plan development.
2) Event-driven rescheduling is carried out for overhaul and minor repairs. This process reduces the impact of repair on the original scheduling plan and ensures that the transportation task is completed.
2 AGV scheduling model considering equipment failure and power management
2.1 Problem description
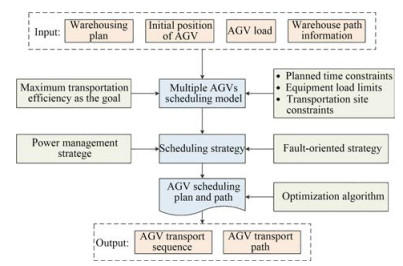
The subject of this study is the AGV transportation system of an outfitting warehouse. This type of AGV transportation system includes multiple charging positions, departure points, and terminal points. At the beginning of scheduling, n static transportation tasks and m AGVs can be found in the warehouse. Each outfitting transportation task includes a task number, departure point, terminal point, time window (spanning the earliest and latest departure times), task type, and outfitting tray weight. The information for each AGV includes the AGV number, rated load, self-weight, initial power, remaining power, and power consumption rate (Vivaldini et al., 2016). Sudden failures occur randomly during scheduling. The information for sudden failures includes the failure type (overhaul and minor repair) and failure maintenance time. A vehicle requiring minor repair can immediately return to operation after being repaired. An AGV requiring an overhaul cannon returns to operation on the same day after failure. A multi-AGV scheduling system should respond quickly to sudden failures, readjust the vehicle scheduling plan, and reduce the impact of sudden failures on overall transportation. The flowchart for multi-AGV scheduling of an outfitting warehouse is shown in Figure 1.
The goal of multi-AGV scheduling is to maximize transportation efficiency under constraints of planning time, equipment load, and transportation site. Scheduling strategies must consider power management and fault-oriented strategies. Finally, an optimization algorithm is used to output the AGV transportation sequence and path.
AGVs perform sorting, handling, and stacking tasks in a storage environment of high-rise 3D shelves. An AGV has different load ratings, and multi-AGVs operate simultaneously in the warehouse area. The characteristics of AGV scheduling for an outfitting warehouse are detailed below. The bottleneck of outfitting accumulation at the buffer of the two systems must be eliminated. The buffer area has a limited capacity for picking up cargo from the conveying area in front of the warehouse. Outfitting has a large weight and volume, but the operation speed of the stackable forklift AGV is low and not sufficiently flexible. The mixed use of vehicles and manual carriers for transportation in the warehouse increases the complexity of vehicle scheduling. AGV operation is disturbed by emergencies in the warehouse. Thus, developing a scheduling strategy in response to sudden failures that occur during outfitting transportation is necessary to reduce interferences from AGV power shortages and sudden failures at any time to the original scheduling plan. Figure 2 shows a forklift AGV and a 3D shelf.
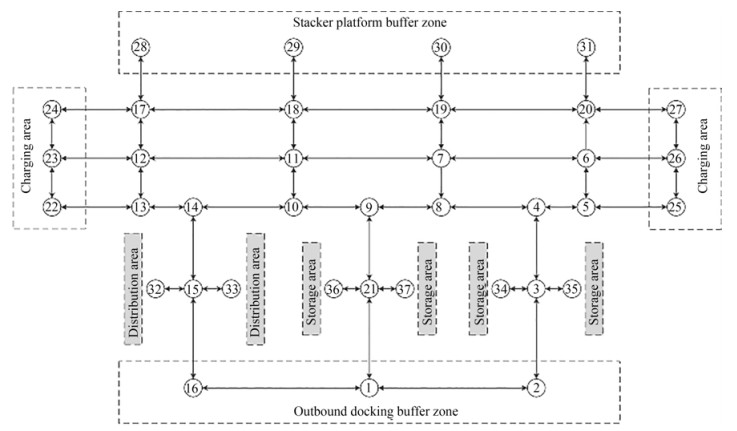
The demand for outfitting delivery is considered in the AGV scheduling model. A delivery order must be fulfilled within a prescribed time window. Outfitting is transported by a stacker from a high rack to the buffer zone of the stacker platform and then taken by the AGV to the buffer zone of the outbound docking, distribution storage, and sorting areas. A dedicated AGV charging area with several positions can be found in the warehouse. A topology diagram of an outfitting warehouse is shown in Figure 3. The proposed model is not limited to the path structure represented by this topology and is suitable for a class of AGV transport scenarios with departure points, terminal points, and charging areas.
The AGV scheduling problem for an outfitting warehouse considering equipment failure and power management is solved under the following assumptions.
1) The remaining power of multi-AGVs is known at the initial scheduling time.
2) An AGV with less than 10% remaining power must return to the charging position.
3) The higher the AGV lifting height, the smaller the load capacity. Heavy goods are placed on the lowest shelf level.
4) A limited number of AGVs can occupy a charging position at a time, and the AGVs have different carrying capacities.
5) The AGV loading and unloading times are fixed.
6) The influence of shelf height on power consumption is considered.
7) The influence of acceleration and deceleration on the power loss of AGVs is not considered.
8) The energy loss of AGVs caused by parking and waiting is not considered.
9) The AGV transportation system includes a stackable forklift AGV, and the energy loss from lifting outfitting is considered.
2.2 Procedure for AGV scheduling considering equipment failure and power management
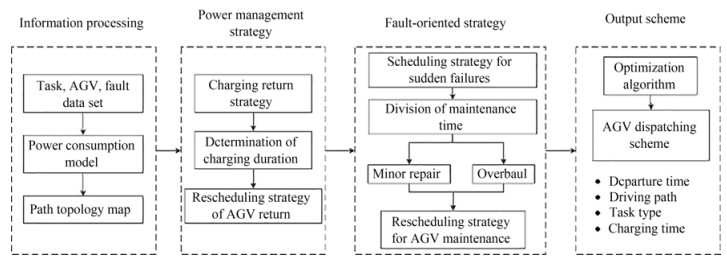
The multi-AGV scheduling problem for transportation tasks consists of assigning vehicles to transportation tasks and task sequencing to minimize the task completion time under various constraints. First, environmental variables, such as task, vehicle, and fault information, are modeled. Mathematical models are established for the power consumption, path topology map, path node relationship, and distance map. A charging return strategy is set for AGV scheduling. The charging time of the vehicle is calculated according to the power consumption model, and multiple vehicles due for charging at the same time are rescheduled.
In case of vehicle failure, overhaul and minor repair are classified according to the estimated failure maintenance time. Rescheduling strategies are developed for overhaul and minor repairs. Finally, the multi-AGV scheduling plan is determined on the basis of the optimization algorithm results, including departure time, driving path, task type, and charging node. Figure 4 shows the AGV scheduling procedure considering equipment failure and power management.
2.3 AGV power consumption model
A feasible path is generated by combining the node relationship and distance matrix and is then used to calculate the AGV delivery path. A model is applied to calculate the power consumption required to complete a task. The remaining power is updated at the end of each task, and the need for AGV recharging is determined. If any AGV needs to be charged, then the number of AGVs participating in the scheduling must be updated.
2.3.1 Power consumed to complete a transportation task
The power consumption per unit distance has a linear relationship with the total vehicle weight (Xiao et al., 2012). ρ(Q) is the AGV power consumption rate:
$$ \rho(Q)=\alpha(Q)+\beta $$ (1) where α and β are parameters related to the energy consumption rate. Both can be calibrated according to the characteristics of respective AGVs. The load capacity is Q.
If task i is assigned to AGV v, then the power consumption rate for completing the task is ρv (Qi)
$$ \rho_v\left(Q_i\right)=\alpha\left(Q_v+Q_i\right)+\beta $$ (2) where Qi is the weight of the task i. The dead weight of the AGV is Qv.
An additional power of 5% is considered to be consumed by parking, waiting, acceleration, and deceleration for each task. The power consumed in completing the task i is Ei j.
$$ E_{i j}=\rho_v\left(Q_i\right)\left[\mathrm{LD}_{i j}+\mathrm{NLD}_{i j}\right] \times 1.05 $$ (3) 2.3.2 Power consumed by cargo stacking
Given that heavy outfitting is used in ship manufacturing, the power consumed by AGVs in lifting outfitting to different shelf heights cannon be neglected. hi is the height of the shelf to which cargo must be lifted as part of the task i. The powers of the lifting and driving motors are known. The AGV consumes power because of motor lifting and driving. The calculation of the power consumption is simplified by assuming that the power consumed in transporting a high cargo stack is proportional to the stack height. wi is the total weight of the cargo and pallet for task i, the average mechanical efficiency is 80%, and the power consumed in cargo stacking is Ehi.
$$ E_{h i}=\frac{9.8 w_i h_i}{80 \%} $$ (4) A model for the power consumed in task transportation is derived. The power consumed to perform a task is calculated as
$$ T_t=E_{i j}+r_i E_{h i} $$ (5) where ri is the number of cargo stacks lifted in performing task i.
2.4 Scheduling strategy for minor repair and overhaul of AGVs
The fault of vehicle v is denoted by gv, and the fault set is denoted by G.
Faults are classified into overhaul and minor repair. A machine requiring overhaul cannon must be returned to operation on the same day. The maintenance time for a minor repair is estimated. The vehicle can be returned to operation after the estimated maintenance time. Minor repair events drive AGV quantity updates and subsequent task rescheduling.
1) A vehicle that has undergone overhaul failure is returned for maintenance, thus reducing the total number of operating AGVs by 1. The initial parameters are updated, and the subsequent tasks are rescheduled. An overhaul of vehicle v is denoted by gv1.
2) For a vehicle that has undergone minor repair failure, the maintenance task is inserted into the first item of the AGV task sequence in the scheduling calculation. If the time window requirements are met, then no adjustment is made. If the time window requirements are not met, then the maintenance task is inserted into the task sequences for rescheduling. Hence, the maintenance task satisfies the first execution constraint. A minor repair of vehicle v is denoted by gv2.
2.5 Optimization model for AGV scheduling
The variables used in the model are defined in Table 1. A path topology map is used to create a warehouse intersection matrix for the relationship among the path nodes. Each intersection represents a node, and AGVs can travel between nodes. zab ≥ 0 indicates that node a can pass through node b. zab = 0 indicates that the AGV cannot pass through nodes a and b. zab is the distance between nodes a and b:
Table 1 Variables used in the scheduling modelNotation Meaning n Number of transportation tasks N Total number of tasks i, j Two different tasks T Task set vm Travel speed of AGV m vlm Lifting speed of AGV m wi Weight of the ith task os Departure point Oc Charging point set of Terminal point ti Departure time of AGV i ei Earliest departure time of the ith task li Latest departure time of the ith task NLDi j Path distance from the terminal point of the ith task to the departure point of the jth task LDi j Path distance from the departure point of the ith task to the terminal point of the ith task m AGV No. M Total number of AGVs cwv Rated load of AGV x Decision variables on tasks ρv (Q) Power consumption rate of the vehicle v Ev0 Initial power quantity Evm Full power Evi Remaining power after completing the ith task $$ \boldsymbol{Z}=\left[\begin{array}{ccc} z_{1, 1} & \cdots & z_{1, B} \\ \vdots & \ddots & \vdots \\ z_{A, 1} & \cdots & z_{A, B} \end{array}\right] $$ (6) where a and b are the number of path lines and path columns for a single AGV, respectively, and A and B are the total numbers of path lines and path columns for all AGVs, respectively.
For efficient outfitting transportation, the optimization objective is to minimize the total transportation time for scheduling.
The objective function is
$$ \min F=\sum\limits_{m=1}^M \sum\limits_{i=1}^N \sum\limits_{j=1}^N\left(\frac{\mathrm{LT}_{i j}+\mathrm{NLT}_{i j}}{v_m}+\frac{h_i}{v_{l m}}\right) $$ (7) The optimization model is subjected to the following constraints:
1) $\sum\limits_{m=1}^M x_{i m}=1 $, ∀i ∈ { 1, 2, ⋯, N }
2) cwm ≤ cwi, ∀i ∈ { 1, 2, ⋯, N }, m ∈ { 1, 2, ⋯, M }
3) ei ≤ ti ≤ li, ∀i ∈ { 1, 2, ⋯, N }
4) 10% ≤ Evo ≤ Evm, ∀Evo ≤ Evi
5) os ∈ Oc
1) An individual task can only be performed by one AGV. 2) The carrying capacity of an AGV is greater than or equal to the weight of the cargo to be handled. 3) This constraint specifies the limit on the AGV task execution time. 4) An AGV has an initial power greater than 10% and less than or equal to the full power. After task i is completed, the remaining power of the AGV is greater than 10%. 5) This constraint specifies the AGV departure point.
3 Optimization algorithm for AGV scheduling
Multi-AGVs are scheduled according to the proposed strategies for charging and fault maintenance to improve the transportation efficiency for transporting outfitting in and out of the warehouse. Various optimization algorithms have been applied to scheduling, including the Dijkstra algorithm (Deng et al., 2012), butterfly optimization algorithm (Li et al., 2022b), genetic algorithm (Zhang et al., 2002), depth-first search (DFS) algorithm (Chen et al., 2022), and hybrid genetic cloud whale optimization algorithm (Li et al., 2022a). The Dijkstra algorithm was used in this study to integrate the charging and fault maintenance strategies.
The total transportation time for the vehicles is the sum of the travel times for the loaded and unloaded vehicles. The optimization objective of this study is to minimize the total transportation time; that is, the shortest total travel time for the AGVs is determined. The algorithm flow for AGV scheduling considering equipment failure and power management is shown in Figure 5.
The solution procedure consists of calculating the power remaining after each task is completed according to the initial power and the power consumption of each task. The total power consumption of each AGV is then calculated to determine whether the AGV can complete all subsequent tasks. If the vehicle cannot complete a task, then the number of AGVs is updated at the initial time according to the departure point of the task at the time at which the vehicle returns for charging. This time point is used to set the node for the return time for rescheduling.
The last charge for an AGV during a workday may exceed the power required for the remaining tasks. Adjusting the quantity of the last charge according to the remaining tasks can enable the AGV to return to work status as soon as possible, thereby improving transportation efficiency.
The specific calculation procedure is as follows.
Step 1. The departure position and load capacity are determined for the first task in the time list. The task is inserted into a temporary matrix.
Step 2. Among the four AGVs, the AGV closest to the departure position is calculated. The AGVs are sorted by distance from the departure position.
Step 3. The algorithm calculates the transport path to the terminal position of the task. The Dijkstra algorithm (Deng et al., 2012) is used to determine the shortest path. The power consumption is calculated according to the path length and shelf elevation for the task.
Step 4. The constraint on the remaining power is evaluated. If the constraint is satisfied, then the task is assigned to the respective AGVs. If the constraint is not satisfied, then Step 2 is performed, and the task is assigned to the next closest AGV.
Step 5. The task time is calculated according to the velocity, path length, and time required for lifting. The current time, position, and power of the vehicle are updated.
Step 6. The start time, end time, path, power consumption, and other information for the scheme for the first task are saved.
Step 7. The aforementioned steps are performed for the second task, and the departure time is determined (the departure time should be later than the current time of the vehicle).
Step 8. For an overhaul case, the vehicle must be repaired. The number of vehicles is reduced by 1, the initial parameters are updated, and the subsequent tasks are rescheduled.
Step 9. For minor repairs of the vehicle, a maintenance task is inserted as the first item of the AGV task sequence. If the subsequent task can be performed within the respective time window, then no adjustment is made.
Step 10. A maintenance task that cannot be performed within the respective time window is inserted into the task sequences for rescheduling. The maintenance tasks must satisfy the first constraint.
During scheduling, the power loss is calculated according to the transportation distance. Within the predictive power management strategy, the charging threshold is 10%; that is, an AGV with less than 10% remaining power is returned for charging. The total number of AGVs is reduced by 1 and subsequently updated.
4 Numerical experiments and discussion
4.1 Case study
An AGV transportation system for an outfitting warehouse is selected as a case study to verify the effectiveness of the proposed method. The AGV parameters are shown in Table 2. The warehouse shelf has 5 layers, each of which is 1 m high.
Table 2 AGV parametersParameters Values Drive motor power (kW) 1.5 Enhance motor power (kW) 3 Battery power (Ah) 200 Self-weight (kg) 1 300 Running speed (m/s) 1.66 Lifting speed (m/s) 0.5 Four AGVs initially located at the charging position are used in the AGV transportation system. In particular, two AGVs have load capacities of 1.5 t each, and the other two AGVs have load capacities of 1 t each. Without the loss of generality, the initial state of the AGV does not need to be considered a full power state. The AGV status list is shown in Table 3.
Table 3 AGV status listAGV No. Current location Current time (s) Current power (Ah) Load capacity (t) 1 22 0 200 1 500 2 23 0 180 1 000 3 25 0 100 1 500 4 26 0 70 1 000 A few different types of faults can occur in a day. For the verification of the effectiveness of the proposed method in dealing with different fault types, four fault events are predetermined in the case study, namely, three minor repair faults and one overhaul fault with different repair times. The fault event list is shown in Table 4.
Table 4 Fault event listAGV No. Fault occurrence time (s) Fault type Fault repair time (s) 1 3 600 1 600 2 3 000 2 inf 3 7 800 1 1 800 4 5 400 3 3 600 The case study consists of 1 500 transportation tasks. Requirements on the departure point, terminal point, and time window are set for each task. The carrying capacity and shelf height for each task are different. In the calculation for lifting heavy outfitting, the influence of shelf height and load capacity on power consumption is considered. A partial transportation task list is shown in Table 5.
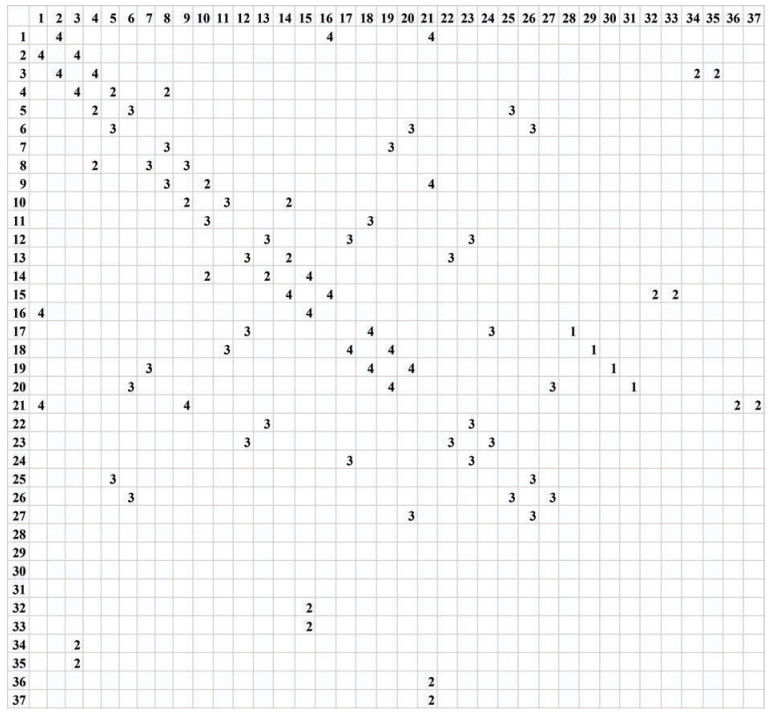
Table 5 Partial list of transportation tasksTask number Departure point Terminal point Departure time (s) Terminal time (s) Weight (t) Shelf number 1 3 18 0 15 1 238 2 2 17 1 0 15 944 4 3 15 20 0 15 964 3 4 19 15 0 15 876 5 5 3 18 0 15 1 280 1 6 19 3 0 15 1283 1 7 17 3 0 15 983 3 8 19 1 0 15 988 3 9 15 18 0 20 996 3 10 3 20 0 20 1 220 2 11 17 15 5 20 920 4 12 19 3 5 20 822 5 13 15 20 5 20 926 4 14 15 18 10 20 1 226 2 15 3 20 10 20 1 242 2 16 17 15 10 20 1 258 1 17 3 18 10 20 1 276 1 18 15 20 10 20 800 5 19 17 3 10 20 1 302 1 20 19 3 10 20 1 324 1 21 3 20 15 30 838 5 22 19 1 15 30 944 4 23 15 18 15 30 1 264 1 24 19 3 15 30 976 3 25 3 18 15 30 1 280 1 26 19 3 15 30 1 283 1 27 17 3 15 30 1 283 1 28 19 1 15 35 912 4 29 15 18 15 35 900 4 30 3 20 15 35 820 5 31 17 15 10 35 920 4 32 19 3 10 35 922 4 33 15 20 10 35 826 5 34 15 18 10 35 926 4 35 3 20 15 35 942 4 36 17 15 15 40 1 258 1 37 3 18 15 40 976 3 38 15 20 15 40 987 3 39 17 3 15 40 1 319 1 40 19 3 15 40 1 322 1 … … … … … … … The environmental setting of the outfitting warehouse is used to establish the relationship between the path nodes and the distance matrix for the warehouse. This relationship and the matrix are shown in Figure 6.
4.2 Analysis of results and discussion
The proposed optimization algorithm and optimization model are applied to the case study to develop a multi-AGV scheduling plan. The scheduling plan for the multi-AGVs is shown in Table 6.
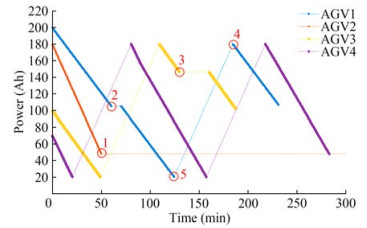
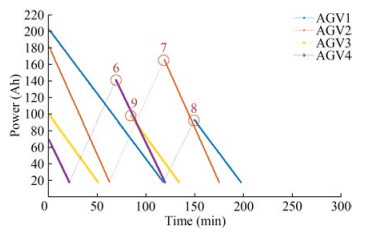
Table 6 Scheduling plan for multi-AGVsAGV No. Path nodes 3 25→5→4→3→4→8→7→19→18 2 23→12→17→12→13→14→15→16→1 1 22→13→14→15→14→10→11→18→19→20 4 26→6→20→19→18→11→10→14→15 1 20→6→5→4→3→4→8→7→19→18 1 18→19→7→8→4→3 3 18→17→18→19→7→8→4→3 1 3→4→8→7→19→7→8→9→21→1 1 1→16→15→14→10→11→18 3 3→4→5→6→20 4 15→14→13→12→17→12→13→14→15 4 15→14→10→11→18→19→7→8→4→3 2 1→16→15→14→10→11→18→19→20 1 18→11→10→14→15→14→10→11→18 3 20→6→5→4→3→4→5→6→20 1 18→17→12→13→14→15 3 20→6→5→4→3→4→8→7→19→18 4 3→2→1→16→15→14→10→11→18→19→20 3 18→17→18→19→7→8→4→3 3 3→4→8→7→19→7→8→4→3 2 20→6→5→4→3→4→5→6→20 2 20→19→7→8→9→21→1 1 15→14→10→11→18 1 18→19→7→8→4→3 1 3→4→8→7→19→18 1 18→19→7→8→4→3 1 3→4→8→7→19→18→17→18→19→7→8→4→3 4 20→19→7→8→9→21→1 2 1→16→15→14→10→11→18 4 1→2→3→4→5→6→20 2 18→17→12→13→14→15 4 20→19→7→8→4→3 2 15→14→10→11→18→19→20 4 3→2→1→16→15→14→10→11→18 2 20→6→5→4→3→4→5→6→20 1 3→4→8→7→19→18→17→12→13→14→15 3 3→4→8→7→19→18 1 15→14→10→11→18→19→20 3 18→17→18→19→7→8→4→3 1 20→19→7→8→4→3 … … For the transportation tasks on the list, the AGV is designated to start from a departure point and deliver cargo to a terminal point. The AGV then drives from the terminal point of the completed task to the departure point of the next task and starts the next delivery. The shortest path between the departure and terminal points is calculated. Vehicle failure, including overhauls and minor repairs, is considered in the calculation. The vehicle returns to the charging position when the power level is less than 10%. The vehicle returns to the nearest charging position. The scheduling result obtained under AGV failure is shown in Figure 7.
The AGV returns to the charging position when the power is less than 10%. Once its power level reaches 90%, the AGV returns to work. Charging the AGV battery from 90% to full charge takes additional time, and aging prevents many batteries from being fully charged. Therefore, a charge level of 90% is predetermined to prevent scheduling interruptions by the AGV returning caused by its battery not fully charging.
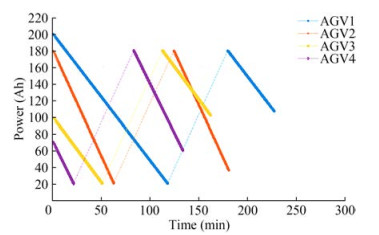
Figure 7 shows that at time node 1, AGV2 has an overhaul fault and terminates operation in 50 min. At time node 2, AGV1 undergoes minor repair failure and returns to operation 60 min after 10 min of repair. At time node 3, AGV3 departs at 130 min, undergoes minor repair failure, and returns to operation after 30 min of maintenance. At time node 4, AGV1 is charged to 90% and returns to operation. At time node 5, AGV1 functions normally up to 10% remaining power, enters the charging position, and returns to operation at time node 4. The scheduling result determined in the absence of AGV failure is shown in Figure 8.
If AGV failure is not considered, then the multi-AGVs perform transportation tasks via the charging management mechanism until the tasks are completed. However, in actual production, AGVs inevitably undergo various types of failure. Therefore, the proposed method is used to consider multiple fault types for the AGV transportation system. The proposed adjustable charging strategy for AGVs is applied to determine and analyze the last charging event for the AGVs in the case study. The scheduling result obtained using the adjustable charging strategy is shown in Figure 9.
After the last charge event, an AGV may carry more power than required to perform the remaining tasks. Therefore, the AGV does not need to be fully charged during the last charge event on a work day but instead should be charged based on the power required to complete the remaining tasks. This strategy optimizes AGV use and ensures the completion of tasks for the workday.
4.3 Comparison of the results of the case study obtained using the proposed algorithm and existing algorithms
In this section, the performance of the DFS algorithm (Chen et al., 2022) is compared against that of the proposed algorithm. On the one hand, the DFS algorithm accesses endpoints by prioritizing depth over breadth. On the other hand, the proposed method is based on the Dijkstra algorithm and integrates charge and fault-event-driven strategies. The scheduling plan for the multi-AGVs obtained using the DFS algorithm is shown in Table 7. Forty tasks in the case study are selected to perform a comparative analysis of the distances traveled and nodes passed by the AGVs. The results for the case study obtained using existing algorithms are compared in Table 8.
Table 7 Scheduling plan of multi-AGVs obtained using the DFS algorithmAGV No. Path nodes 1 3→4→8→9→10→11→18 1 17→12→13→14→10→9→21→1 4 15→14→10→9→8→4→5→6→20 4 19→7→8→9→10→14→15 1 3→4→8→9→10→11→18 3 19→7→8→4→3 4 17→12→13→14→10→9→8→4→3 2 19→7→8→9→21→1 2 15→14→10→11→18 3 3→4→5→6→20 2 17→12→13→14→15 3 19→7→8→4→3 2 15→14→10→9→8→4→5→6→20 3 15→14→10→11→18 1 3→4→5→6→20 3 17→12→13→14→15 3 3→4→8→9→10→11→18 4 15→14→10→9→8→4→5→6→20 3 17→12→13→14→10→9→8→4→3 1 19→7→8→4→3 2 3→4→5→6→20 4 19→7→8→9→21→1 1 15→14→10→11→18 2 19→7→8→4→3 1 3→4→8→9→10→11→18 1 19→7→8→4→3 3 17→12→13→14→10→9→8→4→3 2 19→7→8→9→21→1 4 15→14→10→11→18 2 3→4→5→6→20 4 17→12→13→14→15 2 19→7→8→4→3 2 15→14→10→9→8→4→5→6→20 4 15→14→10→11→18 2 3→4→5→6→20 1 17→12→13→14→15 3 3→4→8→9→10→11→18 4 15→14→10→9→8→4→5→6→20 1 17→12→13→14→10→9→8→4→3 3 19→7→8→4→3 … … Table 8 Comparison of results for the case study obtained using existing algorithmsAGV No. Proposed algorithm Existing algorithm Distance (m) Number of nodes Distance (m) Number of nodes 1 217 84 152 63 2 125 47 160 65 3 144 54 148 62 4 113 44 154 64 Total 599 229 614 254 Table 8 shows that compared with the results obtained using existing algorithms, the scheduling scheme determined using the proposed algorithm exhibits shorter travel distances for the four AGVs and fewer path nodes passed. Thus, the proposed algorithm provides a faster travel path within the prescribed time window than existing algorithms. In summary, the proposed method demonstrates its superiority in power management and emergency response for AGV scheduling.
5 Conclusions
The problems of charging and failure of multi-AGVs are considered in this study, and an approach for scheduling AGVs in warehouses is proposed in consideration of equipment failure and power management. A function for the rate of energy consumption is used to develop a power consumption model for an AGV transportation task. A charging strategy is then established by considering the power consumption of multi-AGVs. An emergency scheduling strategy is proposed for the sudden overhaul and minor repair of AGVs, and a corresponding algorithm is developed.
The effectiveness of the proposed method is verified in a case study. The proposed method can be used to plan the charging time according to vehicle power consumption. A rescheduling strategy is implemented for sudden failure and return to a charging position of outfitting transport vehicles to improve the dynamic response capability of these vehicles.
Further research directions include collaborative scheduling of AGVs with stickers and inbound and outbound vehicles, optimizing the space utilization of buffer zones, and improving the efficiency of outfitting transportation.
Competing interestThe authors have no competing interests to declare that are relevant to the content of this article. -
Table 1 Variables used in the scheduling model
Notation Meaning n Number of transportation tasks N Total number of tasks i, j Two different tasks T Task set vm Travel speed of AGV m vlm Lifting speed of AGV m wi Weight of the ith task os Departure point Oc Charging point set of Terminal point ti Departure time of AGV i ei Earliest departure time of the ith task li Latest departure time of the ith task NLDi j Path distance from the terminal point of the ith task to the departure point of the jth task LDi j Path distance from the departure point of the ith task to the terminal point of the ith task m AGV No. M Total number of AGVs cwv Rated load of AGV x Decision variables on tasks ρv (Q) Power consumption rate of the vehicle v Ev0 Initial power quantity Evm Full power Evi Remaining power after completing the ith task Table 2 AGV parameters
Parameters Values Drive motor power (kW) 1.5 Enhance motor power (kW) 3 Battery power (Ah) 200 Self-weight (kg) 1 300 Running speed (m/s) 1.66 Lifting speed (m/s) 0.5 Table 3 AGV status list
AGV No. Current location Current time (s) Current power (Ah) Load capacity (t) 1 22 0 200 1 500 2 23 0 180 1 000 3 25 0 100 1 500 4 26 0 70 1 000 Table 4 Fault event list
AGV No. Fault occurrence time (s) Fault type Fault repair time (s) 1 3 600 1 600 2 3 000 2 inf 3 7 800 1 1 800 4 5 400 3 3 600 Table 5 Partial list of transportation tasks
Task number Departure point Terminal point Departure time (s) Terminal time (s) Weight (t) Shelf number 1 3 18 0 15 1 238 2 2 17 1 0 15 944 4 3 15 20 0 15 964 3 4 19 15 0 15 876 5 5 3 18 0 15 1 280 1 6 19 3 0 15 1283 1 7 17 3 0 15 983 3 8 19 1 0 15 988 3 9 15 18 0 20 996 3 10 3 20 0 20 1 220 2 11 17 15 5 20 920 4 12 19 3 5 20 822 5 13 15 20 5 20 926 4 14 15 18 10 20 1 226 2 15 3 20 10 20 1 242 2 16 17 15 10 20 1 258 1 17 3 18 10 20 1 276 1 18 15 20 10 20 800 5 19 17 3 10 20 1 302 1 20 19 3 10 20 1 324 1 21 3 20 15 30 838 5 22 19 1 15 30 944 4 23 15 18 15 30 1 264 1 24 19 3 15 30 976 3 25 3 18 15 30 1 280 1 26 19 3 15 30 1 283 1 27 17 3 15 30 1 283 1 28 19 1 15 35 912 4 29 15 18 15 35 900 4 30 3 20 15 35 820 5 31 17 15 10 35 920 4 32 19 3 10 35 922 4 33 15 20 10 35 826 5 34 15 18 10 35 926 4 35 3 20 15 35 942 4 36 17 15 15 40 1 258 1 37 3 18 15 40 976 3 38 15 20 15 40 987 3 39 17 3 15 40 1 319 1 40 19 3 15 40 1 322 1 … … … … … … … Table 6 Scheduling plan for multi-AGVs
AGV No. Path nodes 3 25→5→4→3→4→8→7→19→18 2 23→12→17→12→13→14→15→16→1 1 22→13→14→15→14→10→11→18→19→20 4 26→6→20→19→18→11→10→14→15 1 20→6→5→4→3→4→8→7→19→18 1 18→19→7→8→4→3 3 18→17→18→19→7→8→4→3 1 3→4→8→7→19→7→8→9→21→1 1 1→16→15→14→10→11→18 3 3→4→5→6→20 4 15→14→13→12→17→12→13→14→15 4 15→14→10→11→18→19→7→8→4→3 2 1→16→15→14→10→11→18→19→20 1 18→11→10→14→15→14→10→11→18 3 20→6→5→4→3→4→5→6→20 1 18→17→12→13→14→15 3 20→6→5→4→3→4→8→7→19→18 4 3→2→1→16→15→14→10→11→18→19→20 3 18→17→18→19→7→8→4→3 3 3→4→8→7→19→7→8→4→3 2 20→6→5→4→3→4→5→6→20 2 20→19→7→8→9→21→1 1 15→14→10→11→18 1 18→19→7→8→4→3 1 3→4→8→7→19→18 1 18→19→7→8→4→3 1 3→4→8→7→19→18→17→18→19→7→8→4→3 4 20→19→7→8→9→21→1 2 1→16→15→14→10→11→18 4 1→2→3→4→5→6→20 2 18→17→12→13→14→15 4 20→19→7→8→4→3 2 15→14→10→11→18→19→20 4 3→2→1→16→15→14→10→11→18 2 20→6→5→4→3→4→5→6→20 1 3→4→8→7→19→18→17→12→13→14→15 3 3→4→8→7→19→18 1 15→14→10→11→18→19→20 3 18→17→18→19→7→8→4→3 1 20→19→7→8→4→3 … … Table 7 Scheduling plan of multi-AGVs obtained using the DFS algorithm
AGV No. Path nodes 1 3→4→8→9→10→11→18 1 17→12→13→14→10→9→21→1 4 15→14→10→9→8→4→5→6→20 4 19→7→8→9→10→14→15 1 3→4→8→9→10→11→18 3 19→7→8→4→3 4 17→12→13→14→10→9→8→4→3 2 19→7→8→9→21→1 2 15→14→10→11→18 3 3→4→5→6→20 2 17→12→13→14→15 3 19→7→8→4→3 2 15→14→10→9→8→4→5→6→20 3 15→14→10→11→18 1 3→4→5→6→20 3 17→12→13→14→15 3 3→4→8→9→10→11→18 4 15→14→10→9→8→4→5→6→20 3 17→12→13→14→10→9→8→4→3 1 19→7→8→4→3 2 3→4→5→6→20 4 19→7→8→9→21→1 1 15→14→10→11→18 2 19→7→8→4→3 1 3→4→8→9→10→11→18 1 19→7→8→4→3 3 17→12→13→14→10→9→8→4→3 2 19→7→8→9→21→1 4 15→14→10→11→18 2 3→4→5→6→20 4 17→12→13→14→15 2 19→7→8→4→3 2 15→14→10→9→8→4→5→6→20 4 15→14→10→11→18 2 3→4→5→6→20 1 17→12→13→14→15 3 3→4→8→9→10→11→18 4 15→14→10→9→8→4→5→6→20 1 17→12→13→14→10→9→8→4→3 3 19→7→8→4→3 … … Table 8 Comparison of results for the case study obtained using existing algorithms
AGV No. Proposed algorithm Existing algorithm Distance (m) Number of nodes Distance (m) Number of nodes 1 217 84 152 63 2 125 47 160 65 3 144 54 148 62 4 113 44 154 64 Total 599 229 614 254 -
Chen Y, Jiang Z (2022) Multi-AGVs scheduling with vehicle conflict consideration in ship outfitting Items warehouse. Journal of Shanghai Jiao Tong University (Science) 22: 1–15. https://doi.org/10.1007/s12204-022-2561-z Chiu Y, Shih CJ (2012) Rescheduling strategies for integrating rush orders with preventive maintenance in a two-machine flow shop. International Journal of Production Research 50(20): 5783–5794. https://doi.org/10.1080/00207543.2011.627887 Custodio L, Machado R (2020) Flexible automated warehouse: a literature review and an innovative framework. International Journal of Advanced Manufacturing Technology 106: 533–558. https://doi.org/10.1007/s00170-019-04588-z Dang QV, Singh N, Adan I, Martagan T, Sande D (2021) Scheduling heterogeneous multi-load AGVs with battery constraints. Computers & Operations Research 136: 105517. https://doi.org/10.1016/j.cor.2021.105517 Deng Y, Chen Y, Zhang Y, Mahadevan S (2012) Fuzzy Dijkstra algorithm for shortest path problem under uncertain environment. Applied Soft Computing 12(3): 1231–1237. https://doi.org/10.1016/j.asoc.2011.11.011 Fazlollahtabar H, Saidi-Mehrabad M, Balakrishnan J (2015) Integrated Markov-neural reliability computation method: A case for multiple automated guided vehicle system. Reliability Engineering & System Safety 135: 34–44. https://doi.org/10.1016/j.ress.2014.11.004 Fu JL, Zhang HZ, Zhang J, Jiang LK (2020) Review on AGV scheduling optimization. Journal of System Simulation 32(9): 1664–1675. https://doi.org/10.16182/j.issn1004731x.joss.19-0042 Giglio D (2014) Task scheduling for multiple forklift AGVs in distribution warehouses. Proceedings of the 2014 IEEE Emerging Technology and Factory Automation (ETFA), Barcelona, 1–6. https://doi.org/10.1109/ETFA.2014.7005360 Li MW, Xu DY, Geng J, Hong WC (2022a) A hybrid approach for forecasting ship motion using CNN-GRU-AM and GCWOA. Applied Soft Computing 114: 108084. https://doi.org/10.1016/j.asoc.2021.108084 Li MW, Xu DY, Geng J, Hong WC (2022b) A ship motion forecasting approach based on empirical mode decomposition method hybrid deep learning network and quantum butterfly optimization algorithm. Nonlinear Dynamics 107(3): 2447–2467. https://doi.org/10.1007/s11071-021-07139-y Li R, Liu YJ, Hamada K (2010) Research on the ITOC based scheduling system for ship piping production. Journal of Marine Science and Application 9(4): 355–362. https://doi.org/10.1007/s11804-010-1020-7 Majdzik P, Witczak M, Lipiec B, Banaszak Z (2022) Integrated fault-tolerant control of assembly and automated guided vehicle-based transportation layers. International Journal of Computer Integrated Manufacturing, 35(4–5), 409–426. https://doi.org/10.1080/0951192X.2021.1872103 Mousavi M, Yap HJ, Musa SN, Dawal SZM (2017) A fuzzy hybrid GA-PSO algorithm for multi-objective AGV scheduling in FMS. International Journal of Simulation Modelling 16(1): 58–71. https://doi.org/10.2507/IJSIMM16(1)5.368 Umar UA, Ariffin MK, Ismail N, Tang SH (2015) Hybrid multi-objective genetic algorithms for integrated dynamic scheduling and routing of jobs and automated-guided vehicle (AGV) in flexible manufacturing systems (FMS) environment. The International Journal of Advanced Manufacturing Technology 81(9–12): 2123–2141. https://doi.org/10.1007/s00170-015-7329-2 Vivaldini K, Rocha LF, Martarelli NJ, Becker M, Moreira AP (2016) Integrated tasks assignment and routing for the estimation of the optimal number of AGVS. International Journal of Advanced Manufacturing Technology 82: 719–736. https://doi.org/10.1007/s00170-015-7343-4 Witczak M, Majdzik P, Stetter R, Lipiec B (2020) A fault-tolerant control strategy for multiple automated guided vehicles. Journal of Manufacturing Systems 55: 56–68. https://doi.org/10.1016/j.jmsy.2020.02.009 Wang J, Pan J, Huo J, Wang R, Li L, Nian T (2021) Research on optimization of multi-AGV path based on genetic algorithm considering charge utilization. Journal of Physics: Conference Series 1769(1): 012052. https://doi.org/10.1088/1742-6596/1769/1/012052 Wu B, Chi X, Zhao C, Zhang W, Lu Y, Jiang D (2022) Dynamic path planning for forklift AGV based on smoothing A* and improved DWA hybrid algorithm. Sensors 22(18): 7079. https://doi.org/10.3390/s22187079 Xiao Y, Zhao Q, Kaku I, Xu Y (2012) Development of a fuel consumption optimization model for the capacitated vehicle routing problem. Computers & Operations Research 39(7): 1419–1431. https://doi.org/10.1016/j.cor.2011.08.013 Yan R, Dunnett SJ, Jackson LM (2022) Model-based research for aiding decision-making during the design and operation of multi-load automated guided vehicle systems. Reliability Engineering & System Safety 219: 108264. https://doi.org/10.1016/j.ress.2021.108264 Yan R, Jackson LM, Dunnett SJ (2017) Automated guided vehicle mission reliability modelling using a combined fault tree and Petri net approach. The International Journal of Advanced Manufacturing Technology 92: 1825–1837. https://doi.org/10.1007/s00170-017-0175-7 Zacharia PT, Xidias EK (2020) AGV routing and motion planning in a flexible manufacturing system using a fuzzy-based genetic algorithm. The International Journal of Advanced Manufacturing Technology 109: 1801–1813. https://doi.org/10.1007/s00170-020-05755-3 Zhang MJ, Zheng JX, Zhang J (2002) Selection method of multi-objective problems using genetic algorithm in motion plan of AUV. Journal of Marine Science and Application 1(1): 81–86. https://doi.org/10.1007/BF02921423 Zhen L, Wu YW, Zhang S, Sun QJ, Yue Q (2020) A decision framework for automatic guided vehicle routing problem with traffic congestions. Journal of the Operations Research Society of China 8(3): 357–373. https://doi.org/10.1007/s40305-018-0216-4 Zou WQ, Pan QK, Wang L, Miao ZH, Peng C (2022) Efficient multiobjective optimization for an AGV energy-efficient scheduling problem with release time. Knowledge-Based Systems 242: 108334. https://doi.org/10.1016/j.knosys.2022.108334