1   Introduction

The exploitation of oil and gas deposits in the sea is one of the main uses of offshore platforms. Fixed offshore platforms are widely used in water depths of less than 100 m due to their simple design, handling, and installation, from which simple types can be described as monopiles. Offshore platforms, such as monopiles, are exposed to the forces of the sea from waves, currents, winds, and earthquakes.Therefore, vibration control should be considered to reduce consumption and extend the life, efficiency, and reliability of the structures. The use of a control system by limiting the range of displacements can be effective in increasing the life and efficiency of the structure. The most common method for controlling structures against seismic and wave forces is to simply use active or passive dampers to absorb and dampen energy into the structure. Depending on their performance, dampers are divided into active, inactive, and semi-active categories. Inactive systems apply an indirect attenuation to the structure by modifying and improving the dynamic behavior of the structure. A passive control system does not require external power for the operation and utilizes the motion of the structure to develop the control forces. Therefore, passive dampers have received increased attention because of their relatively lower cost and easier implementation compared to other types of dampers.

In marine structures, such as fixed jackets and floating spars, studies on controlling structure responses due to marine waves and earthquakes are available. However, information regarding the economic monopile response controlling method is limited. A monopile is a marine structure as a substructure for wind turbines or unmanned topside, which tolerates large deflections from lateral forces, such as waves and earthquakes.

As mentioned above, some passive systems are liquid and liquid mass dampers. A detailed study has been conducted to investigate a type of liquid damper, which is categorized as a passive damper, in offshore fixed monopiles. The advantage of such passive dampers is their low main-tenance requirements, and this helpful property will become important when the monopile body can be used as a tank to fill with seawater to reduce structure displacements as a liquid damper. The aforementioned method is economical; thus, implementing an extra tank on the topside of the monopile is unnecessary. The hydrodynamic forces due to the fluid movement inside the body of the structure act as vibration-resistant forces. The fluid inside the body, which is used as a reservoir, fluctuates counterclockwise due to the wave and earthquake forces, causing fluid impingement on the tank wall. Closing the fluid oscillation frequency near the normal frequency of the structural oscillation, which can be determined from modal analysis, is necessary for the fluid movement within the monopile body to reduce the structural displacement significantly.

The present work aims to analyze the feasibility of using a monopile cylindrical body as a water tank for a passive liquid damper against earthquake forces and finding the optimum water level, which would reduce the displacement response of the structure subjected to wave forces using an ANSYS finite element model.

Many types of dampers (passive or active) have been utilized in buildings, and numerous investigations have also been conducted. Nekooei and Ziyaeifar (2018) studied the effect of dampers on reducing building responses against seismic loads, such as using isolators in a structure to reduce building displacement. However, some studies, such as that of Den Hartog (1956), focused on liquid dampers, particularly tuned liquid dampers (TLDs) in offshore platforms. The TLD system was used as a passive control method for the first time in 1909. The system comprised two tanks that were half full of water and aboard a ship.

Carrier and Miles (1960) studied the TLD system as an oscillation dampener in satellites and spacecraft. The dampers were in a liquid-filled loop orbiting satellites and spacecraft to reduce satellite rotation around the cylindrical axis.

In the second half of the eighties and early nineties, applications of liquid dampers adjusted to onshore structures were studied by Modi and Welt (1987), Kareem and Sun (1987), and Fujino and Sun (1992).

Gao and Kwok (1987) studied the effect of columnar fluid dampers adjusted in various forms, such as U and V, for structural control and determining the optimal parameters for designing this type of damper to maximize the structural response to harmonic excitation. The adjustable liquid column damper (TLCD) system should be equally effective under harmonic as well as stationary random excitations. Thus, the gap of the mentioned study is that a TLCD would not be as effective as predicted in this paper in a nonstationary random excitation situation.

Sun et al. (1992) presented nonlinear modeling for liquid dampers with a rectangular tank. This modeling, which is based on the theory of shallow water waves, also considers the effects of fluid damping. The proposed model was obtained by introducing two modified coefficients and em‐pirical relationships for these coefficients to incorporate the brittle waves in the fluid oscillation. Experiments confirmed that the model can successfully predict the response of structures installed with TLDs despite the occurrence of breaking waves. The mentioned study was performed using wave effects; unlike the current study, earthquake effect results are not presented in the study of Sun et al.

Lee (1997) also investigated the behavior of the platforms with and without regulated liquid dampers and concluded that these mechanical dampers reduce the energy input to the structural system. However, results for the structure displacement, which is one of the final aims of this study, are available.

Wu et al. (1998) studied fluid behavior inside the TLD reservoir via numerical simulation of finite elements and compared the results with those of the analytical study. They found compatibility between the analytical and numerical results. However, their study does not include monopile, which is the subject of the current investigation.

Chandrasekaran and Kumar (2013) compared the use of tuned mass dampers (TMD) and multi-TMDs on fixed offshore platforms and concluded that numerical methods in estimating the response of the structure in critical wave conditions showed slightly effective performance of multi-TMDs in controlling the structure response. Moreover, they mainly focused on TMDs but have not investigated TLDs.

Chatterjee and Chakraborty (2014) examined and re-investigated the columnar fluid regulated under wave loading by placing a ball inside the tank (TLCBD). The results show that the new state performs well due to the low oscillation of the fluid surface.

Lotfollahi et al. (2016) investigated the performance of liquid dampers in controlling and reducing the vibration of offshore platforms under earthquake excitation. Three earthquake records were applied to a platform equipped with adjustable liquid dampers, and the displacement response and acceleration were recorded at the highest platform deck level, which showed a significant decrease in the maxi‐mum displacement and acceleration. While the mentioned work studied jackets, analysis of displacement and acceleration in unmanned monopiles was disregarded.

Wu et al. (2016) investigated the effect of adjustable mass dampers (TMD) against earthquake loads on oil rigs by using laboratory and numerical methods. The numerical results are in good agreement with the laboratory ones and show that the platform displacement due to the open earthquake has decreased due to the installation of mass dampers.

Ha and Cheolung (2016) researched the effect of an adjustable fluid damper (TLD) on an offshore floating wind turbine in the laboratory and compared their results with a numerical model. Their results showed that the dynamic response of the structure is improved due to the installation of dampers. Different from the mentioned study, which aims to reduce displacement and acceleration in a wind turbine, the present study focuses on unmanned monopiles.

Zhang and Høeg (2018) investigated the effect of adjustable liquid dampers on the vibration of offshore wind turbine blades. In their research, TLCD and circular liquid column damper (CLCD) have been installed inside the turbine blade. Numerical modeling results have shown that the two types of dampers have a positive effect on reducing the vibration of wind turbine blades.

Zhao et al. (2018) studied the vibration control effects of a TMD on a monopile offshore wind turbine tower under wind–wave and seismic excitations, and shaking table tests on a 1/13-scaled test model equipped with or without TMD were implemented. The seismic responses of a monopile offshore wind turbine attached with/without TMD are also analyzed by the FE software ANSYS according to the test results. The obtained results by numerical simulation fit well with those derived from the experimental tests, demonstrating that the numerical simulation method proposed in this paper is feasible with satisfactory accuracy.

Gharabaghi and Mohasel (2019) numerically modeled the dynamic response of a platform in the waters of South Pars by considering the adjustable liquid damper using Abaqus software and concluded that the platform displacement is reduced due to damper installation. As in the previous studies, the mentioned research did not include unmanned monopiles.

Lu et al. (2017) investigated a particle-TMD on a building and found that the damper has excellent and steady wind-induced vibration control effects. Meanwhile, the parameters (filling ratio, mass ratio, and mass ratio of the container to particles), which have a considerable influ‐ence on the vibration reduction performance of the system, are also analyzed. They found that the particle filling ratio is crucial in deciding the damping effects of the dampers.

However, the investigation of the studies related to unmanned monopiles shows that in some that aim to extract oil and gas in the shortest possible time and cost, liquid damper with high efficiency has been used less and utilizing an adjustable liquid damper can be effective in reducing the response of the structure to environmental factors, including earthquakes.

2   Fixed monopile platforms

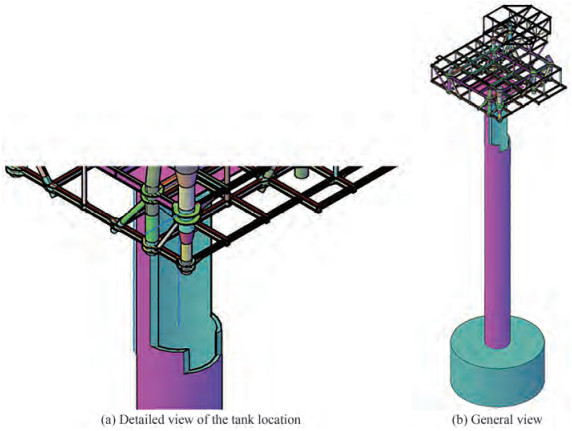
Steel jacket support structures for offshore topside or wind turbines have increasing popularity for different water depths. Traditionally, support structures, such as mono-piles and gravity-based foundations, have dominated shallow water. Figure 1 shows the types of mono columns with a hollow cylindrical tower used as substructures for unmanned or even manned topside.

Figure  1  Monopile Platform Samples

Download: Full-Size Img

One advantage of a cylindrical mono-column is the possibility of using its body as an accessory tank to reserve seawater fluid as a liquid damper.

3   Tuned liquid dampers

In a TLD system, as a passive control method, fluid inertia in a tank is used to control the structure vibration. TLDs were first used in the early 20th century to control the vibrations caused by sea waves in ships and were then applied in the mid-80 s to control the vibrations of civil structures. The operation of this damper is as follows: a number of tanks are installed at the top of the structure, and the vibration energy is depreciated by the inertial behavior of the fluid and its hydrodynamic forces.

The displacement of the structure leads to shaking of the fluid in the tank and causes a difference in the fluid surface level. Consequently, the pressure difference due to this surface difference appears as a shear force at the bottom of the reservoir, which is opposite to the lateral force. Aligning the natural vibration frequency of the structure with the fluid oscillation frequency is suggested to earn the best performance during resonation and optimize the damper design. Different methods have been proposed to simulate the behavior of a finite liquid damper, the most popular of which is the mass-focused method first proposed by Housner (1957). In the Housner model, the hydrodynamic pressures caused by the fluid are simulated by two masses attached to the reservoir wall. One of these masses is related to the pressure due to impact, and the other is considered to model the pressure of fluid oscillation. Figure 2 provides an overview of the proposed model of Housner and its related relationships.

Figure  2  Proposed Model of Housner

Download: Full-Size Img

where m is the mass of the liquid inside the tank and R is the tank radius.

M₁ and M₂ are also defined as shown below:

Linear wave theory is used to calculate the frequency of fluid oscillation inside the tank. The results were as follows:

where h₀ is the fluid height inside the tank, g denotes gravity acceleration, f denotes frequency, and a is the tank diameter for a cylindrical reservoir.

A type of monopile installed at 70 m water depth, which is common in the Persian Gulf, has been chosen to check the effect of liquid damper and structure displacement due to lateral seismic forces. The position and height of the water as a liquid damper, which is placed in the body of the monopile as a water tank, are shown in Figure 3. The height and position of water will also change tower displacement, and this issue will be discussed in the optimization section. The mass of the topside at the top of the monopile was modeled as a concentrated mass. Details of the environmental data and structural properties, such as water depth and topside mass, as an unmanned platform based on the usual situation in the Middle East, especially the Persian Gulf, are described in Table 1.

Figure  3  Inside view of monopile as a water TLD tank

Download: Full-Size Img

4   Water tank as a liquid damper

Water tanks may generally be added at the top of the structures and impart them with a considerable dead load. The water mass can be utilized as a liquid damper to absorb the extra energy imparted on the structure during lateral forces, such as earthquakes. However, the tank body is an extra mass that causes additional weight in the structural mass. In the present work, the water tank is a part of the structure body, and no additional mass is found due to the steel material of the tank. The tank could also be filled when required. The seawater is placed inside the structure body at the top of the monopile. The liquid water cylinder has a plan dimension of proper diameter circle and variable height. The height and dimensions of the water cylinder as a liquid damper were taken to conform to the following condition: the sloshing period of water matches the natural period of the structure, which causes minimal displacement due to resonance situation. However, this type of liquid damper not only aims to reduce the structural response in the resonance condition but also during all lateral forces. Meanwhile, a resonance resistant model has been chosen for the initial dimensions and water height. TLD liquid movement causes a difference in the free surface figure of the liquid in the end walls of the tank, and the pressure difference due to the free surface level difference appears as a shear force on the tank floor, which acts against seismic force and reduces the earthquake displacement response. A detailed model of the tank is shown in Figure 3.

5   Modeling and FEM analysis

An FE study was conducted using the ANSYS software. A model of a steel monopile was taken for investigation. The mass of the topside has been modeled as a concentrated mass at the top of the monopile column, which is a symbol of an unmanned topside with 500 tons of weight that is common in offshore projects. The details of the model, such as diameter, element type, and material properties used in ANSYS, are given in Table 2.

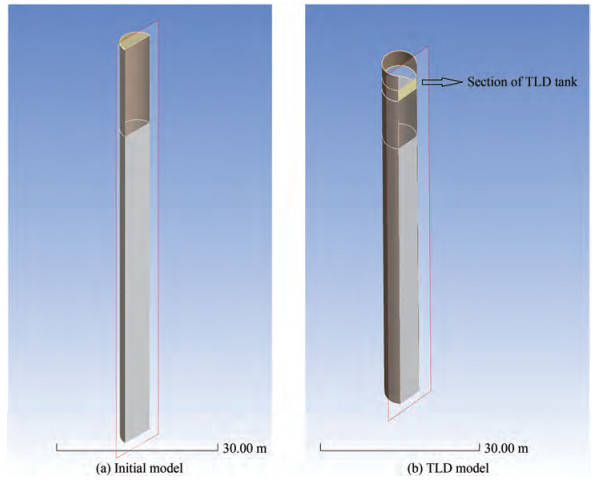
The solid85 element is used to model the monopile body, and the Fluid80 element, which can consider the effects of liquid and structure interaction, is applied to model the fluid inside the monopile body. This element considers the fluid to be homogeneous, nonviscous, incompressible, and nonrotating. Two FE models have been estab‐lished in this research. The first model, namely the "Initial model, " does not contain a liquid damper. A secondary model is created to determine the effects of the inner tank water on the structural response due to earthquake acceleration. The second model, namely the "TLD model, " uses a type of passive liquid damper that contains water inside the monopile body. Figures 4(a) and 4(b) present the schematic of the initial and TLD models, respectively.

Figure  4  Section view of the model

Download: Full-Size Img

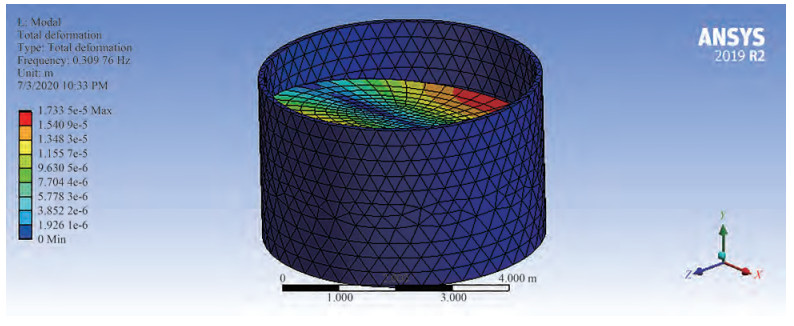
The natural frequency of the monopile will be determined by modal analysis in the ANSYS workbench, which is equal to 0.36 Hz. In the "TLD Model, " the water height inside the body as TLD is determined such that the sloshing frequency due to the vibration is close to the natural frequency of the structure. The sloshing frequency can then be obtained from the Housner equation described in Section 4. Considering 6.5 m for monopile diameter based on Table 2 and the natural frequency of the monopile, which is 0.36 Hz, the water depth inside the monopile as TLD will be 4 m based on the calculations below. With the above-mentioned water depth for TLD, the sloshing frequency will be the same as the natural frequency of the structure, and the "TLD model" containing a water tank with 4 m water depth is chosen as a model to check the structure displacement comparing the "Initial model." By contrast, changing the other parameters, such as tank water height, can verify whether the mentioned parameters will cause improvements in displacement response.

6   Software verification

Figure 5 shows the TLD tank, which is cylindrical and is a part of the monopile body. As mentioned in Section 5, the natural mode and frequency are 0.36 Hz based on modal analysis in the ANSYS workbench. Considering the equations described in Section 4, the first mode frequency of the monopile is near to that provided by the Housner equation. With a 4 m water depth and 6.5 m diameter for the TLD cylindrical tank, the TLD frequency is 0.33 Hz based on Housner equations, and the difference is negligible with software results. Table 3 shows the details.

Figure  5  Close view of the TLD tank

Download: Full-Size Img

7   Time history analysis

One of the methods for earthquake analysis and finding structural responses, such as displacement, is "time history analysis." Using a series of earthquake acceleration records that are applied to the monopile as a lateral load at the base level is effective. Recommendations indicate that at least three accelerometers should be used for time history analysis to obtain substantially accurate results. The accelerated mappings used in this research are related to "Tabas, " "El-Centro, " and "Kobeh" earthquakes. Although they have been used in previous studies, such as Gharabaghi and Mohasel (2019), the three earthquakes have been selected for this research due to their different frequency ranges.

A type of analysis called "transient analysis" has been applied in the ANSYS workbench software to execute time history analysis. The structure is placed in 70 m seawater. Thus, the damping ratio is set to 0.05 in the analysis based on the API RP2A code. However, as a suggestion for future research, finding a suitable model to extract the damping coefficient for analysis can be considered. The current research has a comparative aspect; therefore, 0.05 has been used for simplification based on available references (Tan and Hu 2021).

Notably, the monopile is filled with seawater after installation operation, and this issue is considered in the ANSYS model. Figure 6 shows acceleration mappings for one of the above-mentioned earthquakes (El-Centro), which are applied in software as lateral stimulation. Furthermore, Table 5 presents a brief property of the above-mentioned earthquakes.

Figure  6  El-Centro acceleration map

Download: Full-Size Img

8   Results and discussion

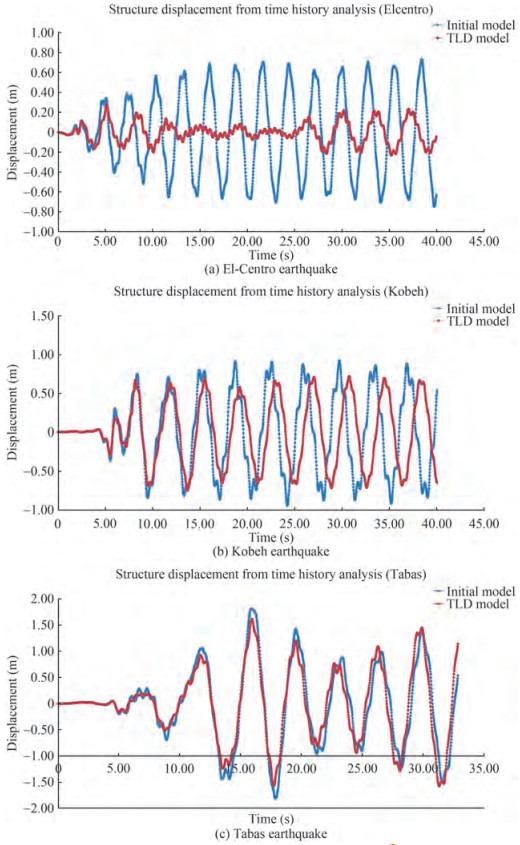
The time histories of the monopile top displacement are presented in Figure 7, which is based on acceleration mapping from El-Centro, Tabas, and Kobeh earthquakes with and without TLD called the "Initial model" and "TLD Model." Furthermore, the maximum displacement values for the above-mentioned models have been compared in Table 4.

Figure  7  Comparison of initial and TLD model displacements for earthquakes

Download: Full-Size Img

Table 4 and Figure 7 show that the TLD effect on displacement reduction in the El-Centro earthquake is more significant than that in others. However, displacement reduction is observed in all cases.

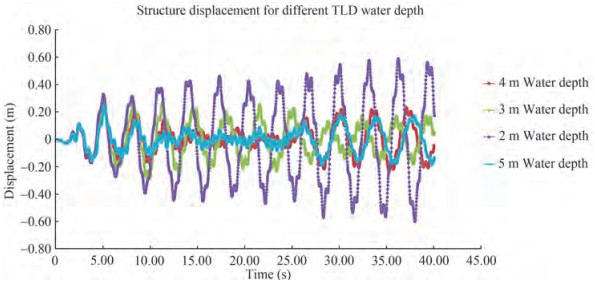
Figure 8 shows that the monopile displacement for the TLD model is related to a situation where the tank water height is 4 m, and its oscillating frequency is tuned with the natural frequency of the structure. In this case, the maximum displacement reduction occurs because of matching the tank water frequency with the structure's natural frequency. The water tank effect will be different by changing the water depth in the tank. Figure 8 shows a comparison of different water depths in the TLD tank for the El-Centro earthquake, which is more TLD influential.

Figure  8  Monopile displacement for different TLD water depths

Download: Full-Size Img

Based on Figure 8, the change in TLD water depth changes the displacements because of the water tilting frequency in the tank, which is close to or far from the earthquake frequency domain and the natural frequency of the structure. The following points are also extracted from the results obtained in this study.

• Based on a review of technical literature and what was mentioned in the introduction section of this article, the fluctuation of fluid inside the tank causes a shear force in the bottom of the tank, which is in contrast to the earthquake force. Matching the frequency of fluid fluctuation inside the tank and the frequency of earthquake leads to the synchronization of the two forces and the significant effect of tank fluid fluctuations in reducing the structure response.

• Another point is that in Housner's equations, the relationship between the oscillation frequency of the reservoir fluid as a hyperbolic function with the height of the water in the reservoir changes nonlinearly and around a certain depth (in this analysis, at a depth of 4 m according to the geometry of the problem and other parameters); thus, matching of the earthquake energy frequency and tank fluid fluctuation occurs. Therefore, considering an upward or downward linear trend for such an occurrence, the hyperbolic tangent function changes in an almost ascending nonlinear curve with its independent variable (herein, reservoir fluid depth). Hence, in shallow depths, such as 1 or 2 m, the oscillation frequency is minimal and has not yet reached the earthquake oscillation frequency. However, the oscillation frequency increased at high depths, such as 4 or 5 m; thus, the approaching oscillation frequency to the earthquake frequency causes a decrease in the response of the structure (Figure 9). In the hyperbolic tangent function, the upward slope of the graph decreases with the increase in the independent variable; thus, the response of the structure is remarkably similar at depths of 4 and 5 m.

• After choosing the optimal height of water in the damper, the behavior of the structure was analyzed, and two modes of the presence and absence of the damper were compared. The obtained results can be used for the design of new marine structures as well as the seismic improvement of monopile platforms. Based on these results, the effect of this type of damper on the monopile displacement is different in various seismic acceleration maps. Consequently, the effectiveness of TLD depends on the frequency range of the earthquake. The results show that the use of this TLD system can significantly reduce the displacement response of the platform.

• Housner's numerical relationship in Section 3, which is used to calculate the fluid oscillation frequency of the tank, was examined. The result shows that when the depth of the fluid inside the tank is 4 m, the earthquake oscillation frequency (of the structure), which can be obtained using modal analysis in ANSYS, is similar to the tank fluid oscillation frequency considering Housner's numerical equation. That is, probably the most opposing force in the direction of earthquake movement at this depth, which is caused by the fluctuation of tank fluid, affects the platform. Therefore, the investigation of the displacement of the structure in three different aforementioned earthquakes has been conducted with the assumption of a 4 m depth of fluid inside the tank, which is presented in Section 7 by providing the displacement graphs.

• The similarity of the oscillation frequency of the tank fluid (assuming that the depth of the fluid inside is 4 m) with the vibration frequency of the structure due to an earthquake can be obtained by comparing the results of the numerical relationship of the frequency in Housner's equations and those of modal analysis.

- The frequency of the first mode of vibration of the structure in ANSYS is 0.31 Hz.

- The vibration frequency of the fluid inside the tank is obtained using Housner's relation according to Table 5.

Therefore, the Housner's equation result (f = 0.33) is similar to ANSYS (f = 0.31).

9   Conclusion

A monopile platform with appropriate dimensions for the Persian Gulf under different earthquakes was investigated in this study in two cases (with and without TLD). In the TLD model, the water tank is a part of the monopile body, and its liquid can be supplied from seawater. Therefore, this type of liquid damper is more economical and lighter than other known items in offshore platforms and buildings. The structural model was created and analyzed in the ANSYS software. After validating the FE model and optimally selecting the water height in the damper, the behavior of the structure was analyzed and compared in two cases (with and without the damper). The results can be useful in designing new marine structures as well as seismic improvement of monopile platforms. According to the obtained results, the effect of this type of damper on the displacement of the monopile is different under various seismic acceleration maps. Consequently, the degree to which the TLD is affected also depends on the frequency domain of the earthquake. The results show that using this system can lead to a significant reduction in the platform displacement response, whereas more than 50% of displacement reduction has been achieved on the basis of Table 4 for the El-Centro acceleration map.

Suggestions for future research are as follows:

1) A mathematical relationship to determine the displacement of the monopile based on various variables, such as the diameter of the monopile, its height, and the depth of the fluid inside the damper tank, is provided to achieve a relationship with specific regression by statistical analysis.

2) In addition, future research will include a comparison of the phase delay amount of superstructure displacement in models with and without dampers, as well as the effective parameters in this issue and the relationship between the amount of this phase delay and its parameters.

3) Monopile connection is rigid in the current research. Therefore, considering the seabed soil in the modeling in future research is suggested.