1   Introduction

Motion of free liquid surface in partially filled containers due to external disturbances is defined as sloshing. For any partially filled tanks, dynamic behaviour is significantly affected by the dynamic motion of the free surface liquid. Sloshing is experienced in various engineering applications such as liquid transporting trains and trucks, oil carrying ships, fuel tanks on space crafts and rockets, water oscillation in liquid storage tanks and reservoirs subjected to earthquake excitations. Oil transportation between countries in terms of both import and export is one of the major trades, supporting the economy of the country. Sloshing is a severe problem in the oil carrying ships. Violent oscillation of the oil inside the tank will lead to the instability and damage of the liquid cargo ships. Understanding the liquid sloshing phenomena will help the Engineers to incorporate the additional loads, in the design of tanks of liquid carrying ships and trucks. Research has been carried out in the field of sloshing from 17^th Century.

2   Background of the Study

A detailed review of the existing literature reveals the importance of sloshing. Numerous works were carried out to study the phenomena of sloshing experimentally, analytically and numerically. Liquid sloshing phenomena was initially investigated by Faraday (1831) which was followed by Benjamin and Ursell (1954). Moiseyev (1958) proposed a nonlinear theory to predict the sloshing behaviour in partly filled sway excited tank. Faltinsen (1974) numerically simulated the nonlinear behaviour of sloshing under sway and roll motions. Nakayama and Washizu (1980) used a finite element based nonlinear approach to investigate the liquid motion and the resulting sloshing pressure in a container excited under forced oscillations. Waterhouse (1994) explicated the significance of aspect ratio in sloshing problem. Armenio and Rocca (1996) developed mathematical models to analyse liquid sloshing in open rectangular tanks. Frandsen (2004) studied the multiple resonance conditions developed in combined heave and sway excitations. Akyildiz and Unal (2005) compared the pressure distribution in a tank excited by roll motion for different fill levels. Jiang et al. (2014) compared the pressure and sloshing elevation by varying excitation frequencies for elastic tank with rigid tank. Kim et al. (2012) studied the scale effects of sloshing under roll and sway motions using three different scaled tanks. The results from the experiment were statistically analysed and a comparison of performance at three different fill levels (0.15 h, 0.70 h and 0.95 h, where h is the height of tank) was also done. Nasar et al. (2008 and 2012)investigated the sloshing behaviour in a rectangular tank mounted on a barge and the barge responses under random excitations.

Umemoto et al. (1997) conducted an experimental work to calculate the sloshing pressures in partially filled double-hulled tanks which are exposed to roll excitation. Cariou and Casella (1999) examined mathematical for the sloshing simulations and emphasized the scope for further research work on impact loads and peak pressures. Tahmasebi et al. (2020) studied different turbulence models to predict sloshing phenomenon and explored their accuracies in prediction. Gurusamy and kumar (2020) conducted a series of experiments to investigate the nonlinear shallow water sloshing. Jin et al. (2020) studied the viscous effects of tap water and glycerin on the horizontally-excited sloshing tank under resonant and off-resonant excitations.

Khezzar et al. and Chen et al. (2009) studied the impact pressure due to sloshing phenomenon in a partly filled tank by using experimental work and numerical simulation, respectively. Rognebakke and Faltisen (2001) investigated the sloshing effects on the partly filled liquid tank subjected to regular beam sea waves. Akyildiz et al. (2013) experimentally explored the sloshing phenomena in a scaled model cylindrical tank with different fill levels excited under roll motion. Graczyk et al. (2007) investigated the structure response of the LNG tank under vertical and horizontal accelerations as well as the sloshing-induced pressure on the tank walls under random stimulation. Liu and Lin (2008) studied the three-dimensional nonlinear sloshing behaviour using numerical model. The numerical study was also validated analytically. Virella et al. (2008) used finite element tool (ABAQUS) to study the influence of non-linear behaviour of sloshing on its pressure and natural periods. The effect of the liquid depth and tank geometry was studied. It was concluded that the surface wave non-linearity does not have considerable effects in the sloshing pressures on the rectangular tank walls. Fully non-linear finite difference modelling was done by Frandsen (2004) and the study was built around equations for inviscid flow. Results of liquid sloshing generated by harmonic base excitations are presented for small to steep non-breaking waves.

There are recent experimental and numerical approaches which discuss the prediction/measurement of sloshing oscillation and induced sloshing pressure. Also, the effectiveness of different baffle configurations in suppressing sloshing oscillation and pressure is explored (Tahmasebi et al. (2020), Guan et al. (2020), Yu et al. (2020a), Pandit and Biswal (2020), Yu et al. (2020b), Jin et al. (2022), Kamath et al. (2021) Tsao and Huang (2021). Xue et al. (2017) reported the influence of vertically arranged baffles on sloshing frequency with shake table tests. Cho et al. (2017) and Saghi et al. (2020) explored the effectiveness of porous baffle in exploiting the sloshing force.

Kim et al. (2017) studied the scale effects on 3-D sloshing flows using three-scaled model tanks of 1:30, 1:50, and 1:70 based on the natural gas carrier of capacity 138, 000 m³. The tanks were excited for various excitation frequencies under roll and harmonic sway motion. Three fill depths of 15%, 70% and 95% were adopted for the study. Peak pressure and rise time of sloshing pressures were studied. It was concluded that the impact pressure reduces at 15% and 70% fill levels when the model scale was increased. Zheng et al. (2021) examined the sloshing characteristics in tanks of various sizes as a result the scaling effect of sloshing is also considered. The study discusses current developments in liquid sloshing hydrodynamics, such as the scaling effect of sloshing. Qiu et al. (2022) studied fluid sloshing hydrodynamic performance in a cryogenic fuel storage tank by utilizing volume of fluid (VOF) method. The numerical model validation is conducted by compared with related experimental results which shows that the η ranges from 30% to 70%, the fluctuation amplitude of M increases about 6.32 times.

The literature reveals that there are numerous experimental and numerical studies are available in understanding the sloshing oscillation and sloshing pressure. Extensive studies on suppression of sloshing oscillation and induced pressure with different baffle configurations are also available. However, studies on estimation of sloshing force in sloshing tank is scarce. Also, studies on different tank size are limited. The estimation of sloshing force from the experimental measurement of sloshing pressure leads to empirical correlation with approximations. Hence, an accurate measurement of sloshing force is inevitable in any experimental program. The estimation of sloshing force is one of the key factors in deciding the appropriate structural configurations in floating tanks and fixed tanks. In view of the importance of above, the present study aims to explore variation of sloshing oscillation and resulting force in different size of the tanks.

3   Experimental Setup

The experimental study is carried out using shake table in the Department of Water Resources and Ocean Engineering at National Institute of Technology Karnataka (NITK), Surathkal. An experimental setup (Figure 1a) is designed and devised to measure the sloshing force based on ballast mass concept. An indigenous make (Geotran, India) servo-hydraulic, single axis shake table of payload capacity 500 kgf is connected to a digital amplifier which is driven by a hydraulic actuator. The inertial forces experienced by the masses placed on the shake table platforms are measured by load cells of capacity 500 N. Capacitance type wave probes are used to capture sloshing motion of liquid inside the tank with range of +20 cm and −20 cm. The horizontal displacement of the shake table is measured using LVDT with displacement range of +50 mm to −50 mm. Wave transformer (Scientech, India) is used to control excitation frequencies and amplitudes. A Data Acquisition System (DAQ) consists of 16 channels of a 16-bit resolution data logger is used to acquire the data. Figure 1(b) shows the calibration charts of different transducers used in the present experimental work.

Figure  1  Experimental and calibration setup

Download: Full-Size Img

Three different rectangular tanks of scale 1:86, 1:57 and 1:43 (Nasar et al., 2008) are fabricated using 12 mm thick acrylic sheets and Table 1 specifies dimensions of rectangular tanks. The photographic view of the three scaled tanks is shown in Figure 2.

Figure  2  Photographic view of rectangular scaled tanks

Download: Full-Size Img

4   Methodology

The tank partially filled with liquid is mounted on the shake table and the table is harmonically excited in sway motion with an excitation amplitude and frequency. Experiments are conducted using Shake table for 25%, 50% and 75% fill levels. Natural frequencies for different fill levels (f_n) are calculated using the mathematical expression (Ibrahim, 2005) as follows:

where, n is the surface mode number, h_s is the static water depth and l is the tank length. The excitation frequencies for 1:86 scaled tank varies from 0.456 6 Hz to 2.794 Hz which covers up to fifth mode of sloshing. Similarly, the frequencies of excitation range from 0.456 6 Hz to 2.813 Hz (f₅) and 0.456 6 Hz to 1.975 7 Hz (f₅) for 1:57 and 1:43 scaled tanks, respectively. In this study, two different excitation amplitudes of 4 mm and 8 mm of are considered.

5   Results and discussion

With the outcomes found from the series of shake table experiments, the sloshing dynamics is explored with the following experimental parameters such as maximum free surface response (ƞ_max), root mean square elevation (ƞ_rms), maximum sloshing force (F'_max), and average of ten largest sloshing peaks (F'_avg), sloshing oscillation spectra and statistical analysis of sloshing force for three scaled tanks in sequence.

5.1   Maximum free surface response (ƞ_max)

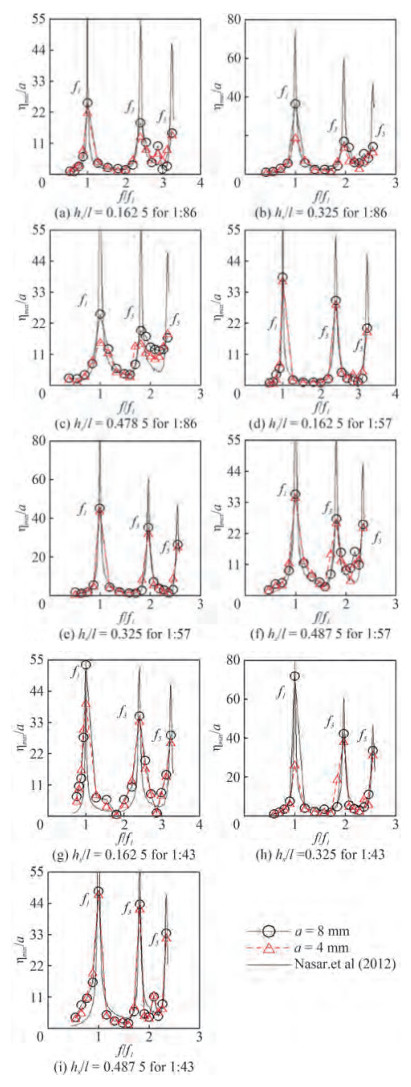
The maximum free surface response gives the maxi‐mum sloshing run-up for given excitation amplitude and excitation frequency. The variation of normalized maximum free response (ƞ_max/a) for different frequency ratio (f /f₁) and different fill levels are projected in Figure 3 for 1:86, 1:57 and 1:43 scaled tanks.

Figure  3  Variation of ƞ_max/a with frequency ratio (f/f₁) for different scaled tanks

Download: Full-Size Img

A comparison of experimental results with numerical results of Nasar et al. (2012) is performed.

The equation of motion of sloshing fluid for the tank subjected to sway excitation,

is given (Warnitchai and Pinkaew, 1998; Frandsen, 2004) as follows:

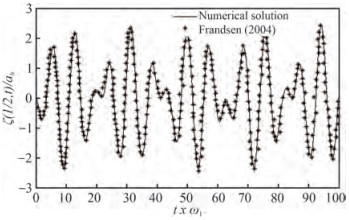
where, q_n(t) is the time evolution function, m_n is the modal mass at nth mode, b is the tank dimension along third axis, and a_h is the sway amplitude. A numerical integration technique by Wilson - θ method has been adopted to solve the equation of motion of sloshing oscillation.

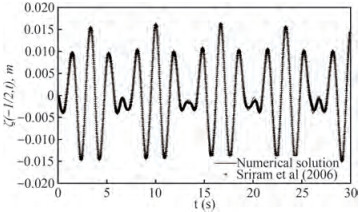
The time histories of free surface elevation ζ(−l/2, t) along the left wall of the tank is compared with numerical findings of Frandsen (2004) and Sriram et al. (2006).

At odd sloshing frequencies, acceptable correlation between maximum free surface responses is observed. Among all the scaled tanks, maximum free surface response is higher for 50% fill depth (h_s/l = 0.325) than the response obtained for 75% fill depth (h_s/l = 0.487 5) and 25% fill level (h_s/l = 0.162 5). It is also experienced that the first mode of sloshing (f = f₁) is the critical mode for partially filled tank under sway excitation. The free surface response is in decreasing order with the wave excitations at f = f₁, f₃ and f₅. On comparison of three different fill levels, higher sloshing oscillations are observed in the order of 50%, 75% and 25% fill levels. Irrespective of the fill depths, the 1:43 scaled tank shows more sloshing response in comparison with 1:57 and 1:86 scaled tanks.

5.2   Root Mean Square Surface Elevation (ƞ_rms)

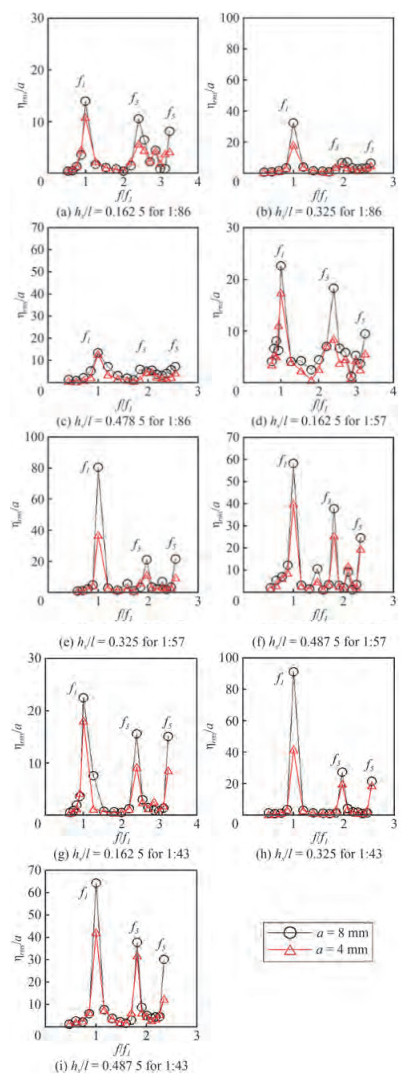
The variation of normalized Root Mean Square surface elevation (ƞ_rms/a) with frequency ratio (f/f₁) is illustrated in Figure 4 for different fill levels and different scaled tanks. By considering all the scaled tanks, normalized root mean square surface elevation is higher for 50% fill depth (h_s/l = 0.325) than the response obtained for 75% (h_s/l = 0.487 5) and 25% (h_s/l = 0.162 5) fill depth. Normalized root mean square surface elevation is observed in the decreasing order, f = f₁, f = f₃, f = f₅ i.e., at odd mode sloshing frequencies. Irrespective of the fill depths, the 1:43 scaled tank experiences more sloshing response in comparison with 1:57 and 1:86 scaled tanks.

Figure  4  Free surface elevation, ζ(−l/2, t) at end of wall for an aspect ratio, h_s/l= 0.5 subjected to sway excitation parameters: a_h= 0.005 h_s and ω_h= 0.7ω₁

Download: Full-Size Img

Figure  5  Free surface elevation, ζ (−l/2, t) at end of wall for an aspect ratio, h_s/l = 0.5 subjected to sway excitation parameters: a_h = 0.005 hs and ω_h = 0.7 ω₁.

Download: Full-Size Img

5.3   Sloshing dynamics

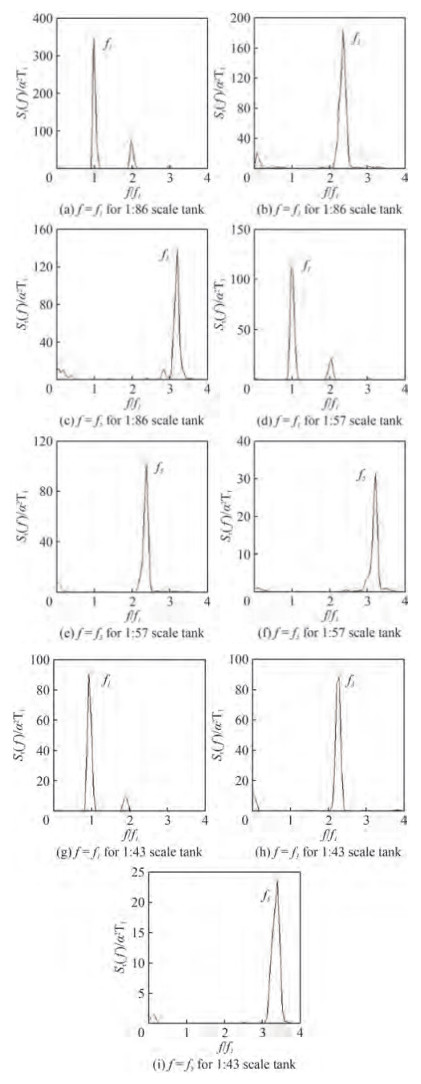
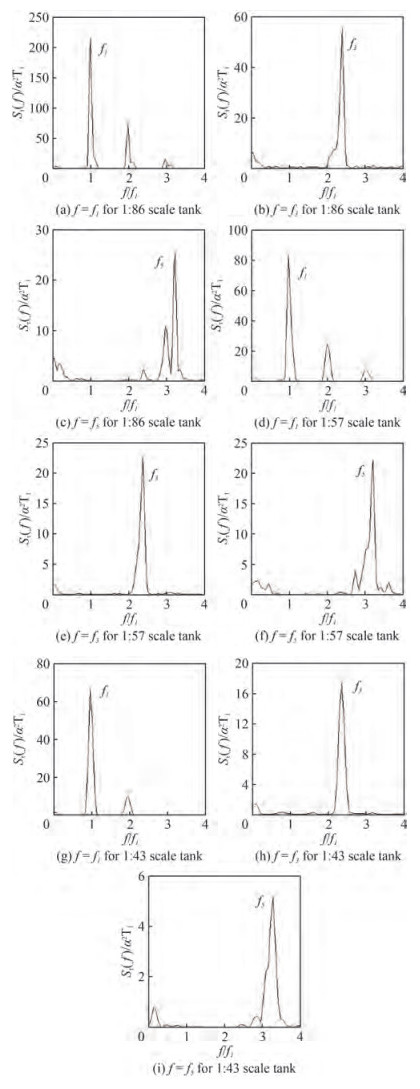
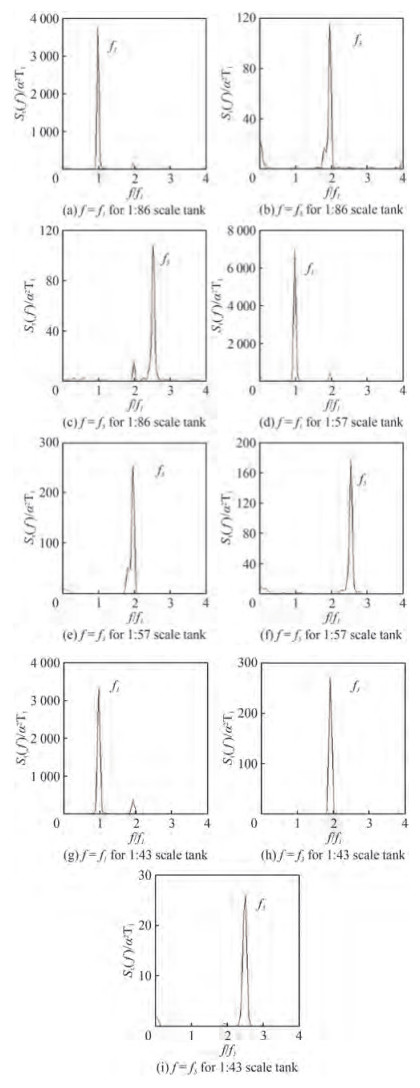
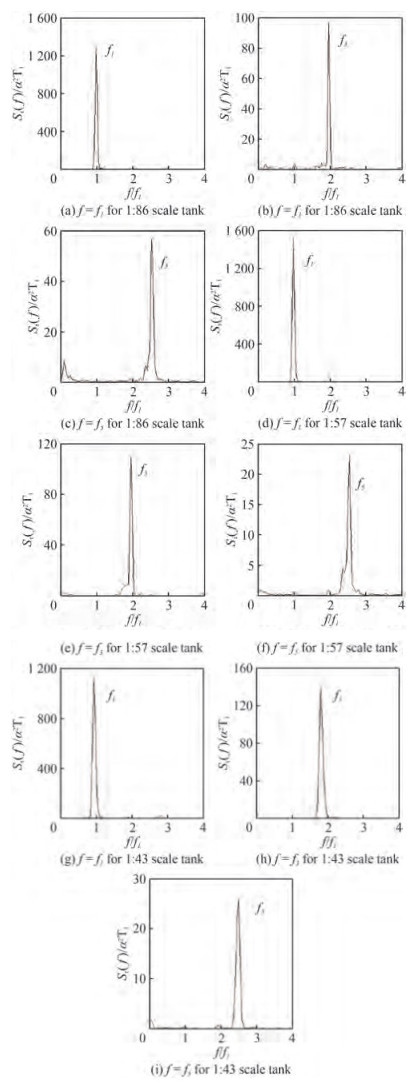
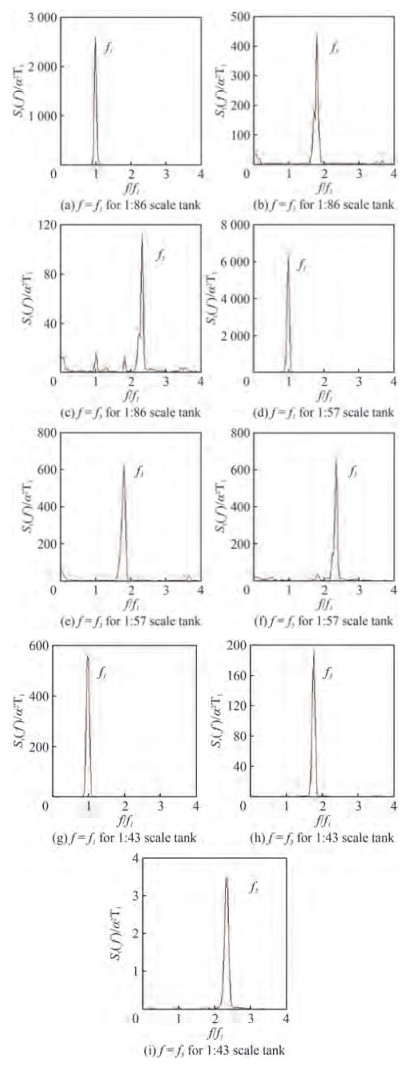
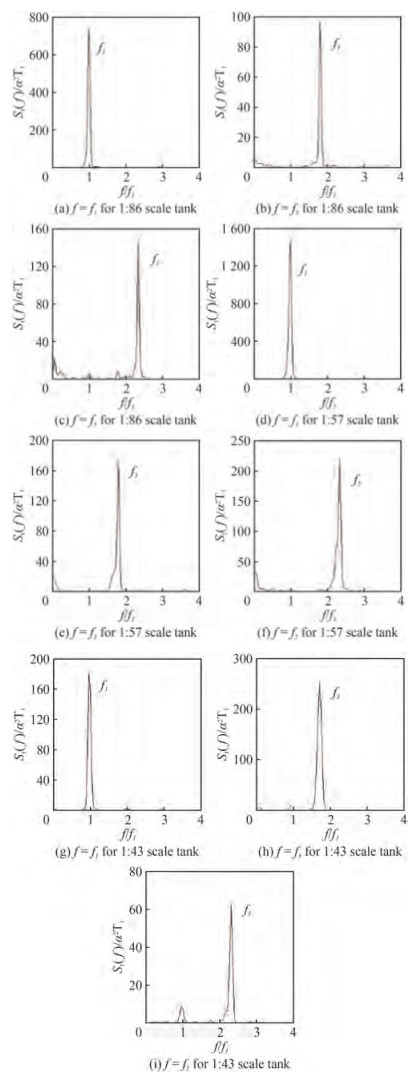
Sloshing dynamics is explored with the help of energy spectrum for three different scaled (i.e; 1:86, 1:57 and 1:43) rectangular tanks at three different fill depths (i.e; 25%, 50% and 75%). It is learnt that odd modes contributions are dominating even modes and hence comparison of sloshing oscillation spectra of f = f₁, f = f₃ and f = f₅ is projected.

From Figures 7 and 8, it is seen that there is an increase in energy absorption for 25% fill level (h_s/l= 0.162 5) as the excitation amplitude increases from 4 mm to 8 mm. Also, it is observed that the energy absorption reduces with increase in sloshing mode for all the scaled tanks. When comparing the three tanks for h_s/l= 0.162 5, the energy concentration in the scaled tank is in the order, 1:86 > 1:57 > 1:43. For 50% (Figures 9 and 10) and 75% fill levels (Figures 11 and 12), the energy concentration is in the order, 1:57 > 1:86 > 1:43.

Figure  6  Variation of ƞ_rms/a with different frequency ratio (f/f₁) for scaled tank

Download: Full-Size Img

Figure  7  Sloshing oscillations spectra for h_s/l = 0.162 5 and excitation amplitude of 4 mm

Download: Full-Size Img

Figure  8  Sloshing oscillations spectra for h_s/l = 0.162 5 and excitation amplitude of 8 mm

Download: Full-Size Img

Figure  9  Sloshing oscillations spectra for h_s/l = 0.325 and excitation amplitude of 4 mm

Download: Full-Size Img

Figure  10  Sloshing oscillations spectra for h_s/l = 0.325 and excitation amplitude of 8 mm

Download: Full-Size Img

Figure  11  Sloshing oscillations spectra for h_s/l = 0.487 5 and excitation amplitude of 4 mm

Download: Full-Size Img

Figure  12  Sloshing oscillations spectra for h_s/l = 0.487 5 and excitation amplitude of 8 mm

Download: Full-Size Img

5.4   Sloshing force

A proper estimation of sloshing force is the significant part of sloshing dynamics and it is the deciding parameter for the design and operation of any moving/fixed vehicle which is carrying/holding a tank with partially filled liquid. Sloshing force mainly depends on the frequency of the moving tank, excitation amplitude, geometry, size of sloshing tank and depth of liquid fill in the tank. In view of importance of measurement of sloshing force, it is measured by ballast mast concept for the different shake table excitation parameters.

The sloshing force is presented in normalized peak sloshing force (F'_max) and normalized average force (F'_avg) of ten largest peaks. According to Jamie (2007), the normalised peak sloshing force and normalised average sloshing force are as follows:

wherea is excitation amplitude, m_w is total mass of the fluid and f is excitation frequency. Liquid is considered as solid mass and its inertial force is used as normalising factor.

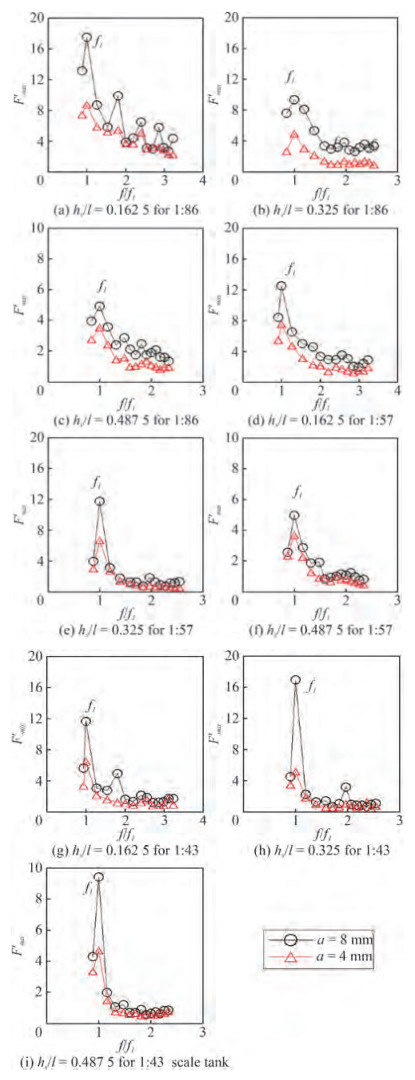
Experimental analysis reveals that as the excitation frequency increases, F'_max and F'_avg decreases. Sloshing force is observed as higher for the first mode of excitation frequency compared with other modes of excitation frequencies. Also, it is understood that sloshing forces increase with increase an excitation amplitude. From Figure 13 and Figure 14, it is observed that 50% (i.e., h_s/l = 0.325) water depth can have higher sloshing force than 25% (i.e., h_s/l = 0.162 5) and 75% (i.e., h_s/l = 0.487 5) water depths. Sloshing force is high for smallest tank (1:86 scale tank) at lowest water depth (25% depth) irrespective of the excitation frequency and amplitude.

Figure  13  Comparison of F'_max with frequencies ratio (f/f₁) for different scaled tanks

Download: Full-Size Img

Figure  14  Comparison of F'_avg with frequencies ratio (f/f₁) for different scaled tanks

Download: Full-Size Img

When the water depth is more than 50% tank height (i.e., h_s/l= 0.325) then sloshing force is maximum in the biggest tank (1:43 scale tank) than other scaled sloshing tanks irrespective of the excitation frequency and amplitude. From experimental observations, it is concluded that proportionate volume of water and tank size would decide the severity of sloshing in the partially filled moving tanks.

5.5   Statistical study

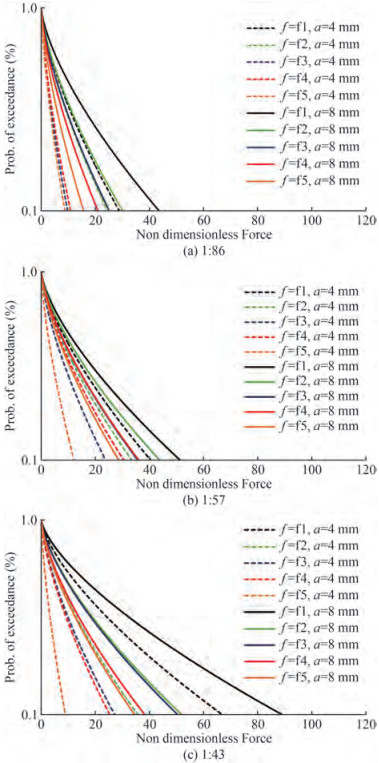
Experimental results are analysed statistically by three parameters Weibull distribution to study the probability of exceedance of forces at different fill depths (25%, 50% and 75%) in scaled rectangular tanks (1:86, 1:57 and 1:43). The probability distribution function (F(x)) of Weibull distribution is represented as,

where β is the scale parameter (β > 0), γ is the shape parameter (γ > 0) and δ is the location parameter.

Method of moments of curve fitting is used to obtain the above-mentioned parameters. Probability of exceedance (S (x))for Weibull distribution is represented as,

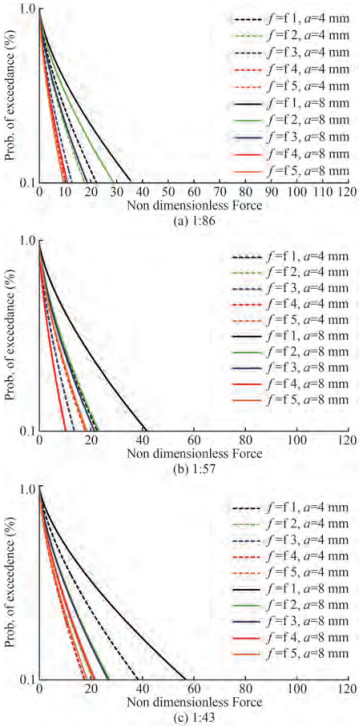
Semi-log graphs are plotted between force and probability of exceedance for the three fill levels and three scaled tanks. For ease of comparison of data, a probability of exceedance of 40% is considered. The results are compared at a probability of exceedance of 40%, which indicates 40% of the force values in sample will be greater than the force corresponds to 40% probability of exceedance.

From Figures 15‒17, a right ward shift in the plot is observed at same probability of exceedance when the excitation amplitude changes from 4 mm to 8 mm. This indicates that the force exerted at 4 mm excitation amplitude is lesser compared to that at 8 mm excitation amplitude. At a specific probability of exceedance, among the five sloshing modes considered, the force exerted with first mode of oscillation is found higher compared to other four modes.

Figure  15  Probability of exceedance of sloshing forces for h_s/l = 0.162 5 for tank scaled

Download: Full-Size Img

Figure  16  Probability of exceedance of sloshing forces for h_s/l= 0.325 for tank scaled

Download: Full-Size Img

Figure  17  Probability of exceedance of sloshing forces for h_s/l= 0.487 5 for tank scaled

Download: Full-Size Img

Among different scaled tanks at 25% fill depth, the 1:86 scaled tank exerts more force in comparison with 1:57 and 1:43 scaled tanks for both 4 mm and 8 mm excitation amplitudes.

At 50% and 75% fill depth, when tanks excite with 4 mm and 8 mm excitation amplitudes, the 1:43 scaled tank exerts additional force in comparison with 1: 57 and 1: 86 scaled tanks.

6   Conclusions

The sloshing phenomena and measurement of sloshing force in rectangular tanks excited in harmonic sway are presented by using shake table experiments. Sloshing behaviour is reported for 1:86, 1:57 and 1:43 scaled tanks with three different fill levels. The key conclusions drawn from the experimental study are given below:

• An experimental setup is designed and devised for measuring sloshing force using ballast mass concept.

• It is concluded from the experimental analysis that the critical mode of sloshing is the first mode of sloshing (f = f₁), for all fill depths (25%, 50% and 75%) and scale ratios (1:86, 1:57 and 1:43) considered.

• Normalised maximum free surface (ƞ_max) response and normalised root mean square of sloshing elevation (ƞ_rms) is noticed in the order f = f₁, f = f₃ and f = f₅ i.e., at odd mode sloshing frequencies.

• Maximum energy (spectral energy) is concentrated for 50% fill level irrespective of the scaled tanks and excitation amplitudes. Energy concentration decreases in the order of 1:86, 1:57 & 1:43 for 25% fill level. For 50% and 75% fill levels, energy concentration decreases in the order of 1:57, 1:86 & 1:43 irrespective of excitation amplitudes.

• Sloshing force (F'_max and F'_avg) is high for 1:86 scaled tank at 25% fill level for all excitation amplitudes and frequencies considered.

• When the fill level is more than 50% (h_s/l = 0.325), sloshing force is maximum in the 1: 43 scaled tank than other scaled sloshing tanks irrespective of the excitation frequency and amplitudes.

• From the experimental observations it is concluded that proportionate volume of water and tank size decides the severity of sloshing in partially filled moving containers.

• It is also concluded that the 50% filled condition experiences violent sloshing irrespective of the scale ratio, excitation amplitudes and excitation frequencies.

Random excitations and typical earthquake accelerations shall be tried in future scope of work. Measurement of sloshing force in different tank geometry shall also be tried for different fill levels. A better correlation in estimating the sloshing force can be obtained by conducting experiments on scaled tanks. Effect of porous baffle in reducing sloshing force shall be explored.