Review of Path-following Control Systems for Maritime Autonomous Surface Ships
https://doi.org/10.1007/s11804-023-00338-6
-
Abstract
A review presents the state-of-the-art path-following control systems for maritime autonomous surface ships, where the special focus is placed on the guidance subsystem and control subsystem. The path following control system is one of the basic requirements for autonomous ships since it guarantees that the ship can track the predefined path with small crosstrack errors. The path following problem is firstly defined, and the cross-track error dynamics are derived from the kinematic equations of marine surface ships. The classical guidance laws are introduced, and the governing equations are also presented in this paper. A review of the guidance laws and controllers for the maritime autonomous surface ships has been carried out based on relevant journal and conference papers. Several important properties and characteristics, such as control structure, guidance law, control method, stability, environmental disturbance and vessel dynamics, are defined for the comparative analysis. Finally, the summary and a discussion on the most used technologies for the path following control of marine autonomous surface ships are presented and highlighted.-
Keywords:
- Maritime autonomous surface ship ·
- Path following ·
- Guidance law ·
- Control method ·
- Stability
Article Highlights• The state-of-the-art path-following control systems for maritime au‐ tonomous surface ships are summarised.• The classical controller and guidance laws as well as the governing equations are presented.• Several important properties and characteristics are defined for the comparative analysis. -
1 Introduction
Maritime accidents usually cause a large loss of human lives, in addition to material losses and damage to the environment. As reported in the safety and shipping review (Allianz Global Corporate and Speciality, 2018), more than 75% of maritime accidents are caused by human errors. It is expected that marine autonomous ships will reduce the number of accidents, by removing human fail‐ ures. In addition, increasing the automation in ships will require fewer onboard seafarers, which is a potential solution for the shortage of workers in the maritime industry in the near future. Meanwhile, as reported in Markets & markets (2021), the global autonomous ships market size is projected to reach 14.2 billion dollars by 2030 with a 9.3% growth rate from 2020 to 2030.
Recent years have seen the rapid development of auton‐ omous ship concepts. To illustrate the situation, RollsRoyce (2015) led a 6.6 million dollar project that brought together universities, ship designers and shipyards to make autonomous ships a reality. It paved the way for autono‐ mous ships. In 2016, Norway opened the World's first offi‐ cial test bed, the Trondheim fjord test bed, for autonomous ships (Maritime, 2016). In 2019, the Minister of the Sea of Portugal presented the first edition of the Bluetech Accel‐ erator Ports & Shipping 4.0, in which, smart shipping and autonomous ships are recognized as the major trends. In 2021, the Maritime Safety Committee of IMO has com‐ pleted the analysis of relevant ship safety conventions, and the next steps for regulating Maritime Autonomous Sur‐ face Ships (MASS) will be assessed (IMO). Recently, the autonomous ship prototype, Yara Birkeland, carried out au‐ tonomous shipping tests in Norway.
One of the basic requirements for the marine autono‐ mous surface ship is to follow the predefined path with small cross-track errors. This property is well known as the path following control system, which mainly consists of the guidance subsystem, navigation subsystem and con‐ trol subsystem. This paper focuses on the state-of-the-art of path following control systems in the published papers, more precisely the guidance and control system, for marine autonomous surface ships. To the authors' best knowledge, few papers give an exhaustive review of the guidance laws and control methodology used for the path following con‐ trol of marine autonomous surface ships. Therefore, it is urgent and necessary to investigate the path following the control system of marine autonomous surface ships and pres‐ ent the statistical distribution of the current guidance technol‐ ogies and control methodologies used in the published pa‐ pers.
This paper is organized as follows: section 2 introduces the path following the control problem, where the error dy‐ namics are presented with the kinematics of marine surface ships. In section 3, the classical guidance laws are firstly in‐ troduced and the state-of-the-art of path following control of marine surface ships is reviewed, as well as the control methodologies. At last, a comparative study is carried out using the defined properties and characteristics based on the selected papers. The conclusions are given in section 4.
2 Path following control problem
The motions of the marine surface ships in waves are usually described in 6 degrees of freedom (DOFs), as presented in Figure 1. They are the surge, sway, and yaw motions, which are described in the horizontal plane, and roll, pitch and heave motion, which is de‐ scribed in the vertical plane. For the path following con‐ trol of marine surface ships, the surge, sway and yaw motions or well known as manoeuvring motions, are typ‐ ically considered, where the hydrodynamic coefficients usually can be approximated using constant values (Faltinsen, 1993). Sometimes roll motion is also augmented to the manoeuvring motions considering its coupling ef‐ fect on yaw and sway motion (Fossen, 2011; Sutulo and Guedes Soares, 2011).
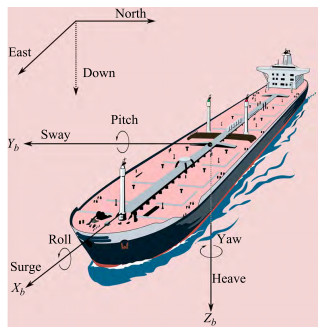 Figure 1 The motions of marine surface ships in waves (Fossen, 2011)
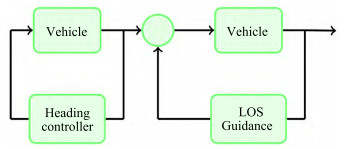
Figure 1 The motions of marine surface ships in waves (Fossen, 2011)A typical autonomous path following system usually consists of the three basic subsystems, guidance, naviga‐ tion, and control system, which are also well known as the GNC system, as presented in Figure 2. The main goal of the GNC system is to control the movement of autonomous ships according to the specified task com‐ mands. The task of the navigation system is to determine the state vectors, including the location and orientation, of the au‐ tonomous ships from the onboard sensors. The guidance system generated the control command according to the ship's state vectors at a given time and the requirement of the task. The control system will execute the guidance commands by manipulating the thruster forces and rud‐ der, to achieve the task.
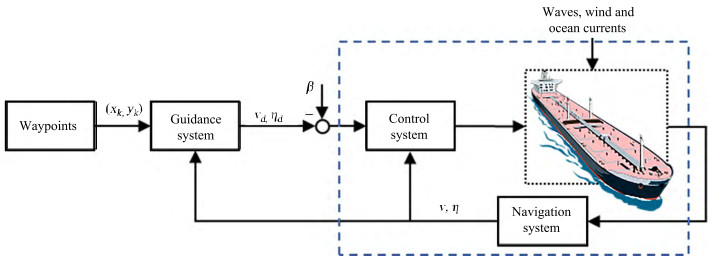 Figure 2 The guidance, navigation, and control system (GNC) for maritime autonomous surface ships (MASS) (Fossen, 2011)
Figure 2 The guidance, navigation, and control system (GNC) for maritime autonomous surface ships (MASS) (Fossen, 2011)2.1 Cross-track error of path following control
The path following control problem of maritime auton‐ omous surface ships is defined by assuming that the pre‐ defined path is described by a curved line in the three-di‐ mensional space, $ \boldsymbol{p}_d(\theta)=\left[x_d(\theta), y_d(\theta), z_d(\theta)\right]^{\mathrm{T}}$ and having the control objective to design a control law for the ships that ensures convergence of the ship's position $\boldsymbol{p}(t)=[x(t), y(t), z(t)]^{\mathrm{T}} $ to the path pd (θ).
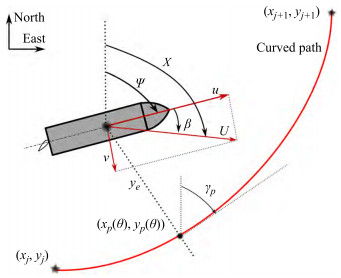
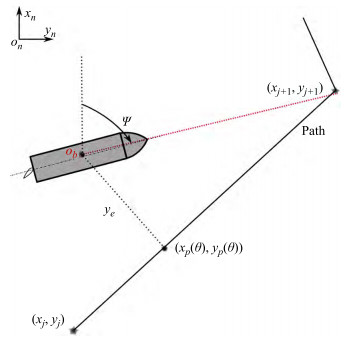
For typical marine surface ships, it is usually assumed that a marine vessel is assigned to follow a two-dimension‐ al parametrized curved path, as presented in Figure 3. Without loss of generality, the curved path is employed for the demonstration of the cross-track error of the path fol‐ lowing control, since the straight-line path can be consid‐ ered as the path with a constant path tangential angle, γp. As presented in Figure 3, a curved path is predefined as (xp(θ), yp(θ)), where θ is a variable, and it is assumed to connect the way-points (xj, yj) for j = 1, ⋯N.
To analyse the motion of the ship in the horizontal plane, three geographic reference frames need to be de‐ fined first. The north-east-down (NED) coordinate sys‐ tem { n } = (xn, yn, zn) with the origin point, on, is defined as the tangent plane on the surface of the earth (Fossen, 2011). The x-axis points toward to true north, the y-axis points toward the east and the z-axis points downwards. The body-fixed coordinate system { b } = (xb, yb, zb) with the origin point, on, is located on the ship and usually coincides with the centre point of the ship. It is moving with the ship and satisfies the righthand rule, where the x-axis points towards the ship's bow, as described in Figure 3. The last reference frame that needs to be defined is the path-tangential reference frame { p } = (xp, yp, zp), which is located on the pre‐ defined path, and it is rotated by an angle γp(θ) from the north-east-down (NED) reference frame using the rota‐ tion matrix (Fossen and Lekkas, 2015):
$$ \boldsymbol{R}\left(\gamma_p(\theta)\right)=\left[\begin{array}{cc} \cos \left(\gamma_p(\theta)\right) & -\sin \left(\gamma_p(\theta)\right) \\ \sin \left(\gamma_p(\theta)\right) & \cos \left(\gamma_p(\theta)\right) \end{array}\right] \in S O(2) $$ (1) where the path tangential angle is given as, γp (θ) = atan2 (x'p (θ), y'p (θ)).
Then, the distance from the ship location (x, y) to the predefined path can be calculated:
$$ \left[\begin{array}{l} x_e \\ y_e \end{array}\right]=\boldsymbol{R}\left(\gamma_p(\theta)\right)\left[\begin{array}{l} x-x_p(\theta) \\ y-y_p(\theta) \end{array}\right] $$ (2) where, the ye is the cross-track error and the xe is the qa‐ long-track error equals zero by choosing the origin op of the path-tangential reference frame to coincide with the vertical projection point of the ship on the path (xp(θ), yp(θ)).
By expanding equation (2), the cross-track error ye is defined as:
$$ y_e=-\left(x-x_p(\theta)\right) \sin \left(\gamma_p(\theta)\right)+\left(y-y_p(\theta)\right) \cos \left(\gamma_p(\theta)\right) $$ (3) Finally, the control objective for the path-following of marine surface ships is defined as:
$$ \mathop {\lim }\limits_{t \to \infty } {y_e}(t) = 0 $$ (4) 2.2 Kinematic equations of path following control
Marine surface ships moving in the horizontal plane, as described in Figure 3, are considered rigid bodies, and the kinematic equations are given as:
$$ \begin{aligned} & \dot{x}=u \cos (\psi)-v \sin (\psi) \\ & \dot{y}=u \sin (\psi)+v \cos (\psi) \\ & \dot{\psi}=r \end{aligned} $$ (5) where, the surge and sway velocity are defined as u and v, respectively. The ψ, r are the yaw (heading) angle and yaw rate, which can be measured using an inertial measurement unit (IMU).
Taking the derivative of Eq. (3) with respect to time and substituting (5) into the results, gives:
$$ \dot{y}_e=U \sin \left(\psi-\gamma_p(\theta)+\beta\right) $$ (6) where, the ground speed of the ship, U, is defined as U =$\sqrt{u^2+v^2} $. The phase angle, β = atan2 (v, u) is the drift angle, and it is the difference in heading angle ψ and course angle χ.
$$ \chi=\psi+\beta $$ (7) The dynamic equation of the cross-track error, ye, can be further simplified as:
$$ \dot{y}_e=U \sin \left(\chi-\gamma_p(\theta)\right) $$ (8) 3 Path following control in autonomous ships
In this section, the path following control state of art for maritime autonomous surface ships is reviewed. The guidance laws and control methods, which are widely used for the path-following control of marine surface ships are described in this section.
3.1 Guidance system
The guidance system can be considered as the command generator for the path following control of autonomous ships. As described in Figure 2, the input of the guidance system is the predefined path and real-time position and state of the ship. The output is the desired speed and head‐ ing angle for the marine surface ships. To achieve the con‐ trol objective, the guidance law must ensure that the crosstrack error will converge to zero in finite time by steering the rudder and rpm of the propeller, as indicated in Eq (4). As it is well known that the sway dynamics of the marine surface ship are underactuated, therefore, the guidance laws need to be designed considering the underactuated sway dynamic.
The most widely used guidance laws for path following control are usually described as geometric techniques, such as line of sight (LOS) guidance law, pure pursuit (PP), and constant bearing (CB). The line of sight guidance law gives the desired heading angle by imitating an ex‐ perienced captain steering the ship towards the desired point, which is the virtual target point (VTP) located on the path. It is classified as a three-point geometric meth‐ od since it involves the position of the ship, the refer‐ ence point and the virtual target point (Fossen, 2011). The pure pursuit guidance law is a simple method and it only involves two points, the position of the ship and the target. The constant bearing is also a two-point guid‐ ance scheme, where the target velocity is considered.
3.1.1 Line of sight guidance law
3.1.1.1 Classical LOS
In the path following control of marine surface ships, the LOS guidance law and its modified version are most widely used considering the simple structure and easy implementation in the ship control systems (Fossen et al., 2003; Moreira et al. 2007). In Figure 4, the classical LOS and look ahead based LOS are presented. For the classical LOS guidance law, the LOS vector needs to be defined first, and usually equal to the nLpp ahead of the ship. As indicated in Figure 4(a), the LOS vector is the vector from the ship position to the virtual target point on the predefined path. Thus, the desired heading angle can be calculated:
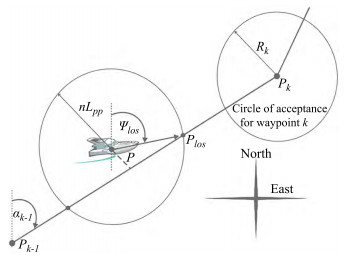 Figure 4 The classical line-of-sight guidance law (Fossen et al., 2003)
Figure 4 The classical line-of-sight guidance law (Fossen et al., 2003)$$ \begin{gathered} \psi_d(t)=\operatorname{atan} 2\left(y_{l o s}-y(t), x_{l o s}-x(t)\right) \\ \left(y_{\text {los }}-y(t)\right)^2+\left(x_{l o s}-x(t)\right)^2=\left(n L_{p p}\right)^2 \end{gathered} $$ (9) Fossen et al., (2003) employed the nonlinear controller for the path following control of a marine craft, and the underactuated control problem was considered, where on‐ ly two controls were used for the 3 DOF motions of the marine surface craft. The control laws for surge and yaw motion were derived using the backstepping control technology and the equilibrium point was proven to be uni‐ formly globally asymptotically stable (UGAS) using the Lyapunov method. The experimental ship model test was carried out for validation.
Fredriksen and Pettersen (2006) studied the way-point manoeuvring of marine surface ships using only two control inputs in surge and yaw motion. The LOS guidance law was used for generating the heading commands. The globally κ exponentially stability of the control law was proved using cascaded control theory, and experimental results using the ship model were presented to validate the proposed control law.
Mu et al., (2018) proposed a fuzzy-based adaptive LOS guidance law for the path-following control of un‐ manned surface vehicles, where the backstepping control technology and neural networks were used for the con‐ trol design. The closed-loop control system was proven to be uniformly ultimately bounded using the Lyapunov stability theory.
An adaptive LOS guidance law and fuzzy heading con‐ trol were used (Niu et al., 2019), for the waypoints-based path following control of unmanned surface vehicles. The experimental tests were carried out to testify to the effectiveness of the proposed control system.
3.1.1.2 Look ahead LOS
A modified version of LOS, look ahead based LOS (Fossen, 2011; Fossen et al., 2015), was proposed for the calculation of the LOS vector, where the look-ahead distance needs to be defined, as described in Figure 5. The heading command is calculated using
 Figure 5 The look-ahead based LOS guidance law (Fossen and Lekkas, 2015)
Figure 5 The look-ahead based LOS guidance law (Fossen and Lekkas, 2015)$$ \psi_d(t)=-\tan ^{-1}\left(\frac{y_e}{\Delta}\right), \quad \Delta>0 $$ (10) Moreira et al., (2007) proposed a dynamic look-ahead LOS guidance for the path following control of autono‐ mous marine surface ships. A new method was proposed for the calculation of the LOS vector to improve the con‐ vergence. The proposed method was implemented in the model of the "Esso Osaka" tank and simulations were presented for showing the effectiveness of the proposed system. A similar study was later performed by (Lekkas and Fossen, 2012), where a time-varying equation was used for the look-ahead distance calculation for the LOS guidance law. A nonlinear sliding mode controller was de‐ signed to control the yaw motion and the coupled guid‐ ance and control system was proved to be globally κ-expo‐ nentially stable. Simulation tests were carried out for the validation of the proposed guidance law.
Fossen and Pettersen, (2014) provide a uniform semiglobal exponential stability (USGES) proof for the path fol‐ lowing control of underactuated marine surface ships using the proportional LOS guidance law. The author extends the previous results, which only guarantee the global κ expo‐ nential stability, by using the cascaded stability theory. Though the USGES is slightly weaker than global exponen‐ tial stability, it is still important for the autonomous system, since it guarantees the robustness of the autonomous system in the presentence of environmental disturbance.
Liu et al.(2017, 2016a) presented an extended state ob‐ server (ESO) based LOS guidance law for the path follow‐ ing control of marine surface ships, where a reduced-order ESO was employed to compensate for the sideslip angle due to environmental disturbance. Both simulation and ex‐ perimental tests were presented in this paper. Further work can be found in (Liu et al., 2016b).
Oh and Sun (2010) used a model predictive control (MPC) for the way-point tracking control of an underactu‐ ated marine surface ship, where the input constraints were considered. LOS guidance law was incorporated into the MPC design, and the performance was improved.
Liu et al. (2018) used a model predictive control method and LOS guidance law for the path following control of AS‐ Vs, where the nonlinear Nomoto model with disturbances was employed for the control design. Simulations were car‐ ried out to show the effectiveness of the proposed method.
Moe et al., (2016a) proposed a guidance and control sys‐ tem for the path following control of autonomous surface vessels using absolute velocity measurements. The proposed system does not need to measure the relative velocities using expensive sensors. The cross-track error dynamics of the closed-loop were proved to be UGAS and USGES, and the results were also verified using the simulations. Further work can be found in (Moe and Pettersen, 2017).
Fossen, (2022) presented the course autopilot design for the path following and an extended Kalman filter (EKF) was used to estimate the course over ground (COG) and speed over ground (SOG) efficiently from global naviga‐ tion satellite systems. The path following tests using LOS guidance law was carried out using a high-fidelity model of a MARINER class cargo ship.
3.1.1.3 Integral LOS
To handle the drift angle due to environmental disturbance, another well-known version of LOS, integral LOS(Børhaug et al., 2011, 2008; Lekkas and Fossen, 2014), was proposed by extending the classical LOS guidance with integral action:
$$ \begin{aligned} & \psi_d(t)=-\tan ^{-1}\left(\frac{y_e+\sigma y_{\mathrm{int}}}{\Delta}\right), \Delta>0 \\ & \dot{y}_{\mathrm{int}}=\frac{\Delta y}{\left(y_e+\sigma y_{\mathrm{int}}\right)^2+\Delta^2} \end{aligned} $$ (11) where, σ is a positive design parameter, and it is an inte‐ gral gain.
Wan et al. (2020), designed the look-ahead distance as a function of the USV's cruising speed and the cross-track‐ ing error for the integral LOS guidance law.
The global asymptotic stability of the proposed control system was proved, and the simulations were carried out to demonstrate its effectiveness.
An integral LOS guidance law was proposed by (Caharija et al., 2012), for the path following control of marine surface vessels, where the integral action was used to com‐ pensate for the slow varying drift angle due to the environ‐ mental disturbance. The closed-loop uniform local expo‐ nential stability was proved, and simulations were carried out to support the theoretical results. The theoretical as‐ pects of the integral LOS guidance law can also be found in (Caharija et al., 2014). An extensive analysis of the inte‐ gral line-of-sight (ILOS) guidance law for path-following control of autonomous surface vessels and underwater ves‐ sels were presented, and both simulation and experiments were used to validate the effectiveness of the proposed sys‐ tem (Caharija et al., 2016).
Fossen et al. (2015), proposed a nonlinear adaptive con‐ troller for the path following control of underactuated ma‐ rine ships by compensating the drift forces due to the envi‐ ronmental disturbance, such as wind, waves and currents. The results were also extended for the path following Du‐ bin's path. The equilibrium points of the proposed sys‐ tem were proven to be USGES, and the simulations show that the cross-track error and the estimated sideslip angle converge exponentially.
A direct and an indirect nonlinear adaptive controller was proposed by Fossen and Lekkas (2015), for the path follow‐ ing control of marine surface ships using LOS guidance law. In this paper, they proposed a disturbance observer to compensate for the drift forces due to ocean currents and proved that the proposed method is globally κ exponentially stable. The simulations for the path following control of ma‐ rine surface vessels were carried out and the case for auton‐ omous underwater vehicles was also validated.
Wiig et al. (2015)presented the uniform semi-global ex‐ ponential stability proof of the integral LOS guidance law for path following control of underactuated marine ves‐ sels. Both the kinematics and dynamics of the system were taken into account, and the simulation results were present‐ ed to support the theoretical analysis.
Su et al. (2021) proposed an adaptive integral LOS guid‐ ance law for the path following control of unmanned sur‐ face vehicles with uncertainties. Three adaptive variables were constructed to eliminate the cross-track errors. The designed guidance subsystem is proved to be uniformly and ultimately bounded by the Lyapunov method.
3.1.1.4 Other works
To avoid collision with the obstacles, Moe and Pettersen, (2016) proposed set-based LOS guidance law for the path following and collision avoidance of autonomous surface vessels. The proposed guidance laws were designed to assure collision avoidance while abiding by the International Regulations for Preventing Collisions at Sea (COLREGs).
Yu et al. (2018) proposed a finite-time predictor LOS guidance law and adaptive neural network controller for the path following of unmanned surface vessels. In this pa‐ per, the author presented the theoretical analysis of the pro‐ posed system, and semi-globally uniformly ultimately bounded was proven by using the Lyapunov method. Rout et al., 2020) also used the adaptive neural network (NN) controller for the path following control of underactuated marine vehicles, where the barrier Lyapunov function (BLF) was used to deal with the system constraints and disturbance. The uniform ultimate boundedness of the closed-loop system was proved and both simulation and experimental tests were carried out for validation.
Miao et al. (2017) used the reduced-order linear extend‐ ed state observer (LESOs) method to estimate the un‐ known sideslip angle. A filtered extended state observer (FESO) was used to estimate the time-varying sideslip an‐ gle(Li et al., 2021a, 2019), where an adaptive fuzzy con‐ troller was used for the heading control of the unmanned surface vehicles. A network-based path-tracking control of an underactuated unmanned surface vehicle was proposed by (Wu et al., 2021), and an extended state observer (ESO) was employed to estimate the unknown disturbances due to the model uncertainties and environmental disturbances. Jiang et al., (2020), used the extended state observer (ESO) to estimate unknown relative velocities together with the ocean currents in real-time.
Wang et al. (2019a) proposed a novel nonlinear adaptive path following controller for the path following of amphibious hovercrafts, where a bounded-gain-forgetting (BGF) adap‐ tive estimator was used to compensate for the drift forces due to the environmental disturbance. A high-gain observ‐ er-based line-of-sight guidance law can be found in (Wang et al., 2019d)
Wang et al., (2019b) proposed a fuzzy observer-based adaptive path following control for an underactuated sur‐ face vehicle (USV). The control laws ensure that the pro‐ posed system was globally asymptotically stable. Simula‐ tion tests were carried out using the proposed method. Similar works can be found in(Wang et al., 2017, 2016).
Right now, the LOS guidance law has been thoroughly studied and well developed, as discussed above. Many re‐ vised versions are proposed to overcome the drawbacks of the classical LOS, for instance, the adaptive LOS, Propor‐ tional LOS, and integral LOS. The main objective of LOS guidance law is to provide the desired heading/course angle for the autonomous ships according to the geometry of posi‐ tions, therefore, it did not account for other information, such as obstacles, collision rules and shipping tasks. In the future, for instance, the LOS guidance law can be extended by considering collision avoidance and COLREGs, as dis‐ cussed in Moe and Pettersen, (2016), however, the stability proof of the whole guidance and control system is a chal‐ lenging problem. Beside the above works, Gu et al., (2022a, 2022b) gave a comprehensive summary of LOS guidance law, disturbance observers and extended state observers for path following of both surface and underwater vehicles.
3.1.2 Pure pursuit guidance law
The pure pursuit (PP) guidance law was typically used for air-to-surface missiles and UAVs (Yamasaki et al., 2009), where the chased targets are usually static or with slow speed. As illustrated in Figure 6, the PP guidance law is the two-point guidance scheme, where only the own ship and the target are considered. In the waypoints following control, the waypoint is usually chosen as the target. The ship aligns the forward speed, vna, along the vector between the ship and the waypoint by choosing the desired velocity as (Breivik and Fossen, 2009):
$$ \boldsymbol{v}_d^n=-\kappa \frac{\boldsymbol{p}^n}{\left\|\boldsymbol{p}^n\right\|} $$ (12) where the κ is the positive constant. As can be observed, the PP guidance law will control ship travel towards the waypoints by neglecting the cross-track error, ye. The ad‐ vantage is that the resulted trajectory is short compared with the LOS guidance law. Papoulias (1993) presented a theoretical analysis of the nonlinear dynamic phenomena when using the pure pursuit guidance for marine vehicles. Xu and Guedes(2018, 2015) proposed an opti‐ mized energy-efficient path-following method by combing the PP and LOS guidance law for autonomous ships. A global optimization algorithm was used to search the regularization factors, which play the trade-off between the total cross-track errors and total control energy.
3.1.3 Constant bearing guidance law
The constant bearing (CB) guidance law is also a twopoint guidance method (Fossen, 2011). The geometry of CB guidance law for tracking a moving ship is presented in Figure 7. It can be assumed to be an extended version of PP guidance law by considering the velocity of the target, vna. CB guidance law is typically used for air-to-air mis‐ siles. Meanwhile, it was also used for collision avoidance at sea for marine vessels, where the own ship needs to steer away from a situation where another ship approaches at a constant bearing. The desired velocity is calculated us‐ ing the following equation,
$$ \begin{aligned} & \boldsymbol{v}_d^n=\boldsymbol{v}_t^n+\boldsymbol{v}_a^n \\ & \boldsymbol{v}_a^n=-\kappa \frac{\boldsymbol{p}^n}{\left\|\boldsymbol{p}^n\right\|} \end{aligned} $$ (13) 3.1.4 Vector field guidance law
The vector field (VF) guidance law is widely used for the path following control of unmanned aerial vehicles (UAVs) (Cho et al., 2015; Lim et al., 2014; Nelson et al., 2007, 2006; Yamasaki et al., 2009; Yanushevsky, 2011). Unlike the guidance law mentioned above, the virtual target point (or LOS vector point) does not need to be defined in the vector field guidance law. The main idea behind VF guidance law is to generate vectors around the predefined path using the mathematical equation, as illus‐ trated in Figure 8. In this Figure, the vectors indicate the desired heading angle of a ship in the position of the ar‐ row. When the ship tracks each vector, it will converge to the desired path eventually.
Nelson et al., (2007, 2006) developed the vector field guidance law for the path following control of air vehicles, where desired course angles are generated using the pre‐ defined function, as given follows:
$$ \chi_d=\chi_p-\chi^{\infty} \frac{2}{\pi} \tan ^{-1}\left(K_p y_e^p\right) $$ (14) where, the χp is the path tangent angle, Kp influences the rate of the transition from χ ∞ to zero. Inspired by the above appli‐ cation, Xu and Guedes Soares, (2016a) proposed the vector field guidance law for the path following control of underac‐ tuated marine surface ships. To improve the robust and con‐ verge rate, the transition region was defined along the pre‐ defined path. The vector field guidance law was defined as:
$$ \chi_d=\left\{\begin{array}{cc} \chi_p-\rho \chi^e, & \text { where }\left|y_e\right|>\tau \\ \chi_p-\rho\left(\frac{\left|y_e\right|}{\tau}\right)^k \chi^e, & \text { where }\left|y_e\right| \leqslant \tau \end{array}\right. $$ (15) where the τ is the distance between the path and the edge of the transition region. χ e is the entering angle, which defined the desired course angle of the ship enter‐ ing the transition region. The Lyapunov method was used to prove that the proposed guidance law is global asymp‐ totic stable. Further work and extended versions of the vec‐ tor field guidance law can also be found in Xu and Guedes Soares(2020, 2018, 2016b, 2015).
Caharija et al. (2015) carried out a comparative study for the two popular guidance laws for straight-line path following purposes of underactuated large AUV vehicles: the integral LOS and the vector field guidance law pro‐ posed by Nelson et al.(2007, 2006). The results show that both guidance laws have a good path following control performance, with the VF guidance law performing slight‐ ly better. However, the significant chattering of the hori‐ zontal rudders can be observed, while the ILOS gives a smooth servo command.
To obtain a strong stability property, Xu et al., (2020a) proposed a time-varying vector field guidance law for both straight path and curved path following control of underac‐ tuated marine surface ships. The guidance law is defined as:
$$ \chi_d=\gamma_p-\operatorname{sgn}\left(y_e\right) \tan ^{-1}\left(\left(\frac{\left|y_e\right|}{\Delta}\right)^{\theta\left(t, y_e\right)}\right) $$ (16) where, the θ(t, ye) is a time-varying function, which con‐ trols the converge rate and ∆ > 0 is a pre-defined constant. The equilibrium point of the guidance and control system is uniform semi-global exponential stable (USGES) using the Lyapunov method and cascaded system theory. The simulation results can be found in Figure 9. Further work can be found in(Hinostroza et al., 2021, 2019; Xu et al., 2021a, 2021b).
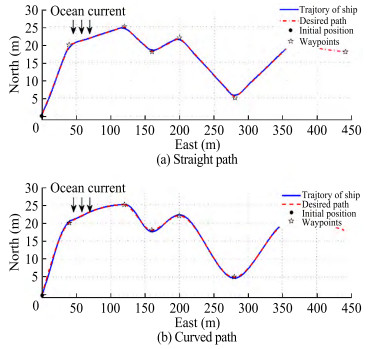 Figure 9 Path following control using the time-varying vector field guidance law (Xu et al., 2020a)
Figure 9 Path following control using the time-varying vector field guidance law (Xu et al., 2020a)From the above discussion, the VF guidance law is more flexible, since only the mathematical equation for generating vectors needs to be defined without considering the physical definition of each parameter. However, LOS guidance laws are geometric techniques, and their parame‐ ters have a physical definition. For instance, The VF guid‐ ance law can be easily extended for collision avoidance by adding one repelling vector field around the obstacles, as discussed in (Xu et al., 2021a).
3.2 Motion control system
The motion control system for marine vessels is an ac‐ tive research field. Many pioneering works and papers have been published in conferences and journals. Roberts, (2008) provide a review of the early developments of marine control systems and discussed the key developments in ship autopilot design. The classical control methods are usually designed based on the knowledge of the plant mod‐ el, for example, Nomoto model (Nomoto et al., 1957; Xu et al., 2020b), Abkowitz models (Abkowitz, 1980; Xu et al., 2018), just to name a few. Recently, model-free datadriven control methodologies were used for the motion control system of marine ships. Its application in the dy‐ namic positioning of marine ships can be found in (Hassani et al., 2018). Considering the fast development of au‐ tonomous ships in recent years, this paper will briefly re‐ view the motion control methodologies, which were used for the path following of underactuated marine ships.
As discussed above, the motion control system works to‐ gether with the guidance system to achieve accurately pathfollowing control of autonomous ships, where the guidance system works like the experienced helmsman to give the de‐ sired ship's speed and the rudder command, and the motion control system will execute the command by changing the speed and heading angle. Therefore, the two systems are coupled together, and form the cascade structure, as dis‐ cussed in (Fossen and Pettersen, 2014; Xu et al., 2020a).
The most popular control method for marine ships is the PID (proportional integral derivative) controller. It is a typi‐ cally model-based linear control method, and the simplified steering model, such as the Nomoto model, is usually em‐ ployed for the control design. However, it is also possible to generalize to the nonlinear systems by using the nonlinear manoeuvring models. The application for the path following control for marine surface ships can be found in papers (Caharija et al., 2016, 2014; Fossen, 2022; Fossen et al., 2015; Fredriksen and Pettersen, 2006; Jiang et al., 2020; Liu et al., 2017, 2016a; Moe and Pettersen, 2017, 2016; Moreira et al., 2007). The detailed design procedure and parameters tuning method will be omitted since they can be easily found in the control books.
Feedback linearization is one of the well-known meth‐ odologies that was used to control nonlinear systems. The main idea is to nonlinear system dynamics into a linear system (Freund, 1973), then the classical linear control technologies, such as pole-placement, can be used to design the control laws. The feedback lineariza‐ tion is also capable of the path following control of marine surface ships, the related works can be found in (Caharija et al., 2012; Moreira et al., 2007; Skjetne et al., 2011; Xu and Guedes Soares, 2016a, 2016b, 2018, , 2020, 2015), just to name a few.
The backstepping control technology was used to design a stable control law for the nonlinear systems by using the con‐ trol Lyapunov functions (CLF) (Kokotović, 1992). The main idea behind the backstepping control method is to replace the control design problem using a sequence of sub-prob‐ lems on lower-order systems, where the virtual control input is defined to obtain the control laws for each sub-system us‐ ing control Lyapunov functions. The application of the back‐ stepping control method for the path following control can be found in(Do et al., 2004, 2002; Fossen et al., 2003; Li et al., 2021b; Mu et al., 2018; Nie and Lin, 2019; Su et al., 2021).
In addition to the control methods mentioned above, there are also many popular control methods for the path following control of marine surface ships, such as the sliding model control (Fossen and Lekkas, 2015; Lekkas and Fossen, 2012; Li et al., 2021a, 2021b, 2019; Moe et al., 2016b), the model prediction control (Liu et al., 2018; Oh and Sun, 2010), the L1 adaptive control method (Breu and Fossen, 2011; Ren et al., 2018; Svendsen et al., 2012; Xu et al., 2021b), the dynamic surface control(Huang et al., 2021a, 2021c; Liu et al., 2016c, 2016b; Wan et al., 2020) and the fuzzy method (Li et al., 2021a; Wang et al., 2019b). Recently, the machine learning methods, such as neural networks, are also employed for the marine control system, as published in(Huang et al., 2021a, 2021b; Liu et al., 2016d; Mu et al., 2018; Rout et al., 2020; Y. Wang et al., 2019b; Wu et al., 2021).
3.3 Comparison
In this part, the comparative study of the path follow‐ ing control system for marine surface ships will be pre‐ sented. There are 80 papers published in journals and in‐ ternational conferences, summarized in Table 1, using the different properties, such as control structure, results (i. e., simulation or experiment), guidance law, control‐ ler, environmental disturbance, vessel dynamics, stabili‐ ty properties, and underactuated control problem.
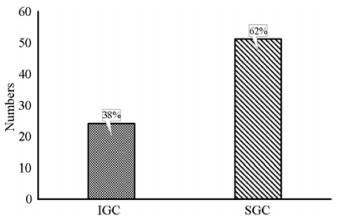
Table 1 Comparison of the path following control system for marine surface shipNo. References Structure Results Guidance law Environmenta l disturbance Controller Vessel Dynamics Stability Under- actuated 1 (Do et al., 2002) IGC Simulation - No Backstepping control Yes Global asymptotic stability Yes 2 (Fossen et al., 2003) SGC Experiment LOS No Backstepping control Yes Uniform global asymptotic stability Yes 3 (Do et al., 2004) IGC Experiment - Yes Backstepping control Yes Global asymptotic stability Yes 4 (Fredriksen and Pettersen, 2006) IGC Experiment LOS Yes Linear control method Yes Global k -exponential stability Yes 5 (Moreira et al., 2007) SGC Simulation Adaptive LOS Yes PID Yes - No 6 (Børhaug et al., 2008) IGC - Integral LOS Yes Adaptive controllers Yes Global asymptotic stability Yes 7 (Pereira et al., 2008) SGC Experiment LOS Yes PD No - No 8 (Oh and Sun, 2010) SGC Simulations LOS No Model predictive control Yes - Yes 9 (Børhaug et al., 2011) IGC Experiment LOS Yes Feedback linearizing control Yes Uniform Global asymptotic stability Yes 10 (Skjetne et al., 2011) IGC Simulation LOS No Feedback linearizing control Yes Global asymptotic stability Yes 11 (Lekkas and Fossen, 2012) IGC Simulation LOS No Sliding mode control Yes Global k -exponential stability Yes 12 (Caharija et al., 2012) IGC Simulation Integral LOS Yes Feedback linearizing control Yes Uniform local exponential stability Yes 13 (Svendsen et al., 2012) - Simulation - Yes L1 adaptive control No - No 14 (Caharija et al., 2014) IGC Simulation Integral LOS Yes Feedback linearizing control Yes Uniform local exponential stability Yes 15 (Fossen and Pettersen, 2014) IGC - Proportional LOS No Yes Uniform semiglobal exponential stability Yes 16 (Lekkas and Fossen, 2014) IGC Simulation Integral LOS Yes Sliding mode control Yes Global k -exponential stability Yes 17 (Fossen and Lekkas, 2015) IGC Simulation Integral LOS Yes Sliding mode control Yes Global k -exponential stability Yes 18 (Fossen et al., 2015) IGC Simulation Integral LOS Yes PID Yes Uniform semiglobal exponential stability Yes 19 (Wiig et al., 2015) IGC Simulation Integral LOS Yes Feedback linearizing controllers Yes Uniform semiglobal exponential stability Yes 20 (Xu and Guedes Soares, 2015) SGC Simulation LOS; PP+ LOS No PID Yes Global asymptotic stability Yes 21 (Caharija et al., 2015) - Experiment LOS; VF Yes PID Yes Global asymptotic stability Yes 22 (Caharija et al., 2016) IGC Simulation; experimenta l Integral LOS Yes Feedback linearizing PD controller Yes Globally asymptotically stable; Uniformly local exponential stable Yes 23 (Moe and Pettersen, 2016) SGC Simulation Set-based LOS No Adaptive feedback linearizing control Yes Uniform global asymptotic stability Yes 24 (Xu and Guedes Soares, 2016a) SGC Simulation VF Yes PID Yes Global asymptotic stability Yes 25 (Niu et al., 2016) SGC Simulation PP+LOS VF Yes PD Yes - No 26 (Xu and Guedes Soares, 2016b) SGC Simulation LOS; VF Yes PID Yes Global asymptotic stability Yes 27 (Liu et al., 2016a) SGC Simulation LOS Yes PID Yes Input-to-state stability Yes 28 (Liu et al., 2016b) SGC Simulation Integral LOS Yes Dynamic surface control Yes Uniformly ultimately bounded Yes 29 (Liu et al., 2016c) SGC Simulation Integral LOS Yes Dynamic surface control Yes Uniformly ultimately bounded Yes 30 (Woo and Kim, 2016) SGC Simulation VF No - No - Yes 31 (Wang et al., 2016) SGC Simulation - Yes Adaptive robust control Yes Finite-time stability No 32 (Shojaei and Dolatshahi, 2017) SGC Simulation LOS Yes Dynamic surface control Neural networks No Uniformly ultimately bounded Yes 33 (Miao et al., 2017) SGC Simulation LOS Yes Backstepping control Yes Asymptotically stability Yes 34 (Liu et al., 2017) SGC Simulation; experimenta l LOS Yes PID Yes Input-to-state stability Yes 35 (Moe and Pettersen, 2017) SGC Simulation Set-based LOS Yes Feedback linearizing control Yes Uniform global asymptotic stability Yes 36 (Wang et al., 2017) SGC Simulation LOS Yes Backstepping control Yes Asymptotically stability Yes 37 (Liu et al., 2018) - Simulation Adaptive LOS Yes Model predictive control Yes - Yes 38 (Mu et al., 2018) SGC Simulation Adaptive LOS Yes Backstepping method Yes Uniformly ultimately bounded Yes 39 (Yu et al., 2018) SGC Simulation LOS No Neural network control No Uniformly ultimately bounded No 40 (Xu and Guedes Soares, 2018) SGC Simulation LOS; PP+ LOS No PID Yes Global asymptotic stability Yes 41 (Mousazadeh et al., 2018) - Experiment Potential field Yes Feedback linearizing control Yes - No 42 (Huang et al., 2018) IGC Simulation LOS Yes Sliding mode control Yes Uniform semiglobal exponential stability Yes 43 (Chen et al., 2018) IGC Simulation Integral LOS Yes Feedback linearizing control Yes Uniform semiglobal exponential stability Yes 44 (Nie and Lin, 2019) SGC Simulation Integral LOS Yes Backstepping control Yes Uniformly ultimately bounded Yes 45 (Li et al., 2019) SGC Simulation LOS Yes Fuzzy logic control No Uniformly ultimately bounded Yes 46 (Niu et al., 2019) - Experiment LOS No Fuzzy logic control No - No 47 (Wang et al., 2019b) SGC Simulation LOS Yes Fuzzy logic control No Global asymptotic stability Yes 48 (Wang et al., 2019c) SGC Simulation LOS Yes PID Yes Input-to-state stability No 49 (Wang et al., 2019d) SGC Simulation LOS Yes Adaptive neural network control No Uniformly ultimately bounded Yes 50 (Xu et al., 2019) IGC Simulation VF Yes Sliding mode control Yes Uniform semiglobal exponential stability Yes 51 (Wang et al., 2019a) SGC Simulation - Yes Sliding mode control Yes Finite-time stability Yes 52 (Hinostroza et al., 2019) SGC Simulation VF Yes PID Yes - Yes 53 (Sans-Muntadas et al., 2019) IGC Experiment - Yes PID No asymptotically stability No 54 (Weng et al., 2020) SGC Simulation LOS Yes Sliding mode control Yes Ultimately bounded No 55 (Bejarano and N-Yo, 2020) SGC Simulation LOS Yes Backstepping control Yes Stable Yes 56 (Xu et al., 2020a) IGC Simulation VF Yes Sliding mode control Yes Uniform semiglobal exponential stability Yes 57 (Wan et al., 2020) SGC Simulation Integral LOS No Dynamic surface control Yes Uniformly asymptotically stability Yes 58 (Rout et al., 2020) SGC Simulation Experiment Modified LOS Yes Adaptive neural network controller Yes Uniformly ultimately bounded Yes 59 (Jiang et al., 2020) SGC Simulation Experiment LOS Yes PID Yes Global asymptotic stability Yes 60 (Xu and Guedes Soares, 2020) SGC Simulation LOS; VF Yes PID Yes Global asymptotic stability Yes 61 (Nie and Lin, 2020) SGC Simulation LOS Yes Fuzzy logic control No uniform ultimate bounded No 62 (Wen et al., 2020) SGC Experiment VF Yes Feedback control Yes Semi-global exponential stable Yes 63 (Wu et al., 2021) SGC Experiment LOS Yes Neural network controller No Input-to-state stability Yes 64 (Su et al., 2021) SGC Simulation LOS NO Backstepping method Yes Uniformly ultimately bounded No 65 (Xu et al., 2021a) IGC Simulation Experiment VF Yes Sliding mode control Yes Uniform semiglobal exponential stability Yes 66 (Liu et al., 2021) SGC Experiment LOS Yes PID No - No 67 (Tian et al., 2021) SGC Simulation LOS Yes Model predictive control Yes Stable No 68 (Xu et al., 2021b) IGC Simulation VF Yes L1 adaptive control Yes Uniform semiglobal exponential stability Yes 69 (Hinostroza et al., 2021) SGC Experiment LOS Yes PID Yes - Yes 70 (Li et al., 2021a) SGC Simulation Integral LOS Yes Sliding mode control Yes Uniformly ultimately bounded Yes 71 (Li et al., 2021b) IGC Simulation LOS Yes Backstepping sliding mode control Yes Uniformly global finitetime stability No 72 (Min and Zhang, 2021) IGC Simulation LOS Yes Fuzzy logic control Yes Uniformly ultimately bounded Yes 73 (Abrougui et al., 2021) SGC Experiment - Yes Sliding mode control No - Yes 74 (Zhang et al., 2021) SGC Simulation LOS No Feedback control Yes Global asymptotic stability No 75 (Fossen, 2022) SGC Simulation Proportional LOS Yes PID Yes Uniformly semiglobally asymptotically stability No 76 (Song et al., 2022) SGC Simulation Experiment VF Yes PID Yes - No 77 (G. Zhang et al., 2022) SGC Simulation Artificial potential field Yes Backstepping method Yes Semi-globally uniform ultimate bounded Yes 78 (Jiang et al., 2022) SGC Simulation - Yes MPC No Input-to-state stable No 79 (H. Zhang et al., 2022) SGC Simulation - Yes Sliding mode control Yes Stable Yes 80 (Wang et al., 2022) SGC Simulation LOS+fast marching method Yes deep reinforcement learning Yes Stable Yes There are two typical approaches for the design of the guidance and control system to solve the path fol‐ lowing problem: The separated Guidance and Control (SGC) approach and the Integrated Guidance and Control (IGC) approach (Rubí et al., 2020). The Separated Guidance and Control (SGC) approach, consists of an outer-loop guidance law for the generation of the desired heading an‐ gle and an inner-loop controller to track the desired head‐ ing angle and generated the output rudder angle. The sta‐ bility property of the whole system is carried out for the outer and inner loop separately, and the coupled term is ne‐ glected. The Integrated Guidance and Control (IGC) ap‐ proach combines the guidance and control system, and the whole system is a cascade where the heading control sys‐ tem is the driving system and the guidance system is the driven system, as presented in Figure 10. As can be ob‐ served, the heading control error will affect the conver‐ gence of the guidance system, which is to minimize the cross-track error, therefore, the coupled term is considered in the Integrated Guidance and Control approach. From ta‐ ble 1. the distribution of the control structure using the SGC and IGC approach is presented in Figure 11. About 62% of papers choose the SGC approach for simplifying the stability analysis, and 38% use the IGC approach.
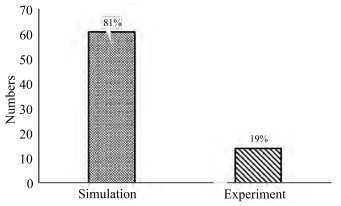
The results are usually validated using the simulations and experiments using the free-running ship model (Xu et al., 2020b). Right now, a large number of papers (81%) are using the simulation for the validation of the path following control, whereas only 19% of papers, the experimental studies were carried out, as indicated in Figure 12. Currently, most experimental studies are carried out using scale ship models in the lab or outdoor water area. The experimental tests in the lab can provide high accuracy position and ve‐ locity with the aid of an advanced position measurement system, meanwhile, the environmental disturbance (wind, wave and current) can also be scaled according to the ship model and can be controlled during the tests. There are some experimental works carried out in the laboratory, such as (Fossen et al., 2003; Fredriksen and Pettersen, 2006). The most convenient way to validate the path-following control system for Maritime Autonomous Surface Ships is using the scaled ship models in the outdoor water area. The sensors for the measurement of the position and velocity and actuators are needed to installed on the ship model, and a data acquisi‐ tion system and remote communication system is also need‐ ed for the data measurement and storage. Some interested works on the autonomous ship model can be found in (Liu et al., 2017; Mousazadeh et al., 2018; Niu et al., 2019; Rout et al., 2020; Sans-Muntadas et al., 2019; Wen et al., 2020; Wu et al., 2021; Xu et al., 2021a, 2020b; Zhu et al., 2020), just to name a few.
As discussed above, there are 4 typical guidance laws, but only LOS and VF guidance laws are widely used for the path following control of marine surface ships, as presented in Figure 13. Right now, LOS and its revised versions take the leading position (about 63%) in the published papers due to the simple structure and easy implementation. The in‐ tegral LOS (18%) is also widely used for cancelling the drift angle due to environmental disturbance. The VF guid‐ ance law (13%) is a novel method for the marine surface ship and it is still under fast development and provides good control performance (Caharija et al., 2015).
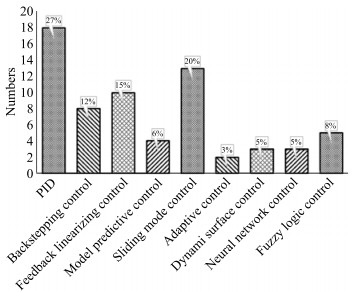
Right now, there are many controllers used to solve the path following problem, both linear controllers and non‐ linear controllers, such as proportional-integral-derivative (PID) controller, Linear control method, backstepping con‐ trol, sliding mode control, feedback linearizing control, sliding mode control, adaptive control, as presented in Figure 14. They are usually designed based on linear or nonlinear ship dynamics, well-known as model-based con‐ trol methodology. PID controller is still popular in the re‐ viewed papers (27%), considering its simple structure and easy implementation.
The nonlinear controllers, such as backstepping control (12%), feedback linearizing control (15%) and sliding mode control (20%) rank second in the reviewed papers. It is worth mentioning that there are some mode-free control methods, such as Neural network control (5%), Fuzzy log‐ ic control (8%). They also provide a good tracking perfor‐ mance, and the stability properties are still a challenge for those control methods.
As can be observed from Table 1 and Figure 15, most of the papers provide the stability proof for their control, such as uniformly ultimately bounded (22%), Finite-time stability (6%), Input-to-state stability (7%), global asymptotic stability (37%), uniformly local exponential stability (4%), globally κ -exponentially stability (7%), and Uniform semi-global expo‐ nential stability (17%).
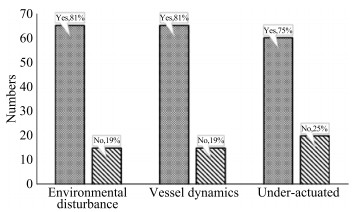
Stability is the most important property of any control sys‐ tem from a control-theoretic perspective since it is closely re‐ lated to the safety, robustness, and reliability of robotic sys‐ tems. Global exponential stability (GES) is usually the most desired quality of a closed-loop control system (Khalil, 2002; Loría and Panteley, 2005), but, it cannot be achieved due to the structural properties of the cross-track error (Fossen and Pettersen, 2014). The uniform semi-global exponential stabil‐ ity (USGES) is slightly weaker than GES and it is important for the performance and robustness of the control system un‐ der environmental disturbance. In Table 1 and Figure 16, most papers will consider the environmental disturbances (81%), such as wind, waves, and currents, the vessel dynamic (81%) and underactuated motions (75%) of marine surface ships.
4 Conclusions
The path following control system is one of the most crit‐ ically important systems for marine autonomous surface ships since it guarantees that the autonomous ship can fol‐ low the predefined path with small cross-track errors. This paper reviews the path following control systems, more pre‐ cisely, guidance systems and control systems, for marine au‐ tonomous surface ships. The path following control prob‐ lem and control objectives are firstly defined and the crosstrack errors function is derived using the kinematic equa‐ tions of marine surface ships. Then, the paper describes the most widely used guidance laws, such as LOS and modified version, PP, constant bearing and VF guidance law. The con‐ trol methodologies, such as PID, feedback linearization, backstepping method, sliding mode control and neural net‐ work-based control are briefly introduced.
To compare the state-of-the-art of path-following control for autonomous ships, 80 papers published in journals and inter‐ national conferences are carefully selected and analysed. Several properties and characteristics are defined, such as the control structure, guidance laws, control method, stability results, envi‐ ronmental disturbance and vessel dynamics, just to name a few.
The conclusions can be summarized:
(1) Most of the papers (62%) choose the separated guidance and control (SGC) for the design of the path following control system.
(2) Simulations are still the main means for validation, tak‐ ing up almost 81% of the selected papers. Experimental stud‐ ies are still very challenging due to many factors, such as the laboratory facility, sensor technology, model scale effect, test location and environmental disturbance, just to name a few.
(3) LOS and its extended versions take the leading posi‐ tion (about 63%) in the selected papers due to the simple structure and easy implementation.
(4) The linear model-based PID controller is still popular in the reviewed papers (27%), and nonlinear control technologies, such as Feedback linearizing, backstepping control and sliding mode control are also widely used in the selected papers.
(5) Most papers provide stability proof for the proposed system, and the global asymptotic stability proof (37%) was proved in most papers.
(6) The environmental disturbance (88%), vessel dynamics (84%) and underactuated motion (79%) are considered for most papers. The wind, wave and current are the typical distur‐ bance considered in the selected paper. The vessel dynamic is typically considered for the model-based control design, and the model-free control method, such as fuzzy logic control, and neutral network control, usually neglected the vessel dynamics.
In the future, the following works on path following control of underactuatd marine surface ships are recom‐ mented. The integrated Guidance and Control (IGC) approach is recommended for the design of the guidance and control for autonomous surface ships, especially the low speed commercial ships, because the coupled terms are ne‐ glected in the separated guidance and control (SGC) ap‐ proach. LOS guidance law can provide a good performance and is still recommented. The vector field guidance law is ex‐ pansible and easy to implement for collision avoidance, but its stability still needs to be investigated. The autonomous ship model is recommended for validation, but the sea trials of autonomous ships are still necessary for the development of automatic control systems.
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http:/creativecommons.org/licenses/by/4.0/.Competing interest C. Guedes Soares is an editorial board member for the Journal of Marine Science and Application and was not involved in the editorial review, or the decision to publish this article. All authors declare that there are no other competing interests. -
Figure 1 The motions of marine surface ships in waves (Fossen, 2011)
Figure 2 The guidance, navigation, and control system (GNC) for maritime autonomous surface ships (MASS) (Fossen, 2011)
Figure 4 The classical line-of-sight guidance law (Fossen et al., 2003)
Figure 5 The look-ahead based LOS guidance law (Fossen and Lekkas, 2015)
Figure 9 Path following control using the time-varying vector field guidance law (Xu et al., 2020a)
Figure 10 The cascaded path following control system (Lekkas and Fossen, 2014, 2012)
Table 1 Comparison of the path following control system for marine surface ship
No. References Structure Results Guidance law Environmenta l disturbance Controller Vessel Dynamics Stability Under- actuated 1 (Do et al., 2002) IGC Simulation - No Backstepping control Yes Global asymptotic stability Yes 2 (Fossen et al., 2003) SGC Experiment LOS No Backstepping control Yes Uniform global asymptotic stability Yes 3 (Do et al., 2004) IGC Experiment - Yes Backstepping control Yes Global asymptotic stability Yes 4 (Fredriksen and Pettersen, 2006) IGC Experiment LOS Yes Linear control method Yes Global k -exponential stability Yes 5 (Moreira et al., 2007) SGC Simulation Adaptive LOS Yes PID Yes - No 6 (Børhaug et al., 2008) IGC - Integral LOS Yes Adaptive controllers Yes Global asymptotic stability Yes 7 (Pereira et al., 2008) SGC Experiment LOS Yes PD No - No 8 (Oh and Sun, 2010) SGC Simulations LOS No Model predictive control Yes - Yes 9 (Børhaug et al., 2011) IGC Experiment LOS Yes Feedback linearizing control Yes Uniform Global asymptotic stability Yes 10 (Skjetne et al., 2011) IGC Simulation LOS No Feedback linearizing control Yes Global asymptotic stability Yes 11 (Lekkas and Fossen, 2012) IGC Simulation LOS No Sliding mode control Yes Global k -exponential stability Yes 12 (Caharija et al., 2012) IGC Simulation Integral LOS Yes Feedback linearizing control Yes Uniform local exponential stability Yes 13 (Svendsen et al., 2012) - Simulation - Yes L1 adaptive control No - No 14 (Caharija et al., 2014) IGC Simulation Integral LOS Yes Feedback linearizing control Yes Uniform local exponential stability Yes 15 (Fossen and Pettersen, 2014) IGC - Proportional LOS No Yes Uniform semiglobal exponential stability Yes 16 (Lekkas and Fossen, 2014) IGC Simulation Integral LOS Yes Sliding mode control Yes Global k -exponential stability Yes 17 (Fossen and Lekkas, 2015) IGC Simulation Integral LOS Yes Sliding mode control Yes Global k -exponential stability Yes 18 (Fossen et al., 2015) IGC Simulation Integral LOS Yes PID Yes Uniform semiglobal exponential stability Yes 19 (Wiig et al., 2015) IGC Simulation Integral LOS Yes Feedback linearizing controllers Yes Uniform semiglobal exponential stability Yes 20 (Xu and Guedes Soares, 2015) SGC Simulation LOS; PP+ LOS No PID Yes Global asymptotic stability Yes 21 (Caharija et al., 2015) - Experiment LOS; VF Yes PID Yes Global asymptotic stability Yes 22 (Caharija et al., 2016) IGC Simulation; experimenta l Integral LOS Yes Feedback linearizing PD controller Yes Globally asymptotically stable; Uniformly local exponential stable Yes 23 (Moe and Pettersen, 2016) SGC Simulation Set-based LOS No Adaptive feedback linearizing control Yes Uniform global asymptotic stability Yes 24 (Xu and Guedes Soares, 2016a) SGC Simulation VF Yes PID Yes Global asymptotic stability Yes 25 (Niu et al., 2016) SGC Simulation PP+LOS VF Yes PD Yes - No 26 (Xu and Guedes Soares, 2016b) SGC Simulation LOS; VF Yes PID Yes Global asymptotic stability Yes 27 (Liu et al., 2016a) SGC Simulation LOS Yes PID Yes Input-to-state stability Yes 28 (Liu et al., 2016b) SGC Simulation Integral LOS Yes Dynamic surface control Yes Uniformly ultimately bounded Yes 29 (Liu et al., 2016c) SGC Simulation Integral LOS Yes Dynamic surface control Yes Uniformly ultimately bounded Yes 30 (Woo and Kim, 2016) SGC Simulation VF No - No - Yes 31 (Wang et al., 2016) SGC Simulation - Yes Adaptive robust control Yes Finite-time stability No 32 (Shojaei and Dolatshahi, 2017) SGC Simulation LOS Yes Dynamic surface control Neural networks No Uniformly ultimately bounded Yes 33 (Miao et al., 2017) SGC Simulation LOS Yes Backstepping control Yes Asymptotically stability Yes 34 (Liu et al., 2017) SGC Simulation; experimenta l LOS Yes PID Yes Input-to-state stability Yes 35 (Moe and Pettersen, 2017) SGC Simulation Set-based LOS Yes Feedback linearizing control Yes Uniform global asymptotic stability Yes 36 (Wang et al., 2017) SGC Simulation LOS Yes Backstepping control Yes Asymptotically stability Yes 37 (Liu et al., 2018) - Simulation Adaptive LOS Yes Model predictive control Yes - Yes 38 (Mu et al., 2018) SGC Simulation Adaptive LOS Yes Backstepping method Yes Uniformly ultimately bounded Yes 39 (Yu et al., 2018) SGC Simulation LOS No Neural network control No Uniformly ultimately bounded No 40 (Xu and Guedes Soares, 2018) SGC Simulation LOS; PP+ LOS No PID Yes Global asymptotic stability Yes 41 (Mousazadeh et al., 2018) - Experiment Potential field Yes Feedback linearizing control Yes - No 42 (Huang et al., 2018) IGC Simulation LOS Yes Sliding mode control Yes Uniform semiglobal exponential stability Yes 43 (Chen et al., 2018) IGC Simulation Integral LOS Yes Feedback linearizing control Yes Uniform semiglobal exponential stability Yes 44 (Nie and Lin, 2019) SGC Simulation Integral LOS Yes Backstepping control Yes Uniformly ultimately bounded Yes 45 (Li et al., 2019) SGC Simulation LOS Yes Fuzzy logic control No Uniformly ultimately bounded Yes 46 (Niu et al., 2019) - Experiment LOS No Fuzzy logic control No - No 47 (Wang et al., 2019b) SGC Simulation LOS Yes Fuzzy logic control No Global asymptotic stability Yes 48 (Wang et al., 2019c) SGC Simulation LOS Yes PID Yes Input-to-state stability No 49 (Wang et al., 2019d) SGC Simulation LOS Yes Adaptive neural network control No Uniformly ultimately bounded Yes 50 (Xu et al., 2019) IGC Simulation VF Yes Sliding mode control Yes Uniform semiglobal exponential stability Yes 51 (Wang et al., 2019a) SGC Simulation - Yes Sliding mode control Yes Finite-time stability Yes 52 (Hinostroza et al., 2019) SGC Simulation VF Yes PID Yes - Yes 53 (Sans-Muntadas et al., 2019) IGC Experiment - Yes PID No asymptotically stability No 54 (Weng et al., 2020) SGC Simulation LOS Yes Sliding mode control Yes Ultimately bounded No 55 (Bejarano and N-Yo, 2020) SGC Simulation LOS Yes Backstepping control Yes Stable Yes 56 (Xu et al., 2020a) IGC Simulation VF Yes Sliding mode control Yes Uniform semiglobal exponential stability Yes 57 (Wan et al., 2020) SGC Simulation Integral LOS No Dynamic surface control Yes Uniformly asymptotically stability Yes 58 (Rout et al., 2020) SGC Simulation Experiment Modified LOS Yes Adaptive neural network controller Yes Uniformly ultimately bounded Yes 59 (Jiang et al., 2020) SGC Simulation Experiment LOS Yes PID Yes Global asymptotic stability Yes 60 (Xu and Guedes Soares, 2020) SGC Simulation LOS; VF Yes PID Yes Global asymptotic stability Yes 61 (Nie and Lin, 2020) SGC Simulation LOS Yes Fuzzy logic control No uniform ultimate bounded No 62 (Wen et al., 2020) SGC Experiment VF Yes Feedback control Yes Semi-global exponential stable Yes 63 (Wu et al., 2021) SGC Experiment LOS Yes Neural network controller No Input-to-state stability Yes 64 (Su et al., 2021) SGC Simulation LOS NO Backstepping method Yes Uniformly ultimately bounded No 65 (Xu et al., 2021a) IGC Simulation Experiment VF Yes Sliding mode control Yes Uniform semiglobal exponential stability Yes 66 (Liu et al., 2021) SGC Experiment LOS Yes PID No - No 67 (Tian et al., 2021) SGC Simulation LOS Yes Model predictive control Yes Stable No 68 (Xu et al., 2021b) IGC Simulation VF Yes L1 adaptive control Yes Uniform semiglobal exponential stability Yes 69 (Hinostroza et al., 2021) SGC Experiment LOS Yes PID Yes - Yes 70 (Li et al., 2021a) SGC Simulation Integral LOS Yes Sliding mode control Yes Uniformly ultimately bounded Yes 71 (Li et al., 2021b) IGC Simulation LOS Yes Backstepping sliding mode control Yes Uniformly global finitetime stability No 72 (Min and Zhang, 2021) IGC Simulation LOS Yes Fuzzy logic control Yes Uniformly ultimately bounded Yes 73 (Abrougui et al., 2021) SGC Experiment - Yes Sliding mode control No - Yes 74 (Zhang et al., 2021) SGC Simulation LOS No Feedback control Yes Global asymptotic stability No 75 (Fossen, 2022) SGC Simulation Proportional LOS Yes PID Yes Uniformly semiglobally asymptotically stability No 76 (Song et al., 2022) SGC Simulation Experiment VF Yes PID Yes - No 77 (G. Zhang et al., 2022) SGC Simulation Artificial potential field Yes Backstepping method Yes Semi-globally uniform ultimate bounded Yes 78 (Jiang et al., 2022) SGC Simulation - Yes MPC No Input-to-state stable No 79 (H. Zhang et al., 2022) SGC Simulation - Yes Sliding mode control Yes Stable Yes 80 (Wang et al., 2022) SGC Simulation LOS+fast marching method Yes deep reinforcement learning Yes Stable Yes -
Abkowitz MA. 1980. Measurement of hydrodynamic characteristics from ship maneuvering trials by system identification. SNAME Trans., 88: 283-318 http://www.researchgate.net/publication/283364635_Measurement_of_hydrodynamic_characteristics_from_ship_maneuvering_trials_by_system_identification Abrougui H, Nejim S, Hachicha S, Zaoui C, Dallagi H. 2021. Modeling, parameter identification, guidance and control of an unmanned surface vehicle with experimental results. Ocean Eng. 241, 110038. https://doi.org/10.1016/J.OCEANENG.2021.110038 Allianz Global Corporate and Speciality. 2018. Safety and Shipping Review 2018. Munich, Germany Bejarano G, N-Yo S. 2020. Velocity estimation and robust nonlinear path following control of autonomous surface vehicles. IFAC-PapersOnLine 53, 14674-14679. https://doi.org/10.1016/J.IFACOL.2020.12.1479 Børhaug E, Pavlov A, Panteley E, Pettersen KY. 2011. Straight line path following for formations of underactuated marine surface vessels. IEEE Trans. Control Syst. Technol., 19: 493-506. https://doi.org/10.1109/TCST.2010.2050889 Børhaug E, Pavlov A, Pettersen KY. 2008. Integral LOS control for path following of underactuated marine surface vessels in the presence of constant ocean currents. In: 47th IEEE Conference on Decision and Control, 4984-4991. https://doi. org/10.1109/ CDC.2008.4739352 https://doi.org/10.1109/CDC.2008.4739352 Breivik M, Fossen T. 2009. Guidance laws for autonomous underwater vehicles. In: inzartsev AV Ed. Underwater Vehicles. IntechOpen, London. 10.5772/6696https://doi.org/10.5772/6696 Breu DA, Fossen TI. 2011. L1 adaptive and extremum seeking control applied to roll parametric resonance in ships. IEEE Int. Conf. Control Autom. ICCA, 871876. 10.1109/ ICCA.2011.6138047 Caharija W, Candeloro M, Pettersen KY, Sørensen AJ. 2012. Relative velocity control and integral LOS for path following of underactuated surface vessels. IFAC Proc. Vol., 45: 380-385. https://doi.org/10.3182/20120919-3-IT-2046.00065 Caharija W, Pettersen KY, Bibuli M, Calado P, Zereik E, Braga J, Gravdahl JT, Sorensen AJ, Milovanovic M, Bruzzone G. 2016. Integral line-of-sight guidance and control of underactuated marine vehicles: theory, simulations, and experiments. IEEE Trans. Control Syst. Technol., 24: 1623-1642. https://doi.org/10.1109/ TCST.2015.2504838 https://doi.org/10.1109/TCST.2015.2504838 Caharija W, Pettersen KY, Calado P, Braga J. 2015. A comparison between the ILOS guidance and the vector field guidance. In: IFAC-PapersOnLine. Elsevier, 89-94. https://doi. org/10.1016/ j.ifacol.2015.10.263 http://www.onacademic.com/detail/journal_1000038977560510_3aa8.html Caharija W, Pettersen KY, Sørensen AJ, Candeloro M, Gravdahl JT. 2014. Relative velocity control and integral line of sight for path following of autonomous surface vessels: merging intuition with theory. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ., 228: 180-191. https://doi. org/10.1177/ 1475090213512293 http://smartsearch.nstl.gov.cn/paper_detail.html?id=6a7ad11c7f6e341b8dd53fe2140ffb5e Chen X, Liu Z, Zhang J, Zhou D, Dong J. 2018. Adaptive slidingmode path following control system of the underactuated USV under the influence of ocean currents. J. Syst. Eng. Electron., 29: 1271-1283. https://doi.org/10.21629/JSEE.2018.06.14 Cho N, Kim Y, Park S. 2015. Three-dimensional nonlinear differential geometric path-following guidance law. 10.2514/1.G001060 https://doi. org/10.2514/1.G001060 Do KD, Jiang ZP, Pan J. 2002. Underactuated ship global tracking under relaxed conditions. IEEE Trans. Automat. Contr., 47: 1529-1536. https://doi.org/10.1109/TAC.2002.802755 Do KD, Jiang ZP, Pan J. 2004. Robust adaptive path following of underactuated ships. Automatica 40, 929-944. https://doi. org/ 10.1016/j.automatica.2004.01.021 doi: 10.1016/j.automatica.2004.01.021 Faltinsen OM. 1993. Sea Loads on Ships and Offshore Structures, Cambridge University Press. Cambridge, UK. Fossen TI (2011) Handbook of Marine Craft Hydrodynamics and Motion Control. John Wiley & Sons, Ltd, Chichester, UK. 10.1002/9781119994138https://doi.org/10.1002/9781119994138 Fossen TI (2011) Handbook of Marine Craft Hydrodynamics andMotion Control. John Wiley & Sons, Ltd, Chichester, UK. 10.1002/9781119994138https://doi.org/10.1002/9781119994138 Fossen TI. 2022. Line-of-sight path-following control utilizing an extended Kalman filter for estimation of speed and course over ground from GNSS positions. J. Mar. Sci. Technol. 1-8. https://doi.org/10.1007/S00773-022-00872-Y/FIGURES/8 doi: 10.1007%2Fs00773-022-00872-y.pdf?pdf=core Fossen TI, Breivik M, Skjetne R. 2003. Line-of-sight path following of underactuated marine craft. IFAC Proc. Vol., 36: 211-216. https://doi.org/10.1016/S1474-6670(17)37809-6 http://pdfs.semanticscholar.org/5848/580d4b40bcca6e16fdc42dc67df8ee33747d.pdf Fossen TI, Lekkas AM. 2015. Direct and indirect adaptive integral line-of-sight path-following controllers for marine craft exposed to ocean currents. Int. J. Adapt. Control Signal Process., 31: 445-463. https://doi.org/10.1002/acs.2550 http://www.dl1.matlabi.ir/vfb/2018/01/fossen2015.pdf Fossen TI, Pettersen KY. 2014. On uniform semiglobal exponential stability (USGES) of proportional line-of-sight guidance laws. Automatica 50, 2912-2917. https://doi.org/10.1016/J. AUTOMATICA.2014.10.018 https://doi.org/10.1016/j.automatica.2014.10.018 Fossen TI, Pettersen KY, Galeazzi R. 2015. Line-of-sight path following for dubins paths with adaptive sideslip compensation of drift forces. IEEE Trans. Control Syst. Technol., 23: 820-827. https://doi.org/10.1109/TCST.2014.2338354 Fredriksen E, Pettersen KY. 2006. Global κ -exponential way-point maneuvering of ships: theory and experiments. Automatica 42, 677-687. ttps: //doi. org/10.1016/J. AUTOMATICA. 2005.12.020 https://doi.org/10.1016/j.automatica.2005.12.020 Freund E. 1973. Decoupling and pole assignment in nonlinear systems. Electron. Lett., 9: 373-374. https://doi. org/10.1049/EL: 19730275 https://doi.org/10.1049/el:19730275 Gu N, Wang D, Peng Z, Wang J, Han QL. 2022a. Advances in Lineof-Sight Guidance for Path Following of Autonomous Marine Vehicles: an Overview. IEEE Trans. Syst. Man, Cybern. Syst. 10.1109/TSMC.2022.3162862 https://doi.org/10.1109/TSMC.2022.3162862 Gu N, Wang D, Peng Z, Wang J, Han QL. 2022b. Disturbance observers and extended state observers for marine vehicles: a survey. Control Eng. Pract., 123: 105158. https://doi.org/10.1016/ J.CONENGPRAC.2022.105158 https://doi.org/10.1016/j.conengprac.2022.105158 Hassani V, Pascoal AM, Onstein TF. 2018. Data-driven control in marine systems. Annu. Rev. Control 46, 343-349. https://doi.org/ 10.1016/J.ARCONTROL.2018.10.006 https://doi.org/10.1016/j.arcontrol.2018.10.006 Hinostroza MA, Xu H, Guedes Soares C. 2021. Experimental results of the cooperative operation of autonomous surface vehicles navigating in complex marine environment. Ocean Eng., 219: 108256. https://doi.org/10.1016/j.oceaneng.2020.108256 Hinostroza MA, Xu H, Guedes Soares C. 2019. Cooperative operation of autonomous surface vehicles for maintaining formation in complex marine environment. Ocean Eng., 183: 132-154. https://doi.org/10.1016/j.oceaneng.2019.04.098 Huang C, Zhang X, Zhang G. 2021a. Decentralized event-triggered cooperative path-following control for multiple autonomous surface vessels under actuator failures. Appl. Ocean Res., 113: 102751. https://doi.org/10.1016/J.APOR.2021.102751 https://doi.org/10.1016/j.apor.2021.102751 Huang C, Zhang X, Zhang G. 2021b. Adaptive neural finite-time formation control for multiple underactuated vessels with actuator faults. Ocean Eng., 222: 108556. https://doi.org/10.1016/J. OCEANENG.2020.108556 https://doi.org/10.1016/j.oceaneng.2020.108556 Huang C, Zhang X, Zhang G, Deng Y. 2021c. Robust practical fixedtime leader-follower formation control for underactuated autonomous surface vessels using event-triggered mechanism. Ocean Eng., 233: 109026. https://doi.org/10.1016/J.OCEANENG.2021.109026 https://doi.org/10.1016/j.oceaneng.2021.109026 Huang H, Li Y, Zhuang Y, Gong M, Sharma S, Xu D. 2018. Lineof-sight path following of an underactuated USV exposed to ocean currents using cascaded theorem. 2018 WRC Symp. Adv. Robot. Autom. WRC SARA 2018 - Proceeding 334-339. https://doi.org/10.1109/WRC-SARA.2018.8584241 http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=8584241 IMO, Autonomous ships: regulatory scoping exercise completed [WWW Document]. URL https://www.imo.org/en/MediaCentre/ PressBriefings/pages/MASSRSE2021. aspx (accessed 5.9.22). Jiang Y, Peng Z, Meng C, Liu L, Wang D, Li T. 2022. Data-driven finite control set model predictive speed control of an autonomous surface vehicle subject to fully unknown kinetics and propulsion dynamics. Ocean Eng., 264: 112474. https://doi. org/10.1016/J. OCEANENG.2022.112474 https://doi.org/10.1016/j.oceaneng.2022.112474 Jiang Y, Peng Z, Wang D, Chen CLP. 2020. Line-of-sight target enclosing of an underactuated autonomous surface vehicle with experiment results. IEEE Trans. Ind. Informatics 16, 832- 841. https://doi.org/10.1109/TII.2019.2923664 Khalil HK. 2002. Nonlinear Systems. Prentice Hall Kokotović PV (1992) The Joy of Feedback: Nonlinear and Adaptive. IEEE Control Syst., 12: 7-17. https://doi.org/10.1109/ 37.165507 http://www.pearsonelt.ch/HigherEducation/ElectricalEngineering/Controls/1471/9780131227408/Nonlinear-Systems-International-Edition.aspx Lekkas AM, Fossen TI. 2014. Integral LOS path following for curved paths based on a monotone cubic hermite spline parametrization. IEEE Trans. Control Syst. Technol., 22: 2287-2301. https://doi.org/ 10.1109/TCST.2014.2306774 Lekkas AM, Fossen TI. 2012. A time-varying lookahead distance guidance law for path following. IFAC Proc. Vol., 45: 398-403. https://doi.org/10.3182/20120919-3-IT-2046.00068 Li M, Guo C, Yu H. 2019. Filtered Extended State Observer Based Line-of-Sight Guidance for Path following of Unmanned Surface Vehicles with Unknown Dynamics and Disturbances. IEEE Access 7, 178401-178412. https://doi.org/10.1109/ACCESS.2019.2958855 Li M, Guo C, Yu H. 2021a. Extended state observer-based integral line-of-sight guidance law for path following of underactuated unmanned surface vehicles with uncertainties and ocean currents. Int. J. Adv. Robot. Syst., 18: 172988142110110. https://doi. org/ 10.1177/17298814211011035 doi: 10.1177/17298814211011035 Li M, Guo C, Yu H, Yuan Y. 2021b. Line-of-sight-based global finite-time stable path following control of unmanned surface vehicles with actuator saturation. ISA Trans. 10.1016/j.isatra.2021.07.009https://doi. org/ 10.1016/j.isatra.2021.07.009 Lim S, Jung W, Bang H. 2014. Vector field guidance for path following and arrival angle control, in: 2014 International Conference on Unmanned Aircraft Systems, ICUAS 2014 - Conference Proceedings. IEEE, pp. 329-338. https://doi. org/ 10.1109/ICUAS.2014.6842271 http://ieeexplore.ieee.org/document/6842271/ Liu C, Negenborn RR, Chu X, Zheng H. 2018. Predictive path following based on adaptive line-of-sight for underactuated autonomous surface vessels. J. Mar. Sci. Technol., 23: 483-494. https://doi.org/10.1007/S00773-017-0486-2/FIGURES/11 https://doi.org/10.1007/s00773-017-0486-2 Liu L, Wang D, Pen, Z. 2017. ESO-based line-of-sight guidance law for path following of underactuated marine surface vehicles with exact sideslip compensation. IEEE J. Ocean. Eng., 42: 477-487. https://doi.org/10.1109/JOE.2016.2569218 Liu L, Wang D, Peng Z. 2016a. ESO-based line-of-sight guidance law for straight line path following with exact sideslip compensation. Proc. World Congr. Intell. Control Autom. 2016-September, 677- 681. https://doi.org/10.1109/WCICA.2016.7578426 http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=7578426 Liu L, Wang D, Peng Z. 2016b. Path following of marine surface vehicles with dynamical uncertainty and time-varying ocean disturbances. Neurocomputing 173, 799-808. https://doi.org/10.1016/J. NEUCOM.2015.08.033 https://doi.org/10.1016/j.neucom.2015.08.033 Liu L, Wang D, Peng Z. 2016c. Predictor-based line-of-sight guidance law for path following of underactuated marine surface vessels. Proc. 6th Int. Conf. Intell. Control Inf. Process. ICICIP 2015 284- 288. https://doi.org/10.1109/ICICIP.2015.7388184 http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=7388184 Liu L, Wang D, Peng Z. 2016d. Path following of marine surface vehicles with dynamical uncertainty and time-varying ocean disturbances. Neurocomputing 173, 799-808. https://doi.org/10.1016/J. NEUCOM.2015.08.033 https://doi.org/10.1016/j.neucom.2015.08.033 Liu Z, Yu L, Xiang Q, Qian T, Lou Z, Xue W. 2021. Research on USV trajectory tracking method based on LOS algorithm. Proc. - 2021 14th Int. Symp. Comput. Intell. Des. Isc. 2021 408-411. https://doi.org/10.1109/ISCID52796.2021.00098 Loría A, Panteley E. 2005. Cascaded Nonlinear Time-Varying Systems: Analysis and Design, in: Lamnabhi-Lagarrigue, F., Loría, A., Panteley, E. (Eds. ), Advanced Topics in Control Systems Theory: Lecture Notes from FAP 2004. Springer London, London, 23-64. https://doi.org/10.1007/11334774_2 http://www.springerlink.com/content/978-1-84628-418-2 Maritime K. 2016. World's First Official Test Bed for Autonomous Shipping Opens in Norway [WWW Document]. URL https://www.km.kongsberg.com/ks/web/nokbg0238.nsf/AllWeb/166309633 F206651C125804200250951?OpenDocument (accessed 9.6.18). MARKETS & MARKETS. 2021. Autonomous Ships Market by Autonomy, Ship Type, End-Use | COVID-19 Impact Analysis | MarketsandMarketsTM [WWW Document]. URL https://www. marketsandmarkets. com/Market-Reports/autonomous-ships-market- 267183224.html (accessed 4.2.21). Miao J, Wang S, Tomovic MM, Zhao Z. 2017. Compound line-ofsight nonlinear path following control of underactuated marine vehicles exposed to wind, waves, and ocean currents. Nonlinear Dyn., 89: 2441-2459. https://doi.org/10.1007/S11071-017-3596-9/ FIGURES/11 https://doi.org/10.1007/s11071-017-3596-9 Min B, Zhang X. 2021. Concise robust fuzzy nonlinear feedback track keeping control for ships using multi-technique improved LOS guidance. Ocean Eng., 224: 108734. https://doi.org/10.1016/ J.OCEANENG.2021.108734 https://doi.org/10.1016/j.oceaneng.2021.108734 Moe S, Pettersen KY. 2017. Set-Based line-of-sight (LOS) path following with collision avoidance for underactuated unmanned surface vessels under the influence of ocean currents. 1st Annu. IEEE Conf. Control Technol. Appl. CCTA 2017 2017-January, 241-248. https://doi.org/10.1109/CCTA.2017.8062470 http://ieeexplore.ieee.org/document/8062470/ Moe S, Pettersen KY. 2016. Set-based Line-of-Sight (LOS) path following with collision avoidance for underactuated unmanned surface vessel, in: 24th Mediterranean Conference on Control and Automation, MED 2016. pp. 402-409. https://doi. org/ 10.1109/MED.2016.7535964 http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=7535964 Moe S, Pettersen KY, Fossen TI, Gravdahl JT. 2016a. Line-of-sight curved path following for underactuated USVs and AUVs in the horizontal plane under the influence of ocean currents. In: 24th Mediterranean Conference on Control and Automation, MED, 2016: 38-45. https://doi.org/10.1109/MED.2016.7536018 http://brage.bibsys.no/xmlui/bitstream/11250/2433975/1/root.pdf Moe S, Pettersen KY, Fossen TI, Gravdahl JT. 2016b. Line-of-sight curved path following for underactuated USVs and AUVs in the horizontal plane under the influence of ocean currents. 24th Mediterr. Conf. Control Autom. MED, 38-45. https://doi. org/ 10.1109/MED.2016.7536018 http://brage.bibsys.no/xmlui/bitstream/11250/2433975/1/root.pdf Moreira L, Fossen TI, Guedes Soares C. 2007. Path following control system for a tanker ship model. Ocean Eng., 34: 2074-2085. https://doi.org/10.1016/j.oceaneng.2007.02.005 Mousazadeh H, Jafarbiglu H, Abdolmaleki H, Omrani E, Monhaseri F, Abdollahzadeh M Reza, Mohammadi-Aghdam A, Kiapei A, Salmani-Zakaria Y, Makhsoos A. 2018. Developing a navigation, guidance and obstacle avoidance algorithm for an Unmanned Surface Vehicle (USV) by algorithms fusion. Ocean Eng., 159: 56-65. https://doi.org/10.1016/j.oceaneng.2018.04.018 Mu D, Wang G, Fan Y, Bai Y, Zhao Y. 2018. Fuzzy-based optimal adaptive line-of-sight path following for underactuated unmanned surface vehicle with uncertainties and time-varying disturbances. Math. Probl. Eng. 2018. 10.1155/2018/7512606https://doi.org/10.1155/2018/7512606 Nelson DR, Barber DB, McLain TW, Beard RW. 2006. Vector field path following for small unmanned air vehicles. 2006 Am. Control Conf. 5788-5794. https://doi.org/10.1109/ACC.2006.1657648 http://www.et.byu.edu/~beard/papers/preprints/NelsonBarberMcLainBeard06.pdf Nelson DR, Barber DB, McLain TW, Beard RW. 2007. Vector field path following for miniature air vehicles. IEEE Trans. Robot., 23: 519-529. https://doi.org/10.1109/TRO.2007.898976 Nie J, Lin X. 2019. Improved adaptive integral line-of-sight guidance law and adaptive fuzzy path following control for underactuated MSV. ISA Trans., 94: 151-163. https://doi.org/10.1016/J.ISATRA. 2019.04.010 https://doi.org/10.1016/j.isatra.2019.04.010 Nie J, Lin X. 2020. FAILOS guidance law based adaptive fuzzy finitetime path following control for underactuated MSV. Ocean Eng., 195: 106726. https://doi.org/10.1016/J.OCEANENG.2019.106726 https://doi.org/10.1016/j.oceaneng.2019.106726 Niu G, Wan L, Zou J, Zeng J, Fan J, Sun C. 2019. Intelligent pathfollowing control of unmanned surface vehicles based on improved line-of-sight guidance. IOP Conf. Ser. Mater. Sci. Eng., 677: 042104. https://doi.org/10.1088/1757-899X/677/4/042104 Niu H, Lu Y, Savvaris A, Tsourdos A. 2016. Efficient path following algorithm for unmanned surface vehicle. Ocean. 2016 - Shanghai. 10.1109/OCEANSAP.2016.7485430https://doi.org/10.1109/OCEANSAP.2016.7485430 Nomoto K, Taguchi T, Honda K, Hirano S. 1957. On the steering qualities of ships. Int. Shipbuild. Prog., 4: 354-370. https://doi.org/10.3233/ISP-1957-43504 Oh S-R, Sun J. 2010. Path following of underactuated marine surface vessels using line-of-sight based model predictive control. Ocean Eng., 37: 289-295. https://doi.org/10.1016/j.oceaneng.2009.10.004 Papoulias FA. 1993. On the nonlinear dynamics of pursuit guidance for marine vehicles. J. Sh. Res., 37: 342-353. https://doi. org/ 10.5957/JSR.1993.37.4.342 https://doi.org/10.5957/jsr.1993.37.4.342 Pereira A, Das J, Sukhatme GS. 2008. An experimental study of station keeping on an underactuated ASV. 2008 IEEE/RSJ Int. Conf. Intell. Robot. Syst. IROS 3164-3171. https://doi. org/ 10.1109/IROS.2008.4650991 http://citeseerx.ist.psu.edu/viewdoc/download;jsessionid=2F2325794225D1815C52C1248263DE60?doi=10.1.1.133.54&rep=rep1&type=pdf Ren RY, Zou ZJ, Wang YD, Wang XG. 2018. Adaptive Nomoto model used in the path following problem of ships. J. Mar. Sci. Technol. 1-11. https://doi.org/10.1007/s00773-017-0518-y Roberts GN. 2008. Trends in marine control systems. Annu. Rev. Control 32, 263-269. https://doi.org/10.1016/J.ARCONTROL.2008.08.002 http://www.sciencedirect.com/science/article/pii/S1367578808000278 Rolls-Royce. 2015. Rolls‐Royce to Lead Autonomous Ship Research Project [WWW Document]. URL https://www. rolls-royce. com/ media/our-stories/press-releases/2015/pr-02-07-15-rolls-royce-tolead-autonomous-ship-research-project. aspx (accessed 9.6.18). Rout R, Cui R, Han Z. 2020. Modified line-of-sight guidance law with adaptive neural network control of underactuated marine vehicles with state and input constraints. IEEE Trans. Control Syst. Technol., 28: 1902-1914. https://doi.org/10.1109/TCST.2020.2998798 Rubí B, Pérez R, Morcego B. 2020. A Survey of Path Following Control Strategies for UAVs Focused on Quadrotors. J. Intell. Robot. Syst. Theory Appl., 98: 241-265. https://doi. org/10.1007/ s10846-019-01085-z https://doi.org/10.1007/s10846-019-01085-z Sans-Muntadas A, Kelasidi E, Pettersen KY, Brekke E. 2019. Path planning and guidance for underactuated vehicles with limited field-of-view. Ocean Eng., 174: 84-95. https://doi. org/10.1016/J. OCEANENG.2019.01.027 https://doi.org/10.1016/j.oceaneng.2019.01.027 Shojaei K, Dolatshahi M. 2017. Line-of-sight target tracking control of underactuated autonomous underwater vehicles. Ocean Eng., 133: 244-252. https://doi.org/10.1016/j.oceaneng.2017.02.007 Skjetne R, Jørgensen U, Teel AR. 2011. Line-of-sight path-following along regularly parametrized curves solved as a generic maneuvering problem. Proc. IEEE Conf. Decis. Control 2467-2474. https://doi. org/10.1109/CDC.2011.6161364 http://www.onacademic.com/detail/journal_1000037030260310_b8a3.html Song D, Gan W, Yao P, Zang W, Zhang Z, Qu X. 2022. Guidance and control of autonomous surface underwater vehicles for target tracking in ocean environment by deep reinforcement learning. Ocean Eng., 250: 110947. https://doi.org/10.1016/j.oceaneng.2022.110947 Su Y, Wan L, Zhang D, Huang F. 2021. An improved adaptive integral line-of-sight guidance law for unmanned surface vehicles with uncertainties. Appl. Ocean Res., 108: 102488. https://doi.org/ 10.1016/J.APOR.2020.102488 https://doi.org/10.1016/j.apor.2020.102488 Sutulo S, Guedes Soares C. 2011. Mathematical models for simulation of manoeuvring performance of ships. In: Guedes Soares C, et al (Eds). Maritime Engineering and Technology. Taylor & Francis Group, London, 661-698. 10.13140/2.1.3538.7209 https://doi.org/10.13140/2.1.3538.7209 Svendsen CH, Holck NO, Galeazzi R, Blanke M. 2012. L1 adaptive manoeuvring control of unmanned high-speed water craft. IFAC Proc. Vol., 45: 144-151. https://doi.org/10.3182/20120919-3-IT-2046.00025 http://www.xueshufan.com/publication/2052220723 Tian Z, Zheng H, Xu W. 2021. Path following of autonomous surface vehicles with line-of-sight and nonlinear model predictive control. 6th Int. Conf. Transp. Inf. Saf. New Infrastruct. Constr. Better Transp. ICTIS 2021 1269-1274. https://doi. org/ 10.1109/ICTIS54573.2021.9798580 doi: 10.1109/ICTIS54573.2021.9798580 Wan L, Su Y, Zhang H, Shi B, AbouOmar MS. 2020. An improved integral light-of-sight guidance law for path following of unmanned surface vehicles. Ocean Eng., 205: 107302. https://doi.org/10.1016/ J.OCEANENG.2020.107302 https://doi.org/10.1016/j.oceaneng.2020.107302 Wang N, Karimi HR, Li H, Su SF. 2019a. Accurate Trajectory Tracking of Disturbed Surface Vehicles: A Finite-Time Control Approach. IEEE/ASME Trans. Mechatronics 24, 1064-1074. https://doi.org/10.1109/TMECH.2019.2906395 http://www.onacademic.com/detail/journal_1000042300177599_123f.html Wang N, Qian C, Sun J-C, Liu Y-C. 2016. Adaptive Robust FiniteTime Trajectory Tracking Control of Fully Actuated Marine Surface Vehicles. IEEE Trans. Control Syst. Technol., 24: 1454-1462. https://doi.org/10.1109/TCST.2015.2496585 Wang N, Sun Z, Yin J, Zou Z, Su SF. 2019b. Fuzzy unknown observerbased robust adaptive path following control of underactuated surface vehicles subject to multiple unknowns. Ocean Eng., 176: 57-64. https://doi.org/10.1016/J.OCEANENG.2019.02.017 https://doi.org/10.1016/j.oceaneng.2019.02.017 Wang N, Sun Z, Yin J, Zheng Z. 2017. Surge-varying LOS based path following control of underactuated marine vehicles with accurate disturbance observation, in: 2017 IEEE 7th International Conference on Underwater System Technology: Theory and Applications (USYS). IEEE, 1-6. https://doi.org/10.1109/USYS.2017.8309464 http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=8309464 Wang S, Yan X, Ma F, Wu P, Liu Y. 2022. A novel path following approach for autonomous ships based on fast marching method and deep reinforcement learning. Ocean Eng., 257: 111495. https://doi. org/10.1016/J.OCEANENG.2022.111495 https://doi.org/10.1016/j.oceaneng.2022.111495 Wang Y, Tong H, Fu M. 2019c. Line-of-sight guidance law for path following of amphibious hovercrafts with big and time-varying sideslip compensation. Ocean Eng., 172: 531-540. https://doi. org/ 10.1016/J.OCEANENG.2018.12.036 https://doi.org/10.1016/j.oceaneng.2018.12.036 Wang Y, Tong H, Wang C. 2019d. High-gain observer-based line-ofsight guidance for adaptive neural path following control of underactuated marine surface vessels. IEEE Access 7, 26088-26101. https://doi.org/10.1109/ACCESS.2019.2900365 Wen Y, Tao W, Zhu M, Zhou J, Xiao C. 2020. Characteristic modelbased path following controller design for the unmanned surface vessel. Appl. Ocean Res., 101: 102293. https://doi. org/10.1016/J. APOR.2020.102293 https://doi.org/10.1016/j.apor.2020.102293 Weng Y, Wang N, Guedes Soares C. 2020. Data-driven sideslip observer-based adaptive sliding-mode path-following control of underactuated marine vessels. Ocean Eng., 197: 106910. https://doi. org/10.1016/J.OCEANENG.2019.106910 https://doi.org/10.1016/j.oceaneng.2019.106910 Wiig MS, Pettersen KY, Krogstad TR. 2015. Uniform Semiglobal Exponential Stability of Integral Line-of-Sight Guidance Laws. IFACPapersOnLine 48, 61-68. https://doi.org/10.1016/J.IFACOL.2015.10.259 http://publications.ffi.no/bitstream/handle/123456789/486/MCMC2015_MartinSyreWiig.pdf?sequence=1&isAllowed=y Woo J, Kim N. 2016. Vector field based guidance method for docking of an unmanned surface vehicle. In: The Twelfth ISOPE Pacific/ Asia Offshore Mechanics Symposium. Gold Coast, Australia, p. ISOPE-P-16-103. Wu W, Peng Z, Wang D, Liu L, Han Q-L. 2021. Network-Based Line-of-Sight Path Tracking of Underactuated Unmanned Surface Vehicles With Experiment Results. IEEE Trans. Cybern. 1-11. https://doi.org/10.1109/TCYB.2021.3074396 http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=9440777 Xu H, Fossen TI, Guedes Soares C. 2020a. Uniformly semiglobally exponential stability of vector field guidance law and autopilot for path-following. Eur. J. Control 53, 88-97. https://doi. org/ 10.1016/j.ejcon.2019.09.007 http://www.sciencedirect.com/science/article/pii/S0947358019302456 Xu H, Guedes Soares C. 2015. An optimized path following algorithm for a surface ship model. In: Guedes Soares, C., et al. (Eds. ). Towards Green Marine Technology and Transport. CRC Press, 151-158. https://doi.org/10.1201/b18855-21 http://www.researchgate.net/publication/294277775_An_optimized_path_following_algorithm_for_a_surface_ship_model Xu H, Guedes Soares C. 2016a. Vector field path following for surface marine vessel and parameter identification based on LS-SVM. Ocean Eng., 113: 151-161. https://doi.org/10.1016/j.oceaneng.2015.12.037 http://smartsearch.nstl.gov.cn/paper_detail.html?id=d2bd9a8c46a963cd4cd971e89e423ab2 Xu H, Guedes Soares C. 2016b. Waypoint-following for a marine surface ship model based on vector field guidance law. In: Guedes Soares C., et al. (Eds. ). Maritime Technology and Engineering 3. Taylor & Francis Group, London, 409-418 Xu H, Guedes Soares C. 2018. An optimized energy-efficient path following algorithm for underactuated marine surface ship model. Int. J. Marit. Eng. Vol 160, A-411-A-421. https://doi.org/ 10.3940/rina.ijme.2018.a4.505 http://www.nstl.gov.cn/paper_detail.html?id=a5328b1f52d631866c082e6ed4562de9 Xu H, Guedes Soares C. 2020. Vector field guidance law for curved path following of an underactuated autonomous ship model. Int. J. Marit. Eng. 162. 10.5750/IJME.V162IA3.1135https://doi.org/10.5750/IJME.V162IA3.1135 Xu H, Hinostroza MA, Guedes Soares C. 2018. Estimation of hydrodynamic coefficients of a nonlinear manoeuvring mathematical model with free-running ship model tests. Int. J. Marit. Eng. Vol 160, A-213-A-226. https://doi.org/10.3940/rina.ijme.a3.2018.448 http://www.nstl.gov.cn/paper_detail.html?id=ed5757a23c56bb9b20b4e519f20bb3dd Xu H, Hinostroza MA, Guedes Soares C. 2021a. Modified vector field path-following control system for an underactuated autonomous surface ship model in the presence of static obstacles. J. Mar. Sci. Eng., 9: 652. https://doi.org/10.3390/jmse9060652 Xu H, Hinostroza MA, Wang Z, Guedes Soares C. 2020b. Experimental investigation of shallow water effect on vessel steering model using system identification method. Ocean Eng., 199: 106940. https://doi.org/10.1016/j.oceaneng.2020.106940 http://www.sciencedirect.com/science/article/pii/S002980182030024X Xu H, Oliveira P, Guedes Soares C. 2021b. L1 adaptive backstepping control for path-following of underactuated marine surface ships. Eur. J. Control 58, 357-372. 10.1016/j.ejcon.2020.08.003https://doi.org/10.1016/j.ejcon.2020.08.003 Xu H, Rong H, Guedes Soares C. 2019. Use of AIS data for guidance and control of path-following autonomous vessels. Ocean Eng., 194: 106635. https://doi.org/10.1016/j.oceaneng.2019.106635 http://www.sciencedirect.com/science/article/pii/S0029801819307553 Yamasaki T, Enomoto K, Takano H, Baba Y, Balakrishnan SN. 2009. Advanced pure pursuit guidance via sliding mode approach for chase UAV. AIAA Guid. Navig. Control Conf. Exhib. 10.2514/6.2009-6298 https://doi. org/10.2514/6.2009-6298 Yanushevsky R. 2011. Guidance of unmanned aerial vehicles. Taylor & Francis Yu Y, Guo C, Yu H. 2018. Finite-time predictor line-of-sight-based adaptive neural network path following for unmanned surface vessels with unknown dynamics and input saturation. Int. J. Adv. Robot. Syst., 15: 172988141881469. https://doi. org/10.1177/ 1729881418814699 http://www.onacademic.com/detail/journal_1000041653537199_42bd.html Zhang G, Han J, Li J, Zhang X. 2022. APF-based intelligent navigation approach for USV in presence of mixed potential directions: Guidance and control design. Ocean Eng., 260: 111972. https://doi.org/10.1016/J.OCEANENG.2022.111972 Zhang H, Zhang X, Bu R. 2022. Sliding mode adaptive control for ship path following with sideslip angle observer. Ocean Eng., 251: 111106. https://doi.org/10.1016/J.OCEANENG.2022.111106 http://www.sciencedirect.com/science/article/pii/S0029801822005182 Zhang Z, Zhao Yuhan, Zhao G, Wang H, Zhao Yi. 2021. Pathfollowing control method for surface ships based on a new guidance algorithm. J. Mar. Sci. Eng., 2021:, 9(2): 166. https://doi. org/10.3390/JMSE9020166 http://www.xueshufan.com/publication/3129121679 Zhu M, Sun W, Hahn A, Wen Y, Xiao C, Tao W. 2020. Adaptive modeling of maritime autonomous surface ships with uncertainty using a weighted LS-SVR robust to outliers. Ocean Eng., 200: 107053. https://doi.org/10.1016/J.OCEANENG.2020.107053 http://www.sciencedirect.com/science/article/pii/S0029801820301268