Numerical Investigation on the Deformation of the Free Interface During Water Entry and Exit of a Circular Cylinder by Using the Immersed Boundary-Multiphase Lattice Boltzmann Flux Solver
https://doi.org/10.1007/s11804-022-00292-9
-
Abstract
In this work, the deformation of free interface during water entry and exit of a circular cylinder is investigated numerically by using the two-dimensional (2D) immersed boundary-multiphase lattice Boltzmann flux solver (IB-MLBFS). The fluid domain is discretized by finite volume discretization, and the flux on the grid interface is evaluated by lattice Boltzmann equations. Both the implicit velocity correction and the surface flux correction are implemented by using the immersed boundary-method to consider the fluid-structure interaction and the contact interface between the multiphase fluids and the structure. First, the water entry of a circular cylinder is simulated and the results are compared with the experiment, which considered the length-diameter ratio of the circular cylinder. The reliability of 2D simulation is verified and the deformation of the free interface is well investigated. Afterward, the water exit of a circular cylinder with constant velocity is simulated, which is less researched. In addition, the results show the advantage of present IB-MLBFS to some extent. Finally, the water exit and re-entry of a circular cylinder are presented, and the results present the complex deformation of the free interface and the dynamic response of the moving structure. Based on the numerical results, the free interface of the multiphase fluids is well captured, and the contact interface on the boundary of the moving structure is accurately presented by the IB-MLBFS.-
Keywords:
- Free interface ·
- Water entry ·
- Water exit ·
- Immersed boundary method ·
- Lattice Boltzmann flux solver
Article Highlights• Implementing the IBM, the implicit velocity correction and surface flux correction were appended to the LBFS, hence, the IB-MLBFS can deal with the multiphase fluids-structure interaction.• The complex deformation of the free interface and hydrodynamic response of the cylinder were well investigated, and all the numerical results were consistent with the experiments.• The IB-MLBFS not only successfully simulated the complex phenomena but also achieved accuracy and stability to a certain extent compared with other solvers. -
1 Introduction
The interaction between multiphase fluids and structure in engineering is ubiquitous, in which the capture of the contact line between the multiphase fluids and the moving structure is challenging for numerical simulation. In inves‐ tigating such problems, numerical methods for multiphase flows and the fluid-structure interaction are equivalently pivotal.
For the computational fluid dynamics in incompressible multiphase fluids, numerical methods can be classified into three categories based on different modeling such as the Navier-Stokes (N-S) solver in the macroscopic domain, the lattice Boltzmann method (LBM) in the mesoscopic domain, and the molecular dynamics (MD) in the microscopic domain. The N-S solvers are governed by mass conservation and momentum conservation on the macroscopic scale, which can be discretized with a high order of accuracy when the computational grids are sufficient. Hence, the N-S solver is considered the commonly used method in computational fluid dynamics, which has been widely developed for commercial applications. Different kinds of N-S solvers have been developed and applied to engineering to investigate multiphase fluids. Bussmann et al. developed a three-dimensional volume tracking model, which was applied to the droplet impact onto a solid surface (Bussmann et al. 1999, 2000). Renardy et al. simulated moving contact line (MCL) problems using a volume-of-fluid method (Renardy et al. 2001). Nevertheless, for most N-S solvers, the computational efficiency is greatly affected by solving Poisson equations for pressure (Wang et al. 2015a, d). Different from N-S solvers, the LBM is sourced from the kinetic theory and the governing equations can be solved directly in an explicit way. This feature ensures efficiency in computing and simplicity in programming and has led the LBM to be a popular method in recent decades (Guo et al. 2002; Mehravaran and Hannani 2008; Huang et al. 2009b; Lee and Liu 2010; Zhou et al. 2012; Galindo-Torres et al. 2013; Lin et al. 2013; Galindo-Torres 2013; Galindo-Torres et al. 2016; de Rosis 2017; Yang et al. 2018, 2019; Chen et al. 2020; Verdier et al. 2020; Ru et al. 2021; Wang et al. 2021; Zhang et al. 2021). Chen et al. developed an improved version of the simplified LBM (SLBM) (Chen et al. 2017, 2018; Chen and Shu 2020a, b). Based on their work, non-uniform meshes can be applied and non-Newtonian power-law fluid flows are investigated. The LBM has great advantages in efficiency, however, there exists a tie-up between the grid size and the time step, which results in the computation domain of the LBM being restricted to uniform mesh, and efficiency and accuracy may not be achieved simultaneously. In addressing the abovementioned challenge, a lattice Boltzmann flux solver (LBFS) has been developed by Wang et al.(2015b, c, 2017, 2019b). In the LBFS, macroscopic property-conserved governing equations recovered by lattice Boltzmann equation (LBE) are discretized by cell-centered finite volume discretization (FVD). Different from other N-S solvers in which the inviscid and viscous fluxes on the cell interface are usually calculated separately, the LBFS reconstructs inviscid and viscous fluxes simultaneously by the local solution to the LBE. Given this feature, the LBFS removes the tie-up to allow its application to the non-uniform mesh and achieve accuracy, and the LBE in evaluating flux escapes from solving Poisson equations to achieve efficiency. Furthermore, Yang et al.(2020b, 2020a, 2021) developed LBFS in multiphase flow, and Chen et al. (2021) coupled the immersed boundary method (IBM) with LBFS in multiphase flow. Based on their work, the LBFS is well implemented and is proven to have wider application space in engineering.
Numerical methods can be classified into two categories based on different frames: the Lagrangian method and the Eulerian method. In investigating fluid-structure interactions (FSI) problems, implementing boundary conditions on the contact line between the structure and fluids remains a challenge (Shao et al. 2013). Thus, a body-fitted grid can be applied, where the grid is generated by concentrating the solid structure and sharing the same grid shape on the boundary line. This discretization of the computational domain ensures the boundary condition imposed with accurate solutions (Mittal and Iaccarino 2005). Nevertheless, generating body-fitted grids with good quality is challenging when the solid structure has a complex geometry, and the computational efficiency may be affected by the regeneration of grids when the solid structure is moving. In addressing the abovementioned drawbacks, nonbody conformal methods were presented (Peskin 1972; DeZeeuw and Powell 1993; LeVeque and Li 1994; Fedkiw et al. 1999; Liu et al. 2000; Li and Lai 2001; Lee and LeVeque 2003; Le et al. 2006), and the IBM, which is a feasible method, was presented by Peskin (2002). This method couples the Lagrangian method and Eulerian method, inheriting their advantages and removing the drawbacks to a certain extent. Wu and Shu (2009) developed an implicit velocity correction-based IBM, Shao et al. (2013) introduced the IBM to the contact line dynamic and Liu et al. (Liu and Ding 2015; Liu et al. 2017) introduced a diffuse-interface IBM for flows with MCLs. Previous research on the IBM has great importance to the multiphase fluids-structure interaction.
Previous work (Yan et al. 2021, 2022; Lu et al. 2022) indicated that the LBFS is efficient and accurate to a certain degree compared with the LBM, which can be successfully implemented for the water entry and exit of rigid bodies (Xiao et al. 2022). In the present work, the IB-MLBFS was developed to investigate the deformation of the free interface during water entry and exit of a circular cylinder (Yan et al. 2022). The implicit velocity correction and surface flux correction are implemented by using IBM to consider the fluid-structure interaction and contact interface between the multiphase fluids and structure. In addition, Sun et al. (2018) developed an accurate and efficient smoothed particle hydrodynamics (SPH) model of the water entry of a circular cylinder. Wang et al. (2019a) improved the model with a novel non-reflecting boundary condition for fluid dynamics, and Sun et al. (2019) presented an investigation on the fully nonlinear water entry of a cone in the Stokes wave. The phenomena in the present simulation have been investigated experimentally by Wei and Hu (2014), Miao (1989), and Colicchio et al. (2009) and numerically by Zhang et al. (2017) with SPH, Zhu et al. (2007) with constrained interpolation profile (CIP), Colicchio et al. (2009) with ever set method (LSM), and Moshari et al. (2014) with the volume of fluid (VOF). The numerical results of the present IB-MLBFS indicate that the free interface deformation of multiphase fluids and the contact interface on the boundary of the moving structure are accurately simulated. The rest of this paper is organized as follows: Section 2 presents the methodology of the computational method and the detailed computation procedure, and Section 3 gives the conversion of units between the computational system and the physical system. The numerical investigation of the deformation of the free interface is presented in Section 4, and the conclusions are drawn in Section 5 at the end.
2 Immersed boundary-multiphase lattice boltzmann flux solver
2.1 Multiphase lattice boltzmann flux solver
2.1.1 Governing equations
For the incompressible multiphase flow, the macroscopic N-S equations recovered by the multiphase lattice Boltzmann model can be written as follows (Wang et al. 2015a):
$$\left(\frac{\partial p}{\partial t}+\boldsymbol{u} \cdot \nabla p\right)+\rho c_s^2 \nabla \cdot \boldsymbol{u}=0$$ (1a) $$\frac{\partial \rho \boldsymbol{u}}{\partial t}+\nabla \cdot(\rho \boldsymbol{u} \cdot \boldsymbol{u})=-\nabla p+\nabla\left[\mu \cdot\left(\nabla \boldsymbol{u}+(\nabla \boldsymbol{u})^{\mathrm{T}}\right)\right]+\boldsymbol{F}_s$$ (1b) where p is the pressure, u is the velocity, ρ is the density, cs is a constant related to the local sound speed, μ is the dynamic viscosity, and Fs is the surface tension force. The relationship between macroscopic properties and the lattice Boltzmann model has been establish, which can be written as follows:
$$p=\sum\limits_{\alpha=0}^{\alpha=8} f_\alpha^{\mathrm{eq}}=\sum\limits_{\alpha=0}^{\alpha=8} f_\alpha$$ (2a) $$\rho \boldsymbol{u} c_s^2=\sum\limits_{\alpha=0}^{\alpha=8} f_\alpha^{\text {eq }} \boldsymbol{e}_\alpha=\sum\limits_{\alpha=0}^{\alpha=8} f_\alpha \boldsymbol{e}_\alpha$$ (2b) where fα represents the particle distribution function in LBE, and fαeq is the equilibrium state of fα, which can be written as follows:
$$f_\alpha^{\mathrm{eq}}(\boldsymbol{r}, t)=w_\alpha\left[p+\rho c_s^2\left(\frac{\boldsymbol{e_\alpha} \boldsymbol{u}}{c_s^2}+\frac{\left(\boldsymbol{e_\alpha} \boldsymbol{u}\right)^2-\left(c_s|\boldsymbol{u}|^2\right)}{2 c_s^4}\right)\right]$$ (3) Then the connection between multiphase N-S equations and LBE is established.
2.1.2 Finite volume discretization
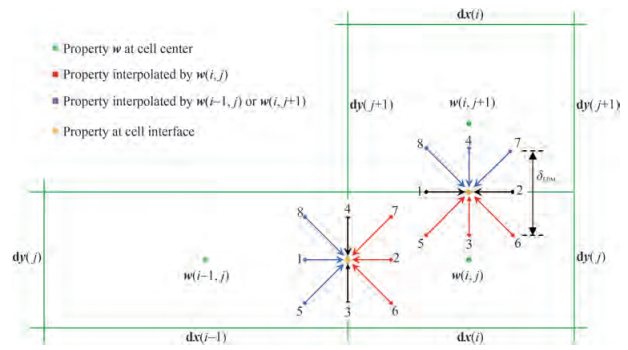
As an FVM-based flux solver, the fluxes at the cell interface between adjacent control cells must be evaluated. After establishing the connection between the N-S equation and LBE, the fluxes can be evaluated by reconstructing a lattice model locally at the cell interface (Figure 1).
For the whole fluids domain, implementing the FVD to Equation (1) over a control cell provides the following property-conserved equations:
$$\frac{\mathrm{d} \boldsymbol{W}_i}{\mathrm{d} t}=-\frac{1}{\Delta V_i} \sum\limits_k \boldsymbol{R}_k \Delta S_k+\boldsymbol{F}_E$$ (4) where FE is the external force given by the source term such as the surface tension force, gravity, and boundary condition. Wi = (p, u) is the macroscopic variables of fluids in the ith control cell. ΔVi represents the volume of the control cell, and ΔSk represents the length/area of the kth interface enclosing the control cell for 2D/3D case. As shown in Figure 1, the fluxes Rk are evaluated by reconstructing a lattice model locally at the cell interface. Rk can be calculated as follows:
$$\boldsymbol{R}_k=\left(\begin{array}{c}\boldsymbol{n} \cdot \sum\nolimits_{\alpha=0}^{\alpha=8} \boldsymbol{e}_\alpha f_\alpha^{\mathrm{eq}} \\ \boldsymbol{n} \cdot \sum\nolimits_{\alpha=0}^{\alpha=8} \boldsymbol{e}_\alpha \boldsymbol{e}_\alpha f_\alpha^{\wedge}\end{array}\right)$$ (5) In addition, the distribution functions in Equation (5) refer to the eight surrounding points in the lattice model. The properties p and u of the surrounding points at (r − eαδt, t − δt) can be considered from that at (rt, t) by interpolation.
2.2 Correction by using the immersed boundary method
2.2.1 Implicit velocity correction
In the present work, the velocity of the flow field is initially predicted without considering the structure and then corrected by considering the solid boundary of the structure. The correction step modifies the velocity of the fluids based on the following relationship:
$$\boldsymbol{u}=\boldsymbol{u}^*+\Delta \boldsymbol{u}$$ (6) where u* is the intermediate velocity of fluids obtained by MLBFS directly without considering FSI, u is the corrected velocity, and Δu is the velocity correction.
The IBM is implemented to obtain the velocity correction on the fluids domain (Peskin 2002; Mittal and Iaccarino 2005; Wu and Shu 2009; Wang et al. 2015b; Yan et al. 2021). As shown in Figure 2, the Lagrangian points indicate the solid boundary whereas the Eulerian points indicate the flow field. The corrected velocity U (XBl) on the Lagrangian point given by the IBM must be identical to the Eulerian point at the same position to satisfy the non-slip boundary condition.
$$\begin{aligned} &\boldsymbol{U}\left(\boldsymbol{X}_\boldsymbol{B}^l\right)=\sum\limits_j \boldsymbol{u}^*\left(\boldsymbol{r}_\boldsymbol{j}\right) \boldsymbol{D}\left(\boldsymbol{r}_\boldsymbol{j}-\boldsymbol{X}_\boldsymbol{B}^l\right) h^2 \\ &\quad+\sum\limits_j \sum\limits_k \delta \boldsymbol{u}_\boldsymbol{B}^k D\left(\boldsymbol{r}_\boldsymbol{j}-\boldsymbol{X}_\boldsymbol{B}^l\right) D\left(\boldsymbol{r}_\boldsymbol{j}-\boldsymbol{X}_\boldsymbol{B}^k\right) \Delta s^k h^\mathit{2} \end{aligned}$$ (7) where U (XBl) presents the corrected velocity on the Lagrangian point XBl, u* (rj) presents the intermediate velocity on the Eulerian point rj, k is the number of Lagrangian points whose effective area of the Dirac function encloses the Eulerian point rj, δuBk presents the velocity correction on the respective Lagrangian point, h represents the grid length of Eulerian mesh, N and M represent the number of Lagrangian and Eulerian points, respectively, and D is the continuous kernel function. We solve Equation (7) implicitly by rewriting it in a matrix form to obtain δuBk:
$$\boldsymbol{AX} = \boldsymbol{B}$$ (8) where
$$\boldsymbol{X}=\left[\delta \boldsymbol{u}_{\boldsymbol{B}}^1 \Delta s^1, \delta \boldsymbol{u}_{\boldsymbol{B}}^2 \Delta s^2, \cdots, \delta \boldsymbol{u}_{\boldsymbol{B}}^N \Delta s^N\right]^{\mathrm{T}}$$ (9a) $$\boldsymbol{A}=h^2\left(\begin{array}{ccc}D_{11} & \cdots & D_{1 M} \\ \vdots & \ddots & \vdots \\ D_{N 1} & \cdots & D_{N M}\end{array}\right)\left(\begin{array}{ccc}D_{11} & \cdots & D_{1 N} \\ \vdots & \ddots & \vdots \\ D_{M 1} & \cdots & D_{M N}\end{array}\right)$$ (9b) $$\boldsymbol{B}=\left(\begin{array}{c}\boldsymbol{U}_{\boldsymbol{B}}^1 \\ \vdots \\ \boldsymbol{U}_{\boldsymbol{B}}^N\end{array}\right)-h^2\left(\begin{array}{ccc}D_{11} & \cdots & D_{1 M} \\ \vdots & \ddots & \vdots \\ D_{N 1} & \cdots & D_{N M}\end{array}\right)\left(\begin{array}{c}\boldsymbol{u}_\mathit{\pmb{1}}^* \\ \vdots \\ \boldsymbol{u}_{\boldsymbol{M}}^*\end{array}\right)$$ (9c) Once δuBkΔsk are obtained, the velocity correction at each Eulerian point can be obtained using the following equation
$$\Delta \boldsymbol{u}=\sum\limits_l \delta \boldsymbol{u_B}^l D\left(\boldsymbol{r}_\boldsymbol{j}-\boldsymbol{X}_{\boldsymbol{B}}^l\right) \Delta s^l$$ (10) Then, the correction can be performed on the whole flow field domain by Equation (6). In this work, the structure was motivated in the fluids thus the U (XBl) on all Lagrangian points is equal to the velocity of the cylinders.
2.2.2 Surface flux correction
For multiphase flows, the density ρ of fluids at the control cell can be determined by the heavy fluid ρH and light fluid ρL:
$$\rho=\phi \rho_H+(1-\phi) \rho_L$$ (11) where ϕ is the order parameter of the heavy fluids in the range of [0, 1]. In capturing the interface of the two immiscible fluids, the Cahn-Hilliard model was applied to compute ϕ, and the conservative equation can be written as follows:
$$\frac{\partial \phi}{\partial t}+\nabla \cdot(\phi \boldsymbol{u})=\nabla \cdot\left[\nabla\left(M \mu_\phi\right)\right]$$ (12) where M is a constant which indicates the mobility; μϕ is the chemical potential determined by the equilibrium state of the interface between fluid and fluid or fluid and structure. In the Cahn-Hilliard model, the boundary condition for ϕ is also determined by the material properties with a contact angle θeq, which is written as follows:
$$\cos \theta^{\mathrm{eq}}=-\omega$$ (13a) $$\left.\boldsymbol{n} \cdot \nabla \phi\right|_{\text {Boundary }}=\omega\left(\phi-\phi^2\right) \sqrt{2 \beta / \kappa}$$ (13b) where ω is the non-dimensional wetting potential determined by Young's Law, and n = (nx, ny) is the external normal unit vector of the respective boundary point. In the present research on water entry and exit, as the impact velocity of the solid structure is high enough and the material properties are not the key issue, we exclude the wetting boundary condition and define the contact angle $\theta^{\mathrm{eq}}=\frac{1}{4} \pi$. Using the Cahn-Hilliard model, Equation (12) can be rewritten as follows:
$$\frac{\partial \phi}{\partial t}=-\nabla \cdot \boldsymbol{q}$$ (14) where q is the surface flux obtained using the following equation:
$$\boldsymbol{q}=-M \cdot \nabla \mu_\phi+\phi \boldsymbol{u}$$ (15) The Cahn-Hilliard only captures the interface of the two fluids hence ϕ and μϕ are obtained without considering the structure. In illustrating the contact line between the boundary of the structure and the interface of multiphase fluids, the ϕ and μϕ obtained by the Cahn-Hilliard model are defined as the intermediate ϕ* and μϕ*, and then the surface flux correction is appended on the predicted intermediate properties of the fluids domain, which is similar to the velocity correction. Notably, for any Eulerian point in the effective area of the Dirac function (Figure 2), its control volume must enclose a small surface area. For this case, the surface fluxes from two opposite directions will contribute positively to ϕ in the control volume. In obtaining the surface flux correction, we initially calculate the derivative on the solid boundary by using the following interpolation formula:
$$\frac{\partial \mu_\phi{ }^*}{\partial x}\left(\boldsymbol{X}_{\boldsymbol{B}}^l\right)=\sum\limits_j \frac{\partial \mu_\phi{ }^*}{\partial x}\left(\boldsymbol{r}_\boldsymbol{j}\right) D\left(\boldsymbol{r}_\boldsymbol{j}-\boldsymbol{X}_{\boldsymbol{B}}^l\right) h^2$$ (16a) $$\frac{\partial \mu_\phi^*}{\partial y}\left(\boldsymbol{X}_{\boldsymbol{B}}^l\right)=\sum\limits_j \frac{\partial \mu_\phi^*}{\partial y}\left(\boldsymbol{r}_\boldsymbol{j}\right) D\left(\boldsymbol{r}_\boldsymbol{j}-\boldsymbol{X}_{\boldsymbol{B}}^l\right) h^2$$ (16b) Then the normal derivative at the boundary point can be illustrated as:
$$\frac{\partial \mu_\phi^*}{\partial n}\left(\boldsymbol{X}_{\boldsymbol{B}}^l\right)=\frac{\partial \mu_\phi^*}{\partial x}\left(\boldsymbol{X}_{\boldsymbol{B}}^l\right) n_x+\frac{\partial \mu_\phi^*}{\partial y}\left(\boldsymbol{X}_{\boldsymbol{B}}^l\right) n_y$$ (17) For all the Eulerian points, the surface flux correction on the Lagrangian points can be written as follows to satisfy the Neumann boundary condition:
$$\Delta q_1\left(\boldsymbol{X}_{\boldsymbol{B}}^l\right)=-2 M \cdot\left[0-\frac{\partial \mu_\phi^*}{\partial n}\left(\boldsymbol{X}_{\boldsymbol{B}}^l\right)\right]$$ (18) Moreover, the Dirichlet boundary condition should be implemented thus the surface correction on the Lagrangian can be written as follows:
$$\Delta q_2\left(\boldsymbol{X}_{\boldsymbol{B}}^l\right)=2 \sum\limits_j \phi^*\left(\boldsymbol{r}_\boldsymbol{j}\right) \Delta \boldsymbol{u}\left(\boldsymbol{r}_{\boldsymbol{j}}\right) \cdot \boldsymbol{n} \cdot D\left(\boldsymbol{r}_{\boldsymbol{j}}-\boldsymbol{X}_{\boldsymbol{B}}^l\right) h^\mathit{2} $$ (19) Given the Neumann boundary condition and Dirichlet boundary, the surface flux correction can be obtained as follows:
$$\Delta q_{\phi n}\left(\boldsymbol{X}_{\boldsymbol{B}}^l\right)=\Delta q_1\left(\boldsymbol{X}_{\boldsymbol{B}}^l\right)+\Delta q_2\left(\boldsymbol{X}_{\boldsymbol{B}}^l\right)$$ (20) In addition, the corrections of ϕ* and μϕ * of the Eulerian point can be calculated using the following relationship
$$\frac{\delta \phi\left(\boldsymbol{r}_\boldsymbol{j}\right)}{\delta t}=\sum\limits_l \Delta q_{\phi n}\left(\boldsymbol{X}_{\boldsymbol{B}}^l\right) D\left(\boldsymbol{r}_\boldsymbol{j}-\boldsymbol{X}_{\boldsymbol{B}}^l\right) \Delta s_l$$ (21) Afterward, the order parameter ϕ can be finally corrected using the following equation:
$$\phi\left(\boldsymbol{r}_\boldsymbol{j}\right)=\phi^*\left(\boldsymbol{r}_\boldsymbol{j}\right)+\delta \phi\left(\boldsymbol{r}_\boldsymbol{j}\right)$$ (22) Then, the whole fluid domain has been corrected by the Dirichlet boundary condition and Neumann boundary condition
2.3 Rigid body dynamics
In the IBM, the inertial or internal mass effects of the structure exist, which may influence the accuracy (Shukla et al. 2007). The flow field within the structure boundary is set as the light fluid to minimize these effects, whose density is 0.001 times that of the heavy fluid, and the noslip boundary is applied at the surface of the structure. The two-dimensional Newton-Euler equations, which describe the rigid body motion, can be written as follows:
$$M_s \frac{\mathrm{d} U_x}{\mathrm{~d} t}=F_{E x}$$ (23a) $$M_s \frac{\mathrm{d} U_y}{\mathrm{~d} t}=-M_s g+F_{E y}$$ (23b) where FE is the external force on the rigid body generated by the surrounding multiphase flows, which can be calculated on the basis of the pressure acting on the structure boundary using the following equation:
$$F_{E x}=\oint\limits_B p\left(\boldsymbol{X}_{\boldsymbol{B}}^l\right) \cdot \boldsymbol{n_x} \mathrm{~d} s$$ (24a) $$F_{E y}=\oint\limits_B p\left(\boldsymbol{X}_{\boldsymbol{B}}^l\right) \cdot \boldsymbol{n}_{\boldsymbol{y}} \mathrm{d} s$$ (24b) $$p\left(\boldsymbol{X}_{\boldsymbol{B}}^l\right)=\sum\limits_j p\left(\boldsymbol{r}_\boldsymbol{j}\right) D\left(\boldsymbol{r}_{\boldsymbol{j}}-\boldsymbol{X}_{\boldsymbol{B}}^l\right) h^2$$ (24c) Using the obtained forces calculated by Equation (20), the motion and velocity of the rigid body can be computed and updated through Equation (19), and then the MCL can be corrected
2.4 Sequence of computation
1) Predict the fluid domain by solving Equation (4) and obtain the intermediate volume factor and intermediate velocity (Section 2.1).
2) Correct the velocity by using the IBM using Equation (10) (Section 2.2.1).
3) Correct the volume factor by using the IBM using Equation (22) (Section 2.2.2).
4) Compute the external force acting on the structure by Equation (24), and then update the location of the moving structure (Section 2.3).
5) Repeat 1 to 4 until the desired iteration number is reached.
3 Dimensional analysis for numerical simulation
For the numerical simulation, all the properties are computed in non-dimensional forms by using a computer. When examining the numerical results with physical experiments, the properties in the LBFS system should be the same as that in the physical system. The conversion of units is conducted as follows to build the connection between the numerical simulation and physical experiment. Let L′, M′ and T′ be the ratios of length, mass, and time, respectively, between the LBFS system and physical system, the conversion formula can be written as follows, and their values are set (Table 1).
$$L^{\prime}=\frac{l_{\mathrm{LBFS}}}{l_{\text {phys }}} M^{\prime}=\frac{m_{\mathrm{LBFS}}}{m_{\text {phys }}} T^{\prime}=\frac{t_{\mathrm{LBFS}}}{t_{\text {phys }}}$$ (25) $$V^{\prime}=L^{\prime} T^{\prime-1} A^{\prime}=L^{\prime} T^{\prime-2} F^{\prime}=M^{\prime} L^{\prime} T^{\prime-2} P^{\prime}=M^{\prime} L^{\prime-1} T^{\prime-2}$$ (26) Table 1 Ratios and values of the basic quantitiesParameter Length Mass Time Ratio L′ = 103 M′ = 106 T′ = 105 Phys 1 (m) 1 (kg) 1 (s) LBFS 103 106 105 Table 2 Ratios and values of the derived quantitiesVelocity Acceleration Force Pressure Ratio L′T′−1 = 10−2 L′T′−2 = 10−7 M′L′T′−2 = 10−1 M′L′1T′−2 = 10−7 Phys 1 (m/s) 1 (m/s2) 1 (N) 1 (Pa) LBFS 10−2 10−7 10−1 10−7 Using the abovementioned relationship, the properties in the physical system can be clearly converted to the respective numerical values in LBFS, hence, the obtained numerical results can be conducted to the physical system, which ensures the implementation of LBFS in engineering.
4 Results and discussions
In this section, the numerical simulations of water entry and exit are presented. The deformation of the free interface is clearly illustrated and the results are compared with experiments. For all the cases, the grid size is set as 10-3 m and the time step is set as 10−5 s. The mobility in the CahnHilliard model is set as M = 20.0, and the grid size ratio between Lagrangian point and Eulerian point is set as 1.0, which has been proven to be suitable values to ensure efficiency and accuracy (Huang et al. 2009a; Wang et al. 2015b; Chen et al. 2020; Yan et al. 2021, 2022). The density of the light gaseous fluid is set as ρL = 1 kg/m3, whereas that of the heavy liquid fluid is set as ρH = 1 000 kg/m3. Moreover, the dynamic viscosity ratio of the liquid fluid and gaseous fluid is defined as μH/μL = 100.
4.1 Water entry of a free circular cylinder
The two-dimensional water entry of a free circular cylinder is presented. In validating the accuracy and investigating the influence of the three-dimensional effect, the experimental study of water entry of a circular cylinder with different densities and length-diameter ratios by Wei and Hu (2014) is referenced. In their experiment, the water in the tank has a depth of 1.0 m, and the cylinder with a diameter of D = 0.05 m is initially placed 2.0 m above the free interface and released horizontally into the water. The impact velocity for the cylinder is U0 = 6.22 m/s hence the Froude number $F r=U_0 / \sqrt{g D}=8.89$.
For numerical simulations, the fluid domain is set as 16D × 30D, and the initial acceleration of the structure in the gaseous fluid is partly simplified, that is, the cylinder is posited near the free-surface with velocity at the beginning to improve the computational efficiency (Figure 3). The cylinders with densities of ρs = 1 370 kg/m3 and ρs = 900 kg/m3 are defined similarly to the experiment. The bounce-back boundary condition is applied to the both sides and the bottom, and the pressure-outlet boundary condition is applied to the top boundary. The moment when the cylinder touches the free interface is defined as t = 0.
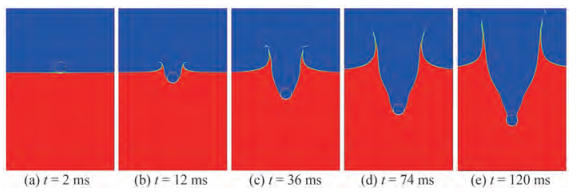
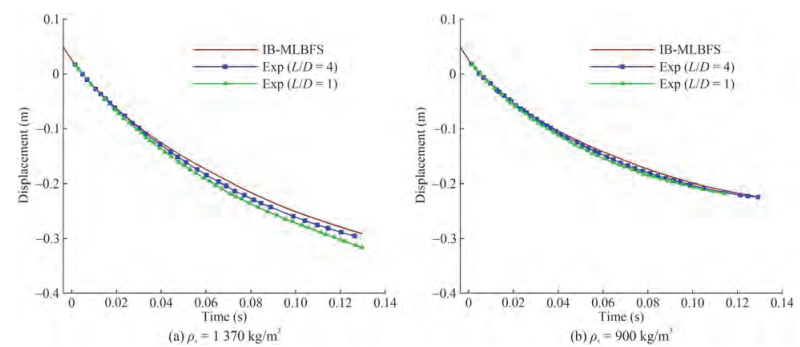
Figure 4 demonstrates the water entry by experiment (Wei and Hu 2014) and the IB-MLBFS at respective times, and the cylinder has a density of ρs = 1 370 kg/m3 and L/D = 4. The development of jets from both sides, the inversion of the cavity shape above the cylinder, and the contact interface surrounding the cylinder are consistent. The surface tension force acting on the free interface maintains the cavity shape, and the cavity is develops with time as the Froude number is large enough. For a detailed illustration, Figure 5 shows the contact interface of the cylinder boundary, gaseous fluid, and liquid fluid. The thickness of the free interface, which maintains the two fluids immiscible by surface tension, is clearly described. In addition, the solid boundary of the cylinder is indicated by dashed lines with no specific color filled inside, hence, the contact line between the structure and multiphase fluids is evident. This feature indicates that the order parameter is well conserved on the solid boundary as the convective and diffusive terms are corrected by the surface flux correction. Moreover, the 2D simulation can represent the phenomenon at L/D = 4. The results show that the present IB-MLBFS satisfies the conserved law on the interface, which can deal with a moving boundary.
When the cylinder has a lower density ρs = 900 kg/m3 than the liquid fluid, the pressure acting on the structure and viscosity of the fluids are considerable, hence, the deformation of the free interface may be different from the abovementioned results. As shown in Figure 6, the evolution of the water entry of a circular cylinder with a density of ρs = 900 kg/m3 is simulated by the current IB-MLBFS. Compared with the results shown in Figure 4, where ρs = 1 370 kg/m3, the cavity shape is nearly the same when t ≤ 74 ms, but the inversion of the cavity shape in the present simulation appears earlier, hence, the deformation of the free interface is quite different at t = 120 ms, and the displacement of the cylinder is shorter. This result can be attributed to the small Froude number in the present case, thus gravity can perform an effective influence on the deformation of the free interface. Nonetheless, the cavity can be observed clearly, and the shape is significant, which indicates that the surface tension force acting on the free interface greatly maintains the contact line among the multiphase fluids. In investigating the influence on the deformation of the free interface by the length-diameter ratio, the instantaneous snapshots at t = 101 ms by the present 2D simulation and experiments (Wei and Hu 2014) with different length-diameter ratios are shown in Figure 7. The comparison shows that the cavity width increases and the jet spreads to both sides with the increase of the length of the cylinder. Notably, the deformation of the free interface in the present 2D simulation results is close to that of the experimental results of L/D = 4, and the comparison of the depth of penetration between the present IB-MLBFS and experiments is shown in Figure 8. The abovementioned results indicate that the length-diameter ratio plays a pivotal rule in the deformation of the free interface, and the 2D simulation is considerable only when the length-diameter ratio is large. Nonetheless, the 2D simulation can accurately predict the displacement of the circular cylinder to a certain extent without the influence of the length-diameter ratio, particularly when ρs = 900 kg/m3.
4.2 Water exit of a circular cylinder with constant velocity
Compared with water entry, the water exit has been less researched. Therefore, the viscosity, gravity, and surface tension of multiphase fluids are particularly important, which lead to the complex deformation shape of the free interface. The abovementioned parameters require the high accuracy of the numerical solver to evaluate the pressure and volume factor. In this section, the 2D water exit of a circular cylinder with constant velocity is presented by IBMLBFS, which has been investigated experimentally by Miao (1989) and simulated numerically by Zhang et al. (2017), Zhu et al. (2007), and Xiao et al. (2022). This case is characterized by the Froude number $F r=v / \sqrt{2 g r}$, where v is the absolute value of the constant velocity in the vertical direction. Based on the experiment, two different Froude numbers, Fr = 0.764 4 and Fr = 0.462 7, were investigated. The circular cylinder is initially posited under the free interface with the distance between the top of the cylinder and the mean free interface is vt/r = −5.5, which reaches the desired constant velocity v after a temporary acceleration at the position vt/r = −5.0. In the present simulation, the Reynolds number Re = 2ρHvr/μH was set similar to that of previous research and defined as 1 000. The computational domain was set as 10D × 10D, and bounce-back boundary condition was applied on the left, right, and bottom sides, whereas the pressure-outlet boundary condition was applied on the top. Instantaneous contours of pressure and density were printed and compared with other numerical solvers, and the coefficient of the vertical force Ce = Fy/ρv2r was presented to compare with experimental and other numerical solvers.
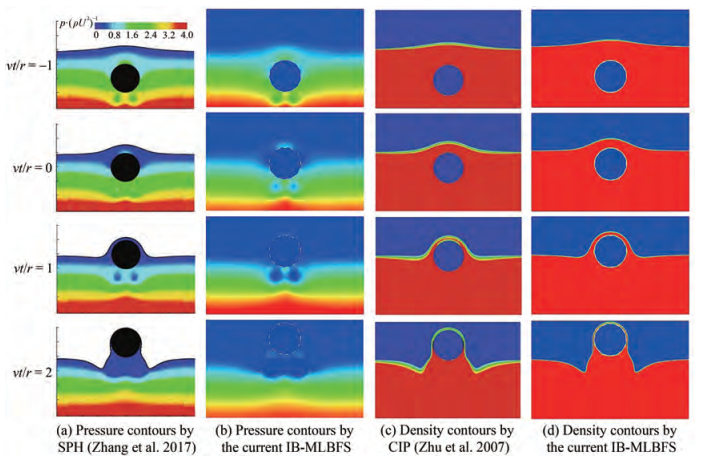
Figure 9 shows the evolution of fluid pressure and deformation of the free interface with Fr = 0.764 4 by SPH (Zhang et al. 2017), CIP (Zhu et al. 2007), and current IB-MLBFS. Evidently, a good agreement is achieved. As shown in Figure 9(a) and Figure 9(b), two regions of the fluid can be observed below the cylinder where the pressure is significantly lower than the surrounding fluid domain, and this phenomenon can still be observed at vt/r = 2 by the IB-MLBFS (Figure 9(b)) but not by SPH (Figure 9(a)). By comparing Figure 9(c) and Figure 9(d), the thickness of the liquid fluid layer and the deformation of the free interface surrounding the cylinder are nearly the same. Nevertheless, the free interface and contact interface of the cylinder presented by the IB-MLBFS in Figure 9(d) show clear deformation because of the surface tension force and surface tension flux correction. Moreover, the fluid layer shown in Figure 9(c) is enclosed because the structure and thickness of the free interface are thick, whereas the layer by the present method shown in Figure 9(d) is conserved well on the solid boundary. Furthermore, the thickness of the free interface is thin enough to represent the detailed deformation.
For Fr = 0.462 7, the gravity and viscosity of the liquid fluid can lead to a complex free interface (Figure 10). Although the fluid below the cylinder still exits two regions with lower pressure, the difference in the pressure is less. For the deformation of the free interface, compared with the results shown in Figure 9, the thickness of the fluid layer above the cylinder is less at vt/r = 0 when Fr = 0.462 7, and then it can hardly maintain but slide to the two sides at vt/r = 1, as the gravity is predominant, and less liquid fluid is lifted at vt/r = 2. As shown in Figure 10(b), two jets appear on the free interface and the gaseous fluid is observed under the free interface, which indicates that the gaseous fluid is mixed with liquid fluid and complex deformation may occur. In investigating this deformation, the detailed density contour at vt/r = 1.5 is shown in Figure 11. Two narrow gaseous gaps are generated on both sides of fluids below the cylinder because the liquid fluid lifted by the cylinder drops, whereas that from each side moves to the middle, and it does not occur at vt/r = 2 (Figure 9(d)) because the viscosity of the fluid is predominant rather than the gravity at that time under Fr = 0.764 4.
Apart from the deformation of the free interface, the time domain Ce under the two different Froude numbers are plotted in Figure 12. Comparing present results with experimental results, the trend of the results by the IBMLBFS is highly consistent with that of the experimental results over time. The amplitude of Ce predicted by the IBMLBFS is close to that predicted by other numerical methods. Although Ce obtained by other solvers are smooth curves, the IB-MLBFS can successfully predict the oscillation curve of Ce with time, which is consistent with the experimental results.
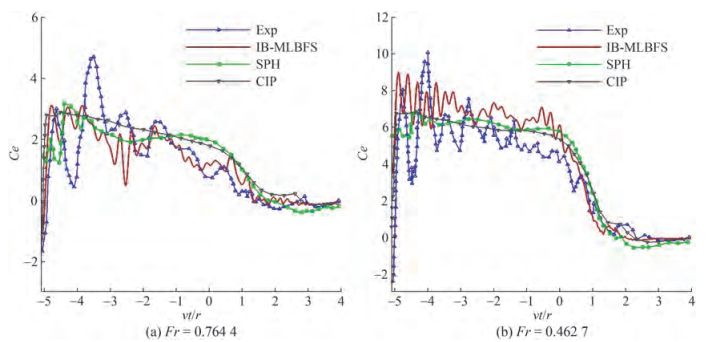 Figure 12 Comparison of the coefficient of the vertical force of the cylinder among the current IB-MLBFS, SPH (Zhang et al. 2017), CIP (Zhu et al. 2007), and experiment (Miao 1989)
Figure 12 Comparison of the coefficient of the vertical force of the cylinder among the current IB-MLBFS, SPH (Zhang et al. 2017), CIP (Zhu et al. 2007), and experiment (Miao 1989)4.3 Water exit and re-entry of a free circular cylinder
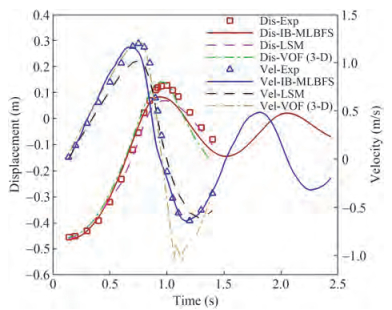
In this section, the water exit and re-entry of a free circular cylinder are presented. Different from water exit with constant velocity, the cylinder in this section is free from gravity, which interacts with fluid dynamically. Once the cylinder is lighter than the heavy fluid and fully submerged under the free interface, the cylinder moves up as it accelerates from a static state under buoyancy and partly exits the free interface as the pressure is predominant. Afterward, it slows down and reaches the summit under the predominant gravity, and finally drops down and re-enters the water. This procedure may repeat several times until the cylinder finally reaches a static state because of the viscosity of the fluids, and the complex deformation of the free interface requires computational stability and accuracy in capturing the contact interface between the multiphase fluids and moving solid structure for the numerical solver. Colicchio et al. (2009) studied the phenomenon by experiment and LSM, and Moshari et al. (2014) represented a numerical study by VOF. The abovementioned solvers successfully simulated the water exit of a free circular cylinder, and the results were consistent with the experiment. Nonetheless, the water re-entry phase has not been well simulated because of the complex deformation shape of the free interface. In this section, the phenomenon obtained by the experiment is represented by the IB-MLBFS. The cylinder, with a density of 0.62 times that of water and a diameter of 0.3 m, is fully submerged with its center at a depth of 0.46 m from the undisturbed free interface. The computational domain is set as 9D × 7D, and the bounceback boundary condition is applied on the left, right and bottom sides of the tank, whereas the pressure-outlet boundary condition is applied on the top.
The pressure and density contours for the evolution of water exit and re-entry of a circular cylinder at time 0.25 s ≤ t ≤ 2.00 s are illustrated in Figure 13 and Figure 14, respectively. Figure 15 shows the time-domain displacement and velocity of the cylinder from water exit to water re-entry. The deformation of the free interface and the hydrodynamic response of the cylinder are clearly demonstrated. In the present simulation results, the cylinder accelerates to the maximum velocity at t = 0.69 s, meanwhile, the fluids are driven with velocity. Hence, the pressure under the cylinder is greater than that at other times (Figure 13(c)). Then, it reaches the summit at t = 0.95 s, and the fluids lifted by the cylinder have dropped and collide with the fluids coming from each side, which leads to complex deformation of the free interface (Figure 14(d)). Afterward, the cylinder drops with the fluids surrounding it, re-enters the water, separates the fluids below to each side, and reaches the lowest depth at t = 1.51 s (Figure 14(f) and Figure 13(f)). In this procedure, the two regions with lower pressure are formed because the fluids slide from the cylinder and move to the sides. Notably, the separated liquid fluid moves back to the middle and climbs up to the surface of the cylinder at t = 1.75 s (Figure 14 (g)), and then slides down again when the cylinder moves up under buoyancy (Figure 14 (h)). This simulation shows the stability and accuracy of the IB-MLBFS as the buoyancy acting on the cylinder is generated by the pressure of the fluids and the complex deformation of the free interface is well captured on the moving boundary of the structure.
5 Conclusions
In this work, the deformation of the free interface during water entry and exit of a circular cylinder was investigated numerically by the IB-MLBFS. Implementing the IBM, the implicit velocity correction and surface flux correction were appended to the LBFS, hence, the IB-MLBFS can deal with the multiphase fluids-structure interaction. The accuracy of the solver was validated and the numerical simulation was well represented.
First, the simulation of water entry of a circular cylinder was presented. The reliability of 2D simulation was verified by comparing with experiment which considered different length-diameter ratios, and the deformation of the free interface was investigated. Then, the less-researched water exit of a circular cylinder with constant velocity was simulated. By considering different Froude numbers, the deformation of the free interface was investigated and the influence of gravity, viscosity and velocity was studied. Finally, the water exit and re-entry of a free circular cylinder were simulated. The complex deformation of the free interface and hydrodynamic response of the cylinder were well investigated, and all the numerical results were consistent with the experiments. The IB-MLBFS not only successfully simulated the complex phenomena but also achieved accuracy and stability to a certain extent compared with other solvers.
In this work, only the circular shape of the moving structure was considered, and the collision and rotation were ignored because the present work focused on the free interface of the fluid domain. Moreover, the present solver is direct numerical simulation, which can hardly apply coarse mehes to a high Reynolds number phenomena, such as the turbulent flow. Future work may introduce the Large Eddy Simulation to the IB-MLBFS and apply the current solver to interacting multi-structures and complex shapes, which may lead to the wider application of the solver in engineering.
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and thesource, provide a link to the Creative Commons licence, and indicateif changes were made. The images or other third party material in thisarticle are included in the article’s Creative Commons licence, unlessindicated otherwise in a credit line to the material. If material is notincluded in the article’s Creative Commons licence and your intendeduse is not permitted by statutory regulation or exceeds the permitteduse, you will need to obtain permission directly from the copyrightholder. To view a copy of this licence, visit http:/creativecommons.org/licenses/by/4.0/. -
Figure 12 Comparison of the coefficient of the vertical force of the cylinder among the current IB-MLBFS, SPH (Zhang et al. 2017), CIP (Zhu et al. 2007), and experiment (Miao 1989)
Table 1 Ratios and values of the basic quantities
Parameter Length Mass Time Ratio L′ = 103 M′ = 106 T′ = 105 Phys 1 (m) 1 (kg) 1 (s) LBFS 103 106 105 Table 2 Ratios and values of the derived quantities
Velocity Acceleration Force Pressure Ratio L′T′−1 = 10−2 L′T′−2 = 10−7 M′L′T′−2 = 10−1 M′L′1T′−2 = 10−7 Phys 1 (m/s) 1 (m/s2) 1 (N) 1 (Pa) LBFS 10−2 10−7 10−1 10−7 -
Bussmann M, Chandra S, Mostaghimi J (2000) Modeling the splash of a droplet impacting a solid surface. Physics of Fluids 12: 3121-3132. https://doi.org/10.1063/1.1321258 Bussmann M, Mostaghimi J, Chandra S (1999) On a three-dimensional volume tracking model of droplet impact. Physics of Fluids 11: 1406–1417. https://doi.org/10.1063/1.870005 Chen GQ, Zhang AM, Liu NN, Wang Y (2021) Development of an immersed boundary-multiphase lattice Boltzmann flux solver with high density ratio for contact line dynamics. Physics of Fluids 33: 057101. https://doi.org/10.1063/5.0043604 Chen Z, Shu C (2020a) Simplified lattice Boltzmann method for non-Newtonian power-law fluid flows. Int J Numer Methods Fluids 92: 38–54. https://doi.org/10.1002/fld.4771 Chen Z, Shu C (2020b) On numerical diffusion of simplified lattice Boltzmann method. Int J Numer Methods Fluids 92: 1198–1211. https://doi.org/10.1002/fld.4823 Chen Z, Shu C, Tan D (2017) A truly second-order and unconditionally stable thermal lattice boltzmann method. Applied Sciences 7: 277. https://doi.org/10.3390/app7030277 Chen Z, Shu C, Tan DS (2018) The simplified Lattice Boltzmann method on non-uniform meshes. Commun Comput Phys 23: 1131–1149. https://doi.org/10.4208/cicp.OA-2016-0184 Chen Z, Shu C, Yang LM, Zhao X, Liu NY (2020) Immersed boundary-simplified thermal lattice Boltzmann method for incompressible thermal flows. Physics of Fluids 32: 013605. https://doi.org/10.1063/1.5138711 Colicchio G, Greco M, Miozzim M, Lugni C (2009) Experimental and numerical investigation of the water-entry and water-exit of a circular cylinder. 24th International Workshop on Water Waves and Floating Bodies, St. Petersburg, Russia de Rosis A (2017) A central moments-based lattice Boltzmann scheme for shallow water equations. Comput Methods Appl Mech Eng 319: 379–392. https://doi.org/10.1016/j.cma.2017.03.001 DeZeeuw D, Powell KG (1993) An adaptively refined cartesian mesh solver for the euler equations. J Comput Phys 104: 56–68. https://doi.org/10.1006/jcph.1993.1007 Fedkiw RP, Aslam T, Merriman B, Osher S (1999) A non-oscillatory Eulerian approach to interfaces in multimaterial flows (the Ghost Fluid method). J Comput Phys 152: 457–492. https://doi.org/10.1006/jcph.1999.6236 Galindo-Torres SA (2013) A coupled discrete element Lattice Boltzmann method for the simulation of fluid-solid interaction with particles of general shapes. Comput Methods Appl Mech Eng 265: 107–119. https://doi.org/10.1016/j.cma.2013.06.004 Galindo-Torres SA, Scheuermann A, Li L (2016) Boundary effects on the soil water characteristic curves obtained from lattice Boltzmann simulations. Comput Geotech 71: 136–146. https://doi.org/10.1016/j.compgeo.2015.09.008 Galindo-Torres SA, Scheuermann A, Li L, Pedrosoa DM, Williams DJ (2013) A Lattice Boltzmann model for studying transient effects during imbibition-drainage cycles in unsaturated soils. Comput Phys Commun 184: 1086–1093. https://doi.org/10.1016/j.cpc.2012.11.015 Guo Z, Zheng C, Shi B (2002) Discrete lattice effects on the forcing term in the lattice Boltzmann method. Phys Rev E 65: 046308. https://doi.org/10.1103/PhysRevE.65.046308 Huang JJ, Shu C, Chew YT (2009a) Mobility-dependent bifurcations in capillarity-driven two-phase fluid systems by using a lattice Boltzmann phase-field model. Int J Numer Methods Fluids 60: 203–225. https://doi.org/10.1002/fld.1885 Huang JJ, Shu C, Chew YT (2009b) Lattice Boltzmann study of droplet motion inside a grooved channel. Physics of Fluids 21: 022103. https://doi.org/10.1063/1.3077800 Le DV, Khoo BC, Peraire J (2006) An immersed interface method for viscous incompressible flows involving rigid and flexible boundaries. J Comput Phys 220: 109–138. https://doi.org/10.1016/j.jcp.2006.05.004 Lee L, LeVeque RJ (2003) An Immersed Interface Method for Incompressible Navier-Stokes Equations. SIAM Journal on Scientific Computing 25: 832–856. https://doi.org/10.1137/S1064827502414060 Lee T, Liu L (2010) Lattice Boltzmann simulations of micron-scale drop impact on dry surfaces. J Comput Phys 229: 8045–8063. https://doi.org/10.1016/j.jcp.2010.07.007 LeVeque RJ, Li Z (1994) The immersed interface method for Elliptic Equations with discontinuous coefficients and singular sources. SIAM J Numer Anal 31: 1019–1044. https://doi.org/10.1137/0731054 Li Z, Lai MC (2001) The immersed interface method for the Navier-Stokes Equations with singular forces. J Comput Phys 171: 822–842. https://doi.org/10.1006/jcph.2001.6813 Lin LS, Chang HW, Lin CA (2013) Multi relaxation time lattice Boltzmann simulations of transition in deep 2D lid driven cavity using GPU. Comput Fluids 80: 381–387. https://doi.org/10.1016/j.compfluid.2012.01.018 Liu H, Li H, Ding H (2017) Simulation of flows with moving contact lines on a dual-resolution Cartesian grid using a diffuse-interface immersed-boundary method. Journal of Hydrodynamics 29: 774–781. https://doi.org/10.1016/S1001-6058(16)60788-6 Liu HR, Ding H (2015) A diffuse-interface immersed-boundary method for two-dimensional simulation of flows with moving contact lines on curved substrates. J Comput Phys 294: 484–502. https://doi.org/10.1016/j.jcp.2015.03.059 Liu XD, Fedkiw RP, Kang M (2000) A boundary condition capturing method for Poisson's equation on irregular domains. J Comput Phys 160: 151–178. https://doi.org/10.1006/jcph.2000.6444 Lu J, Lei H, Dai C, Yang L, Shu C (2022) Analyses and reconstruction of the lattice Boltzmann flux solver. J Comput Phys 453: 110923. https://doi.org/10.1016/j.jcp.2021.110923 Mehravaran M, Hannani SK (2008) Simulation of incompressible two-phase flows with large density differences employing lattice Boltzmann and level set methods. Comput Methods Appl Mech Eng 198: 223–233. https://doi.org/10.1016/j.cma.2008.07.015 Miao G (1989) Hydrodynamic forces and dynamic responses of circular cylinders on wave zones PhD. thesis, Norwegian University of Science and Technology Mittal R, Iaccarino G (2005) Immersed boundary methods. Annu Rev Fluid Mech 37: 239–261. https://doi.org/10.1146/annurev.fluid. 37.061903.175743 https://doi.org/10.1146/annurev.fluid.37.061903.175743 Moshari S, Nikseresht AH, Mehryar R (2014) Numerical analysis of two and three dimensional buoyancy driven water-exit of a circular cylinder. International Journal of Naval Architecture and Ocean Engineering 6: 219–235. https://doi.org/10.2478/IJNAOE-2013-0174 Peskin CS (1972) Flow patterns around heart valves: A numerical method. J Comput Phys 10: 252–271. https://doi.org/10.1016/0021-9991(72)90065-4 Peskin CS (2002) The immersed boundary method. Acta Numerica 11: 479–517. https://doi.org/10.1017/S0962492902000077 Renardy M, Renardy Y, Li J (2001) Numerical simulation of moving contact line problems using a volume-of-fluid method. J Comput Phys 171: 243–263. https://doi.org/10.1006/jcph.2001.6785 Ru Z, Liu H, Xing L, Ding Y (2021) A well-balanced lattice Boltzmann model for the depth-averaged advection-diffusion equation with variable water depth. Comput Methods Appl Mech Eng 379: 113745. https://doi.org/10.1016/j.cma.2021.113745 Shao JY, Shu C, Chew YT (2013) Development of an immersed boundary-phase field-lattice Boltzmann method for Neumann boundary condition to study contact line dynamics. J Comput Phys 234: 8–32. https://doi.org/10.1016/j.jcp.2012.08.040 Shukla RK, Tatineni M, Zhong X (2007) Very high-order compact finite difference schemes on non-uniform grids for incompressible Navier-Stokes equations. J Comput Phys 224: 1064–1094. https://doi.org/10.1016/j.jcp.2006.11.007 Sun P, Zhang AM, Marrone S, Ming F (2018) An accurate and efficient SPH modeling of the water entry of circular cylinders. Applied Ocean Research 72: 60–75. https://doi.org/10.1016/j.apor.2018.01.004 Sun SL, Liu BW, Zhang AM (2019) On the fully nonlinear water entry of a cone in Stokes wave. Eng Anal Bound Elem 98: 232–242. https://doi.org/10.1016/j.enganabound.2018.10.019 Verdier W, Kestener P, Cartalade A (2020) Performance portability of lattice Boltzmann methods for two-phase flows with phase change. Comput Methods Appl Mech Eng 370: 113266. https://doi.org/10.1016/j.cma.2020.113266 Wang N, Korba D, Liu Z, Prabhu R, Priddy MW, Yang S, Chen L, Li L (2021) Phase-field-lattice Boltzmann method for dendritic growth with melt flow and thermosolutal convection-diffusion. Comput Methods Appl Mech Eng 385: 114026. https://doi.org/10.1016/j.cma.2021.114026 Wang P, Zhang AM, Ming F, Sun P, Cheng N (2019a) A novel non-reflecting boundary condition for fluid dynamics solved by smoothed particle hydrodynamics. J Fluid Mech 860: 81–114. https://doi.org/10.1017/jfm.2018.852 Wang Y, Shu C, Huang HB, Teo CJ (2015a) Multiphase lattice Boltzmann flux solver for incompressible multiphase flows with large density ratio. J Comput Phys 280: 404–423. https://doi.org/10.1016/j.jcp.2014.09.035 Wang Y, Shu C, Teo CJ, Wu J (2015b) An immersed boundary-lattice Boltzmann flux solver and its applications to fluid-structure interaction problems. J Fluids Struct 54: 440–465. https://doi.org/10.1016/j.jfluidstructs.2014.12.003 Wang Y, Shu C, Wang TG, Valdivia Y Alvarado P (2019b) A generalized minimal residual method-based immersed boundary-lattice Boltzmann flux solver coupled with finite element method for non-linear fluid-structure interaction problems. Physics of Fluids 31: 103603. https://doi.org/10.1063/1.5119205 Wang Y, Shu C, Yang LM (2015c) An improved multiphase lattice Boltzmann flux solver for three-dimensional flows with large density ratio and high Reynolds number. J Comput Phys 302: 41–58. https://doi.org/10.1016/j.jcp.2015.08.049 Wang Y, Shu C, Yang LM, Teo CJ (2017) An immersed boundary-lattice boltzmann flux solver in a moving frame to study three-dimensional freely falling rigid bodies. J Fluids Struct 68: 444–465. https://doi.org/10.1016/j.jfluidstructs.2016.11.005 Wang Y, Yang L, Shu C (2015d) From lattice Boltzmann method to lattice Boltzmann flux solver. Entropy 17: 7713–7735. https://doi.org/10.3390/e17117713 Wei Z, Hu C (2014) An experimental study on water entry of horizontal cylinders. J Mar Sci Technol 19: 338–350. https://doi.org/10.1007/s00773-013-0252-z Wu J, Shu C (2009) Implicit velocity correction-based immersed boundary-lattice Boltzmann method and its applications. J Comput Phys 228: 1963–1979. https://doi.org/10.1016/j.jcp.2008.11.019 Xiao Y, Zhang G, Hui D, Yan H, Feng S, Wang S (2022) Numerical simulation for water entry and exit of rigid bodies based on the immersed boundary-lattice Boltzmann method. J Fluids Struct 109: 103486. https://doi.org/10.1016/j.jfluidstnicts.2021.103486 Yan H, Zhang G, Wang S, Hui D, Zhou B (2021) Simulation of vortex shedding around cylinders by immersed boundary-lattice Boltzmann flux solver. Applied Ocean Research 114: 102763. https://doi.org/10.1016/j.apor.2021.102763 Yan H, Zhang G, Xiao Y, Hui D, Wang S (2022) A surface flux correction-based immersed boundary-multiphase lattice Boltzmann flux solver applied to multiphase fluids-structure interaction. Comput Methods Appl Mech Eng 400: 115481. https://doi.org/10.1016/j.cma.2022.115481 Yang L, Shu C, Chen Z, Hou G, Wang Y (2021) An improved multiphase lattice Boltzmann flux solver for the simulation of incompressible flow with large density ratio and complex interface. Physics of Fluids 33: 033306. https://doi.org/10.1063/5.0038617 Yang L, Shu C, Yu Y, Wang Y (2020a) A mass-conserved fractional step axisymmetric lattice Boltzmann flux solver for incompressible multiphase flows with large density ratio. Physics of Fluids 32: 103308. https://doi.org/10.1063/5.0022050 Yang L, Yu Y, Hou G, Wang K, Xiong Y (2018) Boundary conditions with adjustable slip length for the lattice Boltzmann simulation of liquid flow. Comput Fluids 174: 200–212. https://doi.org/10.1016/j.compfluid.2018.08.002 Yang L, Yu Y, Pei H, Gao Y, Hou G (2019) Lattice Boltzmann simulations of liquid flows in microchannel with an improved slip boundary condition. Chem Eng Sci 202: 105–117. https://doi.org/10.1016/j.ces.2019.03.032 Yang L, Yu Y, Yang L, Hou G (2020b) Analysis and assessment of the no-slip and slip boundary conditions for the discrete unified gas kinetic scheme. Phys Rev E 101: 023312. https://doi.org/10.1103/PhysRevE.101.023312 Zhang A, Sun P, Ming F, Colagrossi A (2017) Smoothed particle hydrodynamics and its applications in fluid-structure interactions. Journal of Hydrodynamics 29: 187–216. https://doi.org/10.1016/S1001-6058(16)60730-8 Zhang P, Sun S, Chen Y, Galindo-Torres SA, Cui W (2021) Coupled material point Lattice Boltzmann method for modeling fluid-structure interactions with large deformations. Comput Methods Appl Mech Eng 385: 114040. https://doi.org/10.1016/j.cma.2021.114040 Zhou H, Mo G, Wu F, Zhao J, Rui M, Cen K (2012) GPU implementation of lattice Boltzmann method for flows with curved boundaries. Comput Methods Appl Mech Eng 225–228: 65–73. https://doi.org/10.1016/j.cma.2012.03.011 Zhu X, Faltinsen OM, Hu C (2007) Water entry and exit of a horizontal circular cylinder. Journal of Offshore Mechanics and Arctic Engineering 129: 253–264. https://doi.org/10.1115/1.2199558