Overview of Moving Particle Semi-implicit Techniques for Hydrodynamic Problems in Ocean Engineering
https://doi.org/10.1007/s11804-022-00284-9
-
Abstract
With the significant development of computer hardware, many advanced numerical techniques have been proposed to investigate complex hydrodynamic problems. This article aims to provide a detailed review of moving particle semi-implicit (MPS) techniques and their application in ocean and coastal engineering. The achievements of the MPS method in stability and accuracy, boundary conditions, and acceleration techniques are discussed. The applications of the MPS method, which are classified into two main categories, namely, multiphase flows and fluid-structure interactions, are introduced. Finally, the prospects and conclusions are highlighted. The MPS method has the potential to solve practical problems.Article Highlights• A detailed review of MPS techniques and their application in ocean and coastal engineering are presented.• The achievements of the MPS method in stability and accuracy, boundary conditions, and acceleration techniques are discussed.• The applications in multiphase flows and fluid-structure interactions are introduced.• The future perspectives of MPS techniques are highlighted. -
1 Introduction
The ocean environment is closely tied to human life and health. Products are transported from one region to another by sea, and the cost of transport by sea is the lowest, which promotes economic globalization. With the further exploitation of marine resources, industrialization has been further accelerated. Although human beings benefit from marine resources, they also suffer from marine disasters. Tsunamis induced by earthquakes destroy inshore facilities and threaten the safety of people (Hayashi and Hughes 2013). To better adapt to the ocean environment and fully utilize marine resources, the hydrodynamic problems in the field of ocean and coastal engineering were investigated by researchers. In the past decades, computational fluid dynamics techniques have advanced by leaps and bounds. With the assistance of numerical tools, more comprehensive information on the flow field can be obtained at a lower cost.
Particle-based methods exhibit their superiority in three main aspects. First, there are not topological relationships among Lagrangian particles. Therefore, particle-based methods can better capture the free surface and interface with large deformation. Second, in the simulations of moving boundaries with mesh-based methods, errors will be introduced because of the deformation of the mesh. Remeshing is needed to avoid ill-shaped meshes, which is time-consuming (Sun et al. 2019). Particle-based methods can simulate moving boundaries without additional processing. Third, based on the Lagrangian view, the momentum equation of the particle-based method has no convection term. Accordingly, the numerical diffusion induced by the calculation of the advection term is avoided. Smoothed particle hydrodynamics (SPH) and moving particle semiimplicit (MPS) techniques are two mainstream particlebased methods. SPH was first proposed to solve astrophysical problems (Gingold and Monaghan 1977; Lucy 1977) and was subsequently applied to the hydrodynamic (Monaghan 1994) and structural dynamics (Antoci 2007) problems. Based on the hypothesis that the fluid is weakly compressible, the pressure distribution of the flow field can be obtained by explicitly solving the equation of state. The SPH can be easily parallelized with less efficiency loss (Ferrari et al. 2009). However, because of the pressure fluctuation, the original SPH cannot be further extended to complex problems. MPS was first developed to solve the hydrodynamic problems of nuclear engineering (Koshizuka and Oka 1996). The pressure is calculated by solving the pressure Poisson equation (PPE), which consumes the most time during the MPS simulation. The parallelization of MPS, particularly of PPE, is more difficult than that of SPH, and its parallelization efficiency is not as high as that of SPH. Therefore, further enlarging the simulation scale of MPS is difficult. Because of the prediction-correction semi-implicit scheme, the MPS performs better than the original SPH in terms of stability (Luo et al. 2021). In the past years, many numerical techniques have been proposed and introduced to SPH and MPS, and their stability and computational efficiency have been improved dramatically.
Many excellent review articles about particle-based methods have been published. Luo et al. (2021) comprehensively introduced the advances of particle-based methods and their applications in ocean and coastal engineering. The review published by Li et al. (2020) focused on the MPS method and its application in nuclear engineering. Gotch et al. (2021) reviewed the particle-based methods for fluid-structure interactions (FSI) in ocean engineering in three aspects, namely, reliability, adaptivity, and generality. This paper aims to provide a review of the latest advances in the MPS method and their application in the field of ocean and coastal engineering. First, the achievements of the MPS method in stability and accuracy, boundary conditions, and acceleration techniques are briefly summarized. Then, the applications of the MPS method in the field of ocean and coastal engineering are presented. Finally, future works for further improvement and potential application of MPS are discussed. A brief conclusion is drawn as well.
2 Review of the MPS method
2.1 Original MPS method
The governing equations for fluid include the continuity and Navier-Stokes (N-S) equations, which can be written as follows:
$$ \nabla \cdot \boldsymbol{U}=0 $$ (1) $$ \frac{\mathrm{D} \boldsymbol{U}}{\mathrm{D} t}=-\frac{1}{\rho} \nabla P+v \nabla^2 \boldsymbol{U}+\boldsymbol{g} $$ (2) where U, ρ, P, and ν are the velocity, density, pressure, and kinematic viscosity of the fluid, respectively, t is the physical time, and g is the gravity vector.
The particle interaction models, which contain the gradient, divergence, and Laplacian models, are used to discretize the governing equations (Koshizuka and Oka 1996), which can be expressed as follows:
$$ \langle\nabla P\rangle_i=\frac{d}{n^0} \sum\limits_{j \neq i} \frac{P_j-P_i}{\left|\boldsymbol{r}_j-\boldsymbol{r}_i\right|^2}\left(\boldsymbol{r}_j-\boldsymbol{r}_i\right) W\left(\left|\boldsymbol{r}_j-\boldsymbol{r}_i\right|\right) $$ (3) $$ \langle\nabla \cdot \boldsymbol{U}\rangle_i=\frac{d}{n^0} \frac{\left(\boldsymbol{r}_j-\boldsymbol{r}_i\right) \cdot\left(\boldsymbol{U}_j-\boldsymbol{U}_i\right)}{\left|\boldsymbol{r}_j-\boldsymbol{r}_i\right|^2} W\left(\left|\boldsymbol{r}_j-\boldsymbol{r}_i\right|\right) $$ (4) $$ \left\langle\nabla^2 \phi\right\rangle_i=\frac{2 d}{n^0 \lambda} \sum\limits_{j \neq i}\left(\phi_j-\phi_i\right) W\left(\left|\boldsymbol{r}_j-\boldsymbol{r}_i\right|\right) $$ (5) where i and j are the subscripts of fluid particles, d is the dimensions of the space, ϕ is the physical value of the MPS particle, n0 is initial particle density, r is the position vector relative to origin and λ is a parameter used to compensate for the errors resulting from the limited range of the kernel function (Koshizuka and Oka 1996).
The pressure information of MPS particles is obtained by solving the PPE as follows:
$$ \left\langle\nabla^2 P^{n+1}\right\rangle_i=-\frac{\rho}{\Delta t^2} \frac{\left\langle n^*\right\rangle_i-n^0}{n^0} $$ (6) where Pk + 1 is the pressure of the step k + 1 and Δt is the time step.
Based on the difference in the particle density between free-surface and internal particles, the original criteria of free-surface detection can be expressed as follows:
$$ \langle n\rangle_i^* <\beta n^0 $$ (7) 2.2 Stability and accuracy
2.2.1 Modification of gradient model
The original gradient model has several drawbacks. When the interparticle interaction strength increases as the particles approach, the tensile instability may occur because of the presence of attractive interparticle forces (Khayyer and Gotoh 2011). To improve the stability of simulations, Koshizuka et al. (1998) proposed an improved gradient model (Eq. (8)), in which the pressure of particle i was altered by the minimum pressure among the neighboring particles so that the interparticle forces were repulsion. A gradient model (Eq. (9)) with exact conservation of linear momentum and significantly enhanced preservation of angular momentum was proposed by Khayyer and Gotoh (2008). The interparticle forces of two neighboring particles are equal and opposite. Another conservative formulation of the gradient model (Eq. (10)) was proposed by Tanaka and Masunaga (2010). If the MPS particles distribute uniformly, then the aforementioned gradient models are equivalent to the original gradient model. If the MPS particles distribute nonuniformly, then the artificial repulsive force drives the MPS particles from high to low concentrations; its basic concept is similar to that of the particle shifting (PS) technique.
$$ \langle\nabla P\rangle_i=\frac{d}{n^0} \sum\limits_{j \neq i} \frac{P_j-P_{i \min }}{\left|\boldsymbol{r}_j-\boldsymbol{r}_i\right|^2}\left(\boldsymbol{r}_j-\boldsymbol{r}_i\right) W\left(\left|\boldsymbol{r}_j-\boldsymbol{r}_i\right|\right) $$ (8) $$ \begin{aligned} &\langle\nabla P\rangle_i=\frac{d}{n^0} \sum\limits_{j \neq i} \frac{\left(P_j+P_i\right)-\left(P_{j \min }+P_{i \min }\right)}{\left|\boldsymbol{r}_j-\boldsymbol{r}_i\right|^2} \\ &\left(\boldsymbol{r}_j-\boldsymbol{r}_i\right) W\left(\left|\boldsymbol{r}_j-\boldsymbol{r}_i\right|\right) \end{aligned} $$ (9) $$ \langle\nabla P\rangle_i=\frac{d}{n^0} \sum\limits_{j \neq i} \frac{P_j+P_i}{\left|\boldsymbol{r}_j-\boldsymbol{r}_i\right|^2}\left(\boldsymbol{r}_j-\boldsymbol{r}_i\right) W\left(\left|\boldsymbol{r}_j-\boldsymbol{r}_i\right|\right) $$ (10) According to the analysis by Tsuruta (2013), the artificial repulsive force rather than the original gradient force was predominant in Eqs. (8) and (9), which might lead to the unphysical motion and perturbations of fluid particles. To solve this problem, a meticulously adequate stabilizing force was introduced to the original gradient model, as expressed in Eq. (11):
$$ \begin{aligned} &\langle\nabla P\rangle_i=\frac{d}{n^0} \sum\limits_{j \neq i} \frac{P_j-P_i}{\left|\boldsymbol{r}_j-\boldsymbol{r}_i\right|^2}\left(\boldsymbol{r}_j-\boldsymbol{r}_i\right) W\left(\left|\boldsymbol{r}_j-\boldsymbol{r}_i\right|\right) \\ &+\frac{1}{n_0} \sum\limits_{j \neq i} \boldsymbol{F}_{i j}^{\mathrm{DS}} w\left(\left|\boldsymbol{r}_j-\boldsymbol{r}_i\right|\right) \end{aligned} $$ (11) where FijDS is the stabilizing force for target particle i from neighboring particle j.
The error term of the original gradient model is zero-order convergence (Duan et al. 2019). The discretization error can be reduced, and the accuracy of the gradient model can be improved after high-order schemes are adopted. Khayyer and Gotoh (2011) proposed a corrective matrix based on the Taylor series expansion for a more accurate approximation of pressure gradient, as expressed in the following equations:
$$ \langle\nabla P\rangle_i=\frac{d}{n^0} \sum\limits_{j \neq i} \frac{P_j-P_i}{\left|\boldsymbol{r}_j-\boldsymbol{r}_i\right|^2}\left(\boldsymbol{r}_j-\boldsymbol{r}_i\right) \boldsymbol{C}_{i j} W\left(\left|\boldsymbol{r}_j-\boldsymbol{r}_i\right|\right) $$ (12) $$ \boldsymbol{C}_{i j}=\left(\begin{array}{cc} \sum V_{i j} \frac{W_{i j} x_{i j}^2}{r_{i j}^2} & \sum V_{i j} \frac{W_{i j} x_{i j} y_{i j}}{r_{i j}^2} \\ \sum V_{i j} \frac{W_{i j} x_{i j} y_{i j}}{r_{i j}^2} & \sum V_{i j} \frac{W_{i j} y_{i j}^2}{r_{i j}^2} \end{array}\right)^{-1} $$ (13) $$ V_{i j}=\frac{1}{\sum\limits_{i \neq j} W_{i j}} $$ (14) Wang et al. (2017) introduced the corrective matrix to Eq. (8) and obtained a stabilized gradient model as follows:
$$ \langle\nabla \phi\rangle_i=\frac{d}{n^0} \sum\limits_{j \neq i} \frac{P_j-P_{i \min }}{\left|\boldsymbol{r}_j-\boldsymbol{r}_i\right|^2}\left(\boldsymbol{r}_j-\boldsymbol{r}_i\right) \boldsymbol{C}_{i j} W\left(\left|\boldsymbol{r}_j-\boldsymbol{r}_i\right|\right) $$ (15) If the particle distribution is anisotropic, then the zero-order discretization error will be introduced. Hence, dummy particles were introduced to the neighboring field to compensate for the zero-order discretization error of the gradient model (Liu et al. 2018), as shown in Figure 1. The more accurate and stable gradient model can be written as follows
$$ \begin{aligned} &\langle\nabla P\rangle_i=\frac{d}{n^0}\left(\sum\limits_{j \neq i} \frac{P_j-P_{i \min }}{\left|\boldsymbol{r}_j-\boldsymbol{r}_i\right|^2}\left(\boldsymbol{r}_j-\boldsymbol{r}_i\right) \tilde{\boldsymbol{C}}_i W\left(\left|\boldsymbol{r}_j-\boldsymbol{r}_i\right|\right)\right. \\ &\left.+\frac{P_d-P_{i \min }}{\left|\boldsymbol{r}_d-\boldsymbol{r}_i\right|^2}\left(\boldsymbol{r}_d-\boldsymbol{r}_i\right) \tilde{\boldsymbol{C}}_{i j} W\left(\left|\boldsymbol{r}_d-\boldsymbol{r}_i\right|\right)\right) \end{aligned} $$ (16) $$ \tilde{\boldsymbol{C}}_{i j}=\\ \left[\begin{array}{c} \left.\frac{d}{n^0}\left(\sum \frac{W_{i j} x_{i j}^2}{r_{i j}^2}+\frac{W_{i d} x_{i d}^2}{r_{i d}^2}\right) \quad \frac{d}{n^0}\left(\sum \frac{W_{i j} x_{i j} y_{i j}}{r_{i j}^2}+\frac{W_{i d} x_{i d} y_{i d}}{r_{i d}^2}\right)\right]\\ \frac{d}{n^0}\left(\sum \frac{W_{i j} x_{i j} y_{i j}}{r_{i j}^2}+\frac{W_{i d} x_{i d} y_{i d}}{r_{i d}^2}\right) \quad \frac{d}{n^0}\left(\sum \frac{W_{i j} y_{i j}^2}{r_{i j}^2}+\frac{W_{i d} y_{i d}^2}{r_{i d}^2}\right) \end{array}\right]^{-1} $$ (17) 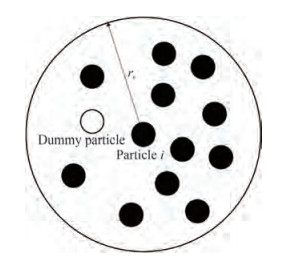 Figure 1 Estimated position of a dummy neighboring particle for particle i (Liu et al. 2018)
Figure 1 Estimated position of a dummy neighboring particle for particle i (Liu et al. 2018)where the subscript d represents the dummy particles.
Duan et al. (2019) developed a second-order corrective matrix (SCM) to further reduce the truncation error of the gradient model. Compared with the first-order corrective matrix, the SCM significantly reduces the discretization error.
$$ \langle\nabla P\rangle_i=\frac{1}{n^0} \sum\limits_{j \neq i} W\left(\left|\boldsymbol{r}_j-\boldsymbol{r}_i\right|\right) \frac{P_j-P_i}{\left|\boldsymbol{r}_j-\boldsymbol{r}_i\right|}\left(\left[\begin{array}{l} \boldsymbol{C}_1 \\ \boldsymbol{C}_2 \end{array}\right] \boldsymbol{P}\right) $$ (18) $$ \boldsymbol{C}_{\boldsymbol{i}}=\left[\begin{array}{cccc} \left(P_1, P_1\right) & \left(P_1, P_2\right) & \cdots & \left(P_1, P_5\right) \\ \left(P_2, P_1\right) & \left(P_2, P_2\right) & \cdots & \left(P_2, P_5\right) \\ \vdots & \vdots & \ddots & \vdots \\ \left(P_5, P_1\right) & \left(P_5, P_2\right) & \cdots & \left(P_5, P_5\right) \end{array}\right]^{-1} $$ (19) $$ \begin{aligned} &\boldsymbol{P}=\left[\begin{array}{lllll} \frac{x_{i j}}{r_{i j}} & \frac{y_{i j}}{r_{i j}} & \frac{x_{i j}^2}{l_0 r_{i j}} & \frac{y_{i j}^2}{l_0 r_{i j}} & \frac{x_{i j} y_{i j}}{l_0 r_{i j}} \end{array}\right]^{\mathrm{T}} \\ &=\left[\begin{array}{lllll} P_1 & P_2 & P_3 & P_4 & P_5 \end{array}\right]^{\mathrm{T}} \end{aligned} $$ (20) where $\left(P_\alpha, P_\beta\right)=\sum\limits_{j \neq i} P_\alpha \cdot P_\beta \frac{W_{i j}}{n_0}$
2.2.2 Modification of the PPE
The pressure distribution of the flow field is obtained by solving the PPE. Therefore, the construction and discretization of the equation are relative to the accuracy of the pressure calculation. The PPE consists of the Laplacian operator (left) and source term (right).
The original Laplacian model exhibits minus first order convergence (Duan et al. 2019). Khayyer and Gotch (2010; 2012) developed high-order Laplacian models (Eqs. (21) and (22)) based on the original MPS kernel function for 2D and 3D simulations. Duan et al. (2018) introduced a corrected vector to the Laplacian model to compensate for anisotropy error. The corrected model was proven to exhibit convergence and reduce unphysical fluctuation. Liu et al. (2018) used the dummy neighboring particle for the discretization of the Laplacian model (Eq. (25)); its basic principle was similar to that of the corrected vector (Duan et al. 2018). Duan et al. (2019) introduced the SCM to the Laplacian model (Eq. (26)), which exhibited first-order convergence.
$$ \left\langle\nabla^2 \phi\right\rangle_i=\frac{1}{n_0} \sum\limits_{i \neq j}\left(\phi_{i j} \frac{\partial^2 w_{i j}}{\partial r_{i j}^2}-\frac{\phi_{i j}}{r_{i j}} \frac{\partial w_{i j}}{\partial r_{i j}}\right) $$ (21) $$ \left\langle\nabla^2 \phi\right\rangle_i=\frac{1}{n_0} \sum\limits_{i \neq j}\left(\phi_{i j} \frac{\partial^2 W_{i j}}{\partial r_{i j}^2}\right) $$ (22) $$ \left\langle\nabla^2 \phi\right\rangle_i=\frac{d}{n^0} \sum\limits_{j \neq i}\left\{\left(\phi_j-\phi_i\right)\left(\frac{2}{\lambda}-\frac{\boldsymbol{L}_i \boldsymbol{C}_{i j}\left(\boldsymbol{r}_j-\boldsymbol{r}_i\right)}{\left|\boldsymbol{r}_j-\boldsymbol{r}_i\right|^2}\right) W_{i j}\right\} $$ (23) $$ \boldsymbol{L}_i=\left(\frac{2 d}{n^0 \lambda} \sum\limits_{j \neq i} x_{i j} W_{i j}, \frac{2 d}{n^0 \lambda} \sum\limits_{j \neq i} y_{i j} W_{i j}\right) $$ (24) $$ \nabla^2 \phi_i=\frac{2 d}{n^0}\left(\sum\limits_{j \neq i} \frac{\phi_j-\phi_i}{r_{i j}{ }^2} w_{i j}+\frac{\phi_d-\phi_i}{r_{i d}{ }^2} w_{i d}\right) $$ (25) $$ \left\langle\nabla^2 \phi\right\rangle_i=\frac{2}{n_0} \sum\limits_{j \neq i}\left\{w_{i j}\left(\phi_j-\phi_i\right) \frac{\left[\boldsymbol{C}_3+\boldsymbol{C}_4\right] \boldsymbol{P}}{l_0 r_{i j}}\right\} $$ (26) The construction of the PPE source term affects the accuracy and smoothness of the numerical flow field. In the original MPS, incompressibility is influenced by the particle number density (PND). However, the PND at each time step would not be exactly equal to the initial particle density, and the numerical errors would accumulate, which may result in considerable pressure fluctuation. Khayyer and Gotoh (2009) developed a high-order source term by calculating the time differentiation of PND based on the original kernel function. To balance the accuracy and continuity, many multiterm formulations for PPE are proposed. Kondo and Koshizuka (2011) derived a more generic formulation, including one main part and two error compensating parts, which could prevent density error accumulation. The coefficients α and β are obtained by hydrostatic pressure calculation, which would not be necessarily appropriate for other simulation cases, particularly for violent flows. Khayyer and Gotoh (2011) proposed the coefficients based on the features of instantaneous flow and applied the high-order schemes for the main part and error compensating parts. The incompressibility of the fluid can also be satisfied by the divergence-free condition. Tanaka and Masunaga (2010) proposed a novel PPE, which had both the advantages of the PND condition that the error was not stored and the advantages of the divergence-free condition that smoother pressure was obtained. The divergence-free term varies smoothly with time, which is similar to the first and second terms in Eqs. (28) and (29).
$$ \left\langle\nabla^2 \phi\right\rangle_i=-\frac{\rho}{n_0 \Delta t} \sum\limits_{j \neq i} \frac{r_e}{r_{i j}^3}\left(x_{i j} u_{i j}^*+y_{i j} v_{i j}^*\right) $$ (27) $$ \begin{aligned} &\frac{\Delta t}{\rho}\left\langle\nabla^2 \phi\right\rangle_i=\frac{n^*-2 n^k+n^{k-1}}{n_0 \Delta t}+\alpha \frac{1}{n_0} \frac{n^k-n^{k-1}}{\Delta t} \\ &+\beta \frac{1}{\Delta t} \frac{n^k-n_0}{n_0} \end{aligned} $$ (28) $$ \begin{array}{l} \frac{{\Delta t}}{\rho }{\left\langle {{\nabla ^2}\phi } \right\rangle _i} = \frac{1}{{{n_0}}}\left( {\frac{{{\rm{D}}n}}{{{\rm{D}}t}}} \right)_i^* + \left| {\left( {\frac{{{n^k} - {n_0}}}{{{n_0}}}} \right)} \right|\left[ {\frac{1}{{{n_0}}}\left( {\frac{{{\rm{D}}n}}{{{\rm{D}}t}}} \right)_i^k} \right]\\ + \left| {\left( {\frac{{\Delta t}}{{{n_0}}}\left( {\frac{{{\rm{D}}n}}{{{\rm{D}}t}}} \right)_i^k} \right)} \right|\left[ {\frac{1}{{\Delta t}}\left( {\frac{{{n^k} - {n_0}}}{{{n_0}}}} \right)} \right] \end{array} $$ (29) $$ \nabla^2 \phi=\frac{\rho}{\Delta t} \nabla \cdot \boldsymbol{U}^*+\frac{\rho}{\Delta t^2} \frac{n^0-n^k}{n^0} $$ (30) 2.2.3 PS schemes
The PS scheme can rearrange seriously distorted particle distribution and consider the transporting effects of shifts, which can also significantly reduce stability errors (Duan et al. 2019). Xu et al. (2009) first proposed the PS scheme based on Fick's law of diffusion, which moved particles from high to low concentrations. The PS scheme was integrated into the incompressible SPH (ISPH) framework and applied to the simulation of internal flows. Because of the incomplete kernel support, the free-surface particles' distribution may be distorted by PS. Lind et al. (2012) suggested reducing or eliminating the normal shifting of free-surface particles and applied the PS to the free-surface flows. However, this treatment may lead to numerical inconsistencies, including the unphysical diffusion of free-surface particles, increased level of perturbations, and/or an unphysical gap between free-surface and nearby particles (Khayyer et al. 2017). To overcome those drawbacks, Khayyer et al. (2017) proposed the optimized PS (OPS) and classified the shifting particles as splashing, free-surface, vicinity, and inner particles. The normal shifting of free-surface and vicinity particles is excluded. Compared with the PS (Lind et al. 2012), the OPS does not include any adjusting parameter and obtains more accurate numerical results. Duan et al. (2018) applied the OPS and conservative gradient model to produce the tangent shifting and normal adjustments of free-surface particles, respectively.
2.3 Boundary conditions
2.3.1 Free surface
In the MPS and other projection-based methods, the pressure exerted by the detected free-surface particles is set to a constant value, which is the Dirichlet boundary condition of PPE. However, if the inner particles are misjudged as the free-surface particles, then their calculated pressure and that of their neighbors would be incorrect, which may lead to pressure fluctuation. Therefore, a high-precision free-surface detection model can enhance the stability and accuracy of the simulation.
The free-surface detection method can be classified into four types of approaches (Luo et al. 2021). The first approach is focused on the concentration of the particles. In the original MPS (Koshizuka and Oka 1996), the PND was used to detect the free-surface particles. Lee et al. (2008) utilized the divergence of particle positions to track the free-surface particles. Although the first approach is efficient, some free-surface particles may be undetected, whereas some inner particles may be incorrectly identified as free-surface particles (Khayyer and Gotch 2008; Khayyer et al. 2008). The nonsymmetric distribution of the neighboring particles of free-surface particles is the basic concept of the second approach. Khayyer et al. (2009) used the summation of the x or y coordinates of neighbors to detect the free-surface particles. Zhang et al. (2014) defined a vector function to detect the free-surface particles. For the third approach, the free-surface particles are detected based on the geometric features of their relative positions. Marrone et al. (2010) defined an umbrella-shaped area and used the conditions expressed in Eq. (31) to evaluate whether the target particle i belongs to the free surface or not (as shown in Figure 2):
$$ \left\{\begin{array}{cl} \forall j \in\left[\left|\boldsymbol{x}_{j i}\right| \geqslant \sqrt{2} h,\left|\boldsymbol{x}_{j T}\right| <h\right] \quad & \Rightarrow b \in S_1 \\ \forall j \in\left[\left|\boldsymbol{x}_{j i}\right|<\sqrt{2} h,\left(\left|\boldsymbol{n}_i \cdot \boldsymbol{x}_{j T}\right|+\left|\boldsymbol{\tau}_i \cdot \boldsymbol{x}_{j T}\right|\right)<h\right] & \Rightarrow b \in S_2 \end{array}\right. $$ (31) 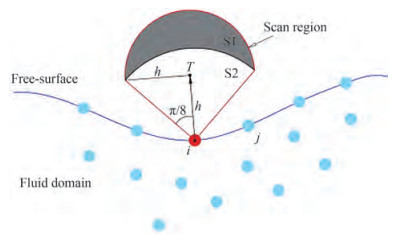 Figure 2 Sketch of the umbrella-shaped region for free-surface detection (Marrone et al. 2010)
Figure 2 Sketch of the umbrella-shaped region for free-surface detection (Marrone et al. 2010)where ni and τi are the local unit normal and tangential vectors of the free surface, respectively. Surface detection with the third approach is accurate but time-consuming. Therefore, many scholars tried to utilize the advantages of the aforementioned approaches and developed several hybrid approaches, i. e., the fourth category of approaches. Wang et al. (2019) coupled the first approach (Lee et al. 2008) and the third approach (Marrone et al. 2010) to track the free surface accurately with low computational cost. Several scholars tried to enforce the Dirichlet boundary condition without free-surface detection and avoid misjudging the free-surface particle. Sun et al. (2014) proposed a novel discretization of the PPE and a new framework of the MPS method (NSD-MPS) using conceptual particles. The pressure fluctuation can be suppressed and the cluster of free-surface particles can be minimized.
2.3.2 Wall boundary condition
The use of dummy particles to discretize solid walls was the most common approach for boundary conditions, which was first proposed by Koshizuka and Oka (1996). This approach can prevent the penetration of fluid particles and provide sufficient kernel support for them. Lee et al. (2011) applied nonslip boundary conditions for simulation by introducing the moving dummy particles. Duan et al. (2020) imposed the Neumann boundary condition on the dummy particles and obtained satisfactory numerical results in the boundary value problem. However, simulating thin-walled structures using the original dummy particles is difficult. If the particles are large, then the fluid particles on both sides of thin-walled structures may unphysically interact with each other, which may affect the accuracy of the simulation. By contrast, the simulation with small particles is time-consuming. To overcome this drawback, He et al. (2018; 2019) proposed a multilayer dummy particle method. The dummy particles in each layer provide support for the fluid particles on their corresponding side, as shown in Figure 3. Even if this boundary condition is satisfactory for the simplified structures, it is difficult for dummy particles to adhere to structures with complex geometries with uniform particle spacing.
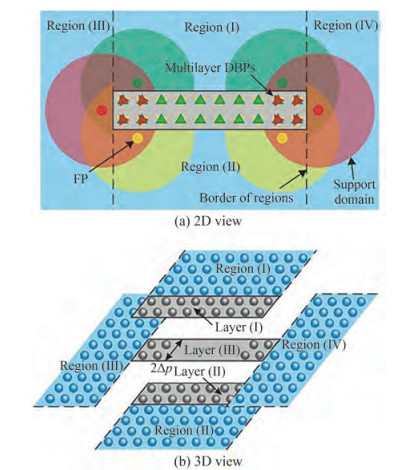 Figure 3 Sketch of a thin-walled structure using the multilayer DBP method (He et al. 2019)
Figure 3 Sketch of a thin-walled structure using the multilayer DBP method (He et al. 2019)The mirror particle method is another widely used boundary condition. A corresponding mirror particle will be generated for the fluid particle near the solid boundaries, which can prevent the fluid particle from penetrating the wall effectively. Colagrossi and Landrini (2003) proposed the mirror particle method, with its physical values deduced from their corresponding fluid particles near the solid boundaries. Park and Jeun (2011) arranged one-line wall particles before the simulation, and the mirror particles reflected from the fluid particles generated at every time step. The mirror particles were only generated when there were fluid particles near the wall. Although the memory was reduced, the computational cost was significantly increased. Akimoto (2013) pointed out that the fluid particles near the corner had multiple imaginary particles associated with each boundary plane, which resulted in the inaccuracy of PND near the corner. A simple split line was used to divide the corner region to prevent the excessive and deficient generation of mirror particles. Because of the complex topological relationships among the fluid particles, solid walls, and mirror particles, extending this approach to complex geometries is difficult.
The repulsive function method can be used to replace the dummy and mirror particles. In this method, the solid boundary is modeled with one-line particles and provides the repulsive force to the fluid particles. The magnitude of the repulsive force is determined by the distance between the fluid particles and the solid boundary. Monaghan (1994) first applied the artificial repulsive forces in the form of Lennard-Jones to the fluid particles near the solid wall. The influence of boundary conditions on the tangential motion of fluid particles is ignored (Violeau and Rogers 2016). Monaghan and Kajtar (2009) used radial forces to obtain suitable boundary forces and the Poisson summation to derive the repulsive function. However, the incomplete kernel support for the fluid particle was not considered in the aforementioned methods. Sun et al. (2021) proposed a generic smoothed wall (GSW) boundary and applied the contact force to repel the fluid particles away from the solid boundary, which is based on the discrete element method (DEM) for solid-solid contact. Moreover, a boundary weight function was applied in the GSW boundary model to compensate for the PND of fluid particles near the wall, which has the same effect on the dummy particles.
Wall boundaries can also be represented by the polygon mesh, which is suitable for solid wall boundaries with complex geometries. Harada et al. (2008) first proposed the polygon wall (PW) boundary conditions without using the wall particles. The boundary contributes to the fluid particles through the distance function. However, severe pressure fluctuation was induced. Zhang et al. (2015) modified the weight function for nonplanar boundaries, which significantly suppressed the pressure fluctuation. Zhang et al. (2016) proposed the boundary particle arrangement technique to make the PND near the nonplanar wall boundaries more accurate. Then, Zhang et al. (2017) proposed a new PPE source term for the PW and obtained a stable pressure distribution. To further improve the accuracy of the simulation, Zhang et al. (2019b) determined the pressure of PW through the Neumann boundary condition and introduced a high-order gradient model to the PW.
2.3.3 Open boundary condition
The open boundary condition (OBC) is widely used in the simulation of ocean engineering problems. Different from the Euler methods, the flow field is discretized as Lagrangian particles. Therefore, how to deal with the fluid particles near the inlet and outlet is a key issue that needs to be considered. The most commonly used OBC was proposed by Lastiwka et al. (2009). The inflow and outflow regions are defined to provide complete kernel support for the particles in the fluid domain. One particle will be generated in the inflow region once one particle is transferred from the inflow region to the fluid domain. The particles will be eliminated when they move out of the flow region. Shakibaeinia and Jin (2009) proposed a similar OBC associated with the particle recycling strategy. Another type of particle called storage particles was defined. The generation and elimination of fluid particles by Lastiwka et al. (2009) corresponds to the addition and subtraction from storage particles by Shakibaeinia and Jin (2009). Wave generation can also be implemented using the OBC. Ni et al. (2018) developed a numerical wave flume (NWF) based on the OBC. The waves were generated by changing the number of fluid particles in the vertical direction in the buffer region. This NWF was able to generate multiple types of waves, including solitary, linear, and second-order regular waves. To further improve the efficiency of NWF, Ni et al. (2020) incorporated the SWE-SPH and NS-SPH. The information was exchanged through the OBC. Tsuruta et al. (2021) proposed a wavy interface model for MPS, which is similar to the NWF. The prescribed wave surface elevation in the buffer region was obtained through the generation and removal of fluid particles, as shown in Figure 4.
 Figure 4 Sketch of the generation and removal of fluid particles in the buffer zone (Tsuruta et al. 2021)
Figure 4 Sketch of the generation and removal of fluid particles in the buffer zone (Tsuruta et al. 2021)2.4 Acceleration technique
In the field of ocean and coastal engineering, the 3D effect cannot be ignored. Therefore, 2D MPS needs to be extended to 3D MPS. However, the computational cost would increase dramatically. Many techniques have been proposed to improve the efficiency of MPS. Those techniques can be classified as multi-resolution, parallel, and graphics processing unit (GPU) acceleration techniques.
2.4.1 Multiresolution technique
The basic concept of the multiresolution technique is that the particles with small spacing are only arranged at the region that needs to be considered, which reduces the computational load and meets the requirements of local accuracy. Introducing the multiresolution technique to the incompressible MPS is difficult because the PPE is solved implicitly. The overlapping particle technique (OPT) was first proposed for MPS by Shibata et al. (2012) and extended to three dimensions by Tang et al. (2016). In the refined domain, the coarse particles can overlap with each other. The PPEs for coarse and fine particles were solved separately, which has only a slight influence on the stability of simulations. However, the interaction between MPS particles of different sizes is a one-way process, and only the coarse particles can affect the fine particles but not the other way around. Shibata et al. (2017) further developed a bilateral OPT and introduced several newly developed techniques to reduce the error in the total fluid mass. Tanaka et al. (2009) proposed a multiresolution technique to generate MPS particles of different sizes before the simulation. Tang et al. (2016) extended the multiresolution technique (Tanaka et al. 2009) to three dimensions and applied the technique to the simulations of the dam break and water entry. Tanaka et al. (2018) further introduced splitting or merging algorithms to the multiresolution technique to change the spatial resolution dynamically. Liu and Zhang (2021) first introduced the multiresolution technique to the least square MPS for the simulation of multiphase flows. The particle resolution near the interface was adaptive.
The FSI phenomena can be frequently observed in ocean and coastal engineering. The plates of marine structures tend to be thin, and the corresponding wall particles tend to be small. Therefore, the total number of particles will be large with a uniform resolution, which results in a heavy computational load. The multiresolution techniques were also introduced to the particle-based FSI solvers to improve their performance. Multiresolution techniques can be classified into two classes, namely, domain and structure refinement methods. Sun et al. (2019; 2021) coupled the SPH method with adaptive particle refinement (APR) to investigate the FSI problems. The APR region was set around the elastic structure. The coarse particles were split into fine particles when they entered the refinement region, and the fine particles were merged into large particles when they left the refinement region. Khayyer et al. (2019; 2021) first introduced a multiresolution technique to MPS and ISPH-SPH to solve hydroelastic problems. The elastic structures were made of fine particles, whereas the flow field was composed of coarse particles. Sun et al. (2021) applied an adaptive high-resolution region to the MPSDEM coupled method (Sun et al. 2019) to improve computational efficiency.
2.4.2 Central processing units (CPU) parallel acceleration technique
The MPS method cannot be applied to large-scale simulation only with multiresolution techniques. Scholars tried to assign the heavy task to multiple central processing units (CPUs) to increase computational efficiency. Two main parallel strategies, namely, open multiprocessing (OpenMP) and message passing interface (MPI), were utilized. For OpenMP, different processors share the memory, which can be easily coded. However, OpenMP is only applicable to a single host with multiple CPUs, and its speedup is limited because of the overhead for data communication (Luo and Koh 2017). Compared with OpenMP, MPI is suitable for largescale computing and can be applied to computer clusters.
The task division approach for particle-based methods can be classified as particle and domain decomposition methods. For the particle decomposition method, the particles are assigned to the processors according to their numbers. Massive data communication is required because the relative position between particles is not fixed (Iribe et al. 2006). To overcome this drawback, Iribe et al. (2010) introduced the renumbering and communication list creation techniques to the particle decomposition method. The communication was significantly reduced. For the domain decomposition method, the calculation domain is divided into several subdomains, and only the particles near the boundary of subdomains exchange the information. Ikari and Gotch (2008) compared the aforementioned decomposition methods and pointed out that the domain decomposition method performed better than the particle decomposition method. Fernandes et al. (2015) proposed a new nongeometric strategy to parallelize the MPS method for fully distributed computing in clusters. The new strategy is based on the domain decomposition method and has been successfully applied to simulations with hundreds of millions of particles. Marrone et al. (2012) proposed a parallel strategy associated with background grids for SPH, which is also suitable for other particle-based methods. The particles are allocated to the background grids that belong to different processors, and the load balance is maintained by redistributing the grids to the processors dynamically. The parallel SPH was applied to the 3D simulation of a ship in steady forward motion. Xie et al. (2021a) introduced this parallel strategy to the MPS-DEM coupled method, which was used to solve the FSI problems.
2.4.3 GPU acceleration technique
Compared with the CPU, one chip area of the GPU has more arithmetic logic units. Therefore, the GPU can achieve high floating-point operations per second and deal with large amounts of data at the same time (Chen and Wan 2019a). CUDA is a general parallel computing platform released by NVIDIA, which enables the GPU to solve complex computing problems. The CUDA platform consists of the host and device parts. The CPU is the host part, whereas the GPU is the device part.
Recently, the GPU acceleration technique has been applied in many fields, including medical imaging and intelligent driving. The GPU acceleration technique has also been used to improve the efficiency of MPS code. Hori et al. (2011) developed a GPU-accelerated MPS method, which was three to seven times faster than the code with a single CPU. Chen et al. (2019) developed the in-house solver MPSGPU-SJTU, which was used to calculate the 3D dam-break problem with 2 678 595 particles. Compared with the computation time of the CPU, the total speedup of GPU code was up to 33.53. Zhang et al. (2021) used the GPU-based MPS to simulate the impinging atomization of two jets, and the speedup is 11.75. To further improve the computational efficiency, Gou et al. (2019) first introduced the multiple GPUs to the incompressible MPS. The domain decomposition method was used to divide tasks and the data communication between GPUs through the MPI. The multiple-GPU-based MPS solver was applied to the simulation of the 3D dam break with 1 million particles.
3 Applications in ocean engineering
3.1 Multiphase flows
3.1.1 Liquid-liquid and liquid-gas flows
The major challenges in extending the MPS method to liquid-liquid/liquid-gas flow problems focus on density and viscosity jump near the interface, surface tension, and compressibility.
Several approaches have been proposed to solve the interface problems. Koshizuka et al. (1999) proposed a multiphase MPS (MMPS) method and solved the pressure fields of two fluids separately to maintain numerical stability. To calculate the pressure head exactly, a buoyancy model was introduced to the MMPS method (Shirakawa et al. 2002; Kim and Kim 2014). However, the adjusting parameter in the buoyancy model was determined through several simple tests, which may be unsuitable for complex multiphase problems (Duan et al. 2017a). Several hybrid methods have also been developed to solve the multiphase problems. Liu et al. (2005) incorporated the MPS and finite volume method (FVM). The heavy phase was simulated by MPS, whereas the light phase was calculated by FVM. The information was exchanged between particles and meshes through extrapolation, which avoided the problems caused by the discontinuity of viscosity and density in the interface. Nevertheless, errors might be induced during the extrapolation process. Several researchers tried to solve the pressure fields of different fluids in one framework. Shakibaeinia and Jin (2012) developed the WCMPS solver, which was suitable for multiphase flow with a low density ratio. The multidensity and multiviscosity models were proposed to handle the interface problem. Khayyer and Gotoh (2013) proposed a high-order density smoothing scheme and extended the incompressible MPS to solve multiphase problems with a high density ratio. Shimizu et al. (2018) dealt with the interface with a high density jump by incorporating the space potential particle concept. Khayyer et al. (2019) further introduced the OPS to the MMPS to maintain the uniform distribution of the particles at the interface. Duan et al. (2017a) proposed two approaches, namely, MMPS-HD and MMPS-CA, to stabilize the multiphase simulations. In the MMPS-HD, harmonic mean density, which was adopted in mesh methods to handle high density ratios, was used to avoid large acceleration at the interface. In the MMPS-CA, new multiphase formulations are proposed based on the local weighted average of particle acceleration to keep the acceleration continuous at the interface.
The surface tension model is important in the simulation of multiphase flows. A continuum surface force (CSF) model was first proposed for mesh-based methods (Brackbill et al. 1992). In particle-based methods, the surface tension is converted into the volume forces exerted on the interface particles. The surface tension is relevant to the local curvature at the interface. Nomura et al. (2001) calculated the curvature through the fan-shaped distribution of the particles near the interface, as shown in Figure 5. This approach of curvature approximation was also used by Rong and Chen (2010) to simulate Taylor bubble formation in microchannels. Based on the classical CSF, Duan et al. (2015) proposed the contoured continuum surface force (CCSF) model, which approximates the phase interface by the contours of the smoothed color function. The CCSF was robust enough and verified through several cases by Wen et al. (2021b).
In the multiphase simulation with a high density ratio, the compressible characteristics cannot be ignored. Ikeda et al. (2001) assumed that density was correlated with pressure and related to sound velocity. Based on this assumption, a compressible term was added to the PPE source term. To reduce the pressure fluctuation, Khayyer et al. (2009) introduced a stabilizing term to the PPE source term, which enabled the slight compressibility of singlephase flows. Then, Khayyer and Gotoh (2016) further developed the compressible-incompressible MMPS method and proposed the compressible-incompressible error compensating source of PPE. The MMPS was used to investigate the cushioning (compressibility) effect of water slamming. Duan et al. (2020) proposed an incompressible-compressible particle method by incorporating incompressible MPS and weakly compressible SPH.
The MMPS has been applied to multiphase problems in ocean and coastal engineering assisted by the advanced techniques mentioned previously.
3.1.1.1 Bubbly flows
Bubbly flow is one of the research highlights in the field of ocean engineering. Tian et al. (2009) adopted MPS to investigate single bubble collapse with noncondensable gas and successfully captured the rebound phenomenon. Guo et al. (2018) introduced the high-order scheme and ECS to the MMPS-CA. The accuracy and stability of the improved MMPS-CA were verified by simulating bubble pairs rising and coalescence. Then, the improved MMPS-CA was employed to investigate the evolution of bubbly flows in a simplified closed air-water separator. Wen et al. (2021b) investigated the violent interactions between a set of 3D bubbles with MPS, as shown in Figure 6. They concluded that bubble interactions in the 3D simulations became more violent, and more complex interfaces were captured by the MMPS method, particularly in cases with a large Bond number, when compared with 2D results. Pipeline transport is an important part of the offshore oil and gas exploitation process. Therefore, bubble motion in the pipeline needs to be investigated. Duan et al. (2017a) adopted MMPS-CA to simulate bubble motion in the rightangle pipe, as shown in Figure 7. The complex breakups or coalescence of the bubbles could be observed clearly, and the breakup of the gas phase frequently occurred in the right-angle region because of the existence of vortices. Rong and Chen (2010) simulated the generation of the Taylor bubble in a T-shaped microchannel using the MMPS method. Then, the influence of junction shape on bubble generation was analyzed.
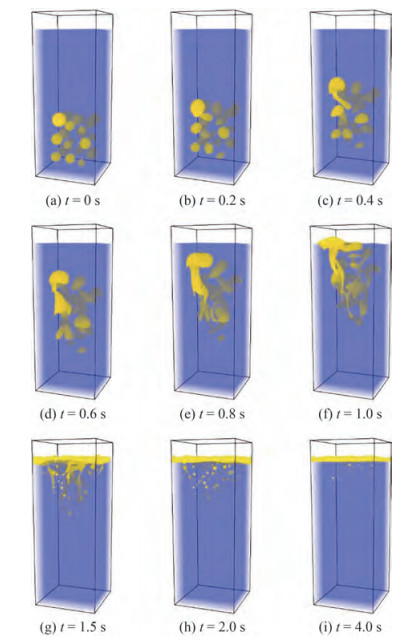 Figure 6 Snapshots of the rising of 3D bubbly flows involving a set of bubbles (Wen et al. 2021b)
Figure 6 Snapshots of the rising of 3D bubbly flows involving a set of bubbles (Wen et al. 2021b)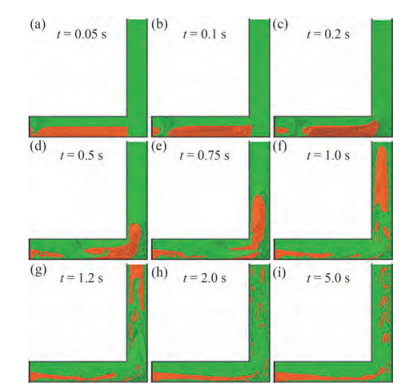 Figure 7 Snapshots of simulated bubble rising in a right-angle tube with complex breakup behavior (Duan et al. 2017a)
Figure 7 Snapshots of simulated bubble rising in a right-angle tube with complex breakup behavior (Duan et al. 2017a)3.1.1.2 Violent flows
The phenomena of air entrapment mainly occur in the problems of violent flows, which affect the characteristics of the local fluid (Luo et al. 2021). Therefore, the air phase should be considered in the simulation of violent flows. Wang and Zhang (2019) proposed a novel MMPS method. The spatial difference form of the governing equation of the original MPS method was replaced by the integral equation based on the theory of peridynamics, which can reduce the numerical instability induced by discontinuity of the physical quantities near the interface. Furthermore, a corrective matrix derived from the shape function in peridynamics was introduced to the gradient and divergence equation to eliminate the error induced by the uneven distribution of particles. The MMPS was applied to simulate the 2D dam break, as shown in Figure 8. The complex interface was successfully captured, and the numerical results are consistent with the experimental data. Wen et al. (2021a) simulated the 3D dam break benefiting from the GPU acceleration technique. Snapshots of 3D two-phase dam-break flows are presented in Figure 9. The numerical results indicated that the air cavity experienced severe pressure and volume oscillations, and the variation trends of pressure and volume were opposite. For multiphase sloshing cases, Shimizu et al. (2018) simulated liquid sloshing with a high filling ratio and small excitation amplitude. A smooth phase interface was captured, and no unphysical gap was observed. However, this method has not been applied to simulate more violent sloshing flows, which can be attributed to the fact that the pressures of different phases were solved separately and the existence of air entrapment that led to the discontinuity of the interface, thereby increasing the difficultly of simulation. Khayyer and Gotoh (2013) utilized the improved MPS with the density smoothing scheme and the Taylor series consistent pressure gradient model to simulate violent sloshing flows. The numerical results presented a smooth interface and uniform distribution of particles. Moreover, coalescence of sloshing-induced secondary jets, entrainment of gas particles, and fragmentation of water particles can be captured clearly. Wen et al. (2022) employed both the singlephase MPS and MMPS to simulate violent sloshing flows, as shown in Figure 10. The comparisons showed that, as the intensity of sloshing increased, the effect of the air cushion became nonnegligible, and the accuracy of the single-phase simulation significantly decreased, whereas the simulation results obtained by the MMPS method were consistent with the experimental results in all cases. Wen et al. (2021c) further investigated the violent multilayer liquid sloshing using the MMPS, as shown in Figure 11 and Figure 12. The phenomenon of internal wave breaking was well captured. Furthermore, the vertical baffle was able to significantly reduce the sloshing intensity and limit the interfacial wave elevations. Water entry is also a significant issue in the field of ocean engineering (Lyu et al. 2022). The multiphase numerical models were also used to predict the pressure distribution and trajectory of structures accurately. Fang et al. (2022) simulated the water entry of the ship panel using a multiphase Riemann-SPH method. The air cushion and slamming load were investigated in detail. Lyu et al. (2021) investigated the water entry with different density ratios using the multiphase SPH model. However, the MPS has not been applied to simulate the multiphase water entry. In the future, the MMPS method should be further modified and employed to solve more complex problems.
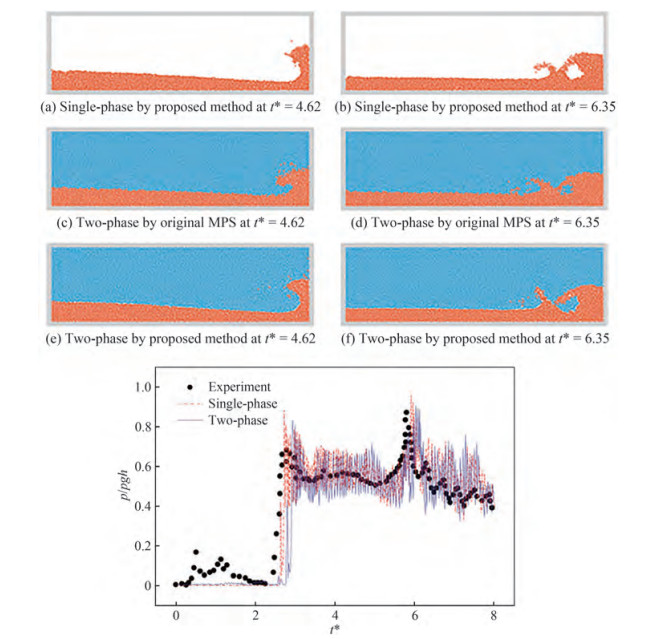 Figure 8 Snapshots of two-phase dam-break flows and the time history of impacting pressure obtained by the different methods (Wang and Zhang 2019)
Figure 8 Snapshots of two-phase dam-break flows and the time history of impacting pressure obtained by the different methods (Wang and Zhang 2019) Figure 9 Snapshots of 3D two-phase dam-break flows (Wen et al. 2021a)
Figure 9 Snapshots of 3D two-phase dam-break flows (Wen et al. 2021a)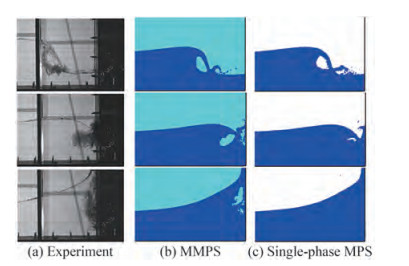 Figure 10 Comparison of air entrapment and cavity evolution captured in the experiment (Rafiee et al. 2010), MMPS simulation, and single-phase MPS simulation (Wen et al. 2022)
Figure 10 Comparison of air entrapment and cavity evolution captured in the experiment (Rafiee et al. 2010), MMPS simulation, and single-phase MPS simulation (Wen et al. 2022) Figure 11 Comparison of phase interfaces in the experiment (Audiffren et al. 2012) and MMPS simulations (Wen et al. 2021c)
Figure 11 Comparison of phase interfaces in the experiment (Audiffren et al. 2012) and MMPS simulations (Wen et al. 2021c)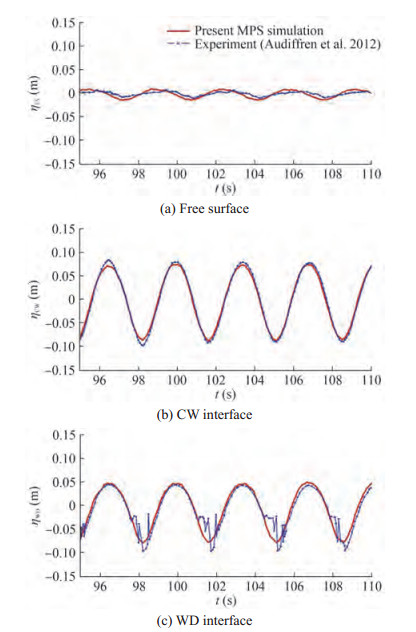 Figure 12 Comparison of the time histories of interfacial wave elevations in the experiment (Audiffren et al. 2012) and MMPS simulations (Wen et al. 2021c)
Figure 12 Comparison of the time histories of interfacial wave elevations in the experiment (Audiffren et al. 2012) and MMPS simulations (Wen et al. 2021c)3.1.1.3 Wave problem
The original single-phase flow MPS method has been widely used in wave problems, which is naturally capable of handling strongly nonlinear free surfaces. In recent years, researchers have tried to employ the MMPS to solve wave problems related to multiphase flows. Khayyer et al. (2019) investigated multiphase standing gravity waves. The time histories of water surface elevation obtained by MMPS incorporated with OPS were consistent with the theoretical solution compared with other numerical results. Duan et al. (2017b) investigated the effect of waves and continuous spills on the oil spreading, as shown in Figure 13. The numerical results showed that the spreading of thick oil slicks could be accelerated when the wave height increased or wave length decreased. Wen et al. (2021a) analyzed internal solitary waves, as shown in Figure 14. The internal solitary wave was able to propagate at a long distance with the waveform maintaining its stability and the wave profile simulated by MMPS being consistent with the experimental data.
 Figure 13 Snapshots of the distributions of oil slicks in the waves (Duan et al. 2017b)
Figure 13 Snapshots of the distributions of oil slicks in the waves (Duan et al. 2017b)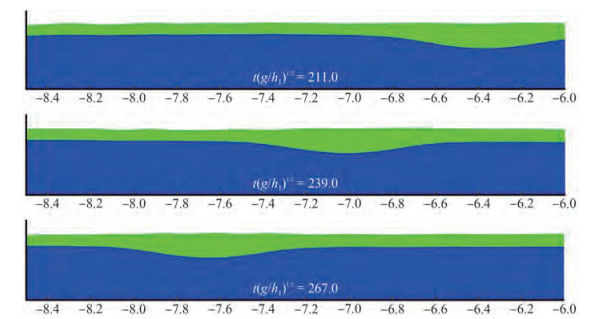 Figure 14 Snapshots of the propagation of internal solitary waves (Wen et al. 2021a)
Figure 14 Snapshots of the propagation of internal solitary waves (Wen et al. 2021a)3.1.2 Liquid-solid flows
The solid phase of liquid-solid flows is considered the continuum field of discrete particles (Feng and Yu 2004). Considering the computational cost, the former is more suitable for large-scale problems. Shakibaeinia and Jin (2011) developed a multiphase non-Newtonian WCMPS to solve the mobile-bed dam-break problem. The liquid and solid phases were solved using a single set of multidensity and multiviscosity equations. Moreover, the generalized viscoplastic fluid model was used to predict the behavior of the solid phase. Fu and Jin (2015) introduced the Herschel-Bulkley rheological model to the WCMPS to simulate the motion of the solid phase, which was regarded as the non-Newtonian fluid. The deformation of landslides could be presented accurately. Tajnesaie et al. (2018) employed the viscoplastic rheological model to simulate the behavior of granular flows. Their numerical results showed that the WCMPS with viscoplastic rheological model performed better than the Herschel-Bulkley rheological model. Jandaghian et al. (2021) developed a 3D liquid-solid two-phase model based on the WCMPS with a regularized visco-inertial rheological model. A new formulation for the effective pressure of solid skeleton was proposed. The WCMPS was applied to simulate the immersed granular collapse, as shown in Figure 15.
 Figure 15 Snapshots of immersed granular collapse (Jandaghian et al. 2021)
Figure 15 Snapshots of immersed granular collapse (Jandaghian et al. 2021)Although the approach with the solid phase being a continuum is more efficient, some important information is neglected, such as the forces acting on a single particle and the motion behavior of a single particle. By contrast, the discrete method emphasizes the interactions among solid particles, and the simulation is more realistic. The DEM is a Lagrangian method based on Newton's second law and is widely employed in simulations of granular flows. In recent years, MPS-DEM coupled methods have been developed for liquid-solid flows. The coupling strategies of MPS and DEM can be classified as resolved and unresolved coupling. For resolved coupling, the fluid force exerted on DEM particles is in the form of pressure and viscous force. Duan et al. (2022) developed a MPS-DEM model to simulate debris remelting in the field of nuclear engineering. Zhou et al. (2021) incorporated SPH and DEM. Then, the SPH-DEM model was applied to represent the tsunamis induced by the 1963 Vajont landslide by Xu et al. (2021). To the best of the authors' knowledge, the MPS-DEM method with resolved coupling has not been applied to investigate the hydrodynamic problems in ocean and coastal engineering.
For unresolved coupling, Sakai et al. (2012) developed a 2D MPS-DEM model with the formulation of the fluid governing equations being Model A, which assumed that the pressure drop is shared between fluid and solid phases (Feng and Yu 2004). Sun et al. (2014) further coupled WCMPS and DEM with the same coupling scheme. Then, Li et al. (2019) extended the WCMPS-DEM coupled method to non-Newtonian solid-liquid flows. Xie et al. (2021b) incorporated the incompressible MPS with DEM with Model B, which assumes that pressure drop is applied to the fluid phase only (Feng and Yu 2004). The authors pointed out that the instability of DEM particles induced by fluid might be avoided because the pressure gradient force was replaced by a more stable term in Model B. The unresolved MPS-DEM model has been used to solve coastal engineering problems. Harada et al. (2019) simulated the swash beach process and investigated the effect of seepage flows on sediment transport. Tazaki et al. (2021) analyzed the vortical sorting process in the swash region using both experimental and MPS-DEM methods. Their numerical results were consistent with the experimental data. Harada et al. (2021) investigated the ripple formation process generated on a movable bed surface with 3D MPS-DEM model. Tazaki et al. (2022) assessed the effect of plunging waves on sediment transport, as shown in Figure 16.
 Figure 16 Comparison of wave profile, sediment shape, and solid-phase velocity between experiments with PIV analysis and numerical simulations (Tazaki et al. 2022)
Figure 16 Comparison of wave profile, sediment shape, and solid-phase velocity between experiments with PIV analysis and numerical simulations (Tazaki et al. 2022)3.2 Interaction between fluid and structures
3.2.1 Elastic structures
The fluid dynamics of severe flows may lead to large deformations and even fractures of offshore structures. Therefore, fluid-elastic structure interaction problems need to be solved. No fixed topological relationships among Lagrangian particles were detected, and information exchange was not restricted to specific nodes. Hence, particle-based methods have the potential to handle severe FSI problems with large deformations.
Particle-based methods can be directly used to simulate elastic structures. Hwang et al. (2014) developed a structural dynamic response model based on MPS. The governing equations of the structures were derived from Hook's law for isotropic linear elastic solids. Khayyer et al. (2018a) employed the projection-based ISPH method for the simulation of fluid and developed a novel SPH-based structure model. The fluid-structure acceleration-based and pressure integration coupling schemes were compared in detail. Khayyer et al. (2018a) proposed Hamiltonian MPS and Hamiltonian SPH structural models based on the application of variational principles for elastodynamics. Then, the Hamiltonian structural models were extended to 3D (Khayyer et al. 2021a) and composite structures (Khayyer et al. 2021c). Particle-based methods can also be coupled with other structural dynamics methods to solve the FSI problems. The finite element method (FEM), as a mature approach, has been widely applied to solve the dynamic problems of complex structures. Lee et al. (2007) first proposed the MPS-FEM coupled method, and the MITC4 shell element was adopted in the FEM analysis of the structure. Fourey et al. (2017) compared the conventional parallel staggered (CPS) and conventional sequential staggered (CCS) algorithms. The CSS algorithm was more stable than the CPS algorithm and was widely used as the coupling algorithm between MPS and other methods. Zhang et al. (2018; 2019) incorporated the incompressible MPS and FEM. The shape-function-based interpolation technique and kernel-function-based interpolation technique were proposed for the information exchange between fluid and structures. Sun et al. (2019) first coupled MPS and DEM. Then, Xie et al. (2021a) extended the MPS-DEM coupled method to the FSI problems with fracture.
The MPS and coupling methods have been applied to solve various FSI problems with deformation. Zha et al. (2021) employed the high-order MPS to simulate the 2D water entry of elastic wedges with different deadrise angles and drop heights. The 3D water entry of elastic wedges was simulated by Khayyer et al. (2021a), and their numerical results with different resolutions were consistent with the experimental data, as shown in Figure 17. Zhang et al. (2016a) analyzed the mitigating effects of the elastic baffle on sloshing using the MPS-FEM. Zhang and Wan (2018a) further investigated the phenomenon in the 2D elastic tank with an elastic wall. By varying Young's modulus of the tank walls, interesting characteristics of the evolution of the free surface, variation of the impact pressures, and dynamic responses of the structures in both time and frequency domains were observed. Rao and Wan (2018) simulated the interactions between solitary waves and elastic plates. The effects of structural flexibility on wave-induced forces were analyzed. Zhang et al. (2022a) used the MPS-FEM to assess the hydroelastic responses of floating structures in waves, as shown in Figure 18 and Figure 19. A series of qualitative analyses were conducted, and the FSI solver could provide reasonable predictions for wave-ship interaction.
 Figure 17 Snapshots of the 3D water entry of elastic structures (Khayyer et al. 2021a)
Figure 17 Snapshots of the 3D water entry of elastic structures (Khayyer et al. 2021a) Figure 18 Snapshots of the interaction between waves and floating structures (Zhang et al. 2022a)
Figure 18 Snapshots of the interaction between waves and floating structures (Zhang et al. 2022a)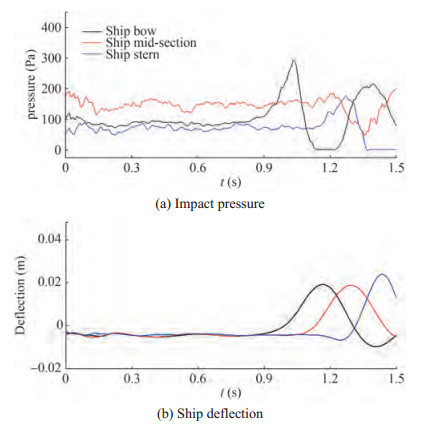 Figure 19 Time histories of impact pressure and ship deflection (Zhang et al. 2022a)
Figure 19 Time histories of impact pressure and ship deflection (Zhang et al. 2022a)3.2.2 Floating structures
The floating structures may be damaged in the harsh marine environment, which could threaten the normal production and life of people. In recent years, many researchers tried to use MPS to investigate the interactions between waves and floating structures.
Shibata et al. (2012) used MPS to investigate the ship's motion in waves. Their numerical results showed that the MPS had the potential to simulate the ship's motion under conditions with high wave height. Zhang et al. (2017) analyzed the roll motion of a rectangular floating body in regular waves with different frequencies. The numerical results of response amplitude operators for roll motions were consistent with the experimental data. Zhang et al. (2020) investigated the effect of the internal baffles on the flooding and motion characteristics of the damaged ship section. Hashimoto et al. (2022) compared MPS and SPH for the simulation of flooding ship sections, as shown in Figure 20. Both the MPS and SPH were able to simulate complex flooding flows. Amaro et al. (2021) developed an MPS-DEM coupled method, which was used to investigate the dynamic behavior of the wave-ice floes interaction.
 Figure 20 Comparison of the simulation snapshots of flooding flows in ships by experiment, MPS, and SPH (Hashimoto et al. 2022)
Figure 20 Comparison of the simulation snapshots of flooding flows in ships by experiment, MPS, and SPH (Hashimoto et al. 2022)3.2.3 Porous structures
Porous structures can dissipate wave energy and are widely used to protect shorelines and bridge piers (Ren et al. 2016).
Porous structure models have been introduced to particle-based methods by many researchers. A macroscopic model is an efficient approach that can address the demand for high accuracy, in which the N-S equation was reformulated based on the volume averaging theory (Xu and Jin 2019) or mixture theory (Khayyer et al. 2018b). Compared with SPH, only a few studies of the MPS porous model have been conducted. Pahar and Dhar (2017) developed a model of flow-porous structure interaction-based incompressible MPS. A concept of apparent density was used to account for increased representative volume by multiplying a coefficient. The numerical solver was applied to solve free-surface flow passing uniform and nonuniform porous block cases. Xu et al. (2019) proposed a transit region between porous and nonporous regions for the smooth transition of porosity. The effects of porosity and mean diameter on the permeability, impact pressure, and reflected wave height were investigated.
3.2.4 Liquid sloshing
Because of the uneven distribution of energy in different regions, a large amount of energy needs to be transported from one area to another every year. Liquid sloshing is a significant issue in the transportation of liquefied natural gas, oil, and liquefied petroleum gas. The liquid inside a partially filled tank will oscillate violently and exert large impact pressure on the tank under external excitation, particularly when the excitation frequency is close to the natural frequency of sloshing. Particle-based methods can easily capture complex free surfaces with large deformation in tanks. In recent years, MPS has been widely applied to liquid sloshing problems.
MPS can be used to investigate the flow mechanics of sloshing. Pan et al. (2008) simulated 2D sloshing with MPS and investigated the effect of kernel functions on the numerical results. Pan et al. (2012) further extended MPS to large eddy simulation (LES) by incorporating it with the subparticle-scale turbulence model. The large impact pressure on the rolling tank wall was predicted accurately by MPS-LES. Jena and Biswal (2017) developed a modified MPS to simulate liquid sloshing in the 2D tank. The wave amplitude and pressure on the tank walls were calculated accurately. Xie et al. (2020) simulated the 3D liquid sloshing in a rectangular tank using the MPS methods assisted by GPU acceleration techniques. Their numerical results showed that the occurrence of the 3D effect was closely related to the excitation frequency, dimensions of the tank, and filling ratio. Zhang et al. (2022b) used MPS to investigated the mechanism of Faraday waves in a vertically excited square tank, as shown in Figure 21. The effects of forcing amplitude and excitation frequency on the formation of Faraday waves were evaluated.
 Figure 21 Comparison of waveforms between experimental results (Frandsen and Peng 2006) and numerical results (Zhang et al. 2022b)
Figure 21 Comparison of waveforms between experimental results (Frandsen and Peng 2006) and numerical results (Zhang et al. 2022b)MPS can also be employed to determine whether certain devices can mitigate sloshing. Tsukamoto et al. (2011) used MPS to analyze the influence of an elastically linked moving body on liquid sloshing. Their numerical results showed that the device can mitigate sloshing in the tank. Tsukamoto et al. (2020) simulated liquid sloshing with stiffeners on the bottom or side wall. For the filling ratio of 5%, the bottom stiffeners could significantly suppress sloshing, whereas the sidewall stiffeners have only a slight effect on sloshing. For the filling ratios of 10% to 20%, the sidewall stiffeners led to significant load mitigation. Bellezi et al. (2022) investigated the effects of floating baffles on liquid sloshing. The heave motion of the baffle was unfixed, and the baffle could significantly reduce liquid sloshing in a wide range of filling conditions.
4 Future perspectives and concluding remarks
The MPS method has been considerably improved and gradually applied to solve the hydrodynamic problems in ocean and coastal engineering since it was proposed. For stability and accuracy, the researchers have proposed many improved schemes for the gradient model, Laplacian model, and PPE source term. However, spurious pressure fluctuations still can be observed in the simulation by MPS, which affects the force exerted on offshore structures. Therefore, the reduction of spurious pressure fluctuations is a significant issue in future work. Furthermore, the stabilizing methods may introduce stabilization errors to the simulation (Duan et al. 2019). Hence, how to balance the accuracy and stability should also be considered.
Another major challenge of the MPS is the boundary condition. The shape of real offshore structures is complex, and slender structures are common. Future boundary conditions should provide adequate support and create accurate physical relationships for the fluids near the complex structures. The MPS method is more suitable for violent flows. However, the computational efficiency of MPS methods is relatively low compared with other methods, such as the FVM and high order spectral method. In the future, the MPS can be coupled with other methods to improve the computational efficiency of the simulation. The region where the waves interact with structures is simulated by MPS, and the wave information is transferred from other methods through OBC. Moreover, the conservation of mass and momentum should be considered during the information transfer process.
In terms of computational efficiency, the GPU technique can significantly improve the performance of MPS. Gou et al. (2019) conducted a simulation with multiple GPUs and determined that the total number of particles was approximately 1.24 million. The advanced task decomposition approaches can be proposed and introduced to fully utilize each GPU. With the further improvement of device memory and parallel strategy, the MPS simulation with particle numbers reaching 10 million should be tried in the future.
Regarding its application in ocean and coastal engineering, MPS was rarely used to solve complex problems. For the FSI problems, the safety of structures needs to be evaluated. MPS and coupled methods can be used to predict the responses of ships and bridges under extreme sea conditions. The stress distribution of overall structures should be presented accurately, which is conducive to the design of offshore structures. Furthermore, the fracture problems should be considered. Accurate fracture models and boundary conditions of fracture surfaces need to be proposed. The wave-ice interaction is also a hot issue, and MPS can be extended to model ice, such as SPH (Zhang et al. 2019a). Both ice and water can be simulated by MPS, which may be beneficial for the information exchange between solid and fluid. As for liquid-solid flows, to simplify the numerical model, the shapes of solid particles are the same. However, granular flows in nature contain multiple nonspherical particles. Therefore, MPS simulation of solid particles with different shapes should be tried in the future. Moreover, the abrasion of solid particles is common. Several novel abrasion models can be introduced to the numerical methods to make the simulation more realistic.
The development of MPS and its application in ocean and coastal engineering are reviewed in detail. The latest advances in stability and accuracy, boundary conditions, and acceleration techniques of MPS methods are presented. The applications of MPS in ocean and coastal engineering, including multiphase flows and fluid-structure interaction, are discussed. Finally, the development direction of MPS methods is predicted. In summary, the MPS method has the potential to solve practical problems. New schemes and techniques need to be proposed to further promote the development of MPS.
Acknowledgement: Supported by the National Key Research and Development Program of China (2019YFB1704200), and the National Natural Science Foundation of China (51879159, 52131102).Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and thesource, provide a link to the Creative Commons licence, and indicateif changes were made. The images or other third party material in thisarticle are included in the article's Creative Commons licence, unlessindicated otherwise in a credit line to the material. If material is notincluded in the article's Creative Commons licence and your intendeduse is not permitted by statutory regulation or exceeds the permitteduse, you will need to obtain permission directly from the copyrightholder. To view a copy of this licence, visit http:/creativecommons.org/licenses/by/4.0/. -
Figure 1 Estimated position of a dummy neighboring particle for particle i (Liu et al. 2018)
Figure 2 Sketch of the umbrella-shaped region for free-surface detection (Marrone et al. 2010)
Figure 3 Sketch of a thin-walled structure using the multilayer DBP method (He et al. 2019)
Figure 4 Sketch of the generation and removal of fluid particles in the buffer zone (Tsuruta et al. 2021)
Figure 6 Snapshots of the rising of 3D bubbly flows involving a set of bubbles (Wen et al. 2021b)
Figure 7 Snapshots of simulated bubble rising in a right-angle tube with complex breakup behavior (Duan et al. 2017a)
Figure 8 Snapshots of two-phase dam-break flows and the time history of impacting pressure obtained by the different methods (Wang and Zhang 2019)
Figure 9 Snapshots of 3D two-phase dam-break flows (Wen et al. 2021a)
Figure 10 Comparison of air entrapment and cavity evolution captured in the experiment (Rafiee et al. 2010), MMPS simulation, and single-phase MPS simulation (Wen et al. 2022)
Figure 11 Comparison of phase interfaces in the experiment (Audiffren et al. 2012) and MMPS simulations (Wen et al. 2021c)
Figure 12 Comparison of the time histories of interfacial wave elevations in the experiment (Audiffren et al. 2012) and MMPS simulations (Wen et al. 2021c)
Figure 13 Snapshots of the distributions of oil slicks in the waves (Duan et al. 2017b)
Figure 14 Snapshots of the propagation of internal solitary waves (Wen et al. 2021a)
Figure 15 Snapshots of immersed granular collapse (Jandaghian et al. 2021)
Figure 16 Comparison of wave profile, sediment shape, and solid-phase velocity between experiments with PIV analysis and numerical simulations (Tazaki et al. 2022)
Figure 17 Snapshots of the 3D water entry of elastic structures (Khayyer et al. 2021a)
Figure 18 Snapshots of the interaction between waves and floating structures (Zhang et al. 2022a)
Figure 19 Time histories of impact pressure and ship deflection (Zhang et al. 2022a)
Figure 20 Comparison of the simulation snapshots of flooding flows in ships by experiment, MPS, and SPH (Hashimoto et al. 2022)
Figure 21 Comparison of waveforms between experimental results (Frandsen and Peng 2006) and numerical results (Zhang et al. 2022b)
-
Akimoto H (2013) Numerical simulation of the flow around a planing body by MPS method. Ocean Eng. 64: 72-79. https://doi.org/10.1016/j.oceaneng.2013.02.015 Amaro RA, Mellado-Cusicahua A, Shakibaeinia A, Cheng LY (2021) A fully Lagrangian DEM-MPS mesh-free model for ice-wave dynamics. Cold Reg. Sci. Technol. 186: 103266. https://doi.org/10.1016/j.coldregions.2021.103266 Antoci C, Gallati M, Sibilla S (2007) Numerical simulation of fluid-structure interaction by SPH. Comput. Struct. 85(11-14): 879-890. https://doi.org/10.1016/j.compstruc.2007.01.002 Audiffren C, Marcer R, Molin B, REMY F, Ledoux A, Helland S, Mottaghi M (2012) Experimental and numerical study of liquid sloshing in a rectangular tank with three fluids. Proceedings of the 22nd International Offshore and Polar Engineering Conference (ISOPE'12), Rhodes, Greece 331-340 Bellezi CA, Cheng LY, Nishimoto K (2022) A numerical study on sloshing mitigation by vertical floating rigid baffle. J. Fluids Struct. 109: 103456. https://doi.org/10.1016/j.jfluidstnicts.2021.103456 Brackbill JU, BKothe D, Zemach C (1992) A continuum method for modeling surface tension. J. Comput. Phys. 100(2): 335-354. https://doi.org/10.1016/0021-9991(92)90240-Y Chen X, Wan D (2019a) GPU accelerated MPS method for large-scale 3-D violent free surface flows. Ocean Eng. 171: 677-694. https://doi.org/10.1016/j.oceaneng.2018.11.009 Chen X, Wan D (2019b) Numerical simulation of three-dimensional violent free surface flows by GPU-based MPS method. Int. J. Comput. Methods 16(4): 1843012. https://doi.org/10.1142/s0219876218430120 Chen X, Xi G, Sun ZG (2014) Improving stability of MPS method by a computational scheme based on conceptual particles. Comput. Methods Appl. Mech. Eng. 278: 254-271. https://doi.org/10.1016/j.cma.2014.05.023 Chen X, Zhang Y, Wan D (2019) Numerical study of 3-D liquid sloshing in an elastic tank by MPS-FEM coupled method. J. Ship Res. 63(3): 143-153. https://doi.org/10.5957/josr.09180082 Colagrossi A, Landrini M (2003) Numerical simulation of interfacial flows by smoothed particle hydrodynamics. J. Comput. Phys. 191(2): 448-475. https://doi.org/10.1016/s0021-9991(03)00324-3 Duan G, Chen B, Koshizuka S, Xiang H (2017a) Stable multiphase moving particle semi-implicit method for incompressible interfacial flow. Comput. Methods Appl. Mech. Eng. 318: 636-666. https://doi.org/10.1016/j.cma.2017.01.002 Duan G, Chen B, Zhang X, Wang Y (2017b) A multiphase MPS solver for modeling multi-fluid interaction with free surface and its application in oil spill. Comput. Methods Appl. Mech. Eng. 320: 133-161. https://doi.org/10.1016/j.cma.2017.03.014 Duan G, Koshizuka S, Chen B (2015) A contoured continuum surface force model for particle methods. J. Comput. Phys. 298: 280-304. https://doi.org/10.1016/j.jcp.2015.06.004 Duan G, Koshizuka S, Yamaji A, Chen B, Li X, Tamai T (2018) An accurate and stable multiphase moving particle semi-implicit method based on a corrective matrix for all particle interaction models. Int. J. Numer. Methods Eng. 115(10): 1287-1314. https://doi.org/10.1002/nme.5844 Duan G, Matsunaga T, Yamaji A, Koshizuka S, Sakai M (2020) Imposing accurate wall boundary conditions in corrective-matrix-based moving particle semi-implicit method for free surface flow. Int. J. Numer. Methods Fluids 93(1): 148-175. https://doi.org/10.1002/fld.4878 Duan G, Yamaji A, Koshizuka S, Chen B (2019) The truncation and stabilization error in multiphase moving particle semi-implicit method based on corrective matrix: Which is dominant? Comput. Fluids 190: 254-273. https://doi.org/10.1016/j.compfluid.2019.06.023 Duan G, Yamaji A, Sakai M (2020) An incompressible-compressible Lagrangian particle method for bubble flows with a sharp density jump and boiling phase change. Comput. Methods Appl. Mech. Eng. 372: 113425. https://doi.org/10.1016/j.cma.2020.113425 Duan G, Yamaji A, Sakai M (2022) A multiphase MPS method coupling fluid-solid interaction/phase-change models with application to debris remelting in reactor lower plenum. Ann. Nucl. Energy 166: 108697. https://doi.org/10.1016/j.anucene.2021.108697 Fang XL, Ming FR, Wang PP, Meng ZF, Zhang AM (2022) Application of multiphase Riemann-SPH in analysis of air-cushion effect and slamming load in water entry. Ocean Eng. 248: 110789. https://doi.org/10.1016/j.oceaneng.2022.110789 Feng YQ, Yu AB (2004) Assessment of model formulations in the discrete particle simulation of gas-solid flow. Ind. Eng. Chem. Res. 43: 8378-8390. https://doi.org/10.1021/ie049387v Fernandes DT, Cheng LY, Favero EH, Nishimoto K (2015) A domain decomposition strategy for hybrid parallelization of moving particle semi-implicit (MPS) method for computer cluster. Cluster Comput 18: 1363-1377. https://doi.org/10.1007/s10586-015-0483-3 Ferrari A, Dumbser M, Toro EF, Armanini A (2009) A new 3D parallel SPH scheme for free surface flows. Comput. Fluids 38(6): 1203-1217. https://doi.org/10.1016/j.compfluid.2008.11.012 Fourey G, Hermange C, Le Touzé D, Oger G (2017) An efficient FSI coupling strategy between smoothed particle hydrodynamics and finite element methods. Comput. Phys. Commun. 217: 66-81. https://doi.org/10.1016/j.cpc.2017.04.005 Frandsen JB, Peng W (2006) Experimental sloshing studies in sway and heave base excited square tanks. Sixth International Conference on Civil Engineering in the Oceans, Baltimore, USA 504-512 Fu L, Jin YC (2015) Investigation of non-deformable and deformable landslides using meshfree method. Ocean Eng. 109: 192-206. https://doi.org/10.1016/j.oceaneng.2015.08.051 Gingold RA, Monaghan JJ (1977) Smoothed particle hydrodynamics: theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 181(3): 375-389. https://doi.org/10.1093/mnras/181.3.375 Gotoh H, Khayyer A, Shimizu Y (2021) Entirely Lagrangian meshfree computational methods for hydroelastic fluid-structure interactions in ocean engineering—Reliability, adaptivity and generality. Appl. Ocean Res. 115: 102822. https://doi.org/10.1016/j.apor.2021.102822 Gou W, Zhang S, Zheng Y (2019) Implementation of the moving particle semi-implicit method for free-surface flows on GPU clusters. Comput. Phys. Commun. 244: 13-24. https://doi.org/10.1016/j.cpc.2019.07.010 Guo K, Chen R, Qiu S, Tian W, Su G (2018) An improved Multiphase Moving Particle Semi-implicit method in bubble rising simulations with large density ratios. Nucl. Eng. Des. 340: 370-387. https://doi.org/10.1016/j.nucengdes.2018.10.006 Harada E, Gotoh H, Ikari H, Khayyer A (2019) Numerical simulation for sediment transport using MPS-DEM coupling model. Adv. Water Resour. 129: 354-364. https://doi.org/10.1016/j.advwatres.2017.08.007 Harada E, Ikari H, Tazaki T, Gotoh H (2021) Numerical simulation for coastal morphodynamics using DEM-MPS method. Appl. Ocean Res. 117: 102905. https://doi.org/10.1016/j.apor.2021.102905 Harada T, Koshizuka S, Shimazaki K (2008) Improvement of wall boundary calculation model for MPS method Trans Jpn. Soc. Comput. Eng. Sci. 20080006-20080006; (in Japanese) Hashimoto H, Grenier N, Sueyoshi M, Touzé DL (2022) Comparison of MPS and SPH methods for solving forced motion ship flooding problems. Appl. Ocean Res. 118: 103001. https://doi.org/10.1016/j.apor.2021.103001 Hayashi M, Hughes L (2013) The Fukushima nuclear accident and its effect on global energy security. Energy Policy 59: 102-111. https://doi.org/10.1016/j.enpol.2012.11.046 He M, Gao X, Xu W, Ren B, Wang H (2019) Potential application of submerged horizontal plate as a wave energy breakwater: A 2D study using the WCSPH method. Ocean Eng. 185: 27-46. https://doi.org/10.1016/j.oceaneng.2019.05.034 He M, Xu W, Gao X, Ren B (2018) The layout of submerged horizontal plate breakwater (SHPB) with respect to the tidal-level variation. Coastal Eng. J. 60(3): 280-298. https://doi.org/10.1080/21664250.2018.1514758 Hori C, Gotoh H, Ikari H, Khayyer A (2011) GPU-acceleration for Moving Particle Semi-Implicit method. Comput. Fluids 51(1): 174-183. https://doi.org/10.1016/j.compfluid.2011.08.004 Hwang SC, Khayyer A, Gotoh H, Park JC (2014) Development of a fully Lagrangian MPS-based coupled method for simulation of fluid-structure interaction problems. J. Fluids Struct. 50: 497-511. https://doi.org/10.1016/j.jfluidstructs.2014.07.007 Ikari H, Gotoh H (2008) Parallelization of MPS method for 3-D wave analysis. Proceedings of 8th International Conference on Hydro-science and Engineering (ICHE), Nagoya, Japan Ikeda H, Koshizuka S, Oka Y, Park HS, Sugimoto J (2001) Numerical analysis of jet injection behavior for fuel-coolant interaction using particle method. J. Nucl. Sci. Technol. 38(3): 174-182. https://doi.org/10.1080/18811248.2001.9715019 Iribe T, Fujisawa T, Koshizuka S (2010) Reduction of communication in parallel computing of particle method for flow simulation of seaside areas. Coastal Eng. J. 52(4): 287-304. https://doi.org/10.1142/S0578563410002221 Iribe T, Fujisawa T, Shibata K, Koshizuka S (2006) Study on parallel computation for fluid simulation using MPS method. Trans Jpn Soc Comput Eng Sci 20060015 (in Japanese) Jandaghian M, Krimi A, Shakibaeinia A (2021) Enhanced weakly-compressible MPS method for immersed granular flows. Adv. WaterResour. 152: 103908. https://doi.org/10.1016/j.advwatres.2021.103908 Jena D, Biswal KC (2017) A numerical study of violent sloshing problems with modified MPS method. J. Hydrodyn. 29(4): 659-667. https://doi.org/10.1016/s1001-6058(16)60779-5 Khayyer A, Gotoh H (2008) Development of CMPS method for accurate water-surface tracking in breaking waves. Coastal Eng. J. 50(2): 179-207. https://doi.org/10.1142/s0578563408001788 Khayyer A, Gotoh H (2009) Modified moving particle semi-implicit methods for the prediction of 2D wave impact pressure. Coastal Eng. 56(4): 419-440. https://doi.org/10.1016/j.coastaleng.2008.10.004 Khayyer A, Gotoh H (2010) A higher order Laplacian model for enhancement and stabilization of pressure calculation by the MPS method. Appl. Ocean Res. 32(1): 124-131. https://doi.org/10.1016/j.apor.2010.01.001 Khayyer A, Gotoh H (2011) Enhancement of stability and accuracy of the moving particle semi-implicit method. J. Comput. Phys. 230(8): 3093-3118. https://doi.org/10.1016/j.jcp.2011.01.009 Khayyer A, Gotoh H (2012) A 3D higher order Laplacian model for enhancement and stabilization of pressure calculation in 3D MPS-based simulations. Appl. Ocean Res. 37: 120-126. https://doi.org/10.1016/j.apor.2012.05.003 Khayyer A, Gotoh H (2013) Enhancement of performance and stability of MPS mesh-free particle method for multiphase flows characterized by high density ratios. J. Comput. Phys. 242: 211-233. https://doi.org/10.1016/j.jcp.2013.02.002 Khayyer A, Gotoh H (2016) A multiphase compressible-incompressible particle method for water slamming. Int. J. Offshore Polar Eng. 26(1): 20-25. https://doi.org/10.17736/ijope.2016.mk42 Khayyer A, Gotoh H, Falahaty H, Shimizu Y (2018a) Towards development of enhanced fully-Lagrangian mesh-free computational methods for fluid-structure interaction. J. Hydrodyn. 30(1): 49-61. https://doi.org/10.1007/s42241-018-0005-x Khayyer A, Gotoh H, Falahaty H, Shimizu Y (2018b) An enhanced ISPH-SPH coupled method for simulation of incompressible fluid-elastic structure interactions. Comput. Phys. Commun. 232: 139-164. https://doi.org/10.1016/j.cpc.2018.05.012 Khayyer A, Gotoh H, Shao S (2009) Enhanced predictions of wave impact pressure by improved incompressible SPH methods. Appl. Ocean Res. 31(2): 111-131. https://doi.org/10.1016/j.apor.2009.06.003 Khayyer A, Gotoh H, Shao SD (2008) Corrected Incompressible SPH method for accurate water-surface tracking in breaking waves. Coastal Eng. 55(3): 236-250. https://doi.org/10.1016/j.coastaleng.2007.10.001 Khayyer A, Gotoh H, Shimizu Y (2017) Comparative study on accuracy and conservation properties of two particle regularization schemes and proposal of an optimized particle shifting scheme in ISPH context. J. Comput. Phys. 332: 236-256. https://doi.org/10.1016/j.jcp.2016.12.005 Khayyer A, Gotoh H, Shimizu Y (2019) A projection-based particle method with optimized particle shifting for multiphase flows with large density ratios and discontinuous density fields. Comput. Fluids 179: 356-371. https://doi.org/10.1016/j.compfluid.2018.10.018 Khayyer A, Gotoh H, Shimizu Y, Gotoh K, Falahaty H, Shao S (2018c) Development of a projection-based SPH method for numerical wave flume with porous media of variable porosity. Coastal Eng. 140: 1-22. https://doi.org/10.1016/j.coastaleng.2018.05.003 Khayyer A, Gotoh H, Shimizu Y, Nishijima Y (2021a) A 3D Lagrangian meshfree projection-based solver for hydroelastic Fluid-Structure Interactions. J. Fluids Struct. 105: 103342. https://doi.org/10.1016/j.jfluidstructs.2021.103342 Khayyer A, Shimizu Y, Gotoh H, Hattori S (2021b) Multi-resolution ISPH-SPH for accurate and efficient simulation of hydroelastic fluid-structure interactions in ocean engineering. Ocean Eng. 226: 108652. https://doi.org/10.1016/j.oceaneng.2021.108652 Khayyer A, Shimizu Y, Gotoh H, Nagashima K (2021c) A coupled incompressible SPH-Hamiltonian SPH solver for hydroelastic FSI corresponding to composite structures. Appl Math Modell 94: 242-271. https://doi.org/10.1016/j.apm.2021.01.011 Khayyer A, Tsuruta N, Shimizu Y, Gotoh H (2019) Multi-resolution MPS for incompressible fluid-elastic structure interactions in ocean engineering. Appl. Ocean Res. 82: 397-414. https://doi.org/10.1016/j.apor.2018.10.020 Kim KS, Kim MH (2014) Dynamic coupling between ship motion and three-layer-liquid separator by using moving particle simulation. Int. J. Offshore Polar Eng. 24(2): 122-128 Kondo M, Koshizuka S (2011) Improvement of stability in moving particle semi-implicit method. Int. J. Numer. Methods Fluids 65(6): 638-654. https://doi.org/10.1002/fld.2207 Koshizuka S, Ikeda H, Oka Y (1999) Numerical analysis of fragmentation mechanisms in vapor explosions. Nucl. Eng. Des. 189: 423-433. https://doi.org/10.1016/S0029-5493(98)00270-2 Koshizuka S, Nobe A, Oka Y (1998) Numerical analysis of breaking waves using the moving particle semi-implicit method. Int. J. Numer. Methods Fluids 26: 751-769. https://doi.org/10.1002/(SICI)1097-0363(19980415)26:7<751::AID-FLD671>3.0.CO;2-C https://doi.org/10.1002/(SICI)1097-0363(19980415)26:7<751::AID-FLD671>3.0.CO;2-C Koshizuka S, Oka Y (1996) Moving particle semi-implicit method for fragmentation of incompressible fluid. Nucl. Sci. Eng. 123(3): 421-434. https://doi.org/10.13182/NSE96-A24205 Lastiwka M, Basa M, Quinlan NJ (2009) Permeable and non-reflecting boundary conditions in SPH. Int. J. Numer. Methods Fluids 61(7): 709-724. https://doi.org/10.1002/fld.1971 Lee BH, Park JC, Kim MH, Hwang SC (2011) Step-by-step improvement of MPS method in simulating violent free-surface motions and impact-loads. Comput. Methods Appl. Mech. Eng. 200(9-12): 1113-1125. https://doi.org/10.1016/j.cma.2010.12.001 Lee CJK, Noguchi H, Koshizuka S (2007) Fluid-shell structure interaction analysis by coupled particle and finite element method. Comput. Struct. 85(11-14): 688-697. https://doi.org/10.1016/j.compstruc.2007.01.019 Lee ES, Moulinec C, Xu R, Violeau D, Laurence D, Stansby P (2008) Comparisons of weakly compressible and truly incompressible algorithms for the SPH mesh free particle method. J. Comput. Phys. 227(18): 8417-8436. https://doi.org/10.1016/j.jcp.2008.06.005 Li G, Gao J, Wen P, Zhao Q, Wang J, Yan J, Yamaji A (2020) A review on MPS method developments and applications in nuclear engineering. Comput. Methods Appl. Mech. Eng. 367: 113166. https://doi.org/10.1016/j.cma.2020.113166 Li JJ, Qiu LC, Tian L, Yang YS, Han Y (2019) Modeling 3D non-Newtonian solid-liquid flows with a free-surface using DEM-MPS. Eng. Anal. Boundary Elem. 105: 70-77. https://doi.org/10.1016/j.enganabound.2019.04.015 Lind SJ, Xu R, Stansby PK, Rogers BD (2012) Incompressible smoothed particle hydrodynamics for free-surface flows: A generalised diffusion-based algorithm for stability and validations for impulsive flows and propagating waves. J. Comput. Phys. 231(4): 1499-1523. https://doi.org/10.1016/j.jcp.2011.10.027 Liu J, Koshizuka S, Oka Y (2005) A hybrid particle-mesh method for viscous, incompressible, multiphase flows. J. Comput. Phys. 202: 65-93. https://doi.org/10.1016/j.jcp.2004.07.002 Liu X, Morita K, Zhang S (2018) An advanced moving particle semi-implicit method for accurate and stable simulation of incompressible flows. Comput. Methods Appl. Mech. Eng. 339: 467-487. https://doi.org/10.1016/j.cma.2018.05.005 Liu X, Zhang S (2021) Development of adaptive multi-resolution MPS method for multiphase flow simulation. Comput. Methods Appl. Mech. Eng. 387: 114184. https://doi.org/10.1016/j.cma.2021.114184 Lucy LB (1977) A numerical approach to the testing of the fission hypothesis. Astron. J. 82: 1013-1024 https://doi.org/10.1086/112164 Luo M, Khayyer A, Lin P (2021) Particle methods in ocean and coastal engineering. Appl. Ocean Res. 114: 102734. https://doi.org/10.1016/j.apor.2021.102734 Luo M, Koh CG (2017) Shared-Memory parallelization of consistent particle method for violent wave impact problems. Appl. Ocean Res. 69: 87-99. https://doi.org/10.1016/j.apor.2017.09.013 Lyu HG, Deng R, Sun PN, Miao JM (2021) Study on the wedge penetrating fluid interfaces characterized by different density-ratios: Numerical investigations with a multi-phase SPH model. Ocean Eng. 237: 109538. https://doi.org/10.1016/j.oceaneng.2021.109538 Lyu HG, Sun PN, Miao JM, Zhang AM (2022) 3D multi-resolution SPH modeling of the water entry dynamics of free-fall lifeboats. Ocean Eng. 257: 111648. https://doi.org/10.1016/j.oceaneng.2022.111648 Marrone S, Bouscasse B, Colagrossi A, Antuono M (2012) Study of ship wave breaking patterns using 3D parallel SPH simulations. Comput. Fluids 69: 54-66. https://doi.org/10.1016/j.compfluid.2012.08.008 Marrone S, Colagrossi A, Le Touzé D, Graziani G (2010) Fast free-surface detection and level-set function definition in SPH solvers. J. Comput. Phys. 229(10): 3652-3663. https://doi.org/10.1016/j.jcp.2010.01.019 Monaghan JJ (1994) Simulating free surface flows with SPH. J. Comput. Phys. 110(2): 399-406. https://doi.org/10.1006/jcph.1994.1034 Monaghan JJ, Kajtar JB (2009) SPH particle boundary forces for arbitrary boundaries. Comput. Phys. Commun. 180(10): 1811-1820. https://doi.org/10.1016/j.cpc.2009.05.008 Ni X, Feng W, Huang S, Zhang Y, Feng X (2018) A SPH numerical wave flume with non-reflective open boundary conditions. Ocean Eng. 163: 483-501. https://doi.org/10.1016/j.oceaneng.2018.06.034 Ni X, Feng W, Huang S, Zhao X, Li X (2020) Hybrid SW-NS SPH models using open boundary conditions for simulation of free-surface flows. Ocean Eng. 196: 106845. https://doi.org/10.1016/j.oceaneng.2019.106845 Nomura K, Koshizuka S, Oka Y, Obata H (2001) Numerical analysis of droplet breakup behavior using particle method. J. Nucl. Sci. Technol. 38(12): 1057-1064. https://doi.org/10.1080/18811248.2001.9715136 Pahar G, Dhar A (2017) Numerical modelling of free-surface flow-porous media interaction using divergence-free moving particle semi-implicit method. Transp. Porous Media 118(2): 157-175. https://doi.org/10.1007/s11242-017-0852-x Pan XJ, Zhang HX, Lun YT (2008) Numerical simulation of viscous liquid sloshing by moving-particle semi-implicit method. J. Marine Sci. App. 7: 184-189. https://doi.org/10.1007/s11804-008-7047-3 Pan XJ, Zhang HX, Sun XY (2012) Numerical simulation of sloshing with large deforming free surface by MPS-LES method. China Ocean Eng. 26(4): 653-668. https://doi.org/10.1007/s13344-012-0049-6 Park S, Jeun G (2011) Coupling of rigid body dynamics and moving particle semi-implicit method for simulating isothermal multiphase fluid interactions. Comput. Methods Appl. Mech. Eng. 200(1-4): 130-140. https://doi.org/10.1016/j.cma.2010.08.001 Rafiee A, Pistani F, Thiagarajan K (2010) Study of liquid sloshing: numerical and experimental approach. Comput. Mech. 47(1): 65-75. https://doi.org/10.1007/s00466-010-0529-6 Rao C, Wan D (2018) Numerical study of the wave-induced slamming force on the elastic plate based on MPS-FEM coupled method. J. Hydrodyn. 30(1): 70-78. https://doi.org/10.1007/s42241-018-0007-8 Ren B, Wen H, Dong P, Wang Y (2016) Improved SPH simulation of wave motions and turbulent flows through porous media. Coastal Eng. 107: 14-27. https://doi.org/10.1016/j.coastaleng.2015.10.004 Rong S, Chen B (2010) Numerical simulation of Taylor bubble formation in micro-channel by MPS method. Microgravity Sci. Technol. 22(3): 321-327. https://doi.org/10.1007/s12217-010-9183-z Sakai M, Shigeto Y, Sun X, Aoki T, Saito T, Xiong J, Koshizuka S (2012) Lagrangian-Lagrangian modeling for a solid-liquid flow in a cylindrical tank. Chem. Eng. J. 200-202: 663-672. https://doi.org/10.1016/j.cej.2012.06.080 Shakibaeinia A, Jin YC (2009) A weakly compressible MPS method for modeling of open-boundary free-surface flow. Int. J. Numer. Methods Fluids 63: 1208-1232. https://doi.org/10.1002/fld.2132 Shakibaeinia A, Jin YC (2011) A mesh-free particle model for simulation of mobile-bed dam break. Adv. Water Resour. 34: 794-807. https://doi.org/10.1016/j.advwatres.2011.04.011 Shakibaeinia A, Jin YC (2012) MPS mesh-free particle method for multiphase flows. Comput. Methods Appl. Mech. Eng. 229-232: 13-26. https://doi.org/10.1016/j.cma.2012.03.013 Shibata K, Koshizuka S, Matsunaga T, Masaie I (2017) The overlapping particle technique for multi-resolution simulation of particle methods. Comput. Methods Appl. Mech. Eng. 325: 434-462. https://doi.org/10.1016/j.cma.2017.06.030 Shibata K, Koshizuka S, Sakai M, Tanizawa K (2012) Lagrangian simulations of ship-wave interactions in rough seas. Ocean Eng. 42: 13-25. https://doi.org/10.1016/j.oceaneng.2012.01.016 Shibata K, Koshizuka S, Tamai T, Murozono K (2012) Overlapping particle technique and application to green water on deck. International Conference on Violent Flows, Nantes, France, 106-111 Shimizu Y, Gotoh H, Khayyer A (2018) An MPS-based particle method for simulation of multiphase flows characterized by high density ratios by incorporation of space potential particle concept. Comput. Math. Appl. 76(5): 1108-1129. https://doi.org/10.1016/j.camwa.2018.06.002 Shirakawa N, Yamamoto Y, Horie H, Tsunoyama S (2002) Analysis of flows around a BWR spacer by the two-fluid particle interaction method. J. Nucl. Sci. Technol. 39(5): 572-581. https://doi.org/10.1080/18811248.2002.9715236 Sun PN, Le Touzé D, Oger G, Zhang AM (2021) An accurate FSI-SPH modeling of challenging fluid-structure interaction problems in two and three dimensions. Ocean Eng. 221: 108552. https://doi.org/10.1016/j.oceaneng.2020.108552 Sun PN, Le Touzé D, Zhang AM (2019) Study of a complex fluid-structure dam-breaking benchmark problem using a multi-phase SPH method with APR. Eng. Anal. Boundary Elem. 104: 240-258. https://doi.org/10.1016/j.enganabound.2019.03.033 Sun X, Sakai M, Sakai MT, Yamada Y (2014) A Lagrangian-Lagrangian coupled method for three-dimensional solid-liquid flows involving free surfaces in a rotating cylindrical tank. Chem. Eng. J. 246: 122-141. https://doi.org/10.1016/j.cej.2014.02.049 Sun Y, Xi G, Sun Z (2019) A fully Lagrangian method for fluid-structure interaction problems with deformable floating structure. J. Fluids Struct. 90: 379-395. https://doi.org/10.1016/j.jfluidstructs.2019.07.005 Sun Y, Xi G, Sun Z (2021) A generic smoothed wall boundary in multi-resolution particle method for fluid-structure interaction problem. Comput. Methods Appl. Mech. Eng. 378: 113726. https://doi.org/10.1016/j.cma.2021.113726 Tajnesaie M, Shakibaeinia A, Hosseini K (2018) Meshfree particle numerical modelling of sub-aerial and submerged landslides. Comput. Fluids 172: 109-121. https://doi.org/10.1016/j.compfluid.2018.06.023 Tanaka M, Cardoso R, Bahai H (2018) Multi-resolution MPS method. J. Comput. Phys. 359: 106-136. https://doi.org/10.1016/j.jcp.2017.12.042 Tanaka M, Masunaga T (2010) Stabilization and smoothing of pressure in MPS method by Quasi-Compressibility. J. Comput. Phys. 229(11): 4279-4290. https://doi.org/10.1016/j.jcp.2010.02.011 Tanaka M, Masunaga T, Nakagawa Y (2009) Multi-resolution MPS method. Trans. Jpn. Soc. Comput. Eng. Sci. 20090001 (in Japanese) Tang Z, Wan D, Chen G, Xiao Q (2016) Numerical simulation of 3D violent free-surface flows by multi-resolution MPS method. J. Ocean Eng. Mar. Energy 2(3): 355-364. https://doi.org/10.1007/s40722-016-0062-6 Tang Z, Zhang Y, Wan D (2016) Numerical simulation of 3-D free surface flows by overlapping MPS. J. Hydrodyn. 28(2): 306-312. https://doi.org/10.1016/s1001-6058(16)60632-7 Tazaki T, Harada E, Gotoh H (2021) Vertical sorting process in oscillating water tank using DEM-MPS coupling model. Coastal Eng. 165: 103765. https://doi.org/10.1016/j.coastaleng.2020.103765 Tazaki T, Harada E, Gotoh H (2022) Numerical investigation of sediment transport mechanism under breaking waves by DEM-MPS coupling scheme. Coastal Eng. 175: 104146. https://doi.org/10.1016/j.coastaleng.2022.104146 Tian W, Ishiwatari Y, Ikejiri S, Yamakawa M, Oka Y (2009) Numerical simulation on void bubble dynamics using moving particle semi-implicit method. Nucl. Eng. Des. 239(11): 2382-2390. https://doi.org/10.1016/j.nucengdes.2009.06.018 Tsukamoto MM, Cheng LY, Kobayakawa H, Okada T, Bellezi CA (2020) A numerical study of the effects of bottom and sidewall stiffeners on sloshing behavior considering roll resonant motion. Mar. Struct. 72: 102742. https://doi.org/10.1016/j.marstruc.2020.102742 Tsukamoto MM, Cheng LY, Nishimoto K (2011) Analytical and numerical study of the effects of an elastically-linked body on sloshing. Comput. Fluids 49(1): 1-21. https://doi.org/10.1016/j.compfluid.2011.04.008 Tsuruta N, Khayyer A, Gotoh H (2013) A short note on dynamic stabilization of moving particle semi-implicit method. Comput. Fluids 82: 158-164. https://doi.org/10.1016/j.compfluid.2013.05.001 Tsuruta N, Khayyer A, Gotoh H, Suzuki K (2021) Development of Wavy Interface model for wave generation by the projection-based particle methods. Coastal Eng. 165: 103861. https://doi.org/10.1016/j.coastaleng.2021.103861 Violeau D, Rogers BD (2016) Smoothed particle hydrodynamics (SPH) for free-surface flows: past, present and future. J. Hydraul. Res. 54(1): 1-26. https://doi.org/10.1080/00221686.2015.1119209 Wang J, Zhang X (2019) Improved moving particle semi-implicit method for multiphase flow with discontinuity. Comput. Methods Appl. Mech. Eng. 346: 312-331. https://doi.org/10.1016/j.cma.2018.12.009 Wang L, Jiang Q, Zhang C (2017) Improvement of moving particle semi-implicit method for simulation of progressive water waves. Int. J. Numer. Methods Fluids 85(2): 69-89. https://doi.org/10.1002/fld.4373 Wang PP, Meng ZF, Zhang AM, Ming FR, Sun PN (2019) Improved particle shifting technology and optimized free-surface detection method for free-surface flows in smoothed particle hydrodynamics. Comput. Methods Appl. Mech. Eng. 357: 112580. https://doi.org/10.1016/j.cma.2019.112580 Wen X, Zhao W, Wan D (2021a) An improved moving particle semi-implicit method for interfacial flows. Appl. Ocean Res. 117: 102963. https://doi.org/10.1016/j.apor.2021.102963 Wen X, Zhao W, Wan D (2021b) A multiphase MPS method for bubbly flows with complex interfaces. Ocean Eng. 238: 109743. https://doi.org/10.1016/j.oceaneng.2021.109743 Wen X, Zhao W, Wan D (2021c) Numerical simulations of multilayer-liquid sloshing by multiphase MPS method. J. Hydrodyn. 33(5): 938-949. https://doi.org/10.1007/s42241-021-0083-z Wen X, Zhao W, Wan D (2022) Multi-phase moving particle semi-implicit method for violent sloshing flows. Eur. J. Mech. B. Fluids 95: 1-22. https://doi.org/10.1016/j.euromechflu.2022.04.002 Xie F, Zhao W, Wan D (2020) CFD simulations of three-dimensional violent sloshing flows in tanks based on MPS and GPU. J. Hydrodyn. 33: 938-949. https://doi.org/10.1007/s42241-020-0039-8 Xie F, Zhao W, Wan D (2021a) MPS-DEM coupling method for interaction between fluid and thin elastic structures. Ocean Eng. 236: 109449. https://doi.org/10.1016/j.oceaneng.2021.109449 Xie F, Zhao W, Wan D (2021b) Numerical simulations of liquid-solid flows with free surface by coupling IMPS and DEM. Appl. Ocean Res. 114: 102771. https://doi.org/10.1016/j.apor.2021.102771 Xu R, Stansby P, Laurence D (2009) Accuracy and stability in incompressible SPH (ISPH) based on the projection method and a new approach. J. Comput. Phys. 228(18): 6703-6725. https://doi.org/10.1016/j.jcp.2009.05.032 Xu T, Jin YC (2019) Modeling impact pressure on the surface of porous structure by macroscopic mesh-free method. Ocean Eng. 182: 1-13. https://doi.org/10.1016/j.oceaneng.2019.04.054 Xu WJ, Zhou Q, Dong XY (2021) SPH-DEM coupling method based on GPU and its application to the landslide tsunami. Part Ⅱ: reproduction of the Vajont landslide tsunami. Acta Geotech. 17: 2121-2137. https://doi.org/10.1007/s11440-021-01387-3 Zha R, Peng H, Qiu W (2021) An improved higher-order moving particle semi-implicit method for simulations of two-dimensional hydroelastic slamming. Phys. Fluids 33(3): 037104. https://doi.org/10.1063/5.0033491 Zhang G, Wua J, Sun Z, Moctarc OE, Zong Z (2020) Numerically simulated flooding of a freely-floating two-dimensional damaged ship section using an improved MPS method. Appl. Ocean Res. 101: 102207. https://doi.org/10.1016/j.apor.2020.102207 Zhang G, Zhao W, Wan D (2022a) Moving particle semi-implicit method coupled with finite element method for hydroelastic responses of floating structures in waves. Eur. J. Mech. B. Fluids 95: 63-82. https://doi.org/10.1016/j.euromechflu.2022.04.005 Zhang G, Zhao W, Wan D (2022b) Numerical simulations of sloshing waves in vertically excited square tank by improved MPS method. J. Hydrodyn. 34(1): 76-84. https://doi.org/10.1007/s42241-022-0008-5 Zhang N, Zheng X, Ma Q (2019a) Study on wave-induced kinematic responses and flexures of ice floe by Smoothed Particle Hydrodynamics. Comput. Fluids 189: 46-59. https://doi.org/10.1016/j.compfluid.2019.04.020 Zhang S, Gou W, Wang Y, Zhang J, Zheng Y (2021) Direct numerical simulation of atomization by jet impact using moving particle semi-implicit method with GPU acceleration. Comput. Part. Mech. 9(3): 499-512. https://doi.org/10.1007/s40571-021-00424-y Zhang T, Koshizuka S, Murotani K, Shibata K, Ishii E (2017) Improvement of pressure distribution to arbitrary geometry with boundary condition represented by polygons in particle method. Int. J. Numer. Methods Eng. 112(7): 685-710. https://doi.org/10.1002/nme.5520 Zhang T, Koshizuka S, Murotani K, Shibata K, Ishii E, Ishikawa M (2016a) Improvement of boundary conditions for non-planar boundaries represented by polygons with an initial particle arrangement technique. Int. J. Comput. Fluid Dyn. 30(2): 155-175. https://doi.org/10.1080/10618562.2016.1167194 Zhang T, Koshizuka S, Xuan P, Li J, Gong C (2019b) Enhancement of stabilization of MPS to arbitrary geometries with a generic wall boundary condition. Comput. Fluids 178: 88-112. https://doi.org/10.1016/j.compfluid.2018.09.008 Zhang TG, Koshizuka S, Shibata K, Murotani K, Ishii E (2015) Improved wall weight function with polygon boundary in moving particle semi-implicit method. Trans Japan Soc Comput Eng Sci 20150012 Zhang Y, Chen X, Wan D (2016b) MPS-FEM coupled method for the comparison study of liquid sloshing flows interacting with rigid and elastic baffles. Appl. Math. Mech. 37(12): 1359-1377 Zhang Y, Wan D (2017) Numerical study of interactions between waves and free rolling body by IMPS method. Comput. Fluids 155: 124-133. https://doi.org/10.1016/j.compfluid.2017.03.019 Zhang Y, Wan D (2018a) MPS-FEM coupled method for fluid-structure interaction in 3D dam-break flows. Int. J. Comput. Methods 16(2): 1846009. https://doi.org/10.1142/s021987621846009x Zhang Y, Wan D (2018b) MPS-FEM coupled method for sloshing flows in an elastic tank. Ocean Eng. 152: 416-427. https://doi.org/10.1016/j.oceaneng.2017.12.008 Zhang Y, Wan D, Hino T (2014) Comparative study of MPS method and level-set method for sloshing flows. J. Hydrodyn. 26(4): 577-585. https://doi.org/10.1016/s1001-6058(14)60065-2 Zhou Q, Xu, WJ, Dong XY (2021) SPH-DEM coupling method based on GPU and its application to the landslide tsunami. Part Ⅰ: method and validation. Acta Geotech. 17: 2101-2119. https://doi.org/10.1007/s11440-021-01388-2


