1   Introduction

Welded tubular assemblies are present in several fields of steel construction including some offshore constructions (Visser, 1974). Namely, handling cranes, bridges, metal supports for platforms and especially marine structures made for the offshore oil industry (Arsem, 1987). These assemblies are formed by welding one or more braces to the chord and are constantly subjected to the combined dynamic forces of waves, wind, current, and even seismic activity (API, 1993). Such loading results in a large number of stress cycles leading to fatigue damage (Bellagh, 2001). In addition, the complex intersections of these tubular joints represent structural discontinuities leading to high stress concentrations near the welds (Mohamad, 2007). Therefore, an accurate assessment of the magnitude of stress concentrations is necessary to properly address the problem of fatigue damage and to make more reliable and resilient tubular joints (N'Diaye et al., 2007).

Extensive research has been conducted on various aspects of fatigue performance evaluation of tubular joints, in particular the determination of the stress concentration factor on the weld toe of tubular joints (Efthymiou, 1988; Lloyds, 1992; Shao, 2004). The main objective of these research efforts is thus the proposal of parametric equations to determine the stress concentration factor (Chang and Dover, 1996). Kuang et al. (1975), Wordsworth (1981), Efthymiou and Durkin (1985), Hellier et al. (1990) and Smedley and Fisher (1991) worked on analytical studies to determine the stress concentration factor for different configurations of tubular joints. These studies were carried out through experimental studies. In their work the authors showed that the distribution of the stress concentration factor on the weld toe of the tubular T, Y, X, K and KT-joints under various loads is at specific points. Shao et al. (2009) have studied the influence of geometrical parameters on the distribution of the SCF through numerical and experimental studies. They demonstrated the dimensionless parameters have an effect on the positioning of the hot spot along the weld edge of the tubular K and T-joints under balanced axial loads. In the same line, Lotfollahi-Yaghin and Ahmadi(2009, 2010) have numerically indicated dimensionless parameters have an effect on the variation of the stress concentration factors along the weld edge of the tubular KT-joint under balanced axial loads. They proposed a parametric equation to predict the stress concentrations along the weld edge of the tubular KT-joint. Ahmadi et al. (2011) and Ahmadi and Lotfollahi-Yaghin (2012) in their work stated that there are very remarkable differences between the values of the stress concentration factor in a three-plane tubular KT-joint, two-plane and single-plane tubular joints having the same geometrical properties under axial loads. It provides a parametric equation for determining stress concentration factors at various positions. Ahmadi and Lotfollahi-yaghin (2015), Ahmadi and Esmaeil (2015) and Ahmadi and Ali (2016) in their work have shown that the stress concentration factors play a crucial role in evaluating the fatigue performance of tubular K and KT-joints under in-plane and out-of-plane bending loads. Iberahin (2018) and Iberahin and Talal (2019) in their work on the analysis of stress concentration factors under axial loading and out-of-plane bending on the tubular K-joint, show that the effect of dimensionless parameters on stress concentration factors depends on the type of load case undergone by the tubular joint. Lalitesh et al. (2019) in their work on stress concentration factors on the weld toe of T and Y-joints subjected to in-plane bending loads, using numerical analysers, the authors show that the stress concentration factors are high for tubular joints with a larger brace-chord tilt angle. Gho and Gao (2004) in their work proposed a set of parametric formulae for determining the stress concentration factor (SCF) in the tubular K(N)-joints under various axial, in-plane bending and outof-plane bending loads. In-Gyu et al. (2014) in their work on the distribution of stress concentration factors in hollow and concrete-filled tubular TY(N)-joints for bridges using a numerical study, reported dimensionless parameters have a negligible effect on concrete-filled tubular TY(N)-joints than on hollow tubular TY(N) -joints. They proposed a parametric equation to determine the sensitivity of the dimensionless parameters.

In the majority of the works presented in the literature, it can be said that stress concentration factors in particular are one of the most influential factors in the fatigue strength of tubular joints than other factors such as frequency, temperature, corrosion, etc (Vincent, 2011). This justifies a lot of work on stress concentration factors on different shapes of tubular joints. Although tubular TY-joints are commonly used in offshore jacket structures, stress concentration factors on TY-joints under axial loads have not been addressed in this case.

In this work, the influence of dimensionless parameters on the stress concentration factor of tubular TY-joints are studied. This analysis is performed by the finite element method on 81 models of TY tubular structures under axial loading conditions using Comsol Multiphysics software. The results of the analysis are used to examine the evaluation of the influence on the fatigue strength of tubular joints, which plays an important role in safeguarding the integrity of structures. In addition, a new set of SCF parametric equations has been developed, based on the non-linear regression method, for the fatigue analysis and design of TY-joints subjected to axial loads.

2   Finite element modeling

In parallel with the various experimental works, numerous numerical simulation studies have been carried out to determine the behavior of tubular joints under loads that best reflect the operating conditions of offshore platforms.

Due to the high cost of materials and the restrictions of its facilities, the experimental method is difficult to use for a thorough study of tubular joints with various parameters without real dimensions. Nevertheless, the finite element method has been successfully used to examine the behavior of tubular joints with fairly realistic geometrical dimensions (Shao, 2004). In this work, we apply the finite element method to perform our study. Better accuracy of the results of a finite element stress analysis in tubular joints depends on the elements used, the fineness of the mesh especially near areas of high stress concentrations, whether the weld toe is modelled and the boundary conditions adopted.

2.1   Parametric study

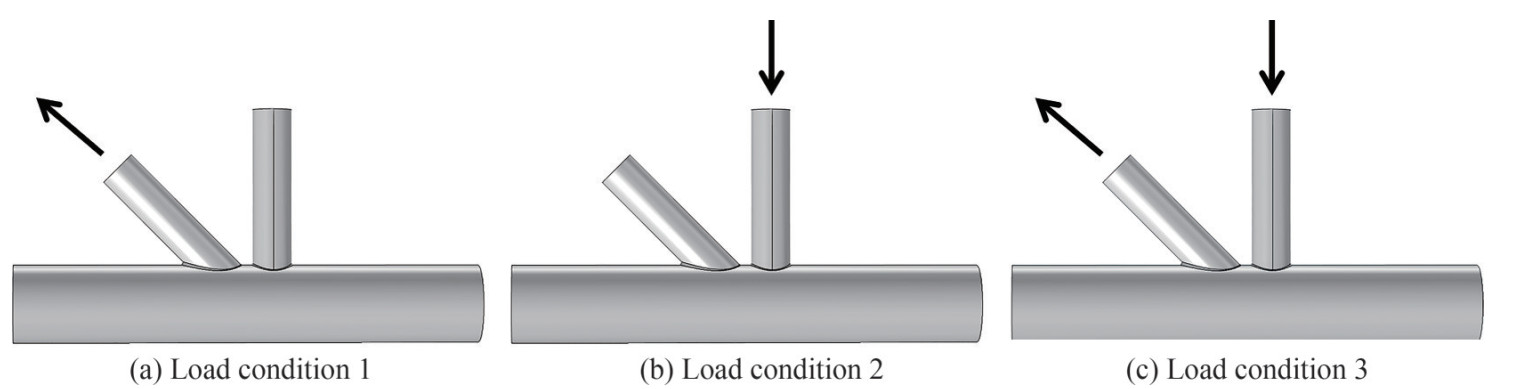
In this work, we analyze the behavior of tubular gap TYjoints (illustrated in Figure 1) subjected to axial loads. This tubular joint has a circular cross-section often found in offshore marine platforms. This is one of the tubular joints found in many of the offshore structures. It is composed of two secondary tubes (brace) connected to a main tube (chord) by welding. One of the brace forms an angle of θ = 90° and the other one inclined at an angle of θ < 90° respectively with chord.

Figure  1  Geometric representation of a tubular gap TY-joint

Download: Full-Size Img

To avoid a very large gap between the braces, we have studied the effect of seven models with different values of the length of the gap between the braces on the hot spot stress shown in Table 1. Then, from Table 1, it appears that the length of the braces gap (g) has no significant effect on the hot spot stress values. Therefore, a typical value of gap parameter ξ = 0.15 is assigned to all our models.

Efthymiou (1988), in his work have explained that, to avoid an impact on stresses at the chord/brace intersection that may be affected by the boundary conditions applied at the chord levels, the length of the chord must be really long. In order to choose a value for the chord length parameter α for our type of tubular joint, we have performed a study of the effect of this parameter on the SCF. Therefore, the results of this partial study have been presented in Table 2. From this analysis on the six models with different values of α given in Table 2, it appears that the value of this parameter has no effect on the values of the SCF. A realistic value of α = 12 is assigned in all models in the current study.

In previous works, Chang and Dover (1999) showed that the brace length parameter has no influence on the hot spot stress when the value of α_B is greater than the threshold value. In the present study, a realistic value α_B = 8 is used for all models in the current study to avoid of short length brace. Steel with a Young's modulus of 207 GPa and a Poisson's ratio of 0.3 was used as material for our model.

The geometric parameters considered for our models are summarized in the Table 3. These geometric parameters cover actual practical values that are commonly found for making tubular joints in offshore platform structures. The geometric values of all braces are the same for different specific design models similar to the one proposed by In-Gyu et al. (2014). Depending on the values of γ, τ and β of each joint, the diameter and wall thickness parameters of the brace are changed from one study model to another.

2.2   Mesh generation procedure and defined boundary conditions

The mesh used to discretise our tubular gap TYjoints (see Figure 2a) are Lagrangian and the element type used is triangular. This type of element has 6 nodes. It favours the representation of affine stress fields per element and are isoparametric because they are derived from these reference elements by a transformation that is also quadratic. However, they also have richer basis functions and therefore lead to smaller deviations from reality. In practice, experience shows that these elements generally lead to a better accuracy/cost ratio than their first order counterparts. The chord, brace and weld toe have acceptable displacements and are well suited to the curved boundary profile. By applying this type of 3D element, the weld toe profile can be modelled as a clean notch. This approach provides a more accurate and detailed stress distribution near the intersection than a single envelope analysis. It should be noted that the size of the weld toe connecting the chord and the brace is in accordance with the AWS (2002).

Figure  2  Meshed TY-joint in Comsol multiphisi

Download: Full-Size Img

The mesh generated for the weld toe profile and the area near the intersection is illustrated in Figure 2b. Our structures are meshed in such a way as to achieve a balance between the accuracy of the results and the computer by evaluating the time, software, file size produced, etc. However, in finite element calculations, numerical blocking in the convergence of solutions for large shear stiffnesses is encountered in some problems. It is possible to reduce or eliminate this phenomenon by lowering the level of the interpolation functions or by introducing elements with a larger number of degrees of freedom (Bharat et al. 2020). In order to improve the performance of the element and to avoid the phenomenon of shear locking, reduced integration has been employed. To check the convergence of the finite element analysis, a compliance test is performed and meshes of different qualities are used in this framework, before generating our 81 models of the tubular TY-joints.

A convergence study is performed to determine the required mesh division at which the displacement values converge as presented in the work of Ajay et al. (2015) and Bharat et al. (2021). Furthermore, a mesh convergence study is necessary to have more reliable results, we refined the mesh down to 3 mm on the intersection area and as CPU increases, the result converges to a constant value of 10.1 MPa (Table 4) as the maximum stress obtained under a loading condition 3 (Figure 3). Thus, the convergence of the mesh is carried out on one of the tubular joints (Joint Ref. 10/1) in UK HSE (1997).

Figure  3  Representation of the different types of axial load applied

Download: Full-Size Img

As shown in Figure 3 in this work, three different axial loading conditions are considered in order to study stress concentration factors in tubular TY-joints. In the load condition 1, the inclined brace is subjected to axial tensile loading and the straight brace is assumed to be fixed (see Figure 3a). In the load condition 2, the straight brace is subjected to an axial compressive load and the inclined brace is assumed to be fixed (see Figure 3b). In the load condition 3, which is the operating condition of tube joints in practice, the brace (straight and inclined) is subjected to balanced axial loads (see Figure 3c). The boundary conditions considered for all our joints designs are the fixing of the both ends of the chord. The modification of the boundary conditions will change the SCF values accordingly as they are very specific values (Anish et al., 2019; Abhay et al., 2019). Thus, this boundary condition allows for reduced displacements and rotations in all directions.

2.3   Stress concentration factor

The tubular joint has a specific geometry, which results in high stress concentrations near the welds toe. Under repeated loading, these concentrations lead to the creation of cracks, which can become large enough to cause the joint to fail. The location of the maximum stress concentration is called a hot spot. The location of the hot spots, where the stress concentration factor values are highest and which are preferred sites for fatigue crack initiation, is important in assessing the service life. Therefore, it is important to accurately determine the distributions of stress concentration factor values near the intersection lines of the tubular joints.

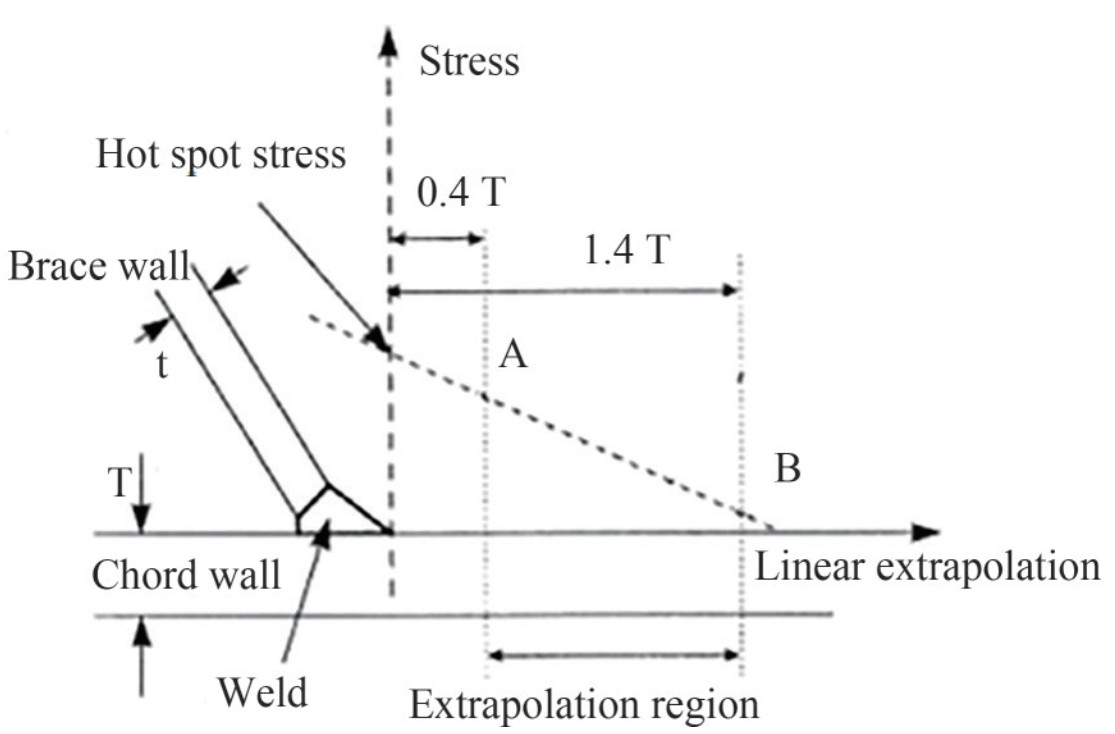
The hot spot stress along the edge of the weld toe is determined by the extrapolation method. As shown in Figure 4, the stresses at points A and B, which lie within a specified extrapolation region, are previously obtained from the finite element analysis (IIW-XV-E, 1999). The hot spot stress is then calculated by extrapolating the stresses at points A and B linearly to the end of the weld. The distribution of the hot spot stress along the edge of the weld toe is absolutely identical to the distribution of the SCF because the nominal stress is determined by applying the beam theory on the brace according to the type of load. However, the Von Mises stress is a better parameter for the analysis (Lalitesh et al. 2018). Therefore, for all FEA analyses in this work, the hot spot stress is given by the value of the Von Mises stress in the results.

Figure  4  Extrapolation method to obtain the hot spot stress

Download: Full-Size Img

The SCF is defined as follows:

where σ_hss is the hot spot stress and σ_n is the nominal stress. For a tubular joint subjected to an axial load Fa on the brace, the nominal stress σ_n is determined as follows:

where d and t are brace diameter and thickness, respectively.

2.4   Validation of the FEM

The accuracy of the predictions of the finite element analysis must be verified against the results of the experimental tests. Therefore, to validate the finite element structure, we will compare our results with those of the tests carried out in the UK HSE (1997). The geometrical characteristics (Table 5) of the finite element model (FEM) were chosen on the basis of the information given by the UK HSE (1997), for a tested steel structure, in order to obtain the maximum value of the SCFs. The results of the process verification are presented in Table 6. A good correlation can be observed on the results of our current model with those of the experimental results. Thus, we see that the maximum difference between the results in the Table 6 is less than 10%. Thus, we observe a slight variation in SCF which could be due to a modelling technique. So, the finite element models generated in this work can be considered as so accurate that they offer reliable results.

3   Results and discussion

In this section, we present the influence of geometrical parameters on the SCF, which is one of the most important factors influencing the fatigue strength of tubular joints. This study is carried out on the tubular TY-joint subjected to axial loads.

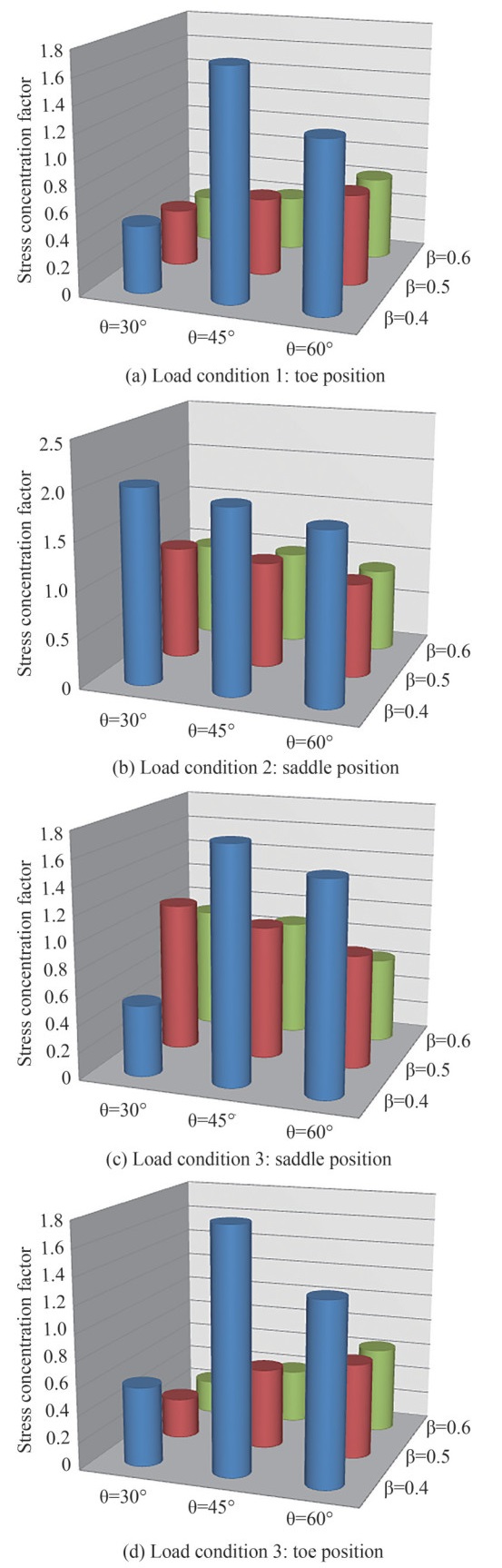
3.1   Analysis of the effects of parameters β on the SCF under axial loading

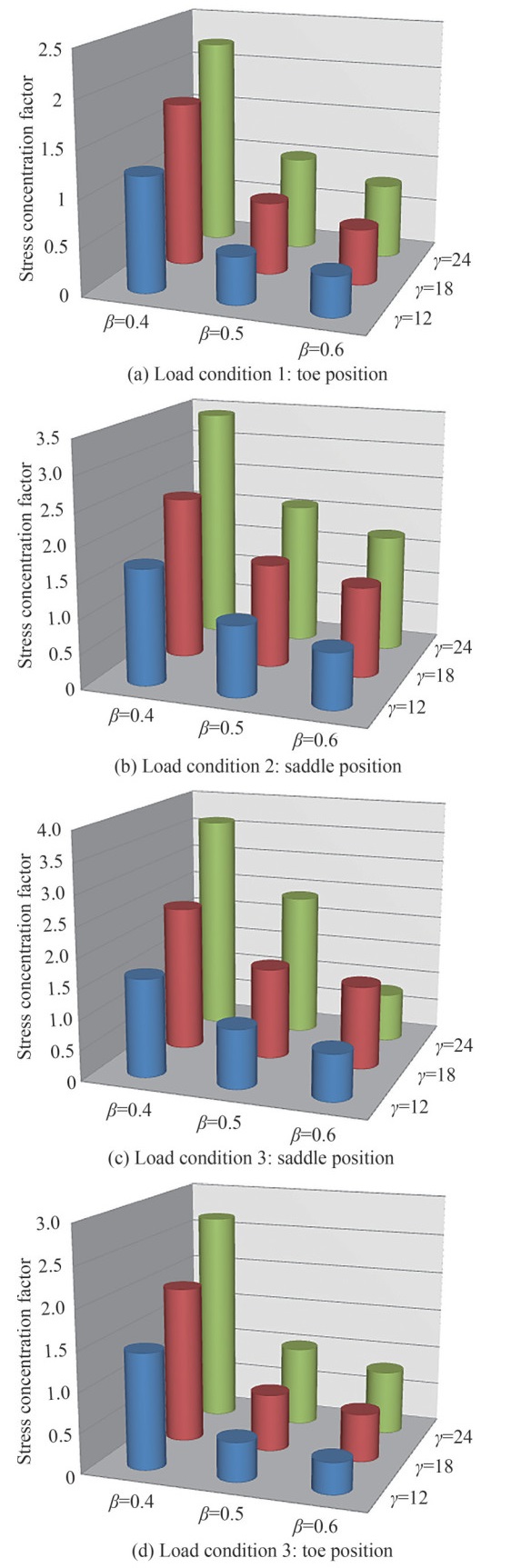
This subsection presents the effects of the brace-tochord diameter ratio parameter β on the SCFs and its interaction with the chord thickness ratio parameter γ. Thus, the influence of the parameters τ, γ and θ on the effect of β on the SCF is also studied. Figure 5 shows the values of the SCF due to the effect of the variations of the parameter β and its interaction with the parameter γ. The effect of the parameter β on the SCF values under load conditions 1 and 3 (Figures 5a and 5d) for β varying from 0.4 to 0.6, leads to a reduction of the SCF values at the position of the tip of the crown of the inclined brace of the tubular TYjoint. On the other hand, under load conditions 2 and 3 (Figures 5b and 5c), the increasing variation of β also leads to a reduction of the SCF values at the position of the saddle of the vertical brace of the tubular TY-joint. Our results thus reveal that the maximum values of the SCF are located at the level of the saddle position. They represent the critical values, which can be responsible for the fatigue failure phenomena. However, the tubular gap TY-joint is more resistant for values of 0.5 < β < 1 and the parameter β is a determining factor in the stress distribution due to the way the load transfer is accomplished. Thus, this result does not depend on the values of the other geometric parameters or on the type of axial loading applied. It is also evident that the parameter γ is more effective in increasing the SCF values compared to the parameter β.

Figure  5  Analysis of the effects of parameters β on the SCF

Download: Full-Size Img

3.2   Analysis of the effects of parameters γ on the SCF under axial loading

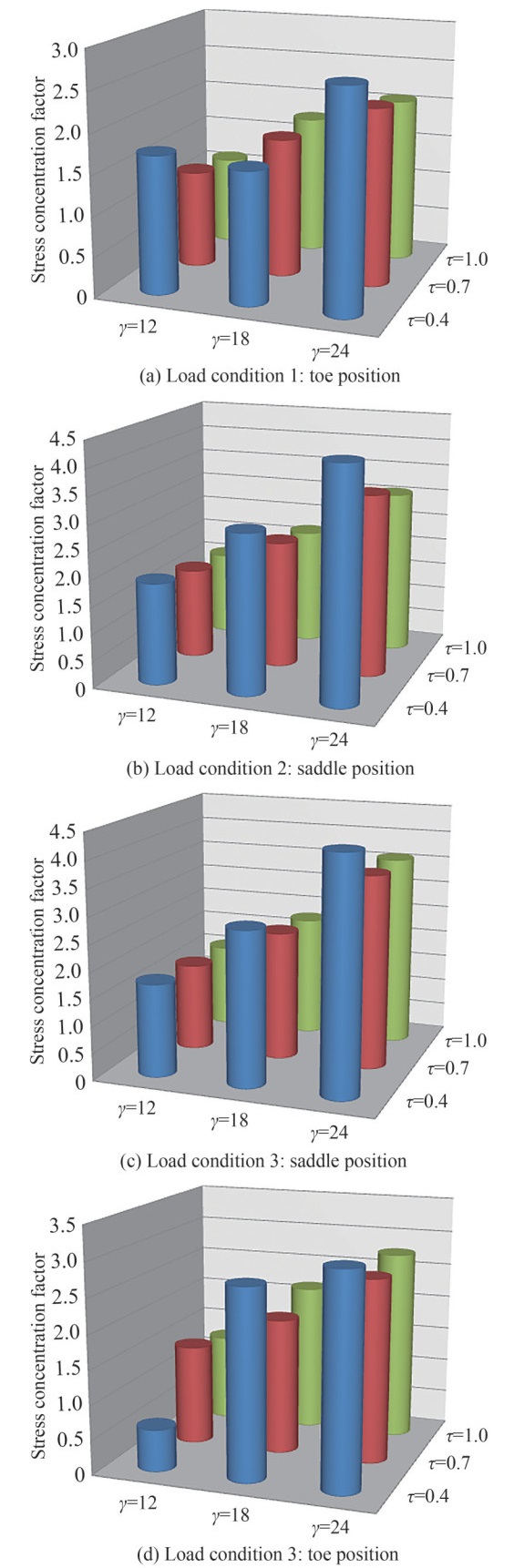
This subsection presents the influence of the chord thickness ratio parameter γ on the SCF and its interaction with the wall thickness ratio parameter τ. The influence of the parameters β, τ and θ on the effect of γ on the SCF is also studied. Figure 6 shows the values of the SCF due to the effect of the parameter γ and its interaction with the parameter τ. The effect of the parameter γ on the SCF values under load conditions 1 and 3 (Figures 6a and 6d) for γ varying from 12 to 24, leads to the increase of the SCF values at the position of the tip of the inclined bracing crown. On the other hand, for loading conditions 2 and 3 (Figures 6b and 6c), the increasing variation of γ leads instead to a significant increase of the SCF values at the position of the saddle of the vertical brace. Thus, for all axial loading conditions studied in Figure 3, the effect of increasing variation of γ increases the hot spot values at the crown and saddle position. Thus, our results show that, the maximum values of the SCF are located at the saddle position towards the side of the chord and thus correspond to the critical point. Therefore, for small variations of γ, by fixing τ, i.e., by increasing the thickness of the chord (T), we obtain an increase in the wall stiffness of the chord of the tubular TYjoint with a small stress distribution. Therefore, this result does not depend on the values of the other geometrical parameters or on the type of axial loading applied. This counterpart, the parameter τ, is more effective in increasing the values of the SCF compared to the parameter γ.

Figure  6  Analysis of the effects of parameters γ on the SCF

Download: Full-Size Img

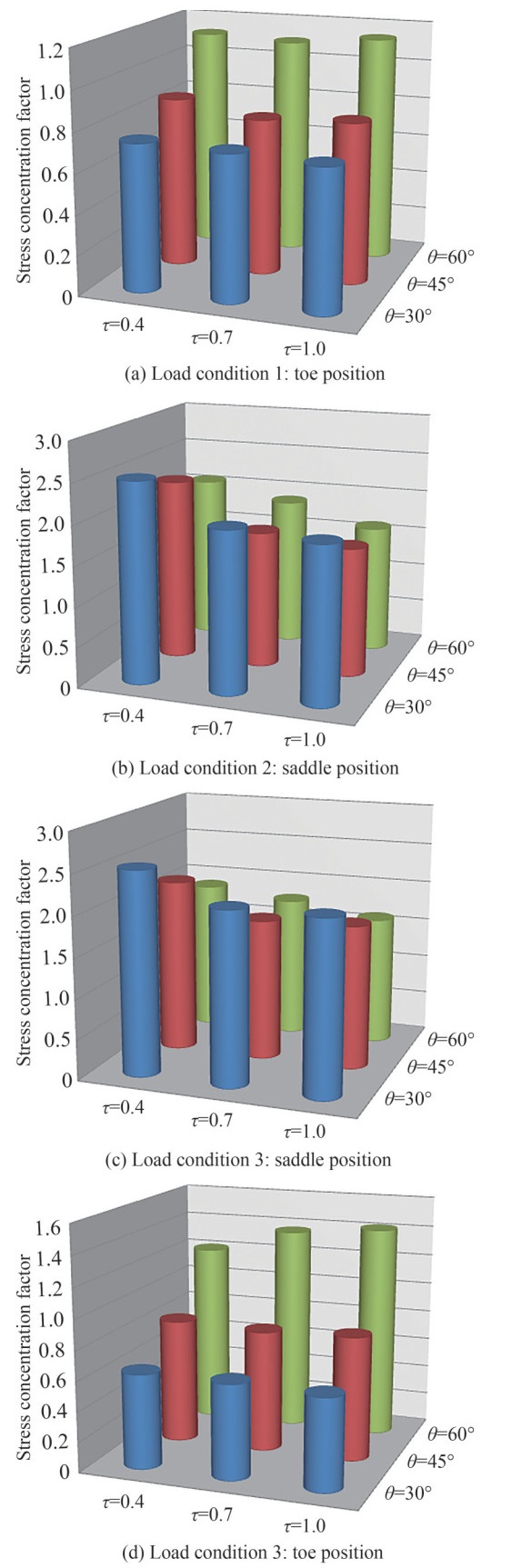
3.3   Analysis of the effects of parameters τ on the SCF under axial loading

The influence of the parameter of the wall thickness ratio τ and its interaction with the angle θ of inclination of the brace on the SCF is illustrated in this subsection. The influence of the parameters β, γ and θ on the effect of the parameter τ on the SCF is also studied. Figure 7 shows the values of the stress concentration factor (SCF) due to the variation of the parameter τ and its interaction with the parameter θ. Consequently, an increasing variation of the parameter τ significantly increases the values of the SCF. Thus, Figures 7a and 7d show the increase of the SCF for variations of the parameter τ during the loading condition 1 and 3 at the crown. However, we observe a low value of SCF for θ= 30° and 45°. Furthermore, Figures 7b and 7c show that the effect of the parameter τ for load conditions 2 and 3 reduces the SCF values at the saddle position. This result does not depend on the other values of the dimensionless parameters. Moreover, we note that the variation of the parameter θ, weakly influences the SCFs values at the saddle position and increases at the toe position. Thus, the critical SCF values are observed in the vicinity of the saddle position. However, the parameter τ is an indication of the relative bending stiffness of the brace and chord. The effect of the variation of the parameter τ on the SCF values is less important than the effect of the parameter β.

Figure  7  Analysis of the effects of parameters τ on the SCF

Download: Full-Size Img

3.4   Analysis of the effects of parameters θ on the SCF under axial loading

This subsection shows the effects of the brace inclination angle θ on the SCFs and its interaction with the parameter β. Thus, Figure 8 shows the effect of the parameter θ on the FSCs under three axial loading conditions (Figure 3). Therefore, Figures 8a and 8d show that for variations of θ for β = 0.4 an increase and decrease in SCF values at the saddle. This is due to a significant increase in the SCF value for θ = 45°. In contrast, for changes in θ for β = 0.5 and 0.6, there is a slight increase in SCF values. Figures 8b and 8c show us a decrease in SCF values for different increasing variations of the parameter θ at the saddle position. Thus, a significant increase in the SCF value for θ = 45° (see Figure 8c). This result does not depend on the type of axial load studied or on the other values of the geometric parameters. Thus, the maximum values of the SCFs are located in the vicinity at the saddle position towards the side of the chord. These values represent critical values in the vicinity of the saddle on the weld toe. However, the parameter β is more effective in significantly varying the SCF values compared to the parameter θ.

Figure  8  Analysis of the effects of parameters θ on the SCF

Download: Full-Size Img

4   Establishing the parametric equations to calculate the SCF

In this paper, four new parametric equations have been developed to determine the stress concentration factor at the crown toe and the saddle point of tubular TY-joints subjected to three types of axial loads. These parametric equations expressed as dimensionless parameters are useful for the fatigue design of tubular joints. The parametric equations to calculate the SCFs were established by the non-linear regression method using the statistical package (SPSS). The SCF values represent the dependent variables and the geometric parameters β, τ, γ, θ the independent variables. These different variables constitute the input information imported in the form of a matrix. The rows of this matrix give information about each value of the SCF on the weld toe in tubular TY-joints with specific geometrical characteristics. Furthermore, when the dependent and independent variables are defined, the expression of the equation has to be elaborated with given parameters, as presented by equation (3).

These parameters are unknown coefficients and exponents (c₁, c₂, c₃, c₄ and c₅ the coefficients defined in Eq. (3)). The researcher should designate an initial value for each factor as close as possible to the expected final answer. Incorrect initial values can lead to the failure of a solution (local or global) to converge. Several expressions of the equation must be developed to derive a parametric equation with a high coefficient of determination of R². In addition, when a large number of non-linear calculations are performed, the following parametric equations are used to obtain the value of the SCF at the Crown toe and Saddle of tubular TY-joints subjected to the three types of axial loads proposed.

• Toe position

Ioad condition 1:

Ioad condition 3:

• Saddle position

Ioad condition 2:

Ioad condition 3:

In equations (4) - (7), the parameter θ is given in radians. The ranges of validity of the geometric parameters for the established equations are defined by Eq. (8).

The commonly used UK DoE (1995), recommends validation criteria for using the established parametric equations calculating the SCF. The validation results compared by the UK DoE (1995) criteria are presented in Table 7.

According to Table 7, all the proposed equations satisfy the UK DoE (1995) criteria and can therefore be reliably used to study the fatigue strength of offshore jacket structures. P/R expressed as a percentage (%) in Table 7, represents the ratio between the SCF predicted by the established parametric equation and the SCF recorded during a test or analysis.

Thus, we compare the equations established with respect to the experimental data and the parametric equations from the literature. For this purpose, we compare Eq. (7) which is one of the equations obtained by the balanced axial load at the Saddle with these different studies published in the literature. According to the UK HSE (1992), a detailed experimental database of SCFs is presented for acrylic complex joints, including uni-planar, multi-planar and K and TY-joints.

This paper deals only with the SCF values at the position of specific points of the weld toe. Experimental data determined from two acrylic specimens (designated 8. A1 and 8.A2) in this paper were used to compare the proposed equations. The geometric parameters of these specimens are shown in Figure 9 and Table 8. In addition to the experimental data, our proposed equations were also compared with the equations proposed by Wordsworth, Efthymiou and Kuang which are specifically set up to predict the value of the SCF at the Saddle position.

Figure  9  Representation geometric of the acrylic specimens (UK HSE 1992)

Download: Full-Size Img

The values obtained by these equations are presented, respectively in UK HSE (1992). In addition, these different equations are used to predict the SCF at the position of the Saddle and Crown points. The validation results for the saddle point position were summarized in Table 9. However, possible reasons for the variation in results from the present work could be due to a different modelling technique. In addition, some authors use the principal constraints while others use the Von Mises constraint as the hot spot stress. Thus, Table 9 presents a good agreement between the results of the proposed equation and the parametric equations proposed in the literature.

5   Conclusions

In this work, the influence of geometrical parameters on the SCF of tubular TY-joints has been studied under three axial loading conditions. 81 models of TY tubular structures were evaluated in this work. The analysis results will be used to show the influence of the geometric parameters brace-to-chord diameter ratio, chord wall slenderness ratio, brace-to-chord thickness ratio and outer brace inclination angle on the values of the SCF at the different saddle and crown toe position. Based on the finite element results, a set of parametric equations calculating the SCF was established using non-linear regression analysis. In the axial load condition 1, the SCF value at the toe position is slightly lower than the corresponding value at the toe position in the load condition 3. Furthermore, we can say that the highest SCF value is at the toe position in the load condition 3. On the other hand, in the axial load condition 2, the SCF value at the position of the saddle point is slightly lower than the corresponding value at this position in the load condition 3. Thus, we obtain the highest SCF value at the saddle point in the case of the load condition 3. Furthermore, among the four parametric equations found, the SCF values at the toe and saddle points are the minimum and maximum values, respectively. The four equations established can be reliably applied to the fatigue strength of TY tubular structures of offshore jacket platforms.