1   Introduction

The design of a submarine, by its nature and by the strong lack of data on this type of unit, brings most of the uncertainties in the preliminary phase. In particular, in this phase potential errors lead to increased design cost, time and design effort. Nevertheless, it is worth noting that a substantial modification of the project in the early stages can be managed quite easily, while in a more advanced stage this may lead to severe consequences. The design is further complicated by the fact that most Classification society rules do not provide precise recommendation about the scantling of the reinforcements and plating thickness of the submarine, only offering prescriptive guidance and formulations for evaluating failure modes (Report of Committee V.5, 2012; American Bureau of Shipping, 2021; Bureau Veritas, 2016). On the contrary, at the moment, the best guidance is provided by DNV-GL rules (DNV-GL, 2018) which offer quite extensive formulation to predict the actual stress distribution, as well as the critical pressure for various buckling limit states, namely global, local and tripping. PD5500 (PD5500, 2021) is also a well assessed code providing formulations for the scantling of pressure vessel.

Clearly, the main loading on submerged structures is the external pressure and the resistant hull is usually checked upon four different failure modes noted as:

1) Yielding of the hull shell;

2) Buckling of the shell between ring stiffeners (local buckling);

3) Global buckling;

4) Annular buckling of frames.

Recently, some scientific papers have been published dealing with the collapse process and ultimate strength prediction of ring stiffened cylinders. Cho et al. (2018) propose a ultimate strength formulation considering failure mode interactions proving the accuracy of the proposed formulation in a empirical way, i.e. with 107 test results.

Reijmers et al. (2022) provide analytical interframe collapse models for axisymmetrically and asymmetrically imperfect cylindrical shells supported by imperfect (i. e., not perfectly circular) rings that are used to qualify the existing and the new model for use in risk-based design.

MacKay et al. (2011) on the contrary deal with collapse predictions for submarine pressure hulls with and without artificial corrosion damage in a numerical way, verifying the accuracy of FE models comparing the results with experimental ones.

It is worth noting, anyway, that the effect of the initial geometrical imperfection on the collapse load, for a specified limit state, has not been fully investigated yet. The objective of this study is the quantification the residual strength of the structure, if any, once one of the four limit states considered in the scantling phase is reached for a certain pressure, and the quantification of the influence of the initial imperfections of the hull on the structural response capacity, in order to obtain information useful for assessing the admissibility of a given operating condition.

The safety factors used in limit state assessment should be defined considering the consequences of the occurrence of a certain failure mode and the residual capacity beyond such limit: e.g., local buckling likely leads to local yielding of plating only, while global buckling may easily lead to overall structural collapse, involving a sudden yielding of wide areas of the structure and a larger safety factor is therefore recommended to keep sufficient margins against complete collapse. The safety factors not supported by clear scientific evidence are used during the scantling phase. Therefore, the residual response to the occurrence of a certain limit state is evaluated, in order to examine the safety coefficients that were defined in the previous activity.

These coefficients are not provided on the basis of particular engineering considerations, but they are defined as input data, based on the experience of the shipyard. Eventually, this study was motivated also by the fact that it is common practice of the shipyards to adopt different safety factors for local and global buckling, assuming that the phenomena lead to a different structural response.

On the basis of the spreadsheet developed for the scantling of a submarine, developed in a related activity, a certain structural layout is therefore identified and verified according to some fixed input data, i.e., the operating draught, the diameter of the submarine and the construction material.

The layout obtained is then verified according to the four limit states that are identified in the preliminary design phase, i.e., global buckling, local buckling, annular buckling and plasticization.

Therefore, the spreadsheet allows creating a certain geometric configuration for the a given operational depth, so that one among the considered states is satisfied according to a minimum margin, while the other three are fully verified with a residual margin of at least 20% with respect to the design load. In this way, it is expected that once the limit state is exceeded, the effects of this exceeding are clearly related to that specific limit state. For example, in order to observe the structural response beyond yielding, where a plastic collapse is expected, without triggering other failure modes, possible occurrences of of local, global or annular should be avoided. In such a way, it is possible to follow the evolution of the plasticization without any overlapping of the collapse modes, and therefore to clearly identify the collapse mechanism. This strategy also allows evaluating the residual strength of the structure, if present, once a given limit state is exceeded.

This is supposed to prevent the interaction between different failure modes in the nonlinear collapse analysis.

The deformed FE model before collapse is also checked to confirm that no failure mode interaction occurs.

In summary, in order to evaluate the effect of the yielding of the material, the critical buckling pressure must be much higher than the pressure that induces yielding, so as to be able to follow the evolution of the structure in the post limit state regime and so to understand if any residual strength is present (i.e., if the structure is able to withstand gradually increasing pressures, or if the limit state coincides with an ultimate state). This type of analysis is followed for each of the four limit states usually considered in the preliminary design stage, in order to draw conclusions relating to all of them.

This study is conducted numerically, using ADINA finite element software, both considering perfect structures and structures characterized by initial imperfections of different shapes. In fact, the geometric imperfection can cause effects of a macroscopic nature, i. e., varying the orientation of the pressure load acting on the hull, but can also influence the buckling strength severely when in presence of submerged structures (Showkati et al., 2008; Wang XY et al., 2011; Wang Z et al., 2011 and Li and Liu, 2020). This involves significant effects related to the dependence of the elastic instability phenomena on the initial geometry, linked to the mode shape assumed by the structure once the critical condition occurs. In particular, the initial imperfections have an important impact on the transition from precritical to post-buckling regime and can influence the structural response greatly, especially when similar eigenvalues make equilibrium conditions, related to different deformations, very close to each other in terms of external load, near the bifurcation points. Basically, a certain imperfection can lead the structure to assume one buckling shape rather than another (Shon et al., 2013), with deeply different structural responses (Figure 1). It is expected that an imperfection having the shape of the first buckling mode, obtained by extracting the eigenvector related to the first eigenvalue from a linearized buckling analysis, is associated with a lower structural response capacity, while different shapes may better approximate the response of the perfect structure or even increase its structural capacity (DNV-GL, 2018).

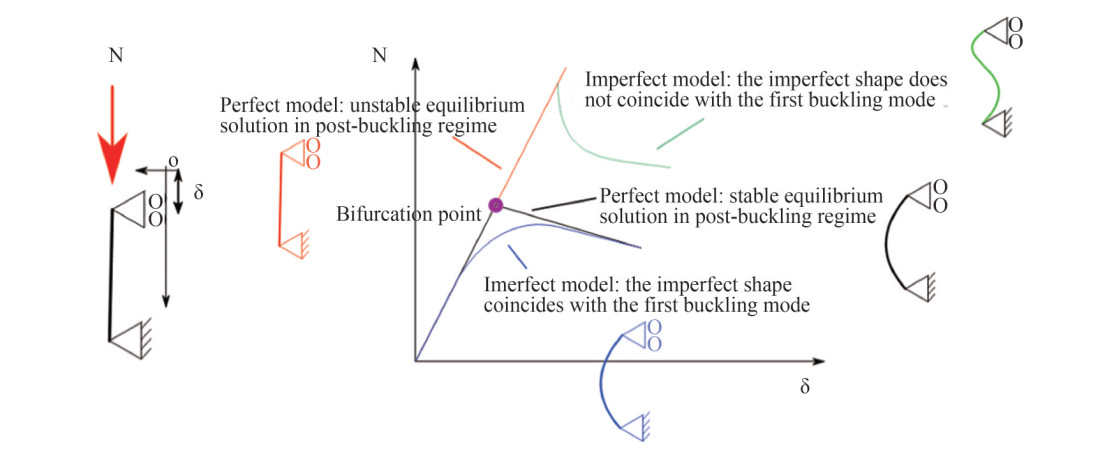Figure  1  Possible structural responses for a model subject to elastic instability, and for different forms of initial imperfection (Showkati et al., 2008)

Download: Full-Size Img

It is very important to define the shape of the imperfection rather than its relative amplitude. In general, imperfections are usually not visible to the naked eye. The imperfections are of the order of a millimeter or fraction of a millimeter; therefore, they are difficult to assess during the construction process. Generally, for a naval structure, e. g., a stiffened panel, a perfect model tends to show a perfectly linear behavior up to the critical load, followed by an abrupt postcritical transition with an important loss of structural stiffness. For a structure with large imperfections, on the other hand, there is a visible non-linearity in an early phase, but the transition towards the postcritical regime is generally more gradual (Figure 2).

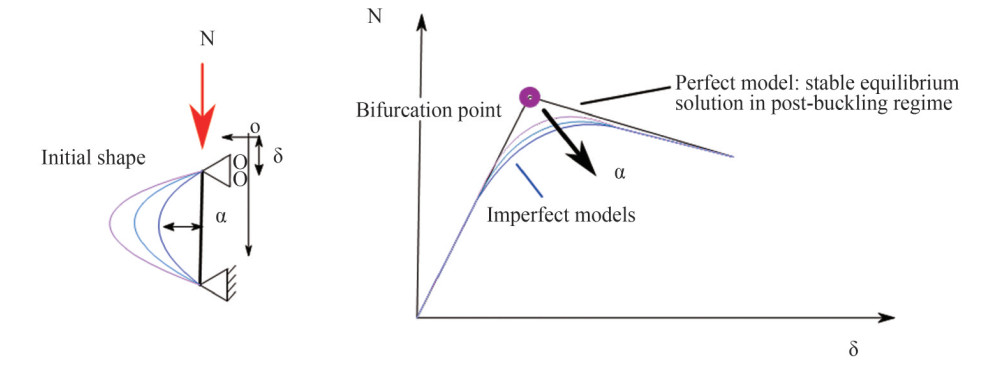Figure  2  Structural response as a function of the extent of the initial imperfection (Showkati et al., 2008)

Download: Full-Size Img

Preliminary studies on reinforced cylindrical structures subjected to external hydrostatic head show that, in addition to the transition from pre to post-critical regime, there is a strong dependence of the ultimate load on the initial imperfection. In this study, two types of initial imperfections are considered: buckling mode and thin-horse shape. The buckling mode imperfection is the most severe type in term of consequences on the capacity of the structure (ISSC, 2012), but at the same time it is less likely to be induced by the manufacturing phase, in which the structure is deformed exactly like the shape of the first mode of instability. The thin-horse imperfection involves the portions of the shell plating farthest from the transverse frames to experience radial displacements, due to the effect of welding shrinkage.

In conclusion, different geometries of FE models were considered in the present study, and tested up to the collapse pressure in the frame of a nonlinear software environment, according to the following principles:

· A set of different geometrical configurations aimed at inducing a clearly defined failure mechanism, to prevent from the interaction of different failure modes;

· Two different imperfection models: first eigen mode and thin-horse mode;

· Different amplitude of initial imperfections.

A total number of more than 40 nonlinear collapse analysis were necessary to draw conclusions (4 structural layouts × 2 different imperfection shapes × at least 5 imperfection amplitudes).

Incremental non-linear collapse analyses were carried out for each combination of parameters. These analyses can take account of the geometric and material non-linearities, updating the stiffness matrix at each load increment.

2   Numerical analysis

2.1   Numerical model–Geometry and configurations

The numerical model consists of a 15 meters hull section between two primary transverse stiffening members (i.e., transverse bulkheads or stiffening rings of higher order than common frames), represented by means of rigid-links. The diameter of the cylinder measures 5 meters. The hull areas extending within the first three common transverse rings are modeled using an elastic constitutive model (Figure 3): this makes the model unsuitable for studying the connection with the primary stiffening members, but this choice allows to solve criticalities related to stress concentrations and, at the same time, to study phenomena of global instability. The number of at least three elastic spacings was derived from a preliminary analysis conducted by the authors, showing that after such interval displacements converge to those of an infinitely long stiffened cylinder, calculated according to analytical formulations (Pulos and Salerno, 1961; Vergassola et al., 2019):

Figure  3  Numerical model: green areas represent the zones where an elastic material model was adopted

Download: Full-Size Img

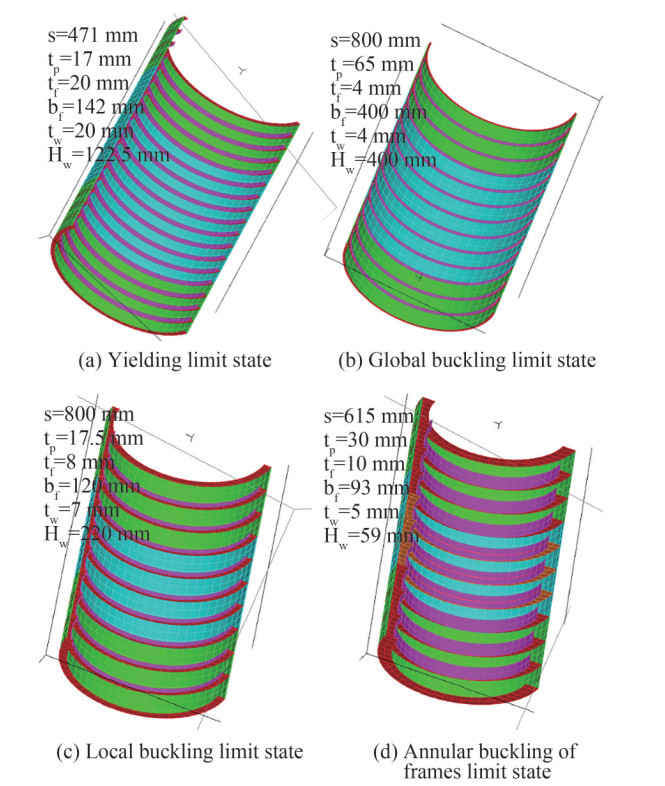
Different geometric configurations are analyzed in this study. These are identified for each of the four limit states described above, for a design depth of 300 m. In particular, each configuration is subjected to the onset of a single limit state, but satisfies the other three with a capacity margin of at least 20% of the design load. To do this, three geometric parameters are selected, i.e., number of transverse rings between the primary stiffening members (spacing of ordinary stiffeners), thickness of the plating and cross-sectional area of the common ring, which combined in an appropriate way, provide the four geometric configurations used for this study (Figure 4). The goal is to obtain a clear separation between the collapse modes, in order to avoid a difficult interpretation of the collapse mechanism linked to the interaction of different non-linear phenomena (failure mode). Therefore, three geometric parameters are selected, i. e., the number of transverse rings between the primary stiffeners (distance of the ordinary stiffeners), the thickness of the plating and the cross-sectional area of the common ring, which, appropriately combined, provide four geometric configurations used for this study (Figure 4). Being s the frame spacing, t_p is the thickness of plating, t_f is the thickness of flange, b_f is the flange breadth, t_w is the thickness of the web and the H_w is the web height of the frame.

Figure  4  The four geometric configurations used for this study

Download: Full-Size Img

Each of the following configurations satisfies, for a hydrostatic head of 300 m, a certain limit state with a minimum margin, while retaining a margin of at least 20%, in terms of external applied load, with respect to the other three limit states.

Four FE models were built-up in ADINA environment, a convergence analysis was carried out and it was found that the best option in terms of convergence vs. time was MITC 16 nodes shell element with a mesh density resulting in an edge length of 150 mm and, as a consequence, a node distance of a about 50 mm. The convergence was checked comparing resulting stress at different locations, namely on the hull shell both at the frame intersection and at mid-span. Furthermore, a ISSC benchmark study (ISSC, 2012) conducted an experimental numerical analysis to study the collapse of a cylinder under external pressure, and it was found that a 5 mm mesh was suitable for the study. The model radius measured 123 mm, hence the model counted about 150 elements on the circumference of the shell. The present model has a diameter of 5 m, hence about 200 elements are modelled on the circumference, but, since a 16 nodes element is adopted, the actual node density is by far greater.

In the present study the effect of residual stresses has not been included. Residual stresses due to the welding of plating characterized by such a high thickness definitely plays a role in the structural response at collapse. By the way, the present paper is focused on highlighting the effect of initial geometric imperfection rather than thermal effects due to the manufacturing process. Introducing initial stresses in the model will be considered as a step forward for a future work.

2.2   Numerical model–Boundary conditions and material model

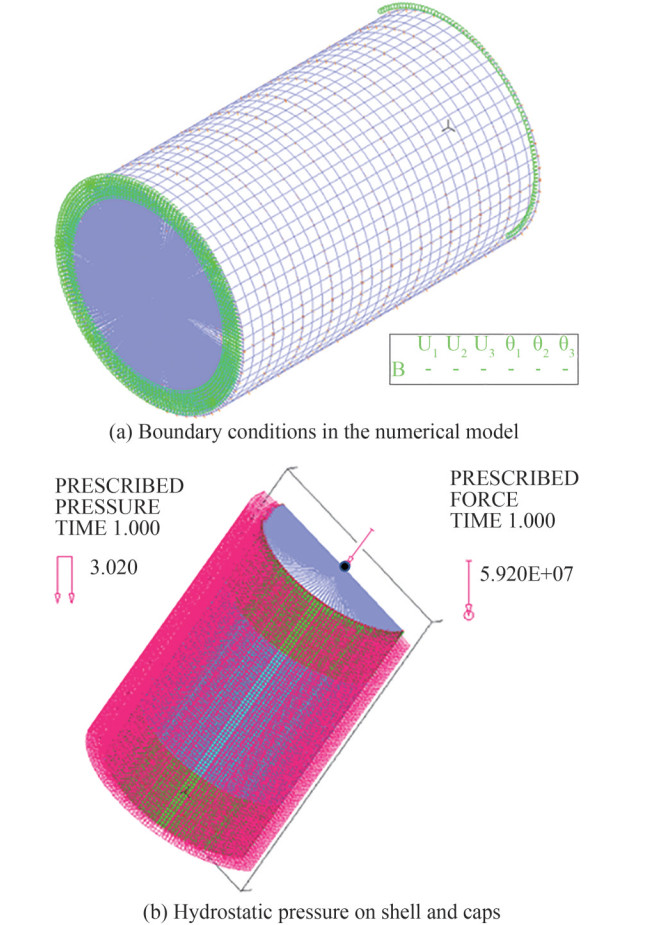
In Figure 5a, the boundary conditions applied to the numerical model are shown. All the degrees of freedom of each single node of one end of the cylindrical body are constrained, while the nodes of the opposite end is connected by "rigid-link"at the central node of the cross section, which has all degrees of freedom restrained except for the axial translation. The hydrostatic pressure relative to the depth of immersion is applied to all the elements in correspondence with the outer shell of the submarine as shown in Figure 5b. Finally, the force equivalent to the hydrostatic pressure acting on the spherical cap, responsible for the axial compression of the plating is calculated and applied in the central node as show in Figure 5c.

Figure  5  The evaluation of axial displacement at the nodes indicated by black dots

Download: Full-Size Img

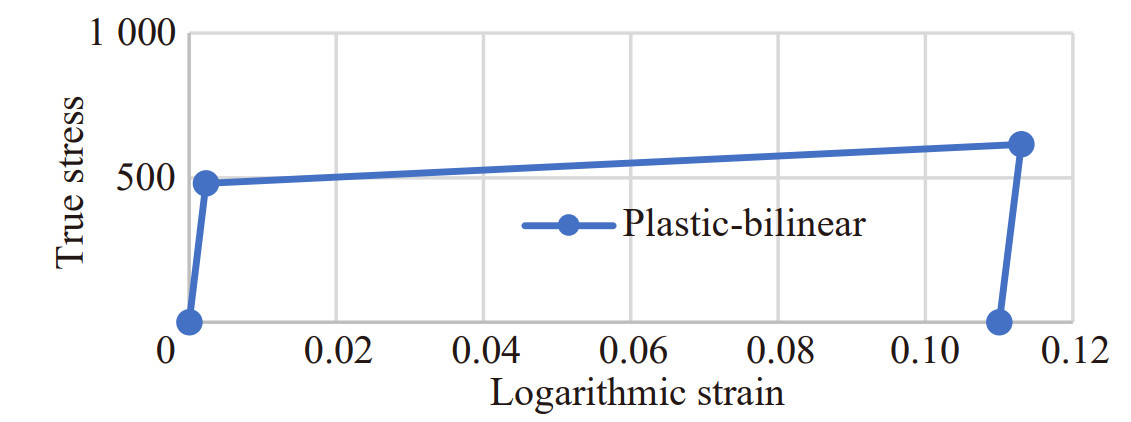
A non-linear plastic material model, with hardening, was hypothesized, capable of simulating the behavior of the AMANOX.

The material model is therefore defined as follows:

· Young's modulus = 213 000 MPa;

· Yield stress = 480 MPa;

· The hardening modulus is equal to 0.6% of the Young's Modulus, or 1 278 MPa;

· Maximum allowable effective plastic strain = 0.11

· An isotropic yield model was defined.

Figure 6 shows the stress strain curve of the defined material model.

Figure  6  Model of material used for buckling analyzes

Download: Full-Size Img

2.3   Numerical model–Type of analysis

The current loading condition, involving a distributed pressure load, in association with a model characterized by nonlinear displacements is not suitable for a displacement-controlled analysis, which is the typical method adopted to assess for the ultimate strength of a structure. In particular, collapse analyses are usually run under displacement control, because it is intended to map a structural response that at some point decreases in terms of internal forces. On the contrary, a collapse analysis using incremental load steps is particularly complex, since beyond the ultimate capacity an equilibrium condition may no longer be identified. E.g., when the ultimate capacity in terms of internal forces is exceeded, the structure can no longer be in equilibrium with increasing external loads.

In the present case, increasing the imposed displacement is suitable for evaluating the ultimate response of the structure due to the difficulty in mapping the displacements, as they involve both axial and transverse displacements at nodes subjected to external loads, whose proportion does not remain constant since the model is subjected to different nonlinear phenomena.

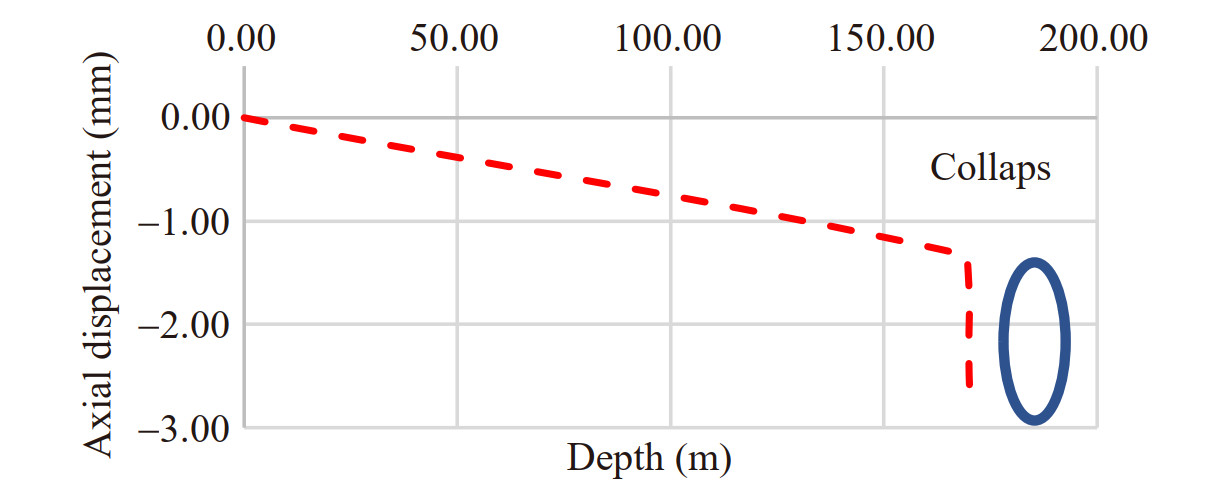
In order to assess for the ultimate strength of the structure, authors attempted to map the axial displacement of the 'plugs' of the submarine, to observe how the axial displacement varies as a function of the external pressure, as long as the structure is able to keep itself in equilibrium with the external loads. It is observed that, when the external pressure becomes closer to the ultimate response of the structure, before the collapse the response becomes highly nonlinear, where very small load increases generate relatively large displacements, highlighting a very strong non-linear transition of the load-displacement curve, as shown in Figure 7.

Figure  7  Example of displacement-load graph that shows the collapse condition

Download: Full-Size Img

In order to describe the collapse behavior of the structure, the method adopted by the authors in the present paper represents a possible alternative to the well-established Riks method. In ADINA software environment collapse analysis adopting Riks method are a possibility, by the way in the present case it was found that achieving convergence was very challenging and time consuming (very often did not lead to convergence at all). The proposed method, with the modelled inertia effect, represents a valid alternative as reported i. e. by the ABAQUS software manual (The Riks Method, 2022).

A nonlinear implicit calculation is performed, which sometimes can generate convergence problems, especially in the pre-collapse stage where the model becomes highly nonlinear. Hence, it is decided to run dynamic analyses although the load increment is very slow, because the small component of kinetic energy associated with a dynamic model significantly facilitates the convergence of the calculation. Consequently, it is observed that once the point of collapse is reached, the structure shows violent accelerations, suggesting that the condition of static equilibrium has been lost. In conclusion, it was decided to conduct an analysis that allows to map the structural response in analogy with a standard endshortening curve, typically obtained by means of displacement control analysis.

In summary, an implicit dynamic analysis with incremental pressure is used, to track the initiation of the collapse. The collapse condition is identified when the axial displacements grow with an order of magnitude higher than the rate of increase up to that point. Ideally, an 'almost' vertical tangent is observed in the displacement-load graph (Figure 7).

In particular, the Figure 7 shows the trend of the curve that links the depth with the axial displacement of one end (submarine "plug", i. e., transverse bulkheads). The very wide linear regime is clearly identified, followed by a very strong nonlinear transition which clearly determines the collapse. In the graph it is not easy to identify exactly the value of the depth where the collapse occurs. However, since the non-linearity becomes so important that the response in terms of displacement assumes an almost vertical slope with respect to the load, it is possible to estimate the value of the hydrostatic head able to induce the collapse with an uncertainty of a few centimeters.

It is also verified, for a limited number of cases due to the complexity related to this kind of analysis, that there is no subsequent equilibrium condition for higher external loads, meaning that the nonlinear behavior observed clearly represents the beginning of the collapse.

2.4   Numerical model–Initial imperfections

In a nonlinear collapse analysis, it is usually necessary to define the shape and the amplitude of an initial imperfection, as imperfect geometries may influence the ultimate strength, as well as the whole structural response before and after the ultimate load (Simitses, 1986; Sadovskýa et al., 2021). The effect of initial imperfections may vary a lot from a structure to another, while its effect is negligible in some actual cases (Ringsberg et al., 2021), particular geometries may on the contrary show severe sensitivity towards it (Ismailab, 2015).

Indeed, initial imperfections are usually present in the actual structures, often due to manufacturing tolerances, or deriving from residual stresses and strains induced in example by the welding process. Moreover, permanent deformations may also be generated by cyclic loading of great amplitude while in service, or due to accidental conditions.

Additionally, geometrical imperfections are, in some cases, needed to trigger a certain nonlinear response when using nonlinear finite element method, particularly when in proximity of bifurcation points. Introducing an initial imperfection in a nonlinear FE analysis is therefore necessary mostly for two reasons:

· It sometimes affects the structural response, while representing a realistic scenario since real structures are not geometrically perfect;

· It makes the convergence of the calculation in the postbuckling transition easier, since it prevents the model from losing the static equilibrium, numerically identified by a zero eigenvalue of the stiffness matrix, when the applied load equals the critical load.

Recently, the evolution of non-linear methods allows to overcome this criticality and also to run nonlinear analyses of perfect models subjected to elastic instability phenomena; however, the initial imperfection still simplifies the computational phase.

When an initial imperfection shape is modelled, the structure may continue to deform in the prescribed shape as the load increases. It may also snap over to a more preferred shape i. e., a shape requiring less internal strain energy. Such mode snapping leads to unstable response and may give numerical instability and problems with convergence. In general, when an imperfection shape similar to the preferred collapse mode of the panel-usually coinciding with the first mode shape obtained from eigenvalue analysis for estimating the critical load-is assigned, it leads to a cautious result and often solves numerical problems. However, the shape associated with the first buckling mode may be complex and, consequently, the model may substantially diverge from the real imperfections of the structure.

Furthermore, when a very large imperfection is considered, more energy is required to change the buckling mode shape. Thus, if the imperfection amplitude is large, the structure may be forced into a nonpreferred shape.

In conclusion, a large imperfection combined with the preferred collapse mode may give unreasonably conservative prediction of the capacity (DNV, (2009). It is therefore important that the imperfection is carefully chosen both in terms of shape and amplitude.

For buckling and ultimate strength analysis using nonlinear finite element method, a small magnitude should be applied with a shape equal-or similar to the preferred collapse mode of the structure. Possible results of selecting different combinations of imperfection shape and magnitude are summarized in Table 1, as extracted from DNV, (2009).

However, it is extremely important to underline that this discussion is based on the common experience that, usually, deals with stiffened structures subject to axial loads, in which the mode shapes show geometries that are consistent with possible geometric imperfections caused by working processes or operation during the unit life.

As regards to the structures of this study, i.e., stiffened cylinders subjected to external pressure, very peculiar mode shapes were observed, especially when a local buckling mode was consistent with the first eigenvalue (Figure 8). Hence, since the presence of actual imperfections equal to the first local buckling mode are quite unlikely to be found, both buckling mode and thin-horse mode imperfection models were considered, as it follows:

Figure  8  Initial imperfections representations

Download: Full-Size Img

• Imperfections according to the first eigenvector resulting from linearized buckling analysis, gradually increasing (i.e., global, local and annular buckling modes, depending on the case): this imperfection is quite unlikely to be found on actual structures, especially when it is associated to a local mode.

• Imperfections according to thin-horse shape, to simulate changes in shape due to the production process, which are increasing too.

Initial imperfections are one of the most important parameters to be evaluated, since it is fundamental to understand how much they can impact on the ultimate strength of the structure with respect to the perfect model one.

3   Results and discussion

In this section the results for each limit state are discussed. In particular, some graphs are shown, in which it is possible to evaluate the ultimate strength behavior as a function of the amplitude of the initial imperfection. In each graph the ultimate capacity of the structure is represented in terms of depth at collapse, and the variation of the initial imperfection is shown both in terms of typology (i.e. buckling mode and thin horse shapes) and amplitude.

3.1   Yielding limit state

The yielding limit state configuration leads, for the design load, the maximum stress on the plating to be just below the yielding strength of the material, while satisfying all the elastic buckling checks (global, local, tripping of the ring) with a large margin (>20%). Although buckling does not occur at failure, as the configuration is supposed to lead to a plastic collapse failure mode, the mode-1 buckling mode is provided as initial imperfection, where mode-1 buckling mode is a local buckling mode.

The results of the analyses are shown in the graph below (Figure 9). The capacity margin of the structure is about 40% in the case of a perfect geometry, with respect to the design load (i.e. the black dashed line). As regards the imperfect models, it is shown a residual capacity margin up to about 10 mm of geometric imperfections, for both imperfection mode shapes. On the other hand, beyond 10 mm of imperfection amplitude, the ultimate capacity of the thinhorse shaped model continues to decrease, while the buckling mode shaped one stabilizes. That is because the thinhorse shape mode affects the actual stress on the plating, interacting with the load orientation, and therefore it has an impact when the collapse mode is governed by plastic collapse.

Figure  9  Yielding limit state results

Download: Full-Size Img

3.2   Global buckling limit state

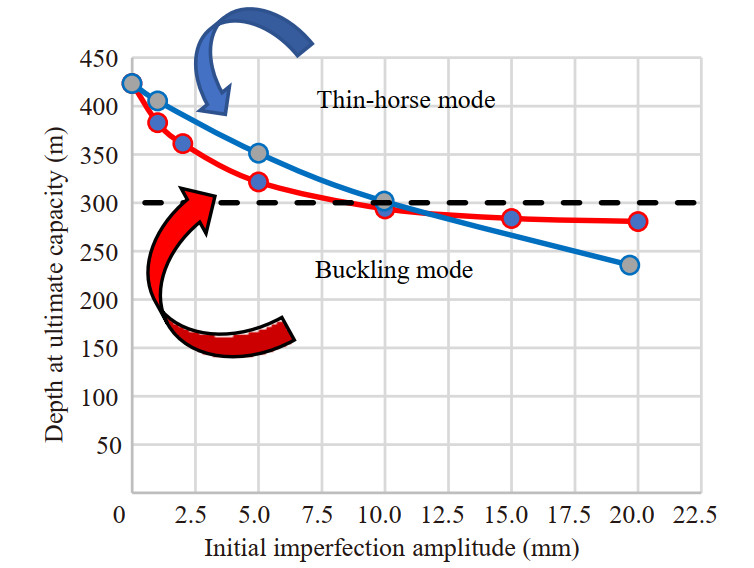
The global buckling limit state configuration leads the critical load for global instability to be just higher than the design load, while the other limit states are widely verified (>20%).

The results of the analyses are shown in the graph below (Figure 10). Negligible capacity margin in the perfect geometry model, compared to the design load, is observed. As a consequence, the condition of global instability can be identified as an "ultimate state". The first buckling mode shape imperfections have a strong impact on the ultimate capacity (i.e. −20% per 2 mm of imperfection). On the other hand, the thin-horse imperfections, increase the structural capacity. This is probably because the structure imperfect shape "moves away" from the preferred shape of collapse. However, it is unlikely that buckling mode imperfections will occur during the production process or due to accidental conditions, while it could occur for cyclic loads (Komoriyama et al., 2018).

Figure  10  Global buckling limit state results

Download: Full-Size Img

Both curves in Figure 10 do not correspond to a zero imperfection, but are referred to an initial imperfection in the order of magnitude of 10-6 mm, so the curves basically show the limit of the functions for an imperfection tending, but not equal to, zero.

3.3   Local buckling limit state

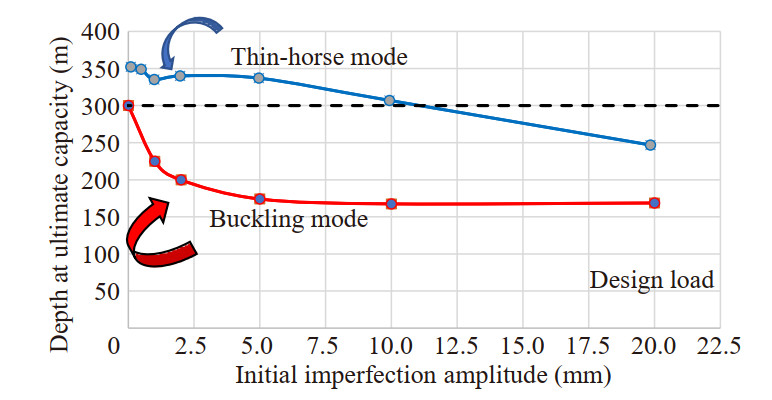
The local buckling limit state configuration leads the critical load for local instability to be just higher than the design load, while the other limit states are widely verified (>20%).

The results of the analyses are shown in the graph below (Figure 11). As for the global buckling, a negligible capacity margin in perfect geometry, compared to the design load, is observed. As a consequence, the condition of local instability can be again identified as an "ultimate state".

Figure  11  Local buckling limit state results.

Download: Full-Size Img

The first buckling mode shape imperfections have a strong impact on the ultimate capacity (i.e., −33% per 2 mm of imperfection). On the other hand, the thin-horse imperfections initially increase the structural capacity. Again, authors believe that this is due by the different shape assumed by the structure, which diverges from the deformed shape of collapse for the perfect model. However, beyond 10 mm of initial imperfection amplitude a reduction in capacity compared to the design value is observed, since the thin-horse imperfection in this case increases the stresses of the plating, as observed before for the plastic collapse case, and a mixed collapse-plastic mode and collapse for local instability is identified. Interaction of failure modes is something beyond this study, and this is the only geometrical configuration in which it was observed.

As for the previous case, both curves in Figure 11 do not correspond to a zero imperfection, but are referred to an initial imperfection in the order of magnitude of 10-6 mm, so the curves basically show the limit of the functions for an imperfection tending, but not equal to, zero.

3.4   Annular buckling of frames limit state

The annular buckling limit state configuration leads the critical load, evaluated according to the Shiomitsu D and Yanagihara D (2020) methodology, to be just higher than the design load, while the other limit states are widely verified. Although a geometric configuration having good analytical/numerical agreement is chosen, the analytical formulations for this particular instability condition are not very reliable. In fact, strong inconsistencies with respect to the numerical model have been observed for some geometric configurations. However, the Yanaghihara formula appears to be the best compromise between the complexity of the method and the accuracy of the result. Other more reliable analytical methodologies involve approaches so complex as to make the numerical model convenient.

By the way, for the selected geometrical configuration, it was found good agreement between the analytical formulation and the linearized method to calculate elastic buckling in the FE model.

As observed by other authors in the literature, the occurrence of annular instability has no impact on the ultimate capacity of the structure. In the graph below (Figure 12) only the buckling-mode imperfection is considered, and it was decided not to proceed with the calculations for thinhorse imperfections, since any impact on the ultimate capacity is not observed even for the mode shape which is supposed to induce the most severe effects on the ultima strength.

Figure  12  Annular buckling limit state results.

Download: Full-Size Img

4   Conclusions

In this study the different limit states to be evaluated in the preliminary design stages of a submarine structure are examined numerically. In particular, collapse modes are assessed, with reference also to the sensitivity of the ultimate strength on the initial imperfections. Main findings may be summarized as below:

· The initial imperfections have a crucial impact on the ultimate strength of the structure, although the shapes which are the most common to be observed in actual structures, i.e. thin-horse imperfections, are less impacting. On the other hand, cyclic loads can induce permanent buckling-mode deformations, through a phenomenon known as fatiguebuckling, that is still scientifically poorly understood, however documented. Such pattern of permanent deformations might significantly reduce the ultimate response of the structure: it is therefore recommended to periodically monitor the shape of the hull with advanced techniques, since imperfections of a few millimeters, difficult to observe macroscopically, are sufficient to drastically reduce the ultimate capacity of the submarine;

· Both the global and local buckling conditions can be considered as ultimate states, highly influenced by the shape and amplitude of the initial imperfection. Therefore, the choice of adopting different safety coefficients for these limit states does not appear justified: currently global instability is considered with greater caution than the local one, but as seen from the results it is recommended to adopt the same level of caution for both;

· A residual capacity of the structure beyond the first yield is observed, which is strongly diminished in the presence of a thin-horse mode imperfection;

· The annular instability appears to be less significative and more difficult to quantify with analytical methods, so it is recommended to verify this limit state according to numerical methods.