Numerical Investigation on the Ultimate Strength of Box Beams with Impact Damage
https://doi.org/10.1007/s11804-020-00177-9
-
Abstract
The objective of this paper is to study the residual ultimate strength of box beams with impact-induced damage, as a model of what may occur in ship hulls. The bottom and side plates of ship hulls can suffer denting or fracture damage due to grounding, collision and other contacts during the ship's service life and these impact-induced damages could result in considerable strength degradation. Box beams are firstly subjected to impact loading and then four-point bending loading is imposed on the damaged structures to assess the residual strength using ANSYS/LS_DYNA. The ultimate moment and collapse modes are discussed considering the effect of impact location. The impact-induced deformation is introduced in the four-point bending simulation, and the impact-induced stress is included or not to determine the effect of residual stress and distortion after impact. It is shown that impact location has significant influence on the residual ultimate bending moment of the damaged box beam providing that the impact energy is kept constant. The collapse modes also change when the impactor strikes on different locations. Damaged hard corner and inclined neutral axes might explain the reduction of ultimate strength and diverse collapse modes. The residual stress in the box beam after impact may increase or decrease the ultimate strength depending on impact location.-
Keywords:
- Impact tolerance ·
- Box beam ·
- Four-point bending ·
- Ultimate moment ·
- Impact location
-
1 Introduction
The longitudinal strength of ships is presently defined by the ultimate hull girder strength. Caldwell (1965) was the first to propose an approach to determine the ultimate strength of ships' hulls presenting a formula for ultimate strength calculation of hull girders. Smith (1977) extended the Caldwell's method by considering the buckling behaviour of ship elements under compression. In his method, the whole structure was firstly divided into elements composed of stiffeners with attached plating. Then, the collapse behaviour of those beam-columns was analysed by FEM with the load-displacement curves stored in a database for further use when calculating their contribution to the overall hull strength. After Smith, several methods were proposed to model the average stress-average strain relationship of the elements composed of stiffeners and attached plating (Dow et al. 1981; Gordo and Guedes Soares 1993).
The ultimate strength of ship hulls has been proposed as the main criteria for ship design (Guedes Soares et al. 1996), substituting the elastic section modulus used at that stage by Classification Societies which have adopted this concept about 10 years later in their Common Structural Rules (Parunov and Guedes Soares 2008; Gaspar et al. 2011; Xu et al. 2015).
Many experimental studies have been performed during the last decades to provide first-hand information for understanding the collapse behaviour of ship structures with simplified box beam models. For example, Reckling (1979) conducted several collapse tests on box girder models under pure bending to study the ultimate strength. Nishihara (1984) tested eight box girder models representing conventional types of ships such as tanker, bulk carrier and container ship. Dow (1991) studied experimentally the collapse behaviour of the 1/3-scale welded steel hull girder model of a frigate under sagging bending moment. Gordo and Guedes Soares (2007) conducted an experimental test on the ultimate bending moment strength of a box girder made of mild steel, where the four-point bending test was applied to obtain pure constant bending throughout the whole specimen. A continuation of the previous work was then performed to account for the effect of high-tensile steel (Gordo and Guedes Soares 2009) and frame spacing (Gordo and Guedes Soares 2014, 2015). In this experimental study, the specimens are made of very high-tensile steel with the 690-MPa nominal yield stress. The box girder is also subjected to pure bending moment to obtain the ultimate strength and collapse behaviour, with tension on the bottom and compression on the top of the box beam. Lin et al. (2019) recently also conducted an experimental and numerical work on this topic. Numerical work can also be found in Pollalis and Samuelides (2013) and Benson et al. (2013).
The ship hull structure can suffer damage due to grounding (Prestileo et al. 2013), collision (Liu et al. 2017a) and any other contacts during the ship's service life. Even minor collisions between ships can be studied by considering the external dynamics (Villavicencio and Guedes Soares 2014), but the final consequences must also account for the internal dynamics (Liu et al. 2017a), including detailed finite element analysis. When only low intensity is involved, both in collisions (Villavicencio et al. 2013; Liu et al. 2015) and in groundings (Liu and Guedes Soares 2015), simplified analytical methods are able to produce acceptable results of the local damage. However, apart from local denting damage, which is observed in minor collisions with neighbouring objects, rupture damage (Liu et al. 2014, 2017b) often appears in serious collision or grounding accidents, some of which may involve high strain rate and appropriate criteria need to be used then (Liu et al. 2018; Liu and Guedes Soares 2019).
Therefore, the study of the impact tolerance of hull girders is necessary in order to assess the residual ultimate strength of the ships after impact-induced damage. There have been several studies related to the residual ultimate strength assessment of hull girder in recent decades. For example, Luís et al. (2009) have studied the effect of damage due to grounding. Notaro et al. (2010) investigated the effect of damage shape on the residual ultimate strength of ship hull girder. Hussein and Guedes Soares (2011) studied the ultimate strength of the intact and damaged bulk carrier in sagging and hogging conditions where two damage scenarios were assumed, collision at the side and grounding at the bottom. Benson et al. (2016) developed a method to assess the global ultimate strength of damaged hull girders.
Considering the complexity of the hull girder and the expensive computational cost of detailed finite element analysis, simplified box beam models have been widely adopted to gain insight into the progressive collapse behaviour of post-accidental strength of the ship structure (Gordo and Guedes Soares 2000; Cho et al. 2016). Putranto and Kõrgesaar (2020) explained the effect of damage shape on the ultimate strength reduction with a simplified box beam model, where the height of the damage was kept constant while the shape and length were varied. The effects of other damage characteristics like damage height and region are investigated herein.
This paper analyses the ultimate strength of box beams after lateral impact loading. Box beams are firstly subjected to impact loading and then four-point bending (FPB) loading is imposed on the damaged structures to assess the residual strength using ANSYS/LS_DYNA. The collapse behaviour of the intact box beam is also studied herein for reference. Both the impact-induced deformation and stress are included in the FPB simulation. The ultimate moment and collapse modes are discussed considering the effect of the impact location.
2 Numerical Simulation
2.1 Four-Point Bending Model Verification
The FPB simulation is verified based on the experimental results given in Gordo and Guedes Soares (2009). The collapse behaviour of three box girders under pure bending moment is presented in the paper, where the H200 model is selected as a reference for model verification herein.
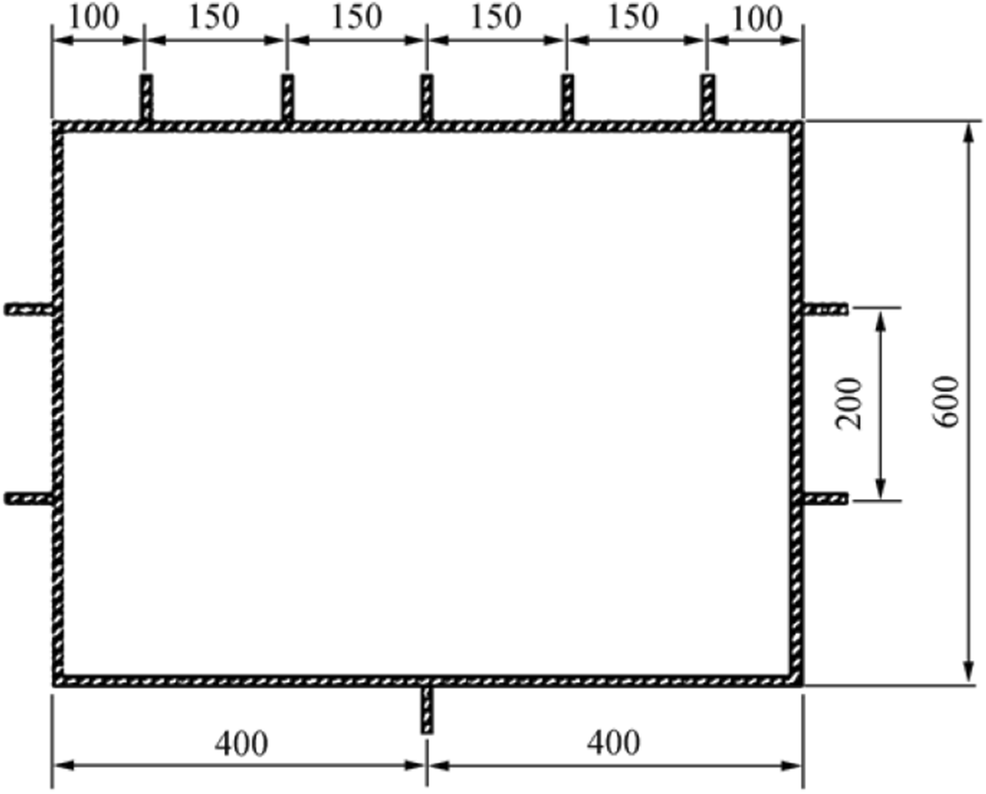
The meshed model is shown in Figure 1. The box girder specimen is 100 + 200 × 4 + 100 mm in length with 5 web transverse frames (L 50 × 20 × 6 mm) inserted in the section. There exist 5, 2 and 1 longitudinal stiffeners (flat bars 20 mm × 4 mm) in the upper plate, side plate and bottom plate, respectively, as shown in Figure 2. All the plates are 4 mm in thickness. The thickness of the supporting parts in two ends was set as 10 mm to avoid buckling at the parts that contact with the loading and supporting hollow cylinders directly. The loading and supporting hollow cylinders are defined as rigid with length of 1000 mm and radius of 50 mm. Shell elements are used for modelling the box beam. After analysing the mesh sensitivity, the mesh size of elements with 25 × 25 is found to be suitable to guarantee both the time saving and accuracy of the calculations. For the extended parts at the two ends, the mesh size is set as 150 mm, with a transition section between the tested box beam and the extended part.
The appropriate and accurate definition of material property is an important part of FEM analysis, which highly affects the numerical results and agreement with the physical experiments. As shown in Benson et al. (2013), the true stress-strain curve could fully describe the material characteristic and ensure a precise treatment of the plasticity. It is vital for the progressive collapse analysis of box beam and also for the simulation of impact scenario.
Benson et al. (2013) take advantage of the complete stress-strain curve of S690 (Sedlacek and Müller 2001) and modified power law to describe the initial yield plateau characteristic. The power law describes the S690 material property as follows:
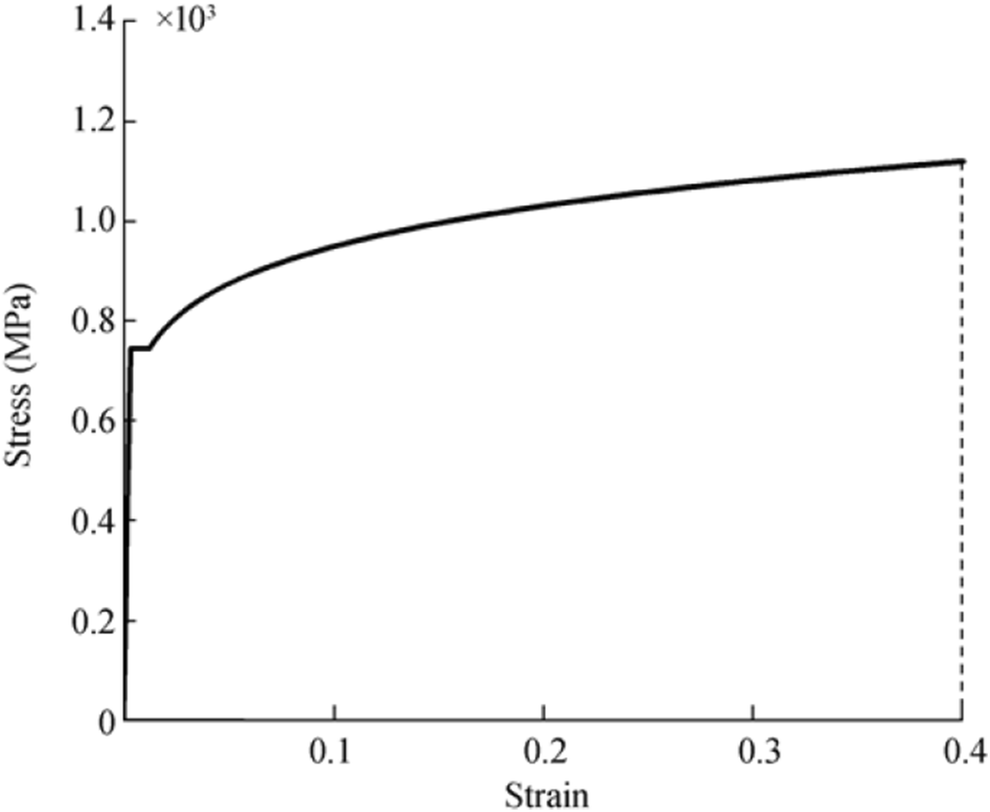
$$ {\sigma}_{\mathrm{ep}}=\left\{\begin{array}{cc}{\sigma}_{\mathrm{Y}}& if\ {\varepsilon}_{\mathrm{ep}}\le {\varepsilon}_{\mathrm{plat}}\ \\ {}K{\left({\varepsilon}_{\mathrm{ep}}-{\varepsilon}_0\right)}^n& \mathrm{otherwise}\end{array}\right. $$ (1) $$ {{\rm{ \mathit{ ε} }}_{\rm{0}}}{\rm{ = }}{{\rm{ \mathit{ ε} }}_{{\rm{plat}}}} - {\left( {\frac{{{{\rm{ \mathit{ σ} }}_{\rm{Y}}}}}{K}} \right)^{1/{\rm{n}}}} $$ (2) where the constants are set as follows: K = 1250 MPa, n = 0.12, εplat = 0.0124, σY = 745 MPa and E = 211 GPa. The given stress-strain relationship is plotted in Figure 3.
Automatic surface-to-surface contact is defined between the hollow cylinders (both loading and supporting cylinders) and the box girder, with the static friction coefficient being 0.3. Prescribed motion is imposed on the top loading cylinders with the vertical velocity of 0.1 m/s, which is faster than the quasi-static loading rate. This is possible since the strain rate sensitivity behaviour of the material is omitted for this simulation. All the other degrees of freedom are fixed and only vertical motion is freed to keep the loading cylinders moving straight. The bottom supporting cylinders are constrained in all directions with no motion during the whole loading process.
For the moment-curvature relationship, the vertical bending moment is calculated as:
$$ M=L\times F/2 $$ (3) where F is the loading force and L is the distance between the loading point and the support. The curvature is calculated by transforming the horizontal displacements of the related four nodes on both ends of the test part, as shown in Figure 4.
There exist two transverse plates at the end of the test part, so the section is stiff enough to keep the length between node A and node B ($ {AB} $) constant in the loading process, which holds for $ {CD} $ as well. The length of arc BD is represented as the straight length of BD for the rotational angle is quite small. The curvature, k, of the arc BD is calculated as:
$$ k=\left[\arcsin \left(\frac{X_1+{X}_2}{H}\right)+\arcsin \left(\frac{X_3+{X}_2}{H}\right)\right]/L $$ (4) where X1, X2, X3 and X4 are horizontal displacements of the node A, B, C and D. H is the height of box beam and L is the length of BD.
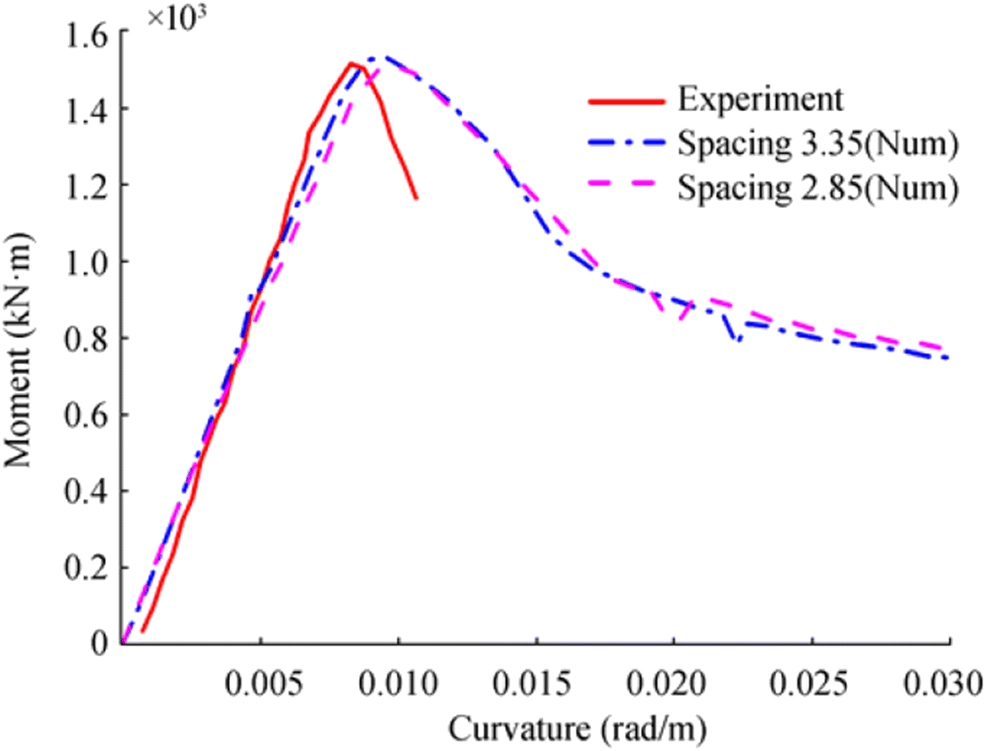
The calculation for the moment-curvature relationship based on the horizontal displacement from the numerical result is shown in Figure 5. The ultimate moments are 1532 kN m and 1508 kN m for the two cases where the spacing between loading point and supporting point is 3.35 m and 2.85 m respectively. The relative difference is about 0.4% and − 1.2%, comparing with the experimental result of 1526 kN m, while the difference between the numerical and experimental results in the plastic stage is obvious. The great discrepancy with the experimental curves may originate from the inaccurate and complicated material property in the plastic stage. It also shows that the effect of spacing between the loading point and supporting point is negligible with the loading point fixed at the ends of test part. The numerical collapse mode is also compared with the experimental result. Figure 6 shows that the numerical model collapses in a similar way with the experimental observation.
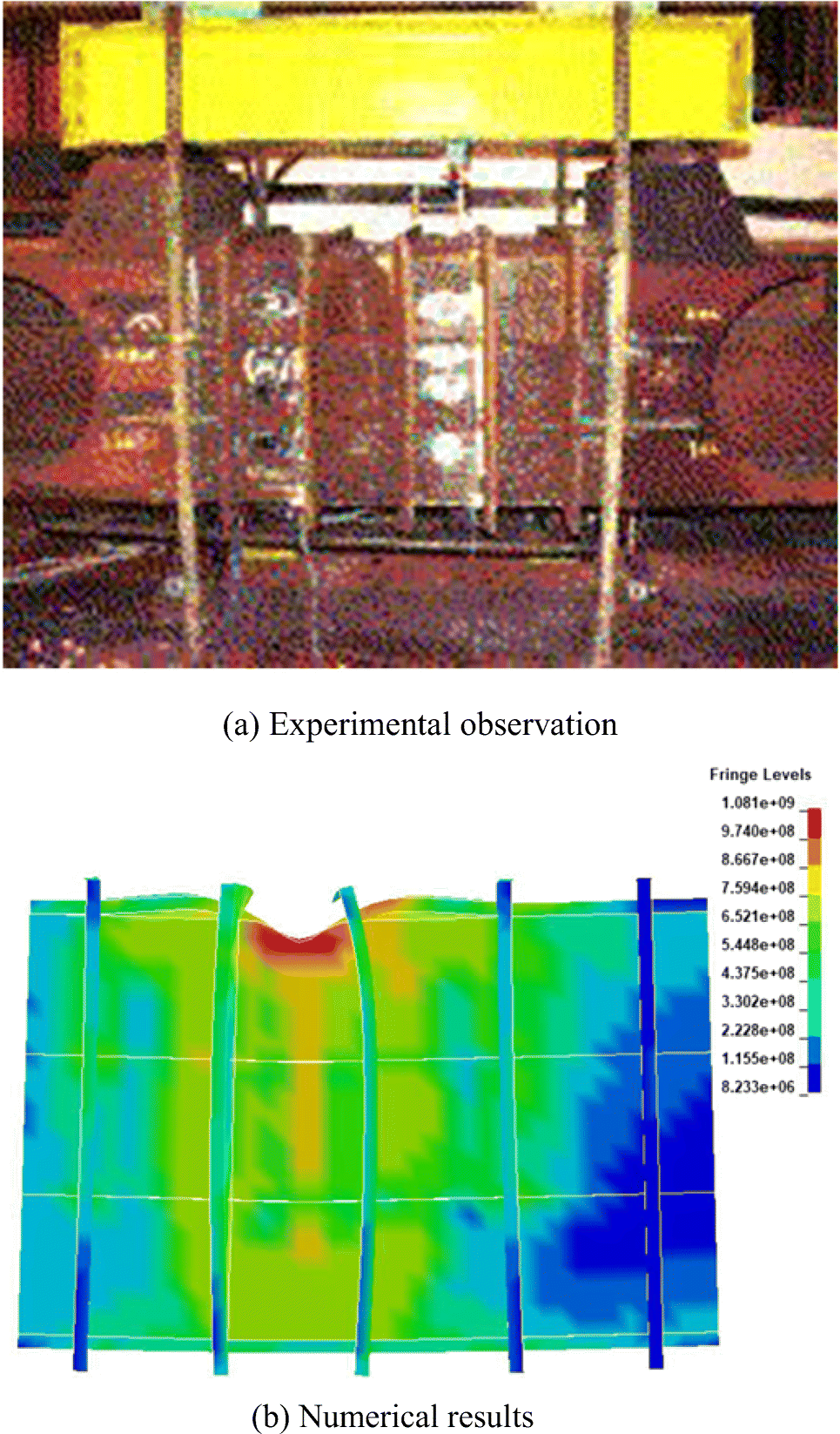 Figure 6 Experimental and numerical collapse modes. (a) Experimental observation (Gordo and Guedes Soares 2009). (b) Numerical results
Figure 6 Experimental and numerical collapse modes. (a) Experimental observation (Gordo and Guedes Soares 2009). (b) Numerical results2.2 Impact Simulation
2.2.1 Impact Model Verification
The impact simulation is verified based on the impact test on the stiffened plates for the lack of existing impact experiments on the box beam with stiffeners. Villavicencio and Guedes Soares (2012) conducted experimental drop weight impact tests and numerical studies to examine the dynamic response of stiffened plates struck by spherical indenters. The specimens in the experiments are supported at two opposite edges and impacted at different locations along the span. Along the unsupported edges, the ends of the stiffeners are either connected to transverse stiffeners or remain free. The end-connected model is adopted here for reference, which is similar to the impact scenario on the upper or side panel of box beams.
The modelling includes the definition of boundary condition to simulate small axial displacement of the specimen, and the definition of strain hardening property of the material using the Cowper-Symonds constitutive model, which is described in detail in Villavicencio and Guedes Soares (2012).
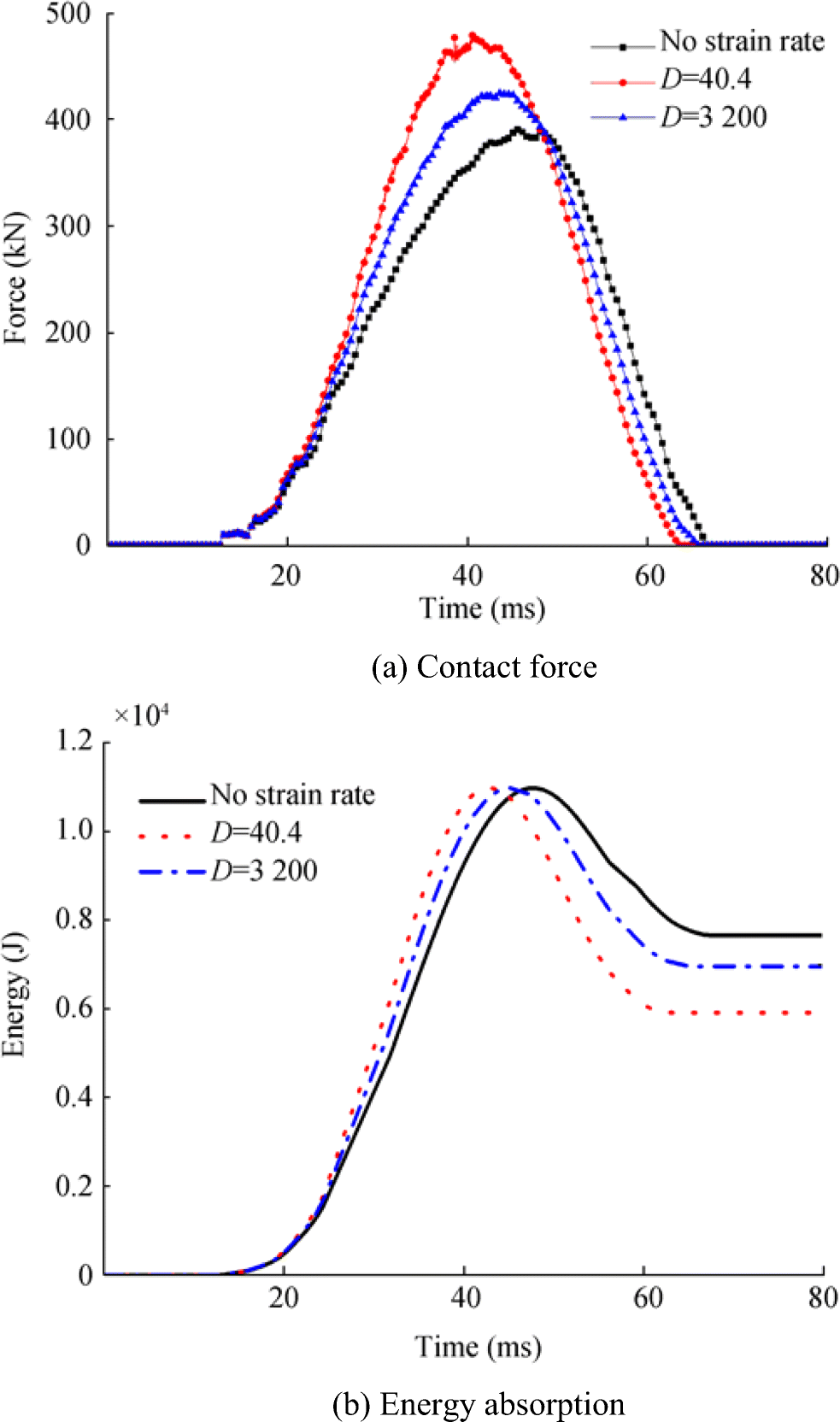
The time history of the contact force and absorbed energy from the numerical results are compared with the experimental response, which is illustrated in Figure 7. It shows that the numerical simulation fits well with the experimental response. The weld joints of the stiffeners are taken into account, so the plate and stiffener thickness at their intersection are increased in this model, which is noted as the welded model. Another model using uniform thickness for the intersection, noted as the uniform model, is also calculated to study the effect of the increased weld intersection. Figure 8 shows that the difference is negligible, so the simple uniform model, where the thickness of the plate and stiffener is uniform, is adopted for all the box beam model in the present study.
2.2.2 Impact Simulation Model
Following the verification of FPB simulation, impact on the box beam is simulated with the model slightly modified, which is shown in Figure 8.
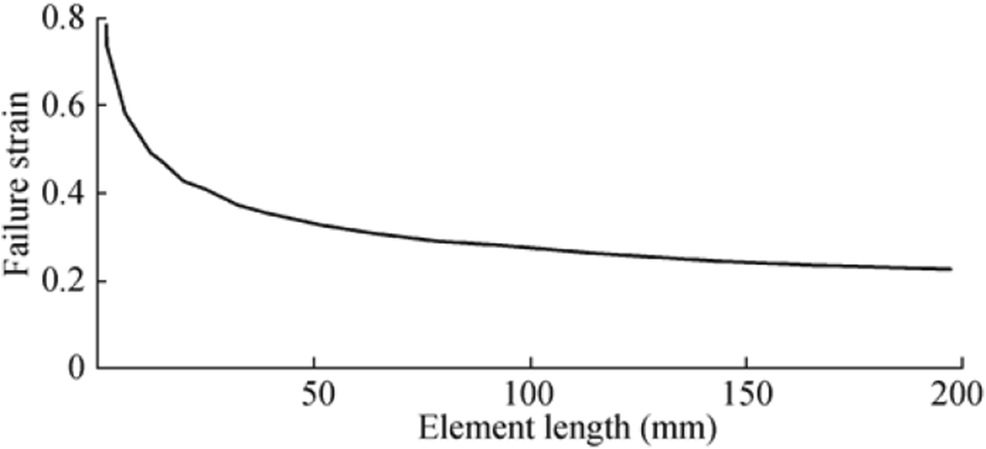
The stiffeners are moved into the inner structure and transverse frames are moved away. The meshing strategy is kept unchanged for the whole box girder model. The material property of the extended parts in two ends is changed from the power law described model to the rigid model, avoiding any deformation in the impact stage. The power law model is adopted for the box beam, as illustrated in section 2.1. The material fails when the strain exceeds the allowable or maximum strain. It should be noted that the rupture strain is highly dependent on the element length in the numerical calculation. According to the relationship curve between element length and failure strain by Ehlers (2010), as shown in Figure 9, the failure strain is set as 0.4 in the present study with the element length of 25 mm.
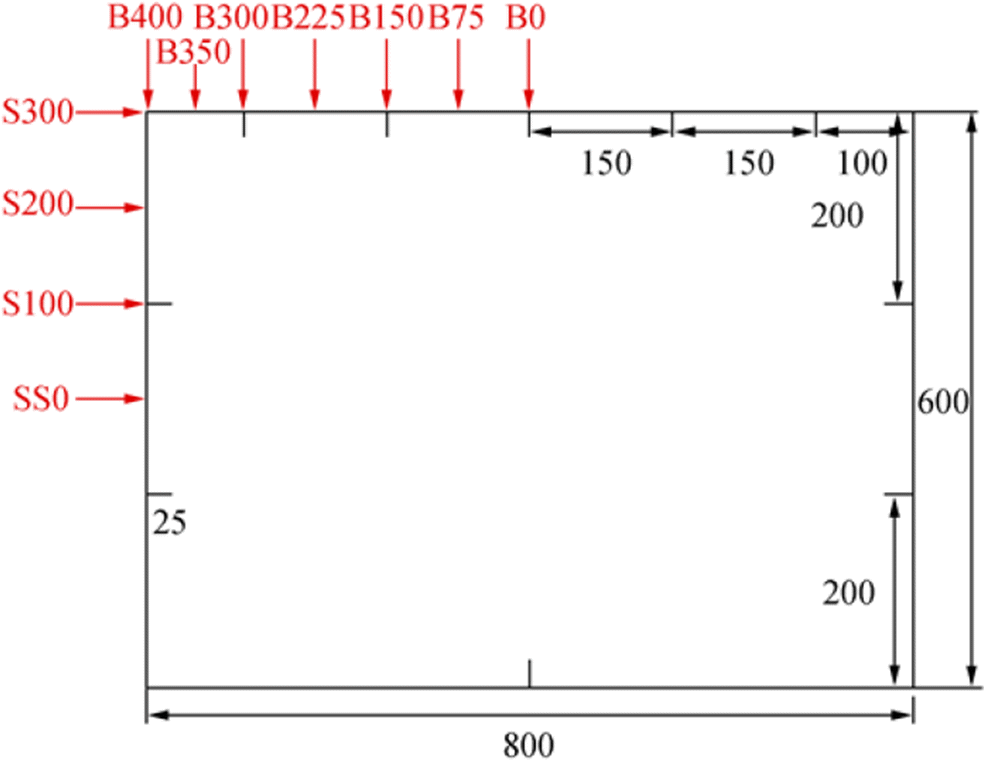
The impactor is modelled as a hemisphere with radius of 50 mm, considering that the minimum spacing between the stiffeners is 100 mm. Shell elements are adopted for the hemispherical impactor and the thickness is set as 10 mm. The mesh size is approximately 10 mm. The MAT_RIGID material model is selected for the impactor to ensure no deformation in the impact process. As the impactor is simply modelled as a hemisphere for the dynamic simulation, an artificially large density is assigned to that striker so as to give an appropriate mass in the real scenario. The initial velocity is set as 3 m/s. The automatic surface-to-surface contact algorithm is defined between the indenter and box beam with the static coefficient of friction set as 0.3. The impact point is changed to study the effect of damage location, as shown in Figure 8. The notations such as B0 and S0 for different impact points represent different cases in the following section.
2.2.3 Effect of Strain Rate
The Cowper-Symonds constitutive equation is introduced to account for the dynamic material characteristics under impact loading:
$$ {\sigma}_{\mathrm{d}}={\sigma}_0\left[1+{\left(\frac{\varepsilon_{\mathrm{r}}}{D}\right)}^{1/q}\right] $$ (5) where σd is the dynamic flow stress corresponding to the uniaxial plastic strain rate εr, σ0 is the associated static plastic flow stress, and D and q are constants for a specific material. The constant D is usually set as 40.4 for the normal steel and 3200 for the high-strength steel, with q being 5 normally (Jones 1981). Benson et al. (2013) studied the effect of impact rupture on the residual strength of a box beam, although it is not clear whether the strain rate effect was included or not in the impact simulation.
To understand the strain rate effect in the impact tolerance study for the box beam with high-strength steel, the constant D is set as 3200 and 40.4, respectively, with the model neglecting the strain rate effect included herein for comparison. Figure 10 presents the contact force and energy absorption characteristics in the impact simulation, where the strain rate constant D is changed. It is found that the maximum force and absorbed energy vary between different cases. The maximum force is lower and the absorbed energy is higher when the strain rate effect is neglected, indicating that the impact resistance is reduced. Hence, the dynamic material characteristics should be accounted for in the impact simulation. The bigger dynamic constant D represents that the strain rate effect is smaller, and vice versa. The dynamic constant D is set as 40.4 for the normal mild steel, as the strain rate effect is obvious. For the high-strength steel, the strain rate effect is always limited and higher dynamic constant (D = 3200) is more appropriate.
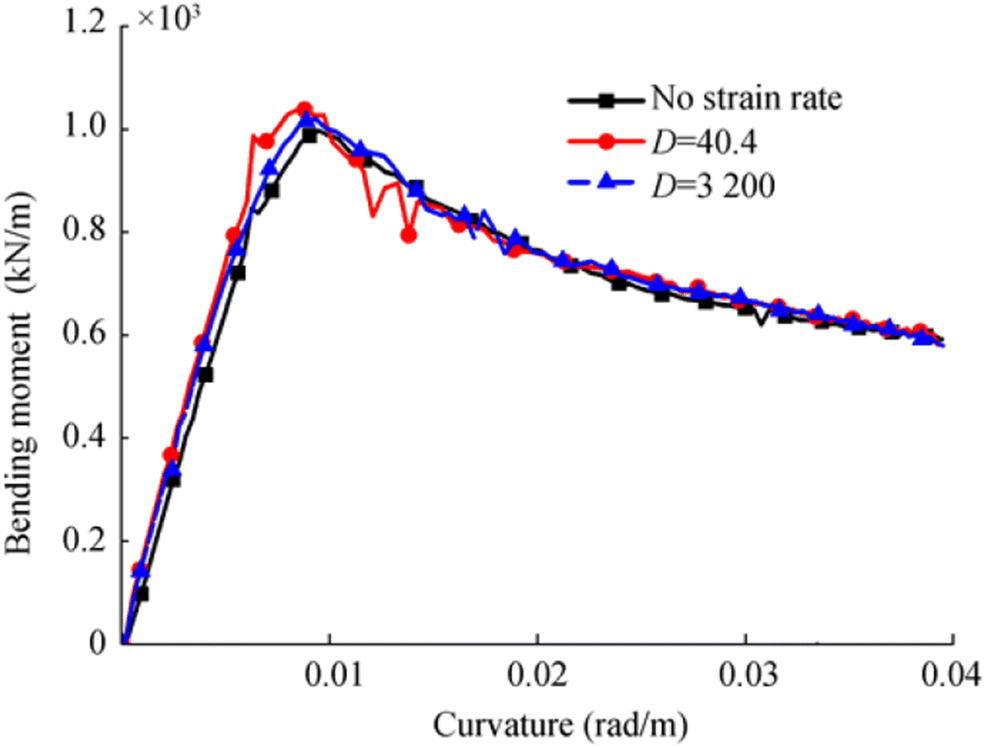
For the residual strength study, the box beams are firstly subjected to impact loading and then a four-point bending (FPB) loading is imposed on the deformed or damaged structures to the strength limit. Accordingly, the effect of the dynamic material characteristics is extended into the FPB simulation. The box beams from the impact simulation above, where the strain rate effect is included or not, are then subjected to FBP loading. Figure 11 shows the moment-curvature relationship of the different cases. It should be noted that the dynamic material characteristics are not included in all the FPB simulations, so the difference results from the different material definitions in the impact simulation. The maximum moment is 999.6 kN m, 1040.4 kN m and 1022.8 kN m for the cases of no strain rate, D = 40.4 and D = 3200, respectively. Although the curves show similar trends, the difference of maximum moment is not negligible. In the impact tolerance study, the strain rate effect cannot be neglected in the first impact simulation.
2.2.4 Impact Results
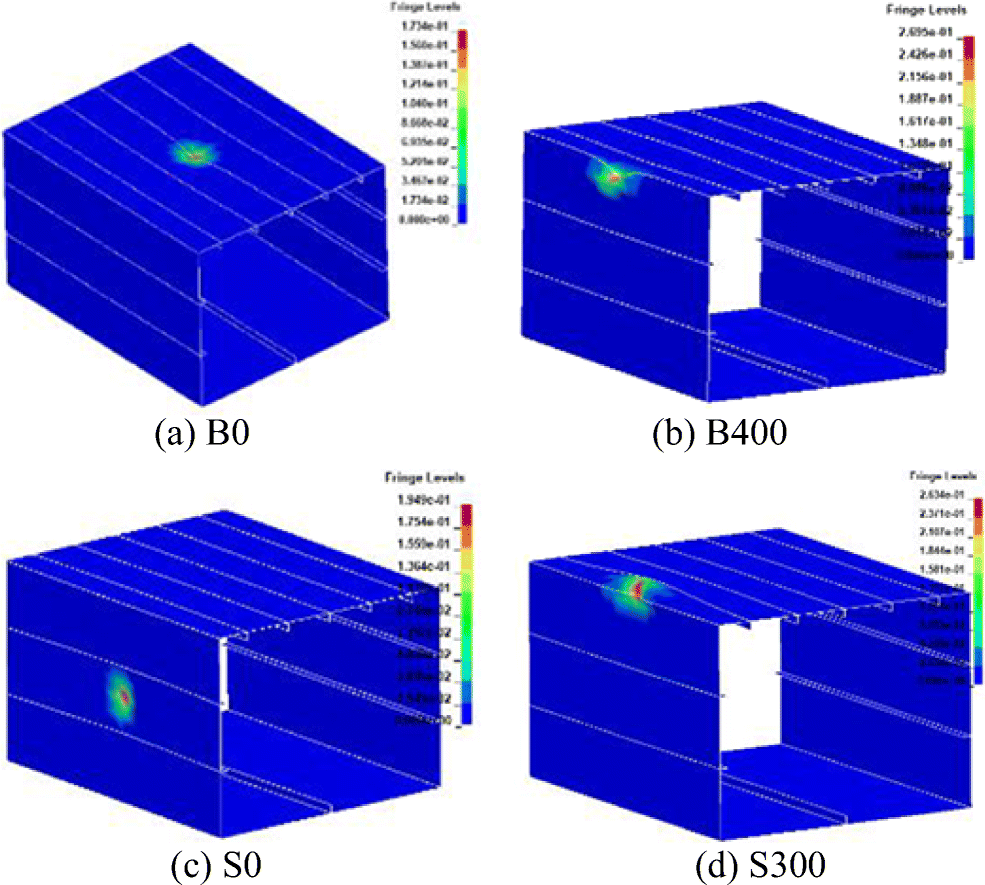
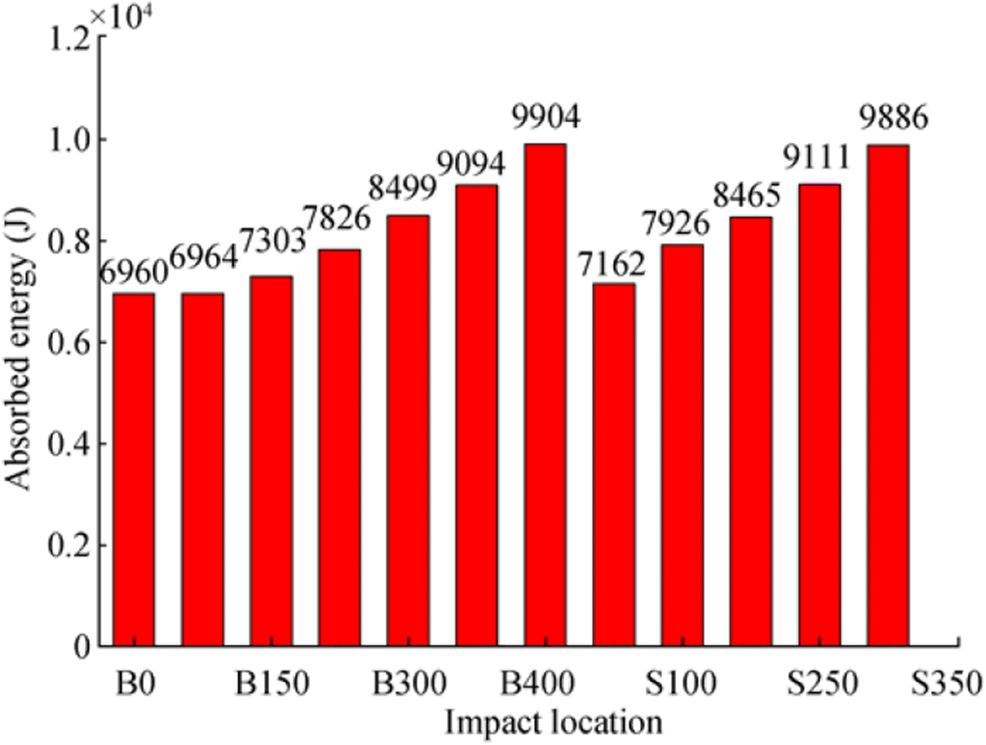
The hemispherical impactor would induce inward deformation and residual tension stress on the box beams. Outward deformation would appear in the side plate when the impactor strikes on the upper corner, and vice versa, which is illustrated in Figure 12. The absorbed energy in different cases is presented in Figure 13, which shows that the plastic energy increases with the impact point moving from the plate centre to the box corner.
2.3 Four-Point Bending After Impact Test
After the impact loading, box beams with impact-induced deformation and stress are then subjected to FPB loading to study the residual ultimate strength and corresponding collapse behaviour. The loading and boundary conditions are set as described in section 2.1. The collapse behaviour of the intact box beam is also studied here for reference.
3 Results
3.1 Moment-Curvature Relationship
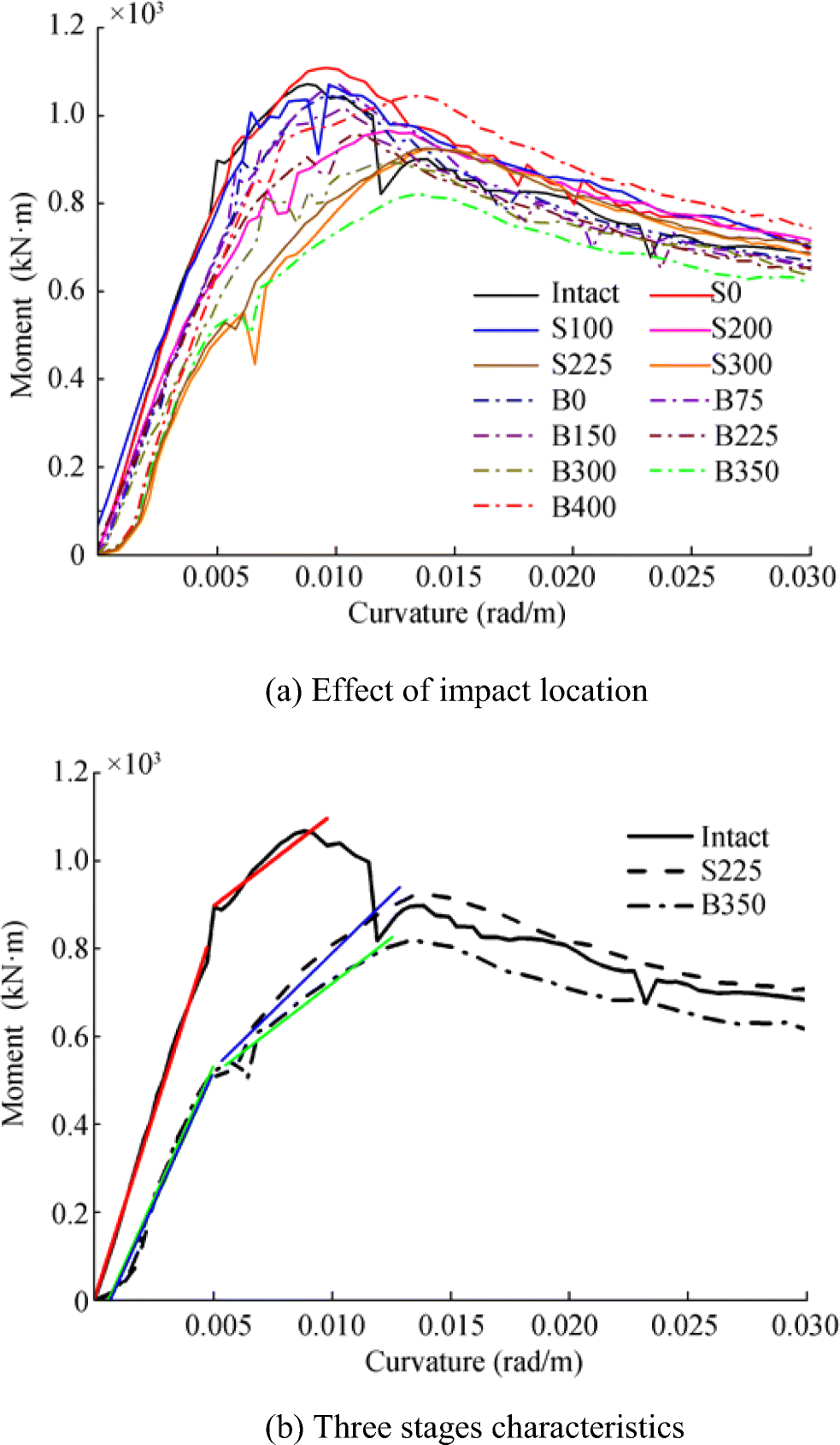
The moment-curvature relationship of box beams under FPB loading is plotted in Figure 14. It displays that the curves may be divided into three regions, as presented in Figure 14b. A similar three-region moment-curvature relationship is also observed in Saad-Eldeen et al. (2010). The first two regions are nearly linear and the corresponding rigidity decreases in the second stage. The large permanent deformation in the third stage leads to great rigidity loss and a nonlinear behaviour.
The slopes of the moment-curvature curves in the first two linear sectors are defined as flexural rigidity EI1 and EI2. The flexural rigidity EI1 and EI2 and the maximum bending moment is 168 649 kN m2, 41 736 kN m2 and 1068 kN m respectively for the intact model, which are taken as reference herein. Table 1 presents the flexural rigidity EI1 and EI2 and the maximum bending moment for intact and deformed box beam. It is found that the residual ultimate strength of box beam after impact loading is highly dependent on the impact location.
Table 1 Flexural rigidity and maximum bending momentCond. EI1 (kN m2) EI2 (kN m2) Max.BM (kN m) Relative diff (%) Intact 168 649 41 736 1068 0.00 S0 166 063 52 246 1104 3.33 S100 145 220 38 603 1067 − 0.09 S200 134 767 47 356 962 − 10.96 S250 106 081 36 872 922 − 15.73 S300 97 891 46 401 921 − 15.92 B0 140 421 56 333 1043 − 2.34 B75 139 648 65 524 1066 − 0.13 B150 130 500 31 928 1010 − 5.72 B225 125 341 33 074 952 − 12.18 B300 115 410 31 280 890 − 19.91 B350 120 253 34 487 818 − 30.49 B400 139 033 15 167 1041 − 2.56 From the case of S0 and S100, it is found that the impact on the centre of the side plate has a minor effect on the ultimate bending moment. The same phenomenon is also found in Putranto and Kõrgesaar (2020), where the ultimate strength drop is about 1.8% with crack or cut-out on the side shell of the box beam. It may be explained that the deformed area is next to the neutral axis and the damage does not cause large loss of inertia moment to the box beam when compared with the intact model. It is interesting that the ultimate moment of the S0 model is larger than that of the intact model. It may be possible for the impact-induced tension stress on the side plate to increase the capacity of box beam to withstand bending moment. When the impact point moves upwards, the ultimate moment loss become prominent, with the percentage loss being 11.0%, 15.7% and 15.9% for the case of S200, S250 and S300 respectively.
When the impactor strikes on the upper plate, it causes large deformation on the upper panel. Because the upper panel is far away from the neutral axis, even small deformation on the upper plate would cause large inertia moment change to the box beam. Consequently, the ultimate bending moment is significantly decreased. As shown in the case of B0, B150 and B225, large deformation appears on the upper plates and the ultimate strength drop is about 3%, 6% and 12%, respectively, which is obviously higher than that of S0 and S100 cases.
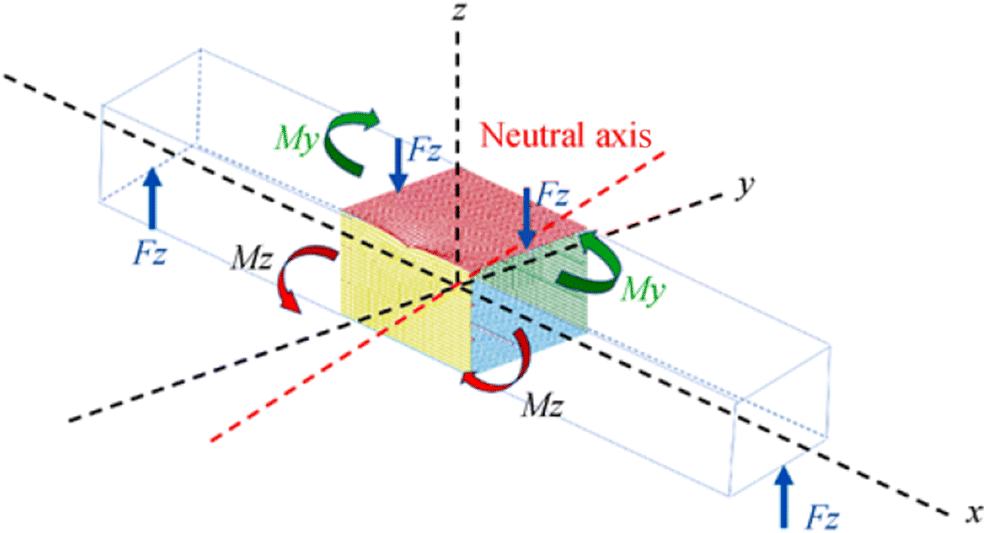
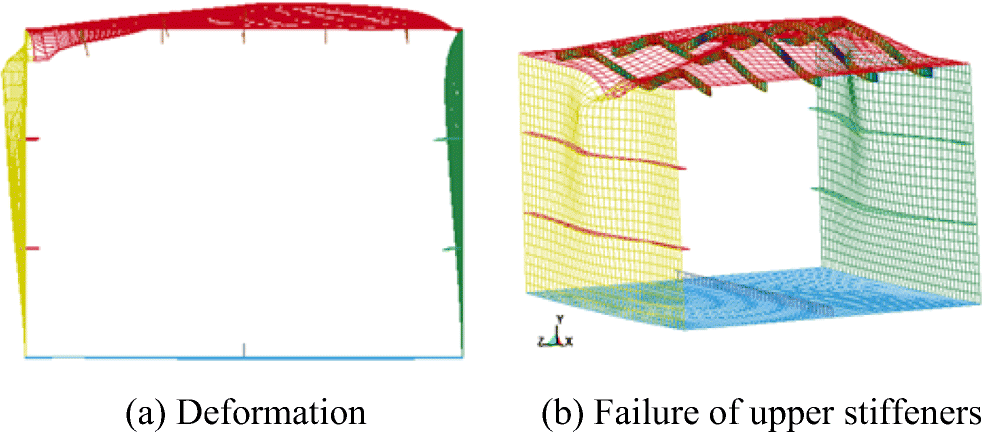
Impact near the box corner affects the ultimate strength of box beam seriously and the ultimate moment reduction is quantified as almost 20%, which could be seen from the case of B300 and B350. Two main reasons lead to the significant strength reduction. Firstly, the damaged hard corner could not provide stiff support for the box beam under FPB loading, which would reduce the structural capacity to resist the bending moment. Secondly, the deformed corner inclined the neutral axis of the box beam, which would induce bending moment in two planes under the same loading force, as shown in Figure 15. For intact model under vertical loading force, it will only deform in the horizontal plane, but when the neutral axis rotates, the vertical loading force causes deformation in both horizontal and vertical planes. It causes asymmetric collapse mode, which will be explained in the next section. As a result, the ultimate bending moment drops greatly. When the indenter impacts on the box corner from the upper side, the strength drop is minor, which is shown in the case of B400.
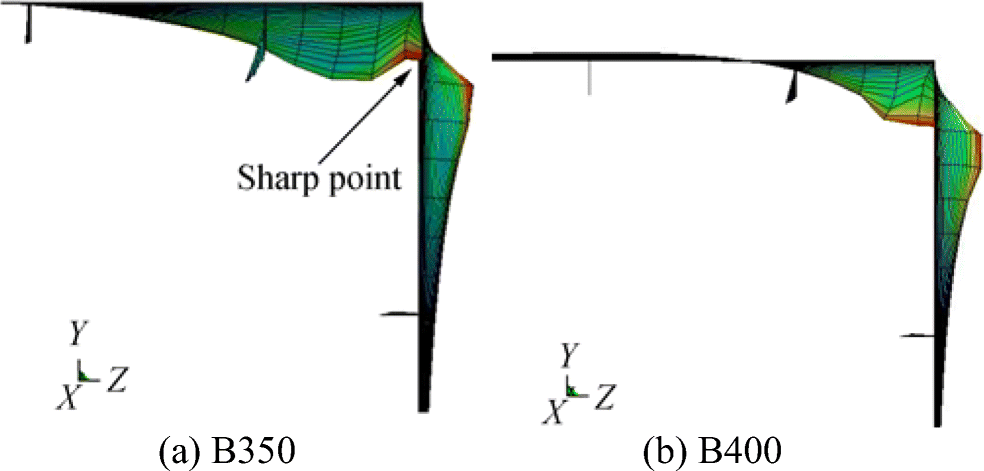
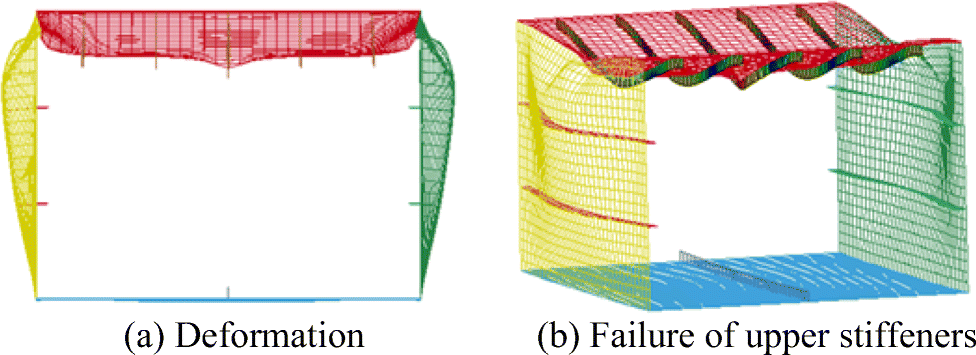
Among all the cases, it is found that the impact on the point that is 50 mm away from the edge (as shown in the cases of B350) leads to the lowest residual strength, namely the minimum ultimate bending moment. It should be noted that the absorbed energy is the largest when the impactor strikes on the edge (case B400), and the ultimate bending moment of case B400 is still greater than that of B350. It is concluded that the most dangerous impact point lies in half space away from the edge of the upper plate in the present study. By checking the deformed box beam after impact (see Figure 16), it is found that the greater deformation and sharp point in the case of B350 may explain the serious strength drop when compared with the case of B400.
3.2 Modes of Collapse
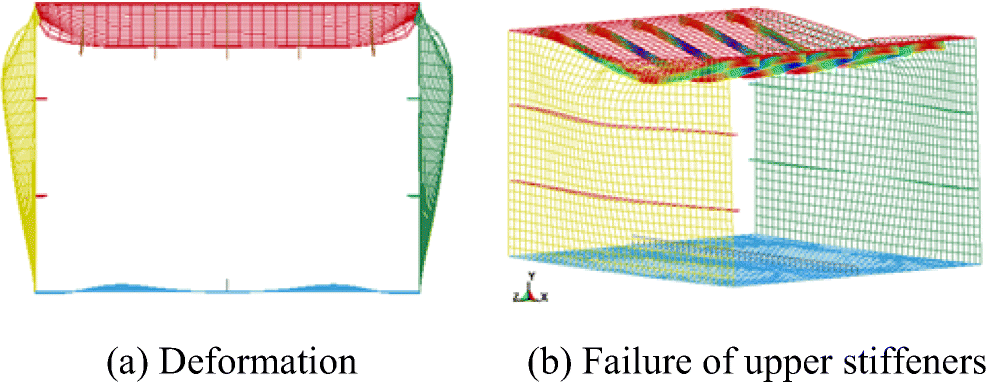
The intact box beam collapses due to the formation of plastic hinges at the middle of the stiffeners under large compressive loading. Plastic hinges in all stiffeners of upper plate mean that they are loaded at stresses close to the yield stress. Numerical results show that the plastic hinges appear almost at the same time. It means that load is transferred quickly between the stiffeners which promotes the simultaneous collapse of the panel. The failure of the compressed upper panel propagates to the side structure leading to the failure of its plating. It needs to be noted that plane sections do not remain plane during the plastic stage and large deformations and rotations appear in the upper and side plates. These axial and rotational deformations are more obvious in the middle of the box beam, as shown in Figure 17.
For the case of B0, impact-induced deformation reduces the inertia moment and leads to the ultimate moment reduction. Because the deformation is symmetric, the structure collapses in the similar way with the intact beam (see Figure 18). Stiffeners of the upper plate yield and lead to the simultaneous collapse of the panel, and failure of the compressed upper panel propagates to the side structure leading to the failure of its plating.
When the impact point moves to the edge of the upper panel, impact-induced deformation causes the inclination of the neutral axis, which leads to the asymmetric collapse mode of the box beam under the same four-point bending load. In the case of B350, the upper stiffener close to the impact point fails firstly, which causes the local collapse of the associated plate, then the local failure of the associated plate propagates to the adjacent side panel leading to the warp of the side panel. The stiffeners next to the other side fail last and the associated plate collapses globally, then the global failure of compressed associated panel propagates to the corresponding side structure leading to the failure of its plating. As a result, the box beam collapses in an asymmetric way with the left side panel warped downward and the right side panel deformed outward, as is shown in Figure 19.
When the impactor strikes on the corner from the upper side, the striker would cause large inward deformation in the upper plate and outward deformation in the side plate, as shown in Figure 12. It should be noted that the upper stiffener close to the impact point failed firstly and deforms inwards under progressive compression, which leads to the local collapse of the associated plate. The local failure of the associated plate propagates to the adjacent side panel leading to the outward deformation of the plating, while the other three stiffeners next to the other side fail lastly and deforms outward and the associated plate collapses globally. The global failure of compressed associated panel propagates to the corresponding side structure causing the failure of its plating. As a result, the box beam collapses in an asymmetric way with the left side panel warped downward and the right side panel deformed inward, which is shown in Figure 20. The two left stiffeners fail inward and the three right stiffeners deform outwards, causing the inward deflection on the left side and outward deformation on the right side in the upper plate.
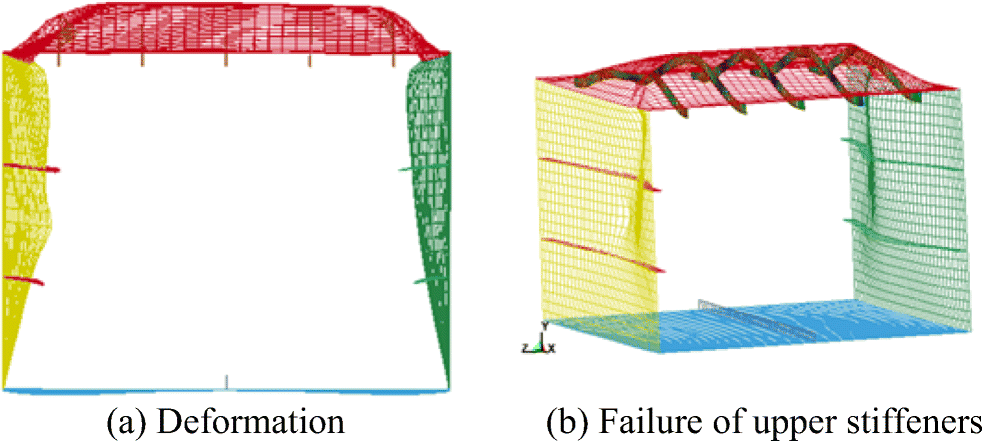
When the impactor strikes on the side plate, it will induce inward deformation and tensile stress on the side panel after rebounding. This initial condition causes a different collapse mode of box beam under FPB loading, as the case of S0. The upper panel deforms outward initially under compression for the initial inward deformation and tensile stress on the side panel. The box beam collapses due to the formation of plastic hinges in the stiffeners under large compressive loading. It should be noted that the position of plastic hinges is not totally the same in the upper stiffeners, as may be seen in Figure 21. The plastic hinges in the stiffener next to the damage side panel appear in the quarter position while the others yield in the middle. The failure of the stiffeners contributes to the collapse of the panel. The failure of the compressed upper panel propagates to the side structure leading to the failure of its plating. The side panels deform inward which is different from the outward deformation in the intact model. Large deformations and rotations also appear in the upper and side plates.
4 Discussion
In all numerical cases above, both the impact-induced stress and deformation are included. In this section, the residual stress after impact is not included, and then the ultimate strength of the damaged box beam with impact-induced deformationis only calculated and compared with the results above to study the effect of residual stress after impact.
Table 2 displays the difference of maximum bending moment between the models with residual stress and those without. It is found that the residual stress in the box beam after impact may increase or decrease the ultimate strength, which depends on the impact location. For example, in the case of B0, the residual stress in the upper plate may increase the ultimate strength of the box beam, where the upper plate is compressed and the bottom plate tensioned under pure bending moment because the indenter would induce tension stress in the upper plate when the impact is on the centre (as shown in Figure 22), which could counteract the compression stress in the FPB loading process. A similar effect is observed in the cases of B75 and B150.
Table 2 Difference of maximum bending momentCond. Max.BM Relative diff With RS Without RS Intact 1068 1068 0 S0 1104 1111 − 0.61 S100 1067 1129 − 5.47 S200 962 989 − 2.77 S250 922 909 1.39 S300 921 907 1.52 B0 1043 1018 2.49 B75 1066 1010 5.56 B150 1010 997 1.30 B225 952 965 − 1.39 B300 890 911 − 2.32 B350 818 818 − 0.01 B400 1041 1074 − 3.11 RS means the residual stress after impact In the case of S0, the residual tension stress after impact in the side plate decreases the ultimate moment of the box beam under pure bending, because the residual tension stress changes the neutral axis of box beam and leads to strength loss of the box beam. Obviously, the stress state is much more complex which needs to be examined in detail. A similar phenomenon is observed in the cases of S100 and S200.
For the cases of S250, S300, B225, B300, B350 and B400, the asymmetric deformation mode and complex residual stress make the stress analysis much more difficult. From the numerical results, the conclusion is only that residual stress after impact increases the ultimate moment in the cases of S250 and S300 and decreases the strength in the cases of B225, B300, B350 and B400 when compared with the corresponding model without residual stress.
5 Conclusion
This paper studies the ultimate strength of box beams after lateral impact loading and presents the collapse behaviour of intact and damaged box beams under four-point bending moment. The influence of the impact location is considered herein, which covers both the side and upper panels. The FPB simulation and impact simulations are validated by comparison with the existing experimental data separately. In addition, the box beams are firstly subjected to impact loading and then four-point bending (FPB) loading is imposed on the damaged structures to assess the residual ultimate strength. Both the impact-induced deformation and initial stress are included in the FPB simulation.
The results clearly show that the impact location has a significant influence on the residual ultimate bending moment of the damaged box beam provided that the impact energy is kept constant. Among all the cases, it is found that impact on the upper plate point that is half spacing away from the edge (as shown in the cases of B350) leads to the minimum ultimate bending moment, namely the lowest residual strength. The most dangerous impact point lies in half spacing away from the edge in the upper panel.
The collapse modes also change much with the impactor striking on different locations. Damaged hard corner and inclined neutral axis may explain the reduction of ultimate strength and diverse collapse modes. It is also found that the residual stress in the box beam after impact may increase or decrease the ultimate strength, when compared with the corresponding model without residual stress, which depends on impact location.
Highlights• The residual stress after impact was included to illustrate the effect of impact-induced stress on the residual strength of the damaged box beams.• The impact location is varied to study the effect of impact point on the residual strength of damaged box beam.• The box beams are firstly subjected to impact loading and then four-point bending (FPB) loading is imposed to assess the residual strength.• The impact tolerance of damaged box beams is numerically investigated.HighlightsOpen Access> This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. -
Figure 6 Experimental and numerical collapse modes. (a) Experimental observation (Gordo and Guedes Soares 2009). (b) Numerical results
Table 1 Flexural rigidity and maximum bending moment
Cond. EI1 (kN m2) EI2 (kN m2) Max.BM (kN m) Relative diff (%) Intact 168 649 41 736 1068 0.00 S0 166 063 52 246 1104 3.33 S100 145 220 38 603 1067 − 0.09 S200 134 767 47 356 962 − 10.96 S250 106 081 36 872 922 − 15.73 S300 97 891 46 401 921 − 15.92 B0 140 421 56 333 1043 − 2.34 B75 139 648 65 524 1066 − 0.13 B150 130 500 31 928 1010 − 5.72 B225 125 341 33 074 952 − 12.18 B300 115 410 31 280 890 − 19.91 B350 120 253 34 487 818 − 30.49 B400 139 033 15 167 1041 − 2.56 Table 2 Difference of maximum bending moment
Cond. Max.BM Relative diff With RS Without RS Intact 1068 1068 0 S0 1104 1111 − 0.61 S100 1067 1129 − 5.47 S200 962 989 − 2.77 S250 922 909 1.39 S300 921 907 1.52 B0 1043 1018 2.49 B75 1066 1010 5.56 B150 1010 997 1.30 B225 952 965 − 1.39 B300 890 911 − 2.32 B350 818 818 − 0.01 B400 1041 1074 − 3.11 RS means the residual stress after impact -
Benson S, Abubakar A, Dow RS (2013) A comparison of computational methods to predict the progressive collapse behaviour of a damaged box girder. Eng Struct 48: 266–280 https://doi.org/10.1016/j.engstruct.2012.09.031 Benson S, Syrigou M, Leelachai A, Dow RS (2016) An extended progressive collapse method for damaged ships. In: Cho SR, Shin HK, Choung J, Jung RT (eds) Collision and grounding of ships and offshore structures. Society of Naval Architects of Korea, Korea, pp 311–318 Caldwell JB (1965) Ultimate longitudinal strength. Trans RINA 107: 411–430 Cho SR, Yoon SH, Park SH, Song SU (2016) Collision damage and residual strength of box girders. In: Cho SR, Shin HK, Choung J, Jung RT (eds) Collision and grounding of ships and offshore structures. Society of Naval Architects of Korea, Korea, pp 325–333 Dow RS, Hugill RC, Clark JD, Smith CS (1981) Evaluation of ultimate ship hull strength. SNAME Symposium on Extreme Loads Response, Arlington: 133–148 Dow RS (1991) Testing and analysis of 1/3-scale welded steel frigate model. Proc. International Conference on Advances in Marine Structures. Dunfermline, Scotland: 749–973 Ehlers S (2010) Strain and stress relation until fracture for finite element simulations of a thin circular plate. Thin-Walled Struct 48: 1–8 https://doi.org/10.1016/j.tws.2009.08.004 Gaspar B, Teixeira AP, Guedes Soares C, Wang G (2011) Assessment of IACS-CSR implicit safety levels for buckling strength of stiffened panels for double hull tankers. Mar Struct 24(4): 478–502 https://doi.org/10.1016/j.marstruc.2011.06.003 Gordo JM, Guedes Soares C (1993) Approximate load shortening curves for stiffened plates under uniaxial compression. In: Faulkner D, Cowling MJ, Incecik A (eds) Integrity of offshore structures, vol 5. EEMAS, Glasgow, pp 189–211 Gordo JM, Guedes Soares C (2000) Residual strength of damaged ship hulls. In: Cassella PSA, Festinese G (eds) Proc of the IX International Maritime Association of Mediterranean Congress (IMAM 2000), Ischia, Italy, pp 79–86 Gordo JM, Guedes Soares C (2007) Experimental evaluation of the behaviour of a mild steel box girder under bending moment. In: Guedes Soares C, Das PK (eds) Advancements in marine structures. Taylor & Francis Group, London, pp 377–383 Gordo JM, Guedes Soares C (2009) Tests on ultimate strength of hull box girders made of high tensile steel. Mar Struct 22(4): 770–790 https://doi.org/10.1016/j.marstruc.2009.07.002 Gordo JM, Guedes Soares C (2014) Experimental analysis of the effect of the frame spacing variation on the ultimate bending moment of box girders. Mar Struct 37: 111–134 https://doi.org/10.1016/j.marstruc.2014.03.003 Gordo JM, Guedes Soares C (2015) Experimental evaluation of the ultimate bending moment of a slender thin-walled box girder. J Offshore Mech Arctic Eng 137(2): 021604 https://doi.org/10.1115/1.4029536 Guedes Soares C, Dogliani M, Ostergaard C, Parmentier G, Pedersen PT (1996) Reliability based ship structural design. Trans Soc Naval Architects Mar Eng 104: 357–389 Hussein AW, Guedes Soares C (2011) Reliability assessment of intact and damaged bulk carriers. In: Guedes Soares C, Fricke W (eds) Advances in marine structures. Taylor & Francis Group, London, pp 679–690 Jones N (1981) Structural impact. Cambridge University Press Luís RM, Teixeira AP, Guedes Soares C (2009) Longitudinal strength reliability of a tanker hull accidentally grounded. Struct Saf 31(3): 224–233 https://doi.org/10.1016/j.strusafe.2008.06.005 Lin Z, Zhu L, Liu JH, Guedes Soares C (2019) Progressive collapse analyses of a stiffened box-girder under pure bending. In: Parunov J, Guedes Soares C (eds) Trends in analysis and design of marine structures. Taylor & Francis Group, London, pp 158–164 Liu B, Guedes Soares C (2015) Simplified analytical method for evaluating web girder crushing during ship collision and grounding. Mar Struct 42: 71–94 https://doi.org/10.1016/j.marstruc.2015.03.001 Liu B, Guedes Soares C (2019) Effect of strain rate on dynamic responses of laterally impacted steel plates. Int J Mech Sci 160: 307–317 https://doi.org/10.1016/j.ijmecsci.2019.06.034 Liu B, Villavicencio R, Guedes Soares C (2014) On the failure criterion of aluminum and steel plates subjected to low-velocity impact by a spherical indenter. Int J Mech Sci 80: 1–15 https://doi.org/10.1016/j.ijmecsci.2013.12.015 Liu B, Villavicencio R, Guedes Soares C (2015) Simplified method for quasi-static collision assessment of a damaged tanker side panel. Mar Struct 40: 267–288 https://doi.org/10.1016/j.marstruc.2014.11.006 Liu B, Villavicencio R, Zhang S, Guedes Soares C (2017a) Assessment of external dynamics and internal mechanics in ship collisions. Ocean Eng 141: 326–336 https://doi.org/10.1016/j.oceaneng.2017.06.053 Liu B, Villavicencio R, Zhang S, Guedes Soares C (2017b) A simple criterion to evaluate the rupture of materials in ship collision simulations. Mar Struct 54: 92–111 https://doi.org/10.1016/j.marstruc.2017.03.006 Liu K, Liu B, Villavicencio R, Wang Z, Guedes Soares C (2018) Assessment of material strain rate effects on square steel plates under lateral dynamic impact loads. Ships Offshore Struct 13(2): 217–225 https://doi.org/10.1080/17445302.2017.1354659 Nishihara S (1984) Ultimate longitudinal strength of midship cross section. Naval Architect Ocean Eng 22: 200–214 Notaro G, Kippenes J, Amlashi H, Russo M, Steen E (2010) Residual hull girder strength of ships with collision or grounding damages, Proc. 11th International Symposium on Practical Design of Ships and Other Floating Structures, Rio de Janeiro, Brazil Prestileo A, Rizzuto E, Teixeira AP, Guedes Soares C (2013) Bottom damage scenarios for the hull girder structural assessment. Mar Struct 33: 33–55 https://doi.org/10.1016/j.marstruc.2013.04.001 Parunov J, Guedes Soares C (2008) Effects of Common Structural Rules on hull-girder reliability of an Aframax oil tanker. Reliab Eng Syst Saf 93(9): 1317–1327 https://doi.org/10.1016/j.ress.2007.07.011 Pollalis C, Samuelides M (2013) Ultimate strength of damaged hulls. In: Amdahl J, Ehlers S, Leira BJ (eds) Collision and grounding of ships and offshore structures. Taylor & Francis Group, London, pp 297–304 Putranto T, Kõrgesaar M (2020). Numerical study on the structural behavior of intact and damaged box beams under four-point bending load, In: Guedes Soares C (ed), Developments in the collision and grounding of ships and offshore structures. Taylor & Francis Group, London, pp 139–143 Reckling KA (1979) Behavior of box girders under bending and shear. Proceedings of the 7th International Ship and Offshore Structures Congress (ISSC). Paris, France: II. 2. 46-49 Smith CS (1977) Influence of local compressive failure on ultimate longitudinal strength of a ship's hull. Proc. of 3rd International Symposium on practical Design in shipbuilding. Tokyo: 73–79 Sedlacek G, Müller C (2001) High strength steels in steel construction. In: Niobium: science and technology. TMS: The Minerals, Metals and Materials Society, Orlando Saad-Eldeen S, Garbatov Y, Guedes Soares C (2010) Experimental assessment of the ultimate strength of a box girder subjected to four-point bending moment. Proc. of the 11th International Symposium on Practical Design of Ships and other Floating Structures (PRADS2010) Villavicencio R, Guedes Soares C (2012) Numerical modelling of laterally impacted plates reinforced by free and end connected stiffeners. Eng Struct 44: 46–62 https://doi.org/10.1016/j.engstruct.2012.05.024 Villavicencio R, Kim Y-H, Cho S-R, Guedes Soares C (2013) Deformation process of web girders inside of a small-scale laterally impacted tanker double hull structure. Mar Struct 32: 84–112 https://doi.org/10.1016/j.marstruc.2013.02.004 Villavicencio R, Guedes Soares C (2014) Analysis of collisions between tugs and tankers. In: Guedes Soares C, Lopez Pena F (eds) Developments in maritime transportation and exploitation of sea resources. Taylor & Francis Group, London, pp 405–414 Xu MC, Teixeira AP, Guedes Soares C (2015) Reliability assessment of a tanker using the model correction factor method based on the IACS-CSR requirement for hull girder ultimate strength. Probabilist Eng Mechan 42: 42–53 https://doi.org/10.1016/j.probengmech.2015.09.003