1   Introduction

Plate panels are used in naval, offshore, mechanical, aerospace, and civil engineering structures as primary strength parts of ships, ship-shaped offshore installations, fuselages, box-girder cranes, and bridges. They are usually designed and built with a uniform thickness over the plating, but nonuniform thickness is sometimes allocated to fulfill practical design requirements (Zenkour 2003; Lee et al. 2019; Tash and Neya 2020).

During the past several decades, the emphasis on structural design has moved from the allowable stress design to the limit state design because the latter approach makes possible a rigorously designed, yet economical, structure that directly takes into consideration the various relevant modes of failure (Paik 2018). Furthermore, limit states are key criteria within the framework of quantitative risk assessment and management which is now recognized to be the best way to effectively manage extreme conditions and accidents associated with the volatile, uncertain, complex, and ambiguous environments at every stage of design, construction, operation, and decommissioining of structures and infrastructure, and ultimately resolve such challenges (Paik 2020).

A limit state is formally defined by the description of a condition for which a particular structural member of an entire structure would fail to perform the function designated beforehand, and four types of limit states are relevant for structures, namely the servicebility limit state (SLS), the ultimate limit state (ULS), the fatigue limit state (FLS), and the accidental limit state (ALS) from the viewpoint of structural design (Paik 2018). This paper deals with the ultimate limit state of a steel-stiffened plate structure under uniaxial compresive loads.

A number of useful studies on the ultimate strength of plate panels for marine applications are found in the literature (Abdussamie et al. 2018; Benson et al. 2011; Gannon et al. 2013, 2016; Iijima et al. 2015; Jagite et al. 2019, 2020; Khan and Zhang 2011; Khedmati et al. 2014, 2016; Kim et al. 2009, 2015; Kumar et al. 2009; Lee and Paik 2020; Magoga and Flockhart 2014; Ozguc et al. 2006; Paik 2007; Paik et al. 2013; Rahbar-Ranji and Zarookoan 2015; Ringsberg et al. 2018; Shi and Gao 2020; Shi and Wang 2012; Zhang 2016; Wang et al. 2009). For plate panels of engineering structures with variable or nonuniform thickness, the structural responses should be characterized by taking into account the effects of variable thickness. Zenkour (2003) and Tash and Neya (2020) studied the bending behavior of transversely isotropic thick rectangular plates with variable thickness. de Faria and de Almeida (2003) and Le-Manh et al. (2017) studied buckling of composite plates with variable thickness. Zhang et al. (2018) studied buckling of egg-shaped shells with variable thickness under external pressure loads. However, no studies on the ultimate strength of isotropic plate panels with variable or nonuniform thickness are found in the literature.

The aim of the present paper is to contribute to developing computational models for the ultimate compressive strength analysis of steel-stiffened plate panels with nonuniform thickness. The paper is a sequel to the articles of Paik et al. (2020a, b, c, d, e) that dealt with full-scale progressive collapse testing on steel-stiffened plate structures under various circumstances such as low temperature or fires.

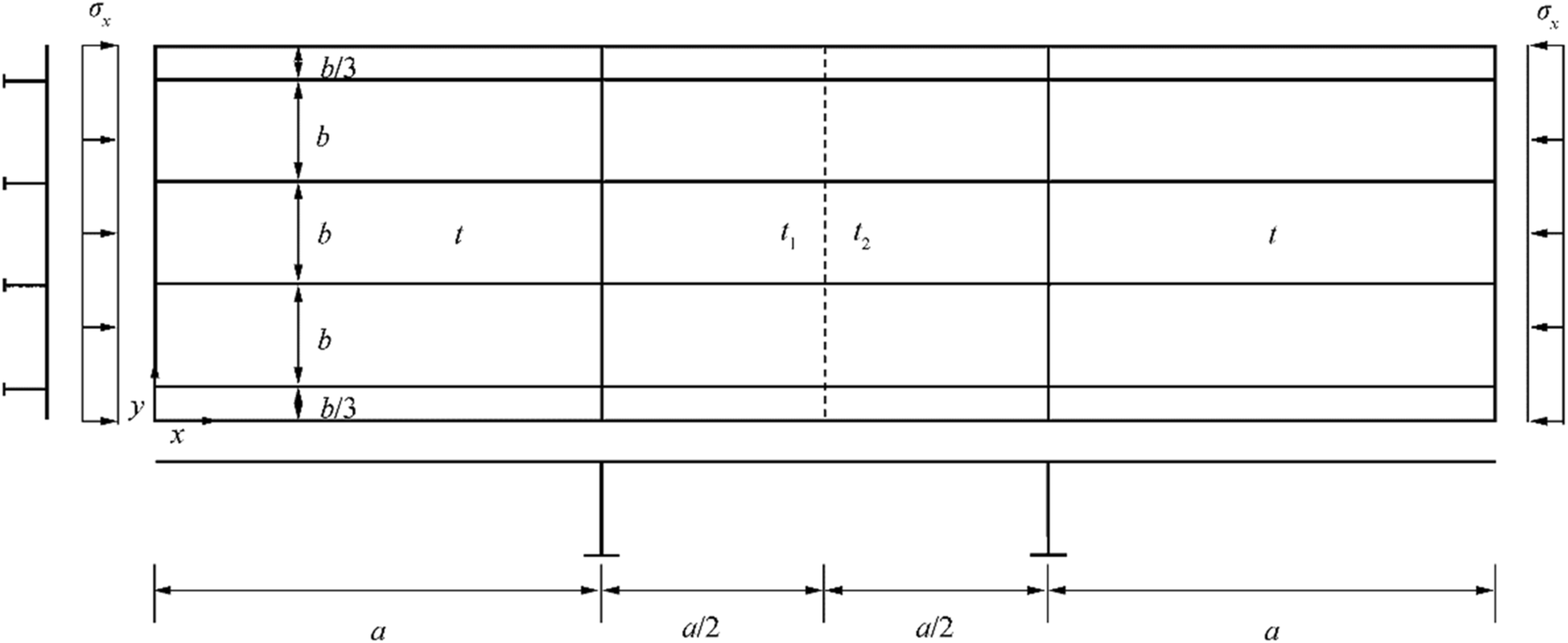
2   A Target Stiffened Plate Panel

A stiffened plate panel subjected to axial compressive loads is considered as shown in Figure 1. The panel is composed of three bays. The plating of outer two bays has a same thickness of t. However, the thickness for a half of the plating in the central bay is t₁ and t₂. The target plate panel with t = t₁ = t₂ was fabricated with the framework of full-scale collapse tests (Paik 2020a, b, c, d and e), where the bottom plate panels of a containership carrying 1900 TEU were a reference.

Figure  1  A stiffened plate panel

Download: Full-Size Img

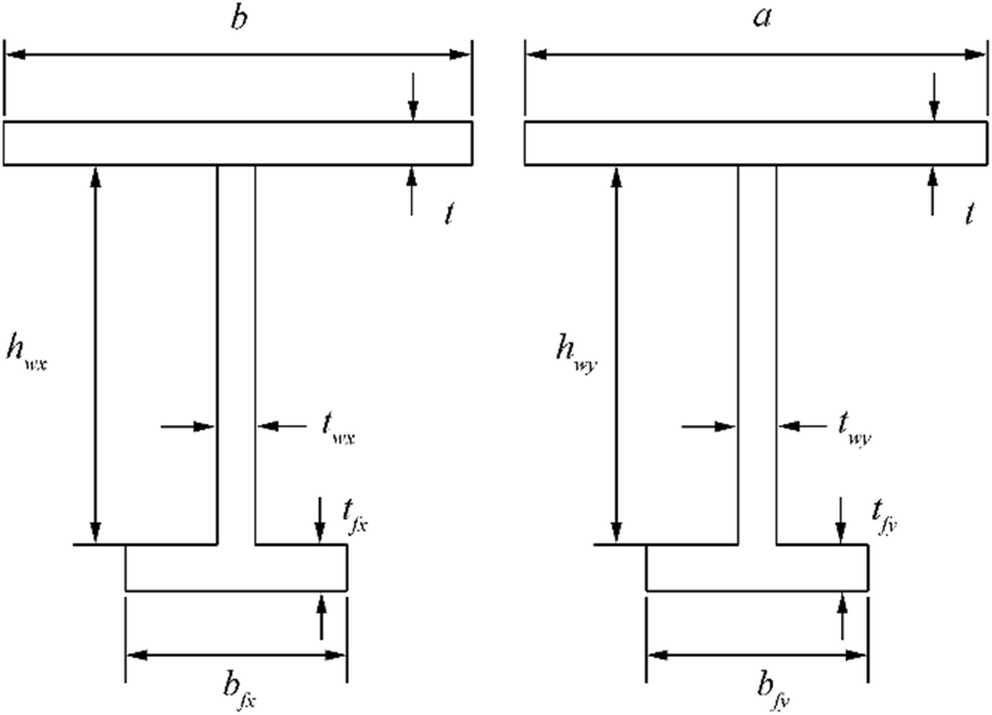
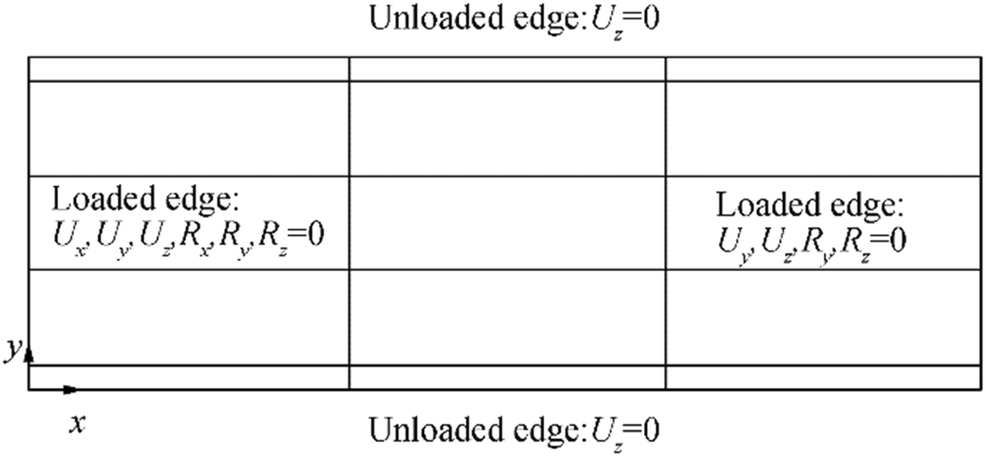
The panel has four longitudinal stiffeners and two transverse frames with T-type as shown in Figure 2. The dimensions of longitudinal stiffeners in outer two bays are the same, but they are larger than from those in the central bay. This means that the outer two bays may not buckle until the central bay reaches the ultimate limit state. Table 1 presents the dimensions of the plate panel. The plate panel is fixed along the loaded edges (i.e., left and right ends), but the unloaded edges are simply supported, i.e., with the constraints of lateral deformation but free rotation. Also, the unloaded edges are allowed to move in-plane freely, implying that they may not keep straight as the plate panel deflects due to buckling.

Figure  2  T-type support members in the x and y directions

Download: Full-Size Img

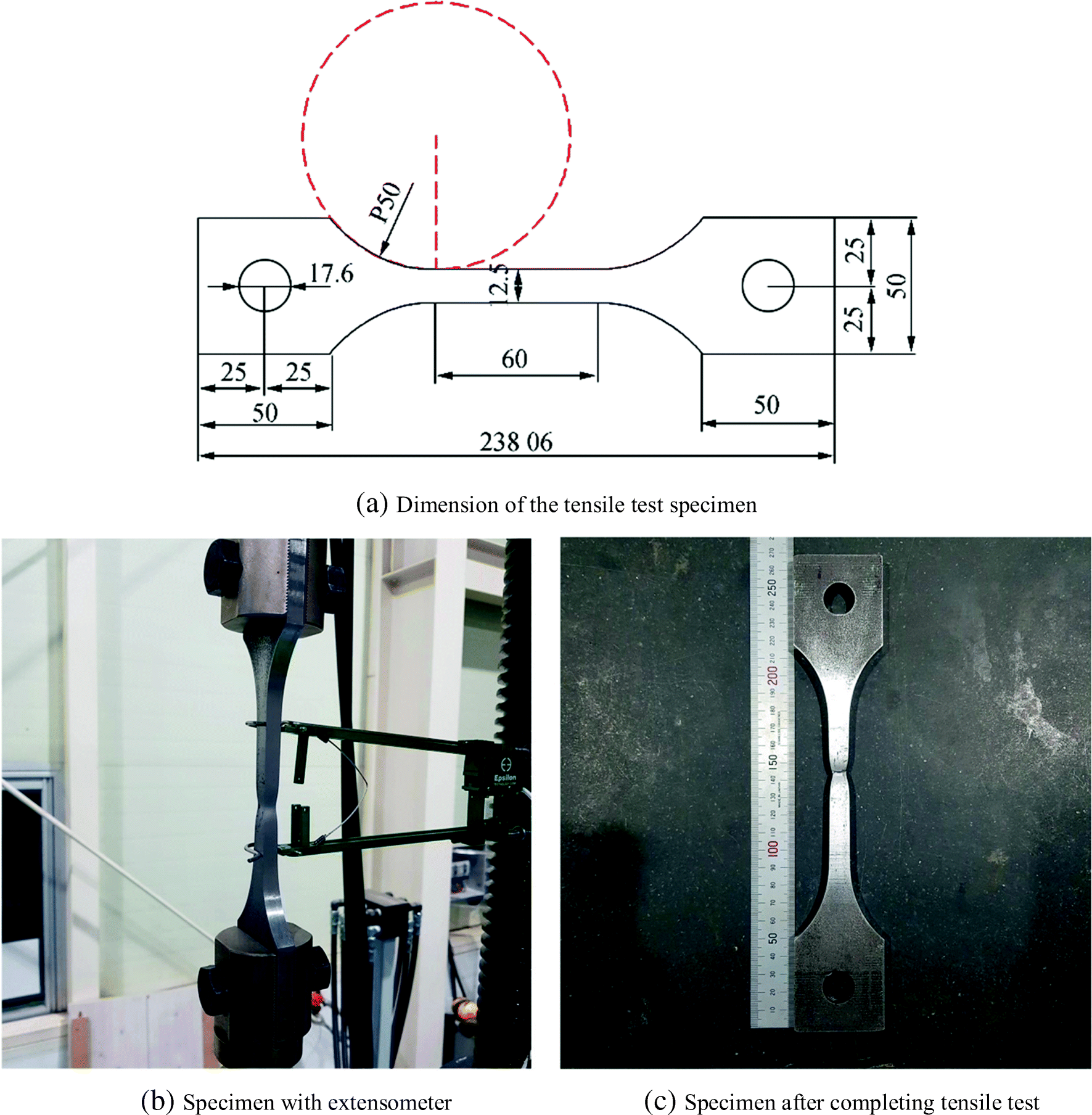
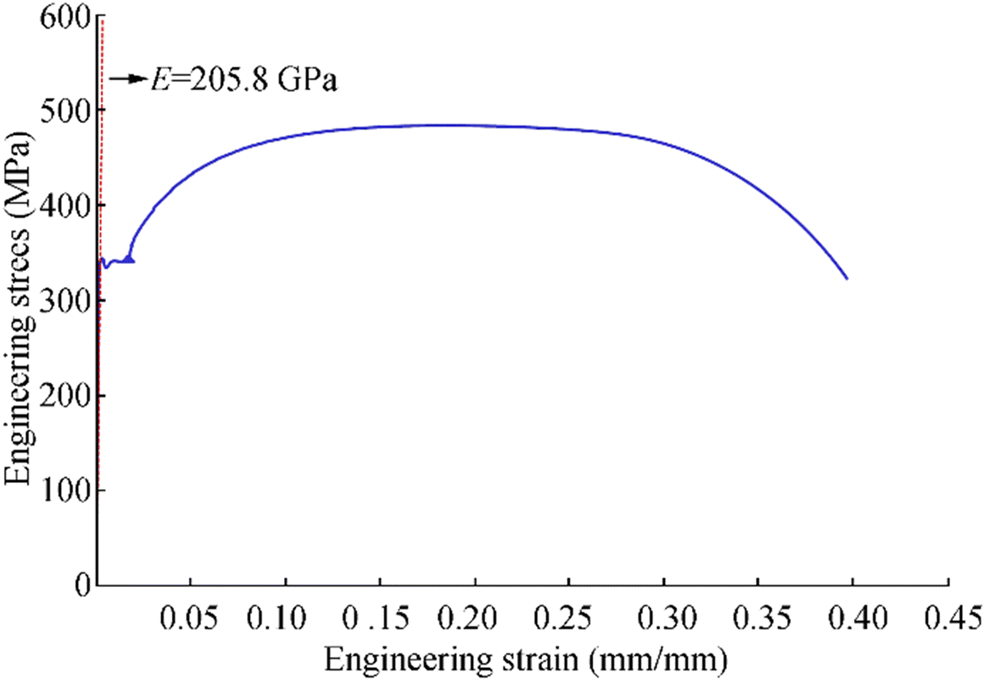
The plate panel is made of high tensile steel with grade AH32. To define the mechanical properties of the material, the tensile coupon tests were conducted with specimens made in compliance with ASTM E8 (ASTM 2011), as shown in Figure 3. Figure 4 shows one of typical engineering stress-engineering strain curves of the material obtained from tensile coupon tests with multiple specimens. Table 2 provides the mechanical properties of the AH32 steel.

Figure  3  Specimen of material used for the structure before and after tensile coupon tests

Download: Full-Size Img

Figure  4  Engineering stress versus engineering strain curve of the AH32 steel

Download: Full-Size Img

3   Modeling of Weld Fabrication-Induced Initial Imperfections of the Plate Panel

The plate panel with t = t₁ = t₂ = 10 mm was fabricated in a shipyard in Busan, South Korea, which builds small and medium-sized merchant and patrol ships. The technology of welding was exactly the same as used for fabrication of real ship structures. The flux-cored arc welding (FCAW) technique was applied in accordance with the welding procedure specification (WPS) requirements as indicated in Table 3. As per the welding requirements of DNVGL (2017), the penetration of welding was fully achieved with a leg length of 7 mm as shown in Figure 5. Figure 6 shows the plate panel after fabrication was completed in the shipyard.

Figure  5  Full penetration of welds with a leg length of 7 mm

Download: Full-Size Img

Figure  6  The plate panel after completing of fabrication in the shipyard

Download: Full-Size Img

3.1   Modeling of the Plate Initial Deflection

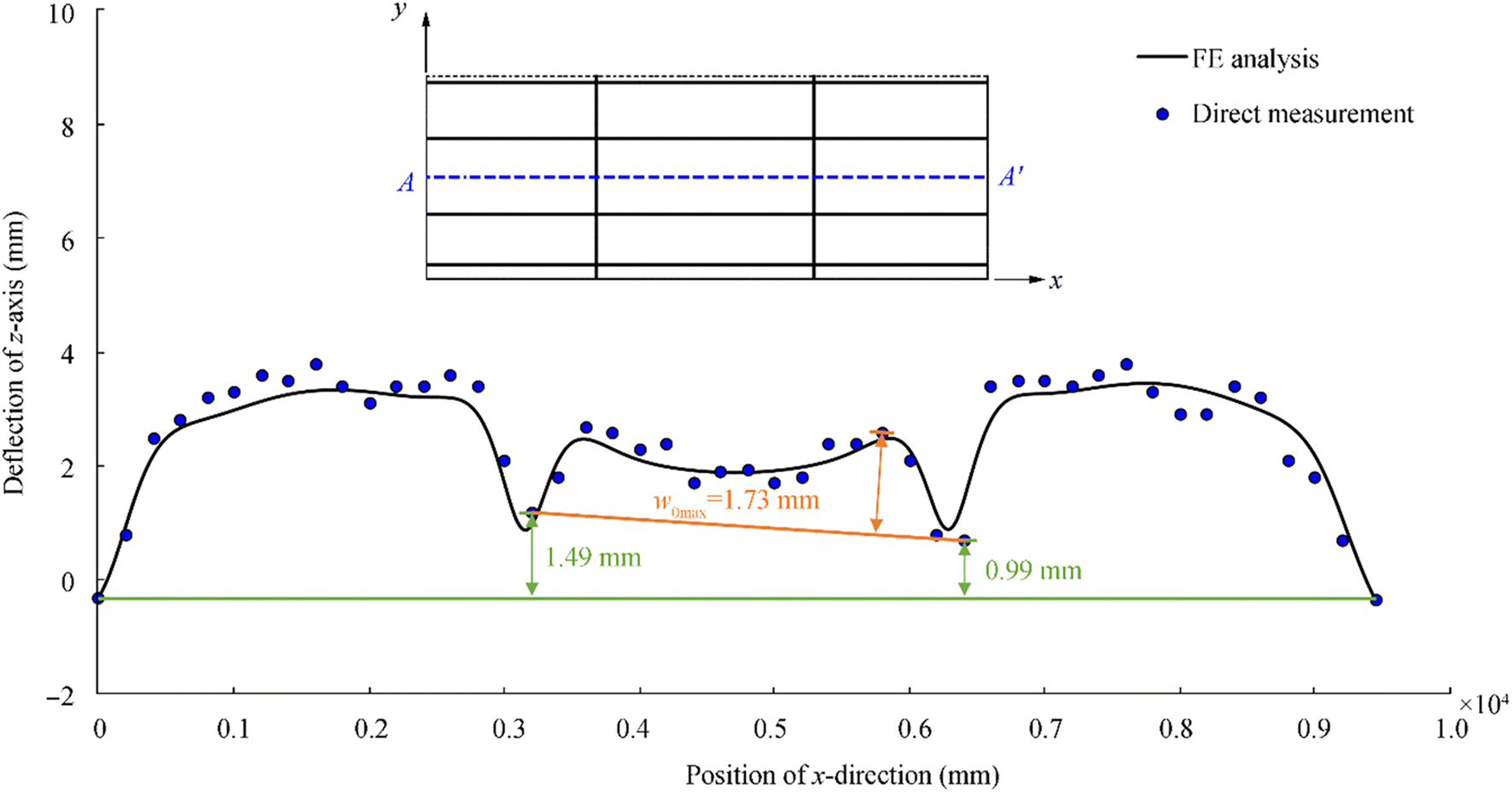
A 3D scanner was used to measure the welding-induced initial deformations for plating and support members. For details of the initial deformation measurements together with the thermal-elastic-plastic large deformation finite element method computations, Yi et al. (2020a) is referred to. Figure 7 presents the welding-induced initial deflection of plating in the plate length and breadth directions. It is seen that not only plating but also transverse frames were deflected by welding, where the relative maximum of the plate initial deflection was found to be 1.73 mm based on the measured data. On the other hand, the maximum sideways deformation of longitudinal stiffeners was 0.42 mm which is 0.000133a. The web initial deflections for both longitudinal stiffeners and transverse frames were negligibly small (Figure 8).

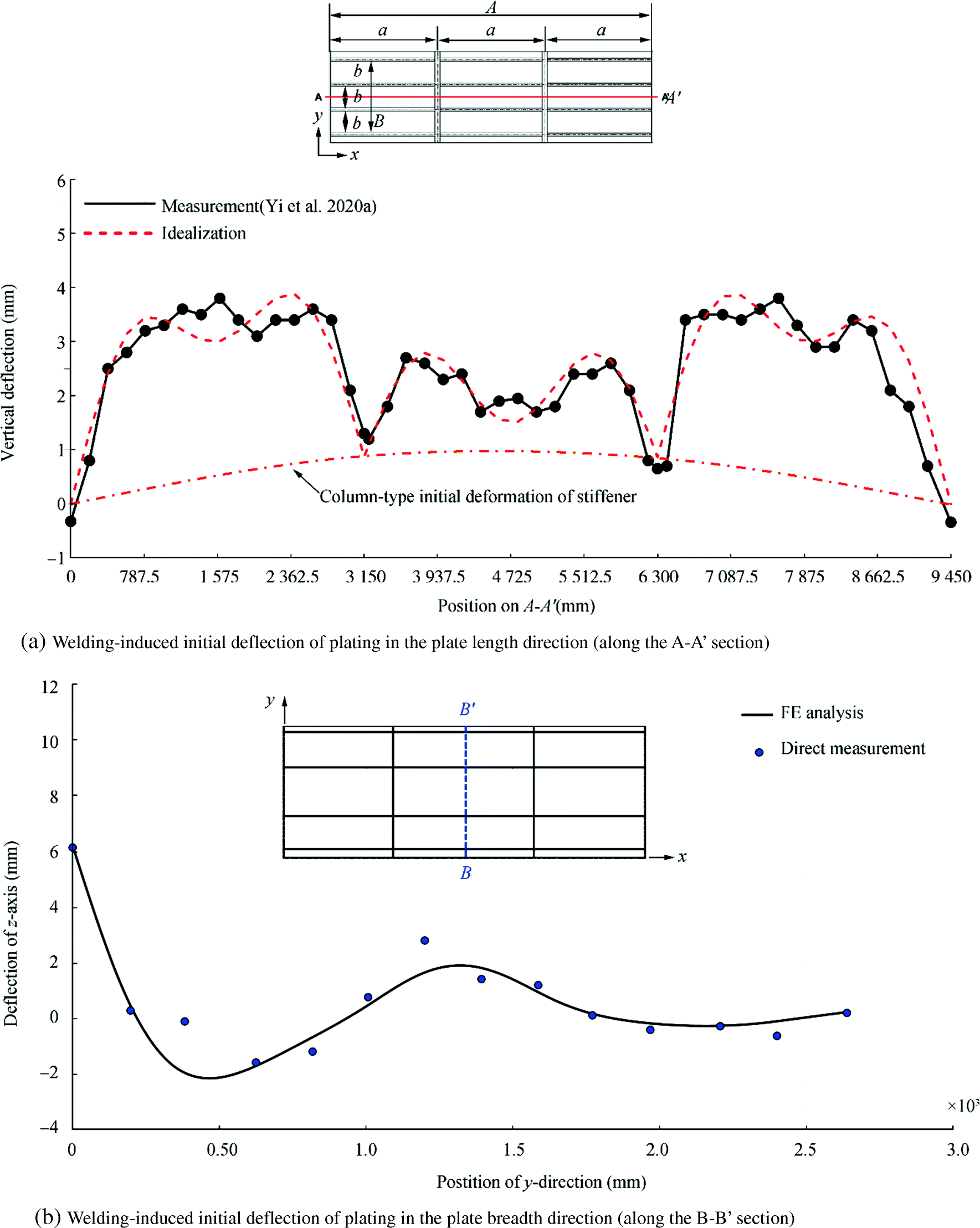Figure  7  Comparison between direct measurements and numerical computations of plate initial deflections (Yi et al. 2020a)

Download: Full-Size Img

Figure  8  The maximum deflections of plating and transverse frames

Download: Full-Size Img

The shape of the plate initial deflection is the so-called hungry horse's back type. In this case, the plate initial deflection of the central bay panel but excluding the unloaded side plates may be formulated by the following Fourier series equation (Paik 2018) where only a single half-wave between longitudinal stiffeners is allocated in the plate breadth direction.

where w₀ is the plate initial deflection function, w_0max is the maximum plate initial deflection, B = 3b is the breadth of the panel, and B_0i3 is the coefficient of the plate initial deflection.

The buckling mode of plating is defined as an integer satisfying the following equation.

where m is the buckling half-wave number. With a = 3150 mm and b = 720 mm, m = 4 is determined.

Equation (1) may be simplified with only the buckling component as follows:

where B₀₄₃ is the buckling component of the plate initial deflection function which may be taken as B₀₄₃ = 0.0259 (Paik 2018) as far as the hungry horse's back shape is applied.

3.2   Modeling of the Residual Stresses

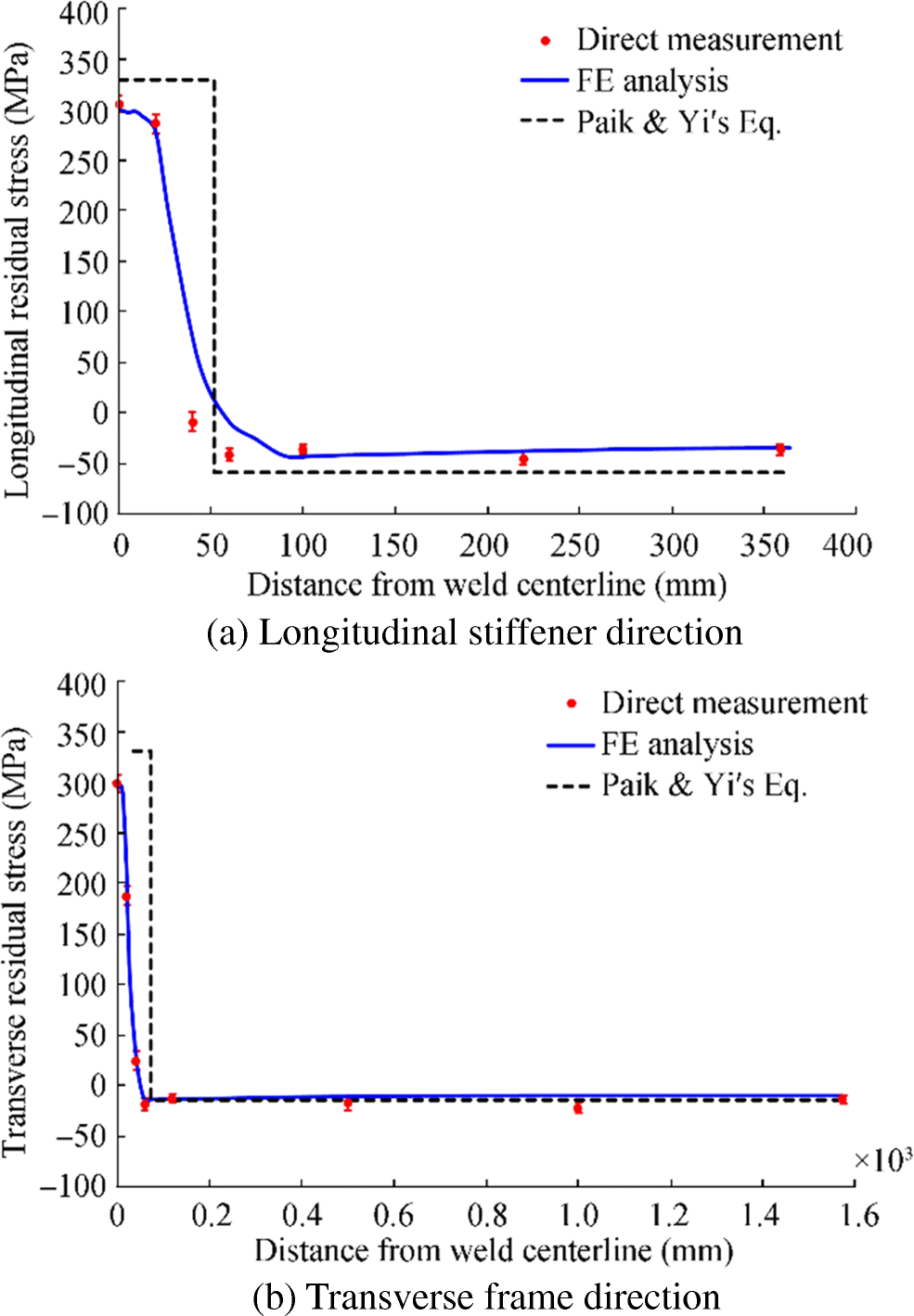
As both longitudinal stiffeners and transverse frames are attached to the plating by welding, residual stresses must be developed in the two directions as shown in Figure 9. Tensile residual stresses are developed in the heat-affected zone, and compressive residual stresses are developed in the middle of plating to fulfill the equilibrium condition between internal forces. The X-ray diffraction (XRD) method was used to measure welding-induced residual stresses in the plate panel. Details of the residual stress measurements together with the thermal elastic-plastic finite element method computations and the simple formula estimations are presented in Yi et al. (2020b). Figure 10 shows the comparison of welding-induced residual stresses between direct measurement, finite element method computations, and simple formula estimations.

Figure  9  Distribution of welding-induced residual stresses in the two directions

Download: Full-Size Img

Figure  10  A comparison of welding-induced residual stresses between direct measurements, numerical predictions, and simple formula estimations

Download: Full-Size Img

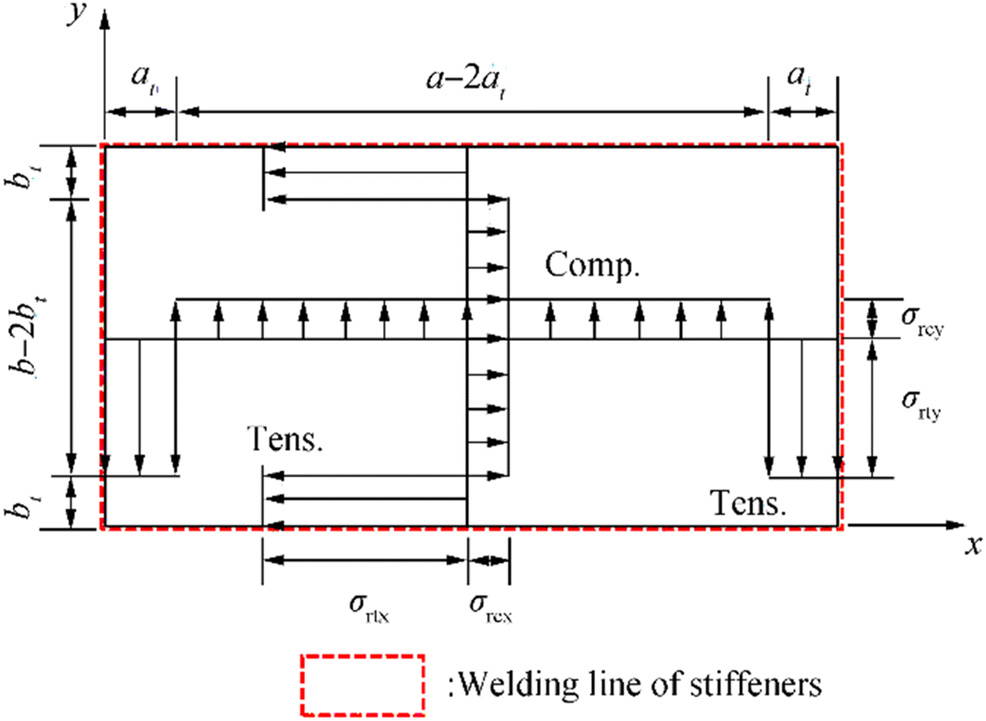
The distribution of welding-induced residual stresses is often modeled as rectangular blocks of tensile and compressive residual stresses as shown in Figure 11. For welded steel plates, the welding-induced residual stresses may be estimated by the following procedure (Paik 2018).

Figure  11  Idealization of the welding-induced residual stresses in a plate

Download: Full-Size Img

From the equilibrium condition, the compressive residual stresses are obtained as follows:

where b_t and a_t are the breadth of tensile residual stress block in the plate breadth or length direction, respectively, σ_rtx, σ_rty are the magnitude of tensile residual stress block in the plate length or breadth direction, respectively, σ_rcx, σ_rcy are the magnitude of compressive residual stress block in the plate length or breadth direction, respectively, a is the plate length (spacing between transverse frames), and b is the plate breadth (spacing between longitudinal stiffeners). σ_rtx and σ_rty are approximately equal to σ_Y (material yield strength) for structural steels.

Equation (4) indicates that the compressive residual stresses can be estimated once the breadths of tensile residual stress blocks are defined. Empirical formulations of b_t and a_t were developed as a function of the weld leg length L_w as follows (Paik 2018):

where $ {c}_1=-0.4562\times {\beta}_x^2+4.1994\times {\beta}_x+2.6354 $, $ {c}_2=1.1352\times {\beta}_x^2-4.3185\times {\beta}_x-11.1750 $ and $ {\beta}_x=\frac{b}{t}\sqrt{\frac{\sigma_Y}{E}} $.

where $ {\displaystyle \begin{array}{c}{d}_1=-0.0399\kern.3em \times \kern.3em {\beta}_y^2\kern.3em +\kern.3em 2.0087\kern.3em \times \kern.3em {\beta}_y\kern.3em +8.7880\\ {}\end{array}} $, $ {d}_2=0.1042\times {\beta}_y^2-4.8575\times {\beta}_y-17.7950 $ and $ {\beta}_y=\frac{a}{t}\sqrt{\frac{\sigma_Y}{E}} $.

Using Eqs. (4)-(6), the magnitude of compressive residual stresses in the longitudinal and transverse directions can be estimated. The yield strength of the AH32 steel is 331 MPa, and thus, σ_Y = σ_rtx = σ_rty = 331 MPa is taken. Also, the leg length for the applied weld condition is L_w = 7 mm. Therefore, the slenderness ratios are calculated as β_x = 2.88 and β_y = 12.63. Equations (5) and (6) provide the breadths of tensile residual stress blocks as follows:

The compressive residual stresses in the longitudinal and transverse directions are estimated from Eq. (4) as follows:

Figure 10 presents the validity of the procedure to estimate the welding-induced residual stresses in the plate panel.

4   Computational Models

4.1   ALPS/ULSAP (2020) Analytical Method

The primary modes of overall failure for a stiffened plate structure are categorized into the following six types (Paik 2018):

· Mode I: overall collapse of plating and stiffeners as a unit

· Mode II: plate collapse without distinct failure of stiffeners

· Mode III: beam column–type collapse

· Mode IV: collapse by local web buckling of stiffener

· Mode V: collapse by lateral-torsional buckling (tripping) of stiffener

· Mode VI: gross yielding

Some collapse modes may in some cases interact and occur simultaneously, but it is typically considered that the collapse of the stiffened panels occurs at the lowest value among the various ultimate loads calculated when considering each of the abovementioned six collapse patterns separately. Details of the ULS computations for each of the six collapse modes are found in Paik (2018), and they have been implemented into the ALPS/ULSAP program (2020). This method accommodates the application of combined load components such as biaxial compression/tension, biaxial in-plane bending, edge shear, and lateral pressure loads. The effects of welding-induced initial imperfections in the form of initial deformations and residual stresses are taken into account.

With ALPS/ULSAP, only the plate panel of the central bay which is assumed to be simply supported is taken as the extent of the analysis as shown in Figure 12. Also, only the buckling mode of the plate initial deflection is considered using Eq. (3). The measured values of the biaxial residual stresses are used but with the idealized distribution as shown in Figure 12. It is assumed that welding-induced residual stresses of longitudinal stiffeners are not considered. The column-type initial deflection of longitudinal stiffeners is assumed to be 0.0015a. The material follows the elastic-perfectly plastic model without considering strain-hardening effect.

Figure  12  Extent of the ALPS/ULSAP and ALPS/SPINE analyses

Download: Full-Size Img

A total of four cases with varying the thicknesses t₁ and t₂ are studied while the average value of them is kept constant at $ t=\frac{t_1+{t}_2}{2} $ as indicated in Table 4. For the ALPS/ULSAP analysis, the smaller value of the plate thickness, i.e., with t_eq = t₂ when t₁ ≥ t₂ is used so that the ultimate strength is computed for the plate panel with a uniform thickness of t_eq = t₂.

4.2   ALPS/SPINE (2020) Incremental Galerkin Method

The incremental Galerkin method developed by Paik et al. (2001) and Paik and Lee (2005) is a semi-analytical method for computing the elastic-plastic large deflection behavior of steel or aluminum plates and stiffened panels up to their ultimate limit state (ULS). This method is designed to accommodate the geometric nonlinearity associated with buckling via an analytical procedure, whereas a numerical procedure accounts for the material nonlinearity associated with plasticity (Paik 2018). The method is unique in its use to analytically formulate the incremental forms of nonlinear governing differential equations for elastic large deflection plate theory. After solving these incremental governing differential equations using the Galerkin approach (Fletcher 1984), a set of easily solved linear first-order simultaneous equations for the unknowns is obtained, which facilitates a reduction in the computational effort.

It is normally difficult, but not impossible, to formulate the nonlinear governing differential equations to represent both geometric and material nonlinearities for plates and stiffened panels. A major source of difficulty is that an analytical treatment of plasticity with increases in the applied loads is quite cumbersome. An easier alternative is to deal with the progress of the plasticity numerically. The benefits of this method are to provide excellent solution accuracy with great savings in computational effort and to handle in the analysis the combined loading for all potential load components, including biaxial compression or tension, biaxial in-plane bending, edge shear, and lateral pressure loads. The effects of initial imperfections in the form of initial deflection and welding-induced residual stresses are also considered. The present theory can be applied to both steel and aluminum plate panels. Details of the IGM theory and applied examples described in Paik (2018) have been implemented into the ALPS/SPINE program.

In the following, some of the more important basic hypotheses used to formulate the incremental Galerkin method for computation of the elastic-plastic large deflection behavior of plate and stiffened panels are described (Paik 2018).

The plate panel is made of isotropic homogeneous steel or aluminum alloys with a Young's modulus of E and a Poisson's ratio of v. For a stiffened panel, Young's modulus of the plate part between stiffeners is the same as that of the stiffeners, but the yield stress of the plate part can differ from that of the stiffeners.

1) The length and breadth of the plate are a and b, respectively, as shown in Figure 13a. The plate thickness is t.

Figure  13  Application of combined in-plane and out-of-plane loads

Download: Full-Size Img

2) The spacing of the stiffeners or the breadth of the plating between stiffeners can differ as shown in Figure 13b.

3) The material follows the elastic-perfectly plastic model without considering the strain-hardening effect.

4) The edge of the panel can be simply supported, clamped, or some combination of the two.

5) The panel is normally subjected to combined loads. Several potential load components act on the panel: biaxial compression or tension, edge shear, biaxial in-plane bending moment, and lateral pressure loads, as shown in Figure 14.

Figure  14  Idealized welding-induced residual stress distributions

Download: Full-Size Img

6) The applied loads are increased incrementally.

7) The shape of the initial deflection in the plate panel is normally complex, but it can be expressed with a Fourier series function. For a stiffened panel, the plate part between stiffeners may have the same set of local plate initial deflections, whereas the stiffeners may have a different set of global column-type initial deflections.

8) Due to the welding along the panel edges and at the intersections between the lower part of the stiffener web and parent plate, the panel has welding-induced residual stresses. These can develop in the plate part in both x and y directions, as welding is normally carried out in these two directions. As shown in Figure 15, the distribution of welding-induced residual stresses for the plate part between stiffeners is idealized to be composed of two stress blocks, i.e., compressive and tensile residual stress blocks. It is assumed that the stiffener webs have uniform compressive residual stresses "equivalent" to that shown in Figure 14.

Figure  15  Example subdivision of mesh regions used for treatment of plasticity

Download: Full-Size Img

9) For evaluation of the plasticity, it is assumed that the panel is composed of a number of membrane fibers in the x and y directions. Each membrane fiber is considered to have a number of layers in the z direction, as shown in Figure 15.

10) It is recognized that the strength of welded aluminum alloys in the softened zone may be recovered by natural aging over a period of time, but the ultimate strength of welded aluminum alloy panels may be reduced by softening phenomenon in the heat-affected zone as far as the material strength is not recovered. The effect of softening is accounted for using the technique noted in item 9 above.

The extent of the ALPS/SPINE analysis was the same as that of the ALPS/ULSAP analysis as shown in Figure 12. The plate initial deflection was assumed as follows:

Furthermore, the added plate deflection under applied loads was assumed to follow the equation.

where w is the added plate deflection and A_i3 is the amplitude of added deflection components.

Similar to the ALPS/ULSAP model, the measured values of the biaxial residual stresses were used but with the idealized distribution as shown in Figure 12. It was assumed that welding-induced residual stresses of longitudinal stiffeners were not considered. The column-type initial deflection of longitudinal stiffeners was assumed to be 0.0015a. Again, a total of four cases including one case with uniform plate thickness were studied as indicated Table 4. The smaller value of the plate thickness, i.e., with t_eq = t₂ when t₁ ≥ t₂ was applied for the ALPS/SPINE analysis.

4.3   ANSYS (2019) Finite Element Method

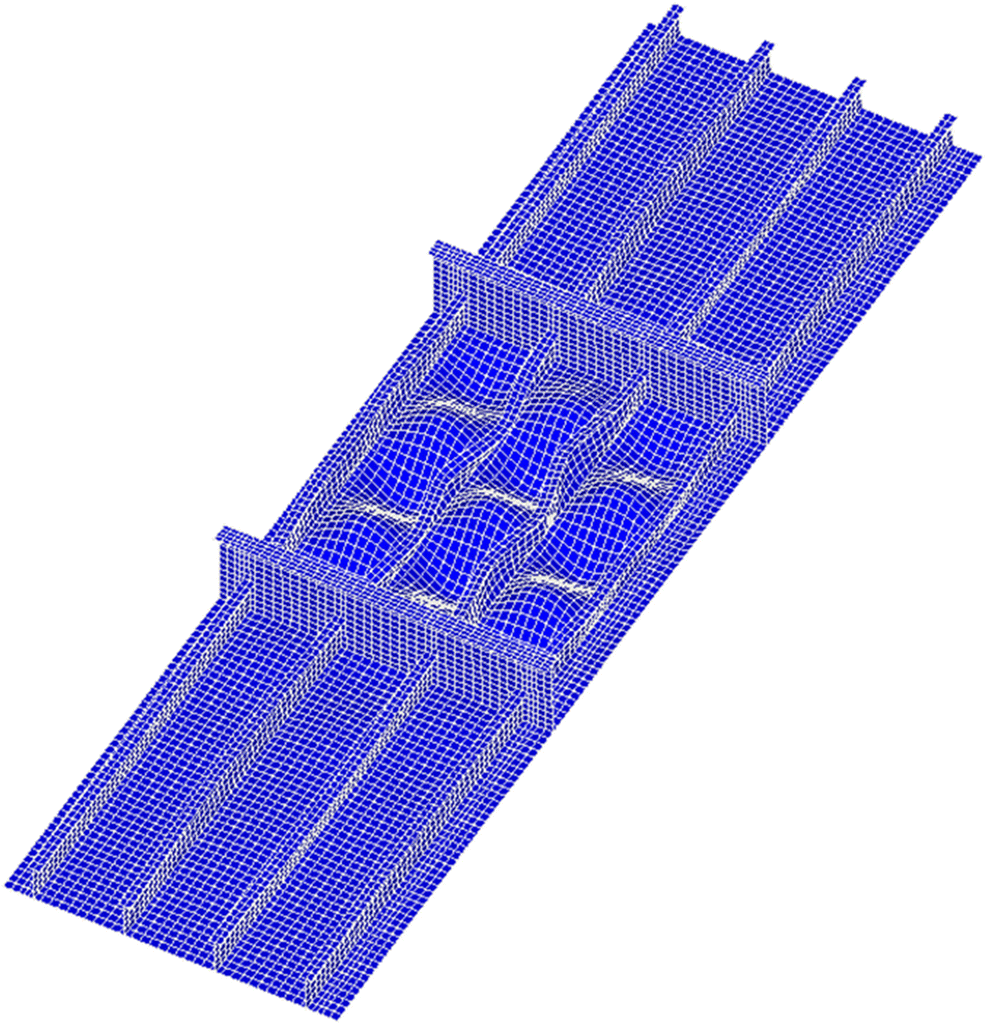
The entire structure was taken as the extent of the analysis as shown in Figure 16. Only plate elements (with an aspect ratio of unity if possible) were used to model not only plating but also support members including both webs and flanges. The mesh size was taken as b / 10 for plating. Two elements (with one element at each side of T-bar) were used for the flange of longitudinal stiffener, and four elements (with two elements at each side of T-bar) were used for the flange of transverse frame.

Figure  16  Extent of the ANSYS finite element method analysis

Download: Full-Size Img

The plate initial deflection was assumed with only the buckling mode of Eq. (3). The measured initial deflection of transverse frames shown in Figure 8 was directly considered. The measured residual stresses were included in the modeling. The maximum sideway deformation of longitudinal stiffeners was applied, and the web initial deflections of both longitudinal stiffeners and transverse frames were neglected. In contrast to ALPS/ULSAP and ALPS/SPINE analyses, the actual plate thicknesses of t₁ and t₂ were directly included in the ANSYS modeling, while a total of four cases were studied as indicated in Table 4. The elastic-perfectly plastic material model was applied for the ANSYS analysis. Figure 17 shows the finite element model of the tested structure. Figure 18 shows the boundary condition applied for the ANSYS finite element analysis which was the same as for the tested structure.

Figure  17  Modeling of initial deformations in the plate and support members

Download: Full-Size Img

Figure  18  Boundary condition applied for the ANSYS finite element method analysis

Download: Full-Size Img

5   Computed Results and Discussion

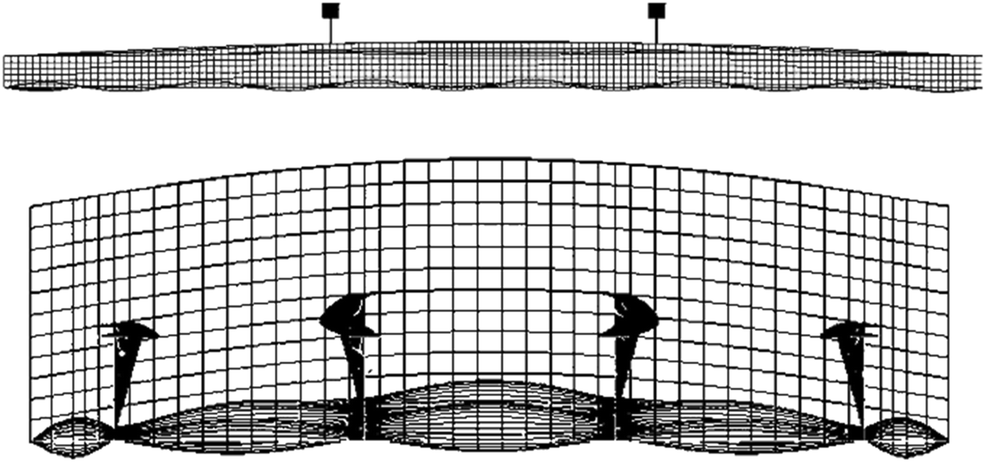
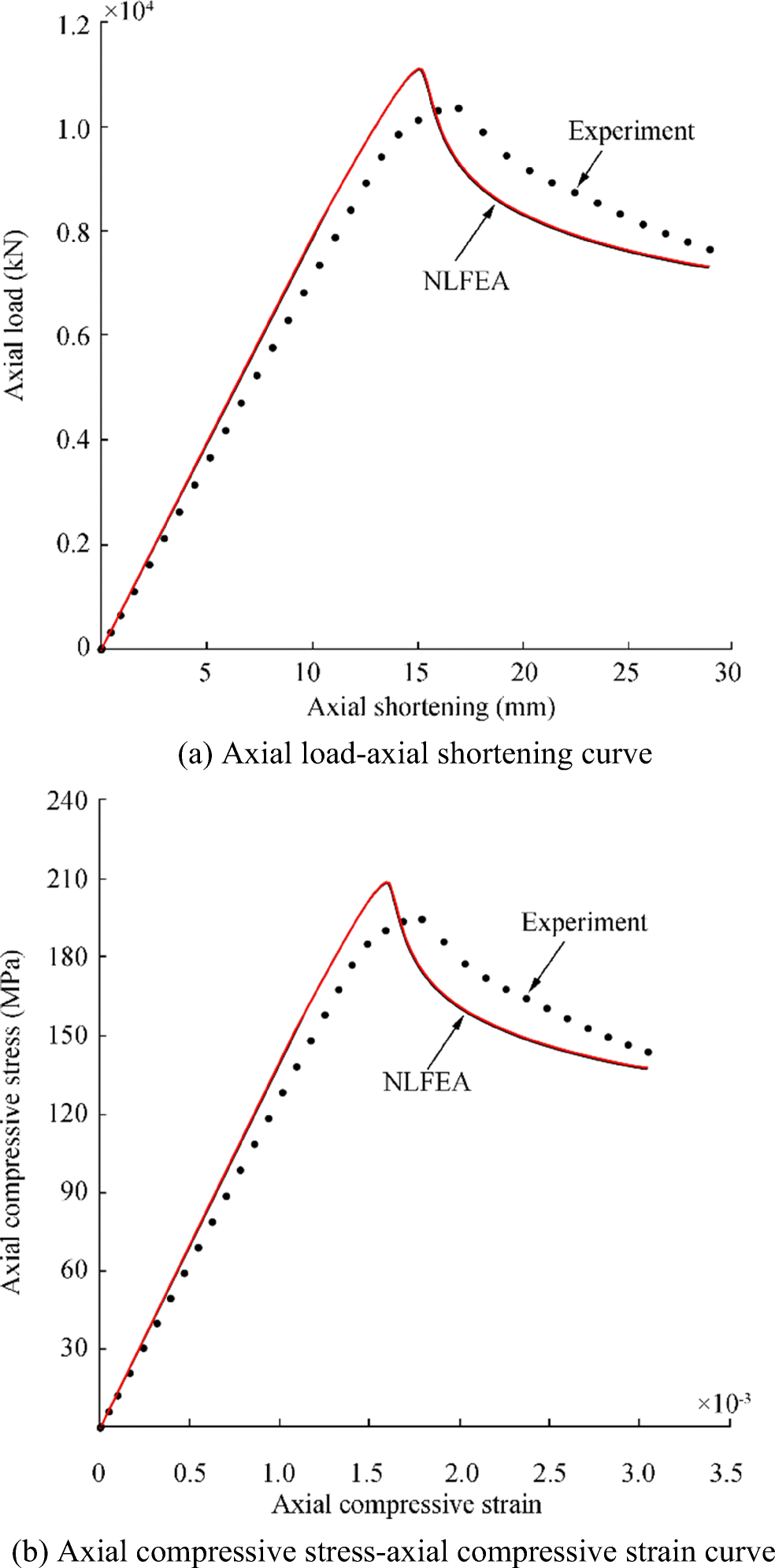
Figure 19 shows the applied compressive load versus axial shortening curves of the plate panel with t = t₁ = t₂ = 10 mm, where unloaded edges are allowed to move in-plane freely without keeping straight. To investigate the effect of the straight edge condition at unloaded edges, a comparison was made in terms of the in-plane displacement as shown in Figure 20. It is obvious from Figure 20 that the in-plane displacement was allowed for the nonstraight condition at unloaded edges, but the difference is very small and can be neglected. In fact, the computed results of the ANSYS finite element method in Figure 19 show identical despite the edge straight condition. Figure 21 shows the deformed shape of the plate panel with t = t₁ = t₂ = 10 mm at the ultimate limit state obtained from the ANSYS finite element method analysis. The deformed shape of the plate panel observed by the ANSYS analysis is comparable with that by the experiment as shown in Figure 22 where the panel reached the ultimate limit state by collapse mode V (tripping of the stiffeners), although the ANSYS computations did not show a clear tripping failure.

Figure  19  Comparison of the ultimate compressive strength behavior of the plate panel between the experiment and ANSYS finite element method analysis

Download: Full-Size Img

Figure  20  Effects of the straight condition at unloaded edges in terms of the in-plane displacement

Download: Full-Size Img

Figure  21  Deformed shape of the plate panel at the ultimate limit state obtained from the ANSYS finite element method analysis (with an amplification factor of 20)

Download: Full-Size Img

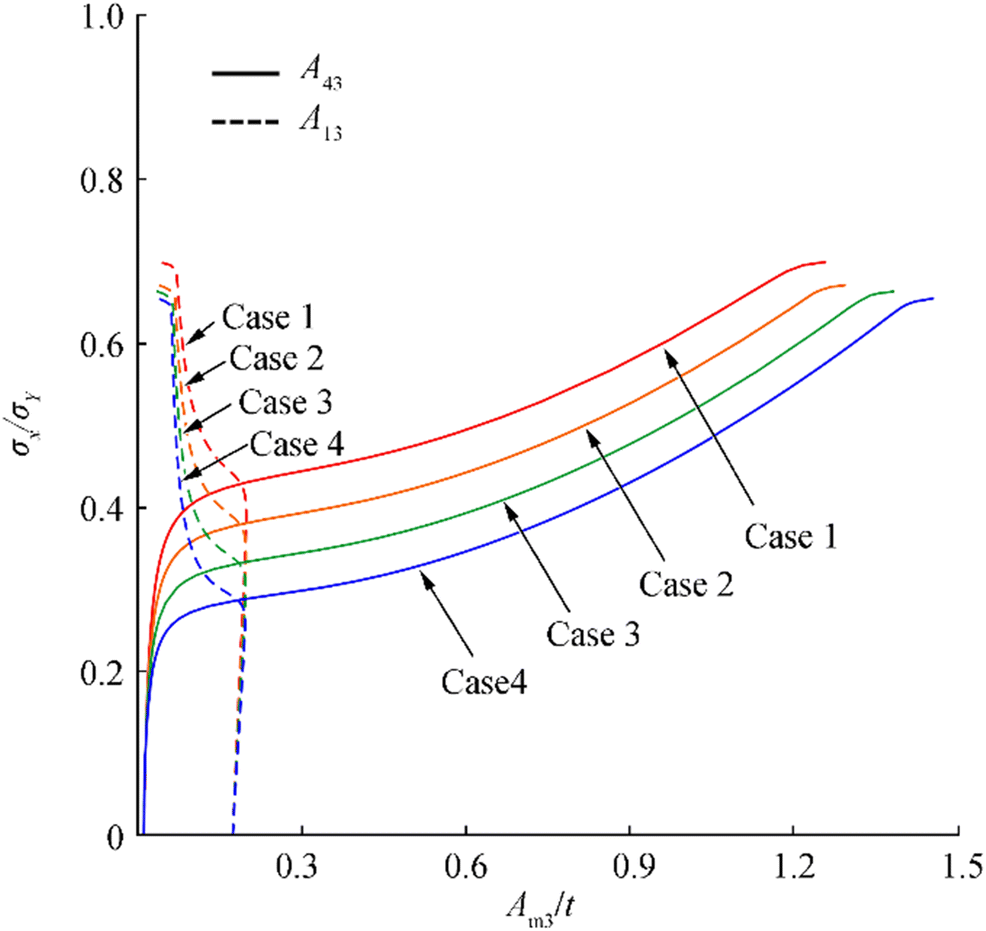
Figure  22  Deformed shape of the plate panel at the ultimate limit state observed from the experiment (Paik et al. 2020a)

Download: Full-Size Img

To examine the effects of nonuniform thickness on the plate ultimate compressive strength, a series analyses were conducted with varying the plate thickness as indicated in Table 4, where the average value of the plate thickness is the same as 10 mm. Figure 23 shows the ultimate compressive strength behavior of the plate panel obtained from the ANSYS finite element method analysis with varying the plate thickness. Figure 24 shows the ALPS/SPINE analysis results in terms of added deflection components until the ultimate strength is reached with varying the plate thickness. It is interesting to see that the global pattern of the plate deflection increases in the beginning as the axial compressive loads are increased, but it eventually decreases (and disappears) as the plate buckles so that the buckling mode becomes dominant.

Figure  23  The ultimate compressive strength behavior of the plate panel obtained from the ANSYS finite element method analysis

Download: Full-Size Img

Figure  24  The ALPS/SPINE ultimate compressive strength behavior of the plate panel in terms of the added deflection components

Download: Full-Size Img

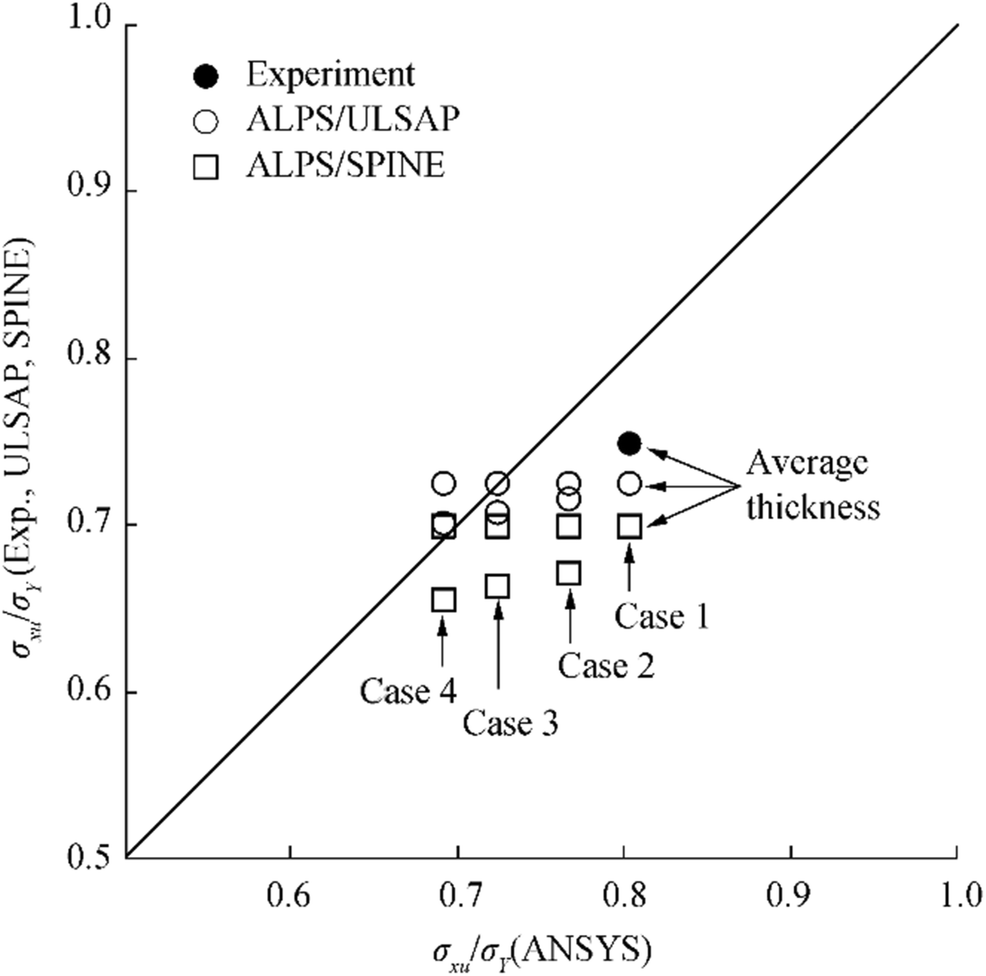
The ALPS/ULSAP predictions were also carried out, and they showed that the panels of the four cases all reached the ultimate limit state by the tripping failure (collapse mode V). Table 5 summarizes the ultimate strength computations together with the experimental result. Figure 25 compares the ultimate compressive strengths obtained from the case studies. The ultimate strength obtained by ANSYS is greater than the experiment by 7.2% for case 1 with t = t₁ = t₂ = 10 mm. It is found that the ANSYS ultimate compressive strength computations of the plate panel with nonuniform thickness decrease as the lower plate thickness t₂ decreases. For case 4 with a thickness difference of t₁ − t₂ = 3 mm, the reduction ratio of the ANSYS ultimate strength computation is 16.1%.

Figure  25  Comparison of the ultimate compressive strength between the analyses and the experiment for the plate panel with varying the thickness

Download: Full-Size Img

On the other hand, the analytical solutions for case 1 are smaller than the experiment by 3.2% for the ALPS/ULSAP analysis and 6.6% for the ALPS/SPINE analysis. By comparing with case 1 and case 4, the reduction rate of the ultimate strength is 3.3% for the ALPS/ULSAP analysis and 6.3% for the ALPS/SPINE analysis. It is obvious that the analytical solution of the panel ultimate strength decreases as the lower thickness decreases, but the reduction rate is much small in contrast to the ANSYS computations.

Based on the case studies, it is considered that the average thickness, i.e., $ {t}_{\mathrm{eq}}=\frac{t_1+{t}_2}{2} $ can approximately be used for the analytical approaches (e.g., ALPS/ULSAP or ALPS/SPINE) of plate panels with nonuniform thickness. The nonlinear finite element method can of course account for actual thicknesses directly.

6   Concluding Remarks

The aim of the paper was to investigate the effects of nonuniform thickness on the ultimate compressive strength of plate panels so that a recommended practice for defining a representative (equivalent) plate thickness was developed. Case studies were conducted by varying the plate thickness. Based on the studies, the following conclusions can be drawn.

1) The modeling techniques of welding-induced initial deflections and residual stresses in plate panels were presented in association with the measure data.

2) The ANSYS ultimate compressive strength computation for the plate panel with a uniform thickness of 10 mm (case 1) was greater than the experiment by 7.2%.

3) The ALPS/ULSAP or ALPS/SPINE ultimate compressive strength solutions for the plate panel of case 1 were smaller than the experiment by 3.2% and 6.6%, respectively.

4) According to the ANSYS computations, the ultimate compressive strength of plate panels with nonuniform thickness decreases as the lower thickness decreases or the thickness difference increases as far as the average thickness is kept constant.

5) The ALPS/ULSAP predictions showed that the plate panels of the four cases all reached the ultimate limit state triggered by tripping of the longitudinal stiffeners. This corresponds to the panel collapse mode of case 1 by the experiment.

6. The ALPS/ULSAP and ALPS/SPINE solutions show a similar trend to the ANSYS finite element method computations, but the reduction rate of the ultimate compressive strength is much smaller.

7. It is concluded that the average thickness for plate panels with nonuniform thickness can approximately be used as a representative for the ultimate compressive strength analysis by analytical methods which model the plate panels with uniform thickness.