Condition Assessment Techniques for Aged Fixed-Type Offshore Platforms Considering Decommissioning: a Historical Review
https://doi.org/10.1007/s11804-020-00181-z
-
Abstract
In this study, the technical papers on structural condition assessment of aged fixed-type offshore platforms reported over the past few decades are presented. Other ancillary related works are also discussed. Large numbers of researches are available in the area of requalification for life extension of offshore jacket platforms. Many of these studies involve reassessment of existing platforms by means of conducting pushover analysis, a static nonlinear collapse analysis method to evaluate the structure nonlinear behaviour and capacity beyond the elastic limit. From here, the failure mechanism and inherent reserve strength/capacity of the overall truss structure are determined. This method of doing reassessment is described clearly in the industry-adopted codes and standards such the API, ISO, PTS and NORSOK codes. This may help understand the structural behaviour of aged fixed offshore jacket structures for maintenance or decommissioning.Article Highlights• Condition assessment (or health monitoring) and life extension techniques are widely reviewed by considering decommissioning of offshore platforms.• The obtained outcomes may help to understand the structural behaviour of aged fixed offshore jacket structures for maintenance. -
1 Introduction
1.1 Offshore Jacket Platform
In the year 1947, in the coast of Louisiana off Gulf of Mexico (GOM), the first offshore oil and gas platform was born in about 5 m of water depth. Since then, offshore platforms have been used actively in the oil and gas industry for decades. The offshore oil and gas industry was having a steep growth thereafter, and it contributed to 14% of the global production in 30 years. By the year 2010, it increased to about 33% of the global production (Kurian et al. 2012). To date, about 10, 000 offshore platforms have been designed and installed throughout the world. The exponential growth of the oil and gas industry was triggered by the development in the energy-hungry post world war countries, the massive industrialisation processes in the 1970s and the liberalisation and the phenomenal growth in the economy of the BRICS countries (Brazil, Russia, India, China and South Africa) by the 1990s.
These factors contributed to the fast expansion and steady growth of the offshore oil and gas industry as well as the utilisation of the offshore platforms. An offshore platform is defined as a structure which has no fixed access to land and is required to stay safe in all weather conditions. Offshore platforms may be fixed to the seabed or floating. Almost all early offshore rigs were fixed-type platforms or fondly known as 'Jackets', mostly in shallow to intermediate waters, located in water depths of not more than 500 m. They are piled to the ground and support decks and/or functional platform facilities as shown in Figure 1. The design life of a typical jacket platform is between 20 and 30 years except for minimal production platforms with a 10-year design life. They are designed to provide support for the exploration and production facilities above the wave elevations. They need to perform under the service conditions which constitute of extreme and operational environmental conditions where the loads are generated from wind, wave and current.
 Figure 1 Typical shape of offshore jacket platform (Fadly 2011)
Figure 1 Typical shape of offshore jacket platform (Fadly 2011)Though offshore oil and gas industry has been active and grown rapidly since 1947, the design standards and guidelines for offshore jacket platform design were only made available in 1969 by publishing the first edition of API RP 2A (American Petroleum Institute Recommended Practice). Before 1969, there were no common design standards or guidelines available. The early platforms were designed based on the industry experience from onshore steel structure design. Since the introduction of the first edition of the API RP 2A document, there have been many revisions to the code over the past couple of decades. This has made the design basis and criteria of the platforms which were designed using the early edition obsolete by now (Mortazavi and Bea 1995).
In the south-east Asian region, the oil and gas industry blossomed in mid-1970s by the setting up of many national oil companies (NOCs). Today, the region is very active with offshore oil and gas exploration and production activities.
Profit sharing contract (PSC) is the term typically coined for the agreement between global players and NOCs for the development of the fields and facilities. Under the contract, NOCs own the assets, and the PSC partners develop and manage the fields and the facilities throughout the contract duration. Profit is shared between the parties with a predetermined ratio. Contract period varies from 20 to 25 years. After the completion of the contract, the platform assets will be returned to the owner, i.e. NOCs. The typical condition of the assets while it is handed over is aged, with high wear and tear and yet acceptably maintained.
In this technical review, the documented researches are grouped into categories based on the sequence of the current research direction. Large numbers of research studies are available in the area of requalification for life extension of offshore jacket platforms. Many of these studies involve reassessment of existing platforms by means of conducting pushover analysis, a static nonlinear collapse analysis method to evaluate the structure nonlinear behaviour and capacity beyond the elastic limit. From here, the failure mechanism and inherent reserve strength/capacity of the overall truss structure are determined. This method of doing reassessment is described clearly in the industry adopted codes and standards such the API, ISO, PTS and NORSOK codes.
1.2 Condition Assessment
Condition assessment or reassessment is defined as "the process of monitoring the integrity of a platform and assessing its fitness for purpose. It is known that remaining structural strength and fatigue performance should be checked by time based on well planned condition assessment procedure (Wong and Kim 2018; Mourão et al. 2019, 2020). In the process, changes in the platform function, estimates of environmental conditions, and physical condition through inspection are evaluated to better quantify the risk associated with its continued operation" mentioned by Banon et al. (1994). Typically, condition assessment is triggered by
1) Changes from original design (e.g. change of platform exposure level such as from unmanned to manned, modification to the facilities, subsidence due to extraction of hydrocarbon and increase of environmental conditions).
2) Damage of structural members due to major events such as dropped objects, small fire and/or blast, boat impact.
3) Deterioration of primary structural components due to ageing effect such as corrosion and fatigue crack.
4) Exceeding original design service life.
From the nonlinear collapse analysis, further progression into structure reliability analysis focusing on system safety is performed to evaluate the probability of failure of ageing platforms. Very few studies have reported on component reliability and component to system reliability. This is despite the fact that offshore platforms are designed on component basis rather than system. It has also been noticed that prior to the platform failure, depending on the degree of determinacy of the platform, several components would have yielded.
This section describes the reassessment procedure outlined in the codes, as practiced by the industry and the works of the researchers in this area. Most of the available codes and standards pay more attention to the design of new platforms. Hence, as mentioned by Nichols et al. (2006), reassessment guidelines recommended by current codes and standards are still immature in terms of its wide applicability and its resilience to variety of nature of design, operation and environment of the platforms. The API (2007) RP 2A WSD code, being the mostly utilised recommended practice (RP) among the industry players, prescribes common guideline for the reassessment of offshore jacket platforms in its Section 17 while the ISO (2007) code in its Section 24. The guideline is prepared from the collective industry experience gained to date as well as from the number of researches have been conducted.
Topside and underwater surveys as well as the soil foundation data are integral of the reassessment procedure. The recommended guide on the reassessment starts with platform risk screening, followed by design level analysis and finally ultimate strength analysis. The risk screening level comprises of platform selection, categorisation and condition assessment. Failure to fulfil this level will lead the platform to design and ultimate strength level analyses. The design level analysis has been described as simpler compared with the complex ultimate strength analysis. In addition, in the ultimate strength, the analysis begins with linear global followed by global inelastic analyses. In performing reassessment for requalification purpose, an ageing platform must demonstrate adequate strength and stability to survive ultimate strength loading criteria prescribed by the codes.
Many NOCs, typically follow own technical standards, which adopt the API guide for reassessment. The primary objective of the reassessment, according to the company, is to predict the strength performance against excessive load and insufficient strength. The reassessment procedure is crafted in such a way that the assessment difficulty increases as it moves from Risk Level to Global Ultimate Strength Analysis (GUSA) Level, i.e. from qualitative to quantitative approach. Risk-level assessment utilises factors influencing the likelihood of failure (LOF) and the consequence of failure (COF) of the platform to establish the risk level and map it into a 5 × 5 risk matrix. That is followed by design level assessment or the static in-place analysis. When a platform fails to comply with the acceptance criteria, load and resistance rationalisation which optimises the inherent conservatism in the initial design is practiced. Followed by reassessment in the form of GUSA is performed (Ayob et al., 2014a). Target reliability typically used in Malaysian industry practice is adopted form API RP 2A-WSD, with RSR value 1.32 for unmanned platform and 1.6 for manned platform. But the last decade has seen that Malaysian industry is looking to adopt ISO 19902 with regional annex for Malaysia. ISO code suggests that the platforms are designed for 100-year return period of load but reassessed for 10, 000-year return period or 1 × 10−4 probability of failure for manned platforms and 1000-year return period or 1 × 10−3 probability of failure for unmanned platforms. In the context of RSR, ISO code suggests RSR value of 1.85 for high-consequence platforms, i.e. manned platforms and RSR value of 1.5 for low-consequence platforms, i.e. unmanned platforms. Since the ISO code is based on probabilistic design, the environmental load factor adopted is 1.35, as has been prescribed by the ISO code, which is derived from studies performed in the Gulf of Mexico and North Sea. But metocean studies performed near Malaysian waters have shown that the environmental condition is more benign than Gulf of Mexico and North Sea. Hence, in a recent study, an environmental load factor ranging from 1.255 to 1.295 was developed, derived from similar target reliability between ISO and API RP 2A-WSD codes.
Since the evolution of the offshore jacket platform in 1947 in the coast of Louisiana off Gulf of Mexico (GOM), it has seen steady growth of the platform installation around the world estimated to be in the order of 10 000 units to date. By industry standard, a jacket platform design life is around 20 to 25 years. Hence, by 1970s to 1990s, many offshore platform installations in the North Sea and Gulf of Mexico were nearing their design life. This has prompted industry wide attention on integrity of the existing ageing jacket platforms. The industry looked into procedural development in reassessing those ageing platforms. Following that, many researchers have studied the field of reassessment of jacket platforms for life extension. In the past few decades, they have contributed to the development of the theoretical background of proper industry-wide accepted procedures and guidelines. Risk assessment and mitigation were the main focus of most of the work, apart from enabling the procedure to be scrutinised, refined and updated further. To their assistance, back then, when those ageing platforms were designed, insufficient location-specific environmental data and computing tools for efficient and easy structural analysis, lead to conservative design in terms of metocean design data and component-based design approach. This has implicitly helped the reassessment of ageing platforms for life extension. The inherent conservatism assisted in providing redundant and robust platforms which weathered the degradation which came with age.
Bea (1974) is among the pioneer in this area. He has devised reliability analysis in the reassessment process into five major parts, namely loading probabilities, resistance probabilities, reliability estimates, value analysis and design criteria. By the 1990s, the state-of-the-art jacket-type platform reassessment issues in GOM has been reviewed by Banon et al. (1994). This is because the number of ageing jacket platforms worldwide has increased, hence reassessment to determine their fitness for purpose has gained considerable attention from the oil and gas industry and the regulatory agencies worldwide. But the reassessment process is found to be time consuming and costly relative to the design of a new platform, as it requires multiple steps such as gathering of information on design and actual physical condition of the platform, modelling of all the significant damages found, structural analysis of the platform, calculation of the safety indices and identifying the necessary mitigation and repair plan. It is also associated with high degree of uncertainty.
Meanwhile, Mobil E & P considered reassessment exercise in the GOM in the 1990s as timely, as it has one third of its 250 platforms aged 20 years or older (Day, 1994). Reassessment is necessary as many of those platforms were, at that time, still having significant economic value due to improved reservoir engineering techniques and advanced secondary and tertiary oil recovery methods. The necessary tools, procedures and expertise needed to conduct reassessment for fitness for purpose is acknowledged available. However this conflicts with the earlier conclusion by Banon et al. (1994). This is because in 1992, API has set-up a task force to develop guidelines for reassessment of existing platforms and the task force members had published their work to be adopted by industry which may be referred to Krieger et al. (1994). The motivation for developing this reassessment guideline was the evolution of jacket platform design practice over the past couple of decades, resulting in new platform design standards getting stringent than those older ones. The concerns raised by the regulating agencies in the USA, among others, are the adequacy of the older platforms to face occurrence of extreme environmental events like hurricane Juan in 1985, the Loma Prieta earthquake in 1989 and hurricane Andrew in 1992. Case studies utilizing the developed procedure were done successfully by Craig and Digre (1994) on three US West Coast production platforms. Following that, API officially issued the guideline as draft Supplement 1 for both the WSD and LRFD, RP2A-LRFD (API 1993), versions of API RP 2A in 1995 and subsequently has included in the new edition of API RP 2A in 1997, which also forms the basis for the analogous guidance in ISO 13813-2 for fixed steel platforms. Details may be referred to Moan (2000). In addition, damage assessment techniques for fixed and offshore platforms subjected to hurricane may be referred to Energo (2007, 2010).
From then onwards, many researchers, i.e. Tromans and van de Graaf (1994), Visser (1995), Sturm et al. (1997), Bea (2000), Hansen and Gudmestad (2001), Capanoglu and Coombs (2009), Bao et al. (2009), Gening and Ruiguang (2010), Håbrekke et al. (2011), Solland et al. (2011), Ayob et al. (2014b), Kurian et al. (2014a, b), George et al. (2016), Kim et al. (2017b) and Mohd Hairil et al. (2019), have utilised the reassessment guideline from the standards to demonstrate the safety of platforms by considering ageing effects as well as the low-risk potential for environmental damage from the operation of those platforms. A study related to the decommisioned offshore platforms converted in offshore wind turbine is also recently introduced by Alessi et al. (2019).
Petruska (1994) has adopted the newly launched code reassessment guide on a 1950 vintage shallow water platform in GOM to assess its fitness of purpose to extend its life span. Visser (1995) has studied reassessment of jacket structures in Cook Inlet, Alaska, utilizing the newly released API guideline on reassessment. Condition survey and reassessment audit of several ageing high-consequence platforms which were designed and installed in the mid-1960s were conducted.
Following Hurricane Roxanne which rocked Bay of Campeche in 1995, PEMEX initiated a program to reassess and requalify the affected platforms according to API guidelines. The findings showed that majority of the platforms would not qualify for the continued service without very expensive and extensive remedial work. Thus, Bea (2000) has conducted study on how risk assessment and management (RAM), a process developed in 1970s, is applied to the requalification of PEMEX platforms. Bea studied the results from field tests to verify loading and capacity analytical models and characterise the bias and uncertainty in the models. Among the biases discovered include wave attenuation due to the soft seafloor soils and extreme condition wave-current directionality.
Banon et al. (1994) reviewed the state-of-the-art jacket reassessment issues in GOM as a result of an effort by ASCE Committee on Offshore Structural Reliability. With the increased usage and confidence in the reassessment method, many researchers studied the effect of controlling variables on the requalification of existing platforms. Dalane and Haver (1995) studied reliability assessment of an existing jacket platform in 70-m water depth at North Sea exposed to reservoir subsidence due to hydrocarbon extraction activities. The safety of the platform is quantified in terms of wave-in-deck due to reduced air gap. Environmental loading, statistical and modelling uncertainties are quantified for the reliability analysis accounted for in the study. Hansen and Gudmestad (2001) also have looked into reassessment of existing jacket platform in North Sea, subjected to wave-in-deck due to subsidence as well as from revised environmental criteria.
Couple of researchers reviewed the development of available methods for safety requalification of jacket platforms. They gave complete picture of the methods, both deterministic and probabilistic, under extreme loading and also on the treatment of the resistance. Key issues like behaviour uncertainties and sensitivities, validation and benchmarking of the methods were examined. Highlighted also are the number of technical and philosophical issues which need to be addressed to increase the benefits from system reliability applications in design and reassessment of offshore jacket platforms as stated by Moan (2000) and Onoufriou and Forbes (2001).
Nichols et al. (2006) addressed the current issues where the continued use of ageing jacket platforms requires reassessment but the code recommended guides are inadequate. Hence, reassessment procedures, tools and technology initiative improvements are imperative. In this work, the challenges and probable solutions in managing the long-term integrity of the ageing platforms were described. The details on how those solutions are assisting in the ongoing development of Carigali Structural Integrity Management System (CSIMS) were presented as well. The adopted process is in line with the recent development of standalone API RP 2SIM, for the structural integrity management (SIM) of existing structures (Westlake et al. 2006).
Contribution to further development in the theoretical background of the procedures for life extension of existing jacket platform is made recently. This includes work on system strength parameters and the use of probabilistic methods in reliability analysis. Criterion for reserve strength ratio, damage strength ratio and reserve freeboard ratio has been suggested. Probabilistic predictive Bayesian method has been proposed for evaluating structural uncertainty for better decision making. The objective was to reevaluate the risk in order to decrease the failure probability (Ersdal 2005). In the Gulf of China, Bao et al. (2009) utilised ultimate strength system reliability analyses and parameters sensitivity to study the effect of parametric variables on the reliability of platform. Elsewhere, stochastic response surface is adopted by Kolios (2010) in the reassessment for better representation of parametric uncertainty. The developed method is simple and efficient, where it allows for reassessment in the form of individual design blocks, opposite to available methods which require deep understanding of mathematical expressions. Global ultimate strength assessment (GUSA) is performed to assist efficiently in identifying and comprehending the failure mechanism and safety indices of platforms that undergo reassessment exercise. Thus, correctly defining risk level and relevant type of required mitigation actions, if necessary for continued use (Ayob et al. 2014a, b).
2 Static Nonlinear Collapse Analysis
In this category, the finite element static nonlinear collapse analysis in obtaining ultimate strength of jacket platform is presented. Almost all the works reported on the reassessment of ageing jacket platforms utilised this method. There are two general approaches. Majority of the researchers adopted the first approach, i.e. incremental load factor for the horizontal environmental load application. The analysis is used in the system-based structural reliability analysis (SRA) to determine platform excess strength capacity fondly known as reserve strength ratio (RSR). RSR is the measure of ductility, and it gives the ultimate strength of a platform. Since all jacket platforms are designed as per their component linear elastic behaviour, the overall available reserve strength in a structural system is made up of combination of the entire components. Static nonlinear collapse analysis is also called as pushover analysis.
RSR compares the collapse capacity with the design capacity to establish excess strength beyond design strength. According to API WSD, the design strength value is determined from the 100-year return period metocean environmental loading. RSR is typically obtained from all directions and the lowest value is devoted as the most critical value from the critical direction. Thus that lowest value will be taken as the platform reserve strength ratio by ISO (2007). The reserve strength ratio (RSR) is defined as in Eq. (1) (Bolt et al. 1996).
$$ \mathrm{RSR}=\left(\mathrm{Ultimate}\ \mathrm{Strength}\right)/\left(\mathrm{Design}\ \mathrm{Strength}\right) $$ (1) According to Krawinkler and Seneviratna (1998) prior to the analysis, the finite element structural stick model in two or three dimension is developed. All the structural members, joints, hinges and its linear and nonlinear response characteristics are appropriately modelled. Gravitational vertical loads are applied as the initial step. Followed by the concurrent environmental lateral loads in chosen direction are applied to the model. The lateral loads are factored incrementally until the platform has been pushed to a specific target displacement or until collapse. The analysis utilises stiffness matrix approach in analysing the member stresses and strains. During the analysis, the program further selects load sub-step sizes, by determining when the next stiffness change occurs and ending the sub-step at the event. This is followed by the modification of the structure stiffness and reanalysis as the next step until the entire load is being applied by Asgarian and Lesani (2009). Further detail into the specific workflow of the analysis could be found in the application manuals of the specific types of computer software such as USFOS and SACS.
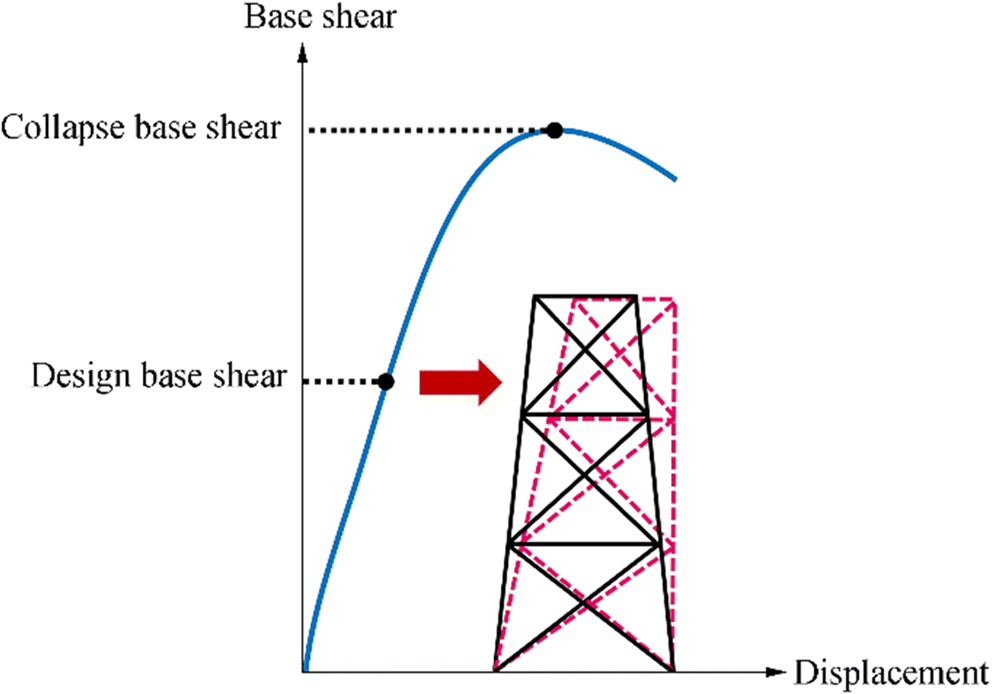
Conventional design of jacket platforms presumes linear elastic behaviour for all relevant analysis limit states as well as perfectly rigid joints. Consequently, members are checked based on linear-elastic theory, and no yield or buckling is permitted. As a result of this approach, conservatively, the jacket collapse is considered equal to first member failure (Golafshani et al. 2011). Figure 2 presents typical static nonlinear collapse analysis procedure. Here, with the gravitational loads already applied, the environmental load is applied horizontally on the jacket structure until it collapses.
The second approach as reported by Golafshani et al. (2011) is called the incremental wave analysis (IWA), in which the wave height is increased instead of the environmental load factor. This method has also been reported elsewhere by Nichols et al. (2006). It is claimed that the typical practice is imperfect as incrementally increasing the wave load factor alone does not depict the real situation. The current nonlinear collapse analysis does not account for the wave-in-deck loading condition where in reality, higher wave load comes from higher wave height, which eventually induces wave-in-deck scenario.
Traditionally, the offshore platforms, just like the land-based structures, are designed by component-based linear elastic method of analysis including the limit state design checks which are formed using empirical expressions. However, since the accidental and natural disasters like Piper Alpha in the North Sea and Hurricane Andrew in GOM, many efforts were made into understanding the nonlinear behaviour of the platforms. This has prompted the code in 1970s to 1980s to put requirements for design and reassessment for accidental and nonlinear loads. The design checks allow for large plastic straining, buckling, plastic mechanism, etc., but not the collapse or overturn of the platform. Hence, Skallerud and Amdahl (2002) mentioned that several efforts were made with the support of major oil and engineering companies, to develop nonlinear analysis programs, which are capable of demonstrating the strength reserves offered by ductile steel material and inherent load redistribution capability in statically indeterminate structures.
Hellan (1995) studied nonlinear collapse analyses and nonlinear cyclic analyses in ultimate limit state design and reassessment of offshore jacket platforms. The aim was to develop an assessment methodology based on system strength rather than component strength and to demonstrate the feasibility of the method. As part of the work, a computer program called USFOS was developed. Six North Sea jacket platforms were analysed according to the developed procedure. The occurrence of the system collapse with first member failure and cases of system strength in excess of first member failure were identified. Probabilistic Monte Carlo simulation was performed with parametric study on yield strength and initial imperfections. Small variation was found in the collapse strength due to variables sensitivity. Latin hypercube sampling method was used to generate random sample vectors. PROBAN software was used to generate statistical inputs and for processing the results of the statistical study.
Prior to that, an extensive study on the development and application of numerical finite element in collapse analysis of plates and truss shaped tubular structures was conducted by Mreide et al. (1986). This work was founded from the previous works of several studies, i.e. Ueda and Rashed (1975), Aanhold (1983) and Rashed (1980), which paved the way for the progressive collapse analysis.
In early 1990s, several researchers have statistically verified the predicted ultimate strength against observed storm damages at GOM by conducting pushover analysis on partially damaged jacket platforms to identify the failure sequence and ultimate collapse load. This is kind of first attempt to rationally evaluate the situation from hurricane damages. Here the extreme hurricane load is predicted probabilistically by adopting new wave theory for extreme random wave kinematics and the effect of current blockage, both introduced in the 1980s. Parametric study was also conducted by van de Graaf and Tromans (1991) to identify magnitude and direction of the load that caused the damage.
To evaluate and validate the performance of the collapse analysis in reality, the Frames project was initiated in 1987. Four units of 2-bay X braced large-scale tubular frames were collapse tested. The test set-up was designed to exhibit different modes of failure allowing for various aspects of reserve and post-failure residual strength to be examined. The project gave an insight into the role of redundancy and failure of tubular joints in a framed structure. This type of work in nature and scale had not been investigated before. A computer program, called SAFJAC, was developed for the nonlinear pushover analysis of framed structures with an aim to accurately represent both the material and geometric nonlinearities. From the study by Bolt et al. (1994), the frame test data from the project correlated well with the experimental results using the developed program. Following this, during the 1990s, many computer programs were developed by several researchers with the aim to improve computational efficiency and to reduce cost. Billington et al. (1993) mentioned that though the structural analysis methodology has advanced considerably over the years, still there exist variable capacities of nonlinear software and their validation with physical tests. Yet, the results from those analyses are well accepted without any prejudice.
Bea and Mortazavi (1996) have developed a simplified assessment method for system strength called ultimate limit state limit equilibrium analysis (ULSLEA). ULSLEA generates shear capacity depth profile based on simplified assumptions, and compares it with storm loading profile. Vannan et al. (1994) presented a simplified ultimate strength assessment procedure, called simplified ultimate strength analysis (SUS) which provides a lower bound estimate of the actual strength utilizing linear collapse analysis instead of nonlinear analysis. The method reasonably predicts the actual failure modes but has some limitations.
Studying parametric effects in collapse analysis, soil resistance has been analysed for wave and current loading (Mostafa et al. 2004). System reserve strength ratio from variations in water depth, topside and metocean loadings has shown significant affection (Pueksap-anan 2010). Study on sensitivity of metocean values on reliability of existing platforms suggested pile soil interaction is to be considered in the pushover analysis to capture foundation failure mechanism (Zaghloul 2008).
Ersdal (2005) has performed pushover analysis to assess the system strength of existing jacket platforms in North Sea. Multiple safety ratios such as RSR, structural redundancy (SR), damaged strength ratio (DSR) and residual strength factor (RIF) were presented as indicators to the level of excess capacity contained by existing platforms. Nevertheless, RSR from the static nonlinear collapse analysis is widely adopted to demonstrate adequate excess strength of existing platforms to withstand specified loading conditions. Apart from RSR, base shear at the bottom of the platforms during collapse could be used to demonstrate the strength of the existing platforms. Figure 3 shows the computation of base shear at different levels of static nonlinear collapse analysis.
3 Structural Reliability Analysis
Until the 1970s, structural engineering was dominated by deterministic approach where the design codes stipulated characteristic resistance and load properties based on past experiences. With the inherent high safety factors which were believed to produce absolute safety, the same was revisited with strings of accidents and their serious consequences. Hence, the work on probabilistic approach with structural reliability analysis gained traction to quantify and control the risks available within a structural system. Offshore jacket platforms demand for high attention in structural reliability analysis perspective as they are placed at random environment with serious consequences for failure. Therefore, probabilistic approach became a necessity (Guenard et al. 1984; Meng et al. 2020). The probabilistic approach was first introduced into the design code by adopting multiple safety factors accounting for various load and resistance uncertainties encountered in the structural design. The factors are determined corresponding to their relative importance (of the reliability of the structure) of the uncertainty it accounts for and following the overall reliability level. The probabilistic approach is also applicable in the reassessment of existing platforms.
The ability of a structure to provide fitness for purpose, under different conditions, i.e. operational, extreme, accidental, fatigue, etc., for a specific time period is, in principle called the structural reliability. The performance of the structure can be calculated mathematically, as the probability of failure, which occurs when the limit state function portraying the evaluated condition is violated. The violation of the performance function is measured in terms of probability of failure, reliability index and/or return period of the event.
Reliability analysis is categorised into four levels. Use of characteristic values alone places the analysis in level I while inclusion of standard deviation, σ and coefficient of correlation (COV) places it at level II. Addition of cumulative distribution function (CDF) puts it in level III. Finally, level IV consists of analysis of engineering economics with uncertainty (Fadly 2011).
Figure 4 shows typical representation of probability density function (PDF) of resistance, R and load, L variables in reliability computation. The central safety margin depicts the reliability of a structural system considering both the characteristic load and resistance parameters. The beginning and end points of the safety margin represent both the central moment (mean, μ) of load and resistance density functions respectively. Probability of failure is the intersection of both density functions as shown shaded in the figure.
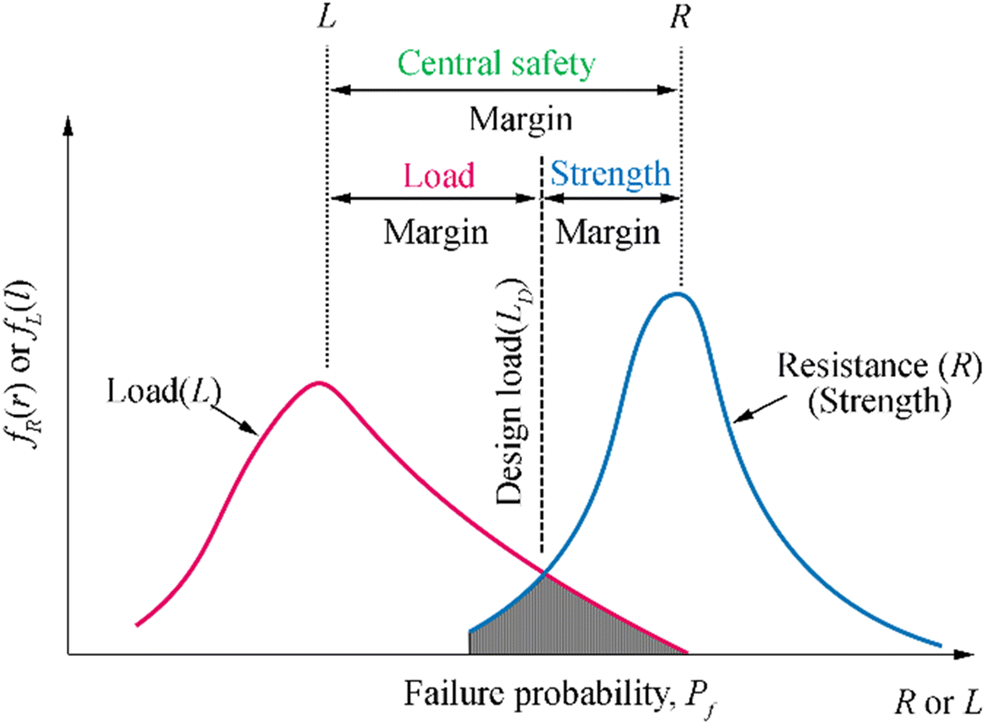 Figure 4 Theoretical representation of probability of failure (Moses and Stahl 1979)
Figure 4 Theoretical representation of probability of failure (Moses and Stahl 1979)In mathematical terms, probability of failure is indicated as the violation of limit state function. Typical limit state function and probability of failure are shown in Eqs. (2.1) and (2.2) respectively.
$$ G=R-L $$ (2.1) $$ {P}_f=P\left[G\left(R,L\right) \lt 0\right] $$ (2.2) where R is the resistance, L is the load, G is the limit state function and Pf is the probability of failure. Here, G < 0 indicates the failure region, G > 0 indicates the safe region and G = 0 as the failure surface. Hence, Pf is accepted as the probability of the limit state function less than zero, i.e. an event where the load exceeds resistance.
For the statistical representation of extreme variables in reliability computation, extreme values distributions such as Gumbel, Fretchet and Weibul are the typical theoretical distributions, commonly adopted to model the uncertainty parameters. These distributions are suitable for the use of maximum of infinite number of extreme events. They represent the maximum intensity by capturing the upper tail characteristics of the distribution. In offshore engineering, type 2 Weibull cumulative distribution function (CDF) is well adopted by many to represent the environmental load uncertainty. The required statistical parameters are the scale and shape parameters of the distribution. This distribution is suitable for rare events of interest such as maximum wave height, wind and current velocity. Typically, wave load is considered as probabilistic, while current and wind loads are deterministic. This is supported by many works in the literature. Recent study on joint density characteristics of measured and Hindcast metocean data in Malaysian waters using Weibull distribution for its extreme event analysis also has verified this (Mayeetae et al. 2012).
Since the preliminary work on structural reliability started in the 1940s to 1950s by Freudenthal, Pugsley and others, and followed by actual works encompassing basic philosophy and some simple calculation procedures were carried out later, there have been extensive and far reaching developments to date (Baker 1998). In the offshore industry, the early works by Bea (1974), Marshall (1979) and Fjeld (1978) have demonstrated the applicability and possible benefits of using reliability analysis as the tool for design and reassessment decision making. Following that several methods in conducting reliability analysis were outlined. The methods could be used in pre-design stage to perform comparative parametric analysis as well to perform overall reliability analysis under extreme conditions (Guenard et al. 1984). That was in accordance with the National Research Council's DIRT (Design, Inspection and Redundancy Triangle) conference, held in 1984, called for expansion of new reliability analysis techniques. Following that, many studies were undertaken to meet the oil industry needs at that time. The gap between the use of probabilistic representation of loads, materials and design criteria and full structural system-level interactions and implications were identified and addressed by Cornell (1987). In addition, extensive study on new methods for reliability analysis was undertaken.
Karamchandani (1990) studied more realistic modelling of nonlinear behaviour of truss and frame-type structures. Member failure sequence leading to system failure was looked into by analysing the union of intersections of member failure events to obtain structural failure event. Branch and Bound method and FORM were utilised in this study. Sensitivity of failure probability due to distribution parameters such as mean and variance of random variables was studied. A new method which could be used with wide range of simulation techniques such as Monte Carlo simulation, latin hypercube sampling and importance sampling was developed for estimating the sensitivity. A different approach using FORM and SORM to estimate the sensitivities was also developed. This work garnered the attention of many researchers till today with regard to the methods to compute structural reliability in component and system levels.
Procedural wise, Tromans and van de Graaf (1994) devised a reliability assessment practice based on Hindcast data and pushover analysis with the help of probabilistic method. This was in the aftermath of Hurricane Camille in GOM, to obtain comparative reliability index and probability failure of jacket platforms affected by the hurricane. They concluded that reliability technique can be confidently applied to the problem of optimisation of design and reassessment. Following that, a method that utilises Hindcast data to generate extreme load distribution function in the load model and resistance model was derived by Efthymiou et al. (1997).
From the mid 1990s, many researchers have looked into more diversified procedures and methods to conduct reliability analysis, mainly for calibration works of limit state design codes. BOMEL Ltd. (2002) has utilised response surface method in performing reliability analysis for calibration of ISO code for North Sea region. Similar methodology was also utilised by many other researchers in many different regions in the development of regional specific environmental load factors (Zafarullah 2013). These works have referred mainly to the works of Moses (1987) who was involved in the development of calibration of API LRFD design code for jacket platforms in the GOM.
Frieze et al. (1997) has also referred to the works of Moses, for his reliability analysis method utilizing response surface for jacket and jack-up platform performance comparison in North Sea. Onoufriou and Forbes (2001) have summarised the available methods for reliability analysis covering both deterministic and probabilistic, under extreme loading condition for design and reassessment cases. Ersdal (2005) has referred to the works of Heideman (1980) whom has provided a simplified expression for the horizontal wave load in load functions of reliability analysis limit state function. He has developed a probabilistic model to establish the annual failure rate of any platform undergoing reassessment. Kolios (2010) in his work, with an objective to provide alternative procedure for reliability analysis, has developed normal and adaptive response surface algorithms that combine FORM/ SORM with linear and quadratic stochastic response surface approximation. He utilised simulation results from finite element collapse analysis combined with numerical reliability procedure via multivariate (quadratic) polynomial regression to compute reliability indices in component level. Lee (2012) has developed finite element–based system reliability analysis framework and method named FE-SRA and B3 respectively.
The proposed framework allows computation of failure probabilities of general system events with respect to design parameters based on component-level finite element reliability analysis. Meanwhile, the developed method helps in identifying critical system failure sequences efficiently and accurately. Thus, it brings significant reduction in computing time and simplicity in the procedure.
In Malaysian waters, in the early years of operation, adopting API WSD code, with a very minimal site specific data and statistics on load and resistance parametric values, platforms that were designed and installed often have the issues ranging from redundancy to overdesigned components. Currently, in managing the integrity issues related to these ageing platforms, industry utilises pushover analysis coupled with simplified structural reliability analysis (SSRA) methodology. SSRA method was jointly developed with DNV in 1999 utilizing 13 jacket platforms in Baram and Balingian fields in Sarawak region. It is a simplified and quick approach to the typical comprehensive SRA. The analysis utilises predetermined covariance and bias values adopted from SRA for a particular type of structure from the same operating region. From the analysis, reliability indices are obtained and subsequently compared with code-specified target reliability indices to make decision. As an alternative to the typical practice of utilizing SSRA, a recent study attempted to establish statistical relationship between reliability index and return period from Malaysian regional specific data (Fadly 2011). From the work, correlation graphs among the reliability parameters with high magnitude of correlation coefficients were established for the region. Comparison between SSRA computed and statistically analysed reliability parameters were done. Table 1 presents the adopted bias and covariance values.
Table 1 Typical bias and covariance values utilised in SSRA (Fadly 2011)Variable Description Bias Covariance Load Dead load 1 0.1 Live/functional load 1 0.2 Environmental load To be fitted 0.3 Resistance Members 1.1 0.15 Joints 1.25 0.2 Piles 1.1 0.2 Soil/foundation 1.30 or 1.13 0.2 In theory, two types of reliability analysis methods are available namely the simulation and analytical-based methods (Melchers 1999). Monte Carlo simulation (MCS) is the main example of simulation-based method while the other method is the moment-based method such as first-order reliability method (FORM). Monte Carlo simulation has been applied in many fields of science to generate random sampling sets of uncertain variables. Typical limit state functions utilised in the reliability analysis are the nonlinear type and consist of both normal and nonnormal basic variables (Cossa 2012). Hence, literature typically suggests using FORM for evaluation of the reliability indices. FORM also has been applied in the development and calibration of the load and resistance factors design codes such API RP2A LRFD and ISO 19902 (Zafarullah 2013; Moses 1987). It is typically used in structural optimisation practices to arrest uncertainties in reassessment parameters which lead to achieving a cost effective structural integrity management practice (Onoufriou and Frangopol 2002; Moses 1997; Toğan et al. 2010).
Describing further on Monte Carlo simulation, it is widely used, robust, easy-to-use and produces high accuracy provided large number of samples is utilised. Yet, it requires significant number of analyses to be performed for achieving quality approximation of values. It helps to approximate the probability of an event from a stochastic process. Many researchers have utilised MCS in offshore engineering as an alternative to evaluate the safety of the structures (Kolios 2010; Cossa et al. 2012; Kurian et al. 2013a). Though it is believed to give crude values, yet it is well adopted due to its simplicity (Veritas 1992). The method generates virtually, large number of random design variables based on statistical distribution of the variables. Later, it will be checked with limit state function against failure. Following a negative value from the evaluation of the limit state function, the structure is considered has failed. This process is repeated for a large number of times and the probability of failure is estimated as the number, of failed samples divided by the total number of simulations.
The number of random simulations generated highly affects the accuracy of this method. Furthermore, the accuracy declines when the probability of failure is estimated to be insignificant. In addition, the computation time increases for small probability of failures (Veritas 1992). Frieze et al. (1997) mentioned that Monte Carlo simulation produces noisy approximation of probability which becomes difficult to use for gradient-based optimisation compared with FORM. For cases of large number of random variables or for a very low probability of failure magnitude, the analysis requires large number of sampling sets, thus increases the computational time and effort (Kolios 2010). Nevertheless, in the literature the method has been widely used for computation of complicated integral of probability of failure using the outputs from multiple computational experiments.
Meanwhile, the FORM has evolved since Cornell in 1969 proposed mean value first-order second moment (MVFOSM) reliability method. The MVFOSM method is applicable for linear and nonlinear limit state function equations. Yet in case of high non linearity, this method is not suitable. This method fails to be invariant with different mathematical equations of similar question (Yu 1996). This method is not further explained as it has not been utilised in this work.
Hasofer and Lind (1974) proposed improvement to the Cornell approach and called their method as HL method. This method produces better results for nonlinear functions as it takes design point as the most probable point (MPP) for the approximation of limit state function instead of mean value. Multiple iterations are able to be run to converge the results. Distributions of variables are utilised in obtaining reliability indices. This method has limitations in nonconvergence issues in certain cases. It only caters for normally distributed random variables. To arrest these, Hasofer Lind-Rackwitz Fiessler (HL-RF) method was adopted. This is an extension of HL method, where the reliability indices could be obtained for the nonnormally distributed variables. The iteration issue for the nonconvergence problem was solved. Detailed analytical description of all these methods are found in Choi et al. (2007).
In summary, the building block of FORM is the HL-RF iteration method which enables the transformation of random variables. The limit state function and its gradients are evaluated in the standard normal space. The design point (MPP) is obtained and for each design point evaluated, the convergence is checked and repeated until convergence is achieved. Finally, the reliability index is calculated as the shortest distance from origin to the MPP.
The origin of HL-RF method is also from the MVFOSM method. In this method, the main variables are the mean and standard deviations; distribution is unnecessary. Taylor series expansion is used to linearise the limit state function as the expansion of limit state equations based on the mean value. From the HL-RF method, utilizing the mean and standard deviations, considering the variables as independently distributed, approximate limit state function at mean value is given by Eq. (3.1).
$$ \overset{\sim }{g}(X)\approx g\left({\mu}_x\right)+\nabla g{\left({\mu}_x\right)}^{\mathrm{T}}\left({X}_i-{\mu_x}_i\right) $$ (3.1) where μx = (μx1, μx2……μxn)T, ∇g(μx) is the gradient of g evaluated at μx as shown in Eq. (3.2).
$$ \nabla g\left({\mu}_x\right)=\left[\frac{\partial_g\left({\mu}_x\right)}{{\partial_x}_1},\frac{\partial_g\left({\mu}_x\right)}{{\partial_x}_2},\dots ..{\frac{\partial_g\left({\mu}_x\right)}{{\partial_x}_n}}^{\mathrm{T}}\right] $$ (3.2) The mean value, $ {\mu}_{\overset{\sim }{g}} $, of the approximate limit state function, $ \overset{\sim }{g}(X) $, is shown in Eq. (3.3).
$$ {\mu}_{\overset{\sim }{g}}\approx E\left\{g\left({\mu}_x\right)\right\}=g\left({\mu}_x\right) $$ (3.3) where variances [g(μx)] and [ ∇ g(μx]) are zero. Hence, the standard deviation, $ {\sigma}_{\overset{\sim }{g}} $, of the limit state function $ \overset{\sim }{g}(X) $ is shown in Eq. (3.4).
$$ {\sigma}_{\overset{\sim }{g}}=\sqrt{\mathrm{Var}\overset{\sim }{g}(X)}= \\ \sqrt{{\left[\nabla g{\left({\mu}_x\right)}^{\mathrm{T}}\right]}^2\mathrm{Var}(X)}={\left[{\sum}_{i=1}^n{\left(\frac{\partial_g\left({\mu}_x\right)}{{\partial_x}_i}\right)}^2{{\sigma^2}_x}_i\right]}^{1/2} $$ (3.4) Thus, the reliability index, β, is given by Eq. (3.5),
$$ \beta =\frac{\mu_{\overset{\sim }{g}}}{\sigma_{\overset{\sim }{g}}} $$ (3.5) The formulation for reliability index above is similar to the linear limit state function where reliability index is defined geometrically as the distance from the failure surface depicting mean margin of safety. Typically, considering R and L as the independent (noncorrelated) and normally distributed resistance and load variables respectively, with central tendency, i.e. means, μR and μL, and standard deviations (dispersion about the mean), σR and σL, reliability index, β, is defined as in Eq. (3.6). Meanwhile, the relationship between reliability index and probability of failure, Pf, is shown in Eq. (3.7) (Choi et al. 2007).
$$ \beta =\frac{\mu_G}{\sigma_G}=\frac{\mu_R-{\mu}_L}{\sqrt{{\sigma_R}^2+{\sigma_L}^2}} $$ (3.6) $$ {P}_f=1-\Phi \left(\beta \right)=\Phi \left(-\beta \right) $$ (3.7) where Φ() is the standard normal cumulative distribution function (CDF), μG is mean of the limit state function and σG is the standard deviation of limit state function. Here, the correlation coefficient between R and L is zero, i.e. non correlated variables. If the variables are correlated, the standard deviation of the limit state function would be as in Eq. (3.8).
$$ {\sigma}_G=\sqrt{{\sigma_R}^2+{\sigma_L}^2-2{\rho}_{RL}{\sigma}_R{\sigma}_L} $$ (3.8) In some instances, time-independent joint probability density functions have to be considered in probabilistic models for reliability analysis. For that purpose, in simplistic manner, the probability of failure, Pf, can be written as in Eq. (3.9).
$$ {P}_f=\int \dots {\int}_{g\ \left(\right) \lt 0}\left({x}_1,{x}_2,\dots, {x}_n\right)d{x}_1{dx}_2\dots {dx}_n $$ (3.9) where fx(x1, x2…xn) is the joint probability density function for the basic random variables of x1, x2…. xn and g() < 0 is the failure region. The direct integration of the above is complicated; hence, the application of moment-based approximate methods such as FORM is used to evaluate the limit state function. Typically, FORM is adopted in cases where the limit state function is linear or when there are uncorrelated normal load/resistance variables or when the nonlinear limit state function is presented by first-order (linear) approximation with equivalent normal variables.
In cases of high nonlinearity in the limit state function, approximation techniques above contain drawbacks in terms of the accuracy of the reliability index. Thus, linear mapping of basic variables into a set of normalised and independent variables is adopted. This approach utilises the design point, i.e. the MPP as the approximation of the limit state function replacing the mean and variance values. The standard normalised random variables for resistance and load are given in Eq. (3.10):
$$ \hat{R}=\frac{R-{\mu}_R}{\sigma_R},\kern0.5em \hat{L}=\frac{L-{\mu}_L}{\sigma_L} $$ (3.10) where μR and μL are mean values of random variables of resistance and load respectively, and σR and σL are standard deviation of random variables of resistance and load respectively.
The transformation of the limit state surface g(R, L) from original coordinate system into standard normal coordinate system $ \left(\hat{R},\hat{L}\right) $ is given in Eq. (3.11).
$$ \hat{g}\left(\hat{R},\hat{L}\right)=\hat{R}{\sigma}_R-\hat{L}{\sigma}_L+\left({\mu}_R-{\mu}_L\right)=0 $$ (3.11) In geometrical form, the shortest distance from origin in the $ \left(\hat{R},\hat{L}\right) $ standard normal coordinate system to failure surface of $ \hat{g}\left(\hat{R},\hat{L}\right) $ is equal to the reliability index, $ \beta =\hat{O}P $* = $ \left({\mu}_R-{\mu}_L\right)/\sqrt{\sigma_R^2+{\sigma}_L^2} $ as shown in Figure 5. Here, the point P* is the MPP.
 Figure 5 Geometrical illustration of reliability index (Choi et al. 2007)
Figure 5 Geometrical illustration of reliability index (Choi et al. 2007)Typically for independent and normally distributed variables, the failure surface is a nonlinear function as given in Eq. (3.12)
$$ g(X)=g{\left({x}_1,{x}_2,\cdots {x}_n\right)}^{\mathrm{T}} $$ (3.12) Hence, the variables are transformed into standardised forms by adopting Eq. (3.13),
$$ {u}_i=\frac{x_i-{\mu_x}_i}{{\sigma_x}_i} $$ (3.13) where μxi and σxi are the mean and standard deviation of xi respectively. The values of mean and standard deviation of standard normal distribution are 0 and 1 respectively. Thus, the reliability index is taken as the shortest distance from the origin to the failure surface as given in Eq. (3.14) and illustrated in Figure 6.
$$ \beta =\min {\left({U}^{\mathrm{T}}U\right)}^{{}^{1}\!\!\diagup\!\!{}_{2}\;} $$ (3.14) 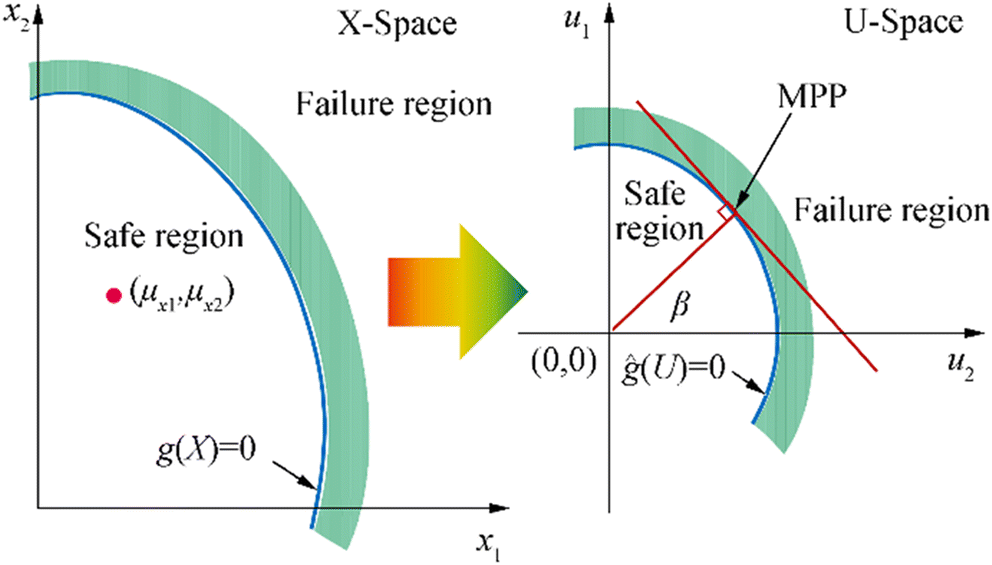 Figure 6 Mapping of failure surface from X space to U space using HL method (Choi et al. 2007)
Figure 6 Mapping of failure surface from X space to U space using HL method (Choi et al. 2007)From the above theoretical computational methods to find reliability index, it is observed that they are utilizing a solution of a constrained optimisation problem into the standard normal U space. Several algorithms were developed by many previously to perform these optimisation procedures. The Finite Element Reliability Using MATLAB (FERUM) which is an open source shell program originated from University of California, Berkeley, (Bourinet 2010) is utilised by many to develop reliability algorithms. The shell program contains probability density function resources which enable random variables to be transformed from its original physical space (X space) to an equivalent standard normal distribution space (U space). It helps to ease the iteration/optimisation process to transform the random variables in finding the design point, i.e. MPP until the convergence is reached and reliability indices are calculated. Here, in analysing the time-independent joint probability density functions, it is replaced with Nataf counterpart specifying marginal distributions and Gaussian correlation structure among the random variables. This in return produces library rich with probability density models.
3.1 Component Reliability Analysis
In the offshore jacket platform reassessment, violation of limit state function occurs when a structure exceeds a particular limit state; hence, the jacket is unable to perform as desired. The main limit state under typical concern is the ultimate limit state which is relevant to collapse of structure or failure of component. Jacket platforms typically have high redundancy and numerous different load paths such that failure of one member/component is unlikely to lead to catastrophic structural collapse. Yet, in minimally braced structures and/or critical members (leg members especially), if a component is damaged or the platform experience extreme loads, it would not have sufficient alternative load paths to redistribute the loads. Hence for component reliability, member internal stresses are obtained from structural analysis.
Handful of studies were reported on component reliability of jacket platforms (Baker 1998; Karamchandani and Cornell 1992; Shabakhty 2004; Chin 2005; Kolios 2010; Lee 2012; Morandi et al. 2015). The aim of most of the works was to evaluate the stresses in each component and compare against the code-determined functions. Most works utilised WSD code as the code produces generally conservative values than the other limit state-based codes. It produces less conservative design values when the stresses due to environmental loading are significantly higher than the gravitational loadings (Zafarullah 2013). The magnitude of the stresses and corresponding strengths determine the failure probability.
Typically, the material yield strength and dimensions of tubular members govern the strength characteristics while the gravitational and environmental loads control the load characteristics of tubular members. In a jacket platform member stress evaluation, typically the gravity load dominates the leg members while the environmental load dominates the brace members (Frieze et al. 1997). The gravitational load consists of the self-weight of the platform and its appurtenances as the dead load and live loads. As for the strength, the yield strength uncertainty dominates the failure probabilities of tubular legs and brace members. Axial tension or compression and bending stresses due to yielding of material (from local or global buckling) and hydrostatic stresses are the common types of stresses found affecting any members.
Typical jacket platform tubular members mostly experience combined compression and bending stresses. Resistance model for tubular members consists of variables of member geometry such as diameter and wall thickness, and material properties such as the yield strength (Zafarullah 2013). The adopted acceptance criteria are the nonviolation of the code prescribed limit state functions. Following that the failure probability of each component are determined. The statistical parameters from a recent local study are given in Table 2. The study was conducted for the purpose of establishing environmental load factors for the regional annex of ISO limit state code calibration.
Table 2 Resistance model variables (Zafarullah 2013)Variable Statistical Parameter Diameter (mm) Distribution Normal MC 1.001 COV 0.0018
(Brace < 1000 mm)
0.0014 (leg > 1000 mm)Wall Thickness (mm) Distribution Normal MC 1.024 COV 0.016 Yield Strength (MPa) Distribution Normal MC 1.230 COV 0.050 Tensile Strength (MPa) Distribution Normal MC 1.183 COV 0.039 In modelling the load and resistance uncertainty for component reliability, the ISO code calibration adopted approach was widely utilised. The uncertainty coefficients depend on the statistical parameters of the basic variables and the applied stresses. Their distribution is also to be identified by Zafarullah (2013). The typical model uncertainty (i.e. bias) coefficient definition is shown by Eq. (4).
$$ {\mathrm{Model}\ \mathrm{uncertainty}}_{\left(\frac{Xm}{Xw}\right)}=\frac{\mathrm{Actiual}\ \mathrm{value}}{\mathrm{Predicted}\ \mathrm{value}} $$ (4) In performing component reliability, the load model consists of gravitational and environmental loads. For gravitational load, its statistical values are obtained from operator from the available structural model, design reports and drawings. The statistical parameters for the environmental load model are determined from platform specific metocean data obtained from operator. These data then approached with statistical analysis using type 2 Weibull CDF, adopted from literature. For determining the resistance model, the typical basic variables for resistance of jacket platform such as member geometry and material properties are sought after. Recently, a study on extensive data from a leading local fabrication yard has established the resistance model and resistance model uncertainty values to be used locally for component reliability (Kurian et al. 2013b). In a separate work, the load model uncertainty values have been established (Zafarullah 2013).
3.2 System Reliability Analysis
Different than component reliability, system reliability manages the uncertainties affecting the overall reliability of a structural system. System reliability of jacket platforms has been studied by many researchers with multiple objectives (Bea 1974; Guenard et al. 1984; Cornell 1987; De 1990; Karamchandani 1990; Tromans and van de Graaf 1994; Onoufriou and Forbes 2001; Chin 2005; Ersdal 2005; Melchers 2005; Kolios 2010).
The analysis is commonly utilised for reassessment, code calibration and optimisation purposes. There are few studies reported on component to system reliability using techniques such as Branch and Bound method and enumeration method.
Offshore jacket platforms are generally comprising of highly redundant structural members; hence, failure of any single member, in principle, would not cause the failure of the overall structure. The reserve capacity between the first member failure to the overall structural failure is, generally, significant (De 1990) except for structures with minimally braced members or having critical members. In structural reliability, redundancy is often defined as the conditional probability of system failure, given the first failure of any member. Meanwhile, the ability of a structure to survive the extreme load demand in different damaged conditions is defined as robustness (Cornell 1987). Robustness and redundancy are inherent in any offshore jacket platforms due to multiple design demand such as loading conditions during load-out, transportation and installation. These provided system effects which bring inherent reserve in the strength of typical offshore jacket platforms.
Guenard et al. (1984) studied the application of developed reliability methods in the early 1980s on system reliability of offshore platforms under extreme metocean condition. Similar study has been conducted elsewhere (Nordal et al. 1987). Improvements were made to the available methodology by including more realistic behaviour of softening/hardening effects instead of plainly assuming strain independent post-limit behaviour of the tubular members (Gierlinski et al. 1993). Later, new methods were developed by applying more realistic modelling of nonlinear behaviour on truss and frame type of structures. Member failure sequence leading to system failure by analysing the union of intersections of member failure events to obtain structural failure event was developed utilizing Branch and Bound method and FORM (Karamchandani 1990). These were referred by many to be adopted with other possible simpler techniques to identify system reliability utilizing component reliability analysis of jacket platforms (Kolios 2010). Many also have studied comprehensively on the available reliability approaches for integrity management of ageing jacket platforms (Onoufriou 1999; Onoufriou and Forbes 2001; Onoufriou and Frangopol 2002). System reliability in the form of SSRA is adopted (Fadly 2011).
Generally, from the nonlinear collapse analysis, RSRs are obtained from 8 or 12 directions of a platform, depending on its number of legs. That is followed by system reliability analysis to evaluate the system reliability indices. RSR helps to demonstrate structure capacity sufficiency and stability against overloading (ISO 2007). Reliability indices obtained from system level analysis are compared with target reliability indices from the codes. The minimum requirement for probability of failure outside of GOM region is 1 × 10−4 for high-consequence platforms and 1 × 10−3 for low-consequence platforms. While, the minimum value of RSR is 1.60 for high-consequence platforms and 0.80 for low-consequence platforms (API 2007).
According to PTS (2010), the minimum value for RSR is 1.50 for high-consequence platforms and 1.32 for low-consequence platforms. These limits are conservative compared with the API prescribed limits. They were established from the risk assessment and acceptable consequence of failure (Ayob et al. 2014a, b). Further detail on the definition of the platform consequences, reference should be made to the platform exposure categories in the appropriate codes. The details of the procedure and methodology for the development of acceptance criteria and target reliability for an example region, Arabian Gulf, may be referred to Amer (2010).
In a recent work on the development of system reliability analysis procedure, Ersdal (2005) has provided a simple probabilistic model function between RSR and reliability indices. The system limit state function, G, is given in Eq. (5).
$$ G=\mathrm{Resistance}-\mathrm{Load}=\mathrm{Load}\times \mathrm{RSR}-\mathrm{Load} $$ (5) where the Load is the design environmental load for 100-year extreme condition that consists of wave height, current velocity, wind speed or combination of any of these. In the above function, a simplified expression of the wave load model (F) following the earlier work by Heideman (1980) is presented. The expression, as given in Eq. (6), utilises wave height (H) and current velocity (u) as the significant environmental parameters.
$$ F={C}_1{\left(H+{C}_2u\right)}^{C_3} $$ (6) Here, C1, C2 and C3 are the curve fitted parameters based on the calculated platform specific loadings. Similar expressions also have been presented elsewhere which will be further explained later.
4 Uncertainty Analysis
Structural reliability analysis is based on probability theory and its treatment to different uncertainties involved. Probability theory treats the likelihood of occurrence of an event and eventually quantifies the uncertainties of random events. Structural reliability analysis is sensitive to uncertainty modelling (Mark et al. 2001). In offshore jacket platform reassessment, probability theory is utilised to manage the risks involved due to the uncertainties from the design parameters. This is because the offshore jacket platforms are placed in random environment and have high failure consequences. Uncertainties are dealt with by taking into consideration random variable parameters of load and resistance. Uncertainty modelling is the first important step in reliability analysis of jacket platforms.
Load and resistance are random variables. Uncertainties due to randomness in applied loads, structural material resistances and errors in computer models are always present and must be considered in structural reliability computation. Load and resistance uncertainty analysis is done utilizing available basic information about the random loads and resistance variables. Meanwhile, modelling uncertainties are analysed utilizing the physical models that predict the load effects and the structural responses. Structural analysis of offshore platforms is also subjected to uncertainties. Strength evaluations are not exact, true values deviate from idealised computer model (Baker 1998).
Uncertainty reflects lack of information. Hence, the randomness typically will be showcased by utilizing the probability density function (PDF) or called frequency function with mean (central tendency), standard deviation and lower and upper tail values of the density function. A PDF represents relative occurrence/frequency of certain events for random variables. Randomness in load and structural resistance variables is identified through either field data collection or from survey of literature, and fitting the data utilizing probability distribution functions to generate statistical parameters such as mean, standard deviation and coefficient of variation. Figure 7 shows a typical density function which presents the centre of the curve as the most probable point while the tail regions as the less probable points in the occurrence of an event. Interval Information is used in situation where incomplete or imperfect data available and this is defined within an interval of known lower and upper bounds (Choi et al. 2007).
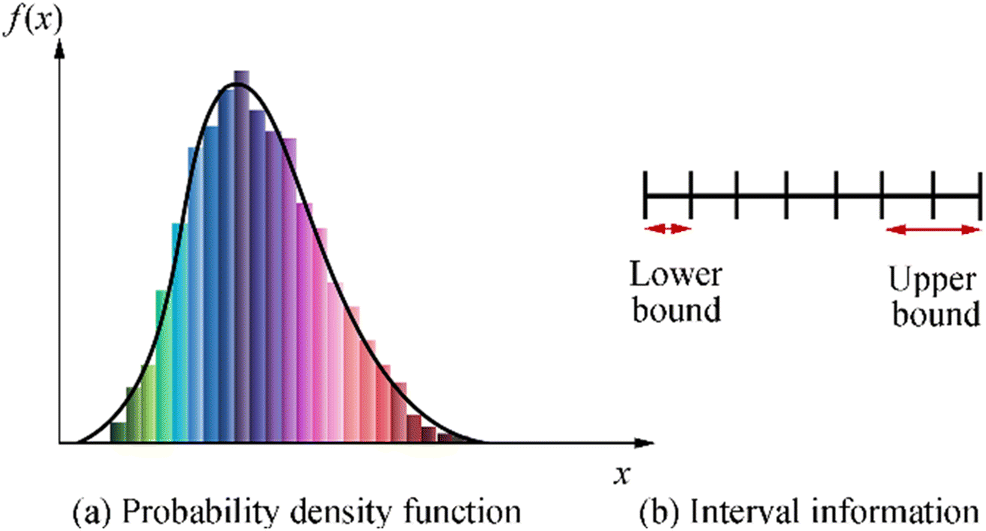 Figure 7 Probability density function and interval information (Choi et al. 2007)
Figure 7 Probability density function and interval information (Choi et al. 2007)Statistical uncertainty is considered in the structural reliability analysis by assessing mean, variance/ standard deviation/ coefficient of variation (COV) and probability distribution for the available random variables. Bias factors have been utilised as modelling error in reliability analysis upon determination of ratio between model predictions and actual test results. Bias is defined as mean over nominal value. Design parameter variation due to uncertainty is able to be modelled and utilised with available probabilistic methods provided reliable statistical parameters can be determined from statistical data. Several analytical and simulation methods are available to address the uncertainty in structural analysis using probability theory.
In structural reliability analysis, commonly adopted probability distribution functions for random variables are the extreme, normal and lognormal types. Rare events such extreme load variables require the extreme types of distributions like Weibull and Gumbel; meanwhile for structural resistance variables, the normal and lognormal distributions are typically fitted in the literature. Wind load which carry insignificant effect to the responses of offshore structures is treated deterministically in most instances, except for very wind sensitive structures.
In system reliability load model computation, to probabilistically arrest the wave loading uncertainty, an uncertainty factor, α, is adopted (Dalane and Haver 1995; Ersdal 2005). The uncertainty factor is normally distributed with mean value 1.0 and COV 0.15. Meanwhile, type 2 Weibull distribution is mostly adopted in the literature to perform the environmental load model computation. Maximum wave height, Hmax, has been utilised typically for the load model computation. Hmax is the design wave for particular platform site for 100-year extreme condition. This maximum load is the most critical variable which could occur during the entire service life of a platform. ISO and API codes insist utilizing 100-year extreme condition of wave parameter for the design and assessment of jacket platforms.
Meanwhile the resistance model in the system reliability limit state function is described as the platform specific design loading multiplied by the platform RSR. Similar to the wave loading uncertainty factor, α, the resistance model uncertainty factor, β, is adopted from the literature. The uncertainty factor for resistance model is normally distributed with mean value 1.0 and COV 0.10, in respectively (Efthymiou et al. 1997; Ersdal 2005).
In the limit state code calibration exercise, for the component reliability analysis, researchers from many regions have undertaken load and material resistance uncertainty studies. The randomness in material comes from geometry and properties such as diameter, thickness, length, yield strength and tensile strength. Zafarullah (2013) has conducted environmental load calibration study for Malaysian waters by collecting material data from materials test report and performing field measurements at an ISO certified leading local fabrication yard. The collected data were used to compute the statistical parameters for the random resistance variables. Similarly, for the modelling of the loading uncertainty, ISO code equations and randomly generated environmental load parameters using type 2 Weibull distribution function from sample platform data, were utilised to obtain member internal stresses and extrapolated return period values of environmental parameters respectively.
Zhang et al. (2010) studied several types of uncertainty models for reliability analysis of an existing offshore jacket structure affected by marine corrosion. They compared and studied the results in terms of numerical efficiency adopting probabilistic models such as pure probabilistic, interval modelling, fuzzy methods and imprecise probabilities. The models were utilised to find upper bound for the failure probability due to the corrosion effect. Kolios (2010) has developed a probabilistic component reliability analysis procedure by arbitrarily utilizing stochastic variables from literature in validating and computing the reliability indices.
5 Response Surface
In this category, the response surface method which has been adopted by many to apprehend the inherent uncertainty in the load and resistance variables represented in the limit state function of reliability analysis is presented. This is considered among the nonintrusive stochastic approaches deployed in the domain of reliability analysis (BOMEL Ltd. 2002; Chin 2005; Kolios 2010). Among the other stochastic approaches are Importance Sampling, Latin Hypercube Sampling, Adaptive Response Surface and so on (Fjeld 1978; Olufsen et al. 1992; van de Graaf et al. 1996; Zhang et al. 2010; Mousavi and Gardoni 2014). In formulating limit state functions utilizing the load and resistance models, response surface method is helpful in generating respective load and resistance coefficients which are eventually utilised in producing response surface equations. Later, these equations are integrated into the limit state functions which are then used in the reliability analyses. According to Shabakhty (2004) in offshore structure reliability analysis, the uncertainty in random variables may have significant effect on the response of platform and therefore affect the probability of failure. Hence, response surface is suitable to be utilised to incorporate the random variables implicitly in the limit state function. Literature claims that response surface method is useful in obtaining parametric representation of environmental loads on jackets. The method evaluates implicitly the limit states at predefined number of points and fits a function to those points. This function is then utilised in reliability analysis (Petrauskas and Botelho 1994). The method has been utilised as an alternative to physical transfer function, using random variables in explicit multivariate functions. It is claimed that the approach is able to reduce the number of structural analyses required for probabilistic analysis (Chin 2005). The effective use of response surface depends on the proper selection of sampling points (Shabakhty et al. 2003). In the method, mean and standard deviation of basic random variables are utilised in enhancing the efficiency and accuracy of the simulations (Bucher and Bourgund 1990). A modified procedure using vector projection approach which provides better results may be available by Kim and Na (1997).
Many researchers agreed that response surface approximates well the limit state functions using simple and explicit mathematical polynomial functions of random probabilistic variables (Shabakhty 2004; Kolios and Brennan 2009). In their works, detailed explanation on the selection and justification of quadratic polynomial function is given. The coefficients of the functions are obtained from fitting the functions to multiple arbitrary member and system responses from the conducted structural analyses. Random variables are simulated using simple algorithm and the response surface function is fitted upon the simulation results. Chin (2005) has categorised response surface into two-level model, i.e. global and local responses prior to computing structural reliability indices in component and system reliability analyses. This approach is able to relate the environmental parameters acting on the structural system such as wave height and current velocity to the member internal stresses. This approach has been adopted by many previously in performing response surface analysis to obtain the system and component responses from the applied environmental loading (Lebas et al. 1992; Karunakaran et al. 1993; Cassidy et al. 2001). Lebas et al. (1992) compared the results from the response surface with results from direct simulations and verified the results.
Global response surface relates the environmental load to the global responses of the structure. Wave height and associated period, current velocity and wind speed are among the typical environmental parameters. The structure base shear and overturning moment are the typical global responses. The local response surface relates the global responses to the local responses namely member internal stresses such as axial and bending stresses of each component. The general limit state functions for the global and local responses are given in Eqs. (7.1) to (7.4) respectively.
$$ G=f\ \left(\mathrm{Wave},\mathrm{Current},\mathrm{Wind}\ \mathrm{etc}.\right) $$ (7.1) $$ g=f\left(\mathrm{BS}\ \mathrm{or}\ \mathrm{OTM}\right) $$ (7.2) where BS = base shear and OTM = over turning moment
$$ {\mathrm{internal}\ \mathrm{stress}}_x=a{\left(\mathrm{BS}\right)}^2+b\left(\mathrm{BS}\right)+c $$ (7.3) $$ {\mathrm{internal}\ \mathrm{stress}}_y=a{\left(\mathrm{BS}\right)}^2+b\left(\mathrm{BS}\right)+c $$ (7.4) where G and g = global and local limit state functions respectively, BS = base shear, OTM = overturning moment and a, b and c are the response surface coefficients. For the internal stresses here, base shear (BS) is used arbitrarily.
In the development of LRFD limit state codes for API, response surface method was utilised to fit the response surface coefficients from multiple simulation of wave height random variable (Moses 1987). Equation (8) was suggested to obtain the environmental load effect from the multiple wave height simulations.
$$ W=A{H}^{\alpha } $$ (8) where W = environmental load, H = wave height and A and α are the response surface coefficients.
Similar approach has been adopted in the ISO limit state code calibration study for North Sea and in a typical jacket structure reliability analysis (Efthymiou et al. 1997). Similar approach has been adopted locally due to its simplicity, in the environmental load factor calibration exercise for the adaptation of the limit state code (Cossa 2012). Adopting from the study by Heideman (1980), Petrauskas and Botelho (1994) have proposed to adopt additional environmental parameter, i.e. current velocity together with the wave height. They believed that the addition of current will better represent the inherent uncertainty in the environmental loading criteria. The suggested response surface function is as in Eq. (6).
Tromans and Vanderschuren (1995) have suggested little complicated response surface analysis method. They studied extreme base shear and mud-line overturning moment responses due to multiple environmental criteria. Hence the function is complicated and contains many unknown coefficients to be fitted from response surface analysis.
In case of any additional environmental parameter is to be included in the response surface function, the approach by Cossa (2012) as in Eq. (9) could be adopted.
$$ w=a{H}^2+ bH+c{V}_c^2+d{V}_c+e{V}_w^2+f{V}_w+g $$ (9) where W = environmental load, H = wave height, Vc = current velocity, Vw = wind speed and a, b, c, d, e, f and g are the response surface coefficients obtained from nonlinear Least Mean Square fitting method with 95% confidence level and R2 value above 0.90.
In Kolios (2010), detail review of the available stochastic methods is given. He advocated for stochastic expansion tools such as Karhunen-Loeve (K-L) expansion and polynomial chaos expansion (PCE) as an efficient approach to treat uncertainties through series of polynomials in computing reliability. But having to analyse complex system such as jacket platforms, simulation techniques such as stochastic response surface method (SRSM) is much preferred. SRSM approximates limit state function using simple and explicit mathematical functions utilizing relevant random variables. The functions are typically simple polynomials with coefficients obtained by fitting the response surface function to a number of sample points from computation of responses of the system and component. Later, algorithms that combine FORM with linear and quadratic response surface approximation technique were developed to estimate the reliability indices.
6 Failure Path
In some instances, for statically determinate structures, the reliability of individual members portrays the reliability of the whole structure as the failure of one member will lead to the structure failure. However, this is not the case for highly redundant structures. The failure of one or few members would not necessarily result in the collapse of the structural system as the system will contain numerous failure paths. From the random nature characteristic, some failure paths are more likely to occur than others. The probability of occurrence of those failure modes and their method of determinations are the basis for the system reliability through failure path analysis.
6.1 System Reliability
Due to typical complicated nature of structural system, direct exact calculation of system reliability is therefore impossible. The structural system is idealised to simplify the analysis process to reduce calculation difficulties, but with utmost care so that the model is able to reflect the real structure properties. The reliability of the system can be estimated by taking into account a specific number of failure modes or failure paths, and combine them in complex reliability system.
A structural system usually can be modelled as a series system, parallel system or combination of both (Mustaffa et al. 2018). A series system shown in Figure 8 (1) is a system in which failure in a structural element will lead the whole system collapse. Meanwhile for parallel system presented in Figure 8 (2), failure in a member does not usually lead to total system collapse. For complex structures illustrated in Figure 8 (3), it is assumed that the structural system is a series of parallel systems, in which each parallel system represents a failure model (Nikolaidis et al. 2014).
To determine the system probability and reliability index, the probability of failure of each component in each failure path (parallel systems) is determined. The probability of each failure path is then evaluated before proceeding to the total system probability of failure.
6.2 Reliability Bounds
Approximate techniques in the form of bounding methods are available to determine the probability of failure of a system event. Simple Bound and Ditlevsen Bound are adopted by many researchers (Kolios 2010; Karamchandani and Cornell 1992; Chin 2005; Kim et al. 2013b).
6.2.1 Simply Bound
Boolean variables are utilised to perform this technique. Consider S to be a system with n failure elements, e1, …., ei, ei + 1, en. For each failure elements, ei, i = 1, …, n, a Boolean variable ei is defined by Eq. (10.1),
$$ {e}_i=\left\{\begin{array}{c}1,\kern0.5em \mathrm{if}\ \mathrm{the}\ \mathrm{failure}\ \mathrm{element}\ \mathrm{is}\ \mathrm{in}\ \mathrm{a}\ \mathrm{non}\ \mathrm{failure}\ \mathrm{state}\\ {}0,\kern0.5em \mathrm{if}\ \mathrm{the}\ \mathrm{failure}\ \mathrm{element}\ \mathrm{is}\ \mathrm{in}\ \mathrm{a}\ \mathrm{failure}\ \mathrm{state}\kern1.25em \end{array}\right. $$ (10.1) For series system, the Simple Bounds is given by Eq. (10.2),
$$ {\max}_{i=1,\dots, n}P\left({e}_i=0\right)\le {P}_{fs}\le 1-{\prod}_{i=1,\dots, n}\left(1-P\left({e}_i=0\right)\right) $$ (10.2) The lower bound in Eq. (10.2) is equal to the exact value of probability of system failure, Pfs, if there is full dependence between all elements and the upper bound corresponds to no dependence between any pair of elements. When the probability of failure of one element is predominant in relation to the other failure elements, the probability of failure of series system is approximately equal to the predominant probability of failure and the gap between the upper bound and lower bound is narrow. However, when the probabilities of failure are in the same order, the Simple Bound is wide.
For parallel system, the Simple Bound formula is given by Eq. (10.3),
$$ {\prod}_{i=1,\dots, n}P\left({e}_i=0\right)\le {P}_{fp}\le \underset{i=1,\dots, n}{\min }\ P\left({e}_i=0\right) $$ (10.3) The lower bound in Eq. (10.3) is equal to the exact value of Pfp if there is no dependence between any pair element and the upper bound corresponds to full dependence between all elements.
6.2.2 Ditlevsen Bound
Since the range provided by the Simple Bound can be very wide, Ditlevsen Bound provides a narrower bound. For series system, it is given by Eqs. (11.1) and (11.2),
$$ {P}_{fs}\le {\sum}_{i=1,\dots, n}P\left({e}_i=0\right)-{\sum}_{i=2,\dots, n}{\max}_{i \lt j}P\left({e}_i=0\cap {e}_j=0\right) $$ (11.1) $$ {P}_{fs}\ge P\left({e}_1=0\right)\\ +{\max}_{i=2,\dots, n}P\left({e}_i=0\right)-{\sum}_{j=1,\dots, i-1}P\left({e}_i=0\cap {e}_j=0,0\right) $$ (11.2) The gap given by Eqs. (11.1) and (11.2) are usually much smaller than the gap provided by the Simple Bound. Nonetheless, the equations require the calculation of the joint probabilities and these calculations are not trivial. They usually require numerical technique. For this reason, the Simple Bound is preferred. With Simple Bound, though the gap between the bounds might be wide, yet it still can provide crude indication of the reliability of the problem. In the literature, many researchers adopted similar approach that when dealing with this sort of difficult situations, a much simpler approach is preferred (Kolios 2010).
6.3 Failure Modes and System Reliability Index
From above, it has been established that a complex structure contains large number of possible failure modes. Including all the possible failure modes in the analysis is an infeasible and inefficient task, since some of the failure modes would have low probability of occurrence. Thus the literature contains many methods to determine system reliability by considering only dominant failure modes with higher probability of failure. Such a method is the Event Tree, or called as Failure Tree. An Event Tree is a diagram showing dominant possible paths of failure, which include sequence of failure members and their probability of failures (Kim et al. 2013b).
Shao and Murotsu (1999) had discussed variety of methods to determine dominant failure modes. They categorised the methods into three types, enumeration approach, plasticity-based approach and simulation-based approach. In Enumeration Approach, Failure Trees are generated by extending the sequence of elements failure step by step until the system collapses. Examples of the approaches are incremental loading method (pushover or collapse analysis) and Branch-and-Bound method. In incremental loading method, the failure modes are generated by incrementally factoring the load to cause sequence of members' failure. The method is deterministic and can obtain crucial failure paths with few repetitions of structural analyses. However, with this method not all dominant failure paths can be determined. The Branch-and-Bound method on the other hand, employs probabilistic search algorithm. It searches possible failures mode by considering their probabilities of occurrences. The Branch and Bound method is theoretically rigorous and requires high computing power.
Plasticity-based approach is found based on the assumption that plastic behaviour is present in the structural materials. The analytical formulation of plastic mechanism can be determined by lower-bound and upper-bound theorem. Among the methods using this approach is β unzipping method and linear programming (LP) method. Simulation-based approach uses simulation methods such as Monte Carlo simulation to generate possible failure modes. This method is computationally expensive.
Apart from the above, Shao and Murotsu (1999) have proposed a method called Selective Searching Technique which is a compromise method combining deterministic and probabilistic approaches. They used Genetic Algorithm (GA) to search for dominant failure paths. β value is used to determine search directions and fitness function. Kim et al. (2013b) have further improved the method by eliminating the use of fitness function, and instead introduced outward searching techniques to determine dominant failure modes. By this way, all critical failure paths can be identified without eliminating potential chromosomes that may lead to system collapse.
To accurately determine the failure paths, considering the sequence of members' failure, post-failure behaviour of the failure elements need to be modelled correctly. Typically, the failure elements are regarded as either perfect brittle or perfect ductile. For a brittle element, it will become ineffective immediately after failure, and loses its load-bearing capacity. However, for a ductile element, it continues to carry the load upon failure. Meanwhile a semi-brittle model as shown in Figure 9 has been widely used. According to the model, during load application, the member force increases elastically to its capacity till failure. Upon failure, if the axial deformation in the element is increased beyond its failure value, the element force abruptly drops to a fraction, φ of its pre-fail capacity. For this, a deterministic value of φ = 0.4 was used for elements failing in compression while φ = 1.0 for elements failing in tension. To conclude the model, it assumes ductile failure behaviour by maintaining the failure load (or the full capacity) upon failure for elements failing in tension and an abrupt drop to 40% of the capacity when elements failing in compression (Karamchandani 1990).
 Figure 9 Component post failure behaviour model (Kolios 2010)
Figure 9 Component post failure behaviour model (Kolios 2010)The elastic load–bearing capacity of the elements is obtained from AISC code formula with safety factors removed. The resistance is further reduced by 15% to account for the neglected moments induced by the frame action (Nordal et al. 1987). For compression capacity, Rc Eqs. (12.1) to (12.3) are applicable.
$$ {R}_c=0.85{f}_y{A}_x\left(1-\frac{{\left(\frac{kl}{r}\right)}^2}{2{C}_c^2}\right) $$ (12.1) $$ {C}_c=\sqrt{\frac{2{\pi}^2E}{f_y}} $$ (12.2) $$ r=\frac{\sqrt{d_o^2+{d}_i^2}}{4} $$ (12.3) where fy = yield strength, Ax = element cross-sectional area, E = modulus of elasticity, r = radius of gyration, d = moment of inertia, k = effective length factor and l = length of element.
For tension capacity, RT presented in Eq. (12.4) is applicable.
$$ {R}_T=0.85{f}_y{A}_x $$ (12.4) where fy = yield strength and Ax = element cross-sectional area.
7 Other Approaches
In this category, other ancillary approaches adopted in this work for the benefit of validation, sensitivity and parametric evaluations are presented. These approaches were utilised on the developed method to study the effect it has on the results.
7.1 Monte Carlo Simulation
The Monte Carlo simulation has been applied in many fields of science to generate random sampling sets of uncertain variables. It helps to approximate the probability of an event from a stochastic process. Many researchers utilised this technique in offshore engineering as an alternative to evaluate the safety of the structures (Kolios 2010; Cossa et al. 2012; Kurian et al. 2013a; Yoo et al. 2020). Though it is believed to give crude values, yet it is well adopted due to its simplicity (Veritas 1992). The method generates virtually, large number of random design variables based on statistical distribution of the variables. Later it will be checked with limit state function against failure.
Following a negative value from the evaluation of the limit state function, the structure is considered failed. This process is repeated for a large number of times and the probability of failure is estimated as the number, of failed samples divided by the total number of simulations. The number of random simulations generated highly affects the accuracy of this method. Furthermore, the accuracy declines and when the probability of failure is estimated to be insignificant. In addition, the computation time increases for small probability of failures (Choi et al. 2007).
7.2 Bayesian Updating
Due to the high uncertainty in the reassessment of existing jacket platforms, probabilistic structural reliability analysis is imperative. And the availability of additional information during the operation tends to reduce the uncertainties especially the uncertainties coming from the load. Hence, utilizing available additional information, computed probability of failure could be enhanced by means of statistical techniques.
Utilisation of the platform prior experience to enhance the outcome of a reliability analysis is feasible. When an existing platform has succeeded in overcoming the extreme load conditions throughout its design lifetime, the confidence level in the platform increases. For an existing jacket platform, its strength and robustness have been proven acceptable from its survival from the experienced environmental and operational loadings throughout its life. Statistical updating methods have been utilised by many researchers (Niu et al. 1990; Ersdal et al. 2003; Moan et al. 2000; Madsen et al. 1989; Melchers et al. 2003; Straub and Papaioannou 2014) to enhance the quantified probability of failure by considering the probability of survival. It is based on Bayes theorem which utilises combined knowledge of statistics and experience to update the probability of occurrence of an event shown in Eq. (13.1). Bayesian Updating method numerically evaluates the posterior probabilistic model given that the prior model and the likelihood function of observation data are available. It requires one to update a prior distribution to a posterior probability distribution with existing data or from observations and judgments (Ang and Tang 2007).
$$ {P}_{uf}=P\left(g\le 0|S \gt 0\right) $$ (13.1) where P(g ≤ 0)= probability of failure of limit state function (Pf) and P(S > 0)=probability of survival of limit state function (Ps).
From above, Eq. (13.1) is expanded into Eq. (13.2),
$$ {P}_{uf}=\frac{P\left[g\le 0\cap S \gt 0\right]}{P\left[S \gt 0\right]} $$ (13.2) The failure probability is calculated by Monte Carlo simulations, and the updated failure probability is given by the number of simulations satisfying g ≤ 0 and S > 0, divided by the number of simulations satisfying S > 0. The probability P(S > 0) means the probability that the structure survived the experienced wave height load level.
Ersdal (2005) analysed North Sea jacket platforms and benefitted with lower updated probability of failure by utilizing Bayesian Updating and Bayesian Updating with Truncation. Figure 10 shows the Bayesian Updating of probability of failure for the North Sea jacket platform from Ersdal. The result shows that the updated probability of failure decreases when the experienced wave height increases. To see a significant difference in the updated probability of failure, the experienced wave loading of 1000 and 10, 000-year return period are used in the survival function. When the experienced wave loading is equal or less than the 100-year return period load, it does not significantly change the updated failure probability.
 Figure 10 Updating probability of failure using Bayes theorem (Ersdal 2005)
Figure 10 Updating probability of failure using Bayes theorem (Ersdal 2005)Frieze et al. (1997) have conducted pushover analysis and utilised Bayesian updating to obtain bias in the RSR values. In most cases, the probability of failure is updated for the purpose of inspection and maintenance planning during the operation. Hence, utilizing this method, with the probable reduction in the probability of failure, the justification for avoiding costly modification and repair for life extension is strengthened.
Zafarullah (2013) has reported that during the design, based on the limited available information and data, assumptions are used against the uncertainty of environmental loading and material resistances. Throughout the platform life, the platform typically experiences some changes from the original condition. Hence, observation and monitoring data from platform operation could be used together with Updating methods to enhance the reliability of existing platforms.
Bayesian Updating with Truncation is another refined approach where it improves the process in obtaining failure probability compared to Bayesian Updating alone. In reliability analysis, the truncation method focuses on the resistance uncertainty model alone compared to Bayesian updating method which considers both load and resistance uncertainty models (Melchers et al. 2003). In truncation, load uncertainty model is not considered due to no additional information is obtained from operators concerning the wave distribution. To update this distribution, it requires sufficient number of wave data and large amount of simultaneous measurement of jacket load experiences. Though the wave height is known, due to uncertainties in load model the value is not accurate. Conclusion could be made that the capacity of a jacket platform could be well estimated from the ability of the platform successfully carrying loads from extreme wave events.
7.3 Corrosion Effect
The nature of offshore jacket platforms, located at harsh and corrosive environment throughout their life time, attract many degradation mechanisms. Corrosion is one of the important degradation mechanisms to be considered in structural design. Due to corrosion, the member capacity deteriorates. Corrosion, a time dependent process, which should be considered throughout the design life, though periodic maintenance and proper protection system (coating and cathodic protection measures) is made available (Paik and Kim 2012; Mohd Hairil et al. 2014; Kim et al. 2020b, c). As awared that the corrosion process is unavoidable. It deteriorates the resistance capacity of structural members of existing platforms. This is further aggravated with poor and less emphasised maintenance scheme by the operators. Limitation of resources, time and cost are to be blamed for the improper platform maintenance. Many researches are available on the effects of corrosion on structural safety (Kim et al. 2012a, b, c, 2014a, b, 2015, 2017b; Park et al. 2015a, b). Melchers (2005) studied the effect of corrosion on structural reliability of an existing facility. He reiterated that corrosion is one of the major degradation mechanisms that reduce strength capacity of offshore structure in a time dependent manner throughout the design life. Based on the deterioration mechanisms present on surface plate materials, marine corrosion is appropriately categorised into immersion, splash/ tidal zone, atmospheric and semi-enclosed space (Melchers 1997).
Refining further, corrosion is divided into pitting and general corrosion. Pitting corrosion refers to corrosion with length and width less than three times of the wall thickness meanwhile length and width more than three times of wall thickness is called general corrosion (Kolios 2010). In structural reliability, corrosion deteriorates resistance capacity. Hence, the uncertainty in remaining strength increases. Figure 11 shows that, the mean resistance value decays in a parabolic shape while uncertainty value increases with time. Meanwhile, as the load value fluctuates randomly with high uncertainty, the margin between the load and resistance decreases by time as the resistance value deteriorates. At one particular random point, the failure occurs when the fluctuating load value crosses the resistance value (Melchers 2005).
Figure 12 shows that, the strength function (R) deteriorates with time (t1, t2, t3 are different time points) due to corrosion, fatigue, etc., while the overlap with load density function (Q) get bigger. This overlapping is the failure criterion for the structure. It can be seen that the resistance probability density function flattens by time as well as the mean value decreases while the standard deviation increases. This explains the effect of corrosion on strength and reliability of offshore structures (Melchers 1999).
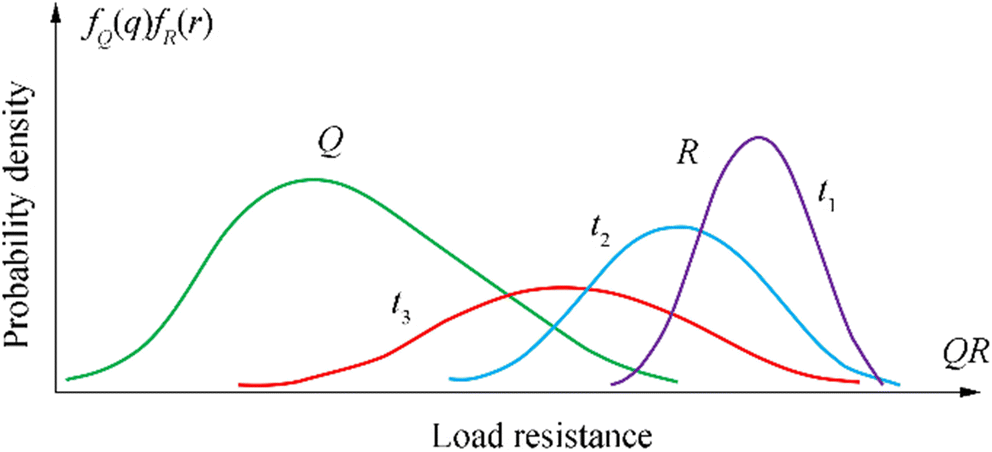 Figure 12 Resistance distribution decay by time (Melchers 1999)
Figure 12 Resistance distribution decay by time (Melchers 1999)Several models have been used for thickness deterioration of offshore structural members due to corrosion, considering different life stages of jacket platform. Most of these models are based on experimental works by many researchers.
Since corrosion affects the probabilistic resistance parameter of a structural member, a probabilistic corrosion model is appropriate. In a corrosion model by Melchers (1999, 2005) is presented as given in Eq. (14) with a mean value expression and an expression for randomness which describe the expected corrosion better.
$$ \complement \left(t,P,E\right)= fn\left(t,P,E\right)+\varepsilon \left(t,P,E\right) $$ (14) where C(t, P, E) is the total weight loss of material, fn(t, P, E) is the mean function, ε(t, P, E) is the zero mean error function, t is the time parameter, P is vector with parameters for the corrosion protection systems included and E is the vector of environmental conditions.
For general corrosion, several models exist. From Southwell's linear and bilinear model (Southwell et al. 1979), Qin and Cui (2003) and Melchers (1998, 2005) extended the model by calculating coefficients based on experimental data. In addition, a trilinear and a power approximation models are available in the literature. Few other different nonlinear models based on observational data are available in the literature which is more biased towards corrosion in plated members in ships and offshore structures (Paik and Kim 2012; Mohd Hairil et al. 2014; Kim et al. 2020b, c).
8 Simplified Approaches
Many software and methods have been developed for modelling, analysing and interpreting structural analysis and structural reliability analysis results. Yet, there are large variations and inconsistencies in the results among the software packages as demonstrated from comparative studies done by HSE (Billington et al. 1993). Furthermore, despite that the developed computer programs allow for efficient design and reassessment of structures, they have many deficiencies like requiring for high degrees of expertise to operate properly, high cost in acquiring and maintaining the products, high manpower and time to conduct the analyses and high chance of human error due to the sophistication in operation.
In lieu of above, many researches, i.e. Bea and Mortazavi (1996), Bea et al. (1993, 1995), Vannan et al. (1994), Bea and Craig (1993), and Stear and Bea (1997), have proposed simplified procedures for both structural and reliability analyses. They concluded that detailed structural analysis and reliability analysis are time consuming and require high cost and competency. Therefore, for any reassessment of offshore jacket structures, these analyses should not be the first step of the processes. This is supported by the fact that the resources are limited and large numbers of ageing platforms are waiting to be reassessed. Hence, Vannan et al. (1994) have proposed a simplified procedure called simplified ultimate strength (SUS) analysis that predicted a lower bound estimate of the ultimate strength of jacket platforms utilizing linear instead of nonlinear collapse analysis. Their prediction of the failure modes compared well with the actual collapse or damage of the platforms. Bea and his group (Bea and Craig 1993; Bea 1996) developed a four-tiered simplified procedure to evaluate the imposing environmental loadings and its structural responses under extreme storm conditions. The results gave a good agreement with the results from commercial software. The intention was to enable the reassessment and requalification activities to be efficient and effective. They utilised qualitative and quantitative methods in coming up with scoring rules for deciding on fitness for purpose of any jacket platform which goes for life extension reassessment. Bea and Craig (1993) have developed a multi-level approach utilizing progressive screening process that involved four cycles of analysis with increasing level of details. Mortazavi and Bea (1995) have developed a simplified structural component and system reliability procedural computer algorithm to identify the potential failure modes and to estimate the failure probability of any jacket-type platform. They suggested that this method could be adopted as a first-hand screening method before a time consuming and costly detailed risk analysis is performed.
Empirical formulation by data processing technique may also be considered as first-cut assessment in predicting remaining structural capacity. Cui and Mansour (1998) and Kim et al. (2018b) summarised historical reviews on existing empirical and design formations in predicting ultimate limit state of plate element. In the similar manner, several empirical formulations and simplification techniques have been proposed for various structures. In particular, damage index versus residual strength concept has been proposed by Paik et al. (2012) and applied to the grounded ships (Paik et al. 2012; Kim et al. 2013a, 2014a, 2020a). In the similar manner, collision (Youssef et al. 2016; Faisal et al. 2017) has also been studied. Various studies have also been conduced to propose empirical formulations in terms of blast wall due to explosion (Kim et al. 2018c; Sohn and Kim 2019), ultimate strength of plate (Paik et al. 2004; Kim et al. 2018d), stiffened panel (Kim et al. 2017a, 2019a, 2020d) and hull girder (Paik et al. 2013; Baek et al. 2018, 2019), fatigue life prediction of offshore riser (Kim et al. 2018a), current profile simplification (Kim et al. 2019b) and many others. Many of them utilised data analysis tool such as regression analysis. Details related to offshore jacket platform will be discussed further.
The previous approaches in performing simplified analyses to obtain the cost effective and quick structural safety are commendable. Besides, the large amount of data from earlier performed structural reliability analyses in the archive of the operators/ owners should be better used to develop a quick method to acquire the structural reliability based on judgment and experience in the region where the platform is situated. This quick method should act as the first level screening method for making a quick and important preliminary decision about any ageing jacket platforms in perspective. Thus, utilizing the available vast data of previously conducted structural reliability analyses, a simplified screening method is imperative for a first-hand rule-of-thumb decision with regard to structural reliability when comes to reassessment. Many researchers have looked into utilizing rich database and have come out with practical screening and prediction methodologies (Pueksap-anan 2010; Liu et al. 2009; Lambert et al. 2012).
Regression is a statistical technique that analyses several variables to formulate relationship between the dependant variable and one or more independent variable(s) to arrive at a function that fits the data and returns an array of values in a matrix form that describes the accuracy of the function (Brown 2001). Regression analysis is made easier nowadays with the availability of efficient computational tools. Microsoft Excel spreadsheet incorporates multiple regression analysis in its Data Analysis ToolPak available in its Excel Option Application Add-ins menu. The basic multiple regression models are expressed in Eq. (15.1) (Freund et al. 2006).
$$ \mathcal{Y}={\beta}_0+{\beta}_1{x}_1+{\beta}_2{x}_2+\dots +{\beta}_m{x}_m+\epsilon $$ (15.1) where $ \mathcal{Y} $ = response/dependent variable, §j, j = 1, 2, …, m. represent m different independent variables, β0 = the intercept (value when all the independent variables are 0), βj, j = 1, 2, …, m represent the corresponding m regression coefficients and ϵ = random error (usually assumed to be normally distributed with mean zero and variance, σ2).
In multiple regression analysis, attention is given to the relationship among the variables. What happens when each variable is varied one at a time, while not changing the values of any others, is of a particular interest. This shows that the coefficient attached to each independent variable should measure the average change in the response variable associated with changes in that independent variable, while the other independent variables remain fixed. This is the interpretation for a regression coefficient in a multiple regression model.
In principle, regression analysis is divided into linear and nonlinear regressions. Linear regression produces linear equation in Eq. (15.2) which forms a straight line for dataset with independent variable, x and dependent variable, y. This is fondly known as univariate linear regression. For a multivariate linear regression, multiple values of independent variables, xn and slopes, mn are produced in Eq. (15.3).
$$ y=b+ mx $$ (15.2) $$ y=b+{m}_1{x}_1+{m}_2{x}_2+{m}_3{x}_3+\dots +{m}_n{x}_n $$ (15.3) where y is dependent variable; x is independent variable; b is y-intercept of the linear function and m is the slope of linear function.
Nonlinear regression generates exponential curve function shown in Eq. (15.4) where x is the independent variable and y is the dependent variable. Equation (15.5) shows multivariate nonlinear regression equation.
$$ y=b\cdotp {m}^x $$ (15.4) $$ y={b}_1\cdotp {m_1}^{x1}\cdotp {m_2}^{x2}\cdotp {m_3}^{x3}\cdotp \dots \cdotp {m_n}^{xn} $$ (15.5) where y is dependent variable; xn is the independent variables; b, mn are the regression coefficients of the function.
Seber and Wild (2003) have stated that it is important in statistics to find the relationship that exists in a set of variables, being subjected to random variations and possible measurement errors. Nonlinear models are used either when they are suggested by theoretical considerations or to build known nonlinear behaviour into a model. Even when a linear approximation works well, a nonlinear model may still be used to retain a clear interpretation of the parameters. The application of nonlinear models is widely used in various situations.
Brown (2001) has described stepwise method for nonlinear regression analysis using Microsoft Excel Data Analysis Toolpak. The first step in analysing data, it was suggested to use a curve to determine the goodness of fit of the data utilizing least square method. This is based on the principal that the magnitude of the difference between the data points and the curve is a good measure of how well the curve fits the data. The best fit of the data is the linear function that has the smallest value for the squared sum (SS) of all the differences. The R2 value, the correlation index or the coefficient of determination, is a value between −1 and 1. It expresses the proportion of variance in the 'dependent' variable explained by 'independent' variable. As the R2 increases towards 1.0, the more accurately the function fits the data.
The analysis returns the best fit for linear function to represent the variables, having similarity to the LINEST function in the Microsoft Excel. Previously, nonlinear data would be transformed to linear form and subsequently analysed by linear regression. However, these transformations could yield inaccurate analysis as the linear regression may distort the experimental error or alter the relationship between y and x. A method that is suitable for this procedure is called iterative nonlinear least squares fitting. It differs from linear regression in a way that it is an iterative process and involves in making an initial estimate of the parameter values. The SOLVER function is utilised to perform iteration to optimise the R2 value which results in a regression function with better prediction power.
Lambert et al. (2012) have conducted a study to describe the method to obtain parameter confidence intervals from the fitting of nonlinear functions to experimental data, using the SOLVER and Analysis ToolPak Add-In from the Microsoft Excel. However, a disadvantage of using the Excel method was the inability to return confidence intervals for the computed parameters or the correlations between them. Using a simple Monte Carlo procedure within the Excel spreadsheet, using SOLVER can provide parameter estimates, for multiple data sets, and obtain the required confidence interval and correlation index.
Spiess and Neumeyer (2010) have mentioned that the R2 observation is still frequently being used in the context of validity of a certain model that fits nonlinear data. R2 is not an optimal choice in a nonlinear analysis as the total sum of squares (TSS) is not equal to the regression sum of squares (REGSS) plus the residual sum of squares (RSS), as is the case of linear regression and hence lacks the appropriate interpretation of the goodness of fit.
Liu et al. (2009) have utilised linear regression in predicting concrete strength taking concrete strength as dependent variable and the experimental surface rebound value and other design parameters as the independent variables. They utilised 146 sets of concrete material design parameters data as training specimens and 20 sets of data for testing the percentage error between the real value and the predicted value to evaluate the accuracy of the prediction model. In addition, correlation analysis was performed to assess the correlation of the utilised independent variables on the dependent powers. From seven design parameters, parameters with positive correlation coefficients were identified. Root mean square error (RMSE) was calculated in order to test the statistical regression analysis. The work explained the regression analysis methodology and sample validation technique in detail.
Pueksap-anan (2010) developed regression formulas for the prediction of ultimate strength in the form of Reserve Strength Ratio (RSR). His aim was to simplify time-consuming and costly structural reliability analysis. The developed nonlinear regression equations were categorised into the incoming wave direction and bracing type. LOGEST function in Microsoft Excel was employed. Metocean return period, topside loading, water depths, and the apparent double batter were considered as the independent variables while the RSR is the dependent variable. Percentage error between the actual and the predicted RSR values were also determined. Finally, the sensitivity of the RSR towards the independent variables was studied.
Ng et al. (2011) performed nonlinear regression analysis on a semi-submersible platform to obtain the response amplitude operator (RAO) based on parameters such as wave frequency, member diameter, and member draft. The nonlinear regression analysis was simplified to become linear regression analysis utilizing the logarithms of parameters (Eq. 16.1). Completing the analysis, the obtained coefficients were utilised in the exponential curve function fit shown in Eq. (16.2). For the validation purpose, the data was grouped according to the frequency and member diameter range. Three motions were considered. The generated regression equations were having a good agreement with the calculated RAO from diffraction theory.
$$ \mathrm{Log}\ R=\mathrm{Log}\ a+b\mathrm{Log}\ f+c\mathrm{Log}\ D+d\mathrm{Log}\ h $$ (16.1) $$ R=a\cdotp {f}^b\cdotp {D}^c\cdotp {h}^d $$ (16.2) where R is dependent variable; f, D and h are independent variables; and a, b, c and d are the regression coefficients.
9 Pile-Soil Ageing Effect
Recently, several studies have been done and are ongoing studying the pile capacity change, especially in offshore foundation by Karlsrud and Nadim (1990), Karlsrud et al. (2005), Nichols et al. (2006), Chen et al. (2009), Jeanjean (2009), Lacasse et al. (2013a, b) and Hajialilue-Bonab et al. (2013). The mechanism behind the change in pile capacity has been represented as mathematical equations known as 'time functions'. The pile capacity is believed to be changing, mostly in a positive manner, from the initial pile capacity since the time of installation. This increase in capacity is called 'set-up'. Nevertheless, the correct mechanism behind this change has not been fully understood. Hence many studies have been undertaken to look into this subject (Komurka et al. 2003; Augustesen 2006; Augustesen et al. 2006; Lied 2010; Jensen et al. 2014).
Bullock et al. (2005a, b) have conducted model test piles to measure the difference in set-up for different layers of soil side shear capacity. The measurement was done for 55 months. Long term effects on side shear set-up was established and a reduction factor of 0.4 was proposed. The linear increase of side shear capacity respect to logarithm of time was confirmed. They were also successful in establishing a minimum set-up factor, Δ10 of 0.1 from their results.
In 2006, studies on vertical bearing capacity of piles in clay soil with regard to long term set-up was performed by Augustesen (2006) and Augustesen et al. (2006). Statistical analysis was carried out using 88 static loading test data. They validated that set-up and established linear increase of the capacity with the logarithm of time. In addition, there are three different models suggested in the literature namely Skov and Denver model (Skov and Denver 1988), Norwegian Geotechnical Institute model (NGI) (Karlsrud et al. 2005; Clausen and Aas 2001) and Bullock model (Bullock et al. 2005a, b) were assessed and compared. Statistical evidence between the magnitude of set-up and soil properties could not be established. Hence, a constant set-up factor, Δ10 for a given time after initial driving was suggested.
NGI with an intention to establish design procedures which account for time effects, has studied pile bearing capacity gain with time from a joint industry project on full scale pile testing from five test sites in Europe with different ground conditions (Lied 2010). Ng et al. (2010) carried out case studies on pile-soil set-up for Malaysian onshore condition. Pile capacities obtained from tests carried out at different elapsed time after installation were studied to determine time effects on pile-soil set-up. They obtained set-up factor, Δ10 ranging from 0.09 to 6.25.
In theory, the pile foundation capacity could be increasing (positive) or decreasing (negative) by time depending on the interaction condition between the pile and the soil stratum, where the pile is installed. Negative change in pile capacity is very rare to occur compared to the positive change. As mentioned above, a positive change in capacity is known as set-up, while the negative change is known as 'relaxation'. The explanation on mechanism behind relaxation can be found in Bullock et al. (2005a) and Rausche et al. (2004). Meanwhile, set-up can be classified into two categories, namely long term and short term effects. The capacity gained in piles at the end of consolidation process is called long term effects or ageing effects. The capacity gained from the end of driving (EOD) of pile to the end of consolidation phase is known as short term effects (Lied 2010). Komurka et al. (2003) stated that there are three phases in the process of set-up shown in Figure 13.
 Figure 13 Idealised set-up phases (Komurka et al. 2003)
Figure 13 Idealised set-up phases (Komurka et al. 2003)First phase accounts for quick capacity increase after installation while the second phase occurs sometime after driving where the dissipation rate becomes constant with respect to the log of time. During the second phase, the soil experiences an increase in effective vertical and horizontal stresses, consolidates, and gains shear strength according to conventional consolidation theory. The duration for pore water pressure dissipation is a function of soil type, permeability, sensitivity, pile type and size. Combination of both phases is known as the short term effects. In the third phase, theoretically, an infinite time period is required for dissipation of the excess pore water pressure, but after a long time period, the rate of dissipation would get slower as the primary consolidation could be considered over and the secondary consolidation continues independent of effective stress. This is referred as the agring, which increases the pile capacity at a rate approximately linear with the log of time. This is valid for uniform soil condition along the pile shaft length and below the pile toe. Typically, at any condition, different layers of soil are present hence different rates for set-up is required for each layer.
9.1 Time Functions
Several time functions describing the pile capacity gain by time are available in the literature. Skov and Denver (1988) proposed a semi-logarithmic empirical relationship to describe set-up as in Eq. (17.1),
$$ {Q}_t/{Q}_o=1+\varDelta 10\ \left[\log\ \left(t/{t}_o\right)\right] $$ (17.1) where Qt = axial capacity at time t after EOD, Qo = axial capacity at reference time to, Δ10 = set-up factor (sand = 0.2, clay = 0.6), to = assumed to be 0.5 day for sand, 1.0 day for clay and EOD = end of driving.
The adopted to ensures a stabilised increase of the capacity with time. Prior to that, the pore pressure has not reached the stationary state, hence soil remoulding occurs. An upper limit for the reference time (to) was proposed however no guideline has been prescribed. Equation (17.2) has been adopted by many and it was developed using combined resistance from lumped pile side shear and toe resistance. In contrast to this, Bullock et al. (2005a, b) found that Δ10 is in the range of 0.1 to 0.32 using the equation for pile side shear capacity only, excluding toe resistance.
Meanwhile, Svinkin (1996) has developed a set of formula as given in Eqs. (17.2) and (17.3) for the set-up in sand based on load test data.
$$ {Q}_t=1.4{Q}_{\mathrm{EOD}}{t}^{0.1}\ \mathrm{upper}\ \mathrm{bound} $$ (17.2) $$ {Q}_t=1.025{Q}_{\mathrm{EOD}}{t}^{0.1}\ \mathrm{lower}\ \mathrm{bound} $$ (17.3) where QEOD is the instantaneous capacity at the end of driving of the pile.
The capacity of piles driven into soft soils is studied by Guang-Yu (1988). It was claimed that sand and gravel do not experience set-up. Hence a formula for predicting set-up in the soft-ground of Shanghai was presented as in Eq. (17.4),
$$ {Q}_{14}=\left(0.375 St+1\right)\ {Q}_{\mathrm{EOD}} $$ (17.4) where Q14 = pile capacity at 14 days after EOD and St = sensitivity of soil.
Svinkin and Skov (2000) presented slight modification to Eq. (17.3) with to equivalent to 0.1 day hence Eq. (17.5),
$$ {Q}_t/{Q}_{\mathrm{EOD}}-1=B\ \left[\log 10\ (t)+1\right] $$ (17.5) where Qt is ultimate resistance at time t days, QEOD is end of driving resistance, B is similar factor like the Δ10 in Eq. (17.3).
In all the above equations, QEOD is obtained from pile dynamic monitoring during pile driving. Augustesen (2006) has proposed different Δ10 values for long and short term effects. For set-up, the short-term component of Δ10 is greater than the long term component, i.e. Δ10 short-term > Δ10 long term shown in Figure 14. The time for equalisation of pore water pressure end of consolidation is denoted teoc and both Δ10 and Q0 depend on whether t < teoc or t > teoc.
From the test results by Clausen and Aas (2001), they claimed that the long term set-up depends on the soil properties. Hence they introduced Δ10 as a function of the plasticity index (Ip) and the over consolidation ratio (OCR) as in Eq. (17.6).
$$ \varDelta 10=0.1+0.4\ \left(1- Ip/50\right)\ OCR-0.8\ \left[ for\ 0.1\le \varDelta 10\le 0.5\right] $$ (17.6) The reference time, t0 is fixed as 100 days. The above equation is also denoted as the NGI equation. Augustesen (2006) recommended the form of Δ10 that best fits the observed results from experimental data, to better depicts the actual behaviour. Hence, Eq. (17.7) is derived.
$$ \varDelta 10=1.24\hbox{--} \left( Suu/60\right)\ 0.03 $$ (17.7) where Suu is the soil un-drained shear strength. This equation is called the AAU equation. In different soil layers average values of Ip, OCR and Suu are recommended by NGI. However, Augustesen et al. (2006) proposed two options to choose from
• Option 1: Equation (17.3) is applied to every single soil layer using Δ10 found using Ip, OCR and Suu of that particular layer.
• Option 2: Equation (17.3) is used for the entire pile. Hence an average value of Ip, OCR and Suu be estimated weighting the soil parameters by surface area or weighting the soil parameters by the calculated capacity of the different layers by means of static design equations for the soil in the pile vicinity.
Equations (17.6) and (17.7) are applicable only for cohesive soil. No equation is available for noncohesive soil. Hence, original constant values for Δ10 are recommended for noncohesive soil (Jensen et al. 2014).
Apart from the pile and soil interaction, pipe and soil interation issues have also been highlighted by invetigating its nonlinear behaviour (Kim et al. 2017c; Yu et al. 2013, 2015, 2017).
10 Concluding Remarks
In this paper, the research studies on structural condition assessment of ageing offshore jacket platforms reported in the literature over the past few decades are presented and discussed. The obtained results may be summarised as follows:
1) Many studies are reported on reassessment of existing offshore jacket platforms by considering maintenance and/or decommissioning. They utilised numerous assessment methodologies, either deterministic or probabilistic types. In lieu of the current practice, probabilistic methodologies to conduct component and system reliability reassessments as an alternative to the current industry adopted approach are needed. In addition, the relationship between component and system reliability is preferred. With the developed methodologies, parametric study affecting the component and system reliability has been performed. The sensitivity study on parameters which contributes to the variation of the reliability indices has been conducted.
2) Large number of studies on corrosion and Bayesian updating methods is available. With the developed methodologies, the effects of corrosion and Bayesian updating on the jacket platforms reliability indices are investigated.
3) Numerous studies have been reported on pile-soil ageing. The effects of pile-soil ageing on the safety indices are investigated. Prior to that, time functions and modification to the pile-soil curves are studied.
4) Large number of studies have been conducted in formulating simplified methodology to determine safety indices of existing jacket platforms. With the available tabulated structural reliability analysis data, the development of simplified methodology to determine reliability indices for Malaysian offshore jacket platforms is performed.
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. -
Figure 1 Typical shape of offshore jacket platform (Fadly 2011)
Figure 4 Theoretical representation of probability of failure (Moses and Stahl 1979)
Figure 5 Geometrical illustration of reliability index (Choi et al. 2007)
Figure 6 Mapping of failure surface from X space to U space using HL method (Choi et al. 2007)
Figure 7 Probability density function and interval information (Choi et al. 2007)
Figure 9 Component post failure behaviour model (Kolios 2010)
Figure 10 Updating probability of failure using Bayes theorem (Ersdal 2005)
Figure 12 Resistance distribution decay by time (Melchers 1999)
Figure 13 Idealised set-up phases (Komurka et al. 2003)
Table 1 Typical bias and covariance values utilised in SSRA (Fadly 2011)
Variable Description Bias Covariance Load Dead load 1 0.1 Live/functional load 1 0.2 Environmental load To be fitted 0.3 Resistance Members 1.1 0.15 Joints 1.25 0.2 Piles 1.1 0.2 Soil/foundation 1.30 or 1.13 0.2 Table 2 Resistance model variables (Zafarullah 2013)
Variable Statistical Parameter Diameter (mm) Distribution Normal MC 1.001 COV 0.0018
(Brace < 1000 mm)
0.0014 (leg > 1000 mm)Wall Thickness (mm) Distribution Normal MC 1.024 COV 0.016 Yield Strength (MPa) Distribution Normal MC 1.230 COV 0.050 Tensile Strength (MPa) Distribution Normal MC 1.183 COV 0.039 -
Aanhold JE (1983) Ultimate strength analysis of framed offshore structures (SINTEF report STF88-A83003). SINTEF, Trondheim Alessi L, Correia JAFO, Fantuzzi N (2019) Initial design phase and tender designs of a jacket structure converted into a retrofitted offshore wind turbine. Energ 12(4): 659. https://doi.org/10.3390/en12040659 Amer MY (2010) Development of structural regional acceptance criteria for existing fixed offshore structures in the Arabian gulf. The Abu Dhabi International Petroleum Exhibition and Conference, 1-4 November, Abu Dhabi, UAE Ang AHS, Tang WH (2007) Probability concepts in engineering: emphasis on applications to civil and environmental engineering (V. 1). John Wiley & Sons, Hoboken, NJ, USA API (1993) Recommended practice for planning, designing and constructing fixed offshore platforms—load and resistance factor design (API RP 2A-LRFD). American Petroleum Institute, Washington API (2007) Recommended practice for planning, designing and constructing fixed offshore platforms–working stress design (2A-WSD 2007). American Petroleum Institute, Washington Asgarian B, Lesani M (2009) Pile–soil-structure interaction in pushover analysis of jacket offshore platforms using fiber elements. J Constr Steel Res 65(1): 209–218. https://doi.org/10.1016/j.jcsr.2008.03.013 Ayob MS, Kajuputra AE, Mukherjee K, Wong BS (2014a) Global ultimate strength assessment of existing offshore jacket structures. The 1st Offshore Technology Conference-Asia (OTC Asia 2014), 25–28 march, Kuala Lumpur Ayob MS, Mukherjee K, Kajuputra AE, Wong BS, Salleh FM (2014b) Requalification of offshore jacket structures in Malaysian waters. The 1st Offshore Technology Conference Asia (OTC Asia 2014), 25–28 march, Kuala Lumpur Augustesen A (2006) The effects of time on soil behaviour and pile capacity. Dissertation, Aalborg University, Aalborg, Ph. D Augustesen A, Andersen L, Sørensen CS (2006) Assessment of time functions for piles driven in clay (DCE Technical Memerandum No. 1). Aalborg University, Aalborg, Denmark Baek SJ, Kim SJ, Paik JK, Sohn JM (2019) Development of an empirical formula for residual strength assessment to prevent sequential events of grounded oil tankers. J Soc Naval Archit Korea 56(3): 263–272. https://doi.org/10.3744/SNAK.2019.56.3.263 Baek SJ, Sohn JM, Paik JK, Kim SJ (2018) Development of a method for prediction of residual strength for prevention of secondary accidents on large oil tankers subjected to collisions. J Soc Naval Archit Korea 55(2): 144–152. https://doi.org/10.3744/SNAK.2018.55.2.144 Baker MJ (1998) Feasibility study on appraisal of methods of structural reliability assessment for offshore structures (HSE Report). Health and Safety Executive (HSE), London, UK Banon H, Bea RG, Bruen FJ, Cornell CA, Krieger WF, Stewart DA (1994) Assessing fitness for purpose of offshore platforms. I: analytical methods and inspections. J Struct Eng 120(12): 3595–3612. https://doi.org/10.1061/(ASCE)0733-9445(1994)120:12(3595) Bao XX, Wang JR, Li HJ (2009) A safety assessment method on aging offshore platforms with damages. The 19th International Offshore and Polar Engineering Conference (ISOPE 2009), 21–26 July, Osaka Bea RG (2000) Criteria for design and requalification of platforms in the bay of Campeche, Mexico. J Waterw Port Coast Ocean Eng 126(5): 254–262. https://doi.org/10.1061/(ASCE)0733-950X(2000)126:5(254) Bea RG (1996) Reassessment and requalification of infrastructure: application to offshore structures. J Infrastruct Syst 2(2): 45–53. https://doi.org/10.1061/(ASCE)1076-0342(1996)2:2(45) Bea RG (1974) Selection of environmental criteria for offshore platform design. J Pet Technol 26(11): 1206–1214. https://doi.org/10.2118/4452-PA Bea RG, Craig MJK (1993) Developments in the assessment and requalification of offshore platforms. The 25th Offshore Technology Conference (OTC 1993), 3–6 May, Houston, Texas Bea RG, Mortazavi MM (1996) ULSLEA: a limit equilibrium procedure to determine the ultimate limit state loading capacities of template-type platforms. J Offshore Mech Arctic Eng 118(4): 267–275. https://doi.org/10.1115/1.2833915 Bea RG, Mortazavi MM, Loch KJ, Young PL (1995) Verification of a simplified method to evaluate the capacities of template-type platforms. The 27th Offshore Technology Conference (OTC 1995), 1–4 May, Houston, Texas Bea RG, Mortazavi MM, Stear JD (1993) Screening methodologies for use in platform assessments and requalifications (final project report). University of California, Berkeley Billington CJ, Bolt HM, Ward JK (1993) Reserve residual and ultimate strength analysis of offshore structures: state of the art review. The 3rd International Offshore and Polar Engineering Conference (ISOPE 1993), 6-11 June, Singapore Bolt HM, Billington CJ, Ward JK (1996) A review of the ultimate strength of tubular framed structures (Report No: OTH 92 365). Health and Safety Executive (HSE), Berkshire, UK Bolt HM, Billington CJ, Ward JK (1994) Results from large-scale ultimate load tests on tubular jacket frame structures. The 26th Offshore Technology Conference (OTC 1994), 2–5 May, Houston, Texas BOMEL Ltd. (2002) System-based calibration of North West European annex environmental load factor to ISO fixed steel offshore structure code 19902 (Report No. C925\04\016R Rev A). BOMEL Ltd, Berkshire, UK Bourinet JM (2010) Ferum 4.1 user's guide. Clermont-Ferrand, France: Institute Français de Mécanique Avancée (IFMA) Brown AM (2001) A step-by-step guide to non-linear regression analysis of experimental data using a Microsoft excel spreadsheet. Comput Methods Prog Biomed 65(3): 191–200. https://doi.org/10.1016/S0169-2607(00)00124-3 Bucher CG, Bourgund U (1990) A fast and efficient response surface approach for structural reliability problems. Struct Saf 7(1): 57–66. https://doi.org/10.1016/0167-4730(90)90012-E Bullock PJ, Schmertmann JH, McVay MC, Townsend FC (2005a) Side shear setup. I: test piles driven in Florida. J Geotech Geoenviron 131(3): 292–300. https://doi.org/10.1061/(ASCE)1090-0241(2005)131:3(292) Bullock PJ, Schmertmann JH, McVay MC, Townsend FC (2005b) Side shear setup. II: results from Florida test piles. J Geotech Geoenviron 131(3): 301–310. https://doi.org/10.1061/(ASCE)1090-0241(2005)131:3(301) Capanoglu C, Coombs S (2009) Requalification process for existing platforms implications of newly acquired criteria on mitigation. The 19th International Offshore and Polar Engineering Conference (ISOPE 2009), 21–26 July, Osaka Cassidy MJ, Houlsby GT, Taylor RE (2001) Application of probabilistic models to the response analysis of jack-ups. The 11th International Offshore and Polar Engineering Conference (ISOPE 2001), 17–22 June, Stavanger, Norway Chen JY, Matarek BA, Carpenter JF, Gilbert RB (2009) Analaysis of potential conseratism in foundation design for offshore platform assessment. Final project report prepared for the minerals management service under MMS award/contract M08PC20002 (MMS project number 612), offshore technology research center, Texas a & M university, Taxas, USA. https://www.bsee.gov/sites/bsee.gov/files/tap-technical-assessment-program/612aa.pdf Chin DCL (2005) A reliability analysis of a Malaysia jacket platform. Dissertation, Universiti Teknologi Malaysia, Johor, Malaysia, MS. c Choi SK, Grandhi RV, Canfield RA (2007) Reliability-based structural design. Springer, London Clausen CJF, Aas PM (2001) Capacity of driven piles in clays and sands on the basis of pile load tests. The 11th International Offshore and Polar Engineering Conference (ISOPE 2011), 17–22 June, Stavanger, Norway Cornell CA (1987) Offshore structural systems reliability (a report to amoco production company for the joint industry project participants), C. Allin Cornell, Inc., Portola Valley Cossa NJ (2012) Environmental load factor for ISO design of tubular joints of a Malaysia fixed offshore steel jacket platform. MS. c. Dissertation, Universiti Teknologi PETRONAS, Seri Iskandar, Perak, Malayisa Cossa NJ, Potty NS, Idrus AB, Hamid A, Foad M, Nizamani Z (2012) Reliability analysis of jacket platforms in Malaysia-environmental load factors. Res J Appl Sci Eng Technol 4(19): 3544–3551 https://maxwellsci.com/print/rjaset/v4-3544-3551.pdf Craig MJK, Digre KA (1994) Assessments of high-consequence platforms: issues and applications. The 26th Offshore Technology Conference (OTC 1994), 2–5 May, Houston, Texas Cui W, Mansour AE (1998) Effects of welding distortions and residual stresses on the ultimate strength of long rectangular plates under uniaxial compression. Mar Struct 11(6): 251–269 https://doi.org/10.1016/S0951-8339(98)00012-4 Dalane JI, Haver S (1995) Requalification of an unmanned jacket structure using reliability methods. The 27th Offshore Technology Conference (OTC 1995), 1–4 May, Houston De RS (1990) Offshore structural system reliability: wave-load modeling, system behavior, and analysis. Dissertation, University of California Berkeley, Berkeley, CA, USA, Ph. D Energo (2007) Assessment of fixed offshore platform performance in hurricanes Katrina and Rita. US Department of Interior Mineral Management Service Engineering and Research Branch & Energo Engineering (Final Report: MMS Project No. 578, Energo Engineering Project No. E06117) https://www.bsee.gov/sites/bsee.gov/files/tap-technical-assessment-program/578aa.pdf Energo (2010) Assessment of damage and failure mechanisms for offshore structures and pipelines in hurricanes Custav and Ike. US Department of Interior Mineral Management Service Engineering and Research Branch & Energo Engineering (Final Report: MMS Project No. 642, Project No. E09180) https://www.bsee.gov/sites/bsee.gov/files/tap-technical-assessment-program//642aa.pdf Efthymiou M, van De Graaf JW, Tromans PS, Hines IM (1997) Reliability-based criteria for fixed steel offshore platforms. J Offshore Mech Arctic Eng 119(2): 120–124. https://doi.org/10.1115/1.2829053 Ersdal G (2005) Assessment of existing offshore structures for life extension. Ph. D. Dissertation, University of Stavanger, Norway Ersdal G, Sørensen JD, Langen I (2003) Updating of structural failure probability based on experienced wave loading. The 13th International Offshore and Polar Engineering Conference (ISOPE 2003), 25–30 May, Honolulu Fadly M (2011) Sensitivity study of environmental load to reliability index for Malaysian region. MS. c. Dissertation, Universiti Teknologi PETRONAS, Malaysia Faisal M, Noh SH, Kawsar RU, Youssef SAM, Seo JK, Ha YC, Paik JK (2017) Rapid hull collapse strength calculations of double hull oil tankers after collisions. Ships Offshore Struct 12(5): 624–639. https://doi.org/10.1080/17445302.2016.1192747 Fjeld S (1978) Reliability of offshore structures. J Pet Technol 30(10): 1486–1496. https://doi.org/10.2118/6963-PA Freund RJ, Wilson WJ, Sa P (2006) Regression analysis: statistical modeling of a response variable. Elsevier, Burlington Frieze PA, Morandi AC, Birkinshaw M, Smith D, Dixon AT (1997) Fixed and jack-up platforms: basis for reliability assessment. Mar Struct 10(2–4): 263–284. https://doi.org/10.1016/S0951-8339(97)00001-4 Gening XU, Ruiguang Y (2010) Methodology to estimate remaining service life of steel structure by possibilistic reliability theory. Chin J Mech Eng 23(6): 780–787. https://doi.org/10.3901/CJME.2010.06.780 George JM, Kurian VJ, Wahab MMA (2016) Changes in the pushover analysis results of offshore jacket platforms due to the incorporation of the aging effects of piles. ARPN J Eng Appl Sci 11(4): 2602–2606 http://www.arpnjournals.org/jeas/research_papers/rp_2016/jeas_0216_3691.pdf Gierlinski JT, Sears RJ, Shetty NK (1993) Integrity assessment of fixed offshore structures: a case study using rasos software. The 12th International Conference on Offshore Mechanics and Arctic Engineering (OMAE 1993), 20–24 June, Glasgow Golafshani AA, Bagheri V, Ebrahimian H, Holmas T (2011) Incremental wave analysis and its application to performance-based assessment of jacket platforms. J Constr Steel Res 67(10): 1649–1657. https://doi.org/10.1016/j.jcsr.2011.04.008 Guang-Yu Z (1988) Wave equation applications for piles in soft ground. The 3rd International Conference on the Application of Stress-wave Theory to Piles, 25-27 may, Ottawa, Canada Guenard YF, Cornell CA, Bea RG, Rackwitz R (1984) Application of system reliability analysis to offshore structures (Standford University report no 71). Stanford University, Stanford Håbrekke S, Bodsberg L, Hokstad P, Ersdal G (2011) Issues for consideration in life extension and managing ageing facilities. The 30th International Conference on Ocean, Offshore and Arctic Engineering (OMAE 2011), 19–24 June, Rotterdam Hajialilue-Bonab M, Levacher D, Chazelas JL, Kaynia AM (2013) Static and dynamic behavior of laterally loaded single piles and determination of P-Y curves. Asian J Civil Eng (BHRC) 14(6): 899–916 https://pdfs.semanticscholar.org/958f/a091f88cd361598b8ffe83fad616ba1fe8e6.pdf?_ga=2.127723597.196045463.1598791769-926310604.1595797586 Hansen K, Gudmestad OT (2001) Reassessment of jacket type of platforms subject to wave-in-deck forces–current practice and future development. The 11th International Offshore and Polar Engineering Conference (ISOPE 2001), 17–22 June, Stavanger, Norway Hasofer AM, Lind MC (1974) An exact and invariant first order reliability format. J Eng Mech 100(1): 111–121 Heideman JC (1980) Parametric response model for wave/current joint probability (submitted to American Petroleum Institute Technical Advisory Committee TAC), 88-20 Hellan Ø (1995) Nonlinear pushover and cyclic analyses in ultimate limit state design and reassessment of tubular steel offshore structures. Norwegian Institute of Technology, Trondheim ISO (2007) Petroleum and natural gas industries—fixed steel offshore structures (ISO 19902: 2007). International Organization for Sandardization, Geneva Jeanjean P (2009). Re-assessment of P-Y curves for soft clays from centrifuge testing and finite element modeling. Offshore Technology Conference (OTC 2009), 4-7 May, Houston, Texas, USA https://doi.org/10.4043/20158-MS Jensen JL, Augustesen A, Sørensen CS (2014) The influence of time on bearing capacity of driven piles. In: The 14th Nordiac Geotechnical Meeting, 19–21 may. Sweden, Ystad Karamchandani AK (1990) New methods in systems reliability. Dissertation, Stanford University, Stanford, CA, USA, Ph. D Karamchandani A, Cornell CA (1992) Reliability analysis of truss structures with multistate elements. II. J Struct Eng 118(4): 910–925. https://doi.org/10.1061/(ASCE)0733-9445(1992)118:4(910) Karunakaran D, Leira BJ, Moan T (1993) Reliability analysis of drag-dominated offshore structures. The 3rd International Offshore and Polar Engineering Conference (ISOPE 1993), 6-11 June, Singapore Karlsrud K, Clausen CJF, Aas PM (2005) Bearing capacity of driven piles in clay, the NGI approach. The 1st International Symposium on Frontiters in Offshore Geotehcnics (ISFOG 2005), 19–21 September, Perth, Australlia Karlsrud K, Nadim F (1990) Axial capacity of offshore piles in clay. The 22nd Offshore Technology Conference (OTC 1990), 7–10 May, Houston Kim DK, Incecik A, Choi HS, Wong EWC, Yu SY, Park KS (2018a) A simplified method to predict fatigue damage of o_shore riser subjected to vortex-induced vibration by adopting current index concept. Ocean Eng 157: 401–411. https://doi.org/10.1016/j.oceaneng.2018.03.042 Kim DK, Kim BJ, Seo JK, Kim HB, Zhang XM, Paik JK (2014a) Time-dependent residual ultimate longitudinal strength-grounding damage index (R-D) diagram. Ocean Eng 76: 163–171. https://doi.org/10.1016/j.oceaneng.2013.06.023 Kim DK, Kim HB, Park DH, Mohd Hairil M, Paik JK (2020a) A practical diagram to determine the residual longitudinal strength of grounded ship in Northen Sea route. Ships Offshore Struct 15(7): 683–700. https://doi.org/10.1080/17445302.2019.1667113 Kim DK, Kim HB, Zhang XM, Li CG, Paik JK (2014b) Ultimate strength performance of tankers associated with industry corrosion addition practices. Int J Naval Archit Ocean Eng 6(3): 507–528. https://doi.org/10.2478/IJNAOE-2013-0196 Kim DK, Kim SJ, Kim HB, Zhang XM, Li CG, Paik JK (2015) Ultimate strength performance of bulk carriers with various corrosion additions. Ships Offshore Struct 10(1): 59–78. https://doi.org/10.1080/17445302.2014.883957 Kim DK, Lim HL, Cho NK (2020b) An advanced technique to predict time-dependent corrosion damage of onshore, offshore, nearshore and ship structures: part II = application to the ship's ballast tank. Int J Naval Archit Ocean Eng 12: 657–666. https://doi.org/10.1016/j.ijnaoe.2020.07.002 Kim DK, Lim HL, Kim MS, Hwang OJ, Park KS (2017a) An empirical formulation for predicting the ultimate strength of stiffened panels subjected to longitudinal compression. Ocean Eng 140: 270–280. https://doi.org/10.1016/j.oceaneng.2017.05.031 Kim DK, Lim HL, Yu SY (2018b) A technical review on ultimate strength prediction of stiffened panels in axial compression. Ocean Eng 170: 392–406. https://doi.org/10.1016/j.oceaneng.2018.10.022 Kim DK, Lim HL, Yu SY (2019a) Ultimate strength prediction of T-bar stiffened panel under longitudinal compression by data processing: a refined empirical formulation. Ocean Eng 192: 106522. https://doi.org/10.1016/j.oceaneng.2019.106522 Kim DK, Ng WCK, Hwang OJ (2018c) An empirical formulation to predict maximum deflection of blast wall under explosion. Struct Eng Mech 68(2): 237–245. https://doi.org/10.12989/sem.2018.68.2.237 Kim DK, Park DK, Kim HB, Seo JK, Kim BJ, Paik JK, Kim MS (2012a) The necessity of applying the common corrosion addition rule to container ships in terms of ultimate longitudinal strength. Ocean Eng 49: 43–55. https://doi.org/10.1016/j.oceaneng.2012.04.012 Kim DK, Park DK, Kim JH, Kim SJ, Kim BJ, Seo JK, Paik JK (2012b) Effect of corrosion on the ultimate strength of double hull oil tankers—part I: stiffened panels. Struct Eng Mech 42(4): 507–530. https://doi.org/10.12989/sem.2012.42.4.507 Kim DK, Park DK, Park DH, Kim HB, Kim BJ, Seo JK, Paik JK (2012c) Effect of corrosion on the ultimate strength of double hull oil tankers—part II: hull girders. Struct Eng Mech 42(4): 531–549. https://doi.org/10.12989/sem.2012.42.4.531 Kim DK, Pedersen PT, Paik JK, Kim HB, Zhang XM, Kim MS (2013a) Safety guidelines of ultimate hull girder strength for grounded container ships. Saf Sci 59: 46–54. https://doi.org/10.1016/j.ssci.2013.04.006 Kim DK, Poh BY, Lee JR, Paik JK (2018d) Ultimate strength of initially deflected plate under longitudinal compression: part I = an advanced empirical formulation. Struct Eng Mech 68: 247–259. https://doi.org/10.12989/sem.2018.68.2.247 Kim DK, Wong EWC, Cho NK (2020c) An advanced technique to predict time-dependent corrosion damage of onshore, offshore, nearshore and ship structures: part I = generalisation. Int J Naval Archit Ocean Eng 12: 657–666. https://doi.org/10.1016/j.ijnaoe.2020.06.007 Kim DK, Wong EWC, Lee EB, Yu SY, Kim YT (2019b) A method for the empirical formulation of current profile. Ships Offshore Struct 14(2): 176–192. https://doi.org/10.1080/17445302.2018.1488340 Kim DK, Yu SY, Lim HL, Cho NK (2020d) Ultimate compressive strength of stiffened panel: an empirical formulation for flat-bar type. J Mar Sci Eng 8(8): 605. https://doi.org/10.3390/jmse8080605 Kim DK, Zalaya MA, Mohd MH, Choi HS, Park KS (2017b) Safety assessment of corroded jacket platform considering decommissioning event. Int J Automot Mech Eng 14(3): 4462–4485. https://doi.org/10.15282/ijame.14.3.2017.6.0353 Kim DS, Ok SY, Song J, Koh HM (2013b) System reliability analysis using dominant failure modes identified by selective searching technique. Reliab Eng Syst Saf 119: 316–331. https://doi.org/10.1016/j.ress.2013.02.007 Kim SH, Na SW (1997) Response surface method using vector projected sampling points. Struct Saf 19(1): 3–19. https://doi.org/10.1016/S0167-4730(96)00037-9 Kim YT, Kim DK, Choi HS, Yu SY, Park KS (2017c) Fatigue performance of Deepwater steel catenary riser considering nonliner soil. Struct Eng Mech 61(6): 737–746. https://doi.org/10.12989/sem.2017.61.6.737 Kolios AI (2010) A multi-configuration approach to reliability based structural integrity assessment for ultimate strength. Dissertation, Cranfield University, UK, Ph. D Kolios A, Brennan FP (2009) Reliability based design for novel offshore structures. The 3rd International Conference of Integrity, Reliability and Failure, 20-24 July, Porto, Portugal Komurka VE, Wagner AB, Edil T (2003) Estimating soil/pile set-up (Wisconsin Highway Research Program Report No. 0092-00-14). Wisconsin Department of Transportation, Wisconsin, USA Krawinkler H, Seneviratna GDPK (1998) Pros and cons of a pushover analysis of seismic performance evaluation. Eng Struct 20(4–6): 452–464. https://doi.org/10.1016/S0141-0296(97)00092-8 Krieger WF, Banon H, Lloyd JR, De RS, Digre KA, Nair D, Guynes SJ (1994) Process for assessment of existing platforms to determine their fitness for purpose. The 26th Offshore Technology Conference (OTC 1994), 2–5 May, Houston Kurian VJ, Goh SS, Wahab MMA, Liew MS (2014a) Reliability assessment model for aging jacket structures in Malaysian waters. Appl Mech Mater 567: 283–288. https://doi.org/10.4028/www.scientific.net/AMM.567.283 Kurian VJ, Nizamani Z, Liew MS (2013a) Bayesian updating for probability of failure of jacket platforms in Malaysia. The Business Engineering and Industrial Applications Colloquium (BEIAC 2013), 7–9 April, Langkawi Kurian VJ, Nizamani Z, Liew MS (2013b) Modelling for uncertainties in resistance for jacket platforms in Malaysia. Res J Appl Sci Eng Technol 5(3): 750–759 http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.1077.1969&rep=rep1&type=pdf Kurian VJ, Wahab MMA, Kheang TS, Liew MS (2014b) System reliability of existing jacket platform in Malaysian water (failure path and system reliability index). Appl Mech Mater 567: 307–312. https://doi.org/10.4028/www.scientific.net/AMM.567.307 Kurian VJ, Yassir MA, Harahap ISH (2012) Dynamic response of semisubmersibles with damaged mooring lines. The 22nd International Offshore and Polar Engineering Conference (ISOPE 2012), June 17–22, Rhodes Lacasse S, Nadim F, Andersen KH, Knudsen S, Eidsvig UK, Yetginer GL, Guttormsen T, Eide A (2013a). Reliability of API, NGI, ICP and Fugro axial pile capacity calculation methods. The 45th Offshore Technology Conference (OTC 2013), 6–9 May, Houston Lacasse S, Nadim F, Langford T, Knudsen S, Yetginer GL, Guttormsen TR, Eide A (2013b) Model uncertainty in axial pile capacity design methods. The 45th Offshore Technology Conference (OTC 2013), 6–9 May, Houston Lambert RJW, Mytilinaios I, Maitland L, Brown AM (2012) Monte Carlo simulation of parameter confidence intervals for non-linear regression analysis of biological data using Microsoft excel. Comput Methods Prog Biomed 107(2): 155–163. https://doi.org/10.1016/j.cmpb.2011.05.009 Lebas G, Lacasse S, Cornell CA (1992) Response surfaces for reliability analysis of jacket structures. The 11th International Conference on Offshore Mechanics and Arctic Engineering (OMAE 1992), 17–22 June, Calgary Lee YJ (2012) Finite-element-based system reliability analysis and updating of fatigue-induced sequential failures. Ph. D. dissertation, University of Illinois at Urbana-Champaign, Champaign Lied EKW (2010) A study of time effects on pile capacity (NGI report). Norwegian Geotechnical Institute, Norway Liu JC, Sue ML, Kou CH (2009) Estimating the strength of concrete using surface rebound value and design parameters of concrete material. Tamkang J Sci Eng 12(1): 1–7. https://doi.org/10.6180/JASE.2009.12.1.01 Madsen HO, Sørensen JD, Olesen R (1989) Optimal inspection planning for fatigue damage of offshore structures. The 5th International Conference on Structural Safety & Reliability (ICOSSAR 1989), 7–11 August, San Francisco, California, USA Mark M, Etterdal B, Grigorian H (2001) Structural reliability assessment of Ekofisk jackets under extreme loading. The 33rd Offshore Technology Conference (OTC 2001), 30 April - 3 May, Houston Marshall PW (1979) Strategy for monitoring, inspection and repair for fixed offshore platforms. Proceedings of the Conference on the Behavior of Offshore Structures (BOSS 1979), London, UK: 97–109 Mayeetae Z, Liew MS, Abdullah MN (2012) Validating hindcast metocean parameter with measured environmental loads of Malaysian water. The 1st International Conference on Civil, Offshore & Environmental Engineering (ICCOEE 2012), 12–14 June, Kuala Lumpur Melchers RE (1997) Modeling of marine corrosion of steel specimens. ASTM Spec Tech Publication 1300: 20–33. https://doi.org/10.1520/STP11356S Melchers RE (1998) Probabilistic modelling of immesion marine corrosion. In: Shimozuka M, Wen YK (eds) Shiraishi N. Balkema, Structural Safety and Reliability, pp 1143–1149 Melchers RE (1999) Structural reliability analysis and prediction. Wiley & Sons, Chichester Melchers RE (2005) The effect of corrosion on the structural reliability of steel offshore structures. Corros Sci 47(10): 2391–2410. https://doi.org/10.1016/j.corsci.2005.04.004 Melchers RE, Ahammed M, Middleton C (2003) FORM for discontinuous and truncated probability density functions. Struct Saf 25(3): 305–313. https://doi.org/10.1016/S0167-4730(03)00002-X Meng D, Hu Z, Wu P, Zhu SP, Correia JAFO, De Jesus AMP (2020) Reliability-based optimisation for offshore structures using saddlepoint approximation. Proc Inst Civ Eng Marit Eng 173(2): 33–42. https://doi.org/10.1680/jmaen.2020.2 Moan T (2000) Recent research and development relating to platform requalification. J Offshore Mech Arctic Eng 122(1): 20–32. https://doi.org/10.1115/1.533720 Moan T, Vårdal OT, Johannesen JM (2000) Probabilistic inspection planning of fixed offshore structures. Proceedings of ICASP8, Sydney, pp. 191-200 Mohd Hairil M, Kim DK, Kim DW, Paik JK (2014) A time-variant corrosion wastage model for subsea gas pipelines. Ships Offshore Struct 9(2): 161–176. https://doi.org/10.1080/17445302.2013.770724 Mohd Hairil M, Zalaya MA, Latheef M, Choi HS, Rahman MAA, Kim DK (2019) Ultimate bending capacity of aged fixed platform by considering the effect of marine fouling. Lat Am J Solid Struct 16(5): e182. https://doi.org/10.1590/1679-78255479 Morandi AC, Frieze PA, Birkinshaw M, Smith D, Dixon AT (2015) Reliability of fixed and jack-up structures: a comparative study. The International Conference on the Behavior of Offshore Structures (BOSS 1979), 28–31 August, London, UK, 111–126 Mortazavi MM, Bea RG (1995) Screening methodologies for use in platform assessments and requalifications. University of California, Berkely Moses F (1987) Application of reliability to formulation of fixed offshore design codes. The Marine Structural Reliability Engineering Symposium (organised by The Society of Naval Architects and Marine Engineers, SNAME), 5-6 October, Arlington, VA, USA Moses F (1997) Problems and prospects of reliability-based optimization. Eng Struct 19(4): 293–301. https://doi.org/10.1016/S0141-0296(97)83356-1 Moses F, Stahl B (1979) Reliability analysis format for offshore structures. J Pet Technol 31(3): 347–354. https://doi.org/10.2118/7203-PA Mostafa YE, Hesham EI, Naggar M (2004) Response of fixed offshore platforms to wave and current loading including soil–structure interaction. Soil Dyn Earthq Eng 24(4): 357–368. https://doi.org/10.1016/j.soildyn.2003.11.008 Mourão A, Correia JAFO, Ávila B, Oliveira C, Ferradosa T, Carvalho H (2020) A combined high- and low-cycle fatigue damage evaluation using local damage parameters for an offshore jacket-type structure. Marit Eng - ICE 173(2): 43–57. https://doi.org/10.1680/jmaen.2019.24 [136] Mourão A, Correia JAFO, Castro JM, Correia M, Lesiuk G, Fantuzzi N, De Jesus AMP, Calcada RAB (2019) Fatigue damage analysis of offshore structures using hot-spot stress and notch strain approaches. Mater Res Proc 12(146–154): 10.21741/9781644900215–10.21741/9781644900221 Mousavi ME, Gardoni P (2014) A simplified method for reliability-and integrity-based design of engineering systems and its application to offshore mooring systems. Mar Struct 36: 88–104. https://doi.org/10.1016/j.marstruc.2014.02.001 Mreide TH, Amdahl J, Granliand T, Astrud OC (1986) Collapse analysis of framed offshore structures. The 18th Offshore Technology Conference (OTC 1986), 5–8 May, Houston Mustaffa Z, Gelder PV, Dawotola AW, Yu SY, Kim DK (2018) Reliability assessment for corroded pipelines in series consdiering length-scale effects. Int J Automot Mech Eng 15(3): 5607–5624. https://doi.org/10.15282/ijame.15.3.2018.16.0431 Ng CY, Kurian VJ, Yassir MEA (2011) Regression Analysis for the Dynamic Responses of Semi-Submersible Platform. The 7th International Conference on Steel and Aluminium Structures (ICSAS 2011), 13–15 July, Kuching, Sarawak Ng WK, Selamat MR, Choong KK (2010) Soil/pile set-up effects on driven pile in malaysian soil. Electron J Geotech Eng 15: 1–11 http://ejge.com/2010/Ppr10.003.pdf Nichols NW, Goh TK, Bahar H (2006) Managing structural integrity for ageing platform. The SPE Asia Pacific Oil & Gas Conference and Exhibition, 11-13 September, Adelaide, Australia Nikolaidis E, Ghiocel DM, Singhal S (2014) Engineering design reliability handbook. CRC Press, London Niu XN, Wickham AHS, Frieze PA (1990) Fracture mechanics and simplified analyses in probabilistic remaining life calculations for jacket structures. The 4th International Symposium on Integrity of Offshore Structures, 2-3 July, Glasgow, Scotland Nordal H, Cornell CA, Karamchandani A (1987) A structural system reliability case study of an eight-leg steel jacket offshore production platform. The Marine Structural Reliability Symposium, 5-6 October, Arlington, VA, USA Olufsen A, Leira BJ, Moan T (1992) Uncertainty and reliability analysis of jacket platform. J Struct Eng 118(10): 2699–2715. https://doi.org/10.1061/(ASCE)0733-9445(1992)118:10(2699) Onoufriou T (1999) Reliability based inspection planning of offshore structures. Mar Struct 12(7): 521–539. https://doi.org/10.1016/S0951-8339(99)00030-1 Onoufriou T, Frangopol DM (2002) Reliability-based inspection optimization of complex structures: a brief retrospective. Comput Struct 80(12): 1133–1144. https://doi.org/10.1016/S0045-7949(02)00071-8 Onoufriou T, Forbes VJ (2001) Developments in structural system reliability assessments of fixed steel offshore platforms. Reliab Eng Syst Saf 71(2): 189–199. https://doi.org/10.1016/S0951-8320(00)00095-8 Paik JK, Kim DK (2012) Advanced method for the development of an empirical model to predict time-dependent corrosion wastage. Corros Sci 63: 51–58. https://doi.org/10.1016/j.corsci.2012.05.015 Paik JK, Kim DK, Park DH, Kim HB, Kim MS (2012) A new method for assessing the safety of ships damaged by grounding. Int J Marit Eng 154(A1): 1–20. https://doi.org/10.3940/rina.ijme.2012.al.218 Paik JK, Kim DK, Park DH, Kim HB, Mansour AE, Caldwell JB (2013) Modified Paik-Mansour formula for ultimate strength calculations of ship hulls. Ships Offshore Struct 8: 245–260. https://doi.org/10.1080/17445302.2012.676247 Paik JK, Thayamballi AK, Lee JM (2004) Effect of initial deflection shape on the ultimate strength behavior of welded steel plates under biaxial compressive loads. J Ship Res 48(1): 45–60 https://doi.org/10.5957/jsr.2004.48.1.45 Park DK, Kim DK, Seo JK, Kim BJ, Ha YC, Paik JK (2015a) Operability of non-ice class aged ships in the Arctic Ocean—part I: ultimate limit state approach. Ocean Eng 102: 197–205. https://doi.org/10.1016/j.oceaneng.2014.12.040 Park DK, Kim DK, Seo JK, Kim BJ, Ha YC, Paik JK (2015b) Operability of non-ice class aged ships in the Arctic Ocean—part II: accidental limit state approach. Ocean Eng 102: 206–215. https://doi.org/10.1016/j.oceaneng.2015.04.038 Petruska DJ, Berek EP, Ingersoil RW, Valdivieso JB (1994) Assessment of vermilion 46-a platform. The 26th Offshore Technology Conference (OTC 1994), 2–5 May, Houstan Petrauskas C, Botelho DL (1994) A reliability model for offshore platforms and its application to ST151 "H" and "K" platforms during Hurricane Andrew (1992). The International Conference on the Behaviour of Offshore Structures (BOSS 1994), 12–15 July. Massachusetts, USA PTS (2010) Design of fixed offshore structures (PTS 34.19.10.30). PETRONAS Technical Standards, Kuala Lumpur, Malaysia Pueksap-anan P (2010) Sensitivity study for RSR of fixed offshore steel type platforms. MS. c. Dissertation, Asian Institute of Technology, Pathum Thani, Thailand Qin S, Cui W (2003) Effect of corrosion models on the time-dependent reliability of steel plated elements. Mar Struct 16(1): 15–34. https://doi.org/10.1016/S0951-8339(02)00028-X Rausche F, Robinson B, Likins G (2004) on the prediction of long term pile capacity from end-of-driving information. Contributions in honor of George G. Gobel (organised by ASCE), 27-31 July, Los Angeles, California Rashed SMH (1980) Behaviour to ultimate strength of tubular offshore structures by the idealized structural unit method (report SK, 51). Norwegian Institute of Technology, Trondheim, Norway Seber GAF, Wild CJ (2003) Nonlinear regression. Wiley, Hoboken, NJ, USA Shabakhty N (2004) Durable reliability of jack-up platforms. Dissertation, Delft University of Technology, Delft, Netherlands, Ph. D Shabakhty N, Boonstra H, van Gelder P (2003) System reliability of jack-up structures based on fatigue degradation. T Bedford & van Gelder (Eds. ), safety and reliability, 1437-1445 Shao S, Murotsu Y (1999) Approach to failure mode analysis of large structures. Probabilistic Eng Mech 14(1–2): 169–177. https://doi.org/10.1016/S0266-8920(98)00028-9 Skallerud B, Amdahl J (2002) Nonlinear analysis of offshore structures. Research Studies Press Ltd., Hertfordshire Skov R, Denver H (1988) Time-dependence of bearing capacity of piles. The 3rd International Conference on the Application of Stress-wave Theory to Piles, 25-27 may, Ottawa, Canada Sohn JM, Kim SJ (2019) Dynamic structural response characteristics of new concept blast walls under hydrocarbon explosions. Latin Am J Soild Struct 16(2): e161. https://doi.org/10.1590/1679-78255351 Solland G, Sigurdsson G, Ghosal A, Veritas DN (2011) Life extension and assessment of existing offshore structures. The SPE Project and Facilities Challenges Conference at METS, 13-16 February, Doha, Qatar Southwell CR, Bultman JD, Hummer CW (1979) Estimating service life of steel in seawater. Seawater Corrosion Handbook, Park Ridge Spiess AN, Neumeyer N (2010) An evaluation of R2 as an inadequate measure for nonlinear models in pharmacological and biochemical research: a Monte Carlo approach. BMC Pharmacol 10(6): 1–11. https://doi.org/10.1186/1471-2210-10-6 Stear JD, Bea RG (1997) Evaluating simplified analysis approaches for estimating the load capacities of Gulf of Mexico jacket-type platforms. The 16th International Conference on Offshore Mechanics and Arctic Engineering (OMAE 1997), 13–17 April, Yokohama Straub D, Papaioannou I (2014) Bayesian updating with structural reliability methods. J Eng Mech 141(3): 04014134. https://doi.org/10.1061/(ASCE)EM.1943-7889.0000839 Sturm A, Bea R, Miller T (1997) Reassessment and requalification of two Gulf of Mexico platforms. The 7th International Conference on Offshore and Polar Engineering (ISOPE 1997), 25–30 May, Honolulu Svinkin MR (1996) Overcoming soil uncertainty in prediction of construction and industrial vibrations. Proceedings of the uncertainty in the geologic environment: from theory to practice, C.D. Shackelford, P. Nelson, and M.J.S. Roth (Eds. ). Geotechnical Special Publications 58(2): 1178–1194 https://cedb.asce.org/CEDBsearch/record.jsp?dockey=0101900 Svinkin MR, Skov R (2000) Set-up effect of cohesive soils in pile capacity. The 6th International Conference on Application of Stress-wave Theory to Piles, 11-13 September, Sao Paulo, Brasil Toğan V, Karadeniz H, Daloğlu AT (2010) An integrated framework including distinct algorithms for optimization of offshore towers under uncertainties. Reliab Eng Syst Saf 95(8): 847–858. https://doi.org/10.1016/j.ress.2010.03.009 Tromans PS, van de Graaf JW (1994) Substantiated risk assessment of jacket structure. J Waterw Port Coast Ocean Eng 120(6): 535–556. https://doi.org/10.1061/(ASCE)0733-950X(1994)120:6(535) Tromans PS, Vanderschuren L (1995) Response based design conditions in the north sea: application of a new method, The 27th Offshore Technology Conference (OTC 1995), 1–4 may. Houston Ueda Y, Rashed SMH (1975) An ultimate transverse strength analysis of ship structures. J Soc Naval Archit Japan 13: 87–104 https://trid.trb.org/view/148397 van de Graaf JW, Tromans PS (1991) Statistical verification of predicted loading and ultimmate strength against observed storm damage for an offshore structure. The 23rd Offshore Technology Conference (OTC 1991), 6–9 May, Houstan van de Graaf JW, Tromans PS, Vanderschuren L, Jukui BH (1996) Failure probability of a jack-up under environmental loading in the Central North Sea. Mar Struct 9(1): 3–24. https://doi.org/10.1016/0951-8339(95)00001-M Vannan MT, Thompson HM, Griffin JJ, Gelpi SL (1994) An automated procedure for platform strength assessment. The 26th Offshore Technology Conference (OTC 1994), 2–5 May, Houston Veritas N (1992) Structural reliability analysis of marine structures (report). Det Norske Veritas (DNV), Oslo, Norway Visser RC (1995) Reassessment of platforms in cook inlet, Alaska, The 27th Offshore Technology Conference (OTC 1995), 1–4 may, Houstan Westlake HS, Puskar FJ, O'Connor PE, Bucknell JR (2006) The Role of Ultimate strength assessments in the structural integrity management (SIM) of offshore structures. The 38th Offshore Technology Conference (OTC 2006), 1–4 May, Houston Wong EWC, Kim DK (2018) A simplified method to predict fiatuge damage of TTR subjected to short-term VIV using artificial neural network. Adv Eng Softw 126: 100–109. https://doi.org/10.1016/j.advengsoft.2018.09.011 Yoo KK, Bacarreza O, Ferri Aliabadi MH (2020) A novel multi-fidelity modelling-based framework for reliability-based design optimisation of composite structures. Eng Comput, In-press https://doi.org/10.1007/s00366-020-01084-x Youssef SAM, Faisal M, Seo JK, Kim BJ, Ha YC, Kim DK, Paik JK, Cheng F, Kim MS (2016) Assessing the risk of ship hull collapse due to collision. Ships Offshore Struct 11(4): 335–350. https://doi.org/10.1080/17445302.2014.993110 Yu SY, Choi HS, Lee SK, Do CH, Kim DK (2013) An optimum design of on-bottom stability of offshore pipelines on soft clay. Int J Naval Archit Ocean Eng 5(4): 598–613 https://doi.org/10.2478/IJNAOE-2013-0156 Yu SY, Choi HS, Lee SK, Park KS, Kim DK (2015) Nonlinear soil parameter effects on dynamic embedment of offshore pipeine on soft clay. Int J Naval Archit Ocean Eng 7(2): 227–243 https://doi.org/10.1515/ijnaoe-2015-0016 Yu SY, Choi HS, Park KS, Kim YT, Kim DK (2017) Advanced procedure for estimation of pipeline embedment on soft clay seabed. Struct Eng Mech 62(4): 381–389 https://koreascience.or.kr/journal/view.jsp?kj=KJKHB9&py=2017&vnc=v62n4&sp=381 Yu X (1996) Reliability and durability based design sensitivity analysis and optimization. Ph. D. Dissertation, University of Iowa, Iowa City, IA, USA Zafarullah N (2013) Environmental load factors and system strength evaluation of jacket platforms in offshore Malaysia. Ph. D. Dissertation, Universiti Teknologi PETRONAS, Seri Iskandar, Perak Zaghloul H (2008) Calibration of deterministic parameters for reassessment of offshore platforms in the Arabian gulf using reliability-based method. Dissertation, The University of Western Australia, Crawley, WA, Australia, Ph. D Zhang MQ, Beer M, Quek ST, Choo YS (2010) Comparison of uncertainty models in reliability analysis of offshore structures under marine corrosion. Struct Saf 32(6): 425–432. https://doi.org/10.1016/j.strusafe.2010.04.003