Buckling Performances of Spherical Caps Under Uniform External Pressure
https://doi.org/10.1007/s11804-020-00125-7
-
Abstract
This study aims to experimentally and numerically examine the buckling performances of stainless steel spherical caps under uniform external pressure. Three laboratory-scale caps were fabricated, measured, and tested. The buckling behaviors of these caps were investigated through experiments and three numerical methods, namely, nonlinear Riks algorithm, nonlinear bifurcation, and linear elastic analysis. The buckling of equal-radius caps was numerically analyzed with different methods to identify their applicability under different wall thicknesses. The results obtained from the nonlinear Riks algorithm are in good agreement with the experimental results, which means the nonlinear Riks algorithm can accurately predict the buckling performances of spherical caps, including the magnitude of critical buckling loads and the deformation of post-buckling modes. The nonlinear bifurcation algorithm is only suitable for predicting the buckling loads of ultra-thin or large-span caps, and the linear buckling method is inappropriate for predicting the buckling of metal spherical caps.-
Keywords:
- Spherical cap ·
- Stainless steel ·
- Buckling ·
- External pressure ·
- Bifurcation buckling ·
- Critical buckling
Article Highlights• The buckling of a series of equal-radius caps of various wall thicknesses is numerically analyzed.• The buckling of three externally pressurized stainless steel spherical caps is experimentally examined.• The experimental data is compared with the predicted values of three different numerical methods. -
1 Introduction
Domed caps have long received considerable research attention owing to their high pressure-supporting capacity. Accordingly, they have been widely used as end closures on cylindrical pressure vessels or as hatches to cover the access holes of subsea pressure hulls (Krivoshapko 2007; Jasion and Magnucki 2015a; Ifayefunmi 2016; Tripathi et al. 2016). However, such caps are prone to lose stability, characteristics that are strongly affected by geometric configurations, inevitable initial imperfections, and wall thickness of the caps (Błachut 2009; Wang et al. 2019; Zhang et al. 2019).
The buckling of domed caps with various geometric configurations and initial geometric imperfections has been extensively studied under uniform external pressure. Domed caps, including hemispheres (Błachut et al. 1990; Błachut and Galletly 1995; Błachut 2009; Błachut 2016a), torispheres (Błachut et al. 1990; Błachut 2016a, b; Warrington 1984), ellipsoids (Błachut 2016a, b; Galletly et al. 1987; Jasion and Magnucki 2015b; Magnucki et al. 2018), toricones (Błachut 2014; Błachut 2016b; Findlay and Timmins 1984; Galletly et al. 1987), and partial spheres (Zhang et al. 2017a, b; Zhang et al. 2018), have been investigated. The buckling performances of spherical caps with initial geometrical imperfections taking the forms of a linear buckling mode (Wang et al. 2019; Zhang et al. 2018; Zhang et al. 2019), local inward dimple (Błachut and Galletly 1990; Błachut 2015; Wang et al. 2019), and increased-radius (Błachut 2015; Wang et al. 2019) and force-induced dimples (Błachut 2015; Wang et al. 2019) have also gained considerable attention. Most related studies have focused on the buckling of caps with medium wall thickness and the buckling based on the Riks algorithm in the ABAQUS code (Lee et al. 2016; López Jiménez et al. 2017; Gerasimidis et al. 2018; Wagner et al. 2018; Zhang et al. 2017b). Moreover, most studies are entirely numerical investigations.
In the present study, the buckling behaviors of stainless steel spherical caps were experimentally and numerically examined under uniform external pressure. Three laboratory-scale spherical caps were fabricated, measured, and tested to collapse. Comparisons between the collapse loads and corresponding buckling loads computed with different numerical methods were carried out. Furthermore, the buckling of spherical caps with different radius-to-thickness ratios was numerically studied to obtain the best method for the buckling prediction of caps with different wall thicknesses. The results of this study may have some potential applications in the deep-sea field.
2 Material and Methods
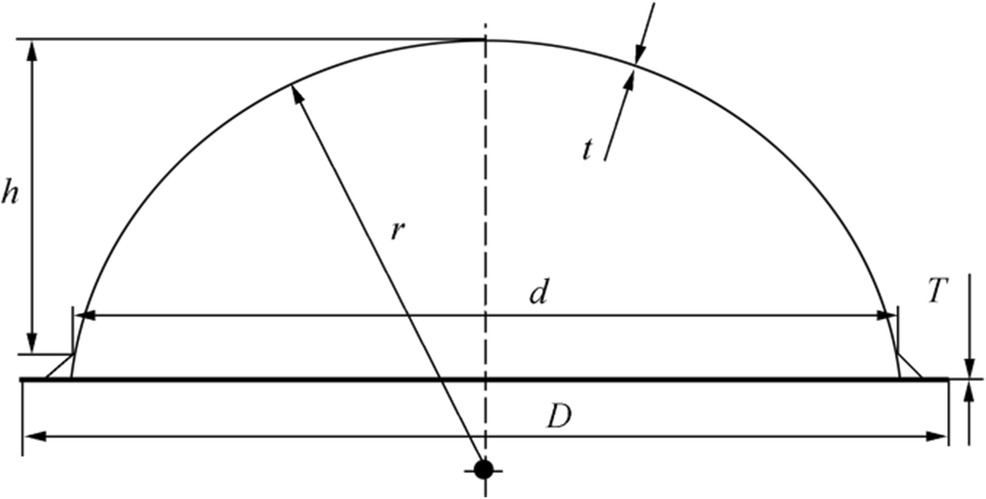
On the basis of a previous study, the optimal configuration of the spherical cap with a height-to-diameter ratio of h/d ≈ 0.274 was conducted (Zhang et al. 2018). A total of 304 stainless steel spherical caps were fabricated with the same nominal base diameter (d) of 145 mm, uniform wall thickness (t) of 1 mm, height (h) of 39.73 mm, and radius (r) of 86 mm. To ensure a nearly fixed constraint, each cap was welded on a heavy metal plate with a nominal diameter of D = 170 mm and nominal wall thickness of T = 20 mm (Figure 1).
The wall thickness of each cap was ultrasonically measured at 10 equidistant points on each of eight equally spaced meridians, yielding a total of 73 measurement sites on each cap. Table 1 lists the obtained minimum tmin, maximum tmax, and average tave magnitudes of wall thickness and the corresponding standard deviations tstd and nominal values tnom. The wall thickness of the caps varied from 1.013 to 1.086 mm, and the average value was 1.040 mm, which was close to the nominal value of 1 mm. Thus, the nominal wall thickness of the spherical caps can be used to study their pressure-supporting capacity.
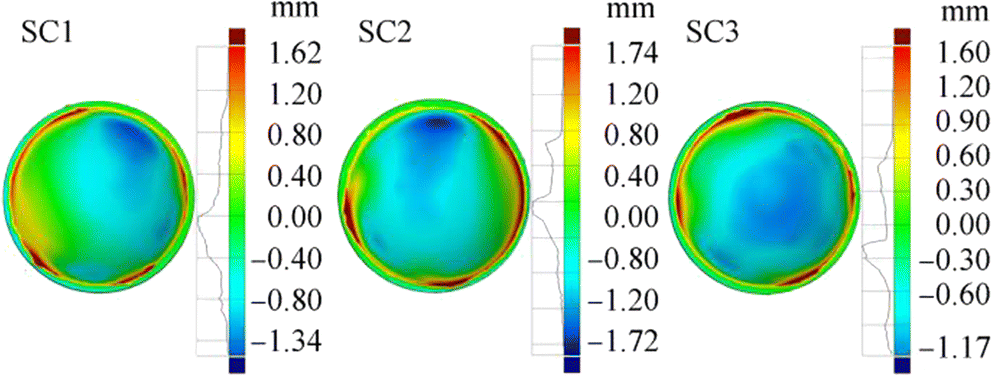
Table 1 Nominal tnom, maximum tmax, minimum tmin, and average tave wall thicknesses of all the fabricated spherical caps and the corresponding standard deviations tstd and experimental and numerical buckling loadsSample tnom (mm) tmin (mm) tmax (mm) tave (mm) tstd (mm) pcoll (MPa) $p_{{\rm{numerics}}}^{{\rm{cri}}}{\rm{ }}({\rm{MPa}})$ $p_{{\rm{numerics}}}^{{\rm{bif}}}{\rm{ }}({\rm{MPa}})$ $p_{{\rm{numerics}}}^{{\rm{lin}}}({\rm{MPa}})$ SC1 1 1.020 1.053 1.032 0.011 5.077 5.423 (1.068) 19.139 (3.822) 22.718 (4.537) SC2 1 1.013 1.080 1.041 0.018 5.036 4.610 (0.915) 14.883 (2.955) 19.006 (3.774) SC3 1 1.028 1.086 1.046 0.017 5.709 5.330 (0.934) 18.253 (3.197) 22.972 (4.024) Before the hydrostatic test, the outer surface of each fabricated cap was scanned in the form of a point cloud using Open Technologies Corporation (accuracy ≤ 0.02 mm) to acquire geometric shapes. The radius deviations between the fabricated and perfect caps are very small (Figure 2); only the base of the cap shows a relatively large deviation owing to the welding deformation. These caps exhibit similar radius deviations, indicating repeatability.
After the pretests, three spherical caps were sequentially immersed into a hydrostatic test rig, which was fabricated for the experiments. To avoid the concentrated force created by the dive, the heavy plate affixed to the experimental cap was required to make contact with the bottom of the chamber to prevent any external force from affecting the experimental results. The pressure inside the vessel was recorded using a pressure sensor, and the pressure was slowly applied through the medium of water in increments of ~ 0.1 MPa using a programmable logic controller.
To characterize the parent material properties, four flat tension coupons were designed in accordance with a modified version of ASTM D638 (ASTM 2003). The measurement approaches are detailed in Zhang et al. (2018). The properties of the experimentally measured cap material (304 stainless steel) are as follows: Young's modulus E = 159.208GPa, yield stress σy = 335.408 MPa, and Poisson's ratio μ = 0.291.
3 Results and Discussion
3.1 Experimental Analysis
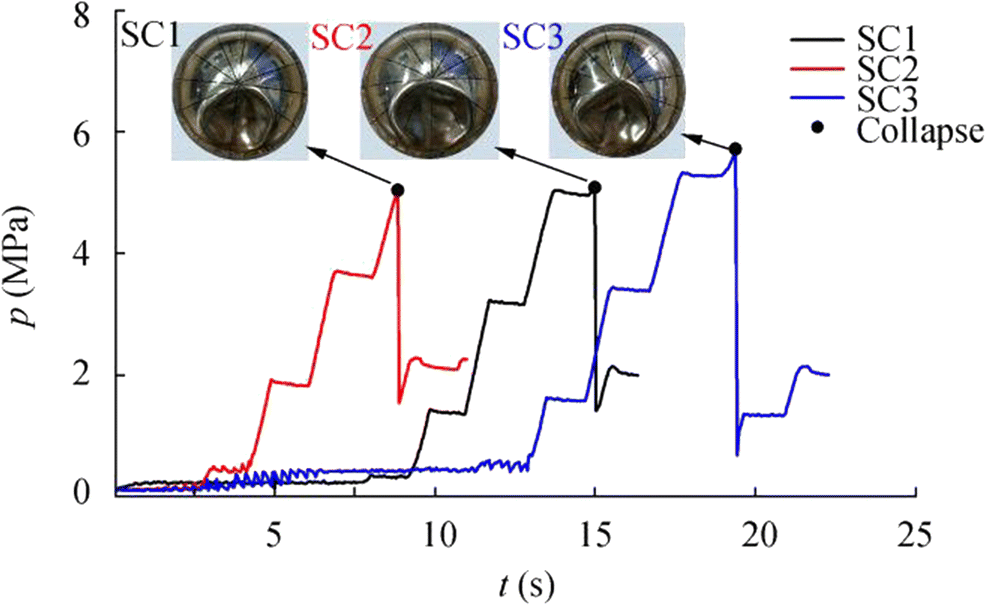
As indicated in Figure 3, all the curves have a similar trend; that is, they first increase up to the peak value (the collapse load), beyond which the pressures drop drastically. The collapse loads can be easily identified in Figure 3, and all caps take the form of a single local dimple near the base, indicating a reasonable repeatability. The collapse loads pcoll from the tests are listed in the seventh column of Table 1. The collapse loads of the spherical caps range from 5.036 to 5.709 MPa. The variations in wall thickness, shape, and material hardening during the stamping and welding processes may have caused the range in collapse loads. Nevertheless, this slight change indicates the adequate repeatability of the hydrostatic tests.
3.2 Analysis of the Numerical Methods
To evaluate the buckling behaviors of the tested spherical caps, their critical, bifurcation, and linear buckling computations were performed. The finite elements of the caps were freely and uniformly generated on the measured geometries (Figure 4). The S4 shell elements and few S3 elements were chosen to prevent hourglassing. Mesh convergence studies were performed to establish approximately 15 000 elements for each model (Zhang et al. 2018). The material properties were the same as those presented in Section 2. For each spherical cap, the wall thickness was assumed to be the average wall thickness presented in Table 1. Fixed boundary conditions were applied, which were consistent with the test conditions presented in Section 2.
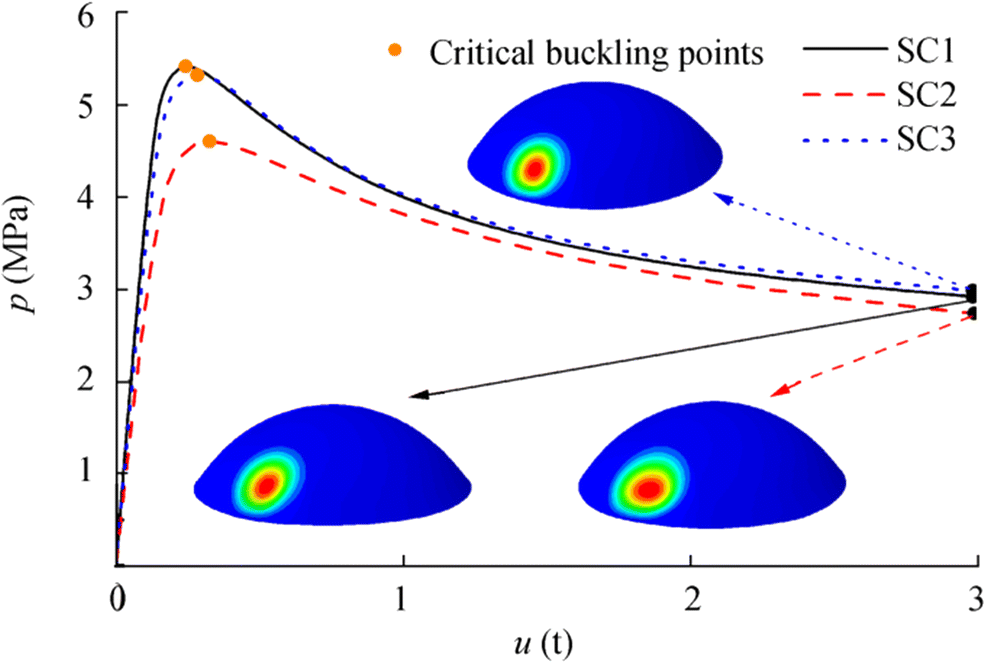
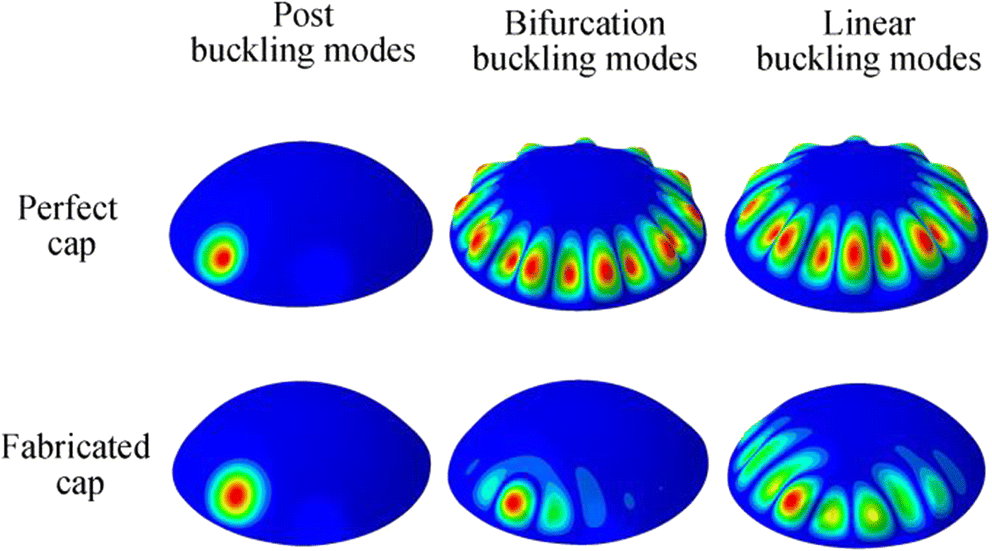
The critical $ \left({p}_{\mathrm{numerics}}^{\mathrm{cri}}\right) $, bifurcation $ \left({p}_{\mathrm{numerics}}^{\mathrm{bif}}\right) $, and linear $ \left({p}_{\mathrm{numerics}}^{\mathrm{lin}}\right) $buckling pressures are listed in the eighth, ninth, and tenth columns of Table 1, respectively, along with the ratios of the numerical values to the experimental values in the parentheses. The ratios of $ {p}_{\mathrm{numerics}}^{\mathrm{cri}} $ to pcoll varied from 0.915 to 1.068. These values were almost equal to those obtained from the experiments, and the slight differences may have been caused by the assumption of the average wall thickness value and the properties of the parent material. However, the magnitude of $ {p}_{\mathrm{numerics}}^{\mathrm{bif}} $ and $ {p}_{\mathrm{numerics}}^{\mathrm{lin}} $ is much larger than that for pcoll, indicating that the two methods are not suitable for the prediction of the pressure-supporting capacity of spherical caps with medium wall thickness. In addition, the post-buckling modes of the three scanned caps were in the form of local dimples, consistent with the experimental results (Figure 5). The modes of bifurcation and linear buckling are far from those in the experimental results (Figure 6). Thus, a nonlinear calculation based on the Riks algorithm in the ABAQUS code may be more suitable for the buckling prediction of spherical caps with medium wall thickness.
3.3 Buckling of Caps with Various Wall Thicknesses
To investigate the effects of the wall thickness on the buckling of spherical caps, equal-radius spherical caps of various wall thicknesses were established. These caps have the same geometrical configurations and material properties as the fabricated caps presented in Section 2, except for the wall thickness. The cap radius-to-thickness ratio ranges from 50 to 1000, which are detailed in Table 2. For each cap, the nonlinear Riks algorithm, nonlinear bifurcation, and linear elastic analysis were conducted. The buckling loads of the three methods are listed in the last three columns in Table 2, and the ratios of the bifurcation (pbif) and linear (plin) buckling loads to the critical buckling loads (pcri) are listed in the parentheses in the corresponding column. In all the analyses, the element type and boundary conditions are the same as those in Section 3.2.
Table 2 Critical, bifurcation, and linear buckling loads for spherical caps with different radius-to-thickness ratiosr (mm) t (mm) r/t Pcri (MPa) Pbif (MPa) Plin (MPa) 86 1.72 50 13.0804 78.2298 (5.981) 79.8670 (6.106) 86 1 86 7.3672 25.5586 (3.469) 26.5910 (3.609) 86 0.860 100 6.2493 18.6212 (2.980) 19.5990 (3.136) 86 0.430 200 2.7521 4.2746 (1.553) 4.8612 (1.766) 86 0.287 300 1.5997 1.7704 (1.107) 2.1598 (1.350) 86 0.215 400 0.9632 0.9724 (1.010) 1.2154 (1.262) 86 0.172 500 0.6205 0.6219 (1.002) 0.7789 (1.255) 86 0.143 600 0.4290 0.4304 (1.003) 0.5415 (1.262) 86 0.123 700 0.3180 0.3185 (1.002) 0.3990 (1.255) 86 0.108 800 0.2457 0.2561 (1.042) 0.3057 (1.244) 86 0.096 900 0.1949 0.1950 (1.001) 0.2421 (1.242) 86 0.086 1000 0.1566 0.1567 (1.001) 0.1962 (1.253) As shown in Table 2, as the radius-to-thickness ratio r/t increases, the ratio of pbif to pcri decreases. When this ratio becomes large enough, such that r/t > 300, the two buckling loads are basically the same. This result indicates that the bifurcation buckling algorithm is more suitable for the buckling prediction of ultra-thin or large-span caps compared with the Riks method because the calculation is simpler and faster. Linear buckling loads share similar trends with bifurcation buckling loads. However, even when the ratio r/t is as large as 1000, the magnitude of plin is still much larger than pcri, indicating that the linear buckling method may not be suitable for the buckling prediction of metal spherical caps. In addition, as indicated in Figure 6, except for the buckling mode of the Riks method that is well consistent with the experimental results, the other two methods cannot predict the damage form of the spherical cap.
4 Conclusions
In this work, the buckling behaviors of three spherical caps with medium wall thickness were experimentally and numerically investigated, and the accuracy of different numerical methods was measured. Furthermore, the numerical results for the buckling of equal-radius spherical caps with various wall thicknesses were obtained.
The results presented in this work show that the critical buckling load, obtained from the Riks method available in the ABAQUS code, can accurately predict the pressure-supporting capacity of spherical caps. Moreover, the bifurcation buckling algorithm is more suitable for predicting the magnitude of buckling loads of ultra-thin or large-span caps. However, the linear buckling method cannot be used to predict the buckling of metal spherical caps. Experiments on the buckling of thin-walled spherical caps can lay a solid foundation for further studies.
-
Table 1 Nominal tnom, maximum tmax, minimum tmin, and average tave wall thicknesses of all the fabricated spherical caps and the corresponding standard deviations tstd and experimental and numerical buckling loads
Sample tnom (mm) tmin (mm) tmax (mm) tave (mm) tstd (mm) pcoll (MPa) $p_{{\rm{numerics}}}^{{\rm{cri}}}{\rm{ }}({\rm{MPa}})$ $p_{{\rm{numerics}}}^{{\rm{bif}}}{\rm{ }}({\rm{MPa}})$ $p_{{\rm{numerics}}}^{{\rm{lin}}}({\rm{MPa}})$ SC1 1 1.020 1.053 1.032 0.011 5.077 5.423 (1.068) 19.139 (3.822) 22.718 (4.537) SC2 1 1.013 1.080 1.041 0.018 5.036 4.610 (0.915) 14.883 (2.955) 19.006 (3.774) SC3 1 1.028 1.086 1.046 0.017 5.709 5.330 (0.934) 18.253 (3.197) 22.972 (4.024) Table 2 Critical, bifurcation, and linear buckling loads for spherical caps with different radius-to-thickness ratios
r (mm) t (mm) r/t Pcri (MPa) Pbif (MPa) Plin (MPa) 86 1.72 50 13.0804 78.2298 (5.981) 79.8670 (6.106) 86 1 86 7.3672 25.5586 (3.469) 26.5910 (3.609) 86 0.860 100 6.2493 18.6212 (2.980) 19.5990 (3.136) 86 0.430 200 2.7521 4.2746 (1.553) 4.8612 (1.766) 86 0.287 300 1.5997 1.7704 (1.107) 2.1598 (1.350) 86 0.215 400 0.9632 0.9724 (1.010) 1.2154 (1.262) 86 0.172 500 0.6205 0.6219 (1.002) 0.7789 (1.255) 86 0.143 600 0.4290 0.4304 (1.003) 0.5415 (1.262) 86 0.123 700 0.3180 0.3185 (1.002) 0.3990 (1.255) 86 0.108 800 0.2457 0.2561 (1.042) 0.3057 (1.244) 86 0.096 900 0.1949 0.1950 (1.001) 0.2421 (1.242) 86 0.086 1000 0.1566 0.1567 (1.001) 0.1962 (1.253) -
ASTM International (2003) ASTM D638-14: standard test method for tensile properties of plastics. ASTM International, West Conshohocken Błachut J (2009) Buckling of multilayered metal domes. Thin-Walled Struct 47: 1429–1438. https://doi.org/10.1016/j.tws.2009.07.011 Błachut J (2014) Externally pressurized toricones-buckling tests. Shell structures–theory and applications, vol. 3, CRC-Press Taylor & Francis, Boca Raton, 183–186 Błachut J (2015) Locally flattened or dented domes under external pressure. Thin-Walled Struct 97: 44–52. https://doi.org/10.1016/j.tws.2015.08.022 Błachut J (2016a) Buckling of composite domes with localised imperfections and subjected to external pressure. Compos Struct 153: 746–754. https://doi.org/10.1016/j.compstruct.2016.07.007 Błachut J (2016b) Buckling of externally pressurized steel toriconical shells. Int J Press Vessel Pip 144: 25–34. https://doi.org/10.1016/j.ijpvp.2016.05.002 Błachut J, Galletly GD (1990) Buckling strength of imperfect spherical caps—some remarks. AIAA J 28(7): 1317–1319. https://doi.org/10.2514/3.25214 Błachut J, Galletly GD (1995) Buckling strength of imperfect steel hemispheres. Thin-Walled Struct 23: 1–20. https://doi.org/10.1016/0263-8231(95)00001-T Błachut J, Galletly GD, Moreton DN (1990) Buckling of near-perfect steel torispherical and hemispherical shells subjected to external pressure. AIAA J 28(11): 1971–1975. https://doi.org/10.2514/3.10506 Findlay GE, Timmins W (1984) Toriconical heads: a parametric study of elastic stresses and implications on design. Int J Press Vessel Pip 15(3): 213–227. https://doi.org/10.1016/0308-0161(84)90058-9 Galletly GD, Kruzelecki J, Moffat DG, Warrington B (1987) Buckling of shallow torispherical domes subjected to external pressure–a comparison of experiment, theory, and design codes. J Strain Anal Eng Des 22(3): 163–175. https://doi.org/10.1243/03093247V223163 Gerasimidis S, Virot E, Hutchinson JW, Rubinstein SM (2018) On establishing buckling knockdowns for imperfection-sensitive shell structures. J Appl Mech 85: 091010-1–091010-14. https://doi.org/10.1115/1.4040455 Ifayefunmi O (2016) Buckling behavior of axially compressed cylindrical shells: comparison of theoretical and experimental data. Thin-Walled Struct 98: 558–564. https://doi.org/10.1016/j.tws.2015.10.027 Jasion P, Magnucki K (2015a) Elastic buckling of Cassini ovaloidal shells under external pressure – theoretical study. Archives of Mechanics 67(2): 179–192 Jasion P, Magnucki K (2015b) Stability of an ellipsoidal head with a central nozzle under axial load. Arch Civ Eng 61(2): 89–98. https://doi.org/10.1515/ace-2015-0016 Krivoshapko SN (2007) Research on general and axisymmetric ellipsoidal shells used as domes, pressure vessels, and tanks. Appl Mech Rev 60(6): 336–355. https://doi.org/10.1115/1.2806278 Lee A, Marthelot J, Hutchinson JW, Reis PM (2016) The geometric role of precisely engineered imperfections on the critical buckling load of spherical elastic shells. J Appl Mech 83: 111005-1–111005-11. https://doi.org/10.1115/1.4034431 López Jiménez F, Marthelot J, Lee A, Hutchinson JW, Reis PM (2017) Technical brief: knockdown factor for the buckling of spherical shells containing large-amplitude geometric defects. J Appl Mech 84: 034501-1–034501-4. https://doi.org/10.1115/1.4035665 Magnucki K, Jasion P, Rodak M (2018) Strength and buckling of an untypical dished head of a cylindrical pressure vessel. Int J Press Vessel Pip 161: 17–21 Tripathi SM, Anup S, Muthukumar R (2016) Effect of geometrical parameters on mode shape and critical buckling load of dished shells under external pressure. Thin-Walled Struct 106: 218–227. https://doi.org/10.1016/j.tws.2016.02.011 Wagner HNR, Hühne C, Niemann S (2018) Robust knockdown factors for the design of spherical shells under external pressure: development and validation. Int J Mech Sci 141: 58–77. https://doi.org/10.1016/j.ijmecsci.2018.03.029 Wang YY, Tang WX, Zhang J, Zhang S, Chen Y (2019) Buckling of imperfect spherical caps with fixed boundary under uniform external pressure. Mar Struct 65: 1–11. https://doi.org/10.1016/j.marstruc.2019.01.004 Warrington B (1984) The buckling of torispherical shells under external pressure. PhD thesis, The University of Liverpool, Liverpool. DOI: https://doi.org/10.1016/j.ijpvp.2018.02.003 Zhang J, Zhu BY, Wang F, Tang WX, Wang WB, Zhang M (2017a) Buckling of prolate egg-shaped domes under hydrostatic external pressure. Thin-Walled Struct 119:296–303. https://doi.org/10.1016/j.tws.2017.06.022 Zhang M, Tang WX, Wang F, Zhang J, Cui WC, Chen Y (2017b) Buckling of bi-segment spherical shells under hydrostatic external pressure. Thin-Walled Struct 120:1–8. https://doi.org/10.1016/j.tws.2017.08.017 Zhang J, Wang YY, Wang F, Tang WX (2018) Buckling of stainless steel spherical caps subjected to uniform external pressure. Ships Offshore Struc 13(7): 779–785. https://doi.org/10.1080/17445302.2018.1459358 Zhang J, Wang YY, Tang WX, Zhu YM, Zhao XL (2019) Buckling of externally pressurised spherical caps with wall-thickness reduction. Thin-Walled Struct 136:129–137. https://doi.org/10.1016/j.tws.2018.12.005