1   Introduction

Ships produce significant noise levels, thus ruining the marine habitat in the oceans. One of the most affected fish is the blue whale because their communication at low frequencies coincides with the acoustic wakes of ship propellers. Changes in blue whales' call level and rate were observed in seas where heavy marine traffic was found (McKenna 2011). The daily lives of other marine animals were also reported to be affected, from searching for food to avoiding danger (Dekeling 2014), resulting in a change of residence, and loss of their original habitat.

The International Maritime Organization plans to limit the noise levels of ships, but such attempts have not yet been finalized due to insufficient knowledge about underwater acoustics (Ianniello et al. 2013). This lack of knowledge in state of the art of hydroacoustics can only be addressed by research developments. To fill this knowledge gap, great interest is being shown recently in the use of advanced acoustic methods, such as acoustic analogies. Some examples will be explained in this section briefly. Mousavi et al. (2014) carried out a numerical simulation of the hydrodynamic noise around a DTMB 4119 marine propeller. Large eddy simulation was adopted to calculate the hydrodynamic parameters, and the Ffowcs Williams-Hawkings (FW-H) model was used to predict the spectral distribution of flow noise for different advance coefficients. As the advance coefficient decreases, acoustic wave pressure periods also decrease, and the acoustic pressure range increases. This finding indicates that the highest intensity of the noise recorded by different hydrophones occurred in the blade passing frequency (BPF). Both hydrodynamic and acoustic performances should be taken into consideration in propeller design. The assessment of the radiated noise is made by model scale tests in cavitation tunnels, which is cheap and available (Bertschneider et al. 2014). However, to deduce the correct far-field noise level, finding an appropriate method of scaling the near-field measurements to full-scale is difficult. Therefore, sea trials and full-scale testing remain the best ways to assess noise levels (Brooker and Humphrey 2014; Aktas et al. 2015).

A numerical analysis on the effect of tip rake angle on sound pressure level around a DTMB 4382 marine propeller was carried out by Ghassemi et al. (2018). They found that increasing the rake in negative or positive values can decrease sound pressure levels to 40% for ± 6° rake angles. Pan and Zhang (2010) studied numerically the hydrodynamic noise of the DTMB 4118 marine propeller in uniform flow by implementing detached eddy simulation. The tonal peaks at multiple BPFs can be clearly seen on the spectrum curves, and the increase in broadband noise is due to vortex shedding separated from the trailing edge and blade tips at a large angle of attack. Bagheri et al. (2015) numerically and experimentally examined the hydrodynamic and hydroacoustic performances of the DTMB 4119 propeller under cavitating and noncavitating cases. To extract the total sound pressure levels, FW-H equations are used. Results reveal the impact of cavitation on propeller noise. Seol et al. (2002) performed a numerical investigation to analyze the noise under noncavitating condition in different operating conditions by using the DTMB 4119 propeller and KA4-70 propeller with and without a duct. The FW-H equation is coupled by the panel method to predict far-field noise levels. Their results suggest that ducts are less effective in the far-field and more effective at higher frequencies.

Propellers behave significantly differently when located behind the stern of a ship. Open-water propeller curves present the general performances of the propeller. However, propellers are subjected to a non-uniform flow under self-propulsion conditions (Kinaci et al. 2018; Gokce et al. 2018; Jasak et al. 2019). Özden et al. (2014) numerically studied the noise of an INSEAN E1619 propeller in open-water and behind a DARPA suboff submarine under a noncavitating condition. The wake profile of the ship was first obtained from resistance tests. Then, it was numerically imposed at the inlet as a boundary condition. Results were compared with the rotating propeller case behind the submarine under self-propulsion condition. Similar noise spectra were obtained in both cases. Sezen et al. (2016) carried out computational analysis to predict hydrodynamic and hydroacoustic performances around a three-bladed marine propeller in a noncavitating case. Hydrodynamic performances were in good agreement with experiments. Hydroacoustic results reveal that the noise level increases proportionally with propeller revolution and is in relation with the vorticity magnitude, which is higher around the propeller blade tip. Ekinci et al. (2010) performed a numerical investigation of the hydrodynamic performances of marine propellers. The open-water characteristics are calculated using lifting surface method, and good agreement with experiment results was obtained. Noise level prediction based on propeller blade cavitation was investigated using empirical formulations for low frequencies under uniform and non-uniform flow conditions. Empirically generated noise spectra showed good agreement, and the method was suggested especially for propellers at preliminary design stages.

This study aims to partially fill this gap by calculating and comparing hydrodynamic performances and noise levels between the highly skewed (HSP) and conventional (CP) Seiun Maru propellers under specific flow conditions. Mathematical background and numerical implementation were briefly explained first. Then, the numerical approach was validated by experiments and the quasi-continuous method (SQCM) found in the literature both for open-water and behind non-uniform ship hull wake cases. With the use of the FW-H equation, near-field noise radiation was predicted by means of Reynolds-averaged Navier-Stokes (RANS) solver. Finally, hydrodynamic and hydroacoustic comparisons were made between the propellers.

2   Propeller Geometry

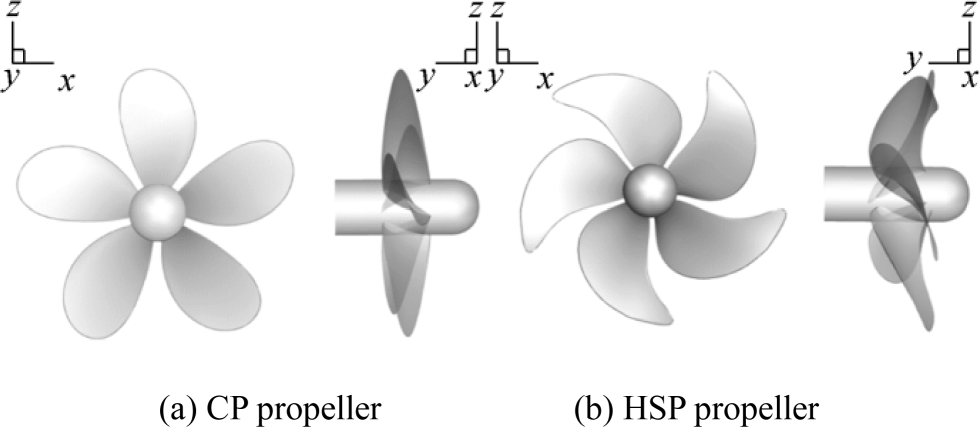
Seiun Maru CP and HSP are five-bladed marine propellers designed in Japan. CP has a modified MAU section with a fixed radial pitch, while HSP has a modified SRI-B section characterized by a variable radial pitch. The propellers have diameters of 3.6 m and are widely used as benchmarks for flow simulations (Carlton 2012). Propellers are modeled using a Fortran code based on the geometric characteristics, and the spatial point coordinates for different cross sections are provided (Belhenniche et al. 2016). The main particulars of the two propellers are summarized in Table 1, and propeller geometries are shown in Figure 1.

Figure  1  Conventional and highly skewed Seiun Maru marine propeller geometries

Download: Full-Size Img

3   Computational Details for Open-Water and Behind-Ship-Hull Conditions

Details of the numerical implementation used are given in this section. Two different cases are examined in this study: open-water and behind-ship-hull cases. The numerical setup was kept similar in both cases as much as possible. Deviations were present where necessary and explained in this section.

3.1   Governing Equations

To obtain the velocity and pressure fields, the conservation form of the unsteady Navier-Stokes equation along with momentum equations was numerically solved. The equations are described as follows:

where u_i is the averaged velocity, p is the averaged pressure, ρ is the density, μ is the dynamic viscosity, and $ -\overline{\rho {u}_i^{\prime }{u}_j^{\prime }} $ is the Reynolds stress. A well-known fact is that the open-water characteristics can be described by the following no dimensional equations:

The Reynolds number of the propeller based on chord length at 0.7R is defined as:

where n denotes the rotational speed; D refers to the propeller diameter; T is the thrust; Q is the torque; ρ and ν are the density and the kinematic viscosity of water, respectively; and C_0.7R is the chord length at 0.7R. For noise prediction, FW-H method is a solution developed from the Lighthill equation (Lighthill 1954; Ffowcs Williams and Hawkings 1969) and is derived from continuity and momentum equations. This equation is a good approach to extract sound pressure levels to the far field. Lighthill's acoustic analogy is given as follows:

where

where T_ij is the Lighthill stress sensor, the first term in the right side represents the Reynolds stresses, the second term is due to changes in pressure and density, and the last term is due to the shear stress tensor. The FW-H equation is represented as follows:

where p^′ is the sound pressure defined by p^′ = p − p₀ and c₀ denotes the sound speed in the far field. δ(f) is the Dirac delta function, and f is the function of the moving boundary f(x,  t) = 0. P_ij is the compressive stress tensor defined as follows:

The first term on the right-hand side of Eq. (9) is the quadruple source, which was neglected in this study because the speed of sound is faster than the propeller rotational speed. This term is considered only for high Mach numbers. Brentner and Farassat proposed a correlation (Farassat 2007), which is a solution to the FW-H equation in the time domain. In their formulation, the pressure field is defined as follows:

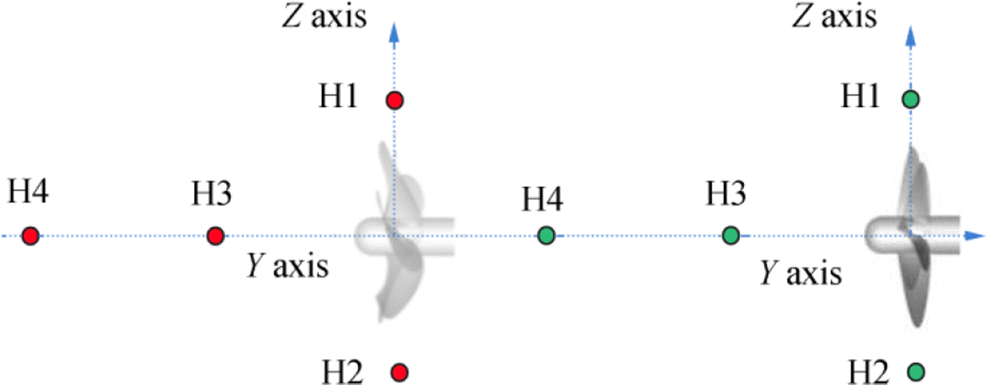
where $ {P}_T^{\prime } $ denotes the acoustic pressure level due to thickness and $ {P}_L^{\prime } $ describes the acoustic pressure level due to loading. The two acoustic pressures, $ {P}_T^{\prime } $ and $ {P}_L^{\prime } $, correspond to the monopole and the dipole sources, respectively, e.g., blade thickness rotation and unsteady sheet cavity volume fluctuations are modeled as monopole sources, and blade surface pressure fluctuations are modeled as a dipole source term (Seol et al. 2005). Four receivers were located in the wake and propeller disk. Figure 2 represents the hydrophone arrangements around CP and HSP Seiun Maru marine propellers.

Figure  2  Arrangement of hydrophone locations. Locations are similar for both propellers

Download: Full-Size Img

Hydrophones were positioned on the radial and rotation axis, with two hydrophones for each axis. Table 2 shows the geometrical arrangement of all hydrophones used in this study.

3.2   Grid Sensitivity Study

Determining the correct pressure distributions on the propeller surfaces is vital to obtain reliable hydroacoustic results.

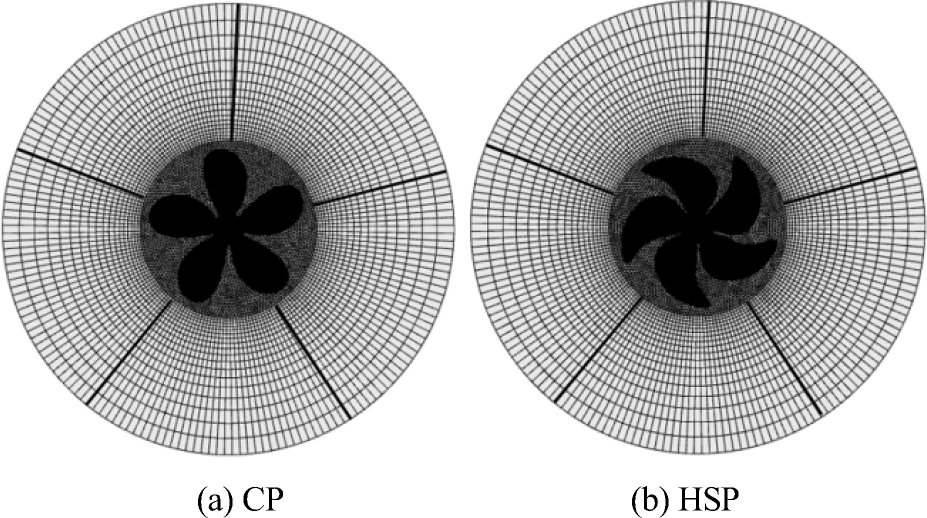
Therefore, at this point of the study, we present a grid sensitivity study that was carried out before continuing on to numerically solve propeller noise. To control the mesh size, the computational domain was divided into 18 blocks. Three inner blocks with one inner block surrounded the propeller, and these inner blocks were covered by 15 outer blocks. A hybrid mesh was adopted for the computational domain; tetrahedral elements were applied for the inner blocks, while hexahedral elements were used for the outer blocks. The blades and the shaft were meshed using constant tetra cells. As stated before, grid structure is important in resolving the pressure distribution along the propeller; therefore, we abstained from using an automatic meshing software. We used a relatively old software called Gambit to manually discretize the fluid domain with a meticulous grid structure.

To determine the effect of grid systems on the results, the grid sensitivity was studied by using a grid refinement ratio $ {r}_G=\sqrt{2} $ (Stern et al. 1999). Three grids were used and referred to as coarse, medium, and fine grids. Illustrations of the grids generated on the propeller are shown in Figure 3. ANSYS TGrid 14.0 was used to solve the turbulent boundary layer on solid surfaces. The propeller domain generated in Gambit was exported into TGrid, where four layers of prismatic cells were attached to the blade surface. For the medium mesh, the first cell height of the solid surface was approximately 0.001065D, and the average y⁺ on the propellers was within 10–120 (see Figure 4), which was suitable for the turbulence model implemented in this study. Propulsion parameters K_T, 10K_Q, and η₀ were evaluated to assess the suitability of the grid structure. Details of the grid system used for the sensitivity study are shown in Tables 3 and 4.

Figure  3  Grid implementation on the surfaces of Seiun Maru conventional and highly skewed propellers

Download: Full-Size Img

Figure  4  Wall y + distribution on HSP and CP

Download: Full-Size Img

Figure 5 shows a layout of the fine grid at a cross section of the full domain. Although the block covering the propeller (block 3) might have a different number of elements for the HSP and CP cases, the number of elements in the rest of the domain was strictly the same.

Figure  5  Fine grid generation for the steady simulation

Download: Full-Size Img

3.3   Boundary and Working Conditions

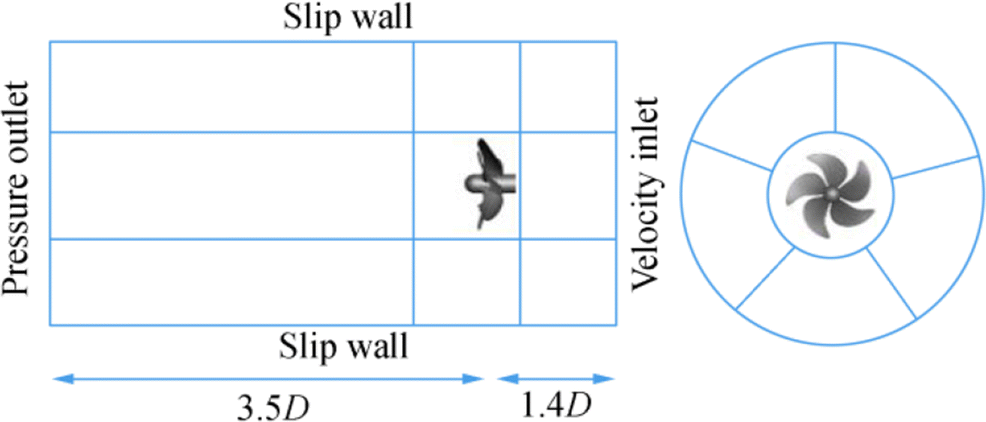
For the boundary conditions of the steady simulation:

– Velocity inlet was located at 1.4D characterized by a uniform flow depending on the advance coefficient J.

– Pressure outlet was located at 3.5D.

– Slip condition was set for the side wall at 1.4D (Belhenniche et al. 2012).

– No slip condition was imposed for the shaft and the propeller (see Figure 6).

Figure  6  Computational domain for steady simulation (shown for HSP in the figure but similar for CP)

Download: Full-Size Img

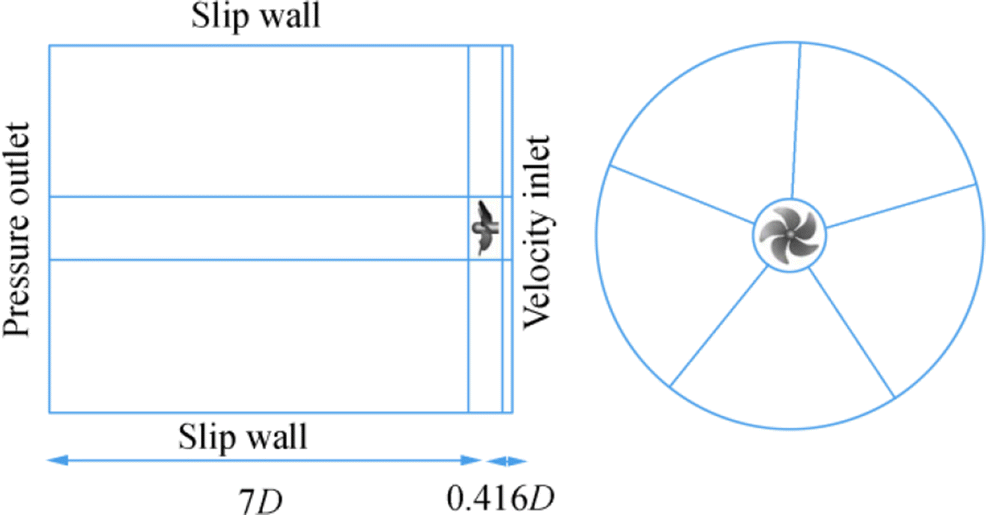
For transient simulations, the same conditions were adopted with the only exception at the inlet, where the axial velocities calculated from a non-uniform ship wake were given as input (Belhenniche et al. 2016).

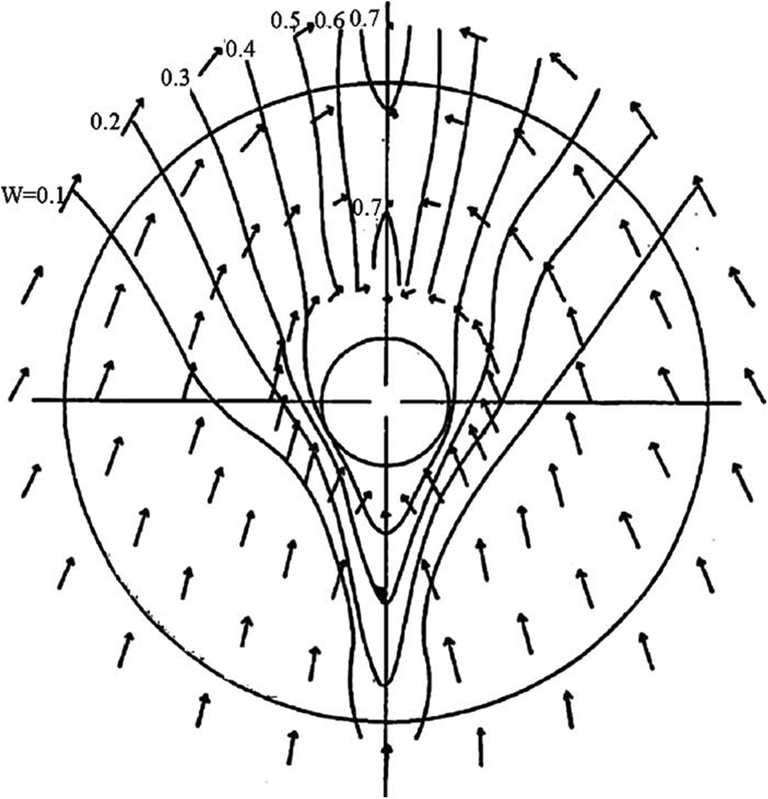
To maintain the non-uniform wake in the propeller plane, the inlet must not be too distant, which would lead to a dissipation of the non-uniform wake and becoming uniform (Ji et al. 2012a, b). The inlet, outlet, and side wall were located at 0.416D, 7D, and 3D, respectively, from the propeller plane, as shown in Figure 7. The distribution of the nominal ship wake is illustrated in Figure 8.

Figure  7  Computational domain for transient simulation (shown for HSP in the figure but similar for CP)

Download: Full-Size Img

Figure  8  Wake distribution given as input for transient simulations

Download: Full-Size Img

To match the conditions in the experiments, open-water simulations were performed for CP and HSP Seiun Maru propellers at a model scale with a diameter of 0.4 m and a revolution of 217.8 r/min. Computational results were compared with the experimental data presented in Ukon et al. (1989, 1990, 1991). Simulations were performed to cover the entire advance coefficient range J, i.e., 0.1 ≤J≤1.0. However, for the case of propellers operating behind the ship hull, full-scale propellers were used with rotation rates of 91.3 and 90.7 r/min for CP and HSP respectively, both working at an advance coefficient of J = 0.85. Computational results were also compared with those of the SQCM method (Nakatake et al. 2002). Hydroacoustic calculations were performed behind a non-uniform ship wake (behind-ship-hull condition) (Özden et al., 2016; Yao and Zhang 2018; Ji et al. 2012a, b) for both HSP and CP Seiun Maru marine propellers under the abovementioned conditions for different hydrophone positions by using a transient solver. Although the hull can be included in simulations, such as in (Long et al. 2019), we abstained from modeling the ship due to high-computer memory requirements. Reference pressure was set as 1 μPa, while the velocity of sound in the undisturbed medium was 1500 m/s.

3.4   Details of Numerical Implementation

Farkas et al. (2018) stated that "numerical results are very similar, regardless of turbulence model" for an open-water propeller. Therefore, k − ε turbulence model (Launder and Spalding 1972) was used for both steady (uniform flow) and transient (non-uniform ship wake) simulations to close Reynolds' stress term $ -\overline{\rho {u}_i^{\prime }{u}_j^{\prime }} $. It is a widely used turbulence model in solving the flow around marine propellers; see, for instance, Ji et al. (2012a, b). Numerical equations were solved using ANSYS Fluent 14.0 based on the finite volume method. For the steady simulation, a second-order scheme was selected for pressure discretization, and second-order upwind was chosen to discretize momentum, turbulent kinetic energy, and specific dissipation rate. A moving reference frame approach was used, and velocity-pressure coupling was made by the Semi-Implicit Method for Pressure-Lined Equation algorithm.

For transient simulations, the standard scheme was chosen for pressure discretization, and the QUICK scheme was selected for the momentum equation. A first-order upwind scheme was used for the discretization of turbulent kinetic energy and specific dissipation rate. Velocity and pressure coupling was made by the Pressure-Implicit with Splitting of Operators algorithm. Sliding mesh technique was applied for the transient simulation, which was accomplished by directly rotating the internal domain, including the propeller. Time step size was set to 1.83756 × 10⁻³ s for HSP and 1.82548 × 10⁻³ s for CP, which correspond to rotation angles of 1 degree for each.

The number of iterations between each physical time step was set to 80 to achieve better convergence. For the acoustic simulation, with the use of the time-dependent flow field data as an input, simulation results were used to solve the FW-H equation to extract the acoustic pressure and the sound pressure level for four hydrophones. Time step was again set to correspond to a rotation angle of 1 degree for propellers operating in non-uniform ship wake simulation. In this case, 10 inner iterations between each physical time step were set. All residuals for simulations involved in both cases were below 10⁻⁶.

The computer used in this study was an ordinary computer with Intel Core i7-3632QM with 2.20 GHz CPU. The open-water case contained about 3 million elements, and simulations at each advance coefficient took around 12 h. All simulations were performed by assuming a steady state as hypothesis. For the non-uniform ship wake condition, the number of elements was slightly higher. The only simulation carried out for this case was transient. A total of 3.5 million elements with a time step size of about ∆t ≈ 1.8 × 10⁻³ took about 30 days to finish.

4   Hydrodynamic Results

The numerical results of open-water and behind-ship-hull conditions for Seiun Maru CP and HSP are given in this section. Section "Performance Prediction in Open-Water" presents the hydrodynamic performances of the propeller in the open-water case. However, the presence of a ship hull in front of a working propeller changes propulsion characteristics considerably (Kinaci and Gokce 2015). Section "Performance Prediction in Non-uniform Ship Wake" presents the calculated hydrodynamic performances behind a non-uniform ship wake. These two sections are given to provide validations and a solid background for hydroacoustic simulations. Section 4.3 presents the numerical hydroacoustic simulation results.

4.1   Performance Prediction in Open-Water

Numerical simulations were carried out for a wide range of advance coefficients and similar to experiments. Inlet velocity was adjusted to vary the advance coefficient. Results of the grid sensitivity study at J = 0.8 are illustrated in Table 5. Error percentages in this table were calculated by:

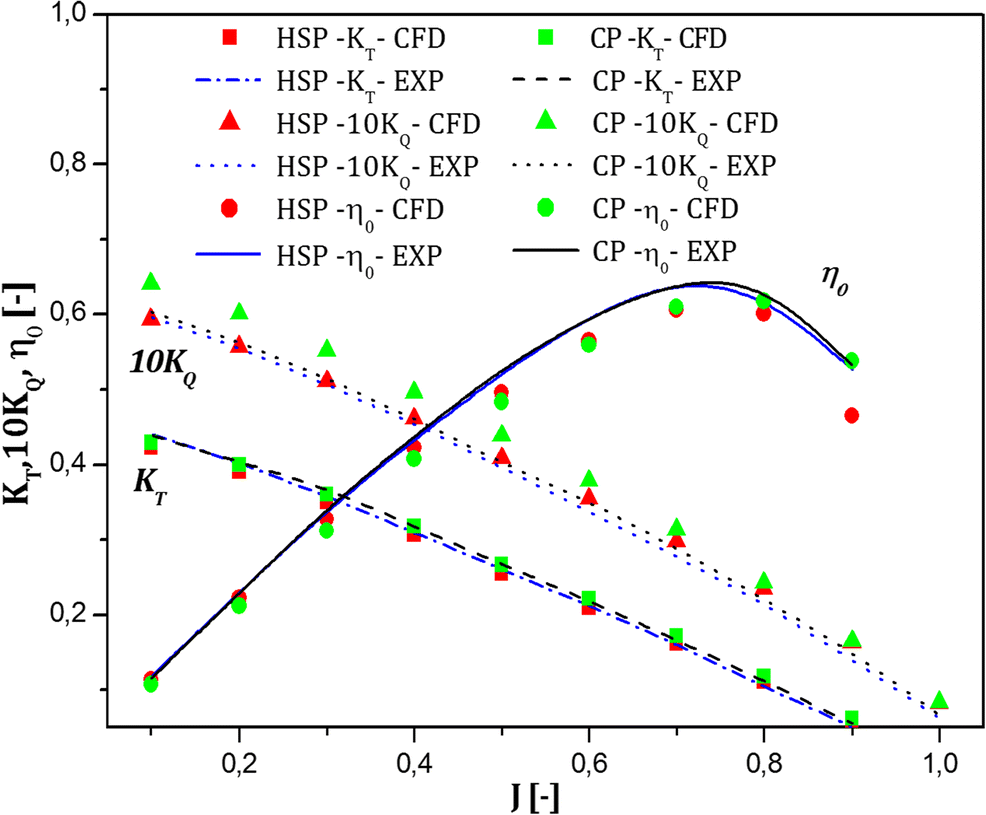
Table 5 shows that the discrepancy between experimental and numerical solutions decreases with an increasing number of elements. Thus, fin grid system was adopted to present the numerical results. The open-water characteristics for CP and HSP are shown in Figure 9. Results show a comparison of the computed thrust and torque curves predicted against experimental values (Ukon et al. 1989, 1990, 1991), and the computed results fit the experimental ones well.

Figure  9  Open-water propeller characteristics of CP and HSP in comparison with experiments (Ukon et al. 1989, 1990, 1991)

Download: Full-Size Img

Similar to experiments, numerical results also suggest that the CP generates higher thrust and torque. Open-water propeller efficiencies seem to be similar both experimentally and numerically. Numerical prediction of torque was somehow higher than that of experiments, which led to lower predicted open-water efficiency; see Eq. (5).

4.2   Performance Prediction in Non-uniform Ship Wake

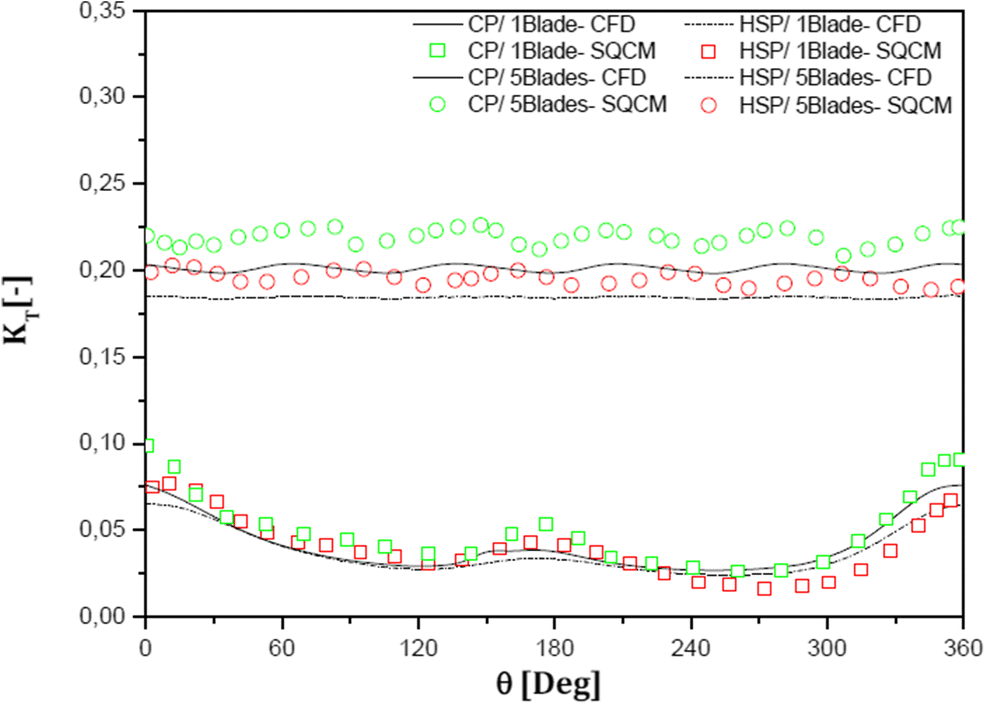
Figure 10 shows the thrust coefficient distributions generated by one-bladed and five-bladed propellers. Qualitatively, thrust predictions are in accordance with the calculations of Nakatake et al. (2002), who used a surface panel method (SQCM). This figure shows that the CFD results are slightly lower than those of SQCM. This result is due to the viscous approach implemented in this study unlike the potential-based SQCM method where the flow is assumed to be inviscid. Another notable detail in this figure is that CP generates higher thrust than HSP. This result is also in accordance with the open-water case, in which CP thrusts were higher than HSP thrusts in the advance coefficient range covered in this study (see Figure 9).

Figure  10  Thrust coefficients generated by both propellers during one revolution

Download: Full-Size Img

An interesting point that can be observed from this figure is the interaction between propeller blades. Mean thrust coefficients during one revolution of CP and HSP for the one-blade and five-blade cases are given in Table 6. The CP generates a higher thrust than the HSP, as also stated previously. This finding is also valid for the one-blade case.

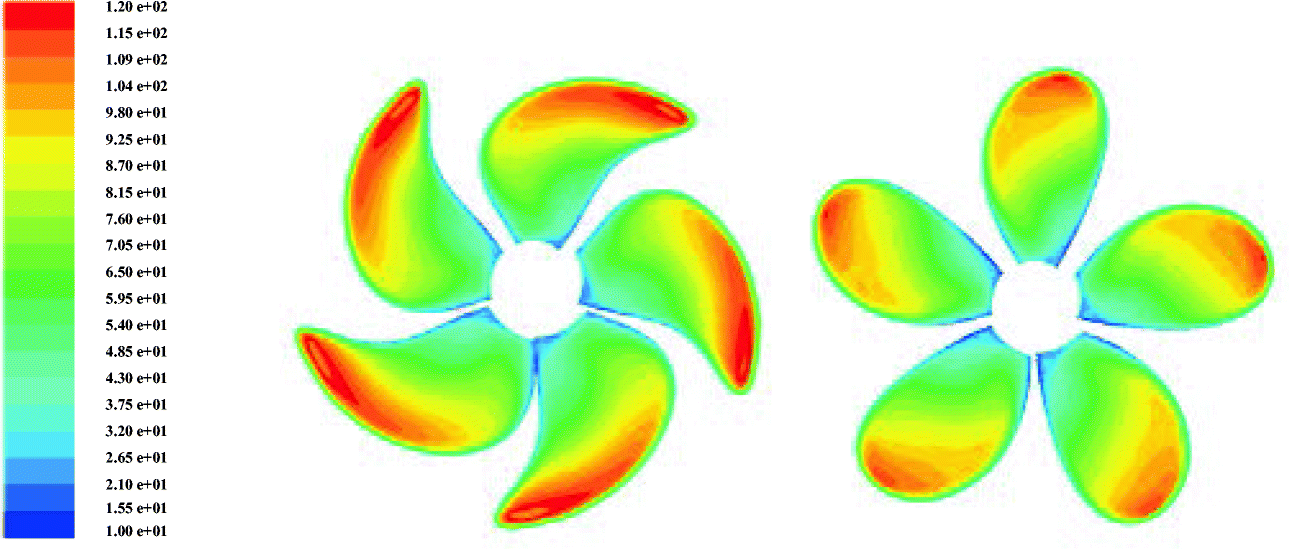
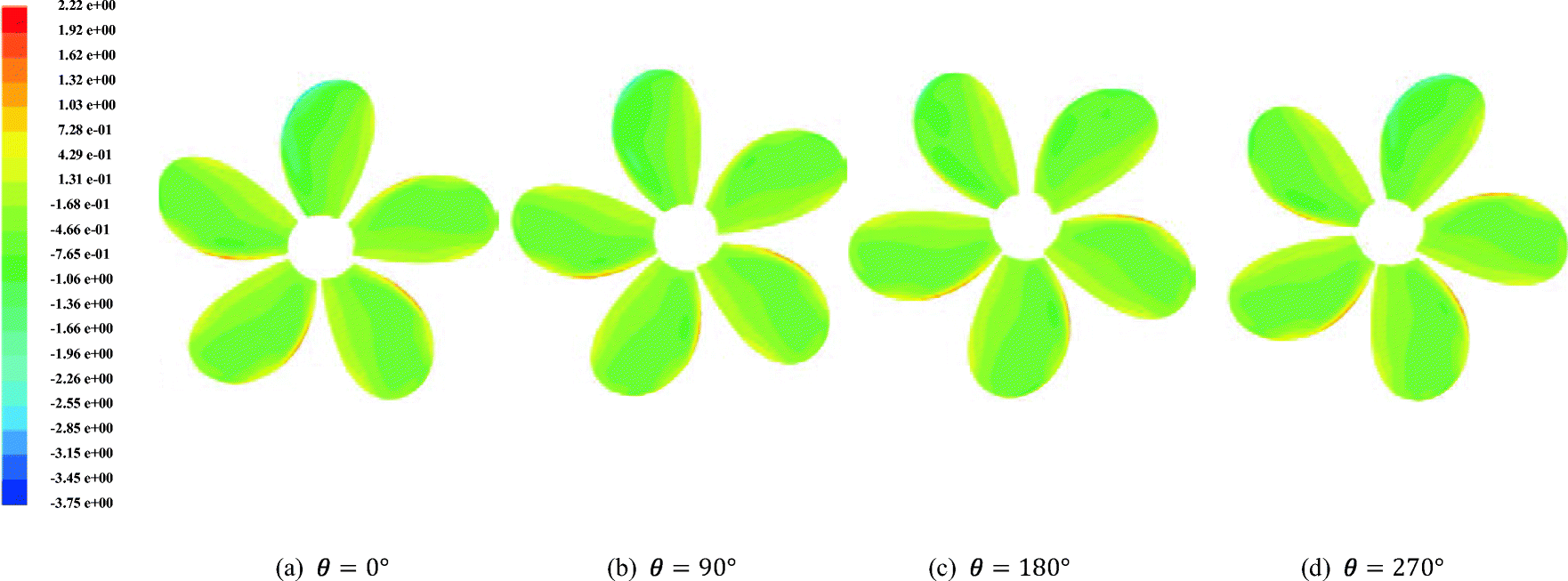
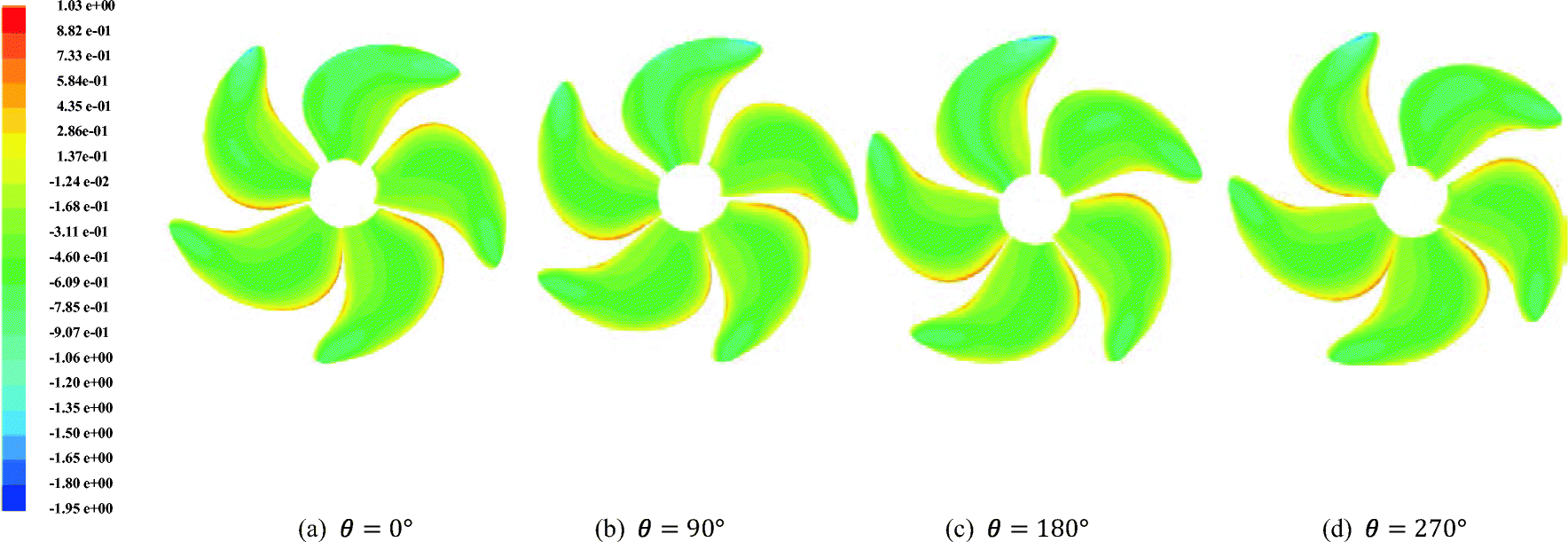
Figures 11 and 12 show pressure coefficient distributions over CP and HSP on the suction side, respectively, for different angle positions. This figure notes the differences in pressure at each angle. This difference is due evidently to the propeller being subjected to a non-uniform flow. A detail that should be noted from this figure is that the regions of blades closer to the hull have lower pressures, as indicated by blue colors at the upper part of the propeller. In this region, the flow becomes stuck in between the propeller and the bottom side of the hull. The region behaves like a jet, and the velocity increases, thereby decreasing the pressure, which is a sign of the possible occurrence of cavitation.

Figure  11  Pressure coefficients at the suction side of CP

Download: Full-Size Img

Figure  12  Pressure coefficients at the suction side of HSP

Download: Full-Size Img

5   Hydroacoustic Results

After satisfactory agreement with experiments was obtained for the hydrodynamic properties of both Seiun Maru propellers, the noise levels generated by these propellers were predicted numerically. However, hydroacoustic experiments for propellers are difficult to conduct. Full-scale experiments are prone to background noise, and the repeatability of these experiments is nearly impossible to achieve because controlling all environmental conditions to the same levels is difficult. Experiments carried out in towing tanks suffer from refractions from the side walls of the tank (Ianniello et al. 2013). In addition, eliminating noise generated by the towing tank itself is a difficult task. Given all these reasons, the numerical approach is generally validated by hydrodynamic data in many studies. Some examples that adopt such an approach are Ianniello et al. (2013), Bagheri et al. (2015), and; Yao and Zhang (2018). Our numerical approach was validated both in open-water and non-uniform flow conditions previously. However, an additional validation study was carried out and presented in this section to validate our hydroacoustic results before we present our findings.

5.1   Hydroacoustic Validation: the DTMB 4119 Case

A validation test of the FW-H equation was carried out for the well-known DTMB 4119 marine propeller. Numerical results presented in other studies (Bagheri et al. 2015; Sezen et al. 2016) were used for comparison. The same mesh structure and numerical implementation was used here.

First, the open-water characteristics were calculated and compared with experiments and panel method (Brizzolara et al. 2008) at a revolution rate of 600 r/min. Then, the time-dependent pressure data were used as input for the FW-H formulation to predict the far-field noise levels. The propeller had a revolution rate of 960 r/min and was operating at an advance coefficient of J = 0.54. Figure 13 shows the open-water performances of DTMB 4119 and the noise levels calculated at 10R and θ=90°. A comparison with available results (Bagheri et al. 2015; Sezen et al. 2016; Brizzolara et al. 2008) shows good agreement for both hydrodynamic and hydroacoustic calculations. Although these are all numerical results and further validation with experiments is required, the general trends of the curves agree, and the BPF is observable in all of them.

Figure  13  DTMB 4119 open-water propeller performances and sound pressure levels at a distance of 10R and θ = 90°

Download: Full-Size Img

5.2   Noise Predictions in the Behind-Ship-Hull Condition: Non-uniform Ship Wake Case

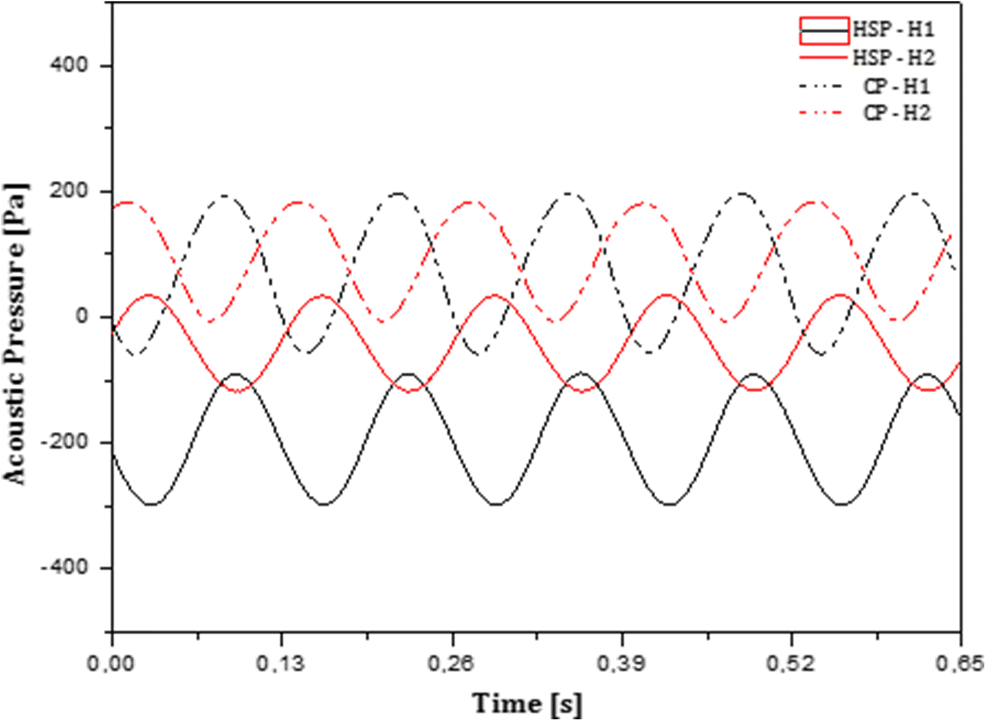
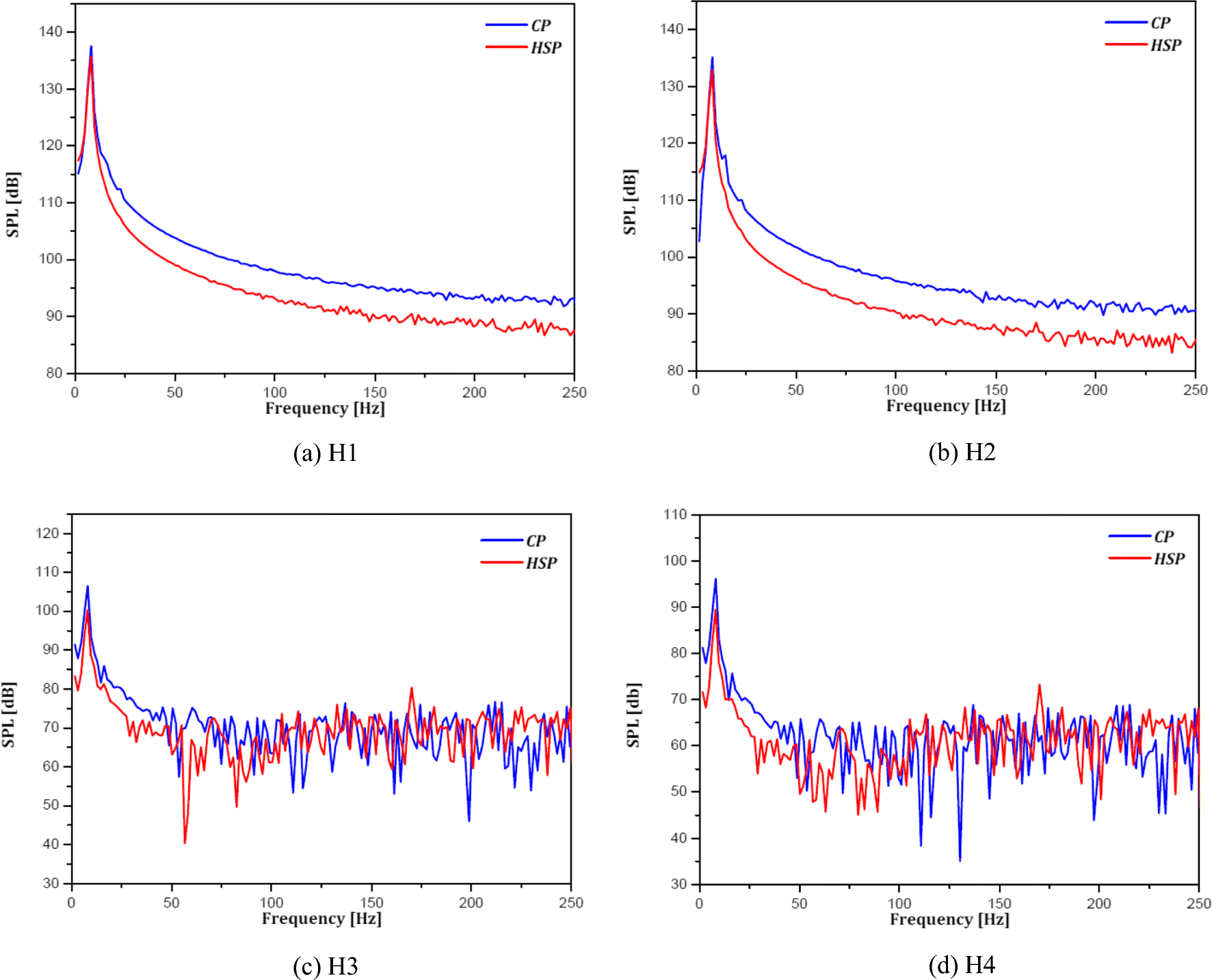
Pressure fluctuations in time for the last rotation are presented in Figure 14 for hydrophones 1 and 2. Five peaks in pressure record correspond to five blades of CP and HSP. The difference in acoustic pressures between hydrophones 1 and 2 for both propellers is due to the non-uniform ship wake, where the lack of axial velocity is more pronounced at the blade top position than at the lowest position. Acoustic pressures for hydrophones 3 and 4 were not presented because pressure peaks could not be identified at these locations. Indeed, pressure signals in time were complex in this chaotic region. The URANS approach may be unable to accurately predict the hydroacoustic signal in the wake generated by the propeller because the method cannot capture almost turbulent structures (Wu et al. 2018). Even so, peaks at noise spectra were identifiable; see Figure 15.

Figure  14  Pressures obtained at hydrophones 1 and 2 for both propellers

Download: Full-Size Img

Figure  15  Sound pressure levels at H1, H2, H3, and H4

Download: Full-Size Img

Figure 15 shows the sound pressure levels for hydrophones 1–4. In these figures, frequency f is given by:

However, only frequencies up to 250 Hz are given in these figures. A different time step size selection process was proposed recently by Sezen and Kinaci (2019), thereby allowing higher harmonics of noise to be captured by setting smaller time steps. However, considering only the peaks at the first BPF, accordance may exist in the first harmonics of both propellers. BPF is given by:

Fundamental (first) harmonics should be 7.602 Hz for CP and 7.558 Hz for HSP. First harmonics were captured clearly at all hydrophone locations, while subharmonics and higher harmonics could hardly be observed. A possible reason for this condition might be the implementation of RANS as a turbulence model, in which many aspects of the flow are averaged. Other harmonics might have been lost during this process, but stronger evidence is needed, and further study must be carried out before pointing out the exact source of this deficiency in results.

Results show that highest values of the sound pressure levels are largely intense in the low-frequency range (0–50), while they are low at higher frequencies. The sound pressure level reaches its maximum at the first order of BPF (1st BPF) and gradually decreases at higher harmonics. Overall sound pressure levels (OASPLs) were also calculated at these hydrophone locations by the following:

Table 7 shows the OASPLs for both CP and HSP at different hydrophone positions. This table indicates that HSP exhibits slightly less noise than CP. Nevertheless, a minor reduction in the hydrodynamic efficiency of HSP compared with CP should also be noted. An important detail to mention is that these results are for the noncavitating case. However, the hydroacoustic performances will probably be more amplified in the presence of cavitation.

6   Conclusions

Numerical investigations were performed to predict and compare the noise characteristics of CP and HSP Seiun Maru marine propellers behind non-uniform ship wake. Numerical calculations were carried out under noncavitating conditions. RANS equations were coupled with the FW-H equation. The numerical approach was first validated from the hydrodynamic aspect for both open-water and behind-ship-hull conditions. Experimental noise data are not available for the tested marine propellers in the literature. Therefore, the hydroacoustic numerical approach was validated by the DTMB 4119 propeller before moving any further with the study. After satisfactory agreement with other studies in the literature was observed, numerical comparisons of hydrodynamic and hydroacoustic performances of CP and HSP marine propellers were carried out. The following are some highlights and conclusions drawn from this study:

1) The predicted open-water characteristics of CP and HSP agree well with the experimental measurements for a wide range of advance coefficients.

2) The calculated thrust coefficient of both propellers behind a non-uniform ship wake during propeller revolution shows good agreement with the SQCM.

3) Periodic features of the thrust coefficient were observed under non-uniform ship wake by using the unsteady solver. Findings show that CP generates higher thrust.

4) The RANS method with the k − ε turbulence model indicates that it is an effective tool to predict the hydrodynamic performances for both steady (open-water) and transient (non-uniform ship wake) conditions. It also generated satisfactory results for hydroacoustic calculations.

5) Noise levels were presented for several hydrophones. The positions of SPL peaks are in good agreement with the theoretical values of BPF. The highest values of SPL are concentrated in the low-frequency range and decrease at high frequencies.

6) OASPLs were calculated both for CP and HSP behind a non-uniform ship wake. HSP generates less noise than CP, but it is also less hydrodynamically efficient. Thus, a trade-off exists between the hydrodynamic and hydroacoustic performances of a marine propeller, and an optimization study is required prior to the selection of the propulsion system of the ship.

Nomenclature