1 Introduction

Transfer alignment is an automatic alignment process in the Slave Inertial Navigation System (SINS), which uses reference coordinate information from the main inertial navigation system before initiating navigation. The purpose of transfer alignment is to provide a measurable or calculable reference for accelerometers and gyros, and to provide the necessary initial conditions for the calculation of navigation parameters (Crassidis, 2006; Allan, 1987; Andrews, 1968; Grewal et al., 2007). Over time, transfer alignment technology with respect to moving bases has become the basic navigation and guidance technology utilized in the carrier aircraft and missile fields.

The performance indicators of transfer alignment include the alignment accuracy, alignment time, and maneuver -ability requirements. However, the performance evaluation standards for transfer alignment are not consistent between countries. Even within one country, different measurements can be used and professionals can use different standards. For example, some use the accuracy of the navigation parameters, including position, velocity, and attitude, which can be determined for a certain period of time after transfer alignment takes place, to indirectly determine the transfer alignment accuracy (Gao et al., 2012). Others use different forms of attitude error, which can be determined once the process of transfer alignment is complete (Zhang et al., 2008), such as the Root-Mean-Square Error (RMSE), the standard error (σ), and the Probability Error (PE or CPE) (Wang et al., 2012; Miao et al., 2000; Grewal et al., 2007; Rogers, 1991). As such, there is a need for a standard evaluation method and index to allow for the analysis of performance evaluations of the transfer alignment on a moving base.

In this study, we investigated a number of possible approaches to the evaluation and identification of transfer alignment on a moving base, and propose the following:

1) We propose the use of a DOA index, which has been applied in transfer alignment performance evaluations, with the statistical methods and application conditions provided (Grewal et al., 2007);

2) We design and establish a comprehensive assessment scheme using a 15-dimensional state-space evaluation model for transfer alignment on a moving base;

3) We verify and discuss the results of four indirect estimation methods, including Fixed Point Smoothing (FPS), Returns to Scale (RTS), the Kalman Filter (KF), and Inverted Sequence Recursive Estimation (ISRE) for application in transfer alignment evaluation and with respect to specific project applications (Przemyslaw, 2012; Leng et al., 2012; Zheng et al., 2011; Wang et al., 2014; Rogers, 1996);

4) Based on our simulations and analyses, we verify the filtering and smoothing effects, calculate the DOA, and provide project proposals.

2 DOA definition and statistical evaluation

The evaluation of the transfer alignment on a moving base involves an evaluation of the SINS performance when the transfer alignment process is complete and has switched into navigation mode. This evaluation includes a determination of the attitude precision, velocity precision, position precision, the calibration precision of the gyros and accelerometers, the adaptation of the transfer alignment method, and the reaction ability during various maneuvers.

Due to the different indexes for different INSs, it is not reasonable to estimate the transfer alignment based only on the alignment accuracy and time. Nor is this approach comparable with different systems that use the same evaluation method. There are many parameters in the INS and there is some confusion regarding which parameters best characterize the transfer alignment effect. We suggest the DOA as an evaluation standard for determining transfer alignment accuracy.

2.1 Definition

The DOA (η) is defined as the degree of similarity (stated as a percentage) between the attitude alignment accuracy and the ideal value for the stated alignment time and maneuvering conditions. It is mathematically expressed as follows (Chen et al., 2014; Han et al., 2010):

$ \begin{array}{c} \eta = \mathop \eta \nolimits_{{\rm{RMS}}} \times 100{\rm{\% }}/(T, M) = \\ \frac{{\mathop {{\rm{RMS}}}\nolimits_0 }}{{\mathop {{\rm{RMS}}}\nolimits_1 }} \times 100\% /(T, M) \end{array} $

(1)

where η_RMS is the degree of similarity between the attitude alignment accuracy (root-mean-square value) and the ideal root-mean-square value, RMS₀ is the desired precision of the INS with a normal alignment, RMS₁ is the INS precision regarding transfer alignment on a moving base, and T is the alignment time. The ideal accuracy can be replaced by the nominal accuracy in engineering applications. In this case, the calculation result may be greater than 100%, which indicates that the transfer alignment scheme is better than the normal alignment scheme.

2.2 DOA statistical evaluation

If the attitude error (Δϕ_x, Δϕ_y, Δϕ_z) can be directly obtained using true-value measurement equipment, we can calculate the DOA according to the following statistical formulas (Hinneburg et al., 2006; Cheng et al., 2001; Zhang SF, 2002):

$ \mathop T\nolimits_A = \frac{1}{m}\sum\limits_{j = 1}^m {\mathop T\nolimits_{Aj} } $

(2a)

$ \mathop \mu \nolimits_\varphi = \frac{1}{{mn}}\sum\limits_{j = 1}^m {\sum\limits_{i = 1}^n {\mathop {\Delta \varphi }\nolimits_{ij} } } $

(2b)

$ \mathop \sigma \nolimits_{i\varphi } = \sqrt {\frac{1}{{m - 1}}\sum\limits_{j = 1}^m {\mathop {(\Delta \mathop \varphi \nolimits_{ij} - \mathop \mu \nolimits_\varphi)}\nolimits^2 } } $

(2c)

$ \mathop \sigma \nolimits_\varphi = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {\mathop {\mathop \sigma \nolimits_{i\varphi } }\nolimits^2 } } $

(3a)

$ \mathop {\Delta \varphi }\nolimits_{{\rm{RMS}}} = \sqrt {\mathop \mu \nolimits_\varphi ^2 + \mathop \sigma \nolimits_\varphi ^2 } $

(3b)

$ \mathop \eta \nolimits_\varphi = \frac{{\mathop \varphi \nolimits_{\mathop {{\rm{RMS}}}\nolimits_0 } }}{{\mathop \varphi \nolimits_{\mathop {{\rm{RMS}}}\nolimits_1 } }} \times 100{\rm{\% }}/(\mathop T\nolimits_A, M) $

(3c)

where n is the number of sampling points in each test, m is the number of effective tests, T_A is the mean value of the transfer alignment time(s), T_Ai is the transfer alignment time of j-time effective test(s), μ_ϕis the system error (′or″), Δφ_ij is the attitude error of the sampling time for the j effective test(′or″), σ_iϕ is the attitude standard error within the sampling time, σ_ϕ is the total attitude standard error, $\mathop {\Delta \varphi }\nolimits_{{\rm{RMS}}} $ is the root mean square value of the attitude error, and $\mathop \eta \nolimits_\varphi $is the degree of alignment.

3 Comprehensive DOA Evaluation of transfer alignment on moving base 3.1 Comprehensive assessment scheme

When evaluating the accuracy of transfer alignment on a moving base in engineering applications, we cannot directly measure the attitude error. In this case, it is necessary to use a highly accurate reference system such as the Differential GPS (DGPS). Using SINS navigation data and reference data for a period of time under a certain track after alignment, we can evaluate the accuracy of the transfer alignment using KF or smoothing techniques. Ultimately, we can estimate the transfer alignment error and then statistically evaluate the DOA in a number of experiments.

To complete this task, this offline data processing method requires the support of a computer program. In addition, the SINS state model must be able to simulate the actual SINS to ensure rational identification results. Then, we can statistically evaluate the DOA index for the integrated evaluation and identification after evaluating the initial state either by smoothing or filtering in numerous trials, as shown in Fig. 1.

For the DOA evaluation, the number of effective tests should be no less than eight (Wang et al., 2013). We divide the data collection process into two stages. The first stage includes the time from the beginning of the SINS transfer alignment to at least 1min following the end of the transfer alignment, with a measuring frequency of no less than 10Hz. The second-stage begins at the start of the SINS navigation. The shortest second-stage duration is 1 second and the longest is 30 minutes. The DGPS measurement equipment provides the system navigation parameter values synchronously during the two stages. The synchronization time accuracy requirement should be based on actual demand, and is negligible if the synchronous error is generally no more than 0.5 ms.

3.2 Mathematical model

To evaluate the accuracy of the transfer alignment on a moving base when using KF or smoothing, we must establish a space model based on the SINS error model.

The state equation (Wang et al., 2012) is as follows:

$ {\pmb{\dot X}}(t) = {\pmb{FX}}(t) + {\pmb{W}}(t) $

(4)

where ${\pmb{X}} = {[\mathop {\mathit{\pmb{\Phi }}}\nolimits^n, \mathop {\delta {\pmb{V}}}\nolimits^n, \mathop {\delta {\pmb{P}}}\nolimits^n, \mathop {\pmb{\varepsilon }}\nolimits^n, \mathop \nabla \nolimits^n ]^{\rm{T}}}$ is the system-state column vector, ${\pmb{W}} = \mathop {\left[ {\mathop { - \mathop {\pmb{\varepsilon }}\nolimits_w ]}\nolimits_{3 \times 1}, \mathop {[\mathop \nabla \nolimits_w ]}\nolimits_{3 \times 1}, \mathop {\pmb{0}}\nolimits_{9 \times 1} } \right]}\nolimits^{\rm{T}} $ is the process noise column vector, and F is the system matrix.

The five components of the system-state column vector represent the three-dimensional (3D) attitude error of the SINS, the velocity error, the position error, the gyro constant drift, and the accelerometer bias error in the navigation coordinate system, respectively. The system matrix is as follows:

$ {\pmb{F}} = \left[ {\begin{array}{*{20}{c}} {{{\pmb{F}}_1}}&{{{\pmb{F}}_2}}&{{{\pmb{0}}_{{\rm{3}} \times {\rm{3}}}}}&{ - {{\pmb{I}}_{3 \times 3}}}&{{{\pmb{0}}_{{\rm{3}} \times {\rm{3}}}}}\\ {{{\pmb{F}}_3}}&{{{\pmb{F}}_4}}&{{{\pmb{0}}_{{\rm{3}} \times {\rm{3}}}}}&{{{\pmb{0}}_{{\rm{3}} \times {\rm{3}}}}}&{{{\pmb{I}}_{3 \times 3}}}\\ {{{\pmb{0}}_{{\rm{3}} \times {\rm{3}}}}}&{{{\pmb{I}}_{3 \times 3}}}&{{{\pmb{0}}_{{\rm{3}} \times {\rm{3}}}}}&{{{\pmb{0}}_{{\rm{3}} \times {\rm{3}}}}}&{{{\pmb{0}}_{{\rm{3}} \times {\rm{3}}}}}\\ {{{\pmb{0}}_{{\rm{3}} \times {\rm{3}}}}}&{{{\pmb{0}}_{{\rm{3}} \times {\rm{3}}}}}&{{{\pmb{0}}_{{\rm{3}} \times {\rm{3}}}}}&{ - {{\pmb{I}}_{3 \times 3}}}&{{{\pmb{0}}_{{\rm{3}} \times {\rm{3}}}}}\\ {{{\pmb{0}}_{{\rm{3}} \times {\rm{3}}}}}&{{{\pmb{0}}_{{\rm{3}} \times {\rm{3}}}}}&{{{\pmb{0}}_{{\rm{3}} \times {\rm{3}}}}}&{{{\pmb{0}}_{{\rm{3}} \times {\rm{3}}}}}&{{{\pmb{I}}_{3 \times 3}}} \end{array}} \right] $

(5)

where

$ \mathop {\pmb{F}}\nolimits_1 = \left[ {\begin{array}{*{20}{c}} 0&{\Omega {\rm{sin}} L + \frac{{\mathop V\nolimits_e \tan L}}{{\mathop R\nolimits_N + h}}}&{ - \Omega \cos L - \frac{{\mathop V\nolimits_e }}{{\mathop R\nolimits_N + h}}}\\ { - \Omega {\rm{sin}} L - \frac{{\mathop V\nolimits_e \tan L}}{{\mathop R\nolimits_N + h}}}&0&{ - \frac{{\mathop V\nolimits_n }}{{\mathop R\nolimits_N + h}}}\\ {\Omega \cos L + \frac{{\mathop V\nolimits_e }}{{\mathop R\nolimits_N + h}}}&{\frac{{\mathop V\nolimits_n }}{{\mathop R\nolimits_N + h}}}&0 \end{array}} \right] $

$ \mathop {\pmb{F}}\nolimits_2 = \left[ {\begin{array}{*{20}{c}} 0&{\frac{{ - 1}}{{\mathop R\nolimits_M + h}}}&0\\ {\frac{1}{{\mathop R\nolimits_N + h}}}&0&0\\ {\frac{{\tan L}}{{\mathop R\nolimits_N + h}}}&0&0 \end{array}} \right], \mathop {\pmb{F}}\nolimits_3 = \left[ {\begin{array}{*{20}{c}} 0&{\mathop { - f}\nolimits_u }&{\mathop f\nolimits_n }\\ {\mathop f\nolimits_u }&0&{\mathop { - f}\nolimits_e }\\ {\mathop { - f}\nolimits_n }&{\mathop f\nolimits_e }&0 \end{array}} \right] $

$ \mathop {\pmb{F}}\nolimits_4 = \left[ {\begin{array}{*{20}{c}} {\frac{{\mathop V\nolimits_n \tan L - \mathop V\nolimits_u }}{{\mathop R\nolimits_N + h}}}&{2\Omega {\rm{sin}}L + \frac{{\mathop V\nolimits_e \tan L}}{{\mathop R\nolimits_N + h}}}&{ - \Omega \cos L - \frac{{\mathop V\nolimits_e }}{{\mathop R\nolimits_N + h}}}\\ { - 2\Omega {\rm{sin}}L - \frac{{\mathop V\nolimits_e \tan L}}{{\mathop R\nolimits_N + h}}}&{\frac{{ - \mathop V\nolimits_u }}{{\mathop R\nolimits_M + h}}}&{ - \frac{{\mathop V\nolimits_n }}{{\mathop R\nolimits_N + h}}}\\ {2\Omega \cos L + \frac{{2\mathop V\nolimits_e }}{{\mathop R\nolimits_N + h}}}&{\frac{{\mathop {2V}\nolimits_n }}{{\mathop R\nolimits_N + h}}}&0 \end{array}} \right] $

The subscripts e, n, and u indicate the east, north, and vertical components, respectively; L is the latitude, V is the speed, Ω is the angular velocity of the Earth's rotation, R_M and R_N are the Earth's radii of the long and short axes, respectively, and f is the specific force.

By discretizing the continuous state equation Eq. (4), we can obtain the discretization state equation:

$ {{\pmb{x}}_k} = \mathop {\mathit{\pmb{\Phi }}}\nolimits_{k, k - 1} {{\pmb{x}}_{{\bf{k - 1}}}} + \mathop {\pmb{\Gamma }}\nolimits_{k, k - 1} {{\pmb{w}}_{k - 1}} $

(6)

where $\mathop {\mathit{\pmb{\Phi }}}\nolimits_{k, k - 1} $ is the one-step steady-state transition matrix.

To establish the observational equation, we mainly use the data collected during the first stage of each test. To establish the observation vector when the SINS process is complete and the navigation mode has begun, we use the differences between the velocities and positions determined by SINS and by high-precision equipment, such as DGPS, as follows:

$ \begin{array}{1} \mathop {\pmb{z}}\nolimits_k = \mathop {\left[ {\mathop {\pmb{V}}\nolimits_{{\rm{SINS}}}^{\pmb{n }}, \mathop {\pmb{P}}\nolimits_{{\rm{SINS}}}^{\pmb{n }} } \right]}\nolimits_k^{\rm{T}} - \mathop {\left[ {\mathop {\pmb{V}}\nolimits_{{\rm{DGPS}}}^{\pmb{n }}, \mathop {\pmb{P}}\nolimits_{{\rm{DGPS}}}^{\pmb{n }} } \right]}\nolimits_k^{\rm{T}} \\ \;\;\; = \mathop {\left[ {\mathop {\delta V}\nolimits_e, \mathop {\delta V}\nolimits_n, \mathop {\delta V}\nolimits_u, \delta \lambda, \delta \phi, \delta h} \right]}\nolimits_k^{\rm{T}} (k = 1, 2, 3 \ldots) \end{array} $

(7)

where $\mathop {\left[ {\mathop {\pmb{V}}\nolimits_{{\rm{SINS}}}^n, \mathop {\pmb{P}}\nolimits_{{\rm{SINS}}}^n } \right]}\nolimits_{}^{} $ and $\left[ {\mathop {\pmb{V}}\nolimits_{{\rm{DGPS}}}^n, \mathop {\pmb{P}}\nolimits_{{\rm{DGPS}}}^n } \right]$ are the velocity and position components of the SINS and DGPS in the navigation coordinate system (geographic coordinate system), respectively, and $\mathop {{\rm{\delta }}V}\nolimits_e $, $\mathop {{\rm{\delta }}V}\nolimits_n $, $\mathop {{\rm{\delta }}V}\nolimits_u $, $\mathop {{\rm{\delta }}\lambda } $, ${{\rm{\delta }}\varphi }$, ${{\rm{\delta }}h}$ are the east velocity, north velocity, vertical velocity, longitude, latitude, and altitude observation errors, respectively. If we combine the discrete state equation with the state-space model, we obtain the following:

$ \begin{array}{l} {{\pmb{x}}_k} = \mathop {\mathit{\pmb{\Phi }}}\nolimits_{k, k - 1} {{\pmb{x}}_{k - {\rm{1}}}} + \mathop {\pmb{\Gamma }}\nolimits_{k, k - 1} {{\pmb{w}}_{k - 1}}\\ {{\pmb{z}}_k} = \mathop {\pmb{H}}\nolimits_k \mathop {\pmb{x}}\nolimits_k + {{\pmb{v}}_k} \end{array} $

(8)

where $\mathop {\pmb{H}}\nolimits_k $ is the 6 × 15 system observation matrix, $\mathop {\pmb{v}}\nolimits_k $ is the 6 × 1 observation noise matrix that approximates the white noise, $\mathop {\pmb{\Gamma }}\nolimits_{k, k - 1} $ is the 15 × 15 noise input matrix, and ${{\pmb{w}}_{k - 1}}$ and $\mathop {\pmb{v}}\nolimits_k $ are unrelated zero-mean Gaussian white-noise sequences. The resulting observation matrix is as follows:

$ \mathop {\pmb{H}}\nolimits_k = \left[ {\begin{array}{*{20}{c}} {\mathop {\rm{0}}\nolimits_{3 \times 3} }&{\mathop {\pmb{I}}\nolimits_{3 \times 3} }&{\mathop {\rm{0}}\nolimits_{3 \times 3} }&{\mathop {\rm{0}}\nolimits_{3 \times 3} }&{\mathop {\rm{0}}\nolimits_{3 \times 3} }\\ {\mathop {\rm{0}}\nolimits_{3 \times 3} }&{\mathop {\rm{0}}\nolimits_{3 \times 3} }&{\mathop {\pmb{I}}\nolimits_{3 \times 3} }&{\mathop {\rm{0}}\nolimits_{3 \times 3} }&{\mathop {\rm{0}}\nolimits_{3 \times 3} } \end{array}} \right] $

(9)

We then use the rank criterion method after calculating the rank of ${\pmb{Q}}_0$, as follows:

$ {\rm{rank}}{{\pmb{Q}}_0} = {\rm{rank}}\left[ {\begin{array}{*{20}{c}} {\pmb{H}}\\ {{\pmb{HF}}}\\ \vdots \\ {{\pmb{H}}{{\pmb{F}}^{n - 1}}} \end{array}} \right] = 15 = n $

(10)

This system is observable, which means this filtering algorithm works.

4 Filter or smoothing algorithm

The filter or smoothing algorithm is the core of the DOA integrated evaluation of the transfer alignment on a moving base. Its purpose is to estimate the initial state of the system based on the observation sequence. Four algorithms that can be applied to this integrated evaluation are the KF, the FPS, Fixed Interval Smoothing (FIS), and the ISRE.

As an analysis example, we use the FIS algorithm, which uses all of the measurement information $\left({\mathop {\pmb{Z}}\nolimits_1, \mathop {\pmb{Z}}\nolimits_2, \cdots \mathop {\pmb{Z}}\nolimits_k, \cdots, \mathop {\pmb{Z}}\nolimits_n } \right)$ to estimate each time state${\mathit{\boldsymbol{\hat X}}_k}$ at fixed time intervals [0, n]. The concrete RTS smoothing algorithm is as follows:

$ \mathop {{\pmb{\hat X}}}\nolimits_{k, k - 1}^f = \mathop {\mathit{\pmb{\Phi }}}\nolimits_{k, k - 1} \mathop {\pmb{X}}\nolimits_{k - 1}^f $

(11a)

$ \mathop {\pmb{P}}\nolimits_{k, k - 1}^f = \mathop {\mathit{\pmb{\Phi }}}\nolimits_{k, k - 1} \mathop {\pmb{P}}\nolimits_{k - 1}^f \mathop {\mathit{\pmb{\Phi }}}\nolimits_{k, k - 1}^{\rm{T}} + \mathop {\pmb{\Gamma }}\nolimits_{k, k - 1} \mathop {\pmb{Q}}\nolimits_{k - 1}^{} \mathop {\pmb{\Gamma }}\nolimits_{k, k - 1}^{\rm{T}} $

(11b)

$ \mathop {\pmb{K}}\nolimits_k^f = \mathop {\pmb{P}}\nolimits_{k, k - 1} \mathop {\pmb{H}}\nolimits_k^{\rm{T}} \mathop {\mathop {{\rm{(}}{\pmb{H}}}\nolimits_k \mathop {\pmb{P}}\nolimits_{k/k - 1}^f \mathop {\pmb{H}}\nolimits_k^{\rm{T}} + \mathop {\pmb{R}}\nolimits_k)}\nolimits^{ - 1} $

(11c)

$ \mathop {{\pmb{\hat X}}}\nolimits_k^f = \mathop {\pmb{X}}\nolimits_{k, k - 1}^f + \mathop {\pmb{X}}\nolimits_k^f (\mathop {\pmb{Z}}\nolimits_k - \mathop {\pmb{H}}\nolimits_k \mathop {{\pmb{\hat X}}}\nolimits_{k, k - 1}^f) $

(11d)

$ \begin{array}{r} \mathop {\pmb{P}}\nolimits_k^f = ({\pmb{I}} - \mathop {\pmb{K}}\nolimits_k^f \mathop {\pmb{H}}\nolimits_k)\mathop {\pmb{P}}\nolimits_{k/k - 1}^f {({\pmb{I}} - \mathop {\pmb{K}}\nolimits_k^f \mathop {\pmb{H}}\nolimits_k)^{\rm{T}}} + \mathop {\pmb{K}}\nolimits_k^f \mathop {\pmb{R}}\nolimits_k \mathop {\pmb{K}}\nolimits_k^{f{\rm{T}}} \\ \left({k = 1, 2, 3, \ldots, N} \right) \end{array} $

(11e)

Reverse smoothing equations:

$ \mathop {\pmb{P}}\nolimits_{N/N}^S = \mathop {\pmb{P}}\nolimits_N^f $

(12a)

$ \mathop {\pmb{K}}\nolimits_k^S = \mathop {\pmb{P}}\nolimits_k^f \mathop {\mathit{\pmb{\Phi }}}\nolimits_{k + 1, k}^{\rm{T}} \mathop {\left({\mathop {\pmb{P}}\nolimits_{k + 1, k}^{\rm{T}} } \right)}\nolimits^{ - 1} $

(12b)

$ \mathop {{\pmb{\hat X}}}\nolimits_{k/N}^s = \mathop {\pmb{X}}\nolimits_k^f + \mathop {\pmb{X}}\nolimits_k^{\rm{s}} \left({\mathop {{\pmb{\hat X}}}\nolimits_{k + 1/N}^s - \mathop {\mathit{\pmb{\Phi }}}\nolimits_{k + 1, k} \mathop {{\pmb{\hat X}}}\nolimits_k^f } \right) $

(12c)

$ \mathop {{\pmb{\hat X}}}\nolimits_{N/N}^s = \mathop {{\pmb{\hat X}}}\nolimits_N^f $

(12d)

$ \begin{array}{r} \mathop {\pmb{P}}\nolimits_{k/N}^s = \mathop {\pmb{P}}\nolimits_k^f + \mathop {\pmb{K}}\nolimits_k^s \mathop {\pmb{P}}\nolimits_{k + 1/N}^s - \mathop {\pmb{P}}\nolimits_{k + 1/N}^f \mathop {\pmb{K}}\nolimits_k^{s{\rm{T}}} \\ \left({k = N - 1, N - 2, \ldots, 0} \right) \end{array} $

(12e)

where $\mathop {{\pmb{\hat X}}}\nolimits_{0/N}^s $ is the optimal smoothing estimation of the system initial state $\mathop {\pmb{X}}\nolimits_0 $, N is the number of measurement update cycles at fixed time intervals [0, t], i.e., $N = t/T$, and $\mathop {{\pmb{\hat X}}}\nolimits_{k/N}^s $is the optimal smoothing estimation of the K time system state.

5 Simulation and analysis

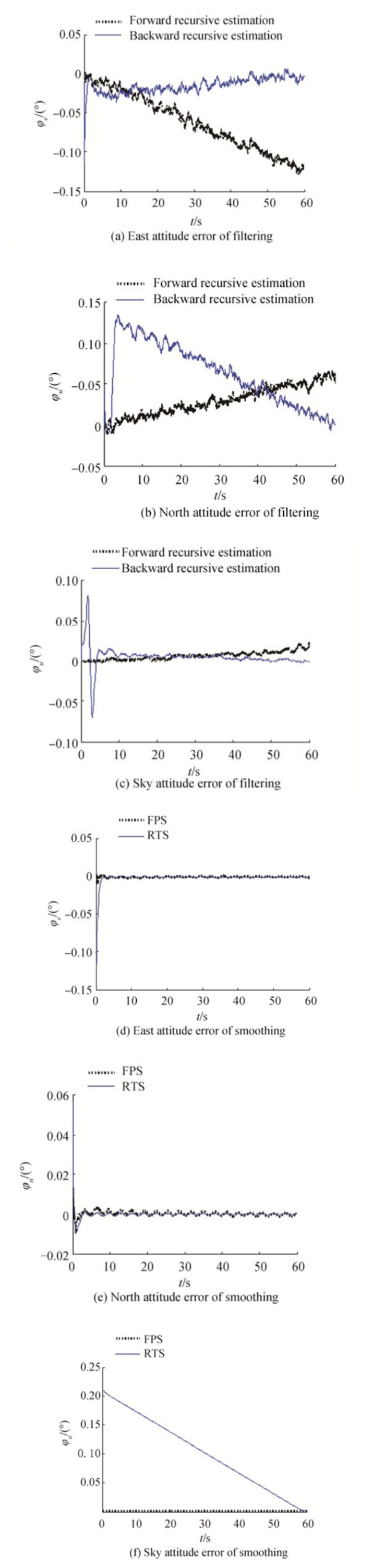
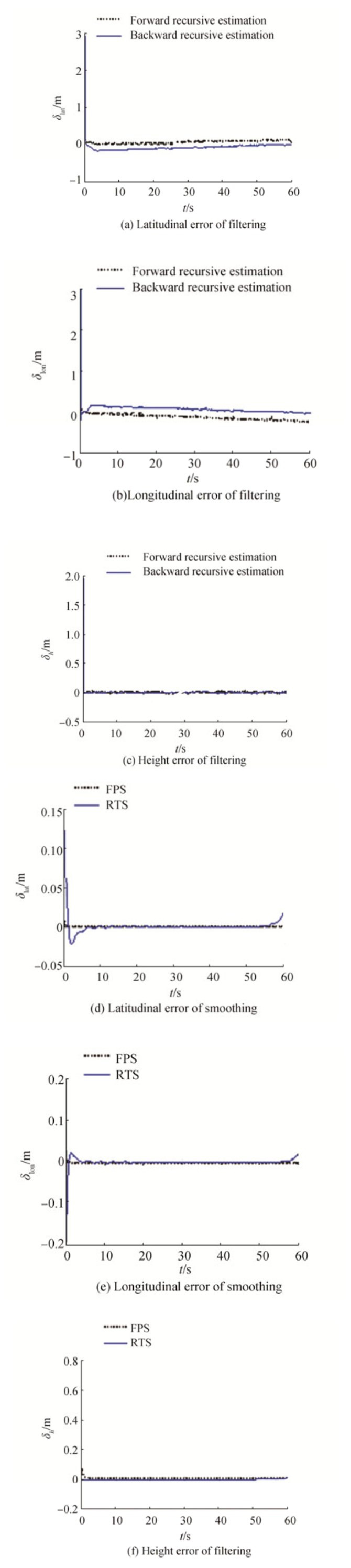
Using the proposed integrated evaluation of the transfer alignment process, we validated the various filtering and smoothing algorithms and compared their results after one minute of ideal SINS simulation output data and using the same SINS model. Figs. 2 (a) and 2(b) show 3D convergence trend charts for position and velocity, respectively. Figs. 3–5 show comparisons of the state errors of the four algorithms. Figs. 3(a), 3(b) and 3(c) show the calculation results of attitude error of the two filtering methods, Figs. 3(d), 3(e) and 3(f) show the calculation results of attitude error of the two smoothing methods. Figs. 4 (a), 4(b) and 4(c) show the comparisons of velocity error of the two filtering methods, Figs. 4(d), 4(e) and 4(f) show the comparisons of velocity error of the two smoothing methods. Figs. 5(a), 5(b) and 5(c) show the calculation results of position error of the two filtering methods, Figs 5(d), 5(e) and 5(f) show the comparisons of attitude error of the two smoothing methods.

From Fig. 3, we can see that the algorithms converge to a very small area ($ \le 4 \times {10^{ - 3}}$), which indicates that the results of this method are correct. Also from the Fig. 4 and Fig. 5, we see that during most of the simulations, the position and velocity errors are small, so we can obtain the velocity of convergence result very fast.

From Figs 3–5, we can conclude that KF and ISRE can both be used to estimate the initial state and that the experimental results are similar. That is, the value at the final ISRE time represents an estimate of the initial error. While the estimation results of two smoothing methods are significantly higher than those of the two filter methods, they are similar in effect. Furthermore, the RTS method can achieve the global optimum by using all the data, which can be represented as a velocity curve.

FPS does not require the storage of a large volume of filter data and its computational burden is lower than that of RTS. However, the transfer-alignment-accuracy integrated evaluation is an offline ex-post evaluation and the computer is fully able to meet performance requirements. Today, RTS is recommended for engineering applications.

As a comprehensive identification index, the DOA or generalized DOA should be calculated according to tactical and technical norms after finishing the above estimation process. For example, in missile applications, the performance requirement relates to the location accuracy index and the generalized DOA of the position parameters can be calculated at this time. As the SINS' RMS0, the statistical result of the SINS simulation was0.99 m/s and the position DOA of an airborne missile was 97.37% (120 s, UVHF, uniform velocity horizontal flight), based on a calculation for which the transfer alignment method is a velocity-and-attitude matching scheme. The position accuracy was 1.016 m/s for a 120-s transfer alignment in the UVHF state.

DOA calculations of a generalized INS extension can employ mature statistical inference evaluation methods and it is unnecessary to update the identification equipment as this evaluation can be performed with the equipment at hand.

6 Conclusions

In this paper, our theoretical calculations and simulated analyses show the DOA concept to be a reasonable, convenient, general, and integrated index for transfer alignment. Not only can it reflect the alignment time and accuracy, but also the differences between different maneuvers or different alignment schemes. This suggests that this index can be reliably used in transfer alignment evaluation and identification. Moreover, we recommend the used of the RTS algorithm in engineering applications. Based on all the evidence, the relationship between different parameters will require further research.