Group of piers are more popular in bridge design for geotechnical and economic reasons (Ataie-Ashtiani et al., 2010) as it is needful to construct multilane bridges in crowded cities or sometimes construction of new pier at upstream or downstream of existing pier is mandatory. Complex piers can significantly affect the hydrodynamic characteristics of the flow field around the piers and lead to develop scour (Ferraro et al., 2013). Scouring around group of piers is significantly different from single pier arrangement (Beg, 2010). A detailed investigation of the turbulent flow structures around the group of the piers can enlighten the process of scouring (Ataie-Ashtiani et al., 2010). Many of the researchers have carried out experimentation on the flow around the piers (Ahmed and Rajaratnam, 1998; Graf and Istiarto, 2002; Izadinia et al., 2013). These studies have focussed on investigation of the flow around single pier with or without scour hole. In the present study tandem arrangement, which is one of the most widely used arrangements of pier groups is studied. For this arrangement, many researchers have carried laboratory work to investigate relation between pier spacing and maximum scour depth (Salim and Jones, 1998; Ataie-Ashtiani and Baheshti, 2006). Igarashi (1981) investigated the change in flow pattern with respect to spacing between the piers. Salim and Jones (1998) predicted that the scour depth decreases as the distance between piers increases. Ataie-Ashtiani and Baheshti (2006) carried out experimental investigation of scour around group of piers and proposed a correction factor for better accuracy of existing equations especially for tandem arrangements of piers. Palau-Salvador et al. (2008) conducted laboratory experiments with numerical simulation around two submerged piers in tandem arrangement and observed that the presence of second pier disturbs the formation of vortices at the downstream of first pier. Zhuang and Liu (2007) have developed an empirical formulation for calculating turbulent flow width generated around bridge piers due to obstruction to flow. Said et al. (2008) carried out laboratory experiments and taken velocity measurements around single pier and two submerged piers in tandem arrangement shows that in case of tandem arrangement the characteristics of flow are depending upon the spacing between the two piers. Tafarojnoruz et al. (2012a) proposed a countermeasure for two piers in tandem arrangement. Ataie-Ashtiani and Aslani-Kordkandi (2013) conducted laboratory experiment on rough bed and compared various turbulence characteristics of flow around single pier and two piers in tandem arrangement. The present study focuses on turbulence characteristics of flow around two piers in tandem and effect of scouring around tandem piers on bed morphology.
In alluvial streams, water is seeping in (upward seepage) or out (downward seepage) from the channel boundaries. Inflow or outflow through porous alluvial boundaries is conditioned upon the difference in water level in channel and ground water table. Tanji and Kielen (2002) evaluated that, seepage losses of 20% -50 % of the total flow in unlined earthen canals can occur in semiarid regions. Kinzli et al. (2010) estimated around 40% losses due to downward seepage. Martin and Gates (2014) evaluated water loss around 15% upstream flow rate due to downward seepage. Apart from losses, the downward seepage significantly affects channel hydrodynamics. Downward seepage influences the flow properties and rate of sediment transport due to momentum exchange between channel boundaries and water in the channel. Most of the researchers have found out that downward seepage may alter channel geometry, increase the Reynolds shear stresses near the boundary and consequently enhance the sediment motion. (Rao et al., 2011; Patel et al., 2015; Deshpande and Kumar, 2016). Qi et al. (2012) have carried out experiments with 2% downward seepage and found a reduction in equilibrium scour depth.
Although there have been previous research on tandem arrangement of piers, still the change in flow characteristics around piers and bed morphology is unclear. Previous researchers have neglected downward seepage parameter, which is incorporated in present work to study the influence of downward seepage on turbulent flow characteristics around tandem piers and corresponding changes in bed geometry.
2 ExperimentationLaboratory experiments were conducted in a tilting flume of length 17.2 m, 1m width and 0.72 m depth. Fig. 1 shows schematic diagram of experimental setup.

|
Figure 1 Schematic diagram of experimental flume set-up |
Experimental setup used in this study is same as detailed in Chavan et al. (2017). Initially plane bed was prepared with two cylindrical piers of perspex material with diameter 75 mm and height 150 mm were placed in tandem arrangement. Flow has been introduced slowly to maintain relatively small velocity of flow and gradually increased so the approaching flow could not wash away the bed material. Front pier was located at 7.5 m from downstream of the channel that is at the middle of the test section of 5 m to 10 m, to ensure fully developed flow. Centre to centre spacing between the two piers was 22.5 cm such that the ratio of centre to centre spacing between the piers and pier diameter is 3 (2 -4) to avoid the interference effect of the piers (Ataie-Ashtiani and Baheshti, 2006). The sediment bed was made up of uniform sand of mean grain diameter 0.418 mm so that D/d50 > 50 where D is diameter of pier, to avoid effect of sediment size on scour depth (Chiew and Melville, 1987) and geometric standard deviation σg is 1.14. Experimental runs were carried for no seepage, 10 % seepage and 20 % seepage conditions. The desired seepage discharges were applied and maintained by electromagnetic flow meters installed at downstream of flume. In this study the incipient motion criterion was used for defining the flow depth in order to investigate effect of seepage on bed mobility. The flow depth and discharge obtained for no seepage condition was 11.4 cm and 0.035 m3/s, respectively. Reynolds number and Froude number obtained with respect to the flow depth were 31 400 and 0.26. The geometry of the bed and scoured region around piers was measured by Ultrasonic ranging system (SeaTek®). The SeaTek instrument measures the distance to a target of wavelength 0.3 mm in water with 5 MHz ultrasound with measurement accuracy of 0.1 mm. Acoustic Doppler Velocimeter (ADV) was used to measure velocity profiles around piers at 20 depths. Once the experimentation started, after one hour, the velocity measurements were taken such that it could be possible to obtain velocity data within the developing scour hole. ADV works with 10 MHz acoustic frequency and has precision of ±0.1 mm. A sampling rate of 200 Hz was used for collecting data up to 5min. Velocity is measured at around 20 points in each velocity profiles. Velocity and turbulence data obtained by ADV are as follow:
| $ u = \frac{1}{N}\sum\limits_{i = 1}^N {{U_i}} $ | (1) |
| $ w = \frac{1}{N}\sum\limits_{i = 1}^N {{W_i}} $ | (2) |
where u, v and w are the time-averaged velocities in the streamwise, spanwise and vertical directions, respectively.
| $ u' = {U_i} - u $ | (3) |
| $ w' = {W_i} - w $ | (4) |
where Ui and Wi are instantaneous velocities in stream wise and vertical directions respectively. u'and w' are fluctuating component in streamwise and vertical direction. N is number of instantaneous velocity samples.
The velocity and turbulence data obtained by ADV need to be post processed as it includes spikes due to interference between transmitted and received signals. Acceleration Threshold method is used (Goring and Nikora, 2002) to remove the spikes with threshold values between 1 to 1.5 based on trial an error method in such a way that velocity power spectra fit with Kolmogorov's -5/3 law in the inertial subrange. Velocity power spectra for streamwise velocities at upstream of piers are shown in Fig. 2. In all experiments an average correlation coefficient between transmitted and received signal is less than 70% and signal to noise ratio kept (SNR) between 10 and 15 (see e.g. Tafarojnoruz et al., 2012b).

|
Figure 2 Velocity power spectra with Kolmogorov's -5/3 at Upstream of piers |
Cross-sectional area of the channel is reduced due to construction of structures like bridge piers in the channel. Presence of piers in the channel, obstruct and divert the path of the flowing stream. Separation of flow due to piers leads to generate higher Reynolds stresses near the bed around piers. Inflation in Reynolds stresses increase the momentum exchange consequently, erodes the bed material around the piers. In this study, two piers are arranged in tandem manner. The approaching flow is obstructed by the front pier, separated in downward direction along the face of the pier and along sides of the pier in the form of side circulations. In front of the pier, the downward flow hits the bed and extract the bed material, which is carried forward by the circulating flow along the sides of the pier and deposited just behind the pier. In the gap between two piers the flow pattern is complicated because of the wake vortices forming at downstream of the front pier and obstruction to flow by rear pier. In case of tandem arrangement of bridge piers, presence of rear pier restrains the wake vortices formed at the downstream of the front pier. The wake vortices are smaller near the bed, as the distance from the bed increases the wake vortices increase in length (Ataie-Ashtiani and Aslani-Kordkandi, 2013) and moves further along the approaching stream flow, obstructed by the rear pier. Hence, the flow obstructed by rear pier is weaker than the fully developed flow which is obstructed by the front pier. The downflow at the front pier has having more potential to scour around front pier than the downflow along the face of rear pier. As the flow passes towards rear pier, wake vortices at the downstream of front pier diminish the velocity of flow, which creates less turbulence at the rear pier and consequently lessens the scour depth at the rear pier.
Fig. 3 shows bed morphology after scouring for no seepage and seepage runs. The scour depth at rear pier is reduced nearly about 50% than the scour depth occurred at front pier for all the runs. In case of 10% seepage, scour depth at front pier is reduced by 16% and at rear pier by 14% and for 20% seepage scour depth at is decreased by 23% at front piers whereas by 26% at rear pier. The extracted bed material is deposited further along the centreline produces hump at the downstream of the piers.

|
Figure 3 Scour around piers (All dimensions are in mm) |
The height of hump is lesser for no seepage run than the seepage runs. Hump height is increased by 10% for 10%seepage and again increased by 22% for 20% seepage. In this study, depletion in scour depth on application of downward seepage is in agreement with the findings of Chavan et al. (2017).
Development of scour around bridge piers is depending upon time. Vortex around piers expands in lateral and longitudinal direction with time. At different intervals of time, lateral bed profiles are measured at upstream of piers with Ultrasonic ranging system for 20 cm transverse distance at upstream and downstream of the pier by considering the centre of pier as centre of that transverse distance. From Fig. 4 it can be seen that, initially rate of scouring is greater which reduces gradually and decreased up to 50% within 12 hours. Flowing stream is obstructed by piers hence generates pressure gradient at the face of the piers. Adverse pressure gradient at the face of the piers results in unstable strong downflow (Zhao et al., 2015) along the face of the piers. The downflow hits the bed and erode the bed material and moves in reverse direction to that of the flowing stream. The reversal flow removes the bed material from slanting slope of the scour hole and enlarges the vortex size. Hence, the reversal flow at upstream of the piers is responsible for development of scour. As the lateral flow in the form of downward seepage through channel boundaries leads to change channel hydrodynamics, consequently modifies the bed morphology around piers. In case of no seepage runs, rate of development of scour depth is more than seepage runs as the downward seepage curtails the reverse flow near the bed at upstream of piers.
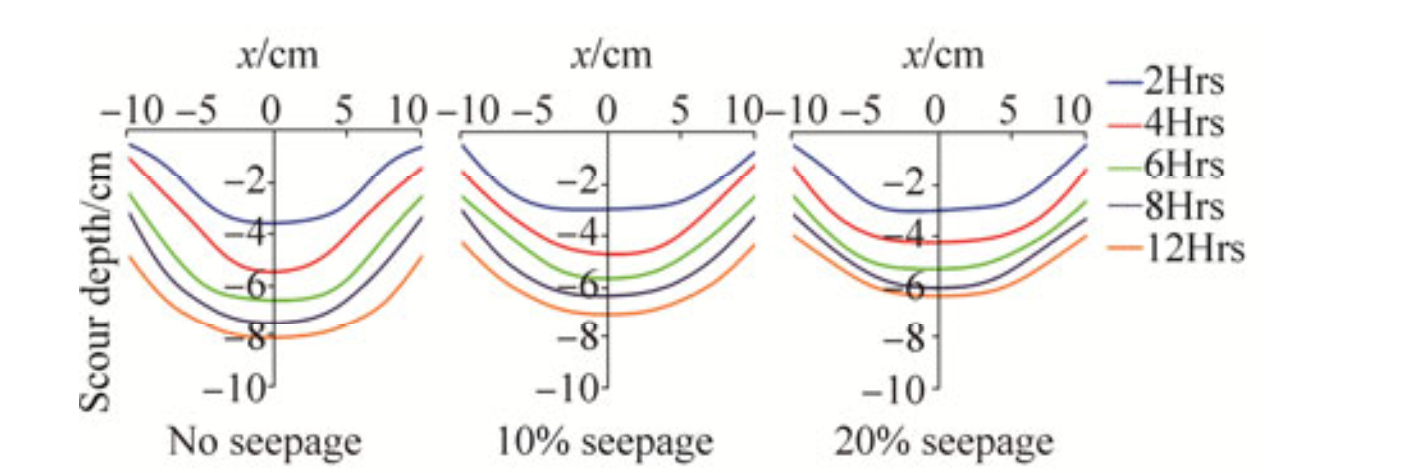
|
Figure 4 Development of scour depth with time at upstream of piers |
The velocity profiles were measured by ADV around piers at three sections, upstream (A) of the front pier, in between both the piers (B) and downstream (C) of the rear pier. Fig. 5 shows velocity profiles at three sections; A (7.597 5, 0.5), B (7.388, 0.5) and C (7.183 5, 0.5) respectively for no seepage, 10% seepage and 20% seepage runs. The velocity profiles are plotted with z/h verses u/u*, where z is the distance of the point from bed, where velocity measurements were taken and h is the total flow depth, u is time averaged velocity and u* is shear velocity.
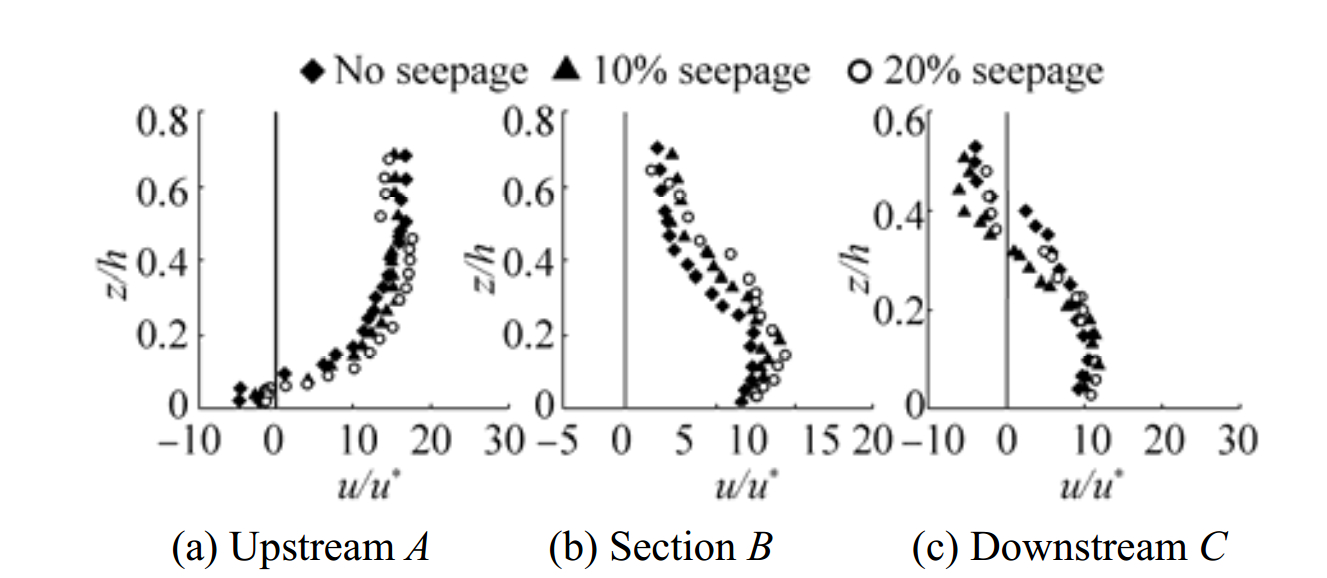
|
Figure 5 Velocity profiles around pier |
At upstream of the front pier that is at section A, as the approach flow is obstructed by the front pier, the reversal velocity can be seen near the bed with in the scour hole where the streamwise component of velocity is found to be negative. With increasing distance from the bed, the stream wise velocity component becomes positive reached to maximum velocity near the edge of the scour hole at (z/h≈ 0.45). At downstream of the pier, at section C, reversal flow can be seen near the free surface and becomes positive with increasing distance from the free surface; the stream wise velocity component attains its maximum value near the bed (z/h≈0.1). Section B is the most critical section where the velocity profile is influenced by flow circulations at the downstream of the front pier and obstruction to the flow by the rear pier. At section B near the free surface the velocity is less positive and gradually increasing near the bed. In case of tandem piers, the flow behaviour between two piers is noticeably complex. The flow leads to the formation of wake vortices at downstream of the pier by moving further along the sides of the front pier due to flow separation at upstream of the front pier. The velocity of flow decreased while approaching the rear pier because of the wake vortices at front pier (Ataie-Ashtiani and Aslani-Kordkandi, 2013). At downstream of rear pier, reversal flow can be seen near the free surface and velocity is increasing gradually with moving towards the bed.
Downward seepage leads increase of the velocity and shear stress near the bed which enhance rate of sediment transport (Devi and Kumar, 2015). In this study, though the velocity increased on application of downward seepage, downward seepage impedes the reversal flow. Consequently, the velocity of flow is less near the bed at upstream of the front pier (Section A) and near the surface at Section C in case of seepage runs.
3.3 Reynolds shear stressFig. 6 shows profiles of Reynolds shear stress (RSS) at sections A, B and C for no seepage, 10% seepage and 20% seepage conditions. Presence of pier diverts the approaching flow at the upstream edge of the pier, leading to create more turbulence around the pier. The flow separation generates higher Reynolds stresses and enhances the momentum exchange owing to scour around piers. Reynolds shear stress becomes negative near the bed at section A and near the free surface at section C. Reynolds stresses are stronger at downstream of piers than those are at upstream of piers due to wake vortices forming at downstream of piers. At section B, Reynolds shear stress fluctuates heavily due to wake vortices generated at the downstream of the front pier and obstruction to the forwarding flow because of rear pier. From fig. 6 it can be perceived that at section A Reynolds stresses are negative near bed and near free surface at section C. At section A, Reynolds stresses are increasing, with moving away from the bed whereas, at section C Reynolds stresses are increasing with moving towards bed. Downward seepage leads to decrease Reynolds stresses near the bed at upstream of the pier. The Reynolds shear stresses are more in case of no seepage run then decrease in case of 10 % seepage and again decrease in case of 15% seepage run.
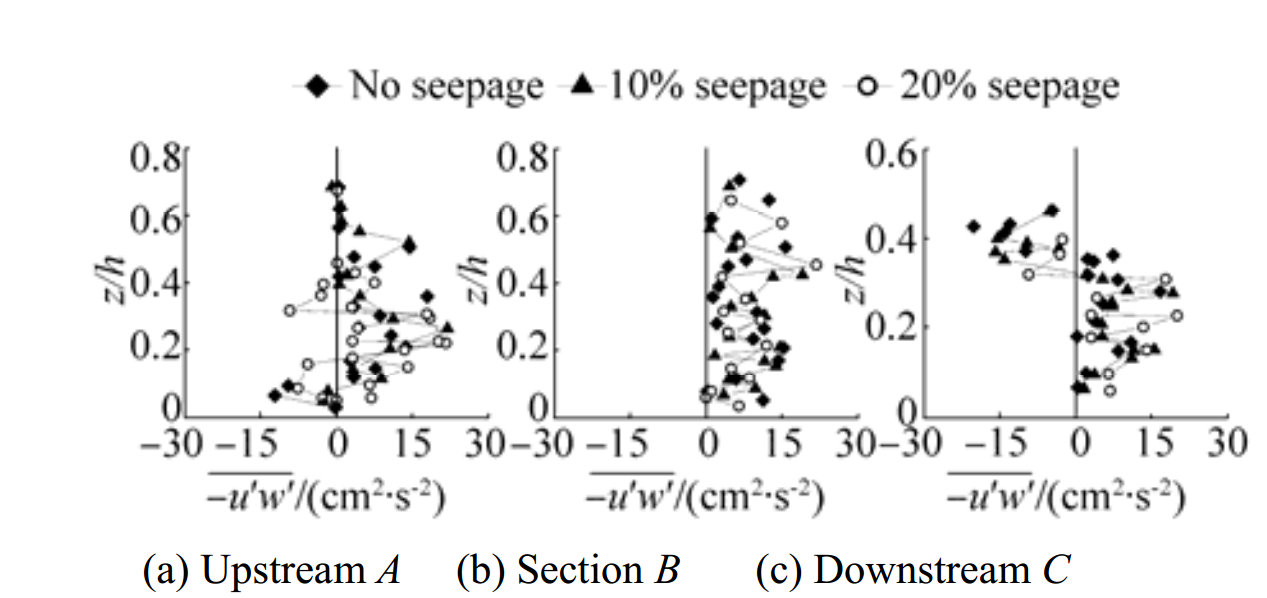
|
Figure 6 RSS profiles |
Lu and Willmarth (1973) have introduced quadrant analysis of Reynolds shear stress which is most frequently used conditional sampling technique, to evaluate the coherent structures of turbulent flow. The bursting phenomenon is quasi-cyclic process in which ejection and sweep are important events describing the sequence of bursting phenomenon. Upward entrainment of low speed fluid particles into the main turbulent flow is called as ejection whereas, these ejected low speed fluid particles are brushed away by high speed fluid particles while sweep events. Sweep is the downward movement of high speed fluid particles towards the bed. To evaluate Reynolds shear stress at a single point as the sum of contribution from different bursting events, the instantaneous values of velocity fluctuations are plotted on plane. The bursting events are defined by four quadrants (q=1, 2, 3, 4), i.e. outward interaction (Q1), ejection (Q2), inward interaction (Q3) and sweep (Q4), respectively.
Contribution to the total Reynolds shear stress through different events can be calculated as:
| $ u'{w'_{{\rm{q}}, H}} = \mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\int\limits_0^T {u'\left(t \right)w'\left(t \right){I_{{\rm{q}}, H}}\left({z, t} \right){\rm{d}}t} $ | (5) |
where T is sampling time, angle bracket indicates conditional averaging, Iq, H is the indicator function which is defined as:
| $ {I_{q, H}}\left[ {u'\left(t \right)w'\left(t \right)} \right] = \left\{ \begin{array}{l} 1, {\rm{if}}\left({u', w'} \right)\;{\rm{is}}\;{\rm{in}}\;{\rm{quadrant}}\;q\\ {\rm{and}}\left| {u'w'} \right| \ge H{\left({\overline {{{u'}^2}} } \right)^{0.5}}{\left({\overline {{{w'}^2}} } \right)^{0.5}}\\ 0, {\rm{otherwise}} \end{array} \right. $ | (6) |
where H is hyperbolic hole size defined by curve (Nezu and Nakagawa, 1993),
| $ \left| {u'w'} \right| = H\sqrt {\overline {{{u'}^2}} } \sqrt {\overline {{{w'}^2}} } $ | (7) |
H indicates threshold level. The hole size H=0, suggests that all data from and corresponding are taken into account. Fractional contribution to the total Reynolds shear stress from different events is defined as:
| $ {S_{q, H}} = \frac{{u'{{w'}_{q, H}}}}{{\overline {u'w'} }} $ | (8) |
Sq, H is positive for sweeps and ejection and negative for outward and inward interactions.
When H = 0:
| $ {S_{10}} + {S_{20}} + {S_{30}} + {S_{40}}{\rm{ = 1}} $ | (9) |
Vertical distribution of stress fraction for H = 0, for no seepage and seepage runs are shown in Fig. 7.

|
Figure 7 Stress fraction Si, H against z/h |
At upstream of the front pier in near bed region, the reversal flow lifts the sediment particles from the scour hole however; the particles are unable to move forward as the flow is not having sufficient capacity to carry the particles. It can be also seen visually during the experiments that particles dislodged by the reversal flow from the slanting slope of the scour hole are again settled down on the bed. From Fig. 7 it can be observed that near the bed with in the scour hole (z/h≤0.1) at upstream of the pier, Q1 and Q3 events contribute more to the total Reynolds shear stress than Q2 and Q4. Contributions from sweep and ejection events are more than inward and outward interaction at outside the scour hole. Near the edge of the scour hole, sweep events are more dominating. Sweep events are governing mechanism for the threshold condition of mobile bed channel due to arrival of high speed fluid particles which enhance the momentum exchange and lead to develop the scour depth. In the downstream of the piers (section C) within the scour hole (z/h > 0.38), ejection events are dominant over sweep events as low speed fluid parcels arrive due to reversal flow which is contributing greater in streamwise direction. Ejection events brought the sediment in suspension which reduces towards the water surface. Whereas, above scour hole (z/h > 0.38), probability of occurrence of sweep and ejection events is nearly same. The magnitude of events is greater at this section as the flow is more turbulent due to wake vortices forming at downstream of piers. At section B, throughout the flow depth, contributions coming from sweep and ejection events are more than contributions of inward and outward interaction. At section B, fluctuations of stress fraction are increased. At section A that is upstream of the piers and section C that is downstream of the piers, stress fraction fluctuates more near the bed due to complex flow structure with in the scour hole and fluctuations are reduced gradually towards the surface.
Downward seepage through channel boundaries influences the conditional RSS distribution. Contribution of all four quadrants namely; inward interaction, outward interaction, ejection and sweep to the Reynolds shear stress are increased in case of seepage as compared to no seepage runs. From Fig. 7 it can be perceived that downward seepage results in arrival of low speed fluid particles due to retardation of flow which indicates ejection events. Whereas, above the scour hole contribution of ejection and sweep events are greater, inward and outward interaction contribute weakly to total Reynolds shear stress.
3.5 Moment AnalysisThird order correlations of velocity fluctuations are studied to procure the information of contribution velocity fluctuations in terms of flux and diffusion of the Reynolds stresses (Simpson et al. 1981). The third order correlation is defined as:
| $ {M_{jk}} = \overline {{{\hat u}^j}{{\hat w}^k}} $ |
where, j+k=3,
Fig. 8 shows third order correlation of velocity fluctuations (M30, M03, M12 and M21) for no seepage, 10% seepage and 20% seepage at upstream of piers (section A) and downstream of piers respectively. From Fig. 8 it can be observed that third order moments are fluctuating heavily throughout the flow depth and fluctuations are more near the edge of the scour hole At upstream of piers (section A) M30 and M12 start with positive values near the bed and then changing over to the negative values with increasing z/h, which implies that near the bed
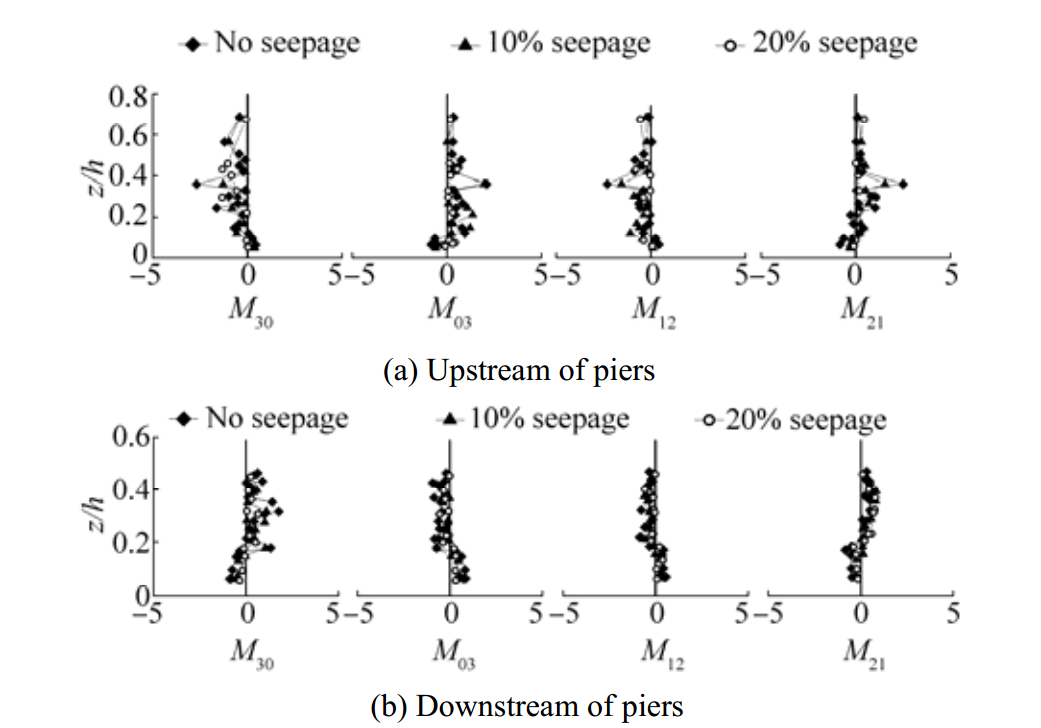
|
Figure 8 Vertical distribution of higher order moments |
The distribution of non-dimensional flux of streamwise (FTKEu = fTKEu/U*3) and vertical (FTKEw = fTKEw/U*3) turbulent kinetic energy is shown in Fig. 9 Which can be calculated as (Raupach, 1981),
| $ {f_{\begin{array}{*{20}{l}} {{\rm{TKEu}}} \end{array}}} = 0.75\left({\overline {u'u'u'} + \overline {u'w'w'} } \right) $ | (10) |
| $ {f_{\begin{array}{*{20}{l}} {{\rm{TKEw}}} \end{array}}} = 0.75\left({\overline {u'u'w'} + \overline {w'w'w'} } \right) $ | (11) |

|
Figure 9 Vertical distribution of TKE fluxes |
Fig. 9 shows graph of non-dimensional flux of turbulent kinetic energy against z/h for no seepage and seepage conditions at upstream and downstream of piers. Presence of piers in flowing stream leads to change flow pattern around piers and turbulent flow characteristics accordingly. At upstream of the piers (section A) for no seepage conditions fTKEu begin with small positive and fTKEw start with negative values. With increasing z/h, fTKEu turns towards negative and fTKEw turns towards positive. Positive values of fTKEu and negative fTKEw are associated with streamwise flux of turbulent kinetic energy in streamwise direction and vertical flux of turbulent kinetic energy is in downward direction. However, away from the bed negative fTKEu and positive fTKEw imply that streamwise flux of turbulent kinetic energy opposite to flow direction and vertical flux of turbulent kinetic energy in the upward direction. Negative fTKEu and positive fTKEw originate retardation process with arrival of low speed fluid parcels. Though same pattern is observed in case of seepage runs, close observation of Fig. 9 shows that near the bed fTKEu and fTKEw have lesser positive and negative values in case of seepage runs than no seepage condition.
At downstream of piers (section C), secondary currents are more dominant due to wake vortices. fTKEu and fTKEw initiate with small negative and positive values respectively. Moving away from the bed, nearly at the edge of the scour hole fTKEu turns towards positive and fTKEw turns towards negative. Near the bed at the downstream of the piers, negative fTKEu and positive fTKEw indicate that streamwise flux of turbulent kinetic energy against the flow direction and vertical flux in upward direction respectively. Negative fTKEu and positive fTKEw, signifies retarding effect due to wake vortices forming at the downstream of the piers which results in arrival of slowly moving fluid parcels. However, near the free surface, positive fTKEu and negative fTKEw corresponds to streamwise flux of turbulent kinetic energy is in flow direction and vertical flux of turbulent kinetic energy is in downward direction results in inrush of fluid parcels. In case of downward seepage conditions, near the bed fTKEubecomes less negative and fTKEw becomes more positive. At section B, it is observed that streamwise and vertical flux of turbulent kinetic energy is more fluctuating and following nearly same trend as it is obtained at section C. On application of downward seepage, the negative fTKEu and positive fTKEw are decreased near the bed, which results in lesser momentum exchange in case of seepage runs than no seepage condition.
3.7 Power spectra analysisFig. 10 shows power spectra plotted against the frequency for velocity components at downstream of piers (section C) for no seepage, 10% seepage and 20% seepage, near free surface (z/h≈0.4). Power spectrum analysis has been carried out to find out strength of wake vortices formed at downstream of piers. Power spectra were obtained from Fast Fourier Transformation (FFT) of auto-covariance function of velocity time series data. The resultant power spectra is calculated as,
| $ S\left(f \right) = {\left\{ {{S_u}{{\left(f \right)}^2} + {S_v}{{\left(f \right)}^2} + {S_w}{{\left(f \right)}^2}} \right\}^{0.5}} $ |
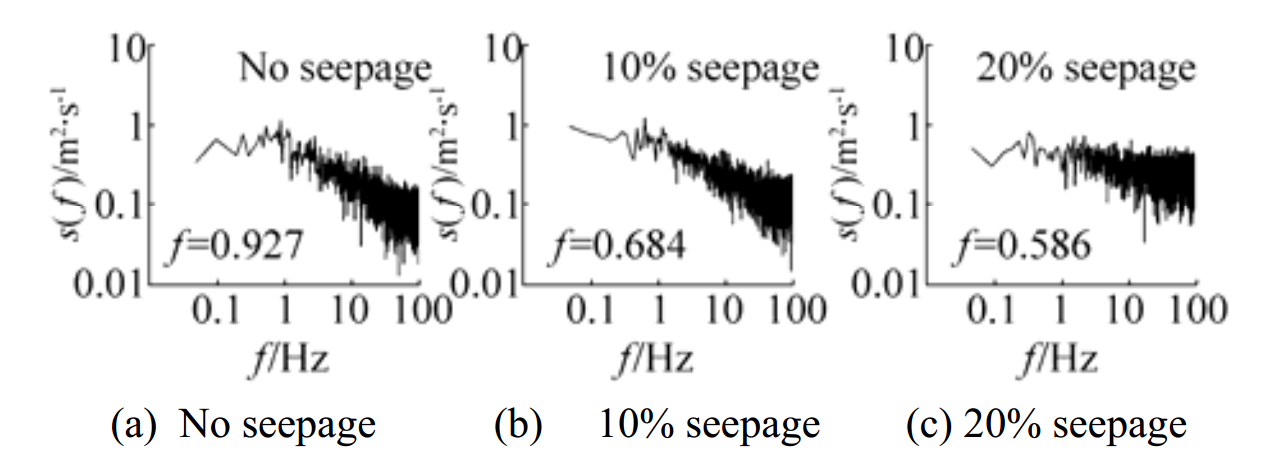
|
Figure 10 Power spectra at downstream of piers |
where Su(f), Sv(f) and Sw(f) are power spectra of velocity components in streamwise, transverse and vertical direction respectively. In the power spectrum distribution, power related to the peak frequency indicates the strength of wake vortices. Strength of vorticity is associated with the capacity of the wake vortices to move the bed particles. From power spectra analysis, Strouhal number is calculated as, fD/U0 where, f is vortex shedding frequency; which is associated with maximum S(f) in Fig. 10, D is diameter of pier and U0 is depth average flow velocity. In this study Strouhal number is calculated at near free surface (z/h≈0.4) and near bed region for no seepage (z/h≈0.07) and seepage conditions and values are mentioned in Table 1.
|
|
Table 1 Strouhal number at downstream of piers |
For no seepage condition, vortex shedding frequency is 0.927 Hz corresponding vortex shedding period is 185 and Strouhal number (St) near the free surface is 0.23 which is comparable with literature (Igarshi, 1981; Sumner et al., 1999; Ataie-Ashtiani and Aslani-Kordkandi, 2013). Inside the scour hole that is near bed region Strouhal number is lesser than it is at near free surface as the strength of wake vortices is least near the bed (Ataie-Ashtiani and Aslani-Kordkandi, 2013).
It has been seen in present study that downward seepage changes the stream flow characteristics and bed morphology around piers. It also shows significant impact on velocity power spectra. From Fig. 10 it can be observed that at downstream of piers, resultant power spectrum is shifted towards lower frequency on application of downward seepage hence, value of Strouhal number is decreasing. At downstream of piers, reduction in strength of wake vortices or decrement in Strouhal number indicates that lateral flow through channel boundaries diminishes the capacity of wake vortices to move bed material.
3.8 Tubulent kinetic energyFig. 11 shows vertical profiles of Turbulent Kinetic Energy (TKE)
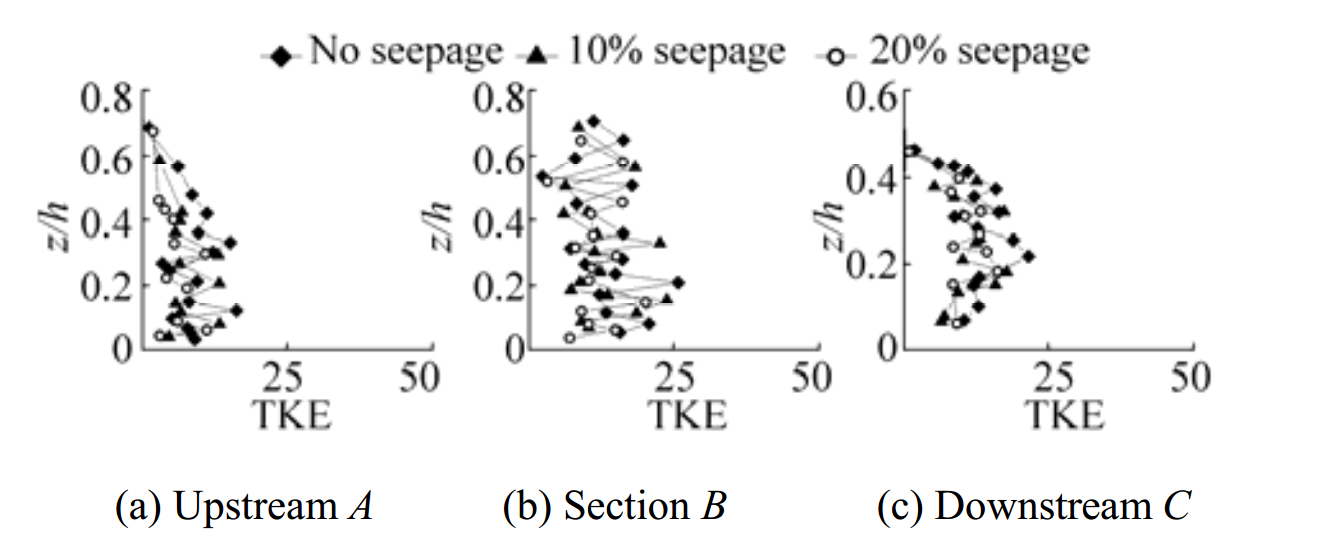
|
Figure 11 Vertical distribution of turbulent kinetic energy |
Laboratory experiments were conducted in a tilting flume to study the effect of downward seepage on the turbulent flow statistics and scouring around tandem piers. Two piers of 75mm diameter are arranged in tandem manner. In the present study various turbulent characteristics were measured no seepage and seepage conditions. Change in bed morphology after scouring and effect of downward seepage on scouring is also studied. Following are the conclusions drawn from the present research:
1) Piers obstruct the flowing stream hence; flow separation around piers leads to erode the bed material, eroded material carried by flowing stream and gets deposited at the downstream of piers. Scour depth at front pier is twice of the scour depth at the rear pier for all the runs and with downward seepage scour depth reduces around both piers. Rate of development of scour depth decreases with downward seepage.
2) At upstream of both piers, near the bed region and near free surface, at downstream of both piers reversal flow is observed. Downward seepage impedes the reversal flow hence controls erosive capacity of reversal flow. Significant decrease in Reynolds shear stress near the bed at upstream of the piers results in lower scour depth in case of seepage runs. In the gap between two piers, wake vortices are forming near the surface due to flow separation at front pier and reversal flow can be seen near the bed due to obstruction by rear pier therefore velocity is less near free surface and is increasing with moving towards bed.
3) At upstream of pier, near the bed, inward interaction and outward interaction contribute more to the Reynolds shear stress whereas away from bed contribution of sweep events are greater. With downward seepage contribution of all events is increasing. At downstream of piers ejection events are more dominant. Whereas in the gap between two piers, contribution of ejection and sweep are stronger towards Reynolds shear stress.
4) In seepage runs, lesser streamwise flux of streamwise Reynolds stress and lesser vertical flux of vertical Reynolds stress is observed near the bed at upstream of piers. Lesser fluxes of streamwise turbulent kinetic energy in streamwise direction and vertical fluxes of turbulent kinetic energy in vertical direction also been observed. Hence, at upstream of piers lower momentum exchange near the bed leads to minimize the scour depth on application of downward seepage. Turbulent kinetic energy is higher near the edge of the scour hole and is decreasing with downward seepage.
5) Power spectral analysis of velocity components has been carried out at downstream of piers. With downward seepage resultant power spectra shifts towards lower frequency, consequently Strouhal number is decreasing. Hence, downward seepage is responsible for decreased strength of wake vortices.
Ahmed F, Rajaratnam N, 1998. Flow around bridge piers. Journal of Hydraulic Engineering, 124(3), 288-300. DOI: http://dx.doi.org/10.1061/(ASCE)0733-9429(1998)124:3(288)
( 0) 0)
|
Ataie-Ashtiani B, Aslani-Kordkandi A. Flow field around single and tandem piers[J]. Flow, Turbulence and Combustion, 2013, 90(3): 471-490. DOI:10.1007/s10494-012-9427-7 ( 0) 0)
|
Ataie-Ashtiani B, Baratian-Ghorghi Z, Beheshti AA. Experimental investigation of clear-water local scour of compound piers[J]. Journal of Hydraulic Engineering, 2010, 136(6): 343-351. DOI:10.1061/(ASCE)0733-9429(2010)136:6(343) ( 0) 0)
|
Ataie-Ashtiani B, Beheshti AA. Experimental investigation of clear-water local scour at pile groups[J]. Journal of Hydraulic Engineering, 2006, 132(10): 1100-1104. DOI:10.1061/(ASCE)0733-9429(2006)132:10(1100) ( 0) 0)
|
Beg M, 2010. Characteristics of developing scour holes around two piers placed in transverse arrangement. Scour and Erosion, ASCE, 76-85. DOI: http://dx.doi.org/10.1061/41147(392)6#sthash.2PdT77GQ.dpuf
( 0) 0)
|
Chavan R, Sharma A, Kumar B. Effect of downward seepage on turbulent flow characteristics and bed morphology around bridge piers[J]. Journal of Marine Science and Application, 2017, 16(01): 60-72. DOI:10.1007/s11804-017-1394-x ( 0) 0)
|
Chiew YM, Melville BW, 1987. Local scour around bridge piers. Journal of Hydraulic Research, 25(1), 15-26. DOI: http://dx.doi.org/10.1080/00221688709499285
( 0) 0)
|
Deshpande V, Kumar B. Turbulent flow structures in alluvial channels with curved cross-sections under conditions of downward seepage[J]. Earth Surface Processes and Landforms, 2016, 41(8): 1073-1087. DOI:10.1002/esp.3889 ( 0) 0)
|
Devi TB, Kumar B, 2015. Turbulent flow statistics of vegetative channel with seepage. Journal of Applied Geophysics, 123, 267-276. DOI: http://doi.org/10.1016/j.jappgeo.2015.11.002
( 0) 0)
|
Ferraro D, Tafarojnoruz A, Gaudio R, Cardoso AH. Effects of pile cap thickness on the maximum scour depth at a complex pier[J]. Journal of Hydraulic Engineering, 2013, 139(5): 482-491. DOI:10.1061/(ASCE)HY.1943-7900.0000704 ( 0) 0)
|
Goring DG, Nikora Ⅵ. Despiking acoustic Doppler velocimeter data[J]. Journal of Hydraulic Engineering, 2002, 128(1): 117-126. DOI:10.1061/(ASCE)0733-9429(2002)128:1(117) ( 0) 0)
|
Graf WH, Istiarto I. Flow pattern in the scour hole around a cylinder[J]. Journal of Hydraulic Research, 2002, 40(1): 13-20. DOI:10.1080/00221680209499869 ( 0) 0)
|
Igarashi T, 1981. Characteristics of the flow around two circular cylinders arranged in tandem: 1st report. Bulletin of JSME, 24(188), 323-331. DOI: http://doi.org/10.1299/jsme1958.24.323
( 0) 0)
|
Izadinia E, Heidarpour M, Schleiss AJ, 2013. Investigation of turbulence flow and sediment entrainment around a bridge pier. Stochastic Environmental Research and Risk Assessment, 27(6), 1303-1314. DOI10. 1007/s00477-012-0666-x
( 0) 0)
|
Kinzli KD, Martinez M, Oad R, Prior A, Gensler D. Using an ADCP to determine canal seepage loss in an irrigation district[J]. Agricultural water management, 2010, 97(6): 801-810. DOI:10.1016/j.agwat.2009.12.014 ( 0) 0)
|
Lu SS, Willmarth WW, 1973. Measurements of the structure of the Reynolds stress in a turbulent boundary layer. Journal of Fluid Mechanics, 60(3), 481-511. DOI: https://doi.org/10.1017/S0022112073000315
( 0) 0)
|
Maity H, Mazumder BS, 2012. Contributions of burst-sweep cycles to Reynolds shear stress over fluvial obstacle marks generated in a laboratory flume. International Journal of Sediment Research, 27(3), 378-387. DOI: https://doi.org/10.1016/S1001-6279(12)60042-0
( 0) 0)
|
Martin CA, Gates TK, 2014. Uncertainty of canal seepage losses estimated using flowing water balance with acoustic Doppler devices. Journal of Hydrology, 517, 746-761. DOI: http://dx.doi.org/10.1016/j.jhydrol.2014.05.074
( 0) 0)
|
Nezu I, Nakagawa H, 1993. Turbulence in open-channel flows.Balkema: Rotterdam, The Netherlands. http://ci.nii.ac.jp/ncid/BA20407467
( 0) 0)
|
Palau-Salvador G, Stoesser T, Rodi W. LES of the flow around two cylinders in tandem[J]. Journal of Fluids and Structures, 2008, 24(8): 1304-1312. DOI:10.1016/j.jfluidstructs.2008.07.002 ( 0) 0)
|
Patel M, Deshpande V, Kumar B, 2015. Turbulent characteristics and evolution of sheet flow in an alluvial channel with downward seepage. Geomorphology, 248, 161-171. DOI: http://doi.org/10.1016/j.geomorph.2015.07.042
( 0) 0)
|
Qi M, Chiew YM, Hong JH. Suction effects on bridge pier scour under clear-water conditions[J]. Journal of Hydraulic Engineering, 2012, 139(6): 621-629. DOI:10.1061/(ASCE)HY.1943-7900.0000711 ( 0) 0)
|
Rao AR, Sreenivasulu G, Kumar B. Geometry of sand-bed channels with seepage[J]. Geomorphology, 2011, 128(3): 171-177. DOI:10.1016/j.geomorph.2011.01.003 ( 0) 0)
|
Raupach MR, 1981. Conditional statistics of Reynolds stress in rough-wall and smooth-wall turbulent boundary layers. Journal of Fluid Mechanics, 108, 363-382. DOI: https://doi.org/10.1017/S0022112081002164
( 0) 0)
|
Said NM, Mhiri H, Bournot H, Le Palec G, 2008. Experimental and numerical modelling of the three-dimensional incompressible flow behaviour in the near wake of circular cylinders. Journal of Wind Engineering and Industrial Aerodynamics, 96(5), 471-502. DOI: 10.1016/j.jweia.2007.12.001
( 0) 0)
|
Salim M, Jones JS, 1998. Scour around exposed pile foundations. Compilation of Conference Scour Papers (1991-1998), ASCE. https://www.mendeley.com/research-papers/scour-around-exposed-pile-foundations/
( 0) 0)
|
Simpson RL, Chew YT, Shivaprasad BG. The structure of a separating turbulent boundary layer. Part 2. Higher-order turbulence results[J]. Journal of Fluid Mechanics, 1981, 113: 53-73. ( 0) 0)
|
Sumner D, Wong SST, Price SJ, Paidoussis MP, 1999. Fluid behaviour of side-by-side circular cylinders in steady cross-flow. Journal of Fluids and Structures, 13(3), 309-338. DOI: https://doi.org/10.1006/jfls.1999.0205
( 0) 0)
|
Tafarojnoruz A, Gaudio R, Calomino F, 2012a. Bridge pier scour mitigation under steady and unsteady flow conditions. Acta Geophysica, 60(4), 1076-1097. DOI: 10.2478/S11600-012-0040-X
( 0) 0)
|
Tafarojnoruz A, Gaudio R, Calomino F, 2012b. Effects of a slotted bridge pier on the approach flow. Proc. XXXⅢ Convegno Nazionale Di Idraulica E Construzioni Idrauliche IDRA 2012, Brescia, Italy, 1-10.
( 0) 0)
|
Tanji KK, Kielen NC, 2002. Agricultural drainage water management in arid and semi-arid areas. FAO.
( 0) 0)
|
Zhao Y, Zong Z, Zou L, Wang TL. Turbulence model investigations on the boundary layer flow with adverse pressure gradients[J]. Journal of Marine Science and Application, 2015, 14(02): 170-174. DOI:10.1007/S11804-015-1303-0 ( 0) 0)
|
Zhuang Y, Liu ZY. Experimental study on the width of the turbulent area around bridge pier[J]. Journal of Marine Science and Application, 2007, 6(1): 53-57. DOI:10.1007/S11804-007-6048-Y ( 0) 0)
|
 2017, Vol. 16
2017, Vol. 16


