1 Introduction
The problems of scattering of water waves by vertical barriers have been drawing a great attention of many researchers for a long time. These problems are important because of their engineering applications such as wavemakers and breakwaters which protect a harbor from the rough sea. Dean (1945) used the complex variable technique to obtain the reflection coefficients from the linearized solution of water wave scattering in the presence of a thin vertical barrier. Ursell (1947) obtained the solution of the problem of water wave diffraction by thin vertical barrier partially immersed in deep water by making use of the singular integral equation along with Havelock's expansion. Porter (1972) derived the solution of the problem involving wave transmission through a gap in a vertical barrier in deep water by using the complex variable technique as well as Green's integral theorem. Banerjea et al. (1996) utilized the one-term and multi-term Galerkin approximation to evaluate the reflection coefficient for the problem considered by Porter (1972). Losada et al. (1992) obtained the reflection and transmission coefficients of the problem involving scattering of water waves by four different types of thin vertical barriers using eigenfunction expansion method. Mandal and Dolai (1994), and Porter and Evans (1995) derived the solution of the problem of Losada et al. (1992) by using the Galerkin approximation. Mandal and Chakrabarti (1999) employed the Galerkin approximation to determine the approximate solutions of a number of water wave scattering problems involving thin vertical barriers in deep water as well as finite depth of water. Sahoo et al. (2000), and Lee and Chawang (2000) analyzed the problem involving the scattering of water waves by permeable vertical barrier using eigenfunction expansion method.
The above works were focused on the scattering of surface water waves by barrier only. On the other hand, the problems involving the scattering of surface water waves by a geometrical disturbance or an obstacle at the bottom are interesting for their possible application in the areas of coastal and marine engineering. The problem consisting of the reflection of surface waves by bottom undulation has been drawing a great attention as its mechanism is important in the development of shore-parallel bars. Such problem was solved by Miles (1981) utilizing the perturbation theory and finite cosine transformation while Davies (1982) employed perturbation theory and Fourier transform technique to obtain the reflection coefficient. Davies and Heathershaw (1984) compared the theoretical results of Davies (1982) by conducting the experiment in a wave tank. Mandal and Basu (1990) generalized the problem of Miles (1981) with inclusion of surface tension at the free surface while Kirby (1993) examined the problem where the incident wave is not necessarily close to the resonant frequency. Martha and Bora (2007) studied the problem for a number of practical examples of bottom undulations. Mandal and Gayen (2006) studied the problem of diffraction of surface water waves by vertical barrier and bottom undulation.
It may be underlined that the combination of vertical barrier and the bottom undulation will serve as an effective breakwater. So it is an endeavor to consider scattering problems involving both barrier and bottom undulation, which help in the real and practical situations. Also, oblique incidence of surface water waves is more natural than the normal incidence. In addition to these, this paper highlights about the applicability of mathematical techniques to solve the mixed Boundary Value Problem (BVP) arising from the scattering problem studied here.
In the present paper, a mixed BVP occurs in a natural way while examining the scattering of oblique water waves by a thin vertical barrier over an undulating bottom topography. With the help of perturbation expansion, many bvps are obtained out of which the first two bvps are considered. The BVP-Ⅰ (zeroth order) corresponds to the problem of scattering of surface waves by barrier over flat bed. This bvp is solved utilizing the eigenfunction expansion method followed by least-squares and QR-factorization giving rise to zeroth order reflection and transmission coefficients. The BVP-Ⅱ represents the radiation problem involving the first order reflection and transmission coefficients. Using the Green's integral theorem, these coefficients are obtained in terms of the integrals involving bottom undulation and the solution of zeroth order BVP. The effect of different parameters involved in the present study, is examined through different graphs. The energy balance relation for the given problem is investigated and checked for assuring the integrity of the theoretical and numerical results of the reflection and transmission coefficients.
2 Formulation of the problemA right handed Cartesian co-ordinate system is taken in which the xz-plane is the undisturbed free surface of the fluid and the y-axis is directed positive vertically downward. The bottom with a small deformation is described by
● Case-Ⅰ:
● Case-Ⅱ:
● Case-Ⅲ:
Partial differential equation and boundary conditions:
It is assumed that the fluid is incompressible, inviscid and the motion to be irrotational and simple harmonic in time. Consider a progressive wave train represented by the velocity potential
| $\hat \phi (x,y) = {\psi _0}(y){{\rm{e}}^{{\rm{i}}\mu x}}$ | (1) |
with
Due to uniformity in the z-direction and the periodicity in time, the velocity potential which describes the fluid motion can be expressed as
| $\frac{{{\partial ^2}\phi }}{{\partial {x^2}}} + \frac{{{\partial ^2}\phi }}{{\partial {y^2}}} - {\nu ^2}\phi = 0,{\rm{in}}\;{\rm{the}}\;{\rm{fluid}}\;{\rm{region}}$ | (2) |
Free surface condition:
| $\,\,\,\,\,\,\,\,\,\frac{{\partial \phi }}{{\partial y}} + K\phi = 0,\,\,\,\,\,\,\,\,\,\,\,{\rm{on}}\,\,y = 0$ | (3) |
Bottom condition:
| $\,\,\,\,\,\,\,\,\,\frac{{\partial \phi }}{{\partial n}} = 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{on}}\,\,y = h + \varepsilon c(x)$ | (4) |
Condition on barrier:
| $\,{\left. {\frac{{\partial \phi }}{{\partial x}}} \right|_{x = {0^ - }}} = {\left. {\frac{{\partial \phi }}{{\partial x}}} \right|_{x = {0^ + }}} = 0,\,\,\,\,\,\,\,\,\,\,\,{\rm{on}}\,\,x = 0,{\kern 1pt} \,y \in B$ | (5) |
Conditions across gap:
| $\,{\left. {\frac{{\partial \phi }}{{\partial x}}} \right|_{x = {0^ - }}} = {\left. {\frac{{\partial \phi }}{{\partial x}}} \right|_{x = {0^ + }}},\,\,\,\,\,\,\,\,\,\,{\rm{on}}\,\,x = 0,{\kern 1pt} \,{\rm{ }}y \in G$ | (6) |
| $\,{\left. \phi \right|_{x = {0^ - }}} = {\left. \phi \right|_{x = {0^ + }}},\,\,\,\,\,\,\,\,{\rm{on}}\,\,x = 0,{\kern 1pt} \,y \in G$ | (7) |
Far field condition:
| $\phi (x,y) \to \left\{ {\begin{array}{*{20}{l}} {\hat \phi (x,y) + R\hat \phi ( - x,y)\;\quad {\mkern 1mu} {\rm{as}}\quad x \to - \infty }\\ {T\hat \phi (x,y)\quad \quad \quad {\mkern 1mu} \;\quad \;\quad \;\;\;{\rm{as}}\quad x \to \infty } \end{array}} \right.$ | (8) |
where
The bottom condition
| $\frac{{\partial \phi }}{{\partial y}} - \varepsilon \left\{ {\frac{{\rm{d}}}{{{\rm{d}}x}}[c(x){\phi _x}] + c(x){\phi _{zz}}} \right\} + O({\varepsilon ^2}) = 0,{\rm{ on}}\,\,y = h$ | (9) |
The approximate boundary condition (9) suggests that
| $\quad \quad \left. \begin{array}{c} \phi \left( {x,y} \right) = {\phi _0} + \varepsilon {\phi _1} + O\left( {{\varepsilon ^2}} \right)\\ R = \;{R_0} + \varepsilon {R_1} + O\left( {{\varepsilon ^2}} \right)\\ T\, = \;{T_0} + \varepsilon {T_1} + O\left( {{\varepsilon ^2}} \right) \end{array} \right\}$ | (10) |
It must be noted that such a perturbation expansion ceases to be valid at Bragg resonance when the reflection coefficient becomes much larger than the dimensionless undulation parameter ε, as noticed by Mei (1985). Also, this theory is valid only for the infinitesimal reflection and away from resonance. It may be reminisced that the Bragg resonance occurs when the wave number of the bottom undulation is twice the wave number of free surface. However, Mei (1985) overcomes this Bragg resonance situation by formulating wave evolution and the reflection theory at and near the Bragg resonance condition for shore-parallel bars. Since, the bottom undulations are small, there is no concern of large reflection in our work. Hence, the perturbation expansion as given by the relation (10) is valid throughout the present work.
On substituting the expressions of
BVP-Ⅰ: The function
| $\frac{{{\partial ^2}{\phi _0}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{\phi _0}}}{{\partial {y^2}}} - {\nu ^2}{\phi _0} = 0,{\rm{in}}\;{\rm{the}}\;{\rm{fluid}}\;{\rm{region}}$ | (11) |
| $\frac{{\partial {\phi _0}}}{{\partial y}} + K{\phi _0} = 0,{\rm{on}}\;y = 0$ | (12) |
| $\frac{{\partial {\phi _0}}}{{\partial y}} = 0,\,\,\,\,\,\,\,\,{\rm{on}}\,\,y = h$ | (13) |
| $\,{\left. {\frac{{\partial {\phi _0}}}{{\partial x}}} \right|_{x = {0^ - }}} = {\left. {\frac{{\partial {\phi _0}}}{{\partial x}}} \right|_{x = {0^ + }}} = 0,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{on}}\,\,x = 0,{\kern 1pt} \,y \in B$ | (14) |
| $\,{\left. {\frac{{\partial {\phi _0}}}{{\partial x}}} \right|_{x = {0^ - }}} = {\left. {\frac{{\partial {\phi _0}}}{{\partial x}}} \right|_{x = {0^ + }}},{\rm{ on}}\,\,x = 0,{\kern 1pt} {\rm{ }}y \in G$ | (15) |
| $\,{\left. {{\phi _0}} \right|_{x = {0^ - }}} = {\left. {{\phi _0}} \right|_{x = {0^ + }}},\,\,\,\,\,\quad \,\,\,\,{\rm{on}}\,\,x = 0,{\kern 1pt} \,{\rm{ }}y \in G$ | (16) |
| ${\phi _0}(x,y) \to \left\{ {\begin{array}{*{20}{l}} {({{\rm{e}}^{{\rm{i}}\mu x}} + {R_0}{{\rm{e}}^{ - {\rm{i}}\mu x}}){\psi _0}(y)\;\quad {\rm{as}}\quad x \to - \infty }\\ {{T_0}{{\rm{e}}^{{\rm{i}}\mu x}}{\psi _0}(y)\quad \quad \quad {\mkern 1mu} \;{\mkern 1mu} \;\quad \;\;\;{\rm{as}}\quad x \to \infty } \end{array}} \right.$ | (17) |
BVP-Ⅱ: The function
| $\frac{{{\partial ^2}{\phi _1}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{\phi _1}}}{{\partial {y^2}}} - {\nu ^2}{\phi _1} = 0,{\rm{in}}\;{\rm{the}}\;{\rm{fluid}}\;{\rm{region}}$ | (18) |
| $\frac{{\partial {\phi _1}}}{{\partial y}} + K{\phi _1} = 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{on }}\,\,y = 0$ | (19) |
| $\frac{{\partial {\phi _1}}}{{\partial y}} = \frac{{\rm{d}}}{{{\rm{d}}x}}\left[ {c(x)\frac{{\partial {\phi _0}}}{{\partial y}}} \right] + c(x){\phi _{zz}},\,\,\,\,\,\,\,\,{\rm{on}}\,\,y = h$ | (20) |
| $\,{\left. {\frac{{\partial {\phi _1}}}{{\partial x}}} \right|_{x = {0^ - }}} = {\left. {\frac{{\partial {\phi _1}}}{{\partial x}}} \right|_{x = {0^ + }}} = 0,\,\,\,\,\,\,\,\,\,\,\,{\rm{on}}\,\,x = 0,{\kern 1pt} \,y \in B$ | (21) |
| $\,{\left. {{\phi _1}} \right|_{x = {0^ - }}} = {\left. {{\phi _1}} \right|_{x = {0^ + }}},\,\,\,\,\,\quad \quad \,\,\,\,\,\,\,{\rm{on}}\,\,x = 0,{\kern 1pt} \,y \in G$ | (22) |
| $\,{\left. {\frac{{\partial {\phi _1}}}{{\partial x}}} \right|_{x = {0^ - }}} = {\left. {\frac{{\partial {\phi _1}}}{{\partial x}}} \right|_{x = {0^ + }}},\,\,\,\,\,\quad \,\,\,\,\,\,\,{\rm{on}}\,\,x = 0,{\rm{ }}{\kern 1pt} \,y \in G$ | (23) |
| ${\phi _1}(x,y) \to \left\{ {\begin{array}{*{20}{l}} {{R_1}{{\rm{e}}^{ - {\rm{i}}\mu x}}{\psi _0}(y)\;{\mkern 1mu} \quad {\rm{as}}\quad x \to - \infty }\\ {{T_1}{{\rm{e}}^{{\rm{i}}\mu x}}{\psi _0}(y)\quad \quad {\rm{as}}\quad x \to \infty } \end{array}} \right.$ | (24) |
Here, the BVP-Ⅰ corresponds to the problem of scattering of water waves by thin vertical barrier in water of finite depth h. The solution for
| ${\phi _0}(x,y) \to \left\{ \begin{array}{l} ({{\rm{e}}^{{\rm{i}}\mu x}} + {R_0}{{\rm{e}}^{ - {\rm{i}}\mu x}}){\psi _0}(y) + \sum\limits_{n = 1}^\infty {{A_n}} {{\rm{e}}^{{s_n}x}}{\psi _n}(y)\;\quad \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad {\rm{as}}\quad x < 0,\\ {T_0}{{\rm{e}}^{{\mathop{\rm i}\nolimits} \mu x}}{\psi _0}(y) + \sum\limits_{n = 1}^\infty {{B_n}} {{\rm{e}}^{ - {s_n}x}}{\psi _n}(y)\quad \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \,\;\,\;\quad {\rm{as}}\quad x > 0, \end{array} \right.$ | (25) |
where
| $\frac{1}{h}\int\limits_0^h {{\psi _n}(y){\psi _m}(y){\rm{d}}y = {\delta _{nm}}} $ |
where δnm is the Kronecker delta.
Now, the relation (15) holds good for 0 < y < h because the horizontal velocity vanishes on the barrier. Using Havelock's inversion formula (Ursell, 1947) in the relation
| ${R_0} + {T_0} = 1\;\;{\rm{and }}\;{A_n} = - {B_n}$ | (26) |
Further, using the boundary condition (16) that the pressure has to be continuous and making use of the relation (26), we have
| $\,\frac{1}{h}{\psi _0}(y) + \frac{1}{h}\sum\limits_{n = 0}^\infty {{A_n}} {\psi _n}(y),\,\,\,\,\,\,\,\,\,\,{\rm{on}}\,\,x = 0,{\kern 1pt} {\rm{ }}\,y \in G$ | (27) |
where
| ${A_0} = {R_0} - 1,\;{k_0} = - {\rm{i}}{\hat k_0}$ | (28) |
Now, using the boundary condition (14), we get
| $\sum\limits_{n = 0}^\infty {{A_n}} ({s_n}h)\frac{1}{h}{\psi _n}(y) = 0,\quad {\rm{on }}x = 0,\;y \in B$ | (29) |
where
The relations (27) and (29) are known as dual series relations and can be combined to make one mixed boundary condition as given by
| $F(y) = 0,\quad 0 < y < h$ | (30) |
where
| $F(y) \to \left\{ {\begin{array}{*{20}{l}} {\frac{1}{h}{\psi _0}(y) + \frac{1}{h}\sum\limits_{n = 0}^\infty {{A_n}} {\psi _n}(y),{\rm{on}}\;y \in G}\\ {\sum\limits_{n = 0}^\infty {{A_n}} ({s_n}h)\frac{1}{h}{\psi _n}(y),\quad \;{\rm{on}}\;y \in B} \end{array}} \right.$ |
The relation (30) represents an over-determined system of equations involving countably infinite number of unknowns
Now, the least-squares error is established as
| ${\rm{Error = }}{\left( {\int\limits_0^h {|F(y){|^2}{\rm{d}}y} } \right)^{1/2}} = {\left( {\int\limits_{y\, \in \,G} {|F(y){|^2}{\rm{d}}y + \int\limits_{y\, \in \,B} {|F(y){|^2}{\rm{d}}y} } } \right)^{1/2}}$ | (31) |
Minimizing the error with respect to An establishing the following normal equations:
| $\int\limits_{y\, \in \,G} {{F^*}(y)\frac{{\partial F(y)}}{{\partial {A_m}}}{\rm{d}}y + \int\limits_{y\, \in \,B} {{F^*}(y)\frac{{\partial F(y)}}{{\partial {A_m}}}{\rm{d}}y} } = 0,\;\;m = 0,{\rm{ }}1,{\rm{ }}2, \ldots ,$ | (32) |
where F*(y) is the complex conjugate of F(y)
On substituting the value of F* and the derivatives of F with respect to the unknowns, the relation (32) gives a system of complex matrix equations which is given by
| $\begin{array}{l} \sum\limits_{n = 0}^\infty {A_n^*\left[ {\frac{1}{h}\int\limits_{y\, \in \,G} {{\psi _n}(y){\psi _m}(y){\rm{d}}y + \frac{{({s_m}h)(s_n^*h)}}{h}\int\limits_{y\, \in \,B} {{\psi _n}(y){\psi _m}(y){\rm{d}}y} } } \right] = } \\ \quad \quad \quad \quad \quad \quad \quad - \frac{1}{h}\int\limits_{y\, \in \,G} {{\psi _0}(y){\psi _m}(y){\rm{d}}y} ,\;\;m = 0,{\rm{ }}1,{\rm{ }}2, \ldots , \end{array}$ | (33) |
For each case (given in Section 2), truncating the series for n and m to a finite number of terms N, a system of N+1 simultaneous equations with N+1 unknowns An
Now, the BVP-Ⅱ represents the radiation problem containing
| $\begin{array}{l} y = 0,\;0 < x \le X;\;x = {0^ + },\;y \in B;\;x = {0^ - },\;y \in B;\;y = 0,\; - X \le x < 0;\\ \quad \quad x = - X,\;0 \le y \le h;\;y = h,\; - X \le x \le X;\;x = X,\;0 \le y \le h \end{array}$ |
where X is positive, large and tends to infinity, we obtain
| ${R_1} = \frac{1}{{2{\rm{i}}\mu }}\int\limits_{ - \infty }^\infty {c(x){{\left( {\frac{{\partial {\phi _0}(x,h)}}{{\partial x}}} \right)}^2}{\rm{d}}x} $ | (34) |
Similarly, applying Green's integral theorem to the functions
| ${T_1} = - \frac{1}{{2{\rm{i}}\mu }}\int\limits_{ - \infty }^\infty {c(x)\left( {\frac{{\partial {\phi _0}(x,h)}}{{\partial x}}} \right)\left( {\frac{{\partial {\phi _0}( - x,h)}}{{\partial x}}} \right){\rm{d}}x} $ | (35) |
It should be realized that in the absence of vertical barrier, the present problem reduces to the problem of scattering of water waves by bottom undulation only. Further, it is noted that in the absence of the barrier, the solution
| ${R_1} = \frac{{ - 2{\rm{i}}\hat k_0^2}}{{2{{\hat k}_0}h + \sinh 2{{\hat k}_0}h}}\int\limits_{ - \infty }^\infty {c(x){{\rm{e}}^{2{\rm{i}}{{\hat k}_0}x}}{\rm{d}}x} $ | (36) |
| ${T_1} = \frac{{2{\rm{i}}\hat k_0^2}}{{2{{\hat k}_0}h + \sinh 2{{\hat k}_0}h}}\int\limits_{ - \infty }^\infty {c(x){\rm{d}}x} $ | (37) |
which exactly match with the results of available in literature (Davies and Heathershaw, 1984; Mandal and Basu, 1990, for normal incidence and negligible surface tension).
The R1 and T1 given in relations (34) and (35) further evaluated for a particular form of the shape function.
5 Particular form of the bottom undulationIn this Section, we consider a particular form of the shape function c(x) to determine the reflection and transmission coefficients respectively, given in the relations (34) and (35). The shape function c(x) is considered in the form of a patch of sinusoidal ripples because the functional form of the uneven bottom closely corresponds to some obstacles which occur in a natural way and formed at the bottom due to the alluviation and ripple growth of sands.
The patch of sinusoidal ripples can be expressed as
| $c(x) = \left\{ \begin{array}{l} {c_0}\sin \lambda x,\quad - l \le x \le l,\\ 0,\quad \quad \quad \quad {\rm{otherwise,}} \end{array} \right.$ | (38) |
where
| $\begin{array}{l} {R_1} = \frac{{{c_0}\mu ({R_0} - 1)}}{{2N_0^2}}\left\{ {\frac{{\sin (\lambda - 2\mu )l}}{{\lambda - 2\mu }} - \frac{{\sin (\lambda + 2\mu )l}}{{\lambda + 2\mu }}} \right\} + \frac{{{\rm{i}}{c_0}\mu {R_0}}}{{2N_0^2}} \times \\ \left\{ {\frac{{2(1 - \cos \lambda l)}}{\lambda } - \frac{{2\lambda }}{{{\lambda ^2} - 4{\mu ^2}}} + \frac{{\cos (\lambda - 2\mu )l}}{{\lambda - 2\mu }}} \right.\left. { + \frac{{\cos (\lambda + 2\mu )l}}{{\lambda + 2\mu }}} \right\} + \\ \frac{{{\rm{i}}{c_0}}}{{{N_0}}}\sum\limits_{n = 1}^\infty {\left[ {\frac{{{s_n}}}{{{{(\lambda - \mu )}^2} + s_n^2}}} \right.} - \frac{{{s_n}}}{{{{(\lambda + \mu )}^2} + s_n^2}} + \\ \left\{ {\frac{{(\lambda - \mu )\sin (\lambda - \mu )l - {s_n}\cos (\lambda - \mu )l}}{{{{(\lambda - \mu )}^2} + s_n^2}}} \right. - \\ \left. {\left. {\frac{{(\lambda + \mu )\sin (\lambda + \mu )l - {s_n}\cos (\lambda + \mu )l}}{{{{(\lambda + \mu )}^2} + s_n^2}}} \right\}{{\rm{e}}^{ - {s_n}l}}} \right]\frac{{{s_n}{A_n}}}{{{N_n}}} \end{array}$ | (39) |
From relation (39), it is observed that when
A MATLAB program is written and is used to investigate the effects of the various parameters such as barrier length, number of ripples, the amplitude of the ripple, the angle of incidence and the gap below/above the barrier on the reflection coefficient |R1| given by relation (39) for a patch of sinusoidal ripples on the sea-bed. The main aim of the present investigation is to observe how the incident wave energy is transformed, after scattered by both obstacles, into the reflected and transmitted waves. The unknowns A0(hence R0 from (28)), A1, A2, ...AN are computed from (33) and then |R1| is computed from (39) and plotted in the Figs. (2)-(4) for different values of different dimensionless parameters. The relation of |R1| is non-dimensionalized by using h as the length scale.
In the numerical computation, the value of Kh=1, angle of incidence
A set of numerical values of |R1| is presented in Table 1 for $N = 5, \; 8, \; 10, \; 15\; {\rm{and}}\; 20$ with different values of Kh and for fixed values of
| Kh | N=5 | N=8 | N=10 | N=15 | N=20 |
| 0.05 | 0.017 8 | 0.017 4 | 0.017 2 | 0.017 0 | 0.016 9 |
| 0.10 | 0.032 0 | 0.031 4 | 0.031 1 | 0.030 8 | 0.030 6 |
| 0.30 | 0.069 4 | 0.068 3 | 0.067 7 | 0.067 0 | 0.066 7 |
| 0.50 | 0.082 1 | 0.080 3 | 0.079 4 | 0.078 3 | 0.077 8 |
To validate the present model, the present results are compared with the results available in the literature. It should be noted that when the length of the vertical barrier
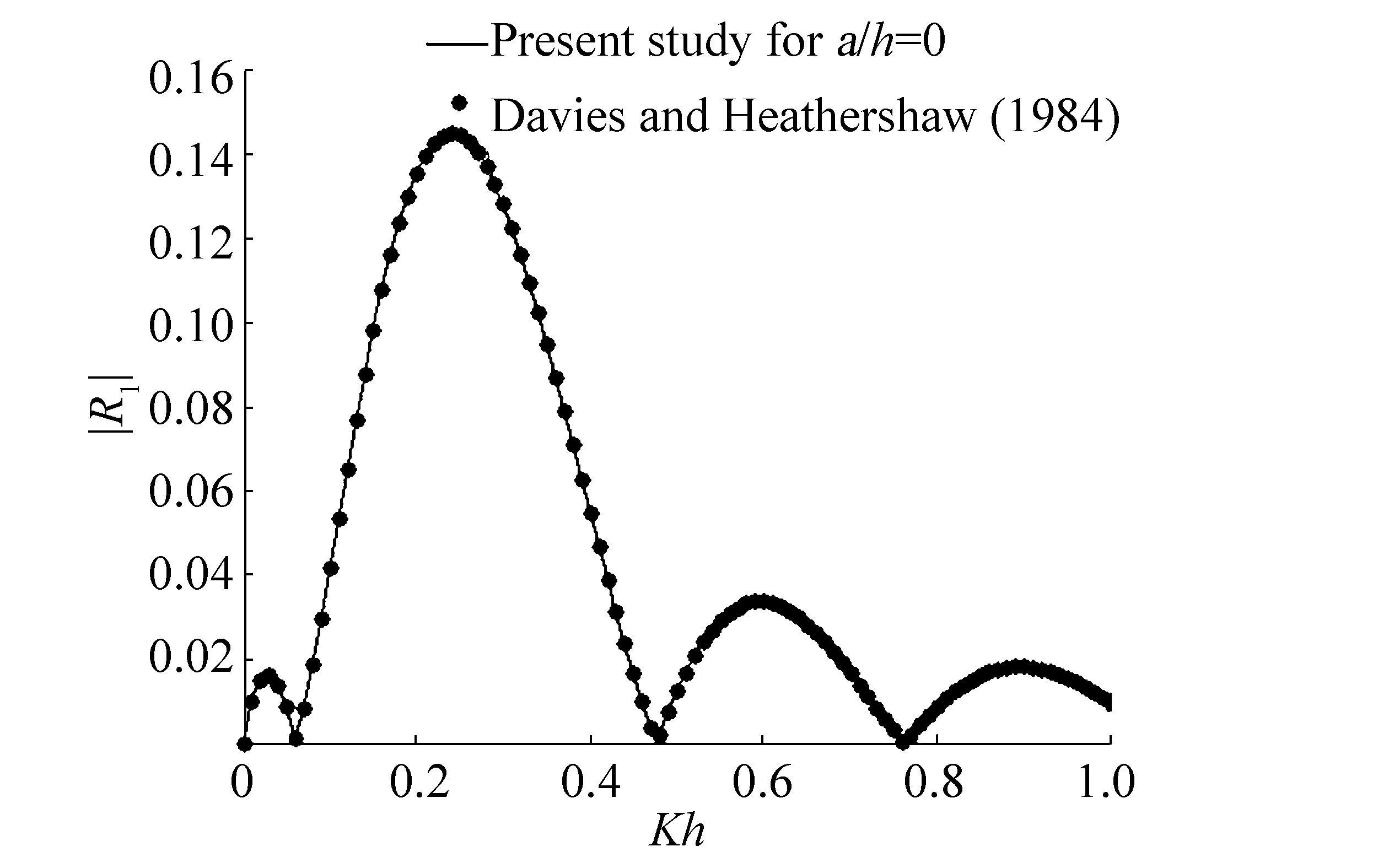
|
| Figure 1 |R1| against Kh for fixed M=2, a/h=0, c0/h=0.1, θ=0 and λh=1 |
Case Ⅰ: A partially immersed barrier
In Fig. 2, the absolute value of the first order reflection coefficient |R1| is plotted against Kh for the different number of ripples,

|
| Figure 2 |R1| versus Kh for different values of M=2, 4, 7 with fixed a/h=0.2, c0/h=0.1 and λh =1 |
Fig. 3shows the variation of the absolute value of the first order reflection coefficient
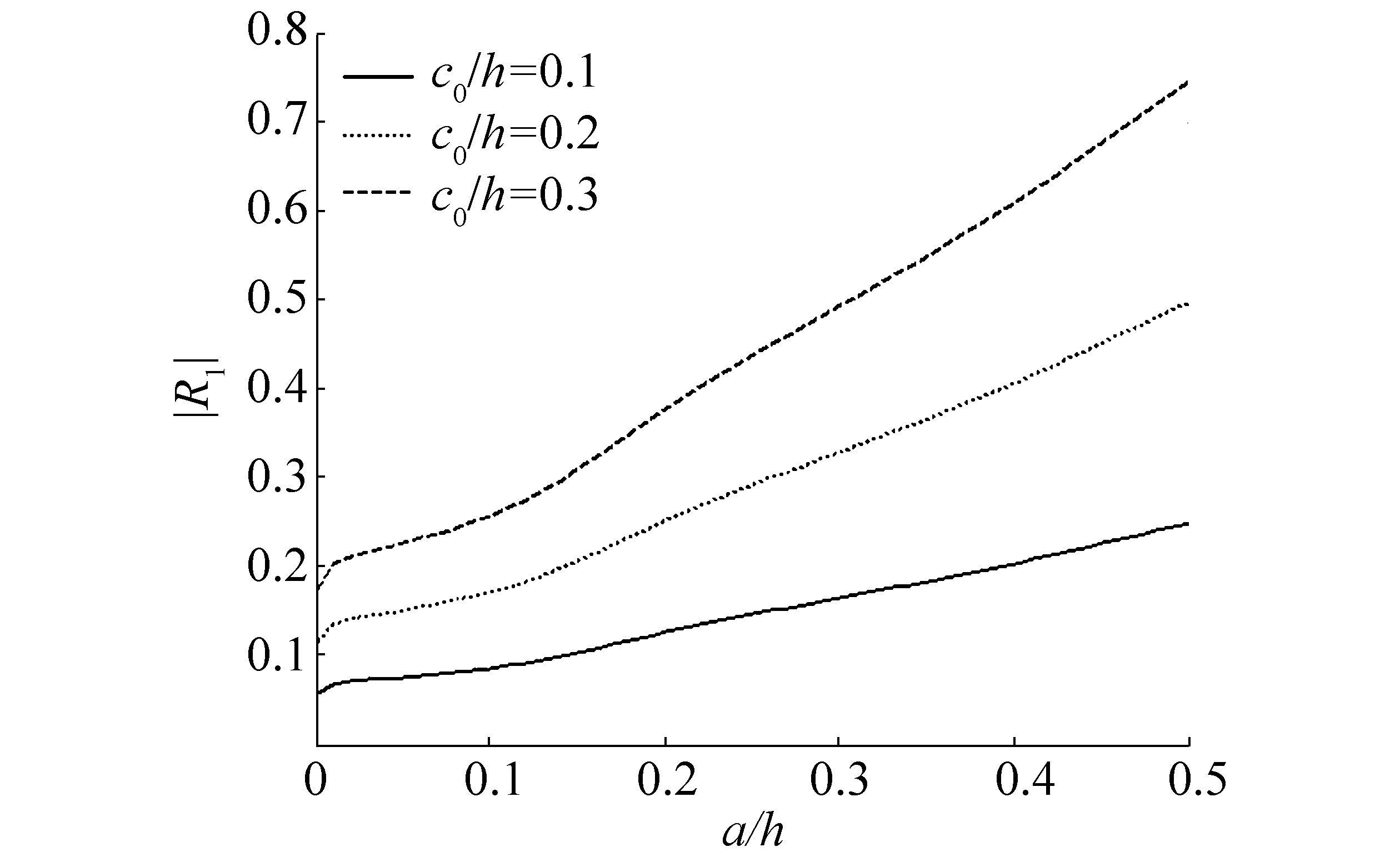
|
| Figure 3 |R1| versus a/h for different values of c0/h=0.1, 0.2, 0.3 with Kh=1, M=1, λh =1 and θ=π/4 |
Case Ⅱ: A bottom standing barrier
In Fig. 4, the reflection coefficientcis |R1| depicted against Kh for different number of ripples
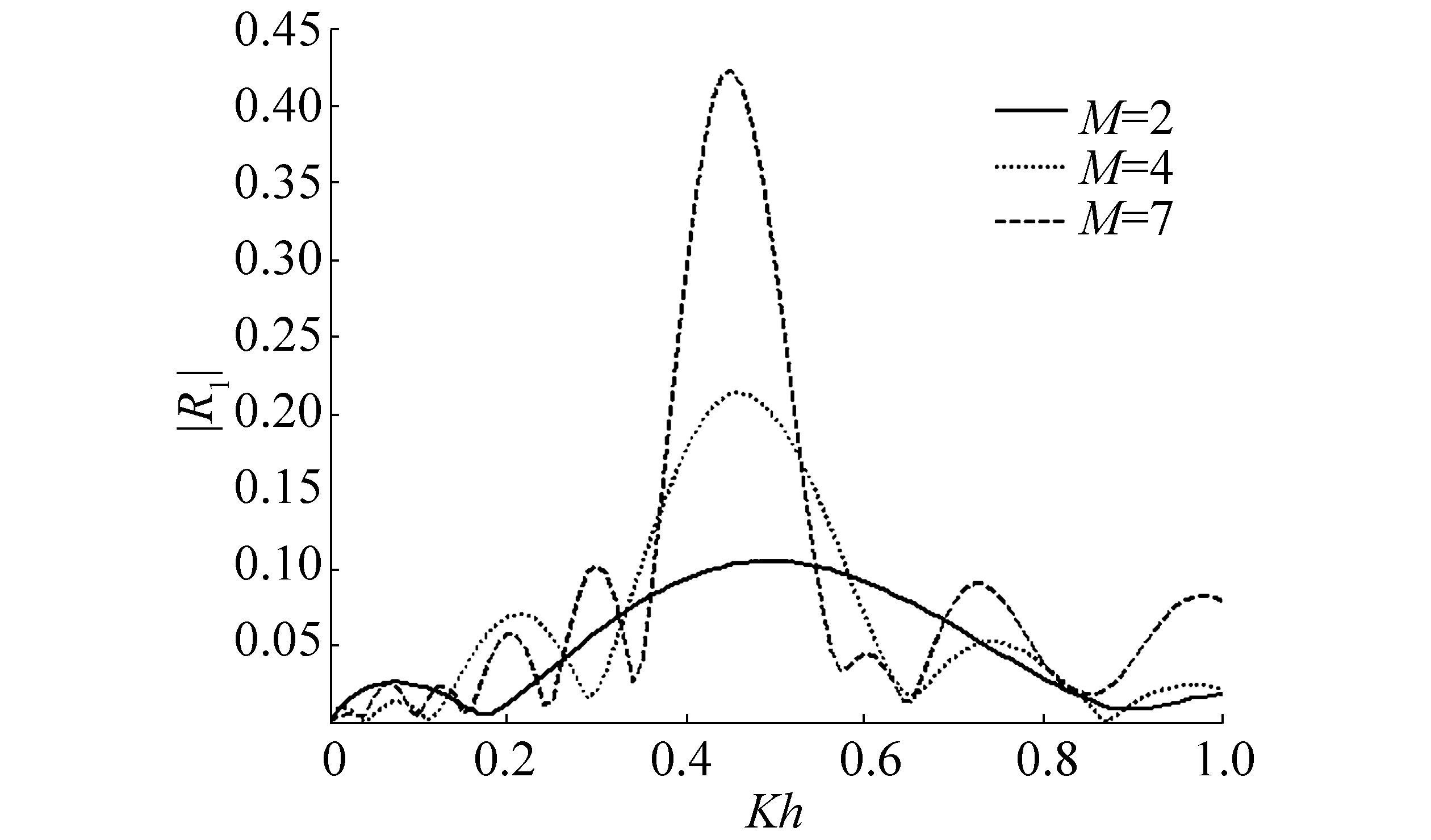
|
| Figure 4 |R1|versus Kh for different number of ripples M=2, 4, 7 with b/h=0.2, c0/h=0.1, λh =1 and θ=π/4 |
In Fig. 5, the reflection coefficient |R1| is plotted against the gap b/h for different values of the ripple amplitude

|
| Figure 5 |R1| versus gap b/h for different values of c0/h=0.10, 0.15, 0.25 with Kh=1, M=1, λh =1and θ=π/4 |
In Fig. 6, the absolute value of the first order reflection coefficient |R1| is plotted against the angle of incidence θ for the gap

|
| Figure 6 |R1| versus θ for b/h=0.2, c0/h=0.1, Kh=1, λh=1 and M=1 |
Case Ⅲ: A barrier with gap
In Fig. 7, the first order reflection coefficient |R1| is plotted against Kh for different number of ripples

|
| Figure 7 |R1|versus Kh for different number of ripples M=2, 4, 7 with d/h=0.2, c0/h=0.1, e/h=0.3, λh =1 and θ=π/4 |
Fig. 8 shows the effect of the amplitude of the bottom undulation
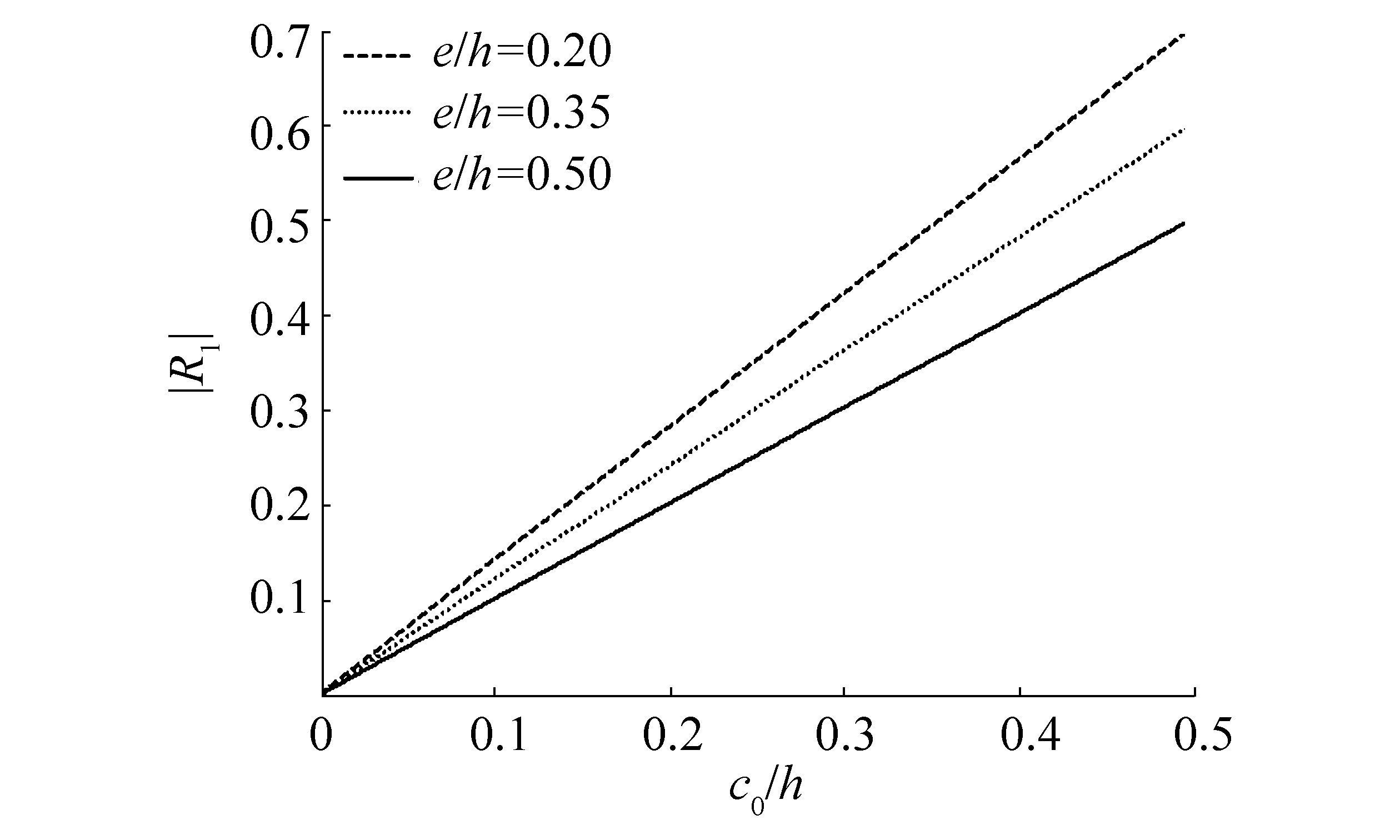
|
| Figure 8 |R1| versus c0/h for different values of e/h=0.20, 0.35, 0.50 with Kh=1, M=1, d/h=0.1, λh =1 and θ=π/4 |
In Fig. 9, the first order reflection coefficient is depicted against the angle of incidence for
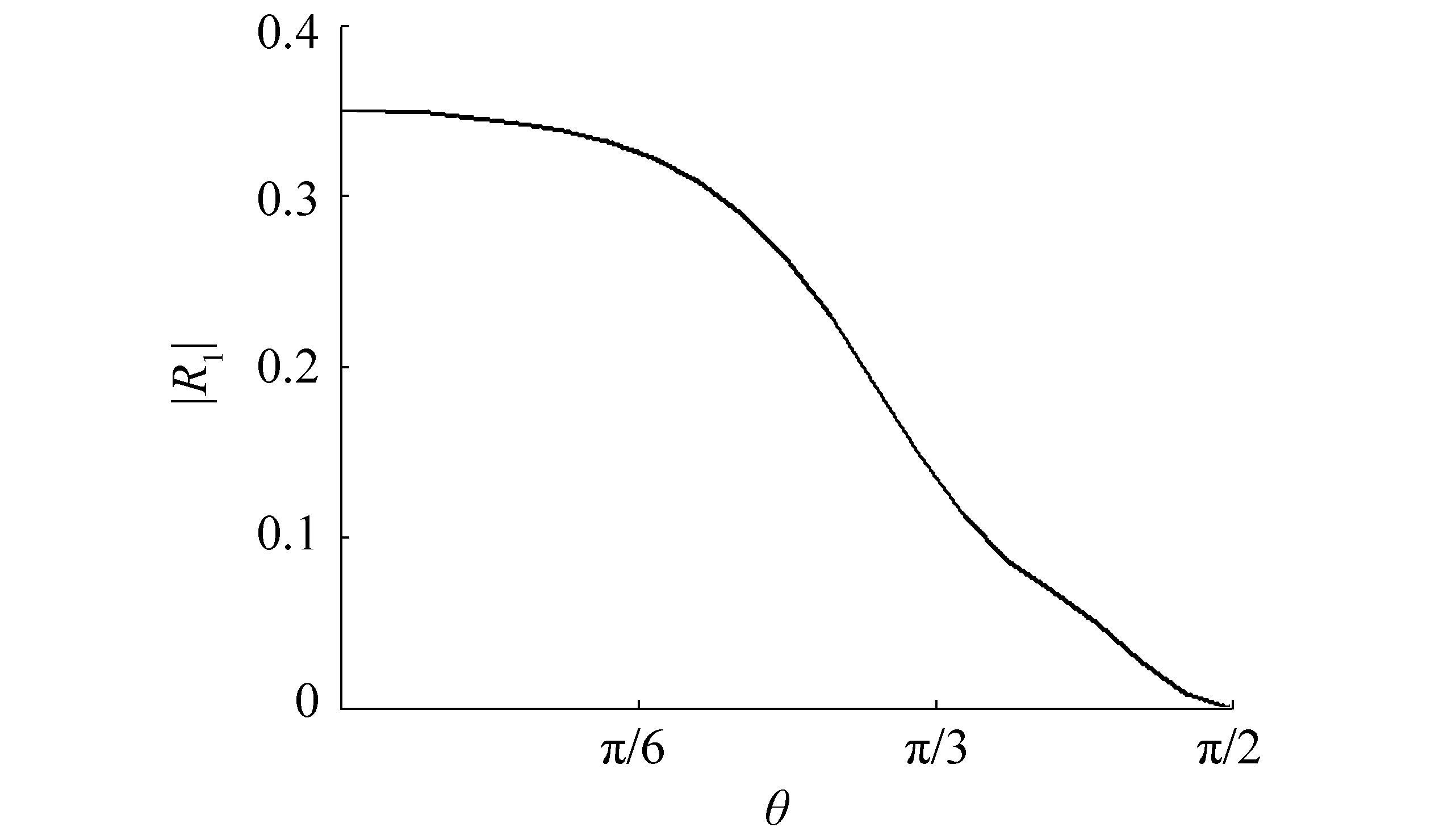
|
| Figure 9 |R1|versus θ for d/h=0.2, e/h=0.2, c0/h=0.1, Kh=1, λh=1 and M=1 |
It is found from the literature (Chakrabarti and Martha, 2009; Chakrabarti and Mohapatra, 2013 etc.) that among many important results in the theoretical study of water waves, the special relation, namely, the "energy identity relation" plays an important role in the water wave scattering problems for checking the correctness of the results. The energy identity, in the cases when one has to rely on the numerical results for these coefficients, confirms the correctness of the numerical results. Using Green's integral theorem involving complex velocity potential and its complex conjugate, the energy identity relation for the present problem can be derived as
| $|R{|^2} + |T{|^2} = 1$ | (40) |
Using relation (10), the numerical values of
| Kh | R0 | R1 | |R| | T0 | |T| | |R|2+|T|2 |
| 0.05 | 0.000+0.006 2i | -0.014 0+0.000 1i | 0.006 3 | 1.000 0-0.006 2i | 1.000 0 | 1.000 0 |
| 0.10 | 0.000 1+0.009 1i | -0.016 1+0.000 1i | 0.009 2 | 0.999 9-0.009 1i | 0.999 9 | 1.000 0 |
| 0.30 | 0.000 4+0.018 7i | -0.079 4+0.001 5i | 0.020 3 | 0.999 6-0.018 7i | 0.999 8 | 0.999 9 |
| 0.50 | 0.001 2+0.030 5i | -0.223 2+0.006 9i | 0.037 6 | 0.998 8-0.030 5i | 0.999 3 | 1.000 0 |
| 0.80 | 0.002 1+0.044 9i | 0.016 6-0.000 7i | 0.045 0 | 0.997 9-0.044 9i | 0.998 9 | 0.999 8 |
| 1.00 | 0.003 8+0.060 4i | -0.021 7+0.001 3i | 0.060 6 | 0.996 2-0.060 4i | 0.998 0 | 0.999 7 |
| Kh | R0 | R1 | |R| | T0 | |T| | |R|2+|T|2 |
| 0.05 | 0.005+0.0224i | -0.013 5+0.000 3i | 0.022 5 | 0.999 5-0.022 4i | 0.999 7 | 1.000 0 |
| 0.10 | 0.001 0+0.031 3i | -0.026 2+0.000 8i | 0.031 4 | 0.999 0-0.031 3i | 0.999 5 | 1.000 0 |
| 0.30 | 0.002 7+0.051 3i | -0.060 0+0.003 1i | 0.051 7 | 0.997 3-0.051 3i | 0.998 6 | 0.999 9 |
| 0.50 | 0.003 9+0.061 9i | -0.069 0+0.004 3i | 0.062 4 | 0.996 1-0.061 9i | 0.998 0 | 0.999 9 |
| 0.80 | 0.004 7+0.068 2i | -0.050 1+0.003 4i | 0.068 5 | 0.995 3-0.068 2i | 0.997 6 | 0.999 9 |
| 1.00 | 0.004 8+0.068 6i | -0.028 8+0.002 0i | 0.068 9 | 0.995 2-0.068 6i | 0.997 6 | 0.999 9 |
| Kh | R0 | R1 | |R| | T0 | |T| | |R|2+|T|2 |
| 0.05 | 0.002 2+0.046 8i | -0.016 0+0.000 8i | 0.046 8 | 0.997 8-0.046 8i | 0.998 9 | 1.000 0 |
| 0.10 | 0.004 4+0.065 8i | 0.007 6-0.000 5i | 0.065 9 | 0.995 6-0.065 8i | 0.997 8 | 1.000 0 |
| 0.30 | 0.013 3+0.113 9i | 0.093 4-0.010 8i | 0.115 0 | 0.986 7-0.113 9i | 0.993 3 | 0.999 8 |
| 0.50 | 0.021 7+0.144 7i | -0.259 2+0.038 5i | 0.148 6 | 0.978 3-0.144 7i | 0.988 9 | 1.000 0 |
| 0.80 | 0.031 5+0.173 9i | 0.005 6-0.001 0i | 0.176 7 | 0.968 5-0.173 9i | 0.984 0 | 0.999 6 |
| 1.00 | 0.037 8+0.190 3i | -0.038 4+0.007 6i | 0.194 0 | 0.962 2-0.190 3i | 0.980 8 | 0.999 6 |
The last column of the Tables 2-5 shows that each value of
| Kh | R0 | R1 | |R| | T0 | |T| | |R|2+|T|2 |
| 0.05 | 0.000+0.005 9i | -0.016 6+0.000 1i | 0.005 9 | 1.000 0-0.005 9i | 1.000 0 | 1.000 0 |
| 0.10 | 0.000 1+0.008 7i | -0.030 2+0.000 3i | 0.008 7 | 0.999 9-0.008 7i | 1.000 0 | 1.000 0 |
| 0.30 | 0.000 3+0.017 8i | -0.065 8+0.001 2i | 0.017 8 | 0.999 7-0.017 8i | 0.999 8 | 0.999 9 |
| 0.50 | 0.000 8+0.027 4i | -0.076 4+0.002 1i | 0.027 4 | 0.999 2-0.027 4i | 0.999 6 | 0.999 9 |
| 0.80 | 0.002 1+0.044 9i | -0.061 8+0.002 8i | 0.044 9 | 0.997 9-0.044 9i | 0.998 9 | 0.999 8 |
| 1.00 | 0.003 8+0.060 4i | -0.044 7+0.002 7i | 0.060 5 | 0.996 2-0.060 4i | 0.998 0 | 0.999 7 |
It is observed from the table 2 (for
Perturbation analysis is used to solve the mixed BVP arising in the study of scattering of oblique incident waves by irregular bottom and thin vertical barrier. The zeroth order reflection and transmission coefficients are obtained by employing the eigenfunction expansion method leading to an over-determined system of equations which is solved with the help of least-squares approximation and thereby employing the QR-factorization. Using the Green's integral theorem, the first order reflection and transmission coefficients are obtained in terms of integrals containing the shape function c(x) and the solution of the problem involving scattering of surface waves by a vertical barrier over uniform finite depth water. The effect of barrier length, amplitude of the ripples, the number of ripples and the angle of incidence on the first order reflection coefficient is demonstrated through different figures. It is found that the global maximum value of the first order reflection coefficient is increasing with increasing the number of ripples and it is also increasing with increasing the barrier length and the amplitude of the ripples. But the reflection coefficient is decreasing with increasing the angle of incidence and the gap. All these numerical results agree with the physical intuitions of the problem. The energy balance relation is derived and used to check the correctness of the numerical results involving the physical quantities obtained by the present method.
Acknowledgement:A. Choudhary is grateful to the University Grants Commission (UGC), Government of India, for providing the research fellowship for pursuing Ph.D. degree at the Indian Institute of Technology Ropar, India. S. C. Martha is grateful to SERB-DST, Govt. of India for financial funding under grant number SB/FTP/MS-034/2013.
| Banerjea S, Kanoria M, Dolai DP, Mandal BN, 1996. Oblique wave scattering by submerged thin vertical wall with a gap in finite-depth water. Applied Ocean Research, 18(6), 319–327. DOI:10.1016/S0141-1187(97)00002-3 |
| Chakrabarti A, Martha SC, 2009. A note on energy-balance relations in surface water wave problems involving floationg elastic plates. Journal of Advances Research in Applied Mathematics, 1(2), 27–34. |
| Chakrabarti A, Mohapatra S, 2013. Scattering of surface water waves involving semi-infinite floating elastic plates on water of finite depth. Journal of Marine Science and Application, 12(3), 325–333. DOI:10.1007/s11804-013-1204-z |
| Davies AG, 1982. The reflection of wave energy by undulations on the seabed. Dynamics of Atmospheres and Oceans, 6(4), 207–232. DOI:10.1016/0377-0265(82)90029-X |
| Davies AG, Heathershaw AD, 1984. Surface wave propagation over sinusoidally varying topography. Journal of Fluid Mechanics, 144, 419–443. DOI:10.1017/S0022112084001671 |
| Dean WR, 1945. On the reflexion of the suface waves by a submerged plane barrier. Mathematical Proceedings of the Cambridge Philosophical Society, 41(3), 231–238. DOI:10.1017/S030500410002260X |
| Kirby JT, 1993. A note on Bragg scattering of surface waves by sinusoidal bars. Physics of Fluids, 5(2), 380–386. DOI:10.1063/1.858861 |
| Lee MM, Chwang AT, 2000. Scattering and radiation of water waves by permeable barriers. Physics of Fluids, 12(1), 54–65. DOI:10.1063/1.870284 |
| Losada IJ, Losada MA, Roldan AJ, 1992. Propagation of oblique incident waves past rigid vertical thin barriers. Applied Ocean Research, 14(3), 191–199. DOI:10.1016/0141-1187(92)90014-B |
| Mandal BN, Basu U, 1990. A note on oblique water wave diffraction by a cylindrical deformation of the bottom in the presence of surface tension. Archives of Mechanics, 42(6), 723–727. |
| Mandal BN, Chakrabarti A, 1999. On Galerkin's method applicable to the problems of water wave scattering by barriers. Proceedings of the Indian National Science Academy:PINSA, 65(1), 61–71. |
| Mandal BN, Dolai DP, 1994. Oblique water wave diffraction by thin vertical barriers in water of uniform finite depth. Applied Ocean Research, 16(4), 195–203. DOI:10.1016/0141-1187(94)90020-5 |
| Mandal BN, Gayen R, 2006. Water wave scattering by bottom undulations in the presence of a thin partially immersed barrier. Applied Ocean Research, 28(2), 113–119. DOI:10.1016/j.apor.2006.06.002 |
| Martha SC, Bora SN, 2007. Oblique surface wave propagation over a small undulation on the bottom of an ocean. Geophysical & Astro Fluid Dynamics, 101(2), 65–80. DOI:10.1080/03091920701208186 |
| Mei CC, 1985. Resonant reflection of surface water waves by periodic sandbars. Journal of Fluid Mechanics, 152, 315–335. DOI:10.1017/S0022112085000714 |
| Miles JW, 1981. Oblique surface-wave diffraction by a cylindrical obstacle. Dynamics of Atmospheres and Oceans, 6(2), 121–123. DOI:10.1016/0377-0265(81)90019-1 |
| Porter D, 1972. The transmission of surface waves through a gap in a vertical barrier. Mathematical Proceedings of the Cambridge Philosophical Society, 71(2), 411–422. DOI:10.1017/S0305004100050647 |
| Porter R, Evans DV, 1995. Complementary approximations to wave scattering by vertical barriers. Journal of Fluid Mechanics, 294, 155–180. DOI:10.1017/S0022112095002849 |
| Sahoo T, Chan AT, Chwang AT, 2000. Scattering of oblique surface waves by permeable barriers. Journal of Waterway, Port, Coastal, and Ocean Engineering, 126(4), 196–205. DOI:10.1061/(ASCE)0733-950X(2000)126:4(196) |
| Ursell F, 1947. The effect of a fixed barrier on surface waves in deep water. Mathematical Proceedings of the Cambridge Philosophical Society, 43(3), 374–382. DOI:10.1017/S0305004100023604 |



