2. Xi'an Institute of Optics and Precision Mechanics of CAS, Xi'an 710119, China
1 Introduction
High Speed Supercavitating Vehicles (HSSVs) have a unique hydrodynamic layout mode, in that they are wholly covered by supercavities, leading to dramatic reduction of sailing drag. Consequently, powerful HSSVs driven by strong propulsion systems can achieve underwater speeds exceeding 200 kn (Savchenko, 2002; Kirschner et al., 2006; Nguyen, 2011; Hassouneh et al., 2013). To satisfy the special requirements of the power and propulsion systems, water ramjets have been proposed and applied to HSSVs owing to their high thrust, high specific impulse, and great energy density (Beckstead, 2004; Timothy et al., 2004). During the functioning of water ramjets, the high-temperature and high-pressure gas generated by the combustion of seawater and metal fuel is ejected through the Laval nozzles at speeds several times higher than the speed of sound and massive thrust is generated (Kirschner et al., 2001; Yang et al., 2009; Hu et al., 2013; Hayati et al., 2013). Moreover, during the functioning of water ramjets, large quantities of seawater need to be introduced into the combustor to meet the demands of reaction and gas refrigeration (Lin et al., 2012; Huang et al., 2013). Furthermore, because of being integrally enveloped in the supercavity and being the only continuously wet zone in HSSVs, the surface of cavitators may be the best place for opening the water inlet. In addition, taking advantage of the high dynamic pressure of the incoming flow, seawater can be unburst into the combustor without having to use any supercharging equipment (Grant et al., 2006; Dominic, 2011).
Regarding the use of water ramjets as thrusters in HSSVs, because plenty of water is taken away from the surface of cavitators, the distribution of pressure and velocity near cavitators will change considerably, which will lead to changes in supercavity shape and cavitator hydrodynamic characteristic (Sun et al., 2011). Li et al. (2014b) studied experimentally the influence of water inlets on the hydrodynamic characteristic and the supercavity shape of conical cavitators when water inflow flux is zero by using conical cavitator models with countersinks in the water tunnel. Huang et al. (2010) established a system for testing water ramjets and researched the impact of water inflow flux on specific impulse, gas temperature, and other important parameters. Feng et al. (2014) discussed the influence of water inflow flux and inlet position on the main performance parameters of water ramjets by using numerical methods.
In the present study, we establish a numerical model of a disk cavitator with water inflow by considering mass transportation between water and vapor, and neglecting the effect of gravity. Furthermore, the mixture multiphase model, realizable k-epsilon turbulence model, and Schnerr–Sauer cavitation model were combined to calculate supercavitation flow field. By changing water inlet area and water flux, numerical simulations were carried out to study the influences of water inflow on supercavity shape and cavitator hydrodynamics. The results obtained herein will be helpful for optimizing the layout and the cavitation flow regime design of HSSVs with water inflow of ramjets.
2 Multiphase flow model and its validation 2.1 Problem descriptionThe typical structure of HSSVs using water ramjets as thrusters is shown in Fig. 1, and this structure is composed mainly of a cavitator, ventilation bowl, fore conic section, cylindrical section, tail section, fins, rudders, and thruster system. The thruster system consists of a water inlet, water pipe, water ramjet, and nozzle (Euteneuer, 2003).
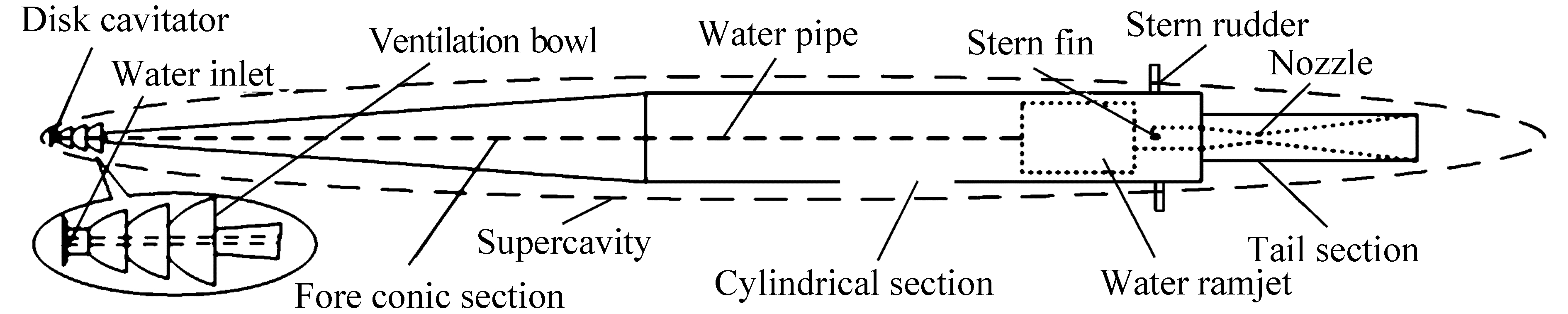
|
| Figure 1 Typical layout of HSSVs |
According to published conclusions (Huang et al., 2010), water ramjets using aluminum as fuel can obtain the highest specific impulse of up to 3 490 N·s/kg when the water-fuel ratio is 3.5. For a 213-mm caliber HSSV using a 48-mm disk cavitator, drag can reach 10 000 N when sailing at a speed of 100 m/s. Under those conditions, a HSSV driven by a water ramjet will consume 2.865 kg of aluminum and 10 kg of water per second. Moreover, the volume flow rate of freshwater would be up to 10 L/s.
Based on the independent expansion principle of Logvinovich, the impact of cavitators will result in expansion of the surrounding liquid to form cavity sections. At a certain moment, the cavity sections at different axial positions will constitute a quasi-ellipsoidal supercavitaty. Accordingly, the initial momentum of one cavity section will decrease owing to the flow of oncoming fluid into the water ramjets at a flux of 10 L/s. The shape of the supercavity will change significantly. Considering that precise forecasting of the supercavity shape is essential for layout design and control strategy of HSSVs, it is imperative to study the influences of water inflow on supercavity shape. Furthermore, the inlet hole opening at the cavitator affects the hydrodynamic characteristics of the cavitator by changing its pressure distribution. As the only stable wetted area in a HSSV, the axial force acting on the cavitator may account for 70% of the entire sailing drag of an HSSV. Thus, it is very urgent to study the impacts of water inflow on the hydrodynamic characteristics as well.
In the present paper, a disk cavitator with a diameter of 48 mm was used to study using numerical methods the influence of water inlet size and water inflow flux on supercavity shape and drag characteristics of cavitators.
2.2 Establishment of numerical modelA numerical model of supercavitation flow involves continuity equations, momentum equations, and turbulence equations. The flow regime of a natural cavitation flow field can be regarded as a homogeneous flow problem and can be solved by using the mixture multiphase model (Yu et al., 2012). The Schnerr–Sauer cavitation model is applied to describe mass transfer between vapor and liquid. Furthermore, the scale wall function is adopted to simulate the flow regime near walls given its reliability in terms of predicting the friction force of the wetted part.
2.2.1 Governing equationsThe homogenous mixture model has been used widely for representing natural cavitating flows, and to maintain the integrity of the content, the mathematical model, including the associated governing equations, and turbulence and cavitation model formulations, is presented in this section.
The governing continuity equation of a homogeneous mixture multiphase flow is as follows:
| $ \frac{\partial }{\partial t}\left( {{\rho }_{m}} \right)+\nabla \left( {{\rho }_{m}}\mathit{\boldsymbol{u}} \right)=0 $ | (1) |
The governing momentum equation of a homogeneous mixture multiphase flow is as follows:
| $ {{R}_{e}}\frac{\partial }{\partial t}\left( {{\rho }_{m}}\mathit{\boldsymbol{uu}} \right)+\nabla \cdot \left( {{\rho }_{m}}\mathit{\boldsymbol{uu}} \right)=-\nabla p+\nabla \cdot \left[ {{\mu }_{m}}\left( \nabla \mathit{\boldsymbol{u}}+\nabla {{\mathit{\boldsymbol{u}}}^{\rm{T}}} \right) \right] $ | (2) |
The volume fraction of the vapor phase is as follows:
| $ \nabla \cdot \left( {{\alpha }_{v}}{{\rho }_{v}}\mathit{\boldsymbol{u}} \right)={{R}_{e}}-{{R}_{c}} $ | (3) |
In Eqs. (1)–(3), u is velocity vector of the mixture phase; p, ρ, α, and μ denote pressure, density, volume fraction, and viscosity, respectively; subscripts m and v represent the mixture phase and the vapor phase, respectively; Re and Rc are the evaporation rate of liquid water and the condensation rate of vapor, separately.
The density and viscosity of the mixture phase are given as follows:
| $ {{\rho }_{m}}={{\alpha }_{v}}{{\rho }_{v}}+\left( 1-{{\alpha }_{v}} \right){{\rho }_{l}} $ | (4) |
| $ {{\mu }_{m}}={{\alpha }_{v}}{{\mu }_{v}}+\left( 1-{{\alpha }_{v}} \right){{\mu }_{w}} $ | (5) |
According to the Schnerr-Sauer cavitation model (Schnerr and Sauer, 2001), the evaporation rate Re and the condensation rate Rc can be determined as follows:
For the condition p≤pB, Re is
| $ {{R}_{e}}=\frac{{{\rho }_{v}}{{\rho }_{l}}}{{{\rho }_{m}}}\frac{3}{{{R}_{B}}}{{\alpha }_{v}}\left( 1-{{\alpha }_{v}} \right)\sqrt{\frac{2}{3}\frac{\left( {{p}_{B}}-p \right)}{{{\rho }_{l}}}} $ | (6) |
For the condition p > pB, Rc is
| $ {{R}_{c}}=\frac{{{\rho }_{v}}{{\rho }_{l}}}{{{\rho }_{m}}}\frac{3}{{{R}_{B}}}{{\alpha }_{v}}\left( 1-{{\alpha }_{v}} \right)\sqrt{\frac{2}{3}\frac{\left( p-{{p}_{B}} \right)}{{{\rho }_{l}}}} $ | (7) |
where pB is the internal pressure of a supercavity, which is slightly higher than the saturation vapor pressure pv due to the effect of turbulence; RB is radius of the bubbles, and it is defined as follows:
| $ {{R}_{B}}={{\left[ \frac{3{{\alpha }_{v}}}{4\pi {{n}_{b}}\left( 1-{{\alpha }_{v}} \right)} \right]}^{\frac{1}{3}}} $ | (8) |
where nb is the number of bubbles in unit volume of liquid and it is set to 1×1013 m-3.
By neglecting the effect of gravity, buoyancy, and compressibility, the realizable k-epsilon turbulence model (Shih et al., 1994) can be simplified as follows:
| $ \frac{\partial \left( {{\rho }_{m}}k \right)}{\partial t}+\frac{\partial \left( {{\rho }_{m}}k{{u}_{j}} \right)}{\partial {{x}_{j}}}=\frac{\partial }{\partial {{x}_{j}}}\left[ \left( {{\mu }_{m}}+\frac{{{\mu }_{t}}}{{{\sigma }_{k}}} \right)\frac{\partial k}{\partial {{x}_{j}}} \right]+{{G}_{k}}-\rho {{\varepsilon }_{m}} $ | (9) |
| $ \begin{align} &\frac{\partial \left( {{\rho }_{m}}\varepsilon \right)}{\partial t}+\frac{\partial \left( {{\rho }_{m}}\varepsilon {{u}_{j}} \right)}{\partial {{x}_{j}}}=\frac{\partial }{\partial {{x}_{j}}}\left[ \left( {{\mu }_{m}}+\frac{{{\mu }_{t}}}{{{\sigma }_{\varepsilon }}} \right)\frac{\partial \varepsilon }{\partial {{x}_{j}}} \right]+ \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ {{\rho }_{m}}{{C}_{1}}S\varepsilon -\frac{{{\rho }_{m}}{{C}_{2}}{{\varepsilon }^{2}}}{k+\sqrt{v\varepsilon }} \\ \end{align} $ | (10) |
where C1=max[0.43, η/η+5] and η=Sk/ε; Gk is the generation of turbulent kinetic energy owing to the mean velocity gradient; C2 is a constant equaling 1.9; σk=1.0 and σε=1.2 are the turbulent Prandtl numbers of k and ε, respectively; and μt denotes the eddy viscosity.
The scale wall function is a near-wall treating method, which is improved by setting a limiter to y* to achieve a higher stability and precision in the simulation of complex flow regime (Launder and Spalding, 1974), and can be expressed as follows:
| $ \left\{ \begin{align} &{{U}^{*}}=\frac{1}{\kappa }\ln \left( E{{y}^{*}} \right) \\ &{{U}^{*}}\equiv \frac{{{U}_{p}}C_{\mu }^{1/4}k_{p}^{1/2}}{{{\tau }_{w}}/\rho } \\ &{{y}^{*}}=\frac{{{\rho }_{m}}C_{\mu }^{1/4}k_{p}^{1/2}{{y}^{+}}}{{{\mu }_{m}}},{{y}^{*}}\ge 11 \\ &{{y}^{*}}=\max \left( {{y}^{*}},y_{\lim }^{*} \right),{{y}^{*}}<11 \\ \end{align} \right. $ | (11) |
where U* is dimensionless velocity, y* is dimensionless distance from the wall, κ is Von Kármán constant equaling 0.418 7, E is an empirical constant equaling 9.793, Up denotes mean velocity of the wall-adjacent cell centroid, kp represents turbulence kinetic energy of the wall-adjacent cell centroid, y+ means distance from the wall-adjacent cell centroid to the wall, μm is dynamic viscosity of the mixture fluid, and ylim*=11.225 is the limiter to prevent the deterioration of numerical results in the y* < 11 region. Regarding HSSVs using water ramjets as thrusters, as shown in Fig. 1, both the hull and the ramjet are enveloped by the supercavity, except the cavitator and the control plane. Considering the emphasis on practical situations in this study, we regard the supercavity as a standard revolving body by neglecting the slight asymmetry induced by gravity and lateral force. Supercavitation flow around the cavitator can be simplified to a two-dimensional problem and simulated using Fluent 17.0 Solver.
Based on a disk cavitator having a diameter of 48 mm, models with inlet areas accounting for 12% and 18% of the cavitator area called model A and model B, respectively, were generated. Then, water inflow flux of 0, 2, 4, 6, 8, and 10 L/s were obtained in turn by adjusting the outlet area of the conduit to investigate the influence of water inflow flux.
2.2.2 Meshing methodSupercavitation flow is sensitive to disturbances in pressure and velocity due to severe turbulence and phase change. Herein, a limited computational domain was used to simulate an infinite flow field. According to extant research (Huang et al., 2015), the computational domain in this study can be distributed as follows: the diameter should be at least 32x larger than the maximum diameter of the theoretical supercavitaty, and the length should be 3x times longer than the theoretical supercavitaty length.
To simulate the supercavitaty more accurately, boundary layer grids were added near the wall and optimized according to the criterion that the value of y+ should be 30–100, which is the basic requirement of the k-epsilon turbulence model in terms of y+. A sufficient number of refining grids were meshed in the zone of phase-change and the near the gas phase–liquid phase interface to ensure that a clear supercavity is formed.
Based on the principle used for simplifying the flow field and the strategy for partitioning the computational domain mentioned above, we built a two-dimensional axisymmetric geometry model of the supercavitation flow field under a water inflow flux range of 0–10 L/s and meshed the structured grid for models A and model B. Finally, 105 000 cells were partitioned for each model, and the distribution of grids near the cavitator is shown in Fig. 2.
|
| Figure 2 Grids near cavitators |
In the inertial frame, the reference was attached to the cavitator, and the inlet speed of the calculation domain was set to 100 m/s. Moreover, by setting the outlet pressure of calculation domain to 123 540 Pa, the cavitation number becomes 0.024, which is equal to that of the HSSV mentioned in an extant reference (Li et al., 2014a). To simulate the flow of water into the combustor, the pressure of the water outlet near the cavitator was set to 2.5 MPa, which was slightly higher than the actual pressure in the combustor (Huang et al., 2010). Slipping wall without shear force was used as the boundary condition of the outer ring of the calculation domain to weaken the influence of boundaries on the flow field. Additionally, the Schnerr-Sauer cavitation model was used to describe mass transfer between gas and liquid to simulate the generation and development of supercavity. The distribution and the boundary conditions of the computational domain are shown in Fig. 3.

|
| Figure 3 Structure of computational domain and boundary conditions |
The principle of independent expansion of the cross cavity section, which was proposed in the 1960s by Logvinovich and has been improved continuously and verified over the past half century, is the theoretical basis for forecasting supercavity shape and cavitator drag. According to the principle, each cross section of a supercavity expands along the plane perpendicular to the trajectory of the cavitator center. The expansion law of a certain cavity section is determined only by the motion velocity, cavitator drag at the time when the cavitator passes the section, and differential pressure between far-field and inside of the cavity, and it does not depend of the movement of the cavitator before or after (Vasin, 2001).
Based on Logvinovich's work (Logvinovich, 1972), the theoretical maximum radius of the supercavity can be described as follows:
| $ {{R}_{m}}={{R}_{n}}\sqrt{{{C}_{x}}/k\sigma } $ | (12) |
| $ \sigma =\frac{2\left( {{p}_{\infty }}-{{p}_{v}} \right)}{\rho v_{\infty }^{2}} $ | (13) |
| $ k=\frac{1+50\sigma }{1+56.2\sigma } $ | (14) |
| $ {{C}_{x}}={{C}_{x0}}\left( 1+\sigma \right) $ | (15) |
Logvinovich's formula (Semenenko, 2001) for forecasting the slender ratio of a supercavity is as follows:
| $ \lambda =\frac{2.077-3.24\sigma }{\sqrt{\sigma \left( 1+\sigma \right)}} $ | (16) |
| $ {{L}_{m}}=2\lambda {{R}_{m}} $ | (17) |
where Cx denotes the drag coefficient of the disk cavitator; Rm and Rn are the theoretical maximum radius of the supercavity cross section and the diameter of the disk cavitator, respectively; σ represents the cavitation number, p∞ and pv are the pressure of far-field and the saturated vapor pressure of water, respectively; v∞ denotes the velocity of incoming flow; k is the correction factor; Cx0 denotes the drag coefficient of the disk cavitator when σ = 0, and it equals 0.827; λ and Lm denote the slender ratio of the supercavity and the theoretical length of the entire supercavity, respectively.
The shape of supercavity is quasi-ellipsoid, which is symmetrical about the maximum cross section. Moreover, the outline of the initial cavity is determined only by the cavitator, and it has no relation with the cavitation number. The outline of the supercavity generated by the disk cavitator can be expressed as follows:
| $ {{R}_{\left( x \right)}}=\left\{ \begin{align} &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{R}_{n}}{{\left( 1+\frac{3x}{{{R}_{n}}} \right)}^{{}^{1}\!\!\diagup\!\!{}_{3}\;}}.x<{{x}_{1}} \\ &{{R}_{m}}\sqrt{1-\left( 1-\frac{R_{1}^{2}}{R_{m}^{2}} \right)\left( 1-\frac{x-{{x}_{1}}}{{{x}_{m}}-{{x}_{1}}} \right)},x\ge {{x}_{1}} \\ \end{align} \right. $ | (18) |
where x1=2Rn, xm denotes the length of the half supercavity, R(x) is the radius of the cross section of the supercavity at an axial position x (mm) away from the cavitator, R1 represents the radius of the cross section of the supercavity at the axial position x=x1, and R1≈1.92Rn can be obtained.
3 Results and discussionsRegarding models A and B, the supercavity shape and the drag coefficients of the disk cavitators under water inflow flux of 0–10 L/s were researched using the numerical method, as described in this section.
3.1 Model validationTaking the 48 mm disk cavitator as an example, when the cavitation number is 0.024, the shape of the supercavity and the drag coefficient of the disk cavitator can be determined using the established model and empirical equations. Furthermore, the accuracy of the established numerical model is verified by comparing the results of the two methods. The drag coefficient of the disks cavitator; and the maximum diameter, length, and shape of the supercavity can be obtained by the empirical equations and the numerical simulation method, respectively. A comparison of the drag coefficients, maximum diameters, and lengths of the supercavities obtained by two methods is given in Table 1, and a comparison of the shapes is shown in Fig. 4.
| Items | Drag coefficient | Maximum diameter/mm | Cavity length/mm |
| Empirical equations | 0.847 | 294.6 | 3757 |
| Numerical methods | 0.861 | 284.9 | 3648 |
| Relative errors/% | 1.6 | -3.3 | -2.9 |

|
| Figure 4 Comparison of supercavity shape obtained using numerical simulation and empirical formulas |
As shown in Table 1, the results of numerical simulation of the disk cavitator coincide with those of the empirical equations, and the errors in the drag coefficient, maximum diameter, and supercavity length are 1.65%, 3.29%, and 2.90%, respectively.
As shown in Fig. 4, the supercavity obtained by numerical simulations is ellipsoidal similar to the supercavity obtained using the empirical equations, and the length and the maximum diameter of the former are slightly smaller than those of the latter.
By considering Table 1 and Fig. 4 together, we can conclude that the numerically obtained drag coefficient of the disk cavitators and the supercavity shape are highly accurate.
3.2 Influence of water inflow flux on cavitator dragAccording to the numerical simulation results, the force acting on the cavitator with the same water inflow flux was calculated separately using models A and B. For disk cavitators, the force acting on the entire cavitator and that acting on the front face are considered, and the former force takes into account the force acting on the shrink part of the intake pipe, while the latter takes into account only the force acting on the circular disk. The force acting on the front face of the cavitator generates the lift component when the cavitator axis and the incoming flow are not in the same direction. Hence, research on the drag feature of the circular front faces of cavitators is required to estimate the lift. The influences of water inflow flux and water inlet size on the drag characteristics of the cavitator are shown in Fig. 5.
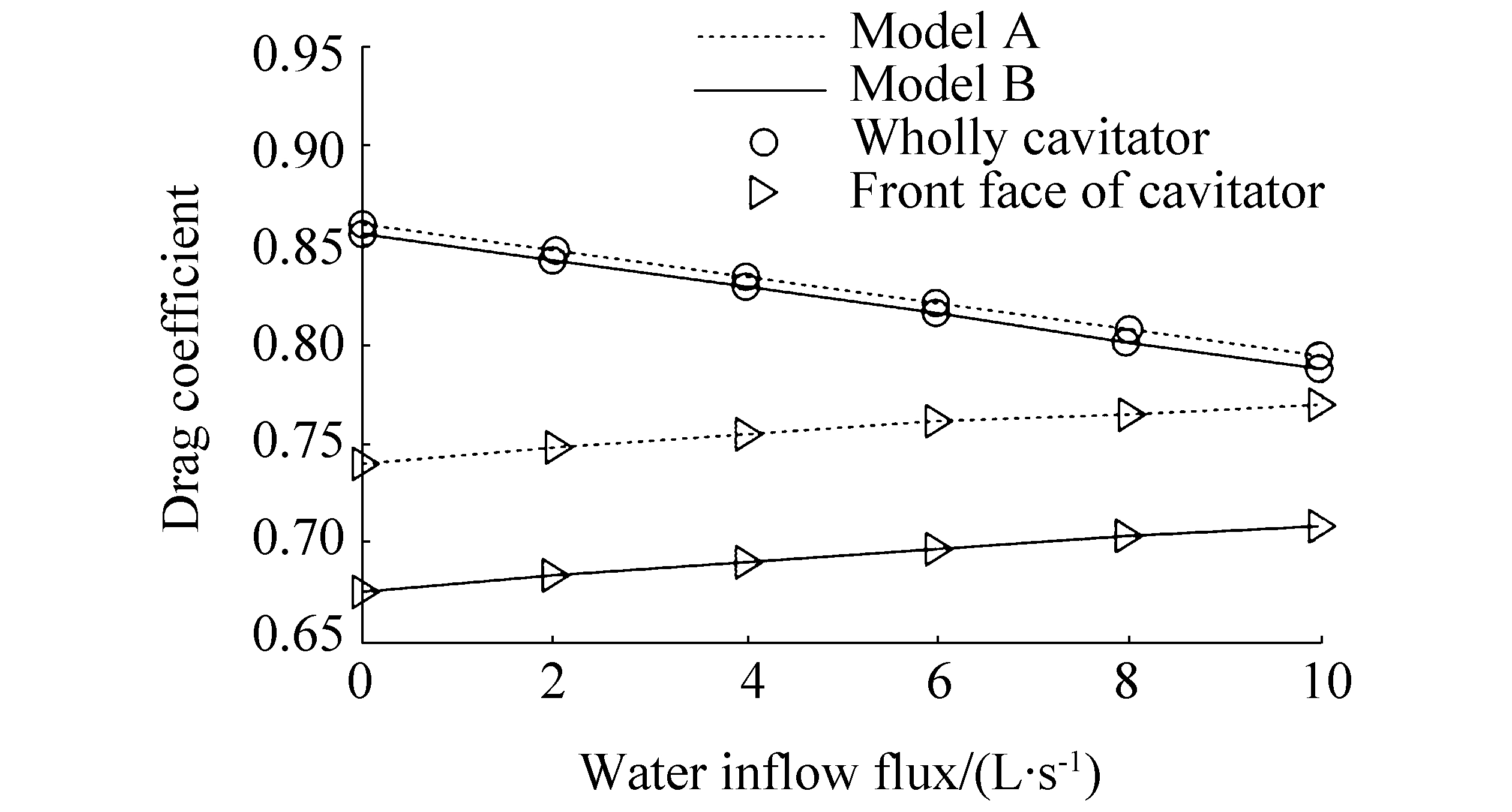
|
| Figure 5 Influences of inflow flux and inlet size on drag characteristics of cavitator |
As can be seen in the figure, the water inflow flux and the size of water inlets have some influence on the drag coefficient of the cavitator. With increasing water inflow flux, the drag coefficient of the entire cavitator decreases gradually, and the drag coefficient of the front face of the disk cavitator increases gradually. Although an increase in the water inlet size will influence the drag coefficient of the entire cavitator slightly, it leads to a sharp decrease in the drag coefficient of the front face of the disk cavitator.
3.3 Influence of water inflow flux on supercavity shapeAccording to the results of the numerical simulations, supercavity shapes with different water inflow fluxes in models A and B were computed to research the influence of water inflow flux on supercavity shape. Taking model A as an example, a comparison of the supercavity outlines for different water inflow fluxes is shown in Fig. 6.
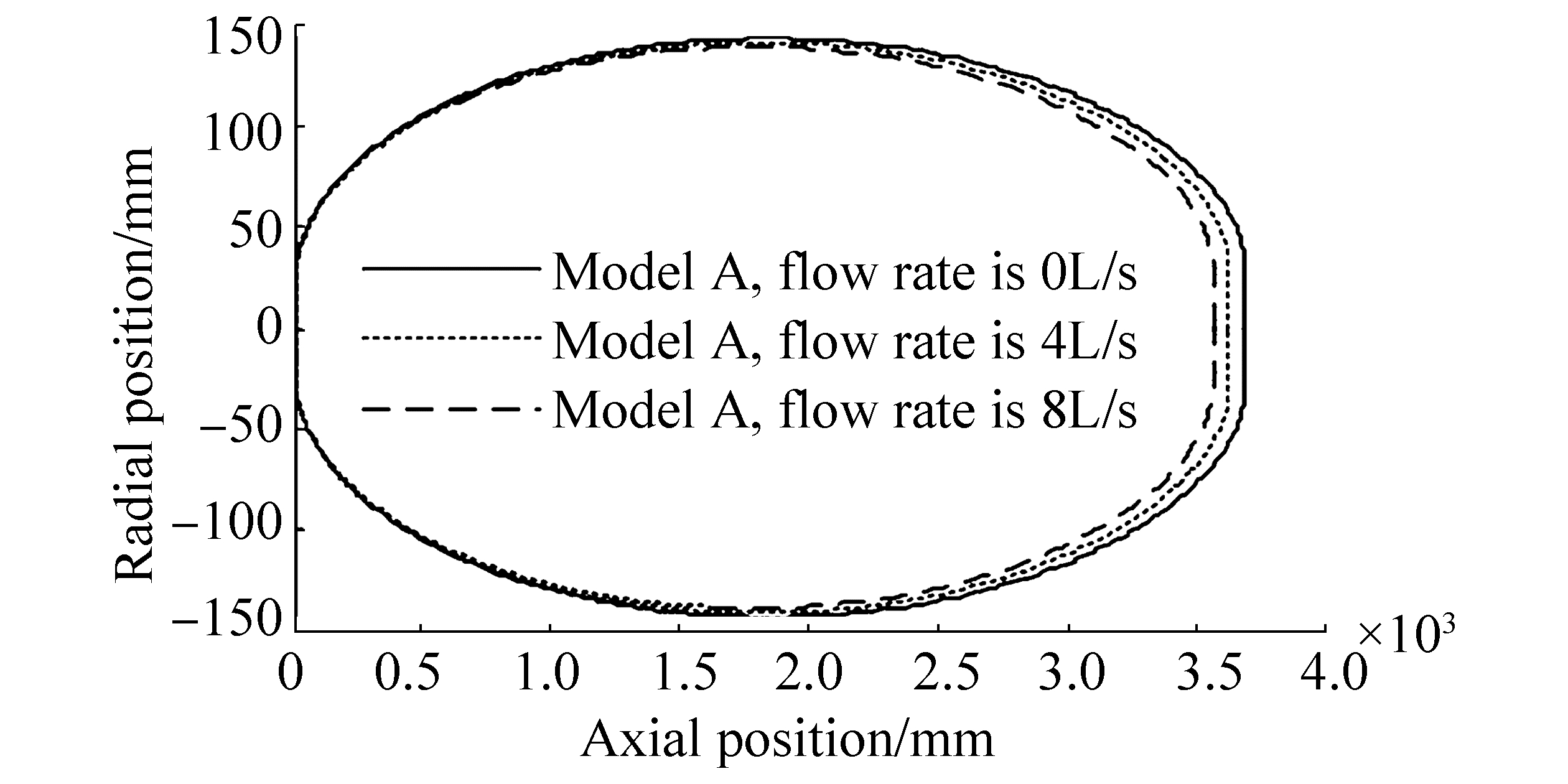
|
| Figure 6 Influence of water inflow flux on supercavity shape |
As shown in Fig. 6, water inflow flux has a significant influence on supercavity shape, and with increasing water inflow flux, the length, and the maximum diameter of the supercavity decrease.
A comparison of maximum diameters of supercavitaties obtained by numerical simulations and those calculated by Eq. (12) for different water inflow fluxes in models A and B is shown in Fig. 7.

|
| Figure 7 Influence of water inflow flux on supercavity size |
As shown in Fig. 7, for models A and B, the influence law of water inflow flux on the maximum diameters of supercavitaties obtained by numerical simulations is essentially the same as that obtained using the empirical equations–the result of numerical simulation is 3.3% smaller. With increasing water inflow flux, the maximum diameter of the supercavitaty in models A and B decreases, and the maximum diameter of the supercavitaty obtained using model A is larger than that of the supercavitaty obtained using model B for the same water inflow flux.
A comparison of the slender ratio of supercavitaties obtained using models A and B under different water inflow fluxes is shown in Fig. 8.

|
| Figure 8 Influence of water inflow flux on supercavity slender ratio |
As can be seen in the figure, water inflow flux has no influence on the supercavity slender ratio of models A and model B. As the water inlet and the water inflow flux change, the supercavity slender ratio obtained by numerical simulation is 12.9±0.1, and this value fits well with 12.75, the supercavitaty slender ratio calculated using the empirical method. Thus, when plenty of water flows into the water ramjet from the cavitator, the slender ratio of the generated supercavity is related only to the cavitation number and the cavitator shape.
4 ConclusionsIn this study, a numerical method was applied to a natural supercavitation flow field, and the method was validated by comparing the obtained results with those obtained using empirical equations. Then, the influence law of water inlet size and water inflow flux on cavitator drag characteristics and supercavity shape were investigated. The following conclusions were drawn.
1) Compared with the calculation result of the empirical equations, the supercavity length obtained from the numerical simulation is 2.9% shorter, maximum supercavitaty diameter is 3.3% smaller, and drag is 1.6% higher.
2) Water inlet size has a considerable influence on cavitator drag coefficient and supercavity shape. When the water inflow flux was kept constant and the water inlet area was increased, the drag coefficient of the entire cavitator decreased slightly, drag coefficients of the front faces of the disk cavitator diminished sharply, maximum supercavitaty diameter decreased slightly, and supercavity slender ratio was not affected.
3) The water inflow flux of ramjets has a significant influence on cavitator drag characteristics and supercavity shape. With an increase in the water inflow flux in the range of 0–10 L/s, the total cavitator drag coefficient decreased sharply, and the drag coefficient of the front face of disk cavitator increased gradually, maximum supercavitaty diameter decreased gradually, and slender ratio of the supercavitaties remained nearly constant.
The results presented herein can be used to optimize the outline and the cavitation flow pattern design of HSSVs.
| Beckstead MW, 2004. A summary of aluminum combustion. Brigham Young University, Provo, Utah, N00014-95-1-1338. |
| Dominic B, Eric L, Paul W, 2011. Feasiblity of water-aluminum reactor powder (WARP) for long endurance UUVs. 9th Annual International Energy Conversion Engineering Conference, 2011-5904. |
| Euteneuer EA, 2003. Further studies into the dynamics of a supercavitating torpedo. University of Minnesota, Twin Cities, USA, 15-35. |
| Feng Xiping, Chen Xianhe, Li Jinxian, 2014. Effect analysis of water spray location and quantity on aluminum water ramjet combustion. Mechanical Science and Technology for Aerospace Engineeing, 33(9), 1423–1427. DOI:10.13433/j.cnki.1003-8728.2014.0929 |
| Grant A, Risha, Huang Y, 2006. Combustion of aluminum particles with steam and liquid water. 44th AIAA Aerospace Sciences Meeting and Exhibit, 2006-1154. DOI: DOI:10.2514/6.2006-1154 |
| Hassouneh MA, Nguyen V, Balachandran B, 2013. Stability analysis and control of supercavitating vehicles with advection delay. Journal of Computational and Nonlinear Dynamics, 8(2), 21003. DOI:10.1115/1.4006835 |
| Hayati AN, Hashemi SM, Shams M, 2013. Design and analysis of bubble-injected water ramjets with discrete injection configurations by computational fluid dynamics method. Proceedings of the Institution of Mechanical Engineers Part C-Journal of Mechanical Engineering Science, 227(9), 1945–1955. DOI:10.1177/0954406212469329 |
| Hu F, Zhang W, Xiang M, Huang L, 2013. Experiment of water injection for a metal/water reaction fuel ramjet. Journal of Propulsion and Power, 29(3), 686–691. DOI:10.2514/1.B34456 |
| Huang C, Luo K, Dang J, Li D, 2015. Influence of flow field's radial dimension on natural supercavity. Journal of Northwestern Polytechnical University, 33(6), 936–941. |
| Huang L, Xia Z, Zhang W, Hu J, Hu F, Zhao Y, 2010. Water/fuel ratio selection method in water ramjet engine test. Acta Aeronautica Et Astronautica Sinica, 31(9), 1740–1745. |
| Huang H, Zou M, Guo X, Yang R, 2013. Analysis of the aluminum reaction efficiency in a hydro-reactive fuel propellant used for a water ramjet. Combustion Explosion and Shock Waves, 49(5), 541–547. DOI:10.1134/S0010508213050055 |
| Kirschner I, Uhlman J, Perkins J, 2006. Overview of high-speed supercavitating vehicle control. AIAA Guidance, Navigation, and Control Conference and Exhibit, Keystone, 6442-1-17. |
| Kirschner IN, Fine NE, Uhlman US, 2001. Supercavitation research and development. Undersea Defense Technologies, Waikiki, 1-10. |
| Launder BE, Spalding DB, 1974. The numerical computation of turbulent flows. Computer Methods in Applied Mechanics and Engineering, 3(2), 269–289. DOI:10.1016/0045-7825(74)90029-2 |
| Li D, Luo K, Huang C, Dang J, Zhang Y, 2014a. Dynamics model and control of high-speed supercavitating vehicles incorporated with time-delay. International Journal of Nonlinear Sciences and Numerical Simulation, 15(3-4), 221–230. DOI:10.1515/ijnsns-2013-0063 |
| Li F, Zhang Y, Dang J, Zhang Y, 2014b. Research on hydrodynamic characteristics of conical cavitator. Acta Armamentarii, 35(7), 1040–1044. |
| Lin Mingdong, Hu Fan, Zhang Weihua, Ma Zhenyu, 2012. Design and analysis of injection tube system of water ramjet. Journal of Solid Rocket Technology, 35(6), 742–746. |
| Logvinovich GV, 1972. Hydrodynamics of free-boundary flows. US Department of Commerce, NASA-TT-F-658, 105-110. |
| Nguyen V, 2011. Dynamics and control of non-smooth systems with applications to supercavitating vehicles. PhD thesis, University of Maryland, College Park, 5-10. |
| Savchenko YN, 2002. Control of supercavitation flow and stability of supercavitating motion of bodies. Proceedings of RTO AVT Lecture Series on Supercavitating Flows, Brussels, 14, 1–29. |
| Schnerr GH, Sauer J, 2001. Physical and numerical modeling of unsteady cavitation dynamics. Fourth International Conference on Multiphase Flow, New Orleans, 1-12. |
| Semenenko VN, 2001. Artificial supercavitation. physics and calculation. VKI Special Course on Supercavitating Flows, Brussels, 1-34. |
| Shih TH, Liou WW, Shabbir A, 1994. A new k-epsilon eddy viscosity model for high Reynolds number turbulent flows:Model development and validation. NASA Sti/recon Technical Report N, 95, 1–30. |
| Sun Z, Deng F, Zhang Y, 2011. Design of the matching pipeline intake of water ramjet with supercavitating vehicle. Mechanical Science and Technology for Aerospace Engineering, 30(7), 1159–1162. |
| Timothy F, Miller, John D, 2004. Green rocket propulsion by reaction of Al and Mg powders and water. 40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Fort Lauderdale, AIAA 2004-4037. |
| Vasin A, 2001. The principle of independence of the cavity sections expansion (Logvinovich's principle) as the basis for investigation on cavitation flows. VKI Special Course on Supercavitating Flows, Brussels, 1-27. |
| Yang Yajing, He Maogang, Xu Houda, 2009. Thermodynamic calculation and analysis for water ramjet. Journal of Propulsion Technology, 30(2), 240–245. |
| Yu K, Zhang G, Zhou J, Zou W, Li Z, 2012. Numerical study of the pitching motions of supercavitating vehicles. Journal of Hydrodynamics, 24(6), 951–958. DOI:10.1016/S1001-6058(11)60323-5 |



