2. Marine Design and Research Institute of China (MARIC), Shanghai 200011, China
1 Introduction
IMO MEPC.212 (63) introduced the Energy Efficiency Design Index (EEDI) to limit the emissions of Greenhouse Gases (GHS) from various types of ships. Although these new regulations were criticized by many parties at the IMO, they are now in the phase of implementation. As these requirements are far more stringent that previous legislation, and will be in force until the end of the implementation period in 2025, this poses serious problems for the maritime industry. There has also been a recent downturn in the shipping market, and fuel costs have become a heavy operational burden to ship owners and operators, and "per ton" fuel prices fluctuate drastically; therefore, ensuring ships to be energy efficient is now a key performance indicator of shipping companies. Shipyards are thus increasingly expected to deliver ships that are more energy-efficient, while simultaneously considering the actual service profile.
It is well established that the engine power of a ship is dependent on the cube of the speed, hence the installed power can be drastically reduced if the design speed is reduced, which thus also reduces fuel consumption and associated ship emissions. However, if EEDI requirements are achieved in practice by simply reducing installed power (but not by improving a ship's efficiency), the ship may not be able to dispose sufficient propulsive power to maintain maneuverability in adverse sea conditions, thereby leading to serious safety issues. In this respect, the " (IMO) 2013 interim guidelines for determining minimum propulsion power to maintain the maneuverability in adverse conditions" (2013 interim guidelines) were compiled to set a lower limit for installed power. The guideline involve the use of two assessment procedures: Level 1 Assessment and Level 2 Assessment. If the ship under assessment passes one of the above assessments, it is considered to have sufficient power to maintain maneuverability in adverse conditions. However, it is of note that the introduction of IMO "minimum power lines" in relation to ship safety, and consideration of "maximum allowable powering" in relation to EEDI requirements have resulted in a dubious min-max ship design problem, for which there may be no design solution if the minimum powering requirement happens to be above the maximum allowable powering requirement. This problem is admittedly related to inadequate statistical analysis of existing speed-powering data of world fleets, on which the min-max powering lines were deduced (Papanikolaou et al., 2015).
Values for the minimum power lines referred to in the above Level 1 Assessment were derived from statistical data of existing ships, and led to calculation of the minimum power line value= a× (DWT) +b, where a and b are ship-type dependent. In Level 2 Assessment, which is a simplified assessment, the required advance speed of a ship in head wind and waves ensuring course-keeping in all wave and wind directions, is firstly determined. The installed power is then assessed in relation to whether it is sufficient enough to enable the ship to achieve its required advance speed in head wind and waves. Application of this method requires knowledge of bare hull ship resistance in calm water, Rcw, resistance due to hull appendages, Rapp, aerodynamic/wind resistance, Rair, (depending on the ship's superstructure and relative wind speed), and the added resistance in waves, Raw. In general, all of these resistance components can be satisfactorily calculated using semi-empirical formulas, except for the more complex added resistance in waves, Raw, which can be obtained from added resistance tests in regular waves at the ship's required advance speed, Vs, as per the ITTC (2002) adopted procedures 7.5-02 07-02.1 and 7.5-02 07-02.2, or by use of equivalent numerical methods verified by the administration.
The dubiousness of the min-max powering lines problem shown above led MEPC-68 to urgently revise the 2013 Interim Guidelines for determining minimum powering of tankers and bulk carriers in adverse weather conditions (IMO MEPC 68/WP.9, 2015), and thus the a and b values used were modified, as shown in Table 1. This essentially means that the minimum power lines for tankers and bulk carriers were raised, and that powering that had originally been specified in the EEDI regulations was increased. Designers had been using the Level 1 assessment procedure defined in MEPC-64 to check installed power until this time, which complied with the EEDI requirements set out in regulations for the energy efficiency of ships. Therefore, by raising the minimum power lines, most of the new designs did not meet the requirements, and hence it was necessary to conduct the simplified Level 2 Assessment, which has now become the only way to prove compliance. Therefore, the current dilemma for the designer is that the installed power needs to be determined in the very early design stages. However, if proceeding to the simplified Level 2 Assessment, then added resistance in waves, Raw, needs firstly to be obtained from model tests conducted in a towing tank, or from an equivalent numerical method verified by the Administration, which at this point does not exist.
| Ship type | MEPC64 | MEPC68 | |||
| a | b | a | b | ||
| Bulk carrier withDWT < 145 000 | 0.068 7 | 2 924.4 | 0.076 3 | 3 374.3 | |
| Bulk carrier withDWT ≥ 145 000 | 0.068 7 | 2 924.4 | 0.049 0 | 7 329.0 | |
| Tankers | 0.068 9 | 3 253 | 0.065 2 | 5 960.2 | |
| Combination carriers | 0.068 9 | 3 253 | 0.065 2 | 5 960.2 | |
In this context, a simplified engineering formula that estimates a ship's added resistance in waves with satisfactory accuracy is urgently required, and would enable designers to determine the required engine power in the early design stage, without incurring delays involved by conducting tank model tests.
In addition to the need for a reliable evaluation method complying with the framework for a minimum power assessment, it is also necessary to develop a simplified method to calculate the fw coefficient, as defined in IMO-EEDI guidelines (IMO MEPC.1/Circ.796, 2012a ), where it is specified that the added resistance of ships in waves needs to be accurately determined "by tank tests or a formula equivalent in terms of accuracy." Again, currently there are no available formulas, but if such a formula were to be determined it could immediately be applied in general ship design (engine selection) where the fast prediction of added resistance in waves is urgently required in the early design stages.
Recent IMO regulations (2013) relating to the determination of minimum propulsion power in adverse conditions have called for a simplified approach for the prediction of added resistance and powering in (head) waves. This approach needs to be able to roughly estimate the added resistance of ships in regular waves, and should be able to be solved using a "pocket calculator" (to the extent possible) and it would essentially involve making an approximation of the added resistance using a semi-empirical formula. The added resistance is commonly treated using potential flow theory (and very often based on slender body theory assumptions) applying the so-called far field method (Maruo, 1960; Newman, 1967; Naito et al., 1988; Kashiwagi, 1992; Liu et al., 2011) or the near field method (Gerritsma and Beukelman, 1972; Salvesen, 1974; Pinkster, 1979; Faltinsen et al., 1980; Papanikolaou and Zaraphonitis, 1987; Kim and Kim, 2011) through pressure integration over the wetted hull surface. More advanced methods include the CFD simulations andexperimental method; however, the use of such methods involves high time/cost and computational effort. Furthermore, all these methods are generally verycomp licated and require extensive input and processing of data, thus this problem needs to be revisited.
In addition, with the continuous increase in ship sizes (in view of economy of scale), the region of relative wave length to ship length, λ/L, that is of practical interest has now been shifted to lower values, which makes the accurate prediction of added resistance in short waves much more important than it used to be. In addition, as confirmed recently by focused experimental studies (for instance, Kim et al., 2014; Valanto and Hong, 2015) and laborious CFD calculations (Ley et al., 2014), viscous effects, which cannot be captured by potential flow theory, appear to play a significant role in the prediction of added resistance in short waves, especially when approaching limiting values. It should be noted, however, that in very short waves both CFD and potential-flow methods are pushed to their limits, due to the need for very dense grids/small size panels in correctly capturing flow changes, as revealed in the study of Söding et al.(2014) . In tank tests, it is a huge challenge to obtain accurate measurements of added resistance in short waves due to the very small measured values. Therefore, tank operators often use steeper incident short waves for respective measurements, which may put the quadratic dependency of the ad ded resistance on wave height under question. Hence, it is imperative, when developing short wave added residence formulas, to use reliable experimental data to fine-tune the properly introduced semi-empirical corrective coefficients.
Following this concept, and while considering the effect of various typical characteristics of a ship hull's form, Liu and Papanikolaou (2016) have proposed a new simple formula to satisfactorily capture the added resistance of various types of modern ships in head waves, based on their research during the SHOPERA project (2013-2016). This formula is based on best fitting of available experimental data for different types of hull forms, and has been simplified to the extent that it uses only the main particulars of the ship and the fundamental wave characteristics to estimate a ship's added resistance, enabling the result to be accessed using only a simple pocket calculator with an EXCEL capability. In addition, this formula has been derived so that it can be applied to both low and moderate speed cases; hence it can be used in a procedure for determining minimum power in adverse sea conditions, or when calculating the weather correction coefficient, fw, of EEDI. In present paper, the authors further simply the formula and verify it by applying it to various case studies, namely to various types of ships operating at different speeds and in various sea conditions, for which experimental results are available. By doing so, the widespread applicability of the proposed new improved formula is verified.
2 Development of formulaFor the prediction of added resistance of a ship in head waves at any wave length, we begin with the following formula,
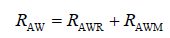
|
(1) |
For short waves, we propose a new practical formula for approximating the added resistance in short waves based on the previous study of Liu et al.(2015) , as

|
(2) |
Simplifying the above expression and using typical design data for various ship types, as shown in Fig. 1, the following formula has been developed for calculating the added resistance in short waves,

|
(3) |

|
| Figure 1 Bluntness coefficients, Bf, of typical merchant ship vs. block coefficient |
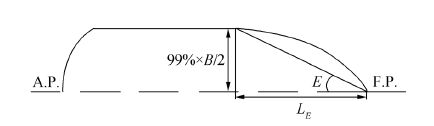
where $E=\arctan \left( \frac{B}{2{{L}_{E}}} \right)$ .
For long waves, the formula of Jinkine and Ferdinande (1974) has been further tuned, particularly in terms of the peak value and forward speed factor. For the peak of added resistance, the following factor is recommended
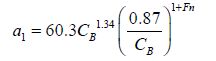
|
(4) |
In addition, after carefully studying the experimental and numerical data, the following expression was proposed for the forward speed factor,
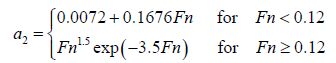
|
(5) |
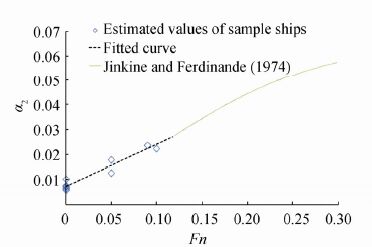
Fig. 2 shows the behavior of this extended speed correction factor, a2, which is valid for Fn=0 to 0.3.
|
| Figure 2 Behavior of speed correction factor, α2 |
Furthermore, the resonance position needs to be extended to the low speed region. It is known that the location of the peak added resistance is related to the location of the peak heave and pitch motions, which are essentially determined by the heave-pitch natural frequencies. The natural frequencies of the uncoupled heave and pitch motions are then found by the following expressions
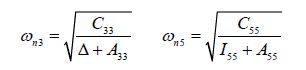
|
(6) |
Although C33 and C55 change with forward speed, this effect for Fn<0.12 is commonly very small (Gerritsma, 1960), which means that there is no radical change in the location of resonance at low speed. Therefore, we revisited the performance of Jinkine and Ferdinande's expression at speeds less than Fn=0.12, and proposed the following expression:
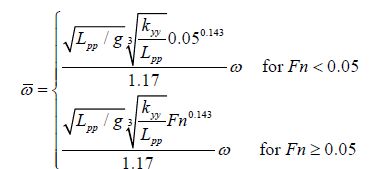
|
(7) |
For short waves, Ursell (1947) derived a theoretical solution for waves reflecting from a vertical wall having a depth, T from a free surface. A number of researchers, namely Fujii and Takahashi (1975) ; Takahashi (1988) ; and Kuroda et al.(2008) , subsequently followed this concept in their models for short wave added resistance prediction. In this approach, the first order Bessel functions of the first and second kind, I1 and K1, were used. However, Valanto and Hong (2015) observed that these formulas do not provide good results in the prediction of added resistance of a cruise ship, and argued that the exponential decay function, e−kT, is somewhat better than that of Kuroda's version of Ursell's solution. On the other hand, following the historical exponential decay concept of Smith (1883) , Kwon (1981) reached a different solution, where his reasoning in short waves was that if the wave amplitude decay is of an exponential manner, then the added resistance, which is basically an equivalent to the dissipated wave energy, will decay with the square of the exponential function. In this context, the added resistance of the ship equals the drift force generated by the wave pressure, which extends from the free surface and down to the ship's draft, T. Thus, the following draft correction coefficient has been derived:
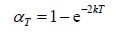
|
(8) |
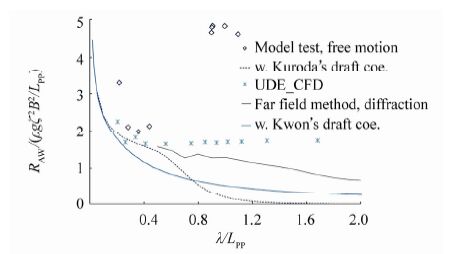
This coefficient appears to be physically very meaningful and is much simpler in practical use. Fig. 3 shows the prediction of added resistance due to the diffraction effect using both Kuroda and Kwon's coefficients. Applying both draft coefficients in very short waves leads to the same results, which shows that in an extreme case both models are valid. However, the two methods deviate from each other in intermediate conditions, and the application of Kuroda's draft coefficient in long waves leads to practically zero added resistance, while the application of Kwon's does not. In view of available results obtained from more advanced numerical tools (namely far field method calculations with potential flow by Liu et al.(2011) , and CFD simulation results by Sigmund of University of Duisburg at Essen (private communication, 2015), Kwon's draft coefficient appears to have more merits, in addition to the fact that it has a simpler expression.
|
| Figure 3 Added resistance due to diffraction effect of DTC containership in head waves using various methods, Fn=0.139 |
LEhas been defined as the distance from the forward perpendicular (F.P.) to the position of maximum ship breadth (beam). However, in practice it has been observed that when approaching the full beam point, there is usually a considerable segment on the water line that changes very slowly in the y direction. This part has a very small projection in the y direction (almost parallel to the centerline), and contributes minimally to added resistance. Hence, LE can be modified to correspond to the point where the width reaches 99%B, as shown in Fig. 4.
|
| Figure 4 Definition of length, LE, and angle, E, of waterline entrance |
Finally the formula takes the following form,
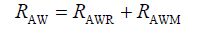
|
(9) |
where
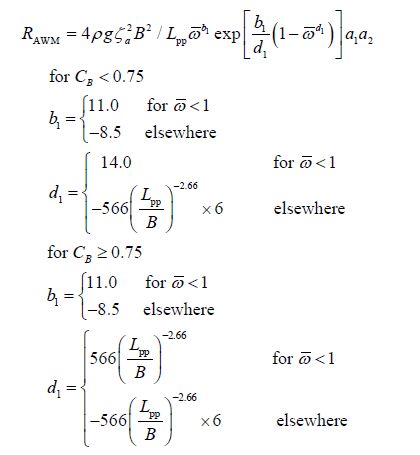
|
and where the definitions of all other parameters can be found in previous sections.
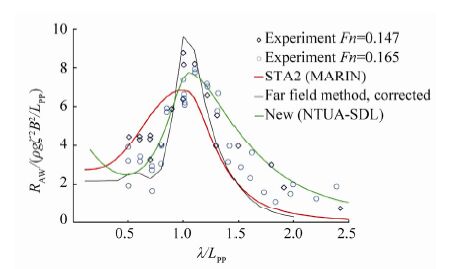
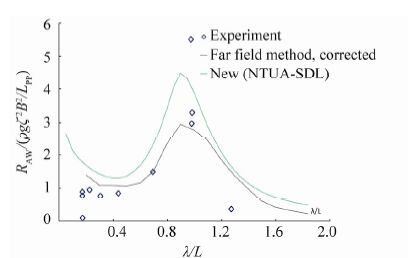
Figs. 5-7 show predictions of added resistance for three ships using application of the refined formula (which is denoted as NEW (NTUA SDL) ), and for reference results using the STA2 formula by MARIN (ITTC, 2012; Grin, 2012) and those based on a more advanced numerical method (the far field method, corrected by Liu et al., 2011) are also plotted. The experimental data of a S60 ship are obtained from Strm-Tejsen et al.(1973) , while those for the RoPAX ship are from the SHOPERA research project (Sprenger et al., 2015). It is observed that, in general, the formula adequately captures added resistance, except in very short waves. However, capturing added resistance in very short waves is a common problem because it is difficult to accurately measure resistance due to its extremely small absolute quantity, and there is thus a lack of valid available data.

|
| Figure 5 Added resistance of S60 model in head waves using different methods, CB=0.60, Fn=0.266 |
|
| Figure 6 Added resistance of S60 model in head waves using various methods, CB=0.80, Fn=0.147 |
|
| Figure 7 Added resistance of a RoPax ship in head waves using various methods, Fn=0.087 |
Present EEDI regulations specify that the only way to obtain mean added resistance is to conduct tank tests in regular waves, which means that it is necessary to use physical model experiments to determine the transfer function of added resistance. Afterwards the mean value of added resistance in irregular seas is calculated by applying some standard wave spectra (tank tests in irregular waves have not yet been adopted due to associated uncertainty of physical phenomenon). Therefore, the new formula is applied herein to estimate the mean value of added resistance of ships in irregular seas, and in this respect various sea states are examined, as shown in Table 2.
| Case | Spectrum | Period/s | HS/m | Speed | Comments |
| Minimum power | ITTC | 7.0-15.0 (peak) | 4.0-5.5 | Low | Deep water |
| Minimum power | JONSWAP | 7.0-15.0 (peak) | 4.0-5.5 | Low | Coastal water, γ=3.3 |
| Weather coefficient fw in EEDI | ITTC | 6.7 (mean) | 3.0 | Design | Deep water |
| Seaways, slow steaming | ITTC | 5.5 (zero crossing) | 1.5 | Moderate | Deep water |
The mean added resistance in irregular waves is calculated as follows
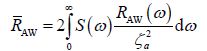
|
(10) |
where S (ω) is the wave spectrum, RAW (ω) the added-resistance response function in regular waves, and ζα the regular wave amplitude.
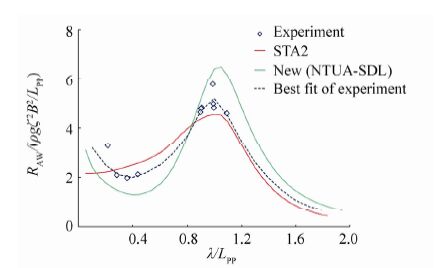
In the following numerical study, two set of results are generated in relation to the following. Firstly, based on the method presented herein, which is denoted as NEW (NTUA-SDL), results in regular waves are obtained, where the mean value in irregular waves is presented as being based on current formula in the following Figs. 9-12. Secondly, based on experimental data from tank tests, a best-fit curve of results in regular waves (best fit of experiment) is derived to calculate the mean value in irregular waves, which is shown as based on tank test in Figs. 9-12. Fig. 8 gives an example of a numerical study conducted on a DTC ship, which was also tested in the SHOPERA project, and results in regular waves based on the afore-defined two methods are plotted. In addition, results based on the STA2 formula are plotted for reference.
|
| Figure 8 Added resistance of DTC ship in head waves using various methods, Fn = 0.139 |
|
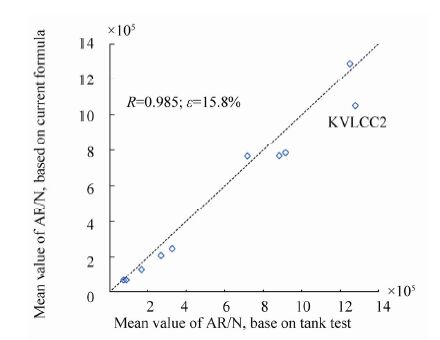
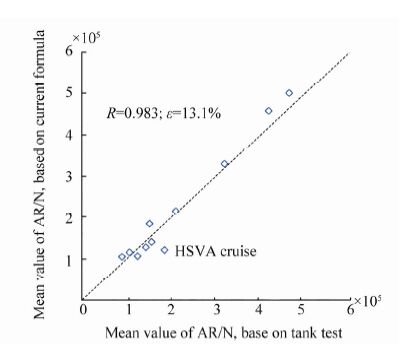
| Figure 9 Correlation between use of current formula and tank test results for various ship types using minimum power assessment |
|
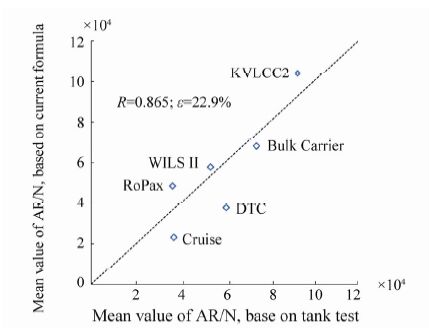
| Figure 10 Correlation between use of current formula and tank test results for various ship types using EEDI calculation |
|
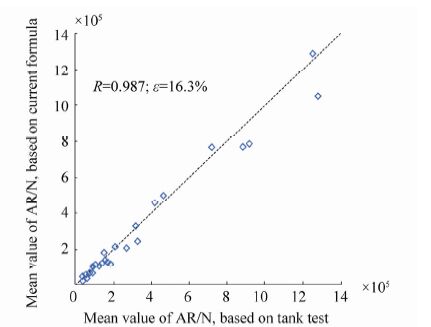
| Figure 11 Correlation between use of current formula and tank test results for various ship types using slow steaming calculation |
|
| Figure 12 Correlation of current formula with tank test results for different ship types and speeds in various sea conditions |
To assess the quality of the prediction in irregular seas, two parameters are used, namely the Pearson's R Correlation and the mean absolute percentage error, which are defined as follows
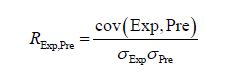
|
(11) |

|
(12) |
where Exp denotes the experimental results, Pre the prediction, cov the covariance, and σ the standard deviation.
3.1 Application to minimum power calculationAs discussed in the introduction, the main thrust of current work has been derived from a demand to predict added resistance in regular waves at a low speed using a simple formula, and this drive was essentially been established in relation to the 2013 Interim Guideline on minimum power assessment. In this study, the KVLCC2 and a bulk carrier are chosen as case studies, as these two ship types are specified in current guidelines. In addition, a containership, namely the DTC, and a RoPax ship are also studied because they were discussed in the SHOPERA project. The main parameters involved in the case study are summarized in Table 3. For the KVLCC2 and bulk carrier, three sea states are studied: two corresponding to open sea cases and the other to coastal water. For the DTC, three sea states are also studied, as specified in the tank test by Sprenger et al.(2015) , and for RoPax, one coastal water case is used in consideration of the vessel's operating characteristics.
| Ship | Spectrum type | Period/s | HS/m | Fn | LE/m | Notes |
| KVLCC2 | ITTC | 15.0 (peak) | 5.5 | 0.09 | At 99%B, 60 | Deep water |
| KVLCC2 | ITTC | 10.0 (peak) | 5.5 | 0.09 | At 99%B, 60 | Deep water |
| KVLCC2 | JONSWAP | 7.0 (peak) | 5.5 | 0.09 | At 99%B, 60 | Coastal water, γ=3.3 |
| Bulk carrier | ITTC | 15.0 (peak) | 5.5 | 0.05 | Estimation, offset N/A, 51 | Deep water |
| Bulk carrier | ITTC | 10.0 (peak) | 5.5 | 0.05 | Estimation, offset N/A, 51 | Deep water |
| Bulk carrier | JONSWAP | 7.0 (peak) | 5.5 | 0.05 | Estimation, offset N/A, 51 | Coastal water, γ=3.3 |
| DTC | JONSWAP | 7.71 | 2.8 | 0.052 | At 99%B, 112 | Deep water |
| DTC | JONSWAP | 9.64 | 5.02 | 0.052 | At 99%B, 112 | Deep water |
| DTC | JONSWAP | 11.86 | 7.38 | 0.052 | At 99%B, 112 | Deep water |
| RoPax | JONSWAP | 7.0 | 4.0 | 0.087 | At 99%B, 35.8 | Coastal water, γ=3.3 |
Figs. 9 shows comparisons between predicted mean values of Added Resistance (AR) and those calculated based on tank tests. In general, the predictions agree well those from the tank tests, and it is shown that the points are set firmly against the line (which means the formula predictions are equal to those of the tank test). The largest discrepancy can be observed for the case of KVLCC2 in Case-2, in which the prediction is 18% smaller, but this can be explained by the significant difference between the prediction and the tank test in regular short waves. It is of note that the experimental results for DTC cases were obtained using tests in irregular waves.
3.2 Application of weather coefficient, fw, calculationIn its 64th session (IMO, 2012a, 2012b), MEPC recognized the need to develop guidelines for calculating the coefficient, fw, contained in the 2012 Guidelines on the method of calculation of the attained Energy Efficiency Design Index for new ships (resolution MEPC.212 (63), 2012b), and thus agreed to circulate interim guidelines for trial use in simulating the coefficient, fw, for a decrease in ship speed within representative sea conditions.
In this section, the formula is applied to the sea condition specified in the EEDI guidelines at the design speed. Experimental data of eleven ships were used to validate the formula, as shown in Table 4, and the mean values of added resistance in representative sea states for EEDI calculation are plotted and shown in Fig. 10. A good agreement between the predicted results and the results based on tank test data can again be observed. The largest discrepancy is related to the cruise ship, but this is a unique case because this type of ship features a very small draft, an excessive large radius of gyration of pitch, and a very sharp bow form, which consequently gives a shifted position of peak added resistance and low values in short waves when using the regular wave prediction formula.
| Ship | Spectrum type | Period/s | HS/m | Fn | LE/m | Notes |
| KVLCC2 | ITTC | 6.7 (mean) | 3.0 | 0.180 | At 99%B, 60 | Deep water |
| VLCC | ITTC | 6.7 (mean) | 3.0 | 0.145 | At 99%B, 54.28 | Deep water |
| Bulk carrier | ITTC | 6.7 (mean) | 3.0 | 0.15 | Estimation, offset N/A, 51 | Deep water |
| HSVA cruise | ITTC | 6.7 (mean) | 3.0 | 0.223 | At 99%B, 72.42 | Deep water |
| WILS II | ITTC | 6.7 (mean) | 3.0 | 0.183 | At 99%B, 99.15 | Deep water |
| S175 | ITTC | 6.7 (mean) | 3.0 | 0.275 | At 99%B, 59.050 | Deep water |
| Series 60, CB=0.60 | ITTC | 6.7 (mean) | 3.0 | 0.266 | At 99%B, 52.000 | Deep water |
| Series 60, CB=0.65 | ITTC | 6.7 (mean) | 3.0 | 0.237 | At 99%B, 46.522 | Deep water |
| Series 60, CB=0.70 | ITTC | 6.7 (mean) | 3.0 | 0.222 | At 99%B, 38.606 | Deep water |
| Series 60, CB=0.75 | ITTC | 6.7 (mean) | 3.0 | 0.177 | At 99%B, 30.480 | Deep water |
| Series 60, CB=0.80 | ITTC | 6.7 (mean) | 3.0 | 0.147 | At 99%B, 22.800 | Deep water |
Slow steaming refers to the practice of operating ships at a speed that is significantly lower than their original design speed. This practice was initially used in containership transportation and is now observed in other ship markets. It was introduced during a time of high fuel prices, but it was soon discovered that in addition to saving money on fuel there were other merits to this practice, such as reducing greenhouse gas emission and absorbing fleet overcapacity (Psaraftis and Kontovas, 2013). Therefore, in ship design, the concept of multi-speed optimization has become important, and it is thus necessary to accurately predict added resistance at an intermediate speed together with the design speed.
Table 5 shows the main parameters involved in the slow steaming case study, where the sea states used are represented by typical ITTC seaway spectra, with HS=1.5 m. In very mild sea conditions, and in the absence of ship motion, it is mainly the short wave results that play a significant role (diffraction/reflection effect). As shown in Fig. 11, in such a case, much lower absolute values of added resistance are observed in comparison with results from the cases studied in the previous two sub-sections. In addition, values of scattering are also much larger, which is actually related to the larger discrepancy in the prediction of added resistance in short waves, in addition to the lack of reliable tank test results in very short waves.
| Ship | Spectrum type | Period/s | HS/m | Fn | LE/m | Notes |
| KVLCC2 | ITTC | 5.5 (zero-crossing) | 1.5 | 0.142 | At 99%B, 60 | Deep water |
| Bulk carrier | ITTC | 5.5 (zero-crossing) | 1.5 | 0.10 | Estimation, offset N/A, 51 | Deep water |
| DTC | ITTC | 5.5 (zero-crossing) | 1.5 | 0.139 | At 99%B, 112 | Deep water |
| WILS II | ITTC | 5.5 (zero-crossing) | 1.5 | 0.183 | At 99%B, 99.15 | Deep water |
| HSVA cruise | ITTC | 5.5 (zero-crossing) | 1.5 | 0.166 | At 99%B, 72.42 | Deep water |
| RoPax | ITTC | 5.5 (zero-crossing) | 1.5 | 0.242 | At 99%B, 35.8 | Deep water |
This paper presents a refined formula for the calculation of added resistance in head waves. With the introduction of an alternative draft coefficient, the formula that was previously introduced by the main authors has been further simplified by avoiding calculation of the Bessel functions. In this respect, it is on step forward in terms of engineering applicability.
The refined formula was applied to typical case studies of various popular ship types, to determine minimum power in adverse conditions, to calculate the EEDI weather (fw), and to predict added resistance in the context of slow steaming. The formula was then verified using a tanker (VLCC), a bulk carrier, two containerships, a RoPax, a cruise ship, and all the S60 series ships in terms of ship type. The length between the perpendiculars of the ships varied between 90 m and 355 m in terms of ship size, and the ships' speed also varied from low, to intermediate and moderate. Essentially by applying the formula to specific ships, for which experimental data were available for validation, its widespread applicability was demonstrated. Fig. 12 shows the overall comparison between predicted mean values of added resistance and results based on tank tests, demonstrating encouraging results. For the 27 pairs of observations, Pearson's R Correlation value was 0.987 and the mean absolute percentage error 16.3%. Overall, it appears that predictions based on the present formula are slightly lower than those based on tank tests, but this is considered minor and can be readily accounted for in engineering applications, where the simplicity of the formula will dominate other aspects.
Nevertheless, further validation is required with other types and sizes of ships. However, this will take some time, as it is necessary to wait for more experimental results to become available for validation. Another foreseeable future task is to extend this formula to cover a wider range of wave headings, which will enable many more applications (e.g., simulation of maneuvering of ships in waves). Finally, the development of the present formula and associated validation work were conducted using full load conditions, and thus caution is needed when applying it to ships in a ballast condition as the associated physical phenomena will change drastically.
AcknowledgementThe work presented in this paper was partly supported by the Collaborative Project (Grant Agreement number 605221) SHOPERA (Energy Efficient Safe SHip OPERAtion), which is co-funded by the Research DG of the European Commission within the RTD activities of the FP7 Thematic Priority Transport / FP7-SST-2013-RTD-1/ Activity 7.2.4 Improving Safety and Security / SST.2013.4-1: Ships in operation. The European Union shall not in any way be liable or responsible for the use of any knowledge, information, or data contained in the present paper, or of any associated consequences thereof. The views expressed in this paper are those of the authors and do not necessarily reflect the views and policies of the European Union.
NomenclatureA33 Coefficient of heave added mass
A55 Coefficient of pitch added inertia moment
B Breadth of ship
Bf Bluntness coefficient
C33 Heave restoring force coefficient
C55 Pitch restoring moment coefficient
CB Block coefficient
E Angle of waterline entrance, as defined in Fig. 4
EEDI Energy Efficiency Design Index
Fn Froude number
g Gravitational acceleration
HS Significant wave height
I1 Modified Bessel function of the first kind of order 1
I55 Massmoment of inertia about the y-axis (pitch)
ke ωe2/g, encountered wave number
K1 Modified Bessel function of the second kind of order 1
kyy Longitudinal mass radius of gyration (pitch)
LE Length of waterline entrance, as defined in Fig. 4
L Length of ship
LPP Length of ship between perpendiculars
MEPC Marine Environment Protection Committee
rAW Non-dimensionaladded resistance coefficient
RAW Total added resistance in regular waves
Mean value of added resistance in irregular seas
RAWR Added resistance in regular waves due to diffraction effect (reflection effect)
RAWM Added resistance in regular waves due to motion effect
S (ω) Wave spectral density
T Draft of ship
TP Spectral peak period
αT Draft correction coefficient
αWL Flare angle at waterline in bow region
Δ Mass of displacement
θ Slope of waterline segment
ζα Incident wave amplitude
λ Wave length
π Ratio of circle circumference to diameter
ρ Density of water
ω Circular wave frequency
ωe Frequency of encounter
ωn3 Natural frequency of heave motion
ωn5 Natural frequency of pitch motion
| Faltinsen OM, Minsaas KJ, Liapis N, Skjordal SO, 1980. Prediction of resistance and propulsion of a ship in a seaway. Proc. 13th Symposium on Naval Hydrodynamics, Tokyo, Japan, 505-529. |
| Fujii H, Takahashi T, 1975. Experimental study on the resistance increase of a ship in regular oblique waves. Proceedings of the 14th International Towing Tank Conference, Ottawa, Canada, 351-360. |
| Gerritsma J, 1960. Ship Motions in longitudinal waves. International Shipbuilding Progress, 7(66), 21–32. |
| Gerritsma J, Beukelman W, 1972. Analysis of the resistance increase in waves of a fast cargo ship. International Shipbuilding Progress, 19(217), 35–43. |
| Grin RA, 2012. On the prediction of wave added resistance. Proceedings of 11th International Marine Design Conference (IMDC), Glasgow, UK, 313-324. |
| International Maritime Organization (IMO), 2012a. MEPC.1/ Circ.796: Interim guidelines for the calculation of the coefficient fw for decrease of ship speed in representative sea condition for trial use. International Maritime Organization, London. |
| International Maritime Organization (IMO), 2012b. IMO MEPC.212(63): Guidelines on the method of calculation of the attained Energy. Efficiency Design Index (EEDI) for new ships. International Maritime Organization, London. |
| International Maritime Organization (IMO), 2013. MEPC.232 (65): Interim guidelines for determining minimum propulsion power to maintain the manoeuvrability in adverse conditions. International Maritime Organization, London. |
| International Maritime Organization (IMO), 2015. MEPC 68/WP.9: The amendments to the 2013 Interim Guidelines for determining minimum propulsion power to maintain the manoeuvrability of ships in adverse conditions, as amended. International Maritime Organization, London. |
| International Towing Tank Conference (ITTC), 2002. Recommended procedures, seakeeping experiments. 7.5-02-07-02.1, Effective Date 2002, Revision 01, Kongens Lyngby (Denmark). International Towing Tank Conference, Venice. |
| International Towing Tank Conference (ITTC), 2012. Recommended procedures and guidelines, speed and power trials, Part 2 Analysis of speed/power trial data. 7.5-04-01-01.2, Effective Date 2012, Revision 00, Kongens Lyngby (Denmark). International Towing Tank Conference, Copenhagen. |
| Jinkine V, Ferdinande V, 1974. A method for predicting the added resistance of fast cargo ships in head waves. International Shipbuilding Progress, 21(238), 149–167. |
| Kadomatsu K, 1988. Study on the required minimum output of main propulsion engine considering maneuverability in rough sea. PhD thesis, Ship Design Lab., Yokohama National University, Yokohama, Japan. |
| Kashiwagi M, 1992. Added resistance, wave-induced steady sway force and yaw moment on an advancing ship. Ship Technology Research (Schiffstechnik), 39(1), 3–16. |
| Kim KH, Kim Y, 2011. Numerical study on added resistance of ships by using a time-domain Rankine panel method. Ocean Engineering, 38(13), 1357–1367. DOI:10.1016/j.oceaneng.2011.04.008 |
| Kim Y, Seo MG, Park DM, Lee JH, Yang KK, 2014. Numerical and experimental analyses of added resistance in waves. Proceedings of 29th Intl Workshop on Water Waves and Floating Bodies, Osaka, Japan, 1–4. |
| Kuroda M, Tsujimoto M, Fujiwara T, 2008. Investigation on components of added resistance in short waves. Journal of Japan Society of Naval Archit and Ocean Eng, 8, 171–176. |
| Kwon YJ, 1981. The effect of weather, particularly short sea waves, on ship speed performance. PhD thesis, University of Newcastle upon Tyne, Newcastle. |
| Ley J, Sigmund S, El Moctar O, 2014. Numerical prediction of the added resistance of ships in waves. Proceedings of 33rd International Conference on Ocean, Offshore and Arctic Engineering, 2, San Francisco, OMAE2014-24216~24225. DOI: 10.1115/OMAE2014-24216 |
| Liu S, Papanikolaou A, 2016. Fast approach to the estimation of the added resistance of ships in head waves. Ocean Engineering, 112–225. DOI:10.1016/j.oceaneng.2015.12.022 |
| Liu S, Papanikolaou A, Zaraphonitis G, 2011. Prediction of added resistance of ships in waves. Ocean Engineering, 38(4), 641–650. DOI:10.1016/j.oceaneng.2010.12.007 |
| Liu S, Papanikolaou A, Zaraphonitis G, 2015. Practical approach to the added resistance of a ship in short waves. Proceedings of the 25th International Offshore and Polar Engineering Conference, 3, Kona, USA, 11-18. |
| Maruo H, 1960. The drift of a body floating on waves. Journal of Ship Research, 4(3), 1–10. |
| Naito S, Yamanoto O, Takahashi T, 1988. Effect of ship hull forms on resistance increase in waves. Proceedings of 5th Marine Dynamics Symposium, Tokyo, Japan, 45–79. |
| Newman JN, 1967. The drift force and moment on ships in waves. Journal of Ship Research, 11, 51–60. |
| Papanikolaou Α, Zaraphonitis G, 1987. On an improved method for the evaluation of second-order motions and loads on 3D floating bodies in waves. Journal Schiffstechnik-Ship Technology Research, 34, 170–211. |
| Papanikolaou A, Zaraphonitis G, Bitner-Gregersen E, Shigunov V, el Moctar O, Guedes Soares C, Reddy D, Sprenger F, 2015. Energy efficient safe ship operation. Proceeding of 2015 World Maritime Technology Conference (SNAME), Providence, USA, 22-35. |
| Pinkster JA, 1979. Mean and low frequency wave drifting forces on floating structures. Ocean Engineering, 6(6), 593–615. DOI:10.1016/0029-8018(79)90010-6 |
| Psaraftis HN, Kontovas CA, 2013. Speed models for energy- efficient maritime transportation: A taxonomy and Survey. Transportation Research Part C, 26, 331–351. DOI:10.1016/j.trc.2012.09.012 |
| Salvesen N, 1974. Second-order steady state forces and moments on surface ships in oblique regular waves. Int. Symp. on Dynamics of Marine Vehicles and Structures in Waves, London, 212–226. |
| SHOPERA Project, 2013-2016. Energy efficient safe ship operation. EU funded FP7 project, http://www.shopera.org |
| Smith WE, 1883. Hogging and sagging strains in a seaway as influenced by wave structure. Trans. Instit. Naval Architects, 24, 135–141. |
| Sprenger F, Maron A, Delefortrie G, Hochbaum A, Fathi D, 2015. Mid-term review of tank test results. SHOPERA Deliverable D3.2, National Technical University of Athens, Athens, Greece. |
| Söding H, Shigunov V, Schellin TE, el Moctar O, 2014. A rankine panel method for added resistance of ships in waves. Journal of Offshore Mechanics and Arctic Engineering, 136(3), 031601. DOI:10.1115/1.4026847 |
| Strøm-Tejsen J, Yeh HYH, Moran DD, 1973. Added resistance in waves. Transactions of the Society of Naval Architects and Marine Engineers, 81, 109–143. |
| Takahashi T, 1988. A practical prediction method for added resistance of a ship in waves and the direction of its application to hull form design. Trans West Jpn Soc Nav Archit, 75, 75–95. |
| Ursell F, 1947. The effect of a fixed vertical barrier on surface waves in deep water. Proceedings of the Cambridge Philosophical Society, 42, 374–382. |
| Valanto P, Hong Y, 2015. Experimental investigation on ship wave added resistance in regular head, oblique, beam, and following waves. Proceedings of the 25th International Offshore and Polar Engineering Conference, Kona, USA, 3, 19–26. |



