2. School of Ocean Science and Technology, Panjin Campus, Dalian University of Technology, Panjin 124221, China
1 Introduction
Ensuring the dynamic performance of offshore structures under ice action is important for structurally optimized designs and safety production. The structural width of a structure at the water line has always been assumed to be the most important parameter, because structural size significantly affects the ice failure mode and determines ice force and broken ice sizes. Ice load is determined by the ice failure process. Through studying the main features of the ice-cone action process, criteria can be determined for wide/narrow structures to verify related ice force conclusions, particularly the applicability of dynamic ice force characteristics within a time history.
In conventional classification methods, wide/narrow structures are mainly quantified according to structure size. However, due to different sea ice conditions, sea ice failure modes and ice force characteristics of same-sized structures are significantly different. Therefore, definitions of wide/narrow structures are relatively vague concepts, and a simple size-based definition cannot be used to guide structure design.
When the structural diameter at waterline varies within a certain range, sea ice failure modes-up against cones (wedge failure mode, plate failure mode, and semi-infinite long beam failure mode) also gradually change (Lau et al., 1999). When the structure size is further increased, there are substantial differences in sea ice failure in relation to ice pile-up against offshore structures. If the structure size is wide enough, a considerable amount of time is taken for the broken ice to slide away from two sides of the structure. However, when broken ice is not cleared in time, ice pile-up directly affects the ice-structure action process, thus changing the ice force application form and ice force. Whether broken ice can be cleared in time is closely related to the structural width at waterline, and mainly depends on size, quantity, clearing track, and clearing velocity of broken ice.
2 Clearing modes of broken ice against conesSea ice impact on a structure (ice load) is produced during the sea ice failure process. Extreme ice force can be interpreted by the internal microstructure changes of sea ice before the sea ice failure limit is met. The ice-cone action process can be used to interpret temporal and spatial features of the dynamic ice force of conical structures, and has been experimentally and theoretically described by many scholars (Frederking, 1980; Frederking and Timco, 1985; Nevel, 1992; Izumiyama et al., 1992; Wang and Xu, 1993; Dempsey et al., 1999; Shkhinek and Uvarova, 2001; Liferov and Bonnemaire, 2005; Paavilainen et al., 2011; Paavilainen and Tuhkuri, 2012, 2013). When ice sheets move toward a cone, subsequent ice sheets push the front ice sheet so that it climbs up the cone, where it circumferentially cracks andforms radial cracks in the vicinity of the cone, thereby leading to ice bending failure. Direct measurements of prototype structures indicate that the bending failure process of level ice-cone action differs significantlybetween the various clearing modes of broken ice against cones (complete clearing, temporary ice pile-up, and sloping ice pile-up mode of broken ice).
2.1 Clearing mode No. 1: Complete clearingThe bending failure process of level ice-cone action had been described according to direct measurements (Qu et al., 2006; Xu and Yue, 2009, 2010). According to existing research findings, the level ice-cone action process can be divided into three stages. In the first stage, ice sheets are bent and fractured; they move towards the cone under an external driving force and the ice sheet edge climbs up the cone. Circumferential cracks and radial cracks are formed in the vicinity of the cone and lead to ice bending failure. In the second stage, broken ice climbs up the cone; under the pushing force from subsequent ice sheets and the inertial effect, broken ice continues to climb up the cone. In the third stage, broken ice sheets slide away from two sides of the cone and are completely cleared before a subsequent ice sheet reaches the cone.
In this clearing mode, the pieces of broken ice are large but there is only a small quantity of it. The broken ice is basically cleared before the subsequent ice sheet reaches the cone, and the ice sheet-cone action process is not affected. The complete clearing mode was observed on JZ20-2MUQ Platform (Qu et al., 2006; Yue and Bi, 1998) (Fig. 1).

|
| Figure 1 Bending failure of ice sheet against on JZ20-2 MUQJacket Platform |
When the amount of broken ice is considerably less than the structure width, it cannot be cleared within several ice force periods, and it either climbs up the cone or is overturned by subsequent ice sheets, thereby forming an ice pile-up. However, the ice pile-up is usually cleared by limited ice force periods. When ice sheets are thin or the ice strength is low, the sea ice fractures easily, then slides down and enters the water, thereby moving away from the cone. Broken ice pile-up does not affect the action of subsequent ice sheets and the cone. Temporary ice pile-up was observed on JZ20-2NW Platform (Xu, 2011) (Fig. 2).

|
| Figure 2 Broken ice temporary pile-up on JZ20-2NWJacket Platform |
Ice pile-up against offshore structures refers torelatively small pieces of broken ice that gradually accumulate between the ice sheets and a structure. Ice sheets are continuously acted on by ice rubbles, until the accumulated broken ice reaches a certain size limit. When the angle of the ice jam slope is smaller than that of the cone angle, the subsequent ice sheet needs to pass through the entire ice jam before reaching the conical structure. However, the large quantity of ice jam hampers ice bending failure against the cone. The common consequence of ice pile-up is that subsequent ice sheets cannot reach the conical structure, but remain on the edge of ice jam, as shown in Fig. 3. A sloping ice jam is generally formed under conditions of overlapping ice, or in relation to a very wide structural size at the waterline, such as JZ9-3 Caisson shown in Fig. 3 (Dalian University of Technology, 2005).

|
| Figure 3 Broken ice pile-up on JZ9-3 Caisson |
According to the determination criteria of dynamic ice force and clearing modes of broken ice formed during ice-structure action, wide/narrow conical structures are respectively defined below.
A “narrow conical structure” refers to a structure where broken ice can be cleared in time to avoid an ice jam and where the subsequent ice sheet is not affected by the ice jam (Fig. 1). A “wide conical structure” refers to a structure where broken ice cannot be cleared in time, and where ice jam is continuously accumulated to form permanent ice jam (Fig. 3). A temporary ice jam is believed to occur with a strucutre that is between that of a “narrow conical structure” and a “wide conical structure” (Fig. 2).
According to the above definitions, the classification results of wide/narrow structures depend on the failure modes of level ice against the structure, as well as the ice-structure action process. Therefore, the type of wide/narrow structure, and whether broken ice can be completely removed from the front of a structure, significantly affect the ice force and ice-induced structural vibration.
For a narrow structure, the broken ice against the structure can be cleared within a short period of time and does not affect the sea ice failure mode and ice-structure action. Thus, continuous ice failure and alternating ice force occur and lead to significant ice-induced structural vibration. The failure processes of sea ice against different narrow structures are basically the same, and the forms of dynamic ice force are widely applicable.
For a wide structure, the broken ice against a structure cannot be cleared, and it forms a long-term ice jam. The subsequent complete ice sheet can then not be applied directly to the structure, and instead is applied to the ice jam. Subsequent ice sheets transfer the ice load to the structure through the ice jam. The alternating ice force that is only produced during sea ice failure is therefore not formed, and ice-induced structural vibration is insignificant.
According to observations of prototype conical structures, whether broken ice against the structures can be cleared within a short time depends on the features of the ice-structure action surface (friction coefficient and cone angle) and the size and quantity of broken ice. If the pieces of broken ice are large in size but there is a small quantity of it, the broken ice against the structure can be easily cleared under the driving force of the subsequent ice sheet. However, if the broken ice consists of small pieces and there is a large quantity of it, it is not possible to clear the broken ice against the structure within a short time and an ice jam is formed. In addition, for the same structure, ice failure modes and clearing modes of broken ice vary with ice conditions. Therefore, a structure under variant ice conditions may be converted from a wide structure to a narrow structure, indicating that alternating ice force or ice jam (which eliminates alternating ice force) can be observed on the same structure (as studiedexperimentally by Timco, 1984).
To verify criteria determining dynamic ice force and definitions of wide/narrow conical structures, ice failure modes and ice clearing processes when acting on field structures were analyzed.
4 Verification using measurement data of prototype structures 4.1 Formation conditions of dynamic ice force and ice-induced vibration on conical structuresAs mentioned above, dynamic ice force is formed only when a complete ice sheet directly impacts a structure to form periodic ice failure. In this regard, broken ice is not accumulated against a structure and the ice-structure action process is not affected. Therefore, the similarity between sea ice failure and the clearing modes of broken ice against a structure lead to similarities in ice force forms. The formation conditions of dynamic ice force can then be determined according to the clearing modes of broken ice against a structure.
If broken ice against a structure can be cleared within a short period of time, the subsequent ice sheet could directly action on ice breaking cone, and clearing modes of broken ice against the structure are not affected. Thus continuous ice failure and alternating ice force occur and lead to significant ice-induced structural vibration. However, if broken ice against a structure cannot be cleared and it forms a long-term ice jam, the subsequent complete ice sheet cannot be directly applied to the structure, and is instead applied to the ice jam; thus the subsequent ice sheet transfers its ice load to the structure through the ice jam. The dynamic features of ice force applied on a structure are not significant, and alternating ice force, which is only produced during sea ice failure, is not formed.
Through the comparison of the ice-induced vibration response before and after ice jam observed on platforms with cones, we verified the relationships between the formation conditions of dynamic ice force and the clearing modes of broken ice against the structures. When dense watertight casings were installed between the legs of narrow jacket structures in the Bohai Sea, ice jam was observed (JZ20-2MUQ Platform). Figs. 4 and 5 show the ice-structure action and ice-induced structural vibration within 3 min prior to, and after, a broken ice jam. In order to provide intuitive vibration comparison results, the same length of 75 s of data was adopted. In the first 100 s, the ice sheet directly impacted the conical structure. The size of the broken ice was relatively large and could be cleared from both sides of the conical structures within a short period of time. However, broken sea ice was completely cleared from the legs with cones. Periodic failure of the sea ice against conical structures produced a significant periodic impact load, and therefore an alternating ice force. The ice-induced vibration signal of the platform deck indicated that the alternating displacement had reached 2 mm. After the first 100 s, broken ice was hampered by the watertight casings between two legs, and formed an ice jam crossing two legs (with a spacing of 10 m) at a small slope angle and over a large area. Subsequent sea ice was then continuously applied onto the ice jam. Although ice conditions were unchanged, the alternating displacement caused by the ice-induced structural vibration was 0.4 mm, and it subsequently decreased. In accordance with the above conclusions, Xu and Yue (2010) indicated that sloping ice pile-up against conical structures would not induce dynamic ice force.
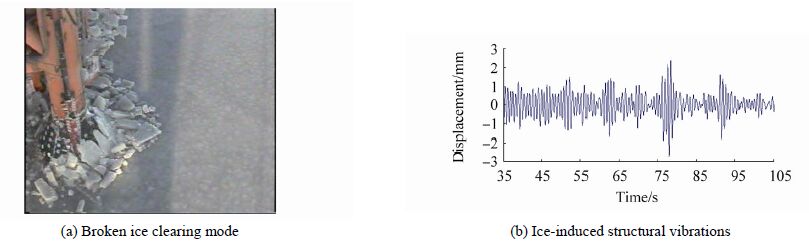
|
| Figure 4 Broken ice clearing mode and ice-induced structural vibration responses before occurrence of sloping ice pile-up |

|
| Figure 5 Broken ice clearing mode and ice-induced structural vibration responses after occurrence of sloping ice pile-up |
According to ice failure modes of a broken ice jam on practical typical conical platforms, we analyzed and verified criteria determining wide/narrow structures with the aim of providing quantitative conclusions.
| Platforms | Cone waterlinediameter/m | The angle between slope andhorizontal surface/ (°) | Maximum level ice thickness/m | Maximum ice velocity/ (m·s−1) | Events of pure bending failure and complete clearing mode | Broken ice pile-up |
| Kemi-I Lighthouse | 10 | 56 | 0.6-0.9 | 0.5 | sometimes | often |
| Confederation Bridge Pier | 14 | 52 | 0.8 | 0.2 (mean) | sometimes | often |
| JZ9-3 Cassion | 30-40 | 58 | 0.45 | 1.2 | n/a | often |
| JZ20-2 Jacket | 2-6 | 60 | 0.3 | 1.2 | often | sometimes |
According to the above definitions of wide/narrow conical structures, combined with data of practical ice-connection processes and broken ice clearing records, it is evident that ice jams can often be observed on structures of a wide size, while ice jams or sea ice clearing phenomenon can sometimes be observed on conical structures of a medium size. Therefore, different sea ice clearing modes can be observed on the same structures under varying sea ice conditions, indicating that a structure can be converted from a wide structure to a narrow structure. According to the direct measurements of Kemi I Lighthouse (Määttänen et al., 1977, 1996; Määttänen, 1990; Brown and Määttänen, 2009), Confederation Bridge Pier (Mayne and Brown, 2000a, 2000b; Brown, 2001; Brown and Määttänen, 2009), JZ9-3 Cassion and JZ20-2 jackets (Yue and Bi, 1998; Qu et al., 2006), we preliminarily summarize sea ice conditions during complete clearing events of broken ice and ice jam events for level ice sheets against various structures, and attempt to provide unified quantitative determination criteria of wide/narrow cones, as shown in Table 1.
Thin ice sheets against structures with a relatively small size are fractured to form small pieces of broken ice. Broken ice remains infront of the cones for a certain period of time and then forms an ice jam before the broken ice is completely cleared. This phenomenon can be observed on jackets with cones. However, if the ice sheet is thick in front of large structures, the fractured ice sheet will also be large and it can be cleared within a short period of time; therefore the action between subsequent ice and the structure is not affected. For example, the significant ice-induced vibration on Confederation Bridge Pier can be interpreted as follows. A dynamic ice force is produced under the complete clearing mode of broken ice, leading to structural vibration.
The size of the broken ice is determined by the ratio of the structure width to the ice thickness. Therefore, the ratio can be considered as the key indicator for quantitative determination criteria of wide/narrow conical structures. If the ratio is below 30, the structure is defined as a narrow conical structure; if above 50 it is defined as a wide conical structure; and if between 30 and 50 the structure should be determined according to the actual size of the broken ice, as shown in Fig. 6.
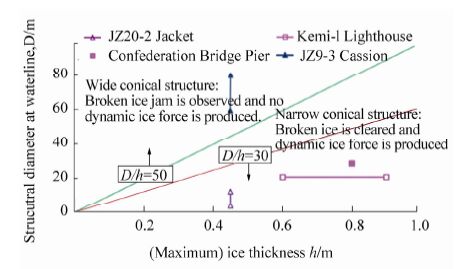
|
| Figure 6 Verification of definition of narrow and wide cones using conical structure parameters and sea ice conditions |
Therefore, in addition to maximum ice force it is necessary to consider ice-induced structural vibration under conditions of thick ice. However, under thin level ice conditions, a large quantity of small pieces of broken ice forms an ice jam and induces additional ice force; therefore it is necessary to consider extreme values of the ice force.
5 ConclusionsIn this paper, definitions of wide and narrow conical structures are proposed. Broken ice against a narrow conical structure can be completely cleared within a short time period and the ice-structure action process and formation of alternating ice force is not be affected. Therefore, the common ice force calculation method and alternating ice force time history are applicable for narrow conical structures. However, broken ice against a wide conical structure forms a continuous ice jam, which hampers the action between the subsequent ice sheet and the structure, thereby producing no significant dynamic ice force or ice-induced structural vibration. According to previously reported direct measurements on prototype conical structures, we provide statistics of ice failures and dynamic ice force events for different structures under different ice conditions. Moreover, we attempt to provide quantitative determination criteria for wide/narrow conical structures according to the ratio of structure width to ice thickness.
| Brown TG, 2001. Four years of ice force observations on the Confederation Bridge. Proceedings of 14th International Conference on Port and Ocean Engineering under Arctic Conditions, Ottawa, 285–299. |
| Brown TG, Määttänen M, 2009. Comparison of Kemi-I and Confederation Bridge cone ice load measurement results. Cold Regions Science and Technology, 55(1), 3–13. DOI:10.1016/j.coldregions.2008.04.005 |
| Dalian University of Technology, 2005. Report on sea ice management. Dalian: Dalian University of Technology2004-2005. |
| Dempsey JP, Fox C, Palmer AC, 1999. Ice-slope interaction: transitions in failure mode. Proceedings of Offshore Mechanics and Arctic Engineering Conference, St. John's, Canada, 225–230. |
| Frederking R, 1980. Dynamic Ice force on an inclined structure. Proceedings of IUTAM Symposium on the Physics and Mechanics of Ice, Copenhagen, 104–116. |
| Frederking R, Timco G, 1985. Quantitative analysis of ice sheet failure against an inclined plane. Journal of Energy Resources Technology, 107(3), 160–169. DOI:10.1115/1.3231205 |
| Izumiyama K, Kitagawa H, Koyama K, Uto S, 1992. A numerical simulation of ice-cone interaction. Proceedings of IAHR Ice Symposium, Banff, 188–199. |
| Lau M, Molgaarad J, Williams FM, A sj, S, 1999. An analysis of ice breaking pattern and ice piece size around sloping structures. Proceedings of 18th International Conference on Offshore Mechanics and Arctic Engineering, St. John's, Canada, 199–207. |
| Liferov P, Bonnemaire B, 2005. Ice rubble behavior and strength: Part I. Review of testing and interpretation of results. Cold Regions Science and Technology, 41(2), 135–151. DOI:10.1016/j.coldregions.2004.10.001 |
| Määttänen M, 1990. The effect of ice pile-up on the ice force of a conical structure. Proceedings of 16th IAHR Ice Symposium, Espoo, 1010–1021. |
| Määttänen M, Hoikkanen AN, Avis J, 1996. Ice failure and ice loads on a conical structure KEMI-I cone full scale ice force measurement data analysis. Proceedings of 19th IAHR Ice Symposium, Beijing, 8–16. |
| Määttänen M, Reddy D, Arockiasamy M, Cheema PS, 1977. Ice-structure interaction studied on a lighthouse in the Gulf of Bothnia using response spectrum and power spectral density function analyses. Proceedings of 4th International Conference on Port and Ocean Engineering under Arctic Conditions. St. John's, Canada, 321–334. |
| Mayne DC, Brown TG, 2000a. Comparison of flexural failure ice-force models. Proceedings of 19th International Conference on Offshore Mechanics and Arctic Engineering, New Orleans, 1269–1276. |
| Mayne DC, Brown TG, 2000b. Rubble pile observations. Proceedings of 10th International Offshore and Polar Engineering Conference, Seattle, 596–599. |
| Nevel DE, 1992. Ice forces on cones from floes. Proceedings of 11th IAHR Ice symposium, Banff, 1391–1404. |
| Paavilainen J, Tuhkuri J, 2012. Parameter effects on simulated ice rubbling forces on a wide sloping structure. Cold Regions Science and Technology, 81(5), 1–10. DOI:10.1016/j.coldregions.2012.04.005 |
| Paavilainen J, Tuhkuri J, 2013. Pressure distributions and force chains during simulated ice rubbling against sloped structures. Cold Regions Science and Technology, 85(1), 157–174. DOI:10.1016/j.coldregions.2012.09.005 |
| Paavilainen J, Tuhkuri J, Polojärvi A, 2011. 2D numerical simulations of ice rubble formation process against an inclined structure. Cold Regions Science and Technology, 68(1-2), 20–34. DOI:10.1016/j.coldregions.2011.05.003 |
| Qu Y, Yue QJ, Bi XJ, Karna T, 2006. A random ice force model for narrow conical structures. Cold Regions Science and Technology, 45(3), 148–157. DOI:10.1016/j.coldregions.2006.05.008 |
| Shkhinek K, Uvarova E, 2001. Dynamics of the ice sheet interaction with the sloping structure. Proceedings 16th International Conference on Port and Ocean Engineering under Arctic Conditions, Ottawa, 639–648. |
| Timco G, 1984. Model tests of ice forces on a wide inclined structure. Proceedings of IAHR Ice Symposium, Hamburg, 87–96. |
| Timco G, Johnston M, 2004. Ice loads on the caisson structures in the Canadian Beaufort Sea. Cold Regions Science and Technology, 38(2-3), 185–209. DOI:10.1016/j.coldregions.2003.10.007 |
| Wang LY, Xu JZ, 1993. Calculation of ice force acting upon a wide cone structure. Engineering Mechanics, 10(3), 71–80. |
| Xu N, 2011. Research on ice force of conical offshore structures. Dalian: PhD thesis, Dalian University of Technology93-95. |
| Xu N, Yue QJ, 2009. The developing process and risk analysis of ice jams based on field test. Proceedings of the 20th International Conference on Port and Ocean Engineering Under Arctic Conditions, Lulea, Sweden, POAC09-49. |
| Xu N, Yue QJ, 2010. Dynamic ice forces analysis of conical structure based on direct measurement. Proceedings of the 29th International Conference on Ocean, Offshore and Arctic Engineering, Shanghai, 771–776. |
| Yue QJ, Bi XJ, 1998. Full-scale test and analysis of dynamic interaction between ice sheet and conical structure. Proceedings of 14th International Association for Hydraulic Research (IAHR) Symposium on Ice, Potsdam, 939–945. |



