Fundamentally,a Tension-Leg Platform(TLP)comprises four circular cylinders interconnected by pontoons. These platforms are commonly configured in a square and are rarely triangular. The TLP hull is like a semisubmersible platform. Some advantages of TLPs include their small vertical motion,high stability,and low rate of cost increase with increasing depth in comparison to other platform types,as well as their deep-sea production capabilities. Disadvantages of the TLP include their high costs associated with the subsea foundation installation,sensitivity of the tethers to fatigue damage,difficulty in repairing and maintaining the tether connections,and low-capacity storage tanks.
Downie et al.(2000) carried out an experimental study on a model truss spar in regular and irregular waves for four different heave plates(two perforated and two solid). In terms of the Response Amplitude Operators(RAOs),the spar similarly behaved with respect to surge and pitch in regular waves. However,there were significant differences in the heave response. Bhattacharyya et al.(2003) developed a numerical model(finite element code)for a typical Sea Star platform at two water depths,215 m and 1 000 m,and carried out experimental work on a scaled model corresponding to the 215 m water depth to validate the numerical model. The authors computed the RAOs for the motions and tether tensions for both prototypes using the Morison wave force model with a wave height of 2 m. Zhang et al.(2007) introduced a new spar concept and used numerical simulation to study its hydrodynamics in both operating and survival conditions. In addition,the authors investigated numerical and experimental RAO results on mooring lines for the surge,heave,and pitch. The predicted RAOs were in excellent agreement with test measurements. Zeng et al.(2007) investigated(6-DOF)coupled motions,the time history of the motions and wetted area,and the free surface and viscous drag effects. To extract the horizontal-plane-motion RAOs,the authors dynamically analyzed the International Ship Structures Committee(ISSC)TLP at a depth of 415 m in regular seas. Joseph et al.(2010) developed a new geometric configuration as a better alternative to existing configurations. The authors also designed a three-column mini TLP and investigated the added mass,radiation damping,transfer functions of wave force,and RAOs of motions for the three-column mini TLP in comparison to the existing four-column mini TLP. Tajali and Shafieefar(2011) carried out a hydrodynamic analysis of a floating multi-body pier interacting with incident waves and presented wave-induced motion and structural response results. They also examined the effect of relevant parameters on the pier hydrodynamic responses and computed the RAO for a wide range of wave frequencies and heading angles. Nallayarasu and Prasad(2012) conducted an experimental and numerical investigation on the hydrodynamic response of a spar and semi-submersible interlinked by a rigid yoke under regular waves. Tabeshpour et al.(2006 ,2013 )carried out a hydrodynamic analysis of the damped pitch and heave motion of TLPs and presented exact solutions for the vibration of a TLP interacting with ocean waves. Wu et al.(2014) investigated the influence of the legs underwater on the hydrodynamic response of the multi-leg floating structure. The authors also numerically simulated the hydrodynamic responses of the structure in different scenarios by applying the three-dimensional potential theory. The hydrodynamic coefficients,wave excitation loads,and RAOs of the 6-DOF at different wave frequencies were also calculated and compared. Nallayarasu et al.(2014) studied the effect of hull geometry on the hydrodynamic response of the spar in regular waves. Das and Baghfalaki(2015) determined the characteristics of the RAO or transfer function of a floating body in the frequency domain for coupled sway,roll,and yaw motions in sinusoidal waves. Abaiee et al.(2015) presented an analytical discussion on the stochastic hydrodynamic modeling of the support structure of the HAWAII WTG offshore wind turbine. They concluded that a simplified hydrodynamic analysis could help researchers to develop a better physical understanding of the hydrodynamics of floating structures and a simpler and quick closed-form analysis would be helpful in solving complicated offshore engineering problems.
In this study,we investigated the portion of the pitch motion in the vertical response of the sides of the TLP in the frequency(RAO)and time domains.
2 Governing equationsWe used the boundary element method as a basis for deriving the dynamic equations of the TLP,as described in the following:
2.1 Diffraction,Froude-Krylov,and radiation wave forcesThis section addresses the hydrodynamic fluid loading of the diffracting bodies in regular waves. The fluid is assumed to be ideal and non-rotational,which allows the use of the potential theory. Velocity potential is defined as follows:
| $$\phi (x,y,z,t) = \phi (x,y,z){{\rm{e}}^{ - {\rm{i}}\omega t}}$$ | (1) |
where $\phi $ is a complex potential function and is separated into radiation waves due to the six modes of body motion and the incident and diffracted waves,and ω is the frequency of the incident wave. To obtain $\phi $,we considered two body problems. The first is related to the floating body undergoing harmonic oscillation in still water. The body motions cause the creation of a radiation force,which is a function of the added mass and wave damping coefficients. The second problem relates to the fixed body being subjected to regular waves. The Froude-Krylov and diffraction forces are components of the wave forces acting on the fixed body. Therefore,the total potential is written as:
| $$\phi (x,y,z,t){{\rm{e}}^{ - {\rm{i}}\omega t}} = [({\phi _I} + {\phi _d}) + \sum\limits_{j = 1}^6 {{\phi _j}{x_j}]} {\rm{ }}{{\rm{e}}^{ - {\rm{i}}\omega t}}$$ | (2) |
where ${\phi _I}$,${\phi _d}$,${\phi _j}$,and xj are the incident wave potential,diffracted wave potential,radiation potential due to the jth motion,and the jth motion(per unit wave amplitude),respectively. We obtained the potential functions for incompressible,non-viscous,and irreversible flows by solving the Laplace equation,as follows:
| $${\nabla ^2}\phi = 0\,\,\,\,\,\,\,\,\,{\rm{or}}\,\,\,\,\,\,\,\,\,\,\,\frac{{{\partial ^2}\phi }}{{\partial {x^2}}} + \frac{{{\partial ^2}\phi }}{{\partial {y^2}}} + \frac{{{\partial ^2}\phi }}{{\partial {z^2}}} = 0$$ | (3) |
Concurrent with the solution of the Laplace equation,certain boundary conditions must be satisfied,as follows:
Free surface boundary condition:
| $$\,{\tau _\omega } = g\frac{{\partial \phi }}{{\partial z}} - {\omega ^2}\phi = 0$$ | (4) |
Bottom boundary condition:
| $$u = \frac{{\partial \phi }}{{\partial z}} = 0\,{\rm{ }}\,{\mathop{\rm in}\nolimits} {\rm{ }}\,\,z = - h$$ | (5) |
Kinematic boundary condition:
| $$\frac{{\partial \phi }}{{\partial n}} = v \cdot n$$ | (6) |
where v is velocity vector and n is surface normal vector.
Far-field boundary condition:
| $$\,\left| {\nabla \phi } \right| \to 0\,\,\,\,\,\,\,{\rm{when}}\,\,{\rm{ }}r \to - \infty $$ | (7) |
where $r = \sqrt {{x^2} + {y^2} + {z^2}} $,$\,{\tau _\omega }$ is the shear stress of a fluid and g is the acceleration of gravity. When the potential functions are known,we can calculate the first-order hydrodynamic pressure distribution using the linearized Bernoulli equation:
| $$p = - \rho \frac{{\partial \phi }}{{\partial t}}$$ | (8) |
We calculate the fluid forces by integrating the pressure over the wetted surface of the body as follows:
| $${F_{{w_j}}} = \, - \int\limits_s {{\rm{i}}\omega \rho ({\phi _I} + {\phi _d}){n_j}{\rm{d}}s} $$ | (9) |
where Fwj is the wave force in jth direction,nj is the generalized surface normal for the jth direction,and S is the wetted surface of the body at equilibrium. The Froude-Krylov and diffraction forces are as follows:
| $${F_{{d_j}}} = - \int\limits_s {{\rm{i}}\omega \rho ({\phi _D}){n_j}{\rm{d}}s} $$ | (10) |
| $${F_{{I_j}}} = - \int\limits_s {{\rm{i}}\omega \rho ({\phi _I}){n_j}{\rm{d}}s} $$ | (11) |
where Fdj and Fij are the diffraction and Froude-Krylov force,respectively. The radiation forces acting on the body due to the body motions are as follows:
| $${F_{{r_{jk}}}} = - \int\limits_s {{\rm{i}}\omega \rho ({\phi _k}){n_j}{\rm{d}}s} = - A{}_{jk}{\ddot x_k} - B{}_{jk}{\dot x_k}$$ | (12) |
where Frjk is the radiated force in the jth direction due to the kth motion. A is the added mass coefficient and B is the damping coefficient:
| $${A_{jk}} = \frac{\rho }{\omega }\int\limits_s {{{({\phi _k})}^{{\mathop{\rm Im}\nolimits} }}{n_j}{\rm{d}}s} $$ | (13) |
| $${C_{jk}} = \rho \int\limits_s {{{({\phi _k})}^{{\mathop{\rm Re}\nolimits} }}{n_j}{\rm{d}}s} $$ | (14) |
Dynamic equations of the heave and pitch of the TLP are expressed as follows:
| $$(M + {A_{33}})\ddot z + {C_{33}}\,\dot z + {K_{33}}z = {F_3}$$ | (15) |
| $$({I_{55}} + {A_{55}})\ddot \theta + {C_{55}}\dot \theta + {K_{55}}\theta = {M_5}$$ | (16) |
where z and θ are the TLP’s heave and pitch degrees of freedom. M is the platform mass,A33 and A55 are the added mass in the heave and pitch directions,respectively; C33 and C55 are the platform stiffness in the heave and pitch directions,respectively; K33 and K55 are the platform stiffness in the heave and pitch directions,respectively,due to the hydrostatic stiffness and coupling of the tendons of the TLP; F3 is the wave force in the vertical direction; and M5 is the pitch moment due to the wave force.
2.3 Frequency domainThe RAO is ratio of the response amplitude to the wave amplitude,as plotted for linear systems,versus the wave frequency or wave period,as follows:
| $${\rm{RAO}} = \frac{{{\delta _j}}}{{{\zeta _a}}}$$ | (17) |
where ${\delta _j}$ and ${\zeta _a}$ are the response and wave amplitude,respectively.
3 Portion of pitch motion in vertical response at sides of TLPThe TLP is a rigid body that is connected to the seabed by vertical tendons(springs). Pitch motion creates vertical motions at the sides of the TLP. Fig. 1 illustrates the position of three points along the TLP as a rigid bar. Point C is in the middle of the bar and θ is the pitch rotation.
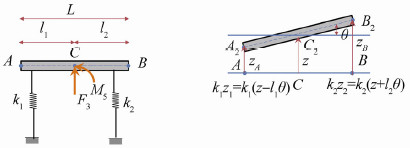
|
| Fig. 1 Schematic of the rigid body motion(pitch at point C and vertical at points A and B) |
The equations of motion for such a two-degrees-of-freedom system are as follows:
| $$m\mathop z\limits^{..} = {F_3} - {k_1}(z - {l_1}\theta ) - {k_2}(z + {l_2}\theta )$$ | (18) |
| $${j_0}\mathop \theta \limits^{..} = {M_5} + {k_1}(z - {l_1}\theta ){l_1} - {k_2}(z + {l_2}\theta ){l_2}$$ | (19) |
where m is the mass of the rigid bar,j0 is the moment inertia of the pitch motion,k1 and k2 are the stiffness of the tendons that are the same here,and l1 and l2 are equal to $\frac{L}{2}$. Eqs.(18)and(19)can be written in matrix form,as follows:
| $$\,\left[ {\begin{array}{*{20}{c}} m&0\\ 0&{{j_0}} \end{array}} \right]\left[ \begin{array}{l} {\ddot z}\\ {\ddot \theta } \end{array} \right] + \,\left[ {\begin{array}{*{20}{c}} {{k_1} + {k_2}}&{ - ({k_1}{l_1} - {k_2}{l_2})}\\ { - ({k_1}{l_1} - {k_2}{l_2})}&{{k_1}{l^2}_1 + {k_2}{l^2}_1} \end{array}} \right]\left[ \begin{array}{l} z\\ \theta \end{array} \right]{\rm{ = }}\left[ \begin{array}{l} {F_3}\\ {M_5} \end{array} \right]$$ | (20) |
where z and $\theta $ are coupled. Coupling can be removed if the term $({k_1}{l_1} - {k_2}{l_2})$ is zero. Also,in this study,${k_1}{l_1} = {k_2}{l_2}$,therefore the heave and pitch motions at the center of the TLP are not coupled.
In the time domain,the vertical motion at points A and B are as follows:
| $${z_A}(t) = {z_C}(t) - \frac{L}{2}{\theta _C}(t)$$ | (21) |
| $${z_B}(t) = {z_C}(t) + \frac{L}{2}{\theta _C}(t)$$ | (22) |
where zA(t) is the time history of the vertical response at point A,zB(t) the time history of the vertical response at point B,zC(t) the time history of the heave response at the center of the TLP,and ${\theta _C}(t)$ the time history of the pitch response at the center of the TLP. Therefore,having the time history of the heave and pitch motions at the center of the TLP,we can obtain the time history of the vertical motion on the side.
In the frequency domain,we obtain the RAOs of the sides as follows:
| $${A_{{\rm{Heav}}{{\rm{e}}_{(A,B)}}}}(\omega ) = {A_{{\rm{Heav}}{{\rm{e}}_{(C)}}}}(\omega ) + \frac{L}{2}{A_{{{({\rm{Pitch}})}_{(C)}}}}(\omega )$$ | (23) |
| $${A_{{\rm{Heav}}{{\rm{e}}_{(A,B)}}}}(\omega ) = {\zeta _a}{\rm{RA}}{{\rm{O}}_{{{({\rm{Heave}})}_{(C)}}}}(\omega ) + \frac{L}{2}{\zeta _a}{\rm{RA}}{{\rm{O}}_{{{(Pitch)}_{(C)}}}}(\omega )$$ | (24) |
| $$\frac{{{A_{{\rm{Heav}}{{\rm{e}}_{(A,B)}}}}(\omega )}}{{{\zeta _a}}} = {\rm{RA}}{{\rm{O}}_{{{({\rm{Heave}})}_{(C)}}}}(\omega ) + \frac{L}{2}{\rm{RA}}{{\rm{O}}_{{{(Pitch)}_{(C)}}}}(\omega )$$ | (25) |
| $${\rm{RA}}{{\rm{O}}_{{{({\rm{Heave}})}_{(A,B)}}}}(\omega ) = {\rm{RA}}{{\rm{O}}_{{{({\rm{Heave}})}_{(C)}}}}(\omega ) + \frac{L}{2}{\rm{RA}}{{\rm{O}}_{{{(Pitch)}_{(C)}}}}(\omega )$$ | (26) |
where $\omega $ is the wave frequency,${A_{{\rm{Heav}}{{\rm{e}}_{(A,B)}}}}(\omega )$ is the amplitude of the vertical response at the sides,${A_{{\rm{Heav}}{{\rm{e}}_{(C)}}}}(\omega )$ is the amplitude of the heave response at the center,${A_{{{({\rm{Pitch}})}_{(C)}}}}$ is the amplitude of the pitch response at the center,${\rm{RA}}{{\rm{O}}_{{{({\rm{Heave}})}_{(A,B)}}}}(\omega )$ is the RAO of the vertical response at the sides,${\rm{RA}}{{\rm{O}}_{{{({\rm{Heave}})}_{(C)}}}}(\omega )$ is the RAO of the heave response at the center,and ${\rm{RA}}{{\rm{O}}_{{{(Pitch)}_{(C)}}}}(\omega )$ is the RAO of the pitch response at the center. Since the RAO is the ratio of the response amplitude to the wave amplitude,the RAO of points A and B are equal.
To compare the RAO of the vertical response at points of B and A,we use the following equation:
| $$R = \frac{{{\rm{RA}}{{\rm{O}}_{{{({\rm{Heave}})}_{(A,B)}}}}}}{{{\rm{RA}}{{\rm{O}}_{{{({\rm{Heave}})}_{(C)}}}}}}$$ | (27) |
The research platform is the ISSC TLP and its specifications are given in Table 1 ,Zeng et al.(2007) .
| Draft/m | 35 |
| Displacement/kg | 54.5×106 |
| Mass/kg | 40.5×106 |
| Roll motion moment of inertia/(kg·m2) | 82.37×109 |
| Pitch motion moment of inertia/(kg·m2) | 82.37×109 |
| Yaw motion moment of inertia/(kg·m2) | 98.07×109 |
| Center of gravity height/m | 38 |
| External radius of tendon/m | 0.3 |
| Internal radius of tendon/m | 0.212 |
| Length of tendon | 195 |
| Pre-tension in tendon/N | 1.44 5×107 |
| Young’s modulus of tendon/(N·m−2) | 2.1×1011 |
| Axial stiffness of tendon/(N·m−1) | 1.5×108 |
| Number of tendons under leg | 3 |
In this section,we illustrate the results of the frequency and time domains. Figs. 2(a) and 2(b) show the RAO of the heave response at point C and the RAO of the pitch response at point C. In Figs. 2(a) and 2(b) ,we can see that the RAO curves of the heave and pitch motions have humps and hollows. At the 6 s wave period,the RAO of the heave is a hollow,and the RAO of the pitch is a hump; at the 7 s wave period the RAO of the heave and pitch motions are both humps; and at the 8 s wave period,the RAOs are both hollow. Figs. 3(a) and 3(b) present the RAO of the vertical response at points A and B that are due only to the portion of the pitch motion and the total RAO of the vertical response at points A and B,respectively.

|
| Fig. 2 RAO of heave and pitch motions at point C |
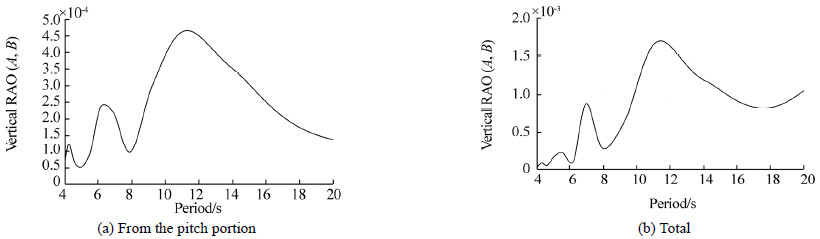
|
| Fig. 3 RAO of vertical motion at points A and B |
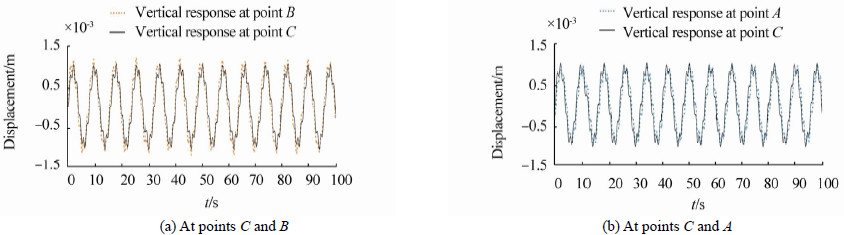
Figs. 4(a) and 4(b) show the vertical responses at points C and A,and the vertical responses at points C and B for the wave(T=6 s and H=4 m),respectively. Fig. 5(a) illustrates the Fast Fourier Transform(FFT)of the vertical response at points A and C. Fig. 5(b) shows the FFTs of the vertical response at points B and C for the wave(T=6 s and H=4 m). From Fig. 4(a) ,we can see that the vertical response at point B is greater than at point C,but in Fig. 4(b) ,the vertical response at point A is less than at point C at certain times. Therefore,the vertical response at the sides of the TLP differ from those at the center.

|
| Fig. 4 Vertical response(T=6 s and H=4 m) |
By comparing Figs. 2 and 4(a) ,it is clear that at the 6 s wave period,the RAO of the heave is a hollow and the RAO of the pitch is a hump. Therefore the pitch response is dominant and the total vertical response at point B is significantly larger than the heave response at point C.
Figs. 4(a) and 4(b) show the vertical responses at points C and A,and the vertical responses at points C and B for the wave(T=6 s and H=4 m),respectively. Fig. 5(a) illustrates the Fast Fourier Transform(FFT)of the vertical response at points A and C. Fig. 5(b) shows the FFTs of the vertical response at points B and C for the wave(T=6 s and H=4 m). From Fig. 4(a) ,we can see that the vertical response at point B is greater than at point C,but in Fig. 4(b) ,the vertical response at point A is less than at point C at certain times. Therefore,the vertical response at the sides of the TLP differ from those at the center.

|
| Fig. 5 FFT of vertical response(T=6 s and H=4 m) |
By comparing Figs. 2 and 4(a) ,it is clear that at the 6 s wave period,the RAO of the heave is a hollow and the RAO of the pitch is a hump. Therefore the pitch response is dominant and the total vertical response at point B is significantly larger than the heave response at point C.
From Fig. 5(a) ,it is clear that the Fourier amplitude of the vertical response at points B and A is greater than at point C in the wave period,because the pitch response is dominant in this period. Also from Figs. 5(a) and 5(b) ,it is clear that at the natural period of the heave,the FFT of the vertical response at points A,B,and C are equal. According to Eqs.(21)and(22),the time histories of the vertical response at points A and B are a combination of the time history of the heave and pitch responses at point C,and both of them have two periods(wave period and natural period). Therefore,the time history of the vertical response at points A and B in the wave period are equal to the combined heave response at point C and the portion of the pitch response in the vertical response. However,in the natural period of the heave time history of the vertical response at points A and B,they are equal to the heave response at point C. Also,the Fourier amplitude of the vertical response at points A and B has three peaks(heave period,pitch period,and wave period)but point C has just two peaks(heave period and wave period).
Figs. 6(a) and 6(b) show the vertical responses at points C and A,and the vertical responses at points C and B for the wave(T=7 s and H=6 m)),respectively. Fig. 7(a) shows the FFT of the vertical response at points of A and C. Fig. 7(b) shows the FFTs of the vertical response at points of B and C for the wave(T=7 s and H=6 m).

|
| Fig. 6 Vertical response(T=7 s and H=6 m) |

|
| Fig. 7 FFT of the vertical response(T=7 s and H=6 m) |
|
| Fig. 8 Vertical response for the wave(T=8 s and H=8 m) |

|
| Fig. 9 FFTs of vertical response for the wave(T=8 s and H=8 m) |
From Figs. 7(a) and 7(b) ,we can see that the FFT of the vertical response has no peak at the natural period of the pitch,because the vertical response is significantly larger than the pitch response. Figs. 8(a) and 8(b) show the vertical response at points C and A and at points C and B for the wave(T=8 s and H=8 m),respectively. Fig. 9(a) shows the FFT of the vertical response at points A and C. Fig. 9(b) shows the FFTs of the vertical response at points of B and C for the wave(T=8 s and H=8 m).
Fig. 10 shows the ratio of the RAOs of the vertical response at points A and B to the RAO of the vertical motion at point C. From Fig. 10 ,it is clear that in low wave periods(high frequency),the ratio of the RAO of the vertical response at points A and B to the RAO of the heave(point C) is greater than 1. For example,at the 6 s wave period this ratio is equal to 5(pitch dominant region). This means that if the combined pitch and heave responses are not considered,there will not be an accurate reflection of the strain on the tendons. From Fig. 2 ,we can see that the RAO curve has humps and hollows in different wave periods. At the 6 s wave period,in the RAO of the heave motion at point C,a hollow occurs,and in the RAO of a pitch motion a hump occurs. Therefore,in this period,the vertical RAO at the sides is significant,as shown in Fig. 10 . From Figs. 2(a) and 2(b) ,it is clear that at the 12-sec wave period,a hump occurs in the RAOs of the heave and pitch motions. Also,because the pitch motion is less than the heave motion,the vertical motion at the sides is approximately equal to that at the center of the TLP(see Fig. 10 ). And from Figs. 2(a) and 2(b) ,at the 7 s wave period,the RAO of the heave and pitch motions are at maximum,but the order of magnitude of the vertical response,rather than pitch response,is dominant; therefore the vertical response at the center and sides of the TLP are the same.

|
| Fig. 10 Ratio of vertical response at points A and B to point C |
Fig. 11 compares the RAOs of the vertical motion at points A and B(total and portion of pitch). From Fig. 11 ,we see that the portion of the pitch response in the vertical response at the sides at higher wave periods is not dominant,but it has effect in wave periods of less than 10 s,which covers most sea states(pitch dominant).

|
| Fig. 11 Comparison of RAOs of vertical motion at points A and B |
An accurate determination of the vertical response at the sides of TLPs is important. The vertical motions at these points are directly related to the stress in the tendons. Usually,time histories and the RAO of the motions of the TLP are noted at the center of gravity and other points are not directly reported. In this study,we investigated the vertical motion at three points: the center of the TLP(point C)and the corner sides(points A and B). From the numerical results obtained in this study,we can make the following conclusions:
The RAO of the corner sides are different from and greater than that of the center of the TLP. The ratio of the total RAO of the vertical response at the sides to the RAO of the center of the TLP in wave periods less than 10 s is significant. Therefore,by considering this portion,we can obtain the true vertical motion of the sides and the strain of the tendons. Combining the vertical portion of the pitch and heave responses facilitates the calculation of the RAO of the stress in the tendons.
The vertical motion at the center of the TLP consists of two periods(the natural period of the heave and the wave period),but at the sides it consists of three periods(the natural periods of the heave and pitch and the wave period).
The vertical response at the sides of the TLP is significant when the pitch response is dominant,rather than the heave response being dominant,at the center of the TLP.
| Abaiee MM, Ahmadi A, Ketabdari MJ, 2015. Analytical discussion on stochastic hydrodynamic modeling of support structure of HAWAII WTG offshore wind turbine. Journal of Advanced Research in Ocean Engineering, 1(1), 55-62.DOI: 10.5574/JAROE.2015.1.1.055 |
| Bhattacharyya SK, Sreekumar S, Idichandy VG, 2003. Coupled dynamics of SeaStar mini tension leg platform. Ocean engineering, 30(6), 709-737. DOI: 10. 10.1016/S0029-8018(02)00061-6 |
| Das SK, Baghfalaki M, 2015. Modeling of response amplitude operator for coupled sway, roll and yaw motions of a floating body in sinusoidal waves using frequency based analysis. Journal of Offshore Mechanics and Arctic Engineering, 137(3), 031303 . |
| Downie MJ, Graham JMR, Hall C, Incecik A, Nygaard I, 2000. An experimental investigation of motion control devices for truss spars. Marine structures, 13(2), 75-90. DOI: 10.1016/S0951-8339(00)00010-1 |
| Joseph A, Mangal L, George PS, 2010. Coupled dynamic response of a three-column mini TLP. Journal of Naval Architecture and Marine Engineering, 6(2), 52-61. DOI: 10.3329/jname.v6i2.2789 |
| Nallayarasu S, Prasad PS, 2012. Hydrodynamic response of spar and semi-submersible interlinked by a rigid yoke–Part I: regular waves. Ships and Offshore Structures, 7(3), 297-309. DOI: 10. 10.1080/17445302.2011.552208 |
| Nallayarasu S, Sreeraj R, Murali M, 2014. Effect of hull geometry on the hydrodynamic response of spar in regular waves. Ships and Offshore Structures, 9(1), 22-37. DOI: 10.1080/17445302.2012.704172 |
| Tabeshpour MR, Ataie Ashtiani B, Seif MS, Golafshani AA, 2013. Hydrodynamic damped pitch motion of tension leg platforms. International Journal of Marine Science and Engineering, 3(2), 91-98. |
| Tabeshpour MR, Golafshani AA, Ataie Ashtiani B, Seif MS, 2006. Analytical solution of heave vibration of tension leg platform. Journal of Hydrology and Hydromechanics, 54(3), 1-10 . |
| Tajali Z, Shafieefar M, 2011. Hydrodynamic analysis of multi-body floating piers under wave action. Ocean Engineering, 38(17-18), 1925-1933.DOI: 10.1016/j.oceaneng.2011.09.025 |
| Wu HL, Chen XJ, Huang YX, Wang B, 2014. Influence of the legs underwater on the hydrodynamic response of the multi-leg floating structure. Ships and Offshore Structures, 9(6), 578-595. DOI: 10.1080/17445302.2013.867646 |
| Zhang F, Yang JM, LI RP, Chen G, 2007. Numerical investigation on the hydrodynamic performances of a new spar concept. Journal of Hydrodynamics, 19(4), 473-481. DOI: 10.1016/S1001-6058(07)60142-5 |
| Zeng XH, Shen XP, Wu YX, 2007. Governing equations and numerical solutions of tension leg platform with finite amplitude motion. Applied Mathematics and Mechanics, 28(1), 37-49. DOI: 10.1007/s10483-007-0105-1 |



