The problems of interaction of surface water waves with a very large floating structure and/or the presence of an obstacle on the ocean-bed are important for their possible applications in the area of coastal and marine engineering. Davies(1982)studied the diffraction of normal incident surface water waves by a patch of sinusoidal ripples on the ocean-bed using the Fourier transform technique. Davies and Heathershaw(1984)analyzed the scattering of water waves by an undulating bottom topography in an ocean-bed. Mei(1985)introduced a theory for the problem of reflection of surface water waves by periodic sandbars at the Bragg resonance condition. For the problem of free surface flow over an undulating bed,the mild-slope equation,initially devised by Kirby(1986). Later on,Chamberlain and Porter(1995)introduced approximate analytical techniques essentially involving depth-averaging under the assumption of the small variation of the ocean-bed. Using linearized water wave theory,Staziker et al.(1996)and Porter and Porter(2003)considered the problem of scattering of surface waves by a small deformation of an impermeable ocean-bed with free surface.
In recent decades,various methods have introduced to study the hydroelastic response of the Very Large Floating Structures(VLFS)in water waves with impermeable ocean-bed. VLFSs can serve as various offshore infrastructure developments,such as oil storage facilities,floating airports,wind and solar power plants,etc. Accordingly,the elastic deformations are predominant over the rigid body motions in the response of the structure to water waves. Thus VLFSs are usually modelled as elastic plates. Water waves interaction by a thin elastic plate modelled as a thin ice-plate creates interesting mathematical problems to marine researchers drawing attention of various types for obtaining their useful solutions,see,Fox and Squire(1994),Linton and Chung(2003),Porter and Porter(2004),Bennetts et al.(2007). Wang and Meylan(2002)obtained a solution by reducing the problem to a finite domain enclosed by a boundary(including the varying part of the bed and the lower surface of the plate)on which the normal derivative of the potential is expressed as a function of the potential itself. The problem was then solved numerically using a boundary-element method.
Assuming that the ocean bed is having a porous type surface,Gu and Wang(1991)studied the propagation of water waves within a porous ocean bed. Later on,employing the complex wavenumber in the poro-elastic model,Jeng(2001)developed the wave dispersion relation in a porous seabed. Mohapatra(2015),Martha and Bora(2007)and Silva et al.(2002)investigated various diffraction problems of water wave by a porous ocean-bed with bottom deformation. Zhu(2001)investigated the propagation of water waves within porous bed on an undulating surface and solved the problem by employing Galerkin eigenfunction expansion technique. They investigated the value of the reflection coefficient numerically. Employing the suitable Green’s function and then using the Green’s integral theorem,Mohapatra(2014)studied the problem of two-dimensional water waves interaction by a small deformation on a porous bed in an ice-covered ocean.
Studies of different types of water wave scattering problems with a permeable ocean-bed of variable depth in presence of a floating elastic plate,have gained reasonable importance due to various reasons. One of these is to understand the effects of wave propagation over a porous ocean-bed with bottom deformations in presence of a floating ice-plate. Another important reason is to construct an effective reflector of the incident wave energy for protecting coastal areas from the rough ocean in the polar regions. Therefore,due to many interesting applications in the theory of scattering of waves,porosity of the ocean-bed along with an infinitely extended floating elastic plate becomes an extremely important aspect to be handled for both the marine and polar researchers.
In the present work,we consider an oblique incident wave propagates in an ocean where the upper surface is covered by an infinitely extended floating elastic plate and the bottom is bounded by a porous surface which has a small deformation. The behaviour of the fluid particles within the permeable ocean-bed is not studied here. Again,we assumed that the fluid motion of the fluid particles is such that the resulting boundary condition on the permeable bed holds good and depends on a parameter P,which is called the porosity parameter in this analysis. In such a case,the waves which is simple harmonic in time can propagate with a particular wavenumber at the surface below the elastic plate. Applying perturbation analysis,the governing BVP reduces to a simpler BVP for the first-order correction of the potential function. The solution of this problem is then obtained by using Green’s integral theorem of the potential function describing the boundary value problem. The first-order reflection and transmission coefficients are evaluated in terms of integrals involving the shape function of the bottom deformation on the porous bed. We present two special forms of bottom deformation,and the first-order reflection and transmission coefficients are depicted graphically for various values of the different parameters. To ensure the correctness of the analytical and numerical results involving reflection and transmission coefficients,“energy balance relation” is checked computationally.
2 Mathematical formulation of the physical problemConsider an incompressible and inviscid fluid which is covered by an infinitely extended thin uniform elastic plate,and lower surface is bounded by a porous bottom surface having a small deformation. The fluid is of infinitely extended in xz- horizontal plane while the depth is considered vertically downwards with y=0 as the mean position of the thin flexible elastic plate. Here the fluid motion is considered to be irrotational in nature and simple harmonic in time with angular frequency ω. The bottom of the fluid with a small deformation is described by $y = h + \delta c\left(x \right)$,where c(x)is a continuous function which describes the shape of bottom deformation on the porous bed and $c\left(x \right)\to 0$ as $\left| x \right| \to \infty $. Under the assumptions of the linear water wave theory,the motion of fluid is described by the potential function $\Phi \left({x,y,z,t} \right)$ can be written as
| $\begin{align} & \Phi \left(x,y,z,t \right)=\operatorname{Re}\left[ \phi \left(x,y \right){{\text{e}}^{\text{i}\left(\upsilon z-\omega t \right)}} \right]\,\,\\ & -\infty <x,\text{ }z<\infty,\,\,\text{ }0\le y\le h+\delta c\left(x \right)\\ \end{align}$ | (1) |
where υ is the component of the incident field wavenumber along z-direction and the function $\phi $ satisfies the modified Helmholtz equation:
| $\begin{array}{l} {\rm{ }}{\phi _{xx}} + {\phi _{yy}} - {\upsilon ^2}\phi = 0\,\,\\ - \infty < x < \infty,\,\,{\rm{ }}0 \le y \le h + \delta c\left(x \right) \end{array}$ | (2) |
The boundary conditions near the floating elastic plate,at the bottom surface and the asymptotic behavior of $\phi $ are given by
| $\begin{array}{l} K\phi + \left[ {D{{\left({\frac{{{\partial ^2}}}{{\partial {x^2}}} - {\upsilon ^2}} \right)}^2} + 1 - \varepsilon K} \right]{\phi _y} = 0\,\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,- \infty < x < \infty,\,\,{\rm{ }}y = 0 \end{array}$ | (3) |
| ${\phi _n} - P\phi = 0,\,\,\,\,\,- \infty < x < \infty,\,{\rm{ }}y = h + \delta c\left(x \right)$ | (4) |
| $\phi \left({x,y} \right)\sim \left\{ \begin{array}{l} \left({{{\rm{e}}^{{\rm{i}}{k_0}x\cos \theta }} + R{{\rm{e}}^{ - {\rm{i}}{k_0}x\cos \theta }}} \right)Z(y)\,\,\,\,\,\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{as}}\,\,x \to - \infty,\\ T{{\rm{e}}^{{\rm{i}}{k_0}x\cos \theta }}Z(y)\,\,\,\,\,{\rm{as}}\,\,x \to \infty \end{array} \right.$ | (5) |
where $K={{{\omega }^{2}}}/{g}\;;$ g is the acceleration due to gravity,$D={F}/{{{\rho }_{1}}g}\;;$ ρ1 is the density of the fluid,F is the flexural rigidity of the floating elastic plate which is given by $F={E{{h}_{i}}^{3}}/{\left[ 12\left( 1-{{\gamma }^{2}} \right) \right]}\;;$E is the Young's modulus and γ is the Poisson's ratio for the floating elastic plate; hi is the small thickness of the elastic plate; $\varepsilon =\left( {{{\rho }_{0}}}/{{{\rho }_{1}}}\; \right){{h}_{0}}$,ρ0 is the density of the flexible elastic plate,${\partial }/{\partial n}\;$is the normal derivative to the bottom surface at a point(x,y,z),P is the porous effect parameter on the ocean bed and Z(y)is gven by
| $Z(y)=\frac{\cosh {{k}_{0}}\left( h-y \right)-\left( {P}/{{{k}_{0}}}\; \right)\sinh {{k}_{0}}\left( h-y \right)}{\cosh {{k}_{0}}h-\left( {P}/{{{k}_{0}}}\; \right)\sinh {{k}_{0}}h}$ | (6) |
The porous boundary condition(4)is the same as that used earlier by Chwang(1983),Sahoo et al.(2000),Martha et al.(2007),Mohapatra(2014,2015). It may be observed that when $P \to 0$,the porous boundary condition(4)reduces to the rigid boundary condition. The condition(5)represents the asymptotic behavior of $\phi $,in which the unknown complex constants R and T are related to the reflection and transmission coefficients,respectively,and are to be determined; θ is the angle of the oblique incident progressive waves; the expression $\cosh {{k}_{0}}h-\left( {P}/{{{k}_{0}}}\; \right)\sinh {{k}_{0}}h$ is non-zero and k0 satisfies the dispersion relation:
| $ \begin{align} & \left[ \left( D{{k}^{4}}+1-\varepsilon K \right)k+\left( {P}/{k}\; \right)K \right]\tanh kh- \\ & \,\,\,\,\,\,\,\,\,\,\left[ \left( D{{k}^{4}}+1-\varepsilon K \right)P+K \right]=0 \\ \end{align} $ | (7) |
In the above dispersion relation(7),there are two non-zero real roots $ \pm {k_0}$,which indicate the propagating waves; four complex roots of type $ \pm \left({\alpha \pm {\rm{i}}\beta } \right)$ with $\alpha > \beta > 0$,which correspond to the damped waves; and an infinite(countable)number of purely imaginary roots $ \pm {\rm{i}}{k_n}$ $\left({{k_n} > 0,\,{\rm{ }}n = 1,{\rm{ }}2,...} \right)$which indicate the evanescent waves,where ${k_n}$’s satisfy the following relation:
| $ \begin{align} & \left[ \left( D{{k}_{n}}^{4}+1-\varepsilon K \right){{k}_{n}}-\left( {P}/{{{k}_{n}}}\; \right)K \right]\tan {{k}_{n}}h+ \\ & \,\,\,\,\,\,\,\,\,\,\left( D{{k}_{n}}^{4}+1-\varepsilon K \right)P+K=0 \\ \end{align} $ | (8) |
It may be noted that the damped propagating waves and the evanescent waves do not affect on the asymptotic behavior of the resulting reflected and transmitted waves. The positive roots of(7)being the wavenumbers of the waves propagating in the positive x-direction,while the negative roots being the wavenumbers of the waves propagating in the negative direction. Since the dispersion relation(7)has one positive real root $k = {k_0}\left({ \ne 0} \right)$,so only one non-zero wavenumber k0 can exists and the wave can propagate near the floating elastic plate along the positive x-direction.
An oblique incident surface waves of wavenumber k0 making an angle $\theta \left( 0\le \theta <{\text{ }\!\!\pi\!\!\text{ }}/{2}\; \right)$,with the positive x-direction is of the form:
$
{{\phi }_{0}}\left( x,y \right)={{\text{e}}^{\text{i}{{k}_{0}}x\cos \theta }}Z\left( y \right),\,\,\text{ }-\infty |
(9)
|
|
When a train of oblique incident surface waves propagates over bottom deformation on a porous bed,then the wave train is partially reflected by it,and partially transmitted over it. The main concern here is to find the reflection and transmission coefficients approximately.
The bottom condition(4)can be expressed approximately as
| $ \begin{align} & {{\phi }_{y}}-\delta \frac{\text{d}}{\text{d}x}\left[ c\left( x \right){{\phi }_{x}}\left( x,h \right)-c\left( x \right){{\upsilon }^{2}}\phi \left( x,h \right) \right]- \\ & P\left[ \phi +\delta c\left( x \right){{\phi }_{y}} \right]+O\left( {{\delta }^{2}} \right)=0\,\,\,\,\text{on }\,y=h \\ \end{align} $ | (10) |
In recent decades,various approaches(both analytical and numerical)have been developed in the literature to deal with the interaction of water waves with a large bottom deformation on an ocean-bed. On the other hand,scattering of surface water waves by a small deformation on the bottom surface of water of finite depth also creates interesting mathematical problems drawing attention of various types for obtaining their useful solutions(Mandal and Gayen, 2006; Martha et al., 2007; Mandal and De, 2009; Mohapatra, 2014,2015). In this paper,we have considered the problem of water wave interaction with a small bottom deformation on a porous ocean-bed. Since the bottom condition given in(4)involves a small parameter δ(<<1),which measures the smallness of the deformation,we can employ the perturbation expansion to solve the problem. Also,the form of the approximate bottom condition(10)suggests that $\phi,\,{\rm{ }}R$ and T have the perturbation expansions,in terms of the small parameter δ which will be discussed in the following section.
3 Solution of the problemIn this section,we consider the scattering problem for an oblique incident waves propagates over a small deformation on a porous ocean-bed,where the upper surface is having a floating flexible elastic plate. Since the bottom condition $\left( {\partial }/{\partial n}\;=0\,\,\text{on}\,\,y=h+\delta c\left( x \right) \right)$ involving a small parameter δ(<<1),which measures the smallness of the deformation,we will employ the perturbation expansion,only to reduce the governing BVP to a simpler BVP for the first-order correction of the potential function. Then the BVP for first-order potential function will be solved using a method based on Green's integral theorem with the introduction of suitable Green’s function.
Let us consider a train of progressive waves of wavenumber k0 is obliquely incident at an angle $\theta \left( 0\le \theta <{\text{ }\!\!\pi\!\!\text{ }}/{2}\; \right)$,with the positive x-axis to the bottom deformation on a porous bed. If there is no bottom deformation,then the oblique incident wave train will propagate without any hindrance and there will be only transmission in this case. This,along with the appropriate form of the boundary condition(10),suggest that the potential function $\phi $,the reflection and transmission coefficients R and T,respectively,can be expressed in terms of the small parameter δ as:
| $\left\{ \begin{array}{l} \phi = {\phi _0} + \delta {\phi _1} + O\left({{\delta ^2}} \right)\,\\ R = \delta {R_1} + O\left({{\delta ^2}} \right)\\ T = 1 + \delta {T_1} + O\left({{\delta ^2}} \right) \end{array} \right.$ | (11) |
where ${\phi _0}$ is given by(9)and,${R_1}$ and ${T_1}$ are the first-order reflection and transmission coefficients,respectively. Here,it may be noted that for large reflection,the expression as given in(11),needs to be refined so that it can deal with the Bragg resonant case,which is discussed in Mei(1985). Also the expression in(11)is only valid for infinitesimal reflection and away from the Bragg resonance case.
Using(11)in(2),the boundary conditions(3),(10),and the asymptotic condition(5); and then compare with the coefficients of zero-order and first-order terms of $\delta $ on both sides,we find that the zero-order and first-order potential functions ${\phi _0}$ and ${\phi _1}$,respectively,satisfy a coupled BVP described by
BVP-Ⅰ,corresponding to${\phi _0}$,is
| ${\phi _0}_{xx} + {\phi _0}_{yy} - {\upsilon ^2}{\phi _0} = 0,\,{\rm{ }}\,\,\,- \infty < x < \infty,\,\,{\rm{ }}0 \le y \le h$ | (12) |
| $\begin{array}{l} K{\phi _0} + \left[ {D{{\left({\frac{{{\partial ^2}}}{{\partial {x^2}}} - {\upsilon ^2}} \right)}^2} + 1 - \varepsilon K} \right]{\phi _0}_y = 0\,\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,- \infty < x < \infty,\,\,{\rm{ }}y = 0 \end{array}$ | (13) |
| ${\phi _0}_n - P{\phi _0} = 0,\,\,{\rm{ }}\,\,y = h$ | (14) |
| ${\phi _0}\left({x,y} \right)\sim {{\rm{e}}^{{\rm{i}}{k_0}x\cos \theta }}Z(y)\,\,\,\,\,\,{\rm{as }}\,\,x \to \pm \infty $ | (15) |
BVP-Ⅱ,corresponding to${\phi _1}$,is
| ${\phi _1}_{xx} + {\phi _1}_{yy} - {\upsilon ^2}{\phi _1} = 0,\,\,\,\,- \infty < x < \infty,\,\,{\rm{ }}0 \le y \le h$ | (16) |
| $\begin{array}{l} K{\phi _1} + \left[ {D{{\left({\frac{{{\partial ^2}}}{{\partial {x^2}}} - {\upsilon ^2}} \right)}^2} + 1 - \varepsilon K} \right]{\phi _1}_y = 0\,\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,- \infty < x < \infty,\,\,y = 0 \end{array}$ | (17) |
| $\begin{align} & {{\phi }_{1}}_{y}-P{{\phi }_{1}}= \\ & \frac{\text{i}{{k}_{\text{0}}}\cos \theta \frac{\text{d}}{\text{d}x}\left[ c\left( x \right){{\text{e}}^{\text{i}{{k}_{\text{0}}}x\text{cos}\theta }} \right]+\left( {{P}^{2}}-{{k}_{0}}^{2}{{\sin }^{2}}\theta \right)c\left( x \right){{\text{e}}^{\text{i}{{k}_{\text{0}}}x\cos \theta }}}{\cosh {{k}_{0}}h-\left( {P}/{{{k}_{0}}}\; \right)\sinh {{k}_{0}}h}\equiv \\ & f(x)\text{ }\,\,\,\,\,\text{on}\,\,\,y=h \\ \end{align}$ | (18) |
| ${\phi _1}\left({x,y} \right)\sim \left\{ \begin{array}{l} {R_1}{{\rm{e}}^{ - {\rm{i}}{k_0}x\cos \theta }}Z(y)\,\,\,\,\,\,{\rm{as}}\,{\rm{ }}\,x \to - \infty \\ {T_1}{{\rm{e}}^{{\rm{i}}{k_0}x\cos \theta }}Z(y)\,\,\,\,\,\,{\rm{as }}\,\,x \to \infty \end{array} \right.$ | (19) |
It may be noted that the BVP-I corresponds to the problem of water waves,where the upper surface is covered by an infinitely extended elastic plate while the lower surface is bounded by a porous surface having no deformation in an ocean of uniform finite depth h. In order that the Eqs.(12)-(15)are satisfied,the above zero-order potential function ${\phi _0}$ is in the same form as given in Eq.(9).
The BVP-II is a radiation problem in water waves involving a bottom deformation on a porous bed in an ocean of uniform finite depth h,in which,the asymptotic condition involves ${\phi _0}$,the solution of BVP-I. In order to solve the above BVP-II for ${\phi _1}$,we need to construct a Green's function for the modified Helmholtz equation. Then employing Green's integral theorem,the first-order reflection coefficient R1 and transmission coefficient T1 will be calculated in terms of integrals involving the shape function representing the bottom deformation on the porous bed.
3.1 Introduction of Green's functionSuppose that the point $\left({{x^ * },{y^ * }} \right)$ being the source term in the fluid region $ - \infty < x < \infty,\,\,0< y < h$ . Then,for $0 < {y^ * } < h,$ the source potential which is referred as the Green's function $G\left({x,y;{x^ * },{y^ * }} \right)$ satisfies the following BVP:
| $\begin{array}{c} {G_{xx}} + {G_{yy}} - {\upsilon ^2}G = 0\,\,{\rm{ }}\\ - \infty < x < \infty,\,\,0 \le y \le h,\,\,{\rm{except}}\,\,{\rm{at}}\,\,\left({{x^ * },{y^ * }} \right) \end{array}$ | (20) |
| $\begin{array}{l} KG + \left[ {D{{\left({\frac{{{\partial ^2}}}{{\partial {x^2}}} - {\upsilon ^2}} \right)}^2} + 1 - \varepsilon K} \right]{G_y} = 0\,\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,- \infty < x < \infty,\,\,{\rm{ }}y = 0 \end{array}$ | (21) |
| ${G_y} - PG = 0\,\,\,\,\,{\rm{on}}\,\,\,- \infty < x < \infty,\,\,\,\,y = h$ | (22) |
| $G\left({x,y;{x^ * },{y^ * }} \right)\to {\rm{multiple}}\,\,{\rm{of}}\,\,{{\rm{e}}^{{\rm{i}}\mu \left| {x - {x^ * }} \right|}}\,\,\,\,{\rm{as }}\,\,\left| {x - {x^ * }} \right| \to \infty $ | (23) |
| $G\left({x,y;{x^ * },{y^ * }} \right)\sim {K_0}(\upsilon {r_1}){\rm{ as }}{r_1}{\rm{ = }}\sqrt {{{\left({x - {x^ * }} \right)}^2} + {{\left({y - {y^ * }} \right)}^2}} \to 0$ | (24) |
where ${K_0}\left({\upsilon {r_1}} \right)$ is the modified Bessel function of the second kind. Now we will solve the BVP defined by(20)-(24)in the form $G\left({x,y;{x^ * },{y^ * }} \right)$,where
| $\begin{array}{l} G\left({x,y;{x^ * },{y^ * }} \right)= {K_0}\left({\upsilon {r_1}} \right)- {K_0}\left({\upsilon {r_2}} \right)+ \\ \int\limits_\upsilon ^\infty {\frac{1}{\mu }\left[ {A\left(\xi \right)\cosh \xi \left({h - y} \right)+ B\left(\xi \right)\sinh \xi y} \right]\cos \mu \left({x - {x^ * }} \right){\rm{d}}\xi } \end{array}$ | (25) |
where $\upsilon =\xi \sin \theta \,\left( 0\le \theta <{\text{ }\!\!\pi\!\!\text{ }}/{2}\; \right),$ $\mu = \sqrt {{\xi ^2} - {\upsilon ^2}} $ and ${r_2} = \sqrt {{{\left({x - {x^ * }} \right)}^2} + {{\left({y + {y^ * }} \right)}^2}} $. Using the boundary conditions near the flexible elastic plate and at the bottom surface,we obtain $A\left(\xi \right)$ and $B\left(\xi \right)$ as
| $\begin{array}{l} A\left(\xi \right)= \\ \frac{{2\left({D{\xi ^4} + 1 - \varepsilon K} \right)\left[ {\xi \cosh \xi \left({h - {y^ * }} \right)- P\sinh \xi \left({h - {y^ * }} \right)} \right]}}{{\cosh \xi h\,\,M\left(\xi \right)}} \end{array}$ | (26) |
| $\begin{array}{l} B\left(\xi \right)= \\ \frac{{2P\left({D{\xi ^4} + 1 - \varepsilon K} \right)\left[ {\xi \cosh \xi \left({h - {y^ * }} \right)- P\sinh \xi \left({h - {y^ * }} \right)} \right]}}{{\cosh \xi h\left({\xi \cosh \xi h - P\sinh \xi h} \right)\,\,M\left(\xi \right)}} \end{array}$ | (27) |
where
| $\begin{align} & M\left( \xi \right)=\left[ \left( D{{\xi }^{4}}+1-\varepsilon K \right)\xi +\left( {P}/{\xi }\; \right)K \right]\sinh \xi h- \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left[ \left( D{{\xi }^{4}}+1-\varepsilon K \right)P+K \right]\cosh \xi h \\ \end{align}$ |
It may be noted here that the integrand in(25)has one simple pole at $\xi = {k_0}$ which will be from $M\left(\xi \right)$ only. However,the terms $\xi $ and $\cosh \xi h-\left( {P}/{\xi }\; \right)\sinh \xi h$ can never be zero as they indicate that there exists a progressive wave in the fluid region. Solving(25)by using(26)and(27),we obtain the solution $G\left({x,{\rm{ }}y;{\rm{ }}{x^ * },{\rm{ }}{y^ * }} \right)$ as:
| $\begin{array}{l} G\left({x,y;{x^ * },{y^ * }} \right)= 2{\rm{\pi i}}\left({D{k_0}^4 + 1 - \varepsilon K} \right){{\rm{e}}^{{\rm{i}}{k_0}\cos \theta \left| {x - {x^ * }} \right|}} \times \\ \left[ {\frac{{\left[ {{k_0}\cosh {k_0}\left({h - {y^ * }} \right)- P\sinh {k_0}\left({h - {y^ * }} \right)} \right]}}{{{k_0}\cos \theta M'\left({{k_0}} \right)\cosh {k_0}h\left({{k_0}\cosh {k_0}h - P\sinh {k_0}h} \right)}}} \right] \times \\ \left[ {\left({{k_0}\cosh {k_0}h - P\sinh {k_0}h} \right)\cosh {k_0}\left({h - y} \right)+ P\sinh {k_0}y} \right] + \end{array}$ |
| $\begin{array}{l} 2{\rm{\pi i}}\left({D{\lambda _1}^4 + 1 - \varepsilon K} \right){{\rm{e}}^{{\rm{i}}\sqrt {{\lambda _1}^2 - {\upsilon ^2}} \left| {x - {x^ * }} \right|}} \times \\ \left[ {\frac{{\left[ {{\lambda _1}\cosh {\lambda _1}\left({h - {y^ * }} \right)- P\sinh {\lambda _1}\left({h - {y^ * }} \right)} \right]}}{{\sqrt {{\lambda _1}^2 - {\upsilon ^2}} M'\left({{\lambda _1}} \right)\cosh {\lambda _1}h\left({{\lambda _1}\cosh {\lambda _1}h - P\sinh {\lambda _1}h} \right)}}} \right] \times \\ \left[ {\left({{\lambda _1}\cosh {\lambda _1}h - P\sinh {\lambda _1}h} \right)\cosh {\lambda _1}\left({h - y} \right)+ P\sinh {\lambda _1}y} \right] + \end{array}$ |
| $\begin{array}{l} 2{\rm{\pi i}}\left({D{\lambda _2}^4 + 1 - \varepsilon K} \right){{\rm{e}}^{{\rm{i}}\sqrt {{\lambda _2}^2 - {\upsilon ^2}} \left| {x - {x^ * }} \right|}} \times \\ \left[ {\frac{{\left[ {{\lambda _2}\cosh {\lambda _2}\left({h - {y^ * }} \right)- P\sinh {\lambda _2}\left({h - {y^ * }} \right)} \right]}}{{\sqrt {{\lambda _2}^2 - {\upsilon ^2}} M'\left({{\lambda _2}} \right)\cosh {\lambda _2}h\left({{\lambda _2}\cosh {\lambda _2}h - P\sinh {\lambda _2}h} \right)}}} \right] \times \\ \left[ {\left({{\lambda _2}\cosh {\lambda _2}h - P\sinh {\lambda _2}h} \right)\cosh {\lambda _2}\left({h - y} \right)+ P\sinh {\lambda _2}y} \right] \end{array}$ |
| $\begin{array}{l} 2{\rm{\pi }}{{\rm{e}}^{ - \sqrt {{k_n}^2 + {\upsilon ^2}} \left| {x - {x^ * }} \right|}} \times \\ \sum\limits_{n = 1}^\infty {\left\{ {\frac{{\left({D{\lambda _n}^4 + 1 - \varepsilon K} \right)\left[ {{k_n}\cos {k_n}\left({h - {y^ * }} \right)- P\sin {k_n}\left({h - {y^ * }} \right)} \right]}}{{\sqrt {{k_n}^2 + {\upsilon ^2}} {M_1}\left({{k_n}} \right)\cos {k_n}h\left({{k_n}\cos {k_n}h - P\sin {k_n}h} \right)}}} \right\}} \times \\ \left[ {\left({{k_n}\cos {k_n}h - P\sin {k_n}h} \right)\cos {k_n}\left({h - y} \right)+ P\sin {k_n}y} \right] \end{array}$ | (28) |
where ${\lambda _1} = \alpha + {\rm{i}}\beta $,${\rm{ }}{\lambda _2} = - {\bar \lambda _1}$,$M'$ denotes the derivative of M with respect to $\xi $ and
| $\begin{align} & {{M}_{1}}\left( {{k}_{n}} \right)= \\ & \left[ \left( D{{k}_{n}}^{4}+1-\varepsilon K \right)\left( 1-Ph \right)+4D{{k}_{n}}^{4}+\left( {PK}/{{{k}_{n}}^{2}}\; \right)-Kh \right]\sin kh+ \\ & \left[ \left( D{{k}_{n}}^{4}+1-\varepsilon K \right){{k}_{n}}h-4D{{k}_{n}}^{3}P-\left( {PK}/{{{k}_{n}}}\; \right)h \right]\cos kh \\ \end{align}$ | (29) |
Since the source potential in terms of Green's function $G\left({x,{\rm{ }}y;{\rm{ }}{x^ * },{\rm{ }}{y^ * }} \right)$ behaves like outgoing waves at infinity,so taking $\left| {x - {x^ * }} \right| \to \infty,$ we obtain the solution $G\left({x,{\rm{ }}y;{\rm{ }}{x^ * },{\rm{ }}{y^ * }} \right)$ as:
| $\begin{array}{l} G\left({x,{\rm{ }}y;{\rm{ }}{x^ * },{\rm{ }}{y^ * }} \right)= 2{\rm{\pi i}}\left({D{k_0}^4 + 1 - \varepsilon K} \right){{\rm{e}}^{{\rm{i}}{k_0}\cos \theta \left| {x - {x^ * }} \right|}} \times \\ \left[ {\frac{{\left[ {{k_0}\cosh {k_0}\left({h - {y^ * }} \right)- P\sinh {k_0}\left({h - {y^ * }} \right)} \right]}}{{{k_0}\cos \theta M'\left({{k_0}} \right)\cosh {k_0}h\left({{k_0}\cosh {k_0}h - P\sinh {k_0}h} \right)}}} \right] \times \\ \left[ {\left({{k_0}\cosh {k_0}h - P\sinh {k_0}h} \right)\cosh {k_0}\left({h - y} \right)+ P\sinh {k_0}y} \right] \end{array}$ | (30) |
To calculate the value of ${\phi _1}\left({{x^ * },{\rm{ }}{y^ * }} \right)$,we apply the Green’s integral theorem to the functions ${\phi _1}\left({x,{\rm{ }}y} \right)$ and $G\left({x,{\rm{ }}y;{\rm{ }}{x^ * },{\rm{ }}{y^ * }} \right)$ in the following form:
| $\int\limits_C {\left({{\phi _1}{G_n} - G{\phi _1}_n} \right)} {\rm{d}}s = 0$ | (31) |
where C is a closed contour consisting of the lines $x = X,\,$ $y = 0,\,{\rm{ }}x = - X,\,{\rm{ }}y = h$ and a small circle ${\left({x - {x^ * }} \right)^2} + {\left({y - {y^ * }} \right)^2} = {d^2}$,and ultimately let $X \to \infty $ and $d \to 0$. Finally,(31)will give the determination of the solution ${\phi _1}$ of the BVP as given by
| ${\phi _1}\left({{x^ * },{y^ * }} \right)= \frac{1}{{2{\rm{\pi }}P}}\int\limits_{ - \infty }^\infty {{G_y}\left({x,h;{x^ * },{y^ * }} \right)f\left(x \right){\rm{d}}x} $ | (32) |
In order to calculate the reflection and transmission coefficients(up to first-order)due to an oblique incident waves of wavenumber k0,we assume ${x^ * } \to \mp \infty $,in(32). Then comparing the resulting integral with ${\phi _1}$ given in(19)at the source point(x,y),we obtain the values of R1 and T1 as:
| $\begin{align} & {{R}_{1}}=\text{i}\left( D{{k}_{\text{0}}}^{4}+1-\varepsilon K \right)\times \\ & \frac{\left( {{P}^{2}}+{{k}_{0}}^{2}\cos 2\theta \right)\sec \theta }{{M}'\left( {{k}_{0}} \right)\left[ \cosh {{k}_{0}}h-\left( {P}/{{{k}_{0}}}\; \right)\sinh {{k}_{0}}h \right]}\int\limits_{-\infty }^{\infty }{c\left( x \right)}\text{ }{{\text{e}}^{\text{2i}\left( {{k}_{\text{0}}}\text{cos}\theta \right)x}}\text{d}x \\ \end{align}$ | (33) |
| ${{T}_{1}}=\frac{\text{i}\left( D{{k}_{\text{0}}}^{4}+1-\varepsilon K \right)\left( {{P}^{2}}-{{k}_{0}}^{2} \right)\sec \theta }{{M}'\left( {{k}_{0}} \right)\left[ \cosh {{k}_{0}}h-\left( {P}/{{{k}_{0}}}\; \right)\sinh {{k}_{0}}h \right]}\int\limits_{-\infty }^{\infty }{c\left( x \right)}\,\text{d}x$ | (34) |
Thus,the integral representation of R1 and T1,due to an oblique incident surface waves propagation over a small bottom deformation on the porous bed,can be evaluated from(33)and(34),once the shape function of the bottom deformation is known. Here,if the angle of incident waves is taken as zero(i.e.,the normal case),then the results(33)and(34)coincide with the corresponding results of Mohapatra(2014). Again,when the flexural rigidity and the density of the elastic plate are taken to be zero,then the results for the problem of water wave scattering by bottom deformation on porous bed with free surface is recovered as a particular case.
4 Particular cases of shape functionHere,we present two different forms of shape function for the bottom deformation: the exponentially damped deformation and the sinusoidal bed,to validate the results.
4.1 The exponentially damped deformationConsider the shape function of the bottom deformation is given by
| $c\left(x \right)= {a_0}{{\rm{e}}^{ - b\left| x \right|}},\,{\rm{ }}\left({b > 0} \right)\,\,\,\,\,\,\,\,\,- \infty < x < \infty $ | (35) |
This shape function corresponds to an exponentially damped deformation on the porous bed. In this example,the top of the elevation lies at $\left({0,{\rm{ }}{a_0}} \right)$ and it decreases exponentially on either side. In order to calculate the reflection coefficient R1,substitute the value of c(x)from(35)into(33),we obtain
| $\begin{align} & {{R}_{1}}=\text{i}\left( D{{k}_{\text{0}}}^{4}+1-\varepsilon K \right)\times \\ & \frac{2b{{a}_{0}}\left( {{P}^{2}}+{{k}_{0}}^{2}\cos 2\theta \right)\sec \theta }{\left[ {{\left( 2{{k}_{0}}\cos \theta \right)}^{2}}+{{b}^{2}} \right]{M}'\left( {{k}_{0}} \right)\left[ \cosh {{k}_{0}}h-\left( {P}/{{{k}_{0}}}\; \right)\sinh {{k}_{0}}h \right]} \\ \end{align}$ | (36) |
In a similar way,we can calculate the transmission coefficient T1 by substituting c(x)from(35)into(34),
| ${{T}_{1}}=\frac{\text{2i }{{a}_{0}}\left( D{{k}_{0}}^{4}+\text{1}-\varepsilon K \right)\left( {{P}^{2}}-{{k}_{0}}^{2} \right)\sec \theta }{b\,{M}'\left( {{k}_{0}} \right)\left[ \cosh {{k}_{0}}h-\left( {P}/{{{k}_{0}}}\; \right)\sinh {{k}_{0}}h \right]}$ | (37) |
We consider another special form of the shape function in the form of a patch of sinusoidal ripples on the porous ocean-bed given by
| $c\left(x \right)= \left\{ \begin{array}{l} a\sin px,\,{\rm{ }}\,{B_1} \le x \le {B_2}\\ 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{otherwise}} \end{array} \right.$ | (38) |
where a is the amplitude of the sinusoidal ripples,${{B}_{1}}={-n\text{ }\!\!\pi\!\!\text{ }}/{p}\;;\,\text{ }{{B}_{2}}={m\text{ }\!\!\pi\!\!\text{ }}/{p}\;\,\left( m,\text{ }n>0 \right)$,p is the wavenumber of the patch in the region ${B_1} \le x \le {B_2}$. The total number of ripples in the patch of sinusoidal ripples on the porous ocean-bed is ${\left( m+n \right)}/{2}\;$ .
Substituting the value of c(x)from(38)into(33)and(34),we obtain R1 and T1,as follows:
| $\begin{align} & {{R}_{1}}=\frac{\text{i}ap\left( D{{k}_{0}}^{4}+1-\varepsilon K \right)\left( {{P}^{2}}+{{k}_{0}}^{2}\cos 2\theta \right)\sec \theta }{{M}'\left( {{k}_{0}} \right)\left[ \cosh {{k}_{0}}h-\left( {P}/{{{k}_{0}}}\; \right)\sinh {{k}_{0}}h \right]}\times \\ & \left[ \frac{{{\left( -1 \right)}^{n}}{{\text{e}}^{2\text{i}\left( {{k}_{0}}\cos \theta \right){{B}_{1}}}}-{{\left( -1 \right)}^{m}}{{\text{e}}^{2\text{i}\left( {{k}_{0}}\cos \theta \right){{B}_{2}}}}}{{{p}^{2}}-4{{k}_{0}}^{2}{{\cos }^{2}}\theta } \right] \\ \end{align}$ | (39) |
| $\begin{align} & {{T}_{1}}=\frac{\text{i}a\left( D{{k}_{0}}^{4}+1-\varepsilon K \right)\left( {{P}^{2}}-{{k}_{0}}^{2} \right)\sec \theta }{{M}'\left( {{k}_{0}} \right)\left[ \cosh {{k}_{0}}h-\left( {P}/{{{k}_{0}}}\; \right)\sinh {{k}_{0}}h \right]}\times \\ & \left[ \frac{\left[ {{\left( -1 \right)}^{n}}-{{\left( -1 \right)}^{m}} \right]}{p} \right] \\ \end{align}$ | (40) |
It may be noted from(39)that when the sinusoidal ripples wavenumber becomes approximately twice of the component of the incident field wave number along x-direction(i.e.,$2{k_0}\cos \theta \approx p$),the theory predicts the possibility of a resonant interaction between the sinusoidal bed and the incident surface wave. Hence,we find that near resonance,i.e., ${{k}_{0}}\approx {\left( p\sec \theta \right)}/{2}\;$ ,the limiting value of R1assumes the value,
| ${{R}_{1}}\approx \,\,-\frac{\text{ }\!\!\pi\!\!\text{ }a\left( m+n \right)\left( D{{k}_{0}}^{4}+1-\varepsilon K \right)\left( {{P}^{2}}+{{k}_{0}}^{2}\cos 2\theta \right)}{4{{k}_{0}}{M}'\left( {{k}_{0}} \right){{\cos }^{2}}\theta \left[ \cosh {{k}_{0}}h-\left( {P}/{{{k}_{0}}}\; \right)\sinh {{k}_{0}}h \right]}$ | (41) |
In such situation,R1 becomes a constant multiple of the total number of ripples in the patch of sinusoidal ripples on the porous ocean-bed ${\left( m+n \right)}/{2}\;$ and hence,R1 increases linearly with m and n. Although the theory breaks down at the point ${{k}_{0}}\approx {\left( p\sec \theta \right)}/{2}\;$,a large amount of reflected energy by this particular form of bottom deformation will be produced in the neighborhood of the point ${{k}_{0}}={\left( p\sec \theta \right)}/{2}\;$. Note that when ${k_0}$ approaches to ${\left( p\sec \theta \right)}/{2}\;$ and the total number of ripples in the patch of sinusoidal ripples on the porous ocean-bed ${\left( m+n \right)}/{2}\;$ becomes large,R1 becomes infinity which contrary to our assumption that R1 is a small quantity. Consequently,we consider only the cases excluding these two conditions in order to avoid the contradiction arising out of resonant cases.
Again,it is clear from(40)that when the total number of ripples in the patch of sinusoidal ripples of the porous ocean-bed is a positive integer(i.e.,both m and n are even or odd),T1 vanishes identically.
It may be noted that the energy balance relation or energy identity plays very important role in checking the method of solution of such mixed boundary value problem. The energy balance relation relates the reflection as well as transmission coefficients associated with the diffraction problem and,in cases when one has to rely only on the numerical results for these important physical quantities,such energy relation supports the validity of the analytical as well as numerical techniques employed to solve the boundary value problem under consideration. Das et al.(2008)derived the energy balance relation for free-surface boundary condition with higher-order derivatives by the appropriate use of Green's integral theorem involving the complex velocity potential and its complex conjugate.
It is known that when an oblique incident surface water waves propagates over a permeable ocean-bed of variable depth in the presence of an infinitely extended floating elastic plate,the energy balance relation involving reflection coefficient $R$ and transmission coefficient $T$ satisfies the following relation:
| ${\left| R \right|^2} + {\left| T \right|^2} = 1$ | (42) |
Here,the numerical computations are shown for R1 and T1,related to two particular types of bottom profiles mentioned in the previous section: the exponentially damped deformation and the sinusoidal bed. In Figs. 1-5,which correspond to the exponentially damped deformation on the porous ocean-bed in section 4.1,the numerical results for the non-dimensionalized $\left| {{R_1}} \right|$ and $\left| {{T_1}} \right|$ due to an oblique incident waves of wavenumber ${k_0}{a_0}$,calculated from(36)and(37),respectively,are plotted against $K{a_0}$. In all the cases,the depth of fluid is taken as ${h}/{{{a}_{0}}=5}\;$. In Fig. 1,the different curves correspond to different incident angles,$\theta =0,\,\text{ }{\text{ }\!\!\pi\!\!\text{ }}/{10}\;,\,{\text{ }\!\!\pi\!\!\text{ }}/{6}\;\,\,\,\text{and}\,\,{\text{ }\!\!\pi\!\!\text{ }}/{5}\;\,,$ while the flexible elastic parameters are fixed at ${D}/{{{a}_{0}}^{4}=1}\;$; ${\varepsilon }/{{{a}_{0}}}\;=0.01$,the porosity of the bed $P{a_0}$ as $0.01$ and the height of the hump ${a_0}b$ as 1. It is observed that whenever the angle of an oblique incident waves increases,the peak value of $\left| {{R_1}} \right|$ decreases. However,for the case of normal incidence(i.e.,$\theta = 0$),the peak value of $\left| {{R_1}} \right|$ is largest. Figs. 2 and 3,respectively,show $\left| {{R_1}} \right|$ due to an oblique incident waves of wavenumber ${k_0}{a_0}$ for four different sets of porosity parameter,(while $\theta $ is fixed at $\pi /6$,the elastic parameters at ${D}/{{{a}_{0}}^{4}=1;\text{ }\,\,{\varepsilon }/{{{a}_{0}}}\;=0.01}\;$)and three different sets elastic parameters($\theta $ is fixed at $\pi /6$,the porosity of the bed $P{a_0}$ as $0.01$). It is observed that the reflected energy is more whenever the porosity of the bed increases,whereas the reflected energy is decreases when the values of elastic parameters ${D}/{{{a}_{0}}^{4};\,\,{\varepsilon }/{{{a}_{0}}}\;}\;$ increase. Here,$\left| {{R_1}} \right|$ is somewhat insensitive to the changes in the flexural rigidity of the floating elastic plate and do not change appreciably when the elastic plate is approximated by a rigid lid. This may be attributed to the fact that,since the elastic plate is somewhat above the bed surface,the surface waves is not much affected by the changes in the flexural rigidity of the elastic plate.
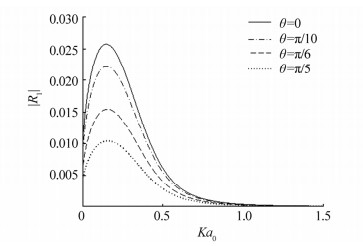 |
| Fig. 1 Variation of reflection coefficient $\left| {{R_1}} \right|$ plotted for various values of incident angle (for exponentially damped bed) |
 |
| Fig. 2 Variation of reflection coefficient $\left| {{R_1}} \right|$ plotted for various values of porosity parameter (for exponentially damped bed). |
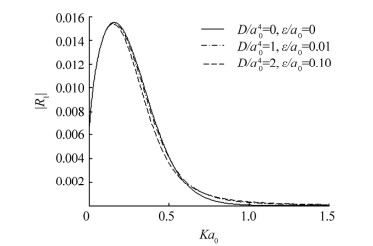 |
| Fig. 3 Variation of reflection coefficient $\left| {{R_1}} \right|$ plotted for various values of elastic parameters (for exponentially damped bed) |
 |
| Fig. 4 Variation of reflection coefficient $\left| {{R_1}} \right|$ plotted for various heights of the hump (for exponentially damped bed) |
 |
| Fig. 5 Variation of transmission coefficient $\left| {{T_1}} \right|$ plotted for various heights of the hump (for exponentially damped bed) |
Figs. 4 and 5,respectively,show $\left| {{R_1}} \right|$ and $\left| {{T_1}} \right|$ for different heights of the hump on the bottom deformation. Here,we consider the angle of incidence waves $\theta $ is $\pi /6$,the depth of the fluid ${h}/{{{a}_{0}}}\;$ is 5,the porous parameter $P{a_0}$ is 0.01 and the elastic parameters are ${D}/{{{a}_{0}}^{4}=1}\;$; $\,{\varepsilon }/{{{a}_{0}}}\;=0.01$. From these figures,it is evident that the values of both $\left| {{R_1}} \right|$ and $\left| {{T_1}} \right|$ decrease when the height of the hump of the bottom deformation increases. This means that when an oblique incident waves propagates over a small bottom deformation on a porous bed,a substantial amount of reflected and transmitted energy can be produced. Moreover,the increasing rate of the reflected and transmitted energy is higher in this case. Again,it is also observed that $\left| {{R_1}} \right|$ is comparatively much smaller than $\left| {{T_1}} \right|$ as
| $\left| {{R}_{1}} \right|=\left| {{T}_{1}} \right|\left[ {\left( {{P}^{2}}+{{k}_{0}}^{2}\cos 2\theta \right)}/{\left( {{P}^{2}}-{{k}_{0}}^{2} \right)}\; \right]{{\left[ {{\left( {2{{k}_{0}}\cos \theta }/{b}\; \right)}^{2}}+1 \right]}^{-1}}$ |
It happens due to the small deformation at the bottom surface of the porous bed. Since the uneven bed(like a hump)decreases exponentially on either side,so both the reflected and transmitted waves exist,and propagate only upto some wavenumbers.
In Figs. 6-10,the numerical computation and graphical presentation are shown for $\left| {{R_1}} \right|$,related to a special form of the bottom surface on the porous bed mentioned in section 4.2. We consider the numerical computations for $\left| {{R_1}} \right|$,which is calculated from(39),due to an oblique incident surface waves of wavenumber ${k_0}h$ propagating along the surface below the floating elastic plate and a patch of sinusoidal ripples with wavenumber ph having ${\left( n+m \right)}/{2}\;$ number of ripple wavelengths in the patch of sinusoidal ripples of the porous bed. Again,in this case we consider the ratio of the amplitude of the ripples and the depth of the fluid(a/h)is taken as $0.1$. The different curves in Fig. 6 correspond to four different angles of incidence,$\theta =0,\,\text{ }{\text{ }\!\!\pi\!\!\text{ }}/{10}\;,\text{ }\,{\text{ }\!\!\pi\!\!\text{ }}/{6}\;$ and ${\text{ }\!\!\pi\!\!\text{ }}/{5}\;$ . For all these curves,the elastic parameters are taken as ${D}/{{{h}^{4}}=1;\,\,{\varepsilon }/{h}\;=0.01}\;$,the porous parameter Ph as 0.1,m and n are fixed at $m = 2;{\rm{ }}n = 3$ and the ripple wavenumber ph as 0.1. It may be noted that for the case of normal incidence(i.e.,$\theta = 0$),the maximum value of $\left| {{R_1}} \right|$ is 0.1931,attained at k0h=0.488377(when $Kh = 0.141$),that is,when the ripple wavenumber ph of the bottom deformation on the porous ocean bed becomes approximately twice as large as the component of the incident field wavenumber ${k_0}h\cos \theta $ along x-direction. The same can be observed when the angle of incidence θ is non-zero(the case of oblique incidence). Another common feature in Fig. 6 is the oscillating nature of $\left| {{R_1}} \right|$ as a function of the wavenumber Kh. As the angle of incidence θ increases,the peak value of $\left| {{R_1}} \right|$ decreases. When the value of $\theta $ approaches to ${\text{ }\!\!\pi\!\!\text{ }}/{4}\;$,the value of reflection coefficient $\left| {{R_1}} \right|$ is much less as compared to the other angles of oblique incidence. In the case of normal incidence,the peak value of $\left| {{R_1}} \right|$ is the largest.
 |
| Fig. 6 Variation of reflection coefficient $\left| {{R_1}} \right|$ plotted for various values of incident angle (for sinusoidal bed) |
In Fig. 7 ,$\left| {{R_1}} \right|$ is plotted against Kh for different porous effect parameter Ph of the undulating bed,while we fixed the angle of incidence θ as ${\text{ }\!\!\pi\!\!\text{ }}/{6}\;$,the ripple wavenumber ph as 0.1,m=2 and n=3. This is most evident in the curves that the peak value of $\left| {{R_1}} \right|$ increases as the porous parameter of the undulating bed increases. This shows that the first-order correction to the reflection coefficient is somewhat sensitive to the changes in the porous parameter of the undulating bed. The peak values of $\left| {{R_1}} \right|$ corresponding to the porous effect parameters Ph=0,0.01,0.05 and 0.1 are attained at k0h=0.56773,0.57425,0.56958 and 0.56528,respectively. Here,it is observed that its peak value is attained when the ripple wavenumber ph of the bottom deformation on the porous bed becomes approximately twice as large as the component of the incident field wavenumber ${k_0}h\cos \theta $ along x-direction. The different curves in Fig. 8 correspond to different sets of elastic parameters of the floating elastic plate(D/h4=0; ε/h=0),(D/h4=1; ε/h=0.01),(D/h4=1.5; ε/h=0.01)and(D/h4=2; ε/h=0.1)while $\theta ={\text{ }\!\!\pi\!\!\text{ }}/{6}\;,\,$ $Ph = 0.1,{\rm{ }}\,ph = 1$ and the number of ripples as 5$\left({m = 2,\,{\rm{ }}n = 3} \right)$are fixed for all these curves. This figure shows that the peak values of $\left| {{R_1}} \right|$ for the oblique incident waves of wavenumber ${k_0}h$ decrease as the values of the flexural rigidity of the elastic plate ${D}/{{{h}^{4}}}\;$ and ${\varepsilon }/{h}\;$ increase. Here also it is observed that the peak values of $\left| {{R_1}} \right|$ are attained when the wavenumber of the bottom undulations on the porous ocean-bed becomes approximately twice the component of the incident field wavenumber along the surface below the floating elastic plate. It may be noted that when ${D}/{{{h}^{4}}}\;$ and ${\varepsilon }/{h}\;$ are taken to be zero(i.e.,the elastic plate is absent),the solution for problems with free surface can be obtained as particular cases.
 |
| Fig. 7 Variation of reflection coefficient $\left| {{R_1}} \right|$ plotted for various values of porosity parameter (for sinusoidal bed) |
 |
| Fig. 8 Variation of reflection coefficient $\left| {{R_1}} \right|$ plotted for various values of elastic parameters (for sinusoidal bed) |
In Fig. 9 ,different curves correspond to different number of ripples in the patch of the deformation on the porous bed. For all these curves,we consider the porous parameter Ph as 0.1,the angle of incidence $\theta $ as ${\text{ }\!\!\pi\!\!\text{ }}/{6}\;$ and the ripple wavenumber ph as 0.1. It is clear from this figure that as the number of ripples in the patch of sinusoidal ripples on the bottom deformation,${\left( m+n \right)}/{2}\;$ increases,the value of ${k_0}h\cos \theta $ converges to a number in the neighborhood of ${k_0}h\cos \theta $ and also the peak value of $\left| {{R_1}} \right|$ increases. On the other hand,when the number of ripples,becomes very large,the reflection coefficient becomes unbounded. That means the perturbation expansion,which is discussed in Eq.(11),ceases to be valid when the reflection coefficient becomes much larger than the deformation parameter,as pointed out by Mei(1985). Its oscillatory nature against Kh is more noticeable with the number of zeros of $\left| {{R_1}} \right|$ increased,but the general feature of $\left| {{R_1}} \right|$ remains the same. In Fig. 10 ,different curves correspond to different ripple wavenumbers ph=0.8,1,1.2 and 1.4 in the patch of the deformation on the porous bed. In this figure,for all curves,we consider $Ph=0.1,\,\text{ }\theta ={\text{ }\!\!\pi\!\!\text{ }}/{6}\;,\,\text{ }m=2$ and n=3. Here also,it has been cleared that the peak values of the reflection coefficient are attained at different values of Kh. The reason is,the value of reflection coefficient $\left| {{R_1}} \right|$(calculated from(39))becomes maximum,only when $ph \approx 2{k_0}h\cos \theta $. It is also observed from this figure that as the ripple wavenumbers increase,the reflection coefficient $\left| {{R_1}} \right|$ becomes smaller than those for the smaller ripple wavenumbers. That means when an oblique incident waves propagates over a porous bed in a fluid having a small ripple wavenumber in the patch of the deformation,a substantial amount of reflected energy can be produced. From the Figs. 5-10,it is also clear that the oscillating nature of $\left| {{R_1}} \right|$ as functions of the wavenumber Kh. Furthermore,the validation of the numerical values of the reflection and transmission coefficients is obtained by showing the energy balance relation(42)is satisfied.
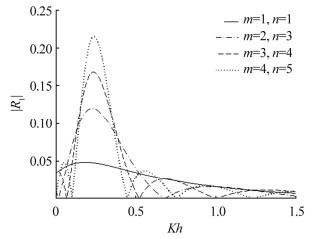 |
| Fig. 9 Variation of reflection coefficient $\left| {{R_1}} \right|$ plotted for various number of ripples in the patch of the deformation (for sinusoidal bed) |
 |
| Fig. 10 Variation of reflection coefficient $\left| {{R_1}} \right|$ plotted for various ripple wave numbers (for sinusoidal bed) |
When an oblique incident surface water waves propagates over a permeable ocean-bed of variable depth in the presence of an infinitely extended floating elastic plate,we have presented the variation of reflection coefficient $\left| R \right|$,transmission coefficient $\left| T \right|$ and the energy balance relation ${\left| R \right|^2} + {\left| T \right|^2}$ for various values of wavenumbers in the following tables. In Table 1,the numerical values for ${k_0}{a_0},\,$ $\left| R \right|,{\rm{ }}\,\left| T \right|$ and ${\left| R \right|^2} + {\left| T \right|^2}$ are given for an exponentially damped deformation profile on the porous bed. In this case,we fixed the elastic parameters as ${D}/{{{a}_{0}}^{4}=1,}\;$ $\,{\varepsilon }/{{{a}_{0}}}\;=0.1$,the angle of incidence waves $\,\theta $ as $\,{\text{ }\!\!\pi\!\!\text{ }}/{6}\;$,the porous parameter $\,P{a_0}$ as 0.1 the depth of fluid taken as $\,{h}/{{{a}_{0}}}\;=5$ and the height of the hump $\,{a_0}b$ as 1. Here we are able to successfully achieve the satisfaction of the energy balance relation almost accurately. Similarly in Table 2,the numerical values for kh,$\left| R \right|,{\rm{ }}\,\left| T \right|$ and ${\left| R \right|^2} + {\left| T \right|^2}$ are given for the particular case of an undulating bottom profile namely a patch of sinusoidal ripples. In this case,we fixed the elastic parameters as ${D}/{{{h}^{4}}=0.1;}\;$ ${\varepsilon }/{h=0.01,}\;$ the angle of incidence waves θ as ${\text{ }\!\!\pi\!\!\text{ }}/{6}\;$,the porous parameter Ph as 0.1,the ripple wavenumber ph as 0.1,the number of ripples as $5\,\left({m = 2,n = 3} \right)$ and the non-dimensional number δ as 0.1. From the numerical values of the reflection and transmission coefficients,we are able to successfully achieve the satisfaction of the energy balance relation or energy identity almost accurately.
| Ka0 | k0a0 | $\,\left| R \right|$ | $\left| T \right|$ | ${\left| R \right|^2} + {\left| T \right|^2}$ |
| 0.01 | 0.159 642 52 | 0.004 243 75 | 1.000 004 84 | 1.000 027 68 |
| 0.21 | 0.277 952 20 | 0.002 821 58 | 1.000 011 55 | 1.000 031 07 |
| 0.41 | 0.430 894 58 | 0.001 034 13 | 1.000 003 78 | 1.000 008 64 |
| 0.61 | 0.583 192 24 | 0.000 236 03 | 1.000 000 38 | 1.000 000 82 |
| 0.81 | 0.700 281 21 | 0.000 063 91 | 1.000 000 04 | 1.000 000 09 |
| 1.01 | 0.787 557 06 | 0.000 023 35 | 1.000 000 00 | 1.000 000 02 |
| Kh | k0h | $\,\left| R \right|$ | $\left| T \right|$ | ${\left| R \right|^2} + {\left| T \right|^2}$ |
| 0.01 | 0.336 159 98 | 0.000 510 92 | 1.000 007 08 | 1.000 014 42 |
| 0.21 | 0.552 970 75 | 0.011 910 71 | 1.000 015 08 | 1.000 172 02 |
| 0.41 | 0.692 330 34 | 0.006 673 32 | 1.000 015 09 | 1.000 074 72 |
| 0.61 | 0.790 438 92 | 0.000 737 09 | 1.000 013 06 | 1.000 026 67 |
| 0.81 | 0.864 497 28 | 0.001 372 77 | 1.000 011 20 | 1.000 024 29 |
| 1.01 | 0.923 590 44 | 0.001 468 67 | 1.000 009 78 | 1.000 021 71 |
In this paper,we have developed a new expression for the Green's function suitable for the solution of scattering problem concerning an oblique incident waves with a small deformation on the ocean-bed,where the upper surface is assumed to be covered by an infinitely extended thin elastic plate and the lower surface is bounded by a porous bottom surface having a small deformation. A simplified perturbation analysis,involving a small parameter δ(<<1),which measures the smallness of the deformation,is employed to reduce the governing BVP to a simpler BVP for the first-order correction of the potential function. The BVP for first-order potential is solved using a method based on Green’s integral theorem with the introduction of suitable Green’s function. This potential function is then utilised to calculate the first-order reflection and transmission coefficients in terms of integrals involving the shape function,representing the bottom deformation. Two special examples of bottom deformation: the exponentially damped deformation and the sinusoidal bed,are considered to validate the results. For the particular example of a patch of sinusoidal ripples,the resonant interaction between the bed and the surface below the elastic plate is attained in the neighborhood of a singularity,when the ripples wavenumbers of the bottom deformation become approximately twice the component of the incident field wavenumber along positive x-directions. This singularity point varies with the flexural rigidity of the floating elastic plate,the angles of incident progressive waves,porous effect parameters of the bed surface and the ripple wavenumbers on the bottom surface. Another result is the reflected energy reduces due to increase in the flexural rigidity elastic plate,the angles of incident progressive waves(except at $\theta ={\text{ }\!\!\pi\!\!\text{ }}/{4}\;$)and the ripple wavenumbers on the bottom surface while the reflected energy increases with porous effect parameters of the bed surface. It is also observed that a very few ripples may be needed to produce a substantial amount of reflected energy so that the amplitude of the generated waves increases. Again,from the derived results,the solutions for problems with impermeable bed can be obtained as particular cases. Also the theory discussed in this paper is valid only for infinitesimal reflection and away from resonance. The main advantage of the present study that follows is that the numerical values of reflection and transmission coefficients are found here to satisfy the energy-balance relation almost accurately which ensures the correctness of the results. The results obtained here are expected to be qualitatively helpful for a wide class of surface waves scattering problems involving an uneven bottom on the porous bed in arctic regions.
| Bennetts, LG, Biggs NRT, Porter D, 2007. A multi-mode approximation to wave scattering by ice sheets of varying thickness. Journal of Fluid Mechanics, 579, 413-443. DOI: 10.1017/S002211200700537X |
| Chamberlain PG, Porter D, 1995. The modified mild-slope equations. Journal of Fluid Mechanics, 291, 393-407. DOI: 10.1017/S0022112095002758 |
| Chwang AT, 1983. A porous-wavemaker theory. Journal of Fluid Mechanics, 132, 395-406 . |
| Das D, Mandal BN, Chakrabarti A, 2008. Energy identities in water wave theory for free-surface boundary condition with higher-order derivatives. Fluid Dynamics Research, 40(4), 253-272. DOI: 10.1016/j.fluiddyn.2007.10.002 |
| Davies AG, 1982. The reflection of wave energy by undulations of the sea bed. Dynamics of Atmosphere and Oceans, 6, 207-232 . |
| Davies AG, Heathershaw AD, 1984. Surface wave propagation over sinusoidally varying topography. Journal of Fluid Mechanics, 144, 419-443. |
| Fox C, Squire VA, 1994. On the oblique reflection and transmission of ocean waves at shore fast sea ice. Philosophical Transactions: Royal Society of London, Series A, 347, 185-218DOI: 10.1098/rsta.1994.0044 . |
| Gu Z, Wang H, 1991. Gravity waves over porous bottoms. Coastal Engineering, 15(5-6), 497-524. DOI: 10.1016/0378-3839(91)90025-C |
| Jeng DS, 2001. Wave dispersion equation in a porous seabed. Coastal Engineering, 28(12), 1585-1599. DOI: 10.1016/S0029-8018(00)00068-8 |
| Kirby JT, 1986. A general wave equation for waves over rippled beds. Journal of Fluid Mechanics, 162, 171-186. |
| Linton CM, Chung H, 2003. Reflection and transmission at the ocean/sea-ice boundary. Wave Motion, 38(1), 43-52. DOI: 10.1016/S0165-2125(03)00003-9 |
| Mandal BN, De Soumen, 2009. Surface wave propagation over small undulations at the bottom of an ocean with surface discontinuity. Geophysical and Astrophysical Fluid Dynamics, 103(1), 19-30. |
| Mandal BN, Gayen R, 2006. Water wave scattering by bottom undulations in the presence of a thin partially immersed barrier. Applied Ocean Research, 28(2), 113-119. DOI: 10.1016/j.apor.2006.06.002 |
| Martha SC, Bora SN, Chakrabarti A, 2007. Oblique water-wave scattering by small undulation on a porous sea-bed. Applied Ocean Research, 29(1-2), 86-90. DOI: 10.1016/j.apor.2007.07.001 |
| Mei CC, 1985. Resonant reflection of surface water waves by periodic sandbars. Journal of Fluid Mechanics, 152, 315-335. DOI: 10.1017/S0022112085000714 |
| Mohapatra S, 2014. Scattering of surface waves by the edge of a small undulation on a porous bed in an ocean with ice-cover. Journal of Marine Science and Application, 13(2), 167-172. DOI: 10.1007/s11804-014-1241-2 |
| Mohapatra S, 2015. Scattering of oblique surface waves by the edge of a small undulation on a porous ocean bed. Journal of Marine Science and Application, 14(2), 156-162. DOI: 10.1007/s11804-015-1298-6 |
| Porter D, Porter R, 2004. Approximations to wave scattering by an ice sheet of variable thickness over undulating topography. Journal of Fluid Mechanics, 509, 145-179. DOI: 10.1017/S0022112004009267 |
| Porter R, Porter D, 2003. Scattered and free waves over periodic beds. Journal of Fluid Mechanics, 483, 129-163. DOI: 10.1017/S0022112003004208 |
| Sahoo T, Chan AT, Chwang AT, 2000. Scattering of oblique surface waves by permeable barrierrs. Journal of Waterway, Port and Coastal Ocean Engineering, 126(4), 196-205. |
| Silva R, Salles P, Palacio A (2002). Linear wave propagating over a rapidly varying finite porous bed. Coastal Engineering, 44(3), 239-260. DOI: 10.1016/S0378-3839(01)00035-7 |
| Staziker DJ, Porter D, Stirling DSG, 1996. The scattering of surface waves by local bed elevations. Applied Ocean Research, 18(5), 283-291. DOI: 10.1016/S0141-1187(96)00021-1 |
| Wang CM, Meylan MH, 2002. The linear wave response of a floating thin plate on water of variable depth. Applied Ocean Research, 24(3), 163-174. DOI: 10.1016/S0141-1187(02)00025-1 |
| Zhu S, 2001. Water waves within a porous medium on an undulating bed. Coastal Engineering, 42(1), 87-101. DOI: 10.1016/S0378-3839(00)00050-8 |



