1 Introduction
Very large floating structures(VLFSs)are floating marine structures measured in kilometers. VLFSs differ from current ship and marine engineering structures that are hundreds of meters long. The current types of VLFS are mainly box and semi-submersible structures. VLFSs generally use a flexible connector that allows the relative motion of modules. Hence, the calculation of connector loads is the key issue that must be addressed in the conceptual design of a multi-module VLFS.
Several studies on VLFS connectors have been conducted in recent years. Connector models generally use the following four forms: rigid module flexible connector(RMFC), flexible module rigid connector(FMRC), flexible module flexible connector, and rigid module rigid connector(RMRC).
The RMFC model assumes that the connector is more flexible than a mobile offshore base(MOB). Each module is considered a rigid body with six degrees of freedom and deformation occurs in the connector. The hydrodynamic interactions between each module are ignored and three-dimensional linear potential flow theory is applied to calculate the hydrodynamic loads in this model.
Wang et al.(1991)considered three-dimensional hydroelastic theory to calculate the hydrodynamic coefficients and wave loads of a multi-module MOB. The study found that unlike that of other monomer and connector modules, the motion response of each MOB module is not greatly affected by hydrodynamics. However, the motions of MOB modules and connector loads are affected by connector stiffness. Du and Ertekin(1991)considered the interaction between modules and used the dual-symmetry composite singularity distribution method to calculate module hydrodynamics.
Wu and Mills(1996)performed a comparative study of rigid splice and elastic connectors. The relative linear displacements between adjacent MOB modules of the rigid splice connector are limited, whereas the relative angular displacements are allowed. Longitudinal motion is allowed when the MOB uses an elastic connector. In the study, the RMFC model was employed to solve the six degrees of freedom motion equation. The hydrodynamic coefficients of each module without speed were subsequently obtained.
Riggs et al.(1998a)assumed that the RMFC model is used in the MOB to simplify connectors to a linear spring and studied the influence of connector stiffness on the response of a five-module MOB. Riggs et al.(1998b)analyzed the motion responses and force among a single module, a five-module disconnected MOB, a five-module MOB with rigid connection, and a five-module MOB with flexible connection.
Riggs et al.(1999), Riggs and Ertekin(1999)analyzed the influence of two different connections and connector damping on MOB motion and explained why different connection schemes have different effects on MOB response. Riggs and Ertekin(1993)used two-dimensional and three-dimensional hydroelasticity methods to predict the responses of a 5-module and 16-module VLFS to regular waves. Kim et al.(1999)compared the motion and connector force of a flexible MOB under eight classes of sea conditions with that of the RMRC and RMFC, respectively. The following conclusions were drawn. The force on the connector of the FMRC model is strongest, followed by that of the RMFC model. The minimum force is observed in the RMRC model connector. The force on the FMRC model connector is twice that on the RMRC model connector. The motion results of the three models have small differences, but the motion results of the RMFC and FMRC models are similar. However, the motion results of the RMFC model are slightly larger.
Several scholars have also proposed the use of the boundary element-finite element method(Hamamoto et al. 1996; Hamamoto and Fujita, 1995)in studying MOB motion response and connector loads. Riggs et al.(2000)compared the MOB responses of the shell finite element and RMFC models. The RMFC model can effectively predict MOB response when the natural frequency and modal of the two models are the same. The results are in good agreement. Edwards and David(1999)attempted to use linear frequency domain hydrodynamic analysis and nonlinear time domain structural analysis to calculate MOB connector loads. The connector load of a nonlinear connector is smaller than that of a linear connector.
Yu et al.(2003, 2004), Shu et al.(2002) and Ding et al.(2005)conducted a numerical simulation and an experimental study on MOB connector loads and dynamic response and obtained meaningful results. The connector stiffness significantly affected its load, wave headings affected the force between modules, the maximum amplitude of connector longitudinal load was greater than the lateral and vertical loads, and the longitudinal load of the connector reached the maximum at the 75° wave direction.
Watanabe and Utsunomiya(1996)used the finite element program and the time domain method to obtain the elastic response of a circular VLFS under impact force. Watanabe et al.(1998)used the time domain method to study the responses of VLFSs on l and ing planes. Endo(2000)analyzed the transient response of VLFSs under dynamic loading caused by plane takeoff and l and ing.
Kashiwagi(2000)studied the calculation method for the elastic response of VLFSs under external force. The study employed the Galerkin method to obtain the amplification factor of the modal function of the linear system synchronization differential equation and discussed the accuracy problems posed by the infinite frequency memory function and added mass. Kashiwagi and Higashimachi(2003)calculated the elastic transient deformation of a pontoon-type VLFS during plane takeoff and l and ing by using the time-domain modal analysis method, which considers the hydrodynamic memory effect problems and the accuracy of hydrodynamic coefficients. Fujikubo(2005)studied VLFSs under unexpected loads to compare the damages under different crash situations.
In the present study, the RMFC model is employed to calculate the time history curves of VLFS connector loads under impact loading. Only the results under wave loads are compared with those under the combined action of wave and impact loads. A time domain calculation method for solving VLFS connector loads is proposed.
2 Mathematical theoryThe dynamic responses of objects under impact load can be analyzed by time domain methods. The various types of coefficients of time domain equations are obtained from the frequency domain equation. However, time domain analysis methods, especially for the calculation of memory function, are time consuming. Time domain and frequency domain differential equations are found to be similar. Time domain differential equations can be obtained through frequency domain differential equations by Fourier transform. The added mass of time domain differential equations is equivalent to the infinite frequency-added mass of the frequency domain. The memory function can be obtained by the convolution of the damping coefficients of each frequency in the frequency domain.
The Longuet-Higgins model is used to simulate r and om wave loads, which can be seen as a superposition of regular waves with different frequencies. The frequency can be selected by applying the Monte Carlo method and the phase angle can be r and omly selected.
2.1 Time domain motion equations of floating body in wavesThe time domain equations of the motion of a floating body in waves are as follows:
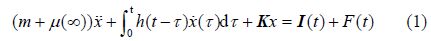
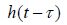 is the memory function, K is the stiffness matrix, including the fluid restoring force and structural stiffness matrix T(t) is the impact load acting on the floating body, and F(t) denotes the wave loads acting on the floating body. The relevant parameters can be found in the work of Guan et al.(2011).
is the memory function, K is the stiffness matrix, including the fluid restoring force and structural stiffness matrix T(t) is the impact load acting on the floating body, and F(t) denotes the wave loads acting on the floating body. The relevant parameters can be found in the work of Guan et al.(2011).
To solve this equation, the infinite frequency-added mass and impulse function should be determined first.
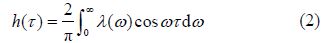
As added mass begins to converge with the increase in frequency, the infinite frequency-added mass in ![]() can be replaced by a relatively high frequency-added mass to meet the accuracy requirements. Impulse function
can be replaced by a relatively high frequency-added mass to meet the accuracy requirements. Impulse function ![]() can be obtained by the convolution of the damping coefficient, which is shown in formula(2).
can be obtained by the convolution of the damping coefficient, which is shown in formula(2).
The Longuet-Higgins model is used to simulate irregular wave loads. The model assumes that the sea comprises finite regular waves at a r and om phase. These waves are limited to a Gaussian r and om distribution, whereas the irregular waves are described by the wave spectrum. The Jonswap spectrum is employed in this study.
The synthesized wave surface is expressed as
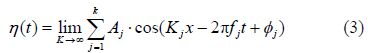
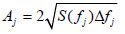 is the wave height of the jth wave, is the jth frequency,
is the wave height of the jth wave, is the jth frequency, This study analyzes a VLFS that is assembled by five identical modules from end to end. Each module consists of an upper body, two parallel lower bodies, and eight columns(four columns on each side). Adjacent modules are connected by two connectors located in the upper deck of the module and symmetrical to the center buttock. In Fig. 1, the modules and connectors are labeled as M1-M5 and C1-C8, respectively. The dimensions of a single VLFS module(Hamamoto et al., 1996)are provided. The upper body length is 300 m, the width is 125 m, the height is 17.5 m, the column height is 27.5 m, the diameter is 25 m, the column transverse spacing is 90 m, and the vertical spacing is 67.5 m. The lower body length is 275 m, the width is 34.5 m, the height is 12.5 m; the center of gravity away from the baseline height is 30.99 m, the design draft is 28.95 m, the design displacement is 2.975×108 kg, and the radius of gyration along the X, Y and Z directions are 50.41 m, 80.49 m, and 90.67 m, respectively(Fig. 2).

|
| Fig. 1 VLFS top view |

|
| Fig. 2 Cross-sectional view of VLFS |
Two methods are used to calculate collision loads: the use of an empirical formula and a numerical simulation through commercial software. The empirical formula of collision forces includes Worthing formula, US highway bridge design specifications, US highway bridges ship collision guide specifications, AASHTO, Norway bridge load specifications, the Norway Public Roads Administration norms, Nordic Public Roads Administration specifications, and the modified Worthing formula. The calculation of ship collision loads shown in Table 1 is different because of these different formulas, specifications, and numerical simulations. The conservative maximum value is selected to calculate the equation.
| Formula or specification | Results of collision load/MN |
| Worthing formula | 82±41 |
| Highway bridge design specifications | 90 |
| AASHTO | 92 |
| Norway bridge load specifications | 84 |
| Norway public roads administration norms | 114 |
| Nordic public roads administration specifications | 94 |
| Modified Worthing formula | 104 |
The conditions set in this study are as follows: a bulk carrier rate of 4 m/s and a displacement of 50000 t(DWT = 35000 t)runs into a column of the VLFS. The impact load, which is the force acting on the VLFS column, is constant at 100 MN, and the duration of the impact load is 3 s(Fig. 3).

|
| Fig. 3 Definition of impact load |
Sea state is calculated as follows: characteristic wave height is Hs=8.8 m and the peak period is Tp=14.2 s. In simulating sea conditions the Jonswap spectrum is used to simulate the sea state spectrum. The low limit frequency is fmin=0.1 rad/s, the upper limit frequency is fmax=5.0 rad/s and the frequency in this range is divided into 50 equal portions to simulate r and om waves. The connector is equivalent to springs in three directions. The stiffness values in three directions are Kx=1×108 N/m, Ky=1×1012 N/m and Kz=1×1012 N/m. The collision positions are presented in Fig. 4. The wave angles are 0° and 75°. The time domain numerical solution method is employed to simulate the connector loads of the VLFS under collision load in 100s waves. Initial displacement, velocity and acceleration are all set to zero. To simulate sea conditions steadily the VLFS under the first 50s of wave action and subjected to an impact load for 3s with a size of 1×108 N is considered.

|
| Fig. 4 Collision load position |
Fig. 5-Fig. 10 show the loads of the connectors C1 and C2 along the X, Y and Z directions at a wave angle of 0°. Fig. 11 and Fig. 16 are the load time curves of connectors C1 and C2 along the X, Y and Z directions at a wave angle of 75°.

|
| Fig. 5 Connector C1 load in X direction(wave direction angle of 0°) |

|
| Fig. 6 Connector C1 load in Y direction(wave direction angle of 0°) |

|
| Fig. 7 Connector C1 load in Z direction(wave direction angle of 0°) |

|
| Fig. 8 Connector C2 load in X direction(wave direction angle of 0°) |

|
| Fig. 9 Connector C2 load in Y direction(wave direction angle of 0°) |

|
| Fig. 10 Connector C2 load in Z direction(wave direction angle of 0°) |

|
| Fig. 11 Connector C1 load in X direction(wave direction angle of 75°) |

|
| Fig. 13 Connector C1 load in Z direction(wave direction angle of 75°) |

|
| Fig. 14 Connector C2 load in X direction(wave direction angle of 75°) |

|
| Fig. 15 Connector C2 load in Y direction(wave direction angle of 75°) |

|
| Fig. 16 Connector C2 load in Z direction(wave direction angle of 75°) |
Only the connector loads of the VLFS under wave loads are compared with those under the combined action of wave and impact loads. Impact load has a significant influence on connector loads. In this work, the connector load increases because of the effects of impact load from 50 s to 100 s.
When the connectors at different wave direction angles are the same, the stiffness of the connector in the Y and Z directions is greater than that in the X direction. This condition causes the change rule of load to be different in the X, Y and Z directions. Similar to connector C1 at 0° and 75° wave headings, the loads along the X direction are 60×106 N as shown in Fig. 5 and Fig. 11. Fig. 6 and Fig. 12 show that the load increases to 10×106 N. Fig. 7 and Fig. 13 show that in the Z direction between the amplitude of X and Y the load increases to 20×106 N.

|
| Fig. 12 Connector C1 load in Y direction(wave direction angle of 75°) |

|
| Fig. 13 Connector C1 load in Z direction(wave direction angle of 75°) |
1)Connector load in Y direction. Under 0° wave heading and under wave loads only, the connector load in the Y direction is zero. From 50 s to 53 s, a rectangular impulse response of the connector load is observed. Due to the impact loads the impulse width is also 3 s. After 3 s, a high-frequency continuous oscillation of load is observed in the Y direction. The maximum load of connector C1 in the Y direction is approximately 10×106 N(Fig. 6).
2)Connector load in Z direction. A rectangular impulse response of the connector load in the Z direction is observed between 50s and 53s. High-frequency oscillations along the Z direction are observed in the connector under the combined action of wave and impact loads because of the high stiffness and natural vibration frequencies in the Z direction. The equilibrium position of the high-frequency oscillations under the combined action of wave and impact loads is the same as that of the connector load under wave load only(Fig. 7, Fig. 10, Fig. 13, and Fig. 16).
3)Comparison of connectors C1 and C2. The maximum load of connectors C1 and C2 are almost the same in the X direction. In the Y and Z directions, the impulse of connector C1 load is more noticeable than that of C2. After collision, the two connector loads are shaken violently at similar oscillation amplitudes. The change laws of the connector loads under wave headings of 0° and 75° are the same, but are greater than that under the wave heading of 75°.
Under the different wave headings of 0° and 75°, the connector loads in the Y direction are different. When the angle of the wave is 0°, the connector load in the Y direction is caused by impact loads only(Fig. 6). The connector load in the Y direction is caused by both impact load and wave force at a wave heading of 75°(Fig. 12).
5 ConclusionsThe time domain method is used to solve the connector load response of a VLFS under impact loads. The connector loads of the VLFS under wave loads only and under the combined action of wave, and impact loads are calculated and the effects of impact load on the connector load are obtained. The results under wave loads only are compared with those under the combined action of wave and impact loads. Under impact loads, the high-frequency oscillation occurs in connectors C1 and C2. The load curve of the connectors gradually becomes smaller at a certain time frame after the impact load is finished. Under different wave headings, the maximum value of the connector loads of C1 and C2 is in the X direction, followed by those in the Z and Y directions. However, the time history curves of the connector loads in the X, Y and Z directions are similar. The loads of connectors C1 and C2 under a wave heading of 75° are greater than those under a wave heading of 0°. The connector loads of C1 and C2 in the Y direction are zero under a wave heading of 0°, but the connector load emerges in t he Y direction under a wave heading of 75°.
The time domain calculation method of connector load in this paper offers a certain reference value for the future research and manufacture of Chinese VLFS.
| Ding W, Yu L, Li RP, Yao MW (2005). Experimental research on dynamic responses of mobile offshore base connector. The Ocean Engineering, 23 (2), 11-15. (in Chinese) DOI: 10.3969/j.issn.1005-9865.2005.02.002 |
| Du S, Ertekin RC (1991). Dynamic response analysis of a flexibly joined-multi-module very large floating structure.Proceedings of Oceans '91, IEEE, Honolulu, USA, 1286-1293 . |
| Edwards MJ, David R (1999). Non-linear time-domain response of connected mobile offshore base unit using linear frequency domain hydrodynamic forces. Proceedings of the Third International Workshop on Very Large Floating Structure. Honolulu, Hawaii, USA, 155-161. |
| Endo H (2000). The behavior of a VLFS and an airplane during takeoff/landing run in wave condition. Marine Structures, 13(4-5), 477-491. DOI: 10.1016/S0951-8339(00)00020-4 |
| Fujikubo M (2005). Structural analysis for the design of VLFS. Marine Structures, 18(2), 201-226. DOI: 10.1016/j.marstruc.2005.07.005 |
| Guan YF, Yuan YB, Gu JY (2011). Influence of ship collision on connector loads of MOB. Shipbuilding of China, 52(4), 177-185. (in Chinese) DOI: 10.3969/j.issn.1000-4882.2011.04.020 |
| Hamamoto T, Fujita K (1995). Three-dimensional BEM-FEM coupled dynamic analysis of module-linked large floating structures.Proc 5th Int Offshore Polar Eng Conf, Hague, Netherlands, 3, 392 . |
| Hamamoto T, Hayashi T, Fujita K (1996). 3D BEM-FEM coupled hydroelastic analysis of irregular shaped module-linked large floating structures. Proc 6th Int Offshore Polar Eng, Conf, Los Angeles, USA, 1, 362-369. |
| Kashiwagi M (2000). A time-domain mode-expansion method for calculating transient elastic responses of a pontoon-type VLFS. Journal of Marine Science and Technology, 5(2), 89-100. DOI: 10.1007/PL00010631 |
| Kashiwagi M, Higashimachi N (2003). Numerical simulations of transient responses of VLFS during landing and take-off of an airplane. Proc Int Symp Ocean Space Utilisation Technol, National Maritime Research Institute, Tokyo, Japan, 83-91. |
| Kim D, Chen L, Blaszkowshi Z, Ray J (1999). Linear frequency domain hydroelastic analysis for McDermon's mobile offshore base using WAMIT. Proceedings of the Third International Workshop on Very Large Floating Structure. Honoluu, Hawaii, USA, 105-133. |
| Riggs HR, Ertekin RC, Mills TRJ (1998a). Impact of connector stiffness on the response of a multi-module mobile offshore base. Proceeding the International Offshore and Polar Engineer Conference, Montréal, Canada, 1, ISOPE, 200-207. |
| Riggs HR, Ertekin RC, Mills TRJ (1998b). Wave-induced response of a 5-module mobile offshore base. 17th International Conference on Offshore Mechanics and Arctic Engineering, Lisbon , Portugal, OMAE98-4440. |
| Riggs HR, Ertekin RC, Mills TRJ (1999). Characteristics of the wave response of mobile offshore bases. Proceeding 18th International Conference on Offshore Mechanics and Arctic Engineering, Saint John's, Canada, 1-9. |
| Riggs HR, Ertekin RC (1999). Response characteristics of serially connected semisubmersibles. Journal of Ship Research, 43(4), 229-240. |
| Riggs HR, Ertekin RC (1993). Approximate methods for dynamic response of multi-module floating structures. Marine Structures, 6(2-3), 117-141. DOI: 10.1016/0951-8339(93)90016-V |
| Riggs HR, Ertekin RC, Mills TRJ (2000). A comparative study of RMFC and FEA models for the wave-induced response of a MOB. Marine Structures, 13(4-5), 217-232. DOI: 10.1016/S0951-8339(00)00029-0 |
| Shu Z, Li RP, Wang ZJ (2002). A study on the motion of very large floating structure in waves. China Offshore Platform, 17(3), 1-5. (in Chinese) DOI: 10.3969/j.issn.1001-4500.2002.03.001 |
| Wang DY, Riggs HR, Eriekin RC (1991). Three-dimensional hydroelastic response of a very large floating structure. Offshore and Polar Engrg., 1(4), 307-316. |
| Watanabe E, Utsunomiya T (1996). Transient response analysis of a VLFS at airplane landing. Proc IntWorkshopon Very Large Floating Structures, Hayama, Kanagawa, Japan, 243-7. |
| Watanabe E, Utsunomiya T, Tanigaki S (1998). A transient response analysis of a very large floating structure by finite element method. Structural Engrg/Earthquake Engrg, JSCE, 15(2), 155-163. |
| Wu CF, Mills TRJ (1996). Wave induced connector loads and connector design for the mobile offshore base. Proceeding of the Second International Workshop on Very Large Floating Structure, Hayama, Japan, 387-392. |
| Yu L, Ding W, Li RP (2004). Effect of the multiple modules interaction on MOB connector loads. The Ocean Engineering, 22(1), 25-31. (in Chinese) DOI: 10.3969/j.issn.1005-9865.2004.01.004 |
| Yu L, Li RP, Shu Z (2003). Dynamic characteristics of mobile offshore base connectors. Journal of Shanghai Jiao Tong University, 37(8), 1159-1163. (in Chinese) DOI: 10.3321/j.issn:1006-2467.2003.08.005 |



