船舶动态路径规划在现代航海领域中扮演着至关重要的角色,船舶在航行过程中面临着复杂的海况、繁忙的航道、多变的天气条件以及严格的环保要求,为船舶设计出一条既安全又经济的航线就需要不断根据外界条件的变化不断调整航线。船舶有效的动态路径规划能够确保船舶在预定时间内,以最小的能耗和最低的风险,从出发点安全、准时地到达目的地。动态路径规划能够显著提高航行的安全性[1]。通过对海洋气象数据、海流情况、障碍物分布等因素的综合分析,规划系统能够为船舶提供避开潜在危险的最优航线。这不仅包括避开已知的障碍物,如冰山、礁石和其他船舶,还包括对突发情况的应对,比如突如其来的风暴或海流变化[2]。通过优化航线,可以减少不必要的航程,从而节省燃料消耗,减少排放,延长船舶的维护周期。此外,优化的航线有助于减少航行时间,提高船舶的周转率,这对于需要快速响应市场需求的航运公司来说尤为重要。
在进行船舶动态协同路径规划时,控制算法是一个研究难点,船舶的动态路径规划是一个多目标优化问题,需要同时考虑多个目标,如最短航程、最快到达时间、最小燃料消耗、避免环境敏感区域等[3 - 4]。这些目标之间可能存在冲突,因而不能使用简单的多元回归来解决此类问题。另外,动态协同路径规划的实现需要实时收集和处理大量的环境数据和船舶状态数据,这要求船舶具备强大的数据处理能力和计算能力。不同船舶之间需要建立有效的协同决策机制,确保各船舶之间的行动协调一致,避免冲突和碰撞。将人工智能算法、大数据收集与分析和卫星通信技术等应用到船舶动态路径规划中,可以实现实时更新和自适应调整,以应对不断变化的海洋环境。本文将模拟退火算法和遗传算法进行有效结合,并将其应用到船舶动态协同路径规划中,并对规划路径进行仿真验证。
1 船舶动态协同路径规划模型 1.1 动态路径规划问题描述船舶动态路径规划是一个复杂的问题,需要考虑多种因素,包括船舶的动态特性、海洋环境、障碍物以及遵守海上交通规则等。最佳路径函数F为:
| $ F = {w_1} \cdot L + {w_2} \cdot S + {w_3} \cdot E + {w_4} \cdot T \text{。} $ | (1) |
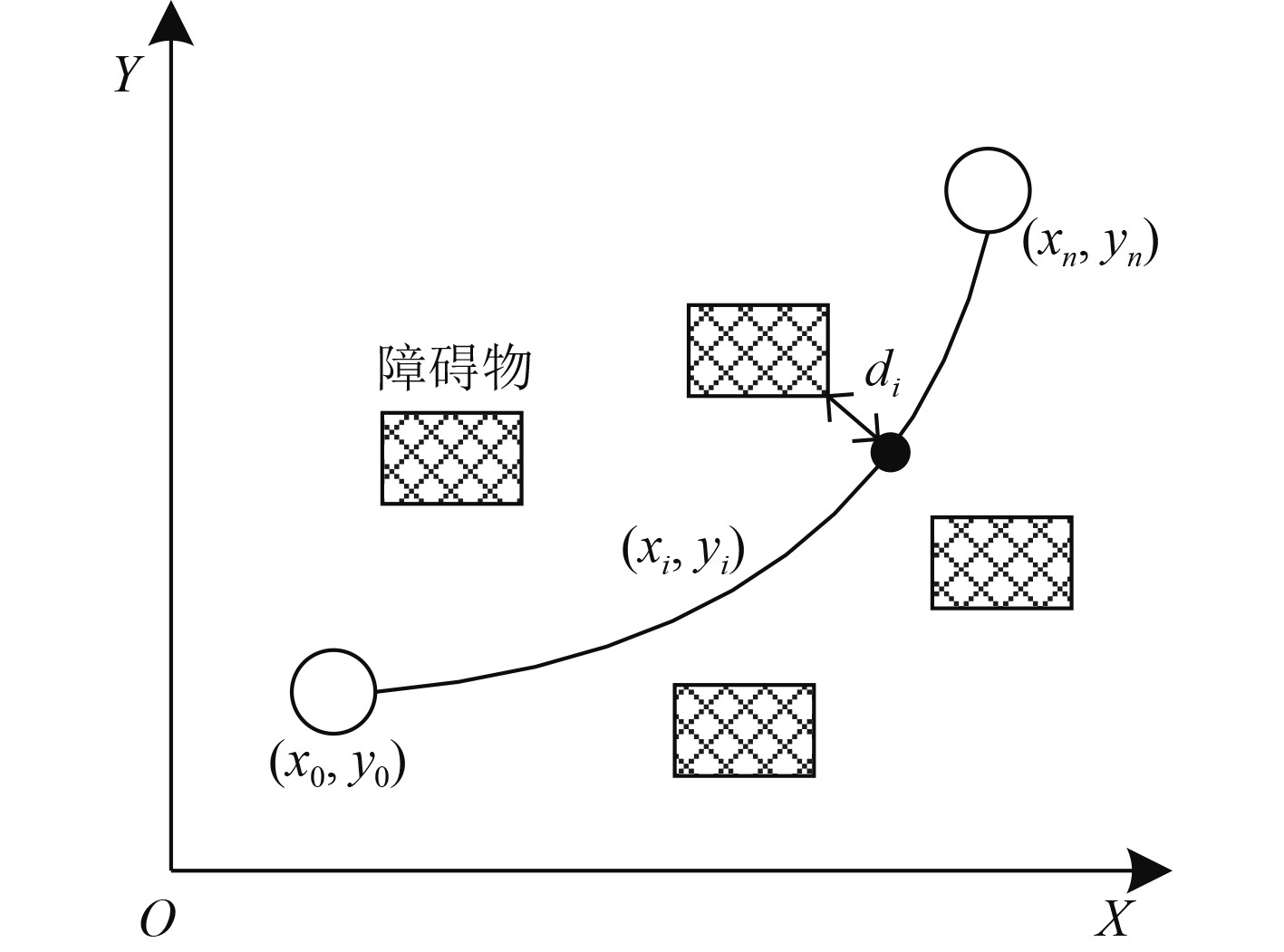
式中:L为路径长度;S为安全性指标,包括与障碍物的距离、水深等;E为经济性指标;T为时间效率指标,如航行时间;w1、w2、w3、w4为权重系数,用于平衡不同指标的重要性。在以上因素中,路径长度最为重要,这是由于路径长度不仅会影响到达时间,同时还会直接影响经济效益,优先对路径长度最优进行规划,其次对安全性进行规划。图1为路径规划示意图。
|
图 1 路径规划示意图 Fig. 1 Path planning diagram |
1)路径长度代价函数
对于路径长度最优的规划而言,确定从起始点到目标点的路径,同时考虑路径的长度、风险因素、规则约束等。定义路径长度代价用于计算船舶在规划路径上行驶的总距离,这个代价需要最小化以找到最优路径。路径长度的代价公式通常是基于路径上各个点之间的距离累加得到[5]。
假设船舶的规划路径由一系列离散的点组成,这些点在二维平面上可以表示为(xi, yi),其中i是点的索引(i=0,1,2,···,n),n是路径上的点的总数,(x0, y0)为起点,(xn, yn)为终点。
对于路径上的任意2个相邻点(xi, yi)和(xi+1, yi+1),它们之间的欧几里得距离di计算式为:
| $ {d_i} = \sqrt {{{({x_{i + 1}} - {x_i})}^2} + {{({y_{i + 1}} - {y_i})}^2}} \text{。} $ | (2) |
路径的总长度L是所有相邻点之间距离的累加,即:
| $ L = \sum\limits_{i = 0}^{n - 1} {{d_i}} \text{。} $ | (3) |
综合式(2)和式(3),可得:
| $ L = \sum\limits_{i = 0}^{n - 1} {\sqrt {{{({x_{i + 1}} - {x_i})}^2} + {{({y_{i + 1}} - {y_i})}^2}} } \text{,} $ | (4) |
代价函数J为:
| $ J = \sum\limits_{i = 0}^{n - 1} {((} {x_{i + 1}} - {x_i}{)^2} + {({y_{i + 1}} - {y_i})^2}) \text{。} $ | (5) |
2)安全性代价函数
在寻求动态最佳路径的过程中,需要不断地对船舶周围的障碍物进行探测,并计算障碍物和船舶之间的距离。动态路径规划中是不断地设置下一个目标点,然后进行动态调整,以达到安全到达的目的。传统方法一般都是通过设置安全距离阈值来实现,这种方法可以在最大程度上保证船舶航行安全,但并不足以体现船舶整体规划路线的安全性代价[6]。本文采用动态惩罚函数来确保船舶安全,即安全性代价函数Jsafety和距离的平方相关,其定义为:
| $ {J_{{\text{safety}}}}({D_{{\text{actual}}}}) = \max (0,k \cdot {({D_{{\text{safe}}}} - {D_{{\text{actual}}}})^2}) \text{。} $ | (6) |
式中:k为一个正常数,用于调整惩罚的强度。指数惩罚函数比线性惩罚函数更加敏感,可以更快地对危险情况进行响应。
1.2 多种算法在路径规划中的应用在船舶路径规划方面,国内外学者已经有了长久的研究,且取得了非常多的理论和实践成果,如LOS循迹控制算法、粒子群算法、自动避碰算法等。本文主要研究模拟退火算法、遗传算法在路径规划中的应用。
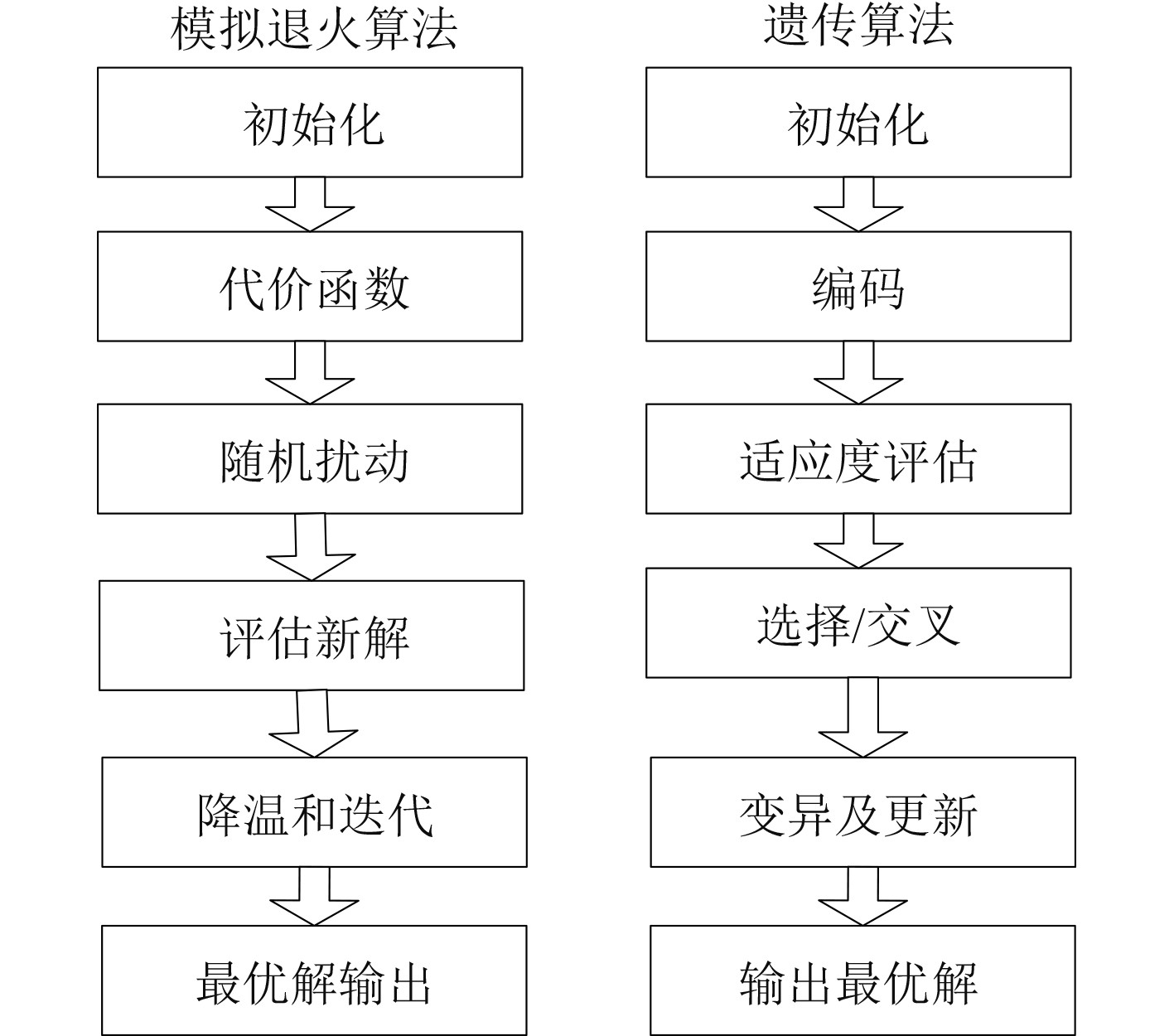
模拟退火算法(Simulated Annealing, SA)和遗传算法(Genetic Algorithm, GA)是2种常用的启发式搜索算法,它们在解决船舶路径规划中有着广泛的应用。图2为2种算法的基本流程。
|
图 2 2种算法的基本流程 Fig. 2 The basic flow of the two algorithms |
模拟退火算法选择一个初始的船舶路径作为当前解,并设定一个初始温度(高温)和冷却速率。定义一个代价函数来评估当前路径的质量,通常包括路径长度、安全性(与障碍物的距离)、遵守海上避碰规则等因素。在当前解的基础上进行随机扰动,生成一个新的路径解。这涉及改变路径上的某些点的位置或改变路径的某些部分。然后计算新解的代价,并与当前解的代价进行比较。如果新解比当前解好(代价更低),则接受新解作为当前解。如果新解比当前解差,根据一定的概率接受新解,这个概率通常与当前温度和新旧解的代价差有关,即Metropolis准则。
逐渐降低温度,并重复上述过程,直到达到预定的终止条件(如温度低于某个阈值或达到最大迭代次数),最终输出最优解。
遗传算法首先会生成一组随机的路径解作为初始种群,每个解称为一个个体。将路径解编码为染色体,通常是一串表示路径点的数字序列。计算每个个体的适应度,即根据代价函数评估其路径的质量,根据适应度选择优秀的个体进行繁殖,较差的个体会被淘汰。随机选择一对个体作为父母,通过交叉操作生成新的个体。这涉及交换父母染色体中的某些部分。以一定的概率对个体的染色体进行变异,以引入新的遗传多样性,涉及随机改变染色体中的某些基因。通过选择、交叉和变异操作生成新的种群。重复上述过程,直到满足终止条件(如达到最大迭代次数或适应度收敛)。在算法结束时,输出种群中适应度最高的个体对应的路径作为最终解。
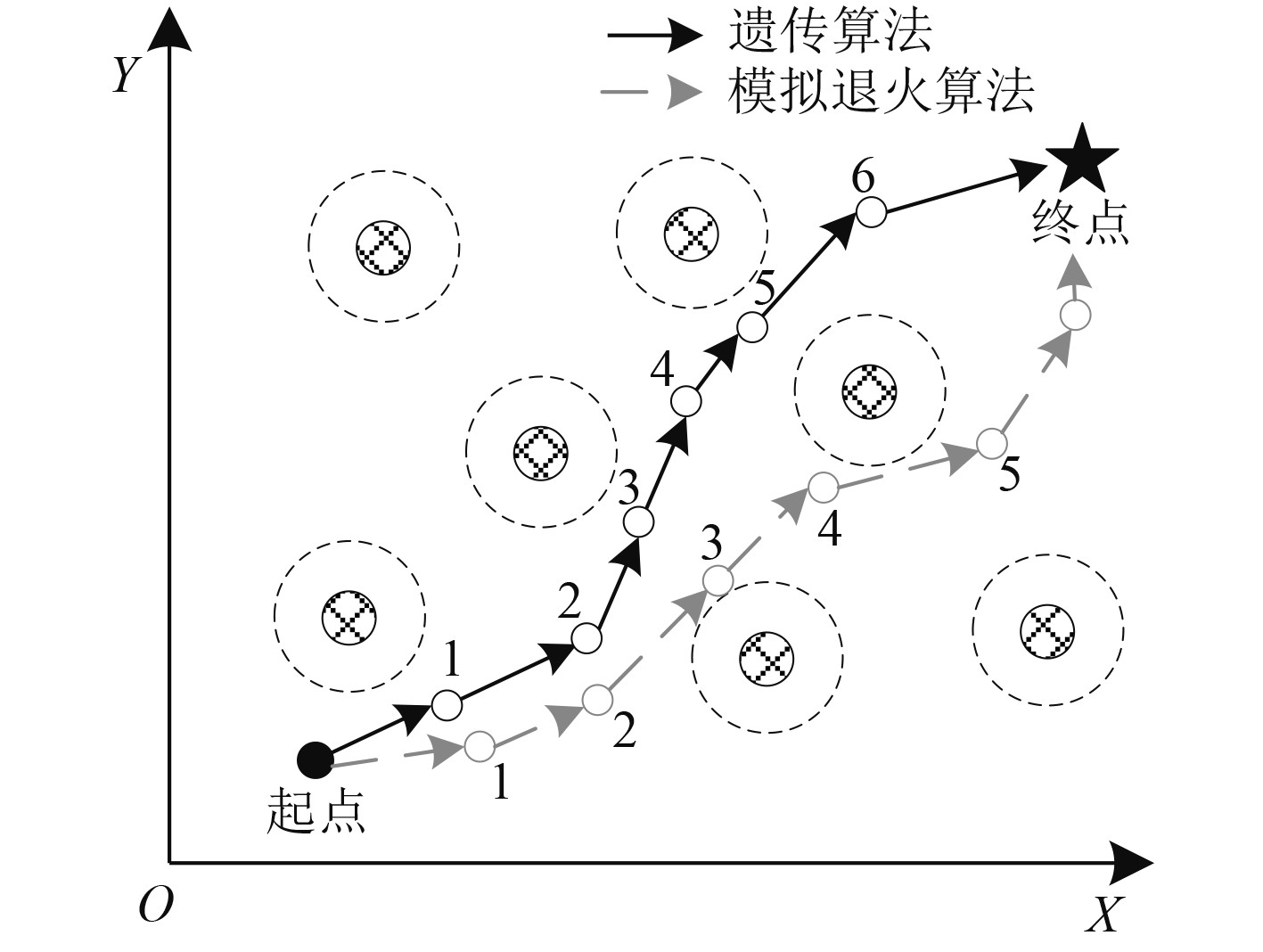
使用2种算法对静态船舶路径进行规划,2种算法均迭代
|
图 3 不同算法静态路径规划仿真对比 Fig. 3 Simulation comparison of static path planning with different algorithms |
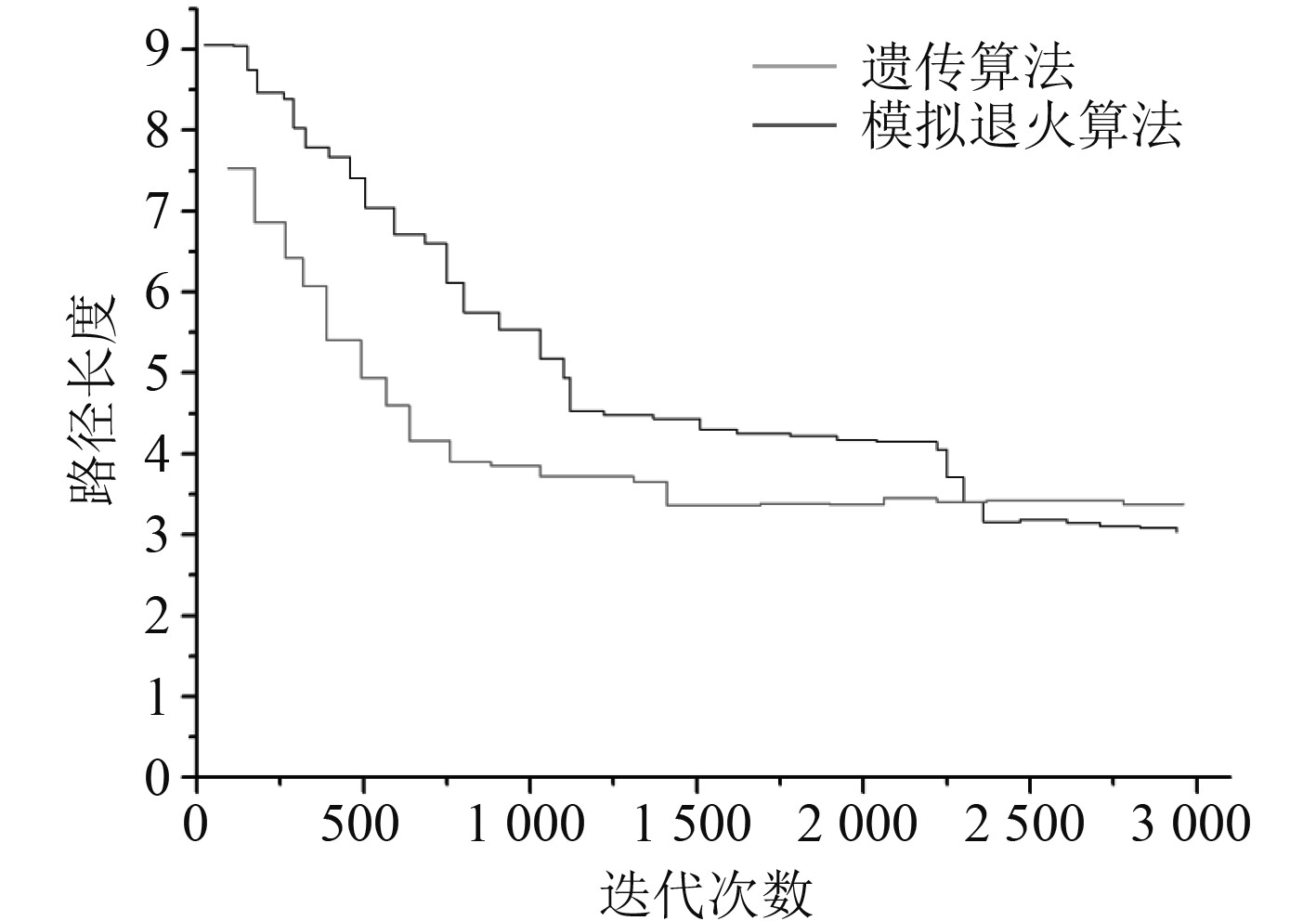
以2种算法迭代次数和最短路径进行对比,得到结果如图4所示。可以发现模拟退火算法在搜索速度上具有一定优势,遗传算法在求解过程中存在速度较慢的问题,但是当迭代超过
|
图 4 不同算法迭代次数 Fig. 4 Different algorithm iteration times |
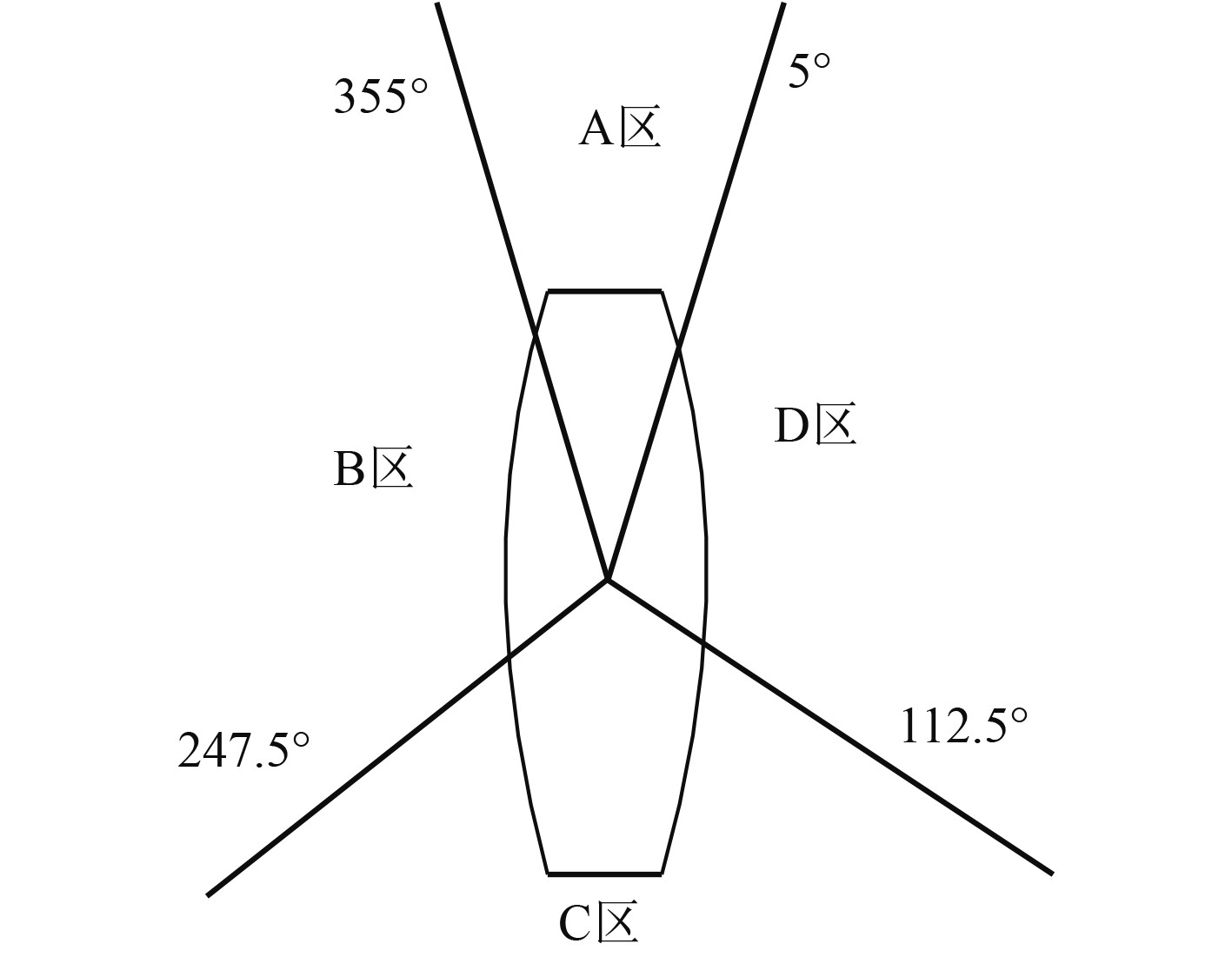
对单船动态路径规划,只需要选择模拟退化算法或者遗传算法对路径进行规划即可,对于多船动态协同路径规划而言,需要考虑船舶自身的速度、航向以及其他船舶的动态情况,如图5所示。在海洋航行中,能见度良好的条件下,国际海上避碰规则对船舶相遇的情况进行了明确的划分,以确保航行安全。
|
图 5 多船舶避碰区域划分 Fig. 5 Multi-ship collision avoidance area division |
1)A区定义为船舶舷角在(0°,5°)和(355°,360°)的范围内,这通常指的是正面接近的情况。在这种情况下,船舶应采取向右转向的避让措施,舵角通常大于15°。
2)B区代表交叉相遇的情况,其舷角范围为(247.5°,355°)。
3)C区则指超车情况,舷角在(112.5°,247.5°)之间,此时被追越的船通常不采取行动。
4)D区同样表示交叉相遇,舷角范围为(5°,112.5°),在这种情况下,船舶应向右转以避让来船。
在能见度受限的海洋环境中,船舶应根据来船的相对方位采取相应的避让行动。具体而言,对于舷角在(0°,90°)和(270°,360°)范围内的来船,船舶应向右转;而对于舷角在(90°,180°)和(180°,270°)范围内的其他船舶,船舶应采取左转避让。
为了将这些避碰规则和船员的航海经验有效地整合到船舶导航模型中,对这些规则进行数学量化并将它们转换为具体的航行限制。当船舶与另一艘船舶的距离小于6 n mile时将设置一个航行限制区域,以确保船舶有足够的时间和空间来采取适当的避让措施。
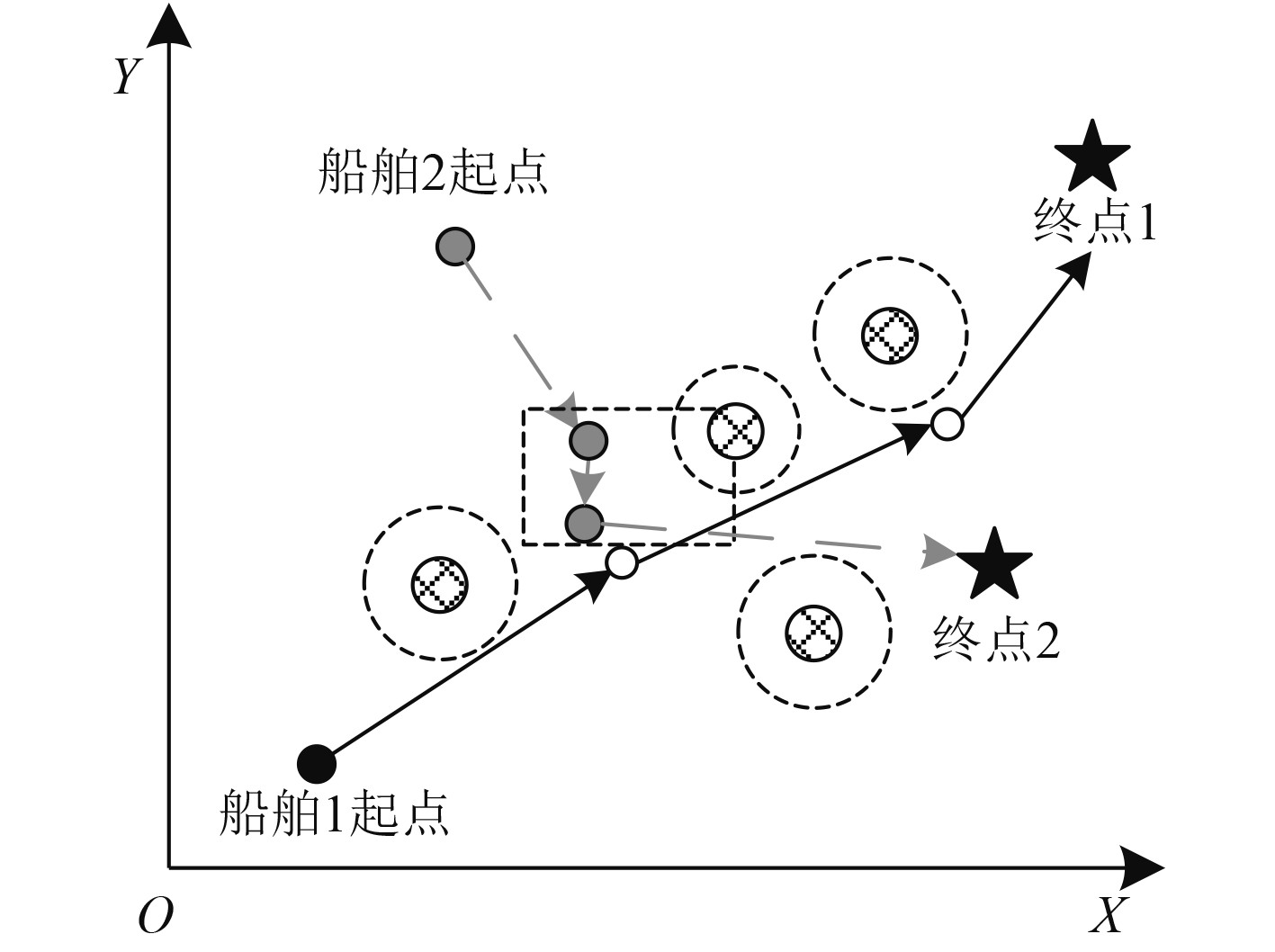
2.2 多船协同动态路径规划实现多船协同动态路径规划的实现过程较为复杂,本文以2艘船舶正面交汇的情况进行说明,最终的仿真结果如图6所示,虚线矩形框中是船舶2采取避让动作向右转向,最终两船安全通过,且避开了所有障碍物。当障碍物和船舶数量较多时,其规划难度将会呈指数级增长。
|
图 6 多船舶动态路径规划 Fig. 6 Multi-ship dynamic path planning |
为了保证船舶航行安全并实现最短路径长度,本文对模拟退火算法和遗传算法在动态协同路径规划中的应用进行研究,对动态路径规划问题进行了数学描述,对模拟退火算法和遗传算法在船舶路径规划中进行仿真,结果表明,遗传算法在求解过程中速度较慢,当迭代超过
| [1] |
陈雯琦. 多无人机协同目标追踪的路径规划研究[D]. 西安:西安工业大学, 2024.
|
| [2] |
戴晟潭, 王寅, 尚晨晨. 基于深度强化学习的多无人车协同路径规划方法[J/OL]. 北京航空航天大学学报, 1−12, 2024. DAI Chengtan, WANG Yin, SHANG Chenchen. A method of multi-UAV cooperative path planning based on deep reinforcement learning [J/OL]. Journal of Beijing University of Aeronautics and Astronautics, 1−12, 2024. |
| [3] |
方城亮, 杨飞生, 潘泉. 基于MASAC强化学习算法的多无人机协同路径规划[J]. 中国科学: 信息科学, 2024, 54(8): 1871-1883. FANG Chengliang, YANG Feisheng, PAN Quan. Multi-UAV cooperative path planning based on MASAC reinforcement learning algorithm[J]. Science China: Information Sciences, 2024, 54(8): 1871-1883. |
| [4] |
屈禹先. 基于自适应策略约束条件下多源异构体的学习路径规划研究[D]. 西安:西安理工大学, 2024.
|
| [5] |
冒如权, 丁峰, 杨恒瑞. 多无人船协同多目标遍历路径规划[J]. 船舶工程, 2024, 46(5): 97-102. MAO Ruquan, DING Feng, YANG Hengrui. Multi-UUV cooperative multi-target traversal path planning[J]. Ship Engineering, 2024, 46(5): 97-102. |
| [6] |
王健雄, 包菊芳. 融合多策略改进的蚁群算法机器人路径规划研究[J]. 重庆工商大学学报(自然科学版), 2024, 8(1): 1-9. WANG Jianxiong, BAO Jufang. Research on robot path planning based on multi-strategy improved ant colony algorithm[J]. Journal of Chongqing Technology and Business University (Natural Science Edition), 2024, 8(1): 1-9. |
 2024, Vol. 46
2024, Vol. 46
