0 引　言

舰船在复杂多变的海域环境中导航，其准确性直接关系到舰船的安全与任务的完成^[1]。然而，舰船导航过程中不可避免地会受到各种噪声和干扰的影响，如海洋环境噪声、电磁干扰、设备误差等，这些因素会严重降低导航信号的精度和稳定性^[2]。因此，对舰船导航信号进行有效的滤波处理，以提高其准确性和抗干扰能力，成为了舰船导航技术中亟待解决的问题。

例如，为解决传统信号滤波方法在处理时变噪声和非线性系统时存在的局限性问题，靳凯迪等^[3]通过引入可变遗忘因子和渐消记忆机制，结合变分贝叶斯框架，实现对信号的自适应滤波。采用可变遗忘因子根据信号的历史信息和当前状态对其进行动态调整，有效应对时变噪声的影响；应用渐消记忆机制逐步遗忘过时信息，突出当前状态的重要性，提高滤波的实时性和准确性。变分贝叶斯方法对初始参数的选择很敏感。不恰当的初始参数会导致算法收敛慢或不收敛，影响信号滤波的稳定性。分数表示模型利用分数阶微积分工具，能够更精确地描述信号的动态特性和复杂系统的响应。为此，鲁大勇等^[4]建立基于分数表示模型的信号数学模型，用于准确描述信号的变化趋势和噪声特性。利用分数阶微积分运算，设计自适应滤波策略，根据信号的当前状态和历史信息动态调整滤波参数，实现对导航信号的高精度滤波。分数阶微积分运算相较于传统的整数阶微积分更为复杂，导致在某些计算资源有限或实时性要求极高的场景中，滤波算法无法及时响应信号的变化，从而影响导航信号的稳定性。小波变换作为一种多尺度分析工具，能够有效地提取信号中的有用信息，同时抑制噪声的干扰。而自寻优技术则通过自动调整算法参数，使得滤波效果达到最优。为此，李冬毅等^[5]提出结合小波变换和自寻优技术的自寻优小波降噪方法，利用小波变换多尺度分解海洋数据，得到不同频率成分的信号。通过自寻优技术，根据噪声的特性自动选择合适的小波基函数和分解层数，以及设定合理的阈值抑制高频噪声。重构处理后的各尺度信号，得到滤波后的海洋数据。海洋环境中的噪声来源多样，包括自然噪声（如风浪、潮汐等）和人为噪声（如船舶活动、海洋开发等）。如果噪声特性复杂多变，自寻优技术则难以准确识别并选择合适的降噪参数，从而影响降噪效果和导航信号的稳定性。Monti等^[6]建立纳米卫星群中各卫星之间的相对距离模型，用于准确反映卫星之间的空间位置和相对运动关系。通过卡尔曼滤波算法实时地根据相对距离信息，对导航信号进行滤波处理，以消除噪声和干扰，提高导航信号的准确性。卡尔曼滤波算法基于线性系统状态方程进行设计，它对于非线性系统的估计效果并不理想。然而，在实际航行环境中，舰船运动模型都是非线性的，这限制了卡尔曼滤波算法的应用范围。在复杂的海洋环境中，舰船导航面临诸多挑战，如风浪、海流、潮汐等因素的影响。通过实时获取海上观测值，导航信号滤波方法能够及时捕捉这些变化，动态调整滤波参数和策略，以适应不同的航行环境。同时还可以弥补单一数据源的不足，保证导航信号的稳定性和可靠性。

为此，本文提出基于海上观测值的舰船导航信号滤波方法。

1 舰船导航信号滤波方法 1.1 基于海上观测值的舰船导航信号模型

为了确保导航信号的稳定性与可靠性，通过建立舰船的运动状态方程和观测方程，能够精确描述舰船在海洋环境中的运动状态，并实时反映舰船的位置、速度、航向等关键信息。这种模型化的方法不仅提高了舰船导航的精确性，也为后续的滤波处理提供了坚实的数据基础。

1）舰船运动状态方程

以纬度、经度弧长$ d $、$ \lambda $，海流东向与背向分量$ {v_E} $、$ {v_N} $，航速$ v $，航向$ C $，以及舰船角速度变化量$ \theta $为海上观测值，建立舰船的运动状态方程。舰船运动的状态向量为：

$ \left\{ \begin{gathered} \dot d = {v_N} + v\cos C + {\varepsilon _1} ，\\ \dot \lambda = {v_E} + v\sin C + {\varepsilon _2}，\\ \dot v = {\varepsilon _5} ，\\ \dot C = \theta + {\varepsilon _6} ，\\ \dot \theta = {\varepsilon _7}。\\ \end{gathered} \right. $

(1)

式中：$ \dot d $、$ \dot \lambda $、$ \dot v $、$ \dot C $、$ \dot \theta $为$ d $、$ \lambda $、$ v $、$ C $、$ \theta $的一阶导数；$ {\varepsilon _1} $、$ {\varepsilon _2} $、$ {\varepsilon _5} $、$ {\varepsilon _6} $、$ {\varepsilon _7} $为对应的白噪声，且均值为0。

令$ {v_E} $与$ {v_N} $满足一阶马尔可夫过程，那么：

$ \left\{ \begin{gathered} {{\dot v}_E} = - k{v_E} + {\varepsilon _3} ，\\ {{\dot v}_N} = - k{v_N} + {\varepsilon _4}。\\ \end{gathered} \right. $

(2)

式中：$ k $为相关时间；$ {\varepsilon _3} $、$ {\varepsilon _4} $为对应的白噪声，且均值为0。

整合式(1)与式(2)。并对展开离散化处理，得到舰船运动状态方程：

$ \left\{ \begin{gathered} {{\dot d}_t} = {{\dot d}_{t - 1}} + \frac{{1 - \exp \left( { - kT} \right)}}{{k{{\dot v}_{N,t - 1}}}} - {{\dot v}_{t - 1}} \times \cos {{\dot C}_{t - 1}} + \\ \frac{T}{{2{\theta _{t - 1}}}} + {\varepsilon _{1,t - 1}} ，\qquad \qquad\qquad\qquad \\ {{\dot \lambda }_t} = {{\dot \lambda }_{t - 1}} + \frac{{1 - \exp \left( { - kT} \right)}}{{\beta {{\dot v}_{E,t - 1}}}} - {{\dot v}_{t - 1}} \times \sin {{\dot C}_{t - 1}} + \\ \frac{T}{{2{\theta _{t - 1}}}} + {\varepsilon _{2,t - 1}} ，\qquad \qquad \qquad \qquad\\ {{\dot v}_{E,t}} = \exp \left( { - kT} \right){{\dot v}_{E,t - 1}} + {\varepsilon _{3,t - 1}} ，\\ {{\dot v}_{N,t}} = \exp \left( { - kT} \right){{\dot v}_{N,t - 1}} + {\varepsilon _{4,t - 1}} ，\\ {{\dot v}_t} = {{\dot v}_{t - 1}} + {\varepsilon _{5,t - 1}}，\\ {{\dot C}_t} = {{\dot C}_{t - 1}} + T{{\dot \theta }_{t - 1}} + {\varepsilon _{6,t - 1}} ，\\ {{\dot \theta }_t} = {{\dot \theta }_{t - 1}} + {\varepsilon _{7,t - 1}}。\\ \end{gathered} \right. $

(3)

式中：$ t $为时间；$ T $为采样间隔。

以矩阵的形式，改写式(3)得到简化的舰船运动状态方程为：

$ {{\boldsymbol{X}}_t} = f\left( {{{\boldsymbol{X}}_{t - 1}},t - 1} \right) + {\boldsymbol{H}}{{\boldsymbol{E}}_{t - 1}}。$

(4)

式中：$ {{\boldsymbol{E}}_{t - 1}} $为白噪声矩阵，且均值为0；$ f $为非线性函数；$ {\boldsymbol{H}} $为舰船运动状态转移矩阵；$ {{\boldsymbol{X}}_t} $为舰船运动状态矩阵，包含$ d $、$ \lambda $、$ {v_E} $、$ {v_N} $、$ v $、$ C $、$ \theta $这7种海上观测值。

2） 舰船运动观测方程

依据1.1.1小节的舰船运动状态方程$ {{\boldsymbol{X}}_t} $，建立舰船导航信号的观测方程$ {{Z}_t} $。其中，$ {{Z}_t} $内包含$ d $、$ \lambda $、$ v $、$ C $这4种海上观测值，表达式如下：

$ {{Z}_t} = {{G}_t}{{\boldsymbol{X}}_t} + {{\boldsymbol{S}}_t} 。$

(5)

式中：$ {{G}_t} $为常数阵；$ {{\boldsymbol{S}}_t} $为白噪声矩阵，且各频率分量之间是互不影响的。

通过联立式(4)与式(5)，便可得到基于海上观测值的舰船导航信号模型。

1.2 舰船导航信号滤波的实现

在舰船导航信号滤波的研究中，观测噪声和模型噪声的不确定性是一个关键的难点问题。为了解决这一难题，提出了利用改进量子粒子群优化算法来优化卡尔曼滤波算法的观测噪声协方差矩阵和舰船导航信号模型噪声协方差矩阵的方法。通过优化算法能够更准确地估计和调整噪声协方差矩阵，从而改进卡尔曼滤波算法的性能。这不仅提高了滤波算法对噪声的适应能力，也增强了滤波结果的准确性和可靠性。结合舰船导航信号模型，应用改进后的卡尔曼滤波算法进行滤波估计，可以更加精确地获取舰船的位置、速度和航向等关键信息，为舰船的安全航行提供有力保障。

利用卡尔曼滤波算法^[7]，对舰船导航信号进行滤波估计的公式如下：

$ \hat Z_t^ - = {\boldsymbol{H}}{{\boldsymbol{X}}_{t - 1}} + V{u_{t - 1}}，$

(6)

$ {\boldsymbol{B}}_t^ - = {\boldsymbol{H}}{{\boldsymbol{B}}_{t - 1}}{\Gamma ^{\hat T}} + {\boldsymbol{W}} ，$

(7)

$ {\delta _t} = {\boldsymbol{B}}_t^ - Z_t^{\hat T}{\left( {{Z_t}{\boldsymbol{B}}_t^ - Z_t^{\hat T} + {\boldsymbol{R}}} \right)^{ - 1}} ，$

(8)

$ {\hat Z_t} = \hat Z_t^ - + {\delta _t}\left( {{{\boldsymbol{X}}_t} - {Z_t}\hat Z_t^ - } \right)。$

(9)

式中：$ \hat Z_t^ - $为一步预测的舰船导航信号滤波估计结果；$ {\boldsymbol{B}}_t^ - $为一步预测的误差方差矩阵；$ {\delta _t} $为滤波增益；$ {u_{t - 1}} $为海上观测值，包含$ d $、$ \lambda $、$ {v_E} $、$ {v_N} $、$ v $、$ C $、$ \theta $；${\boldsymbol{ R}} $为观测噪声协方差矩阵；$ W $为舰船导航信号模型的噪声协方差矩阵；$ V $为$ {u_{t - 1}} $的增益；$ {\hat Z_t} $为舰船导航信号滤波估计结果。

卡尔曼滤波算法的性能高度依赖于$ {\boldsymbol{R}} $和$ {\boldsymbol{W}} $的准确性。而舰船导航环境复杂多变，包括海洋环境、天气状况、舰船运动状态等多种因素^[8]。这些因素的变化会导致$ {\boldsymbol{R}} $和$ {\boldsymbol{W}} $的统计特性发生变化，为此，需要利用改进量子粒子群优化算法实时$ {\boldsymbol{R}} $和$ {\boldsymbol{W}} $，以适应复杂多变的导航环境，提高滤波算法的鲁棒性和适应性。具体步骤如下：

步骤1　初始化$ {\boldsymbol{R}} $与$ {\boldsymbol{W}} $，令$ {\boldsymbol{R}} $与$ {\boldsymbol{W}} $内元素总数，为改进量子粒子群优化算法的初始种群，每个粒子均代表卡尔曼滤波中的一组$ {\boldsymbol{R}} $和$ {\boldsymbol{W}} $的参数组合。

步骤2　以舰船导航信号滤波估计精度为粒子适应度$ f $，求解各粒子的$ f $，按照$ f $调整各粒子的局部最佳位置，指每个粒子在其搜索历史中找到的最佳位置，即最佳$ {\boldsymbol{R}} $和$ {\boldsymbol{W}} $的参数组合。其作用为：当粒子更新其位置时，它们会受到局部最佳位置的吸引，向自己的最佳经验靠拢^[9]，有助于粒子在卡尔曼滤波内$ {\boldsymbol{R}} $和$ {\boldsymbol{W }}$参数组合搜索空间中保持一定的多样性，避免过早收敛到非全局最优解，提升舰船导航信号滤波估计精度。

步骤3　按照局部最佳位置，求解各粒子的平均最佳位置$ {p_b}\left( \tau \right) $，公式如下：

$ {p_b}\left( \tau \right) = l\left( \tau \right){p_i}\left( \tau \right) 。$

(10)

式中：$ l\left( \tau \right) $为随机向量；$ \tau $为迭代次数；$ {p_i}\left( \tau \right) $为第$ i $个粒子的局部最佳位置。对比分析$ {p_i}\left( \tau \right) $，获取全局最佳位置$ {p_g}\left( \tau \right) $，指整个粒子群在搜索卡尔曼滤波内$ {\boldsymbol{R}} $和$ {\boldsymbol{W}} $的参数组合过程中，找到的最佳位置，即对应于所有粒子找到的$ {\boldsymbol{R}} $和$ {\boldsymbol{W}} $最佳参数组合，其作用为：粒子在更新其位置时，不仅会受到$ {p_i}\left( \tau \right) $的吸引，还会受到$ {p_g}\left( \tau \right) $的吸引，有助于粒子群在卡尔曼滤波内$ {\boldsymbol{R}} $和$ {\boldsymbol{W}} $参数组合搜索空间中快速收敛到全局最优解。

步骤4　对比分析邻近两次迭代时$ {p_g}\left( \tau \right) $和$ {p_g} \left( {\tau - 1} \right) $，如果$ {p_g}\left( \tau \right) $优于$ {p_g}\left( {\tau - 1} \right) $，则以为当下最佳全局位置；如果$ {p_g}\left( {\tau - 1} \right) $优于$ {p_g}\left( \tau \right) $，则以$ {p_g}\left( {\tau - 1} \right) $为当下最佳全局位置。

步骤5　求解目前各粒子的吸引子$ {q_i}\left( \tau \right) $，计算公式如下：

$ {q_i}\left( \tau \right) = M\left( {{p_i}\left( \tau \right),{p_b}\left( \tau \right) - {p_i}\left( \tau \right)} \right) 。$

(11)

求解压缩扩张因子$ \beta $，计算公式如下：

$ \beta = {\beta _{\min }} + \frac{{\left( {{\tau _{\max }} - \tau } \right)\left( {{\beta _{\max }} - {\beta _{\min }}} \right)}}{{{\tau _{\max }}}}。$

(12)

式中：$ {\beta _{\max }} $、$ {\beta _{\min }} $为$ \beta $的最大值、最小值；$ {\tau _{\max }} $为$ \tau $的最大值。

步骤6　求解各粒子的最新位置，公式如下：

$ {A_i}\left( {\tau + 1} \right) = \left\{ \begin{gathered} {q_i}\left( \tau \right) + \beta \left| {{p_b}\left( \tau \right) - {A_i}\left( \tau \right)} \right|\ln \left( {\frac{1}{\eta }} \right),\varpi \geqslant \frac{1}{2} ，\\ {q_i}\left( \tau \right) - \beta \left| {{p_b}\left( \tau \right) - {A_i}\left( \tau \right)} \right|\ln \left( {\frac{1}{\eta }} \right),\varpi < \frac{1}{2} 。\\ \end{gathered} \right. $

(13)

式中：$ \eta $为随机因子；$ \varpi \in \left[ {0,1} \right] $为随机数。

步骤7　分析该算法是否达到$ {\tau _{\max }} $，如果达到$ {\tau _{\max }} $，那么结束算法，输出最优的$ {\boldsymbol{R}} $和$ {\boldsymbol{W}} $参数组合，反之，跳转至步骤2。在卡尔曼滤波算法内代入最优的$ {\boldsymbol{R}} $和$ {\boldsymbol{W}} $参数组合，得到最优的舰船导航信号滤波估计结果。

2 实验分析

以某舰船导航定位系统为研究对象，利用所提方法对该舰船导航定位系统的舰船导航信号进行滤波处理，提升舰船导航轨迹的精度，确保舰船安全航行。该舰船导航定位系统的相关参数，如表1所示。

为了更清晰地展示实验分析流程，图1概述了如何使用提出的方法，对舰船导航定位系统的导航信号进行滤波处理的过程：

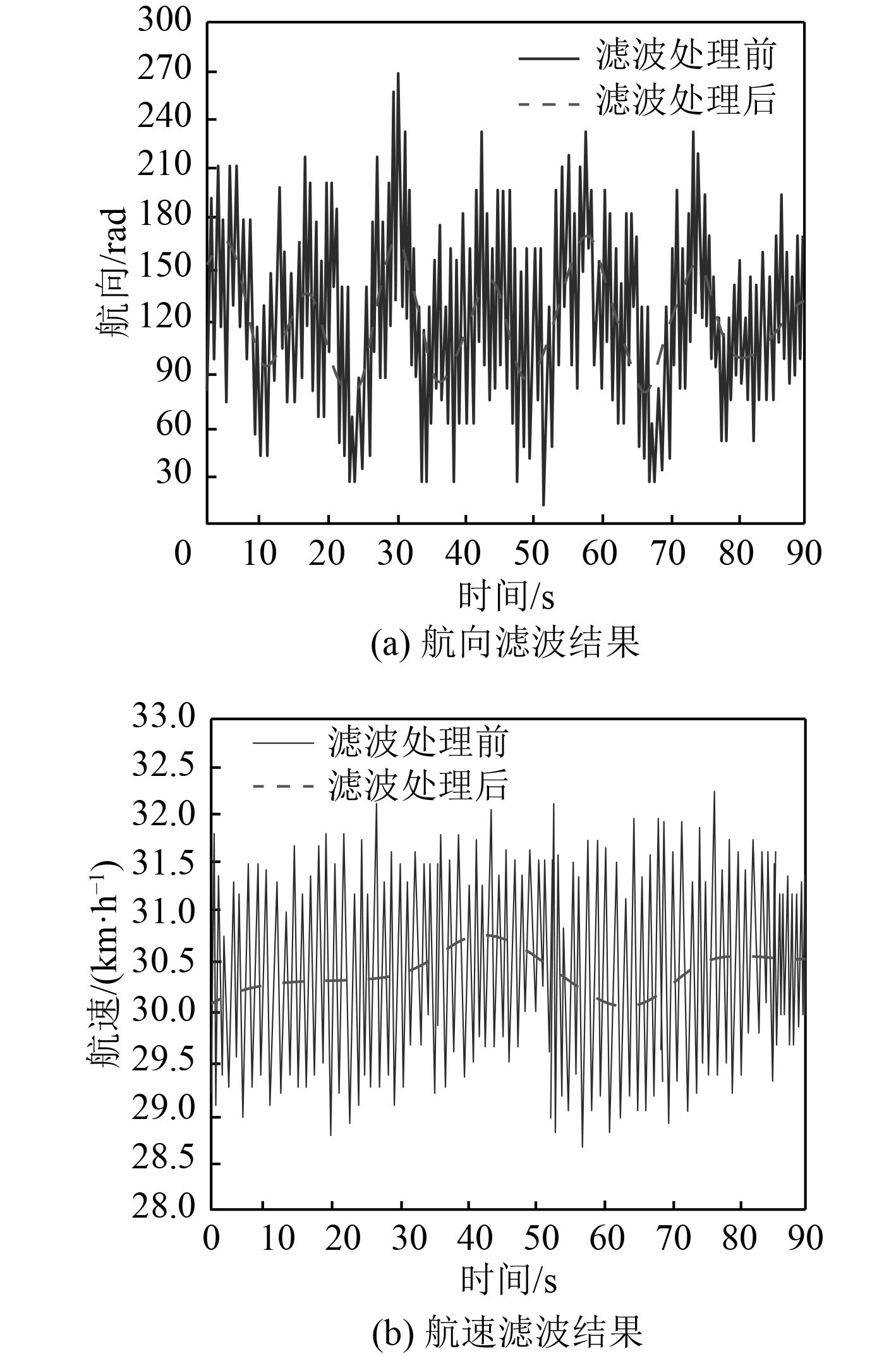
利用所提方法对该舰船导航定位系统内，舰船导航信号进行滤波处理，以航向与航速为例，舰船导航信号滤波结果如图2所示。

由图2(a)可知，所提方法可有效滤波处理舰船的航向信息，未经过所提方法滤波处理前，无法有效为航行人员提供有价值的航向信息，原始航向信息已被噪声完全淹没。经过所提方法滤波处理后，可清晰呈现航向信息的变化信息，为航行人员提供精准的航向信息。

由图2(b)可知，所提方法也可有效滤波处理舰船的航速信息，未经过所提方法滤波处理前，航速信息的波动幅度较大，无法了解不同时刻舰船的实际航速信息。经过所提方法滤波处理后，可清晰呈现不同时刻舰船的实际航速信息。

综合分析可知，所提方法可有效滤波处理舰船导航信号，显著提升舰船导航信号质量，可以为航行人员提供更加清晰、准确的导航信息，及时发现潜在的风险或障碍物，并采取相应的避让措施，大大降低航行事故的发生率，提高舰船航行的安全性。

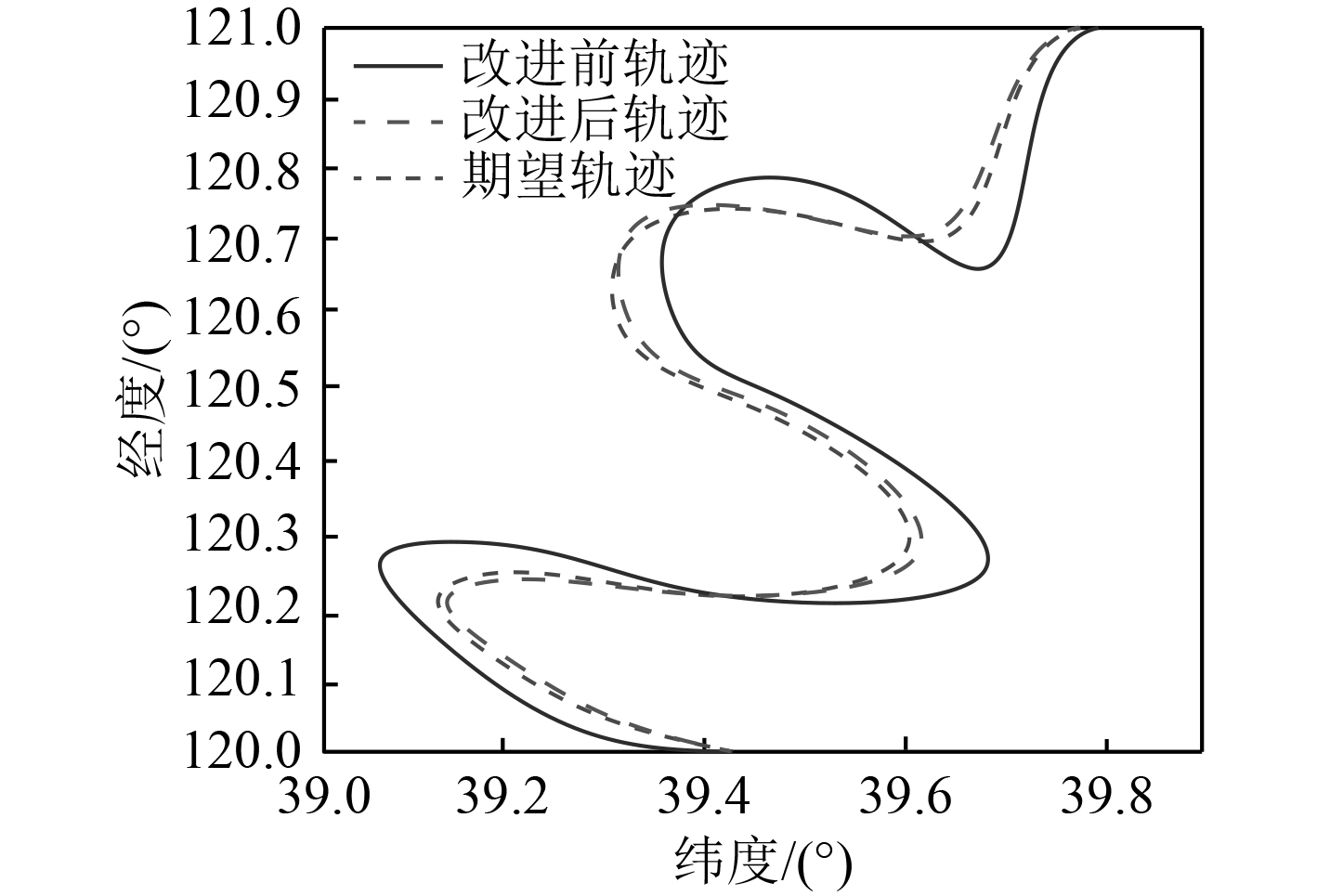
分析所提方法，利用改进量子粒子群优化算法，优化卡尔曼滤波算法的观测噪声协方差矩阵与模型噪声协方差矩阵前后，应用所提方法后的舰船导航效果，分析结果如图3所示。

可知，依据所提方法改进前滤波后的舰船导航信号，得到的舰船导航轨迹，与期望轨迹存在较大差距，因舰船导航环境复杂多变，包括海洋环境、天气状况、舰船运动状态等多种因素，这些因素的变化会导致卡尔曼滤波算法的观测噪声协方差矩阵，以及舰船导航信号模型噪声协方差矩阵的统计特性发生变化，影响舰船导航信号滤波估计精度，进而影响导航轨迹的准确性。依据所提方法改进后滤波后的舰船导航信号，得到的舰船导航轨迹，与期望轨迹非常接近，说明所提方法改进后，滤波后的导航信号更加接近真实值，进而提升舰船导航轨迹，确保舰船航行的安全性。原因是所提方法改进后，可提升观测噪声协方差矩阵，以及舰船导航信号模型噪声协方差矩阵的精度，降低海洋环境、天气状况、舰船运动状态等多种因素，对舰船导航信号滤波效果的影响，提升滤波精度。

3 结　语

在舰船导航中，通过整合纬度、经度、海流、航速、航向和角速度等观测值，构建了导航信号模型。采用改进的量子粒子群优化算法，对卡尔曼滤波的观测噪声和模型噪声协方差矩阵进行优化，进而改进了卡尔曼滤波算法。该算法与导航信号模型相结合，实现了对舰船导航信号的精确滤波估计。实验表明，通过滤波处理后的舰船导航轨迹精度更高，在舰船导航系统中，实时性和鲁棒性为非常重要的指标。未来需要研究如何在保证滤波精度的同时，提高算法的实时性和鲁棒性。