声呐是利用声波进行水下目标探测、定位、识别等方面的电子设备,是水声学中应用最广泛、最重要的一种装备,各种类型的声呐已广泛装备于世界各国海军主战舰艇等,作为海军舰艇水下探测的千里眼和顺风耳,其性能的优劣、稳定性对舰艇执行反潜、侦察和对抗等任务的能力起着决定性作用[1]。
圆柱形声呐又称球鼻艏声呐,指安装在下探到深于龙骨处的声呐导流罩内的声呐基阵,是海军舰艇装备的主要作战声呐之一。目前圆柱形声呐一般以多元基阵为主,具有主被动2种工作模式,声呐工作时需要通过基阵内各阵元换能器互相配合来实现较好的阵列技术处理效果,在这种情况下,阵元换能器性能的差异叠加后可能会造成声呐性能的明显变化,而声呐基阵在列装后,存在以下问题:阵元换能器的性能本身会随着时间而发生变化,声呐导流罩内的换能器受基阵架及导流罩内部结构的散反射影响严重,换能器之间的耦合作用,若是未能有效确定声呐设备的实际使用性能参数,必将影响声呐装备整体作战性能[2]。
声呐各阵元的接收幅度一致性作为关乎声呐技战指标实现的重要参数,有许多学者研究采用离散测量、有源校准和自校准等方法对阵列误差进行校准,建立换能器幅相测量系统,但研究主要集中在实验室环境条件下[3-6],与实际应用环境存在较大差异。为此,需要研究一种圆柱形基阵阵元灵敏度原位校准方法,以贴近于实际环境对安装后的声呐基阵接收性能进行检测,有效确定声呐阵元实际使用性能和一致性,为声呐装备阵列信号处理等算法实现的提供准确的数据作为参考,保障声呐系统有良好工作状态。
1 校准原理采用标准水声源比较法对圆柱形基阵阵元接收幅度一致性进行校准,如图1所示。校准时,被测船舶锚泊,位于球鼻艏内的声呐基阵保持静止,标准水声源由辅助船携带,通过硬/软连接方式下放至与被校声呐有效声中心相同入水深度,辅助船在预定的多个离散点位进行信号发射,离散点位的选取可以呈线性布置或者圆弧布置,覆盖被校声呐一定角度的扇面开角,为方便实际操作,辅助船沿直线运动,到达预定点位后发射信号,采集系统记录声呐各阵元输出信号,完成所有点位校准工作后驶离试验区域,对标准水声源在不同点位时被校声呐阵元输出电压信号进行处理,获取被校声呐阵元对应不同频率下的输出电压幅度包含2个过程,第1个过程是运用圆弧距离修正法将声呐阵元输出换算到同一等效圆弧面上,第2个过程是运用循环叠加平均法对被校准声呐阵元在不同点位下的输出值进行处理。

|
图 1 校准方法示意图 Fig. 1 Schematic diagram of calibration method |
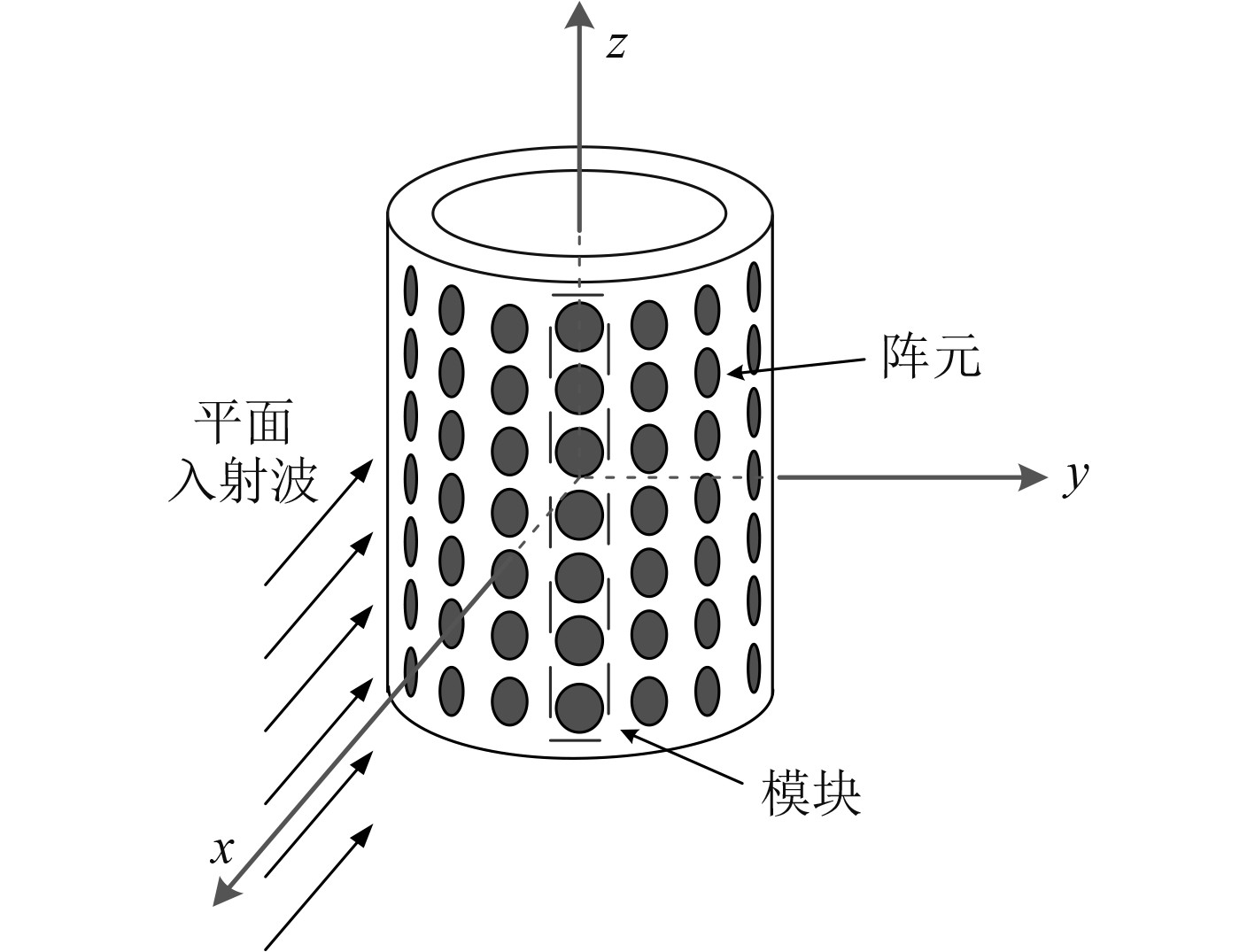
圆柱形声呐立体结构示意图如图2所示,圆柱阵不同模块(将声呐竖向一列阵元视为一组模块)间沿圆弧面等间距布置,这就导致不同模块间的阵元辐射面呈一定夹角,有效接收面出现差异,单个离散点位无法实现声呐全部阵元幅度一致性的校准,因此,必须考虑声呐阵结构,在满足远场条件下,标准水声源发出信号在到达声呐阵处可近似为平面波,根据远场声压与校准距离成反比的声传播规律,将声呐各阵元处的声压换算到同一等效平面S处。
|
图 2 圆柱形基阵结构示意图 Fig. 2 Schematic diagram of cylindrical array structure |
| $ {p_{_{{S}}}} = \frac{{{p_{(ij,\theta )}} \cdot {r_{(ij,\theta )}}}}{d} = \frac{{{p_{(ij,\theta )}} \cdot \left( {{R_\theta } - L} \right)}}{d}。$ | (1) |
式中:
考虑阵元接收灵敏度,则阵元开路输出端电压可表示为:
| $ {U_{(ij,\theta )}} = \frac{{{p_{(ij,\theta )}} \cdot d \cdot {M_{ij}}}}{{{r_{(ij,\theta )}}}}。$ | (2) |
式中:
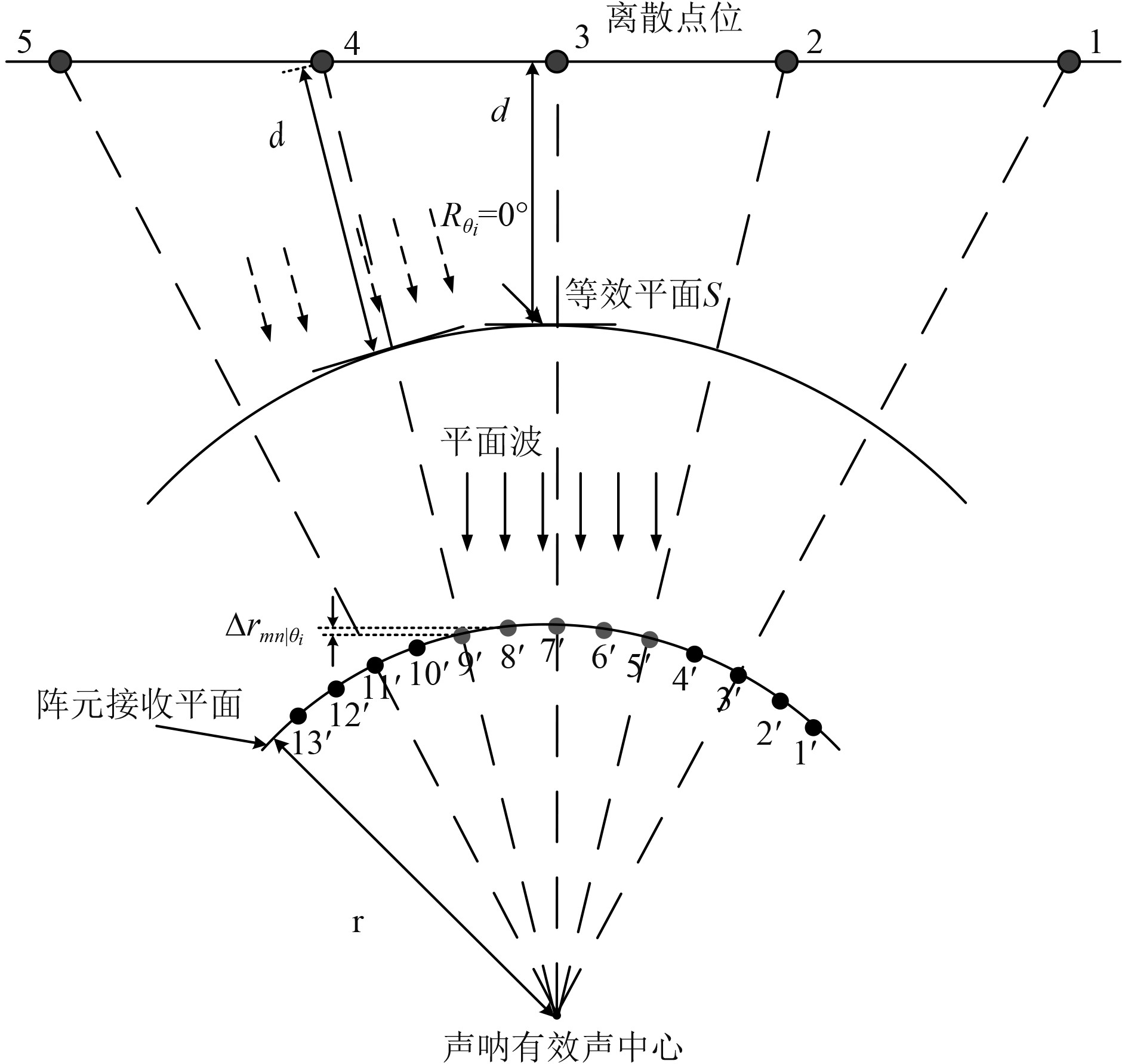
为便于说明,做俯视等效图如图3所示。
|
图 3 校准过程等效图(俯视图) Fig. 3 Equivalent diagram of calibration process (top view) |
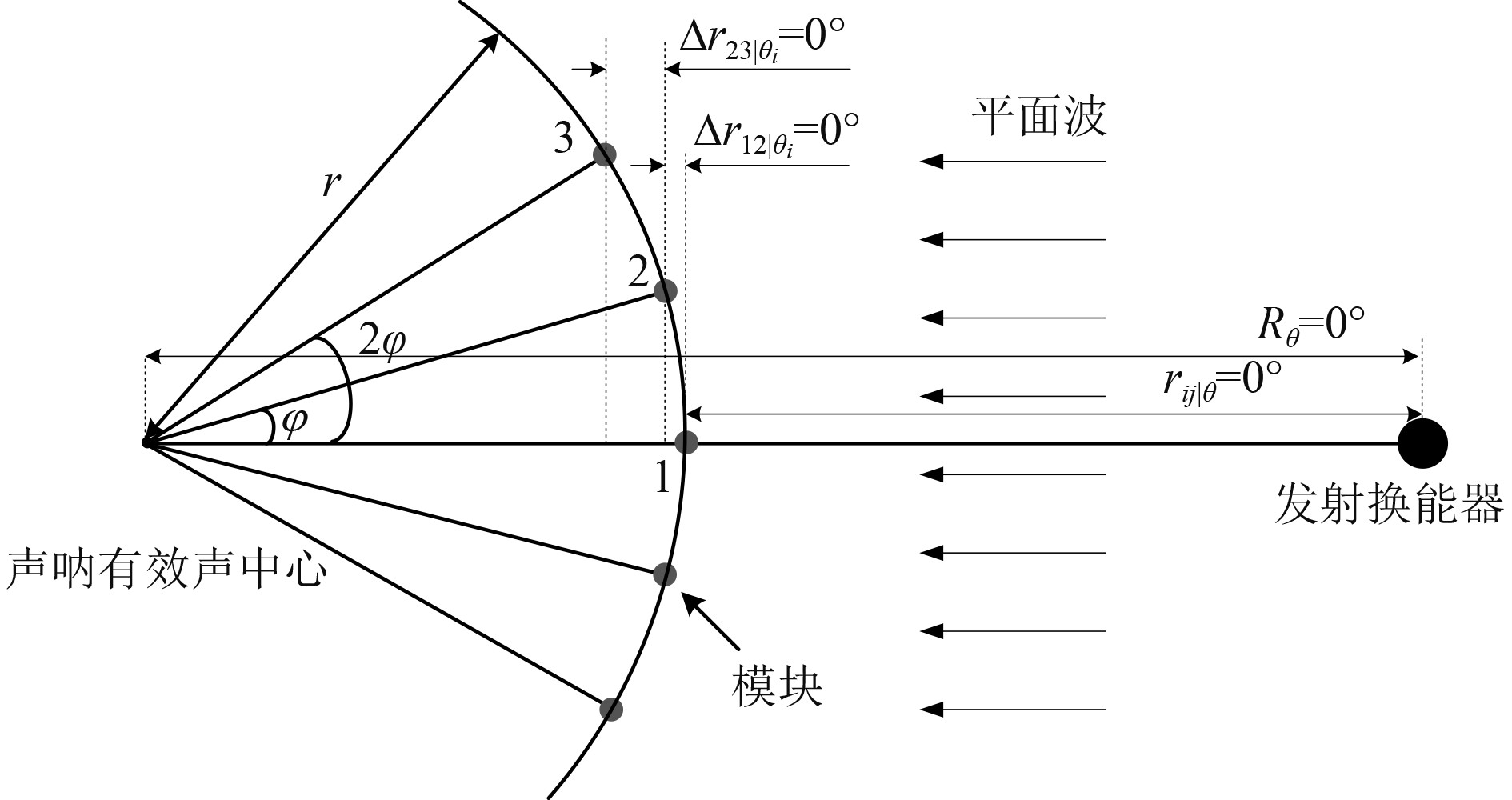
由于不同模块的阵元辐射面存在一定的夹角,需对单次校准时不同模块的接收声压信号进行距离修正。如图4所示,声呐模块于圆弧上均匀布放,平面波从0°方向入射,假设相邻模块中心与声呐等效声中心的连线夹角为
|
图 4 圆弧距离修正法示意图 Fig. 4 Schematic diagram of arc distance correction method |
对图4中的1#、2#、3#模块进行分析,当发射换能器与声呐艏端夹角为0°时,1#模块与发射换能器的距离可以表示为:
| $ {r_{1j|\theta = 0^\circ }} = {R_{\theta = 0^\circ }} - r 。$ | (3) |
则2#模块与发射换能器的距离需进行距离修正,表示为:
| $ \begin{split} {r_{2j|\theta = 0^\circ }} =& {R_{\theta = 0^\circ }} - r + \Delta {r_{12|\theta = 0^\circ }} =\\ & {R_{\theta = 0^\circ }} - r + r \cdot \cos \left( \varphi \right) 。\end{split} $ | (4) |
同理,3#模块与发射换能器的距离表示为:
| $ \begin{split} {r_{3j|\theta = 0^\circ }} =& {R_{\theta = 0^\circ }} - r + \Delta {r_{13|\theta = 0^\circ }} = \\ &{R_{\theta = 0^\circ }} - r + r \cdot \cos \left( {2\varphi } \right)。\end{split} $ | (5) |
根据声呐基阵的密排结构,当标准水声源位于某一离散点位时,直达声波能覆盖多个模块,而不同模块间的阵元辐射面呈一定夹角,为降低辐射面指向及声场起伏等带来的影响,采用循环叠加测试方式,如图5所示,考虑在一个点位校准时覆盖3~5个模块,这就能够保证每个模块(对应多个阵元)至少进行2次校准,并对多次校准值取能量平均作为最终结果,以半声呐阵有27模块,每次测量5个模块为例进行分析。

|
图 5 圆柱形基阵校准分布图 Fig. 5 Calibration distribution map of cylindrical array module |
运用循环叠加平均法对被校声呐阵元在不同夹角下的输出电压进行处理:
| $ {\overline{U}}_{(ij)}=10\mathrm{lg}\left(\frac{{U}_{(ij,\theta {'})}^{2}+{U}_{(ij,\theta {''})}^{2}+{U}_{(ij,\theta {'''})}^{2}}{3}\right)。$ | (6) |
式中,
以声呐基阵有效声中心为原点,建立与水面平行的坐标系,改变发射换能器的声波入射角度,依次对声呐阵模块各阵元的接收性能进行校准,即可获取声呐阵元接收灵敏度结果。
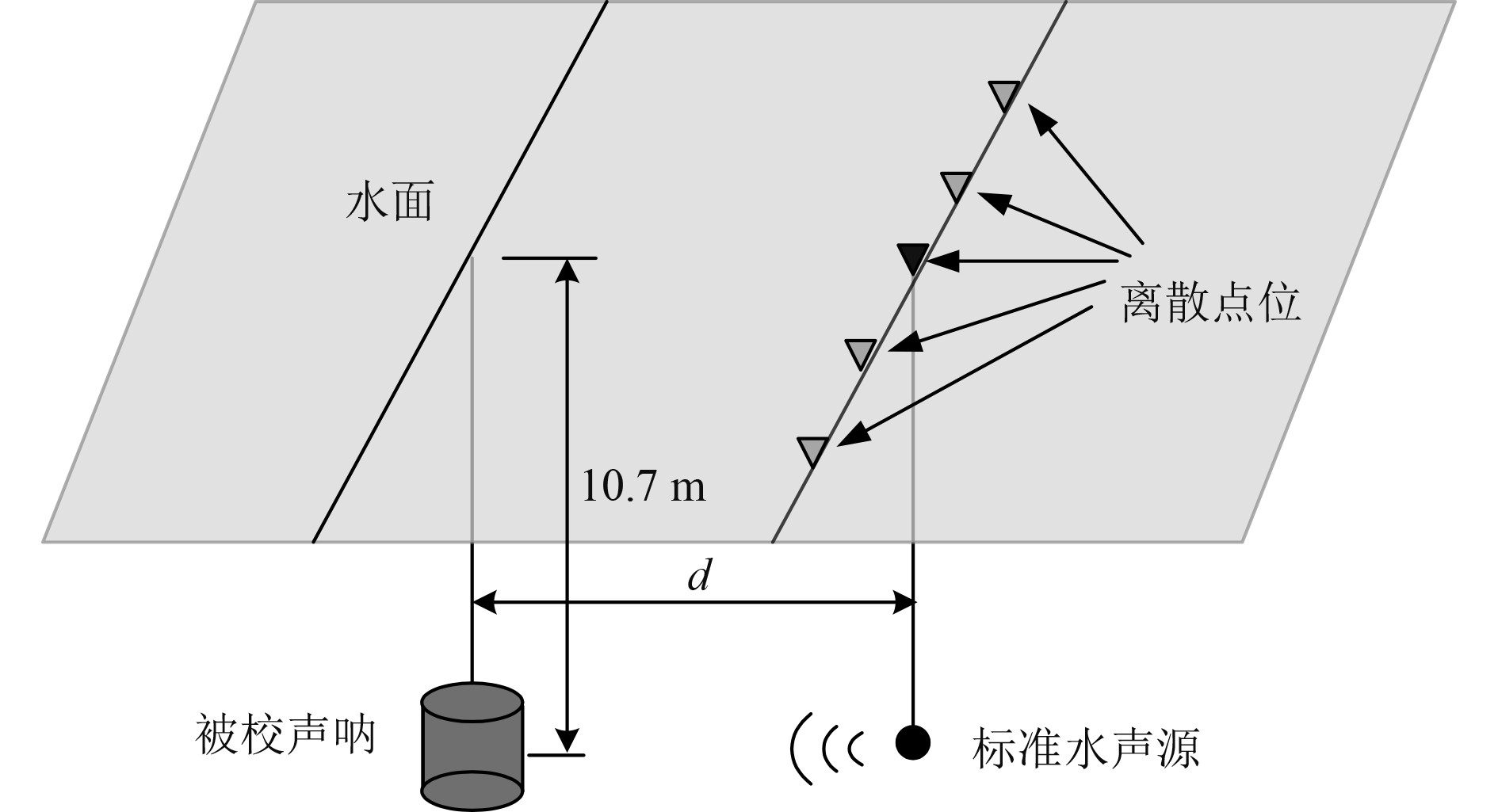
2 验证试验及结果分析 2.1 试验概况为验证所提方法的可行性和准确性,在某水域设计开展了验证试验,试验示意图如图6所示,试验水域开阔,平均水深约为36 m,水面平静,以圆柱形声呐为对象,采用脉冲声校准技术,频率范围1~10 kHz,标准水声源与声呐有效声中心入水深度10.7 m,声呐通过趸船上的升降回转装置布置于水域一定深度,保持声呐阵在水下静止不动,将经过标定的声源通过软连接方式吊放至与声呐有效声中心同一高度的水平面以下,为模拟实际海上试验时的操作流程,标准水声源沿趸船舷侧移动,以声呐阵0#模块为基准,在以15°为步长选取5个离散点进行试验。由于湖上水流较小,可认为声源水下位置不发生大的变化,沿直线改变声源的位置,由于试验范围在百米内,标准水声源离散布置点与声呐有效阵中心的距离采用高频水下同步声应答器测距方式获取。
|
图 6 试验声场布置示意图 Fig. 6 Schematic diagram of experimental sound field layout |
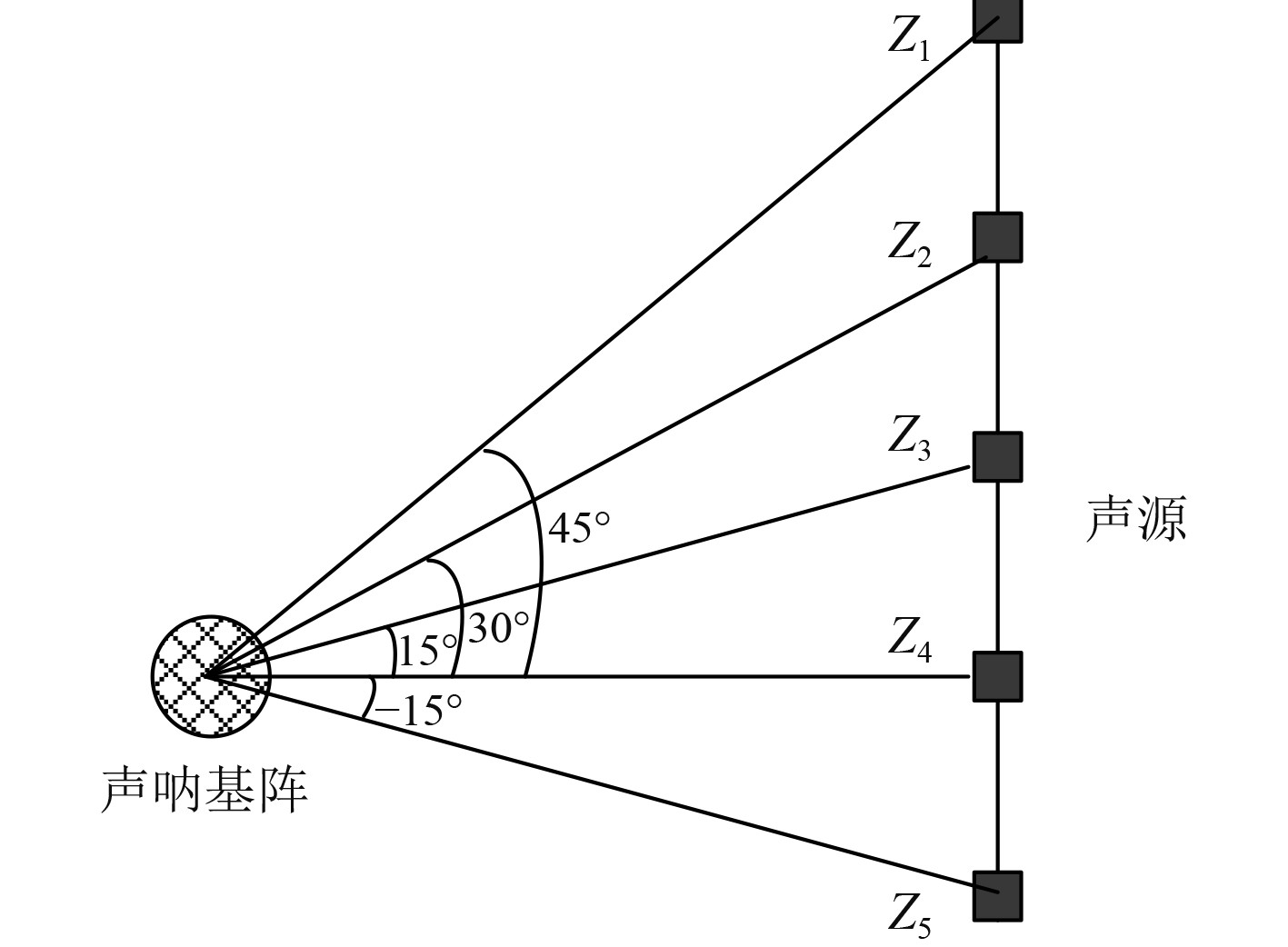
为便于说明,做俯视等效图如图7所示,被校声呐由多条模块组成,每条模块包含多路阵元(选取三路,命名为a、b、c),根据现场环境条件,选取00~06条模块、33路进行接收幅度校准,其中,01b模块正对Z3(15°方位),03b模块正对Z4(0°方位),05b模块正对Z5(−15°方位)。
|
图 7 圆柱形声呐接收特性实测示意图(俯视图) Fig. 7 Schematic diagram of measured reception characteristics of cylindrical sonar (top view) |
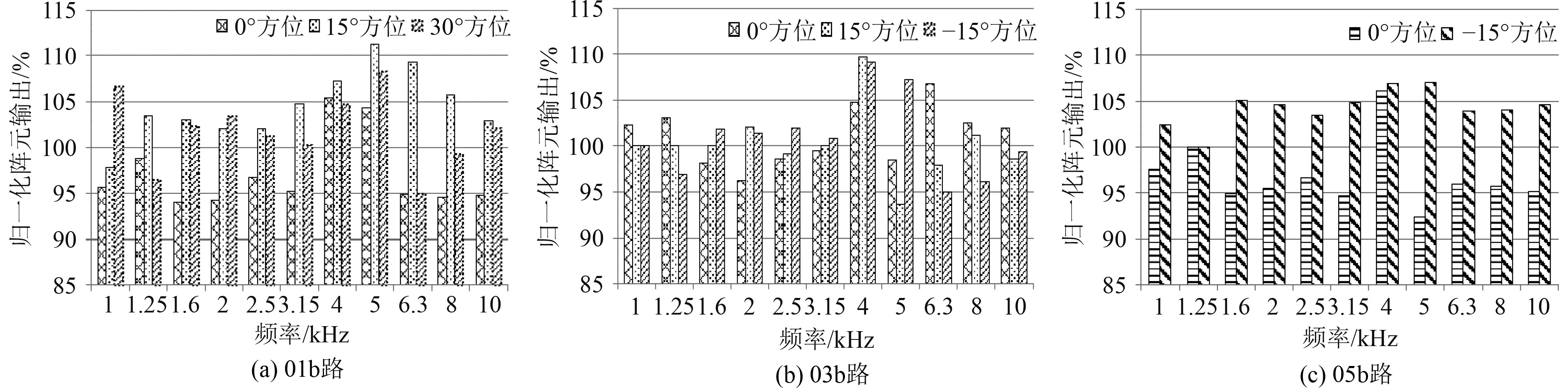
按所述方法对试验数据进行处理分析,得到选取01b、03b和05b三路阵元输出结果(Uoc)见表1,由于阵元频响起伏,为便于对比,以阵元在相邻几个方位下输出结果均值为参考,获取阵元在不同方位下输出结果相对值,得到归一化阵元输出如图8所示。
|
|
表 1 不同方位下被校声呐单路阵元(01b、03b和05b)输出对比 Tab.1 Comparison of output of single channel array elements (01b, 03b and 05b) of calibrated sonar in different orientations |
分析表1和图8可知,在相邻3个方位下,同一路阵元输出有较好的一致性,整体起伏约在10%以内,随着校准方位的增大,阵元输出逐渐降低,分析原因,这是阵元辐射面与入射波夹角增大,而大尺寸声呐基阵阵元均具有一定的指向性。
|
图 8 三路阵元校准归一化结果 Fig. 8 Normalization results of three-way array element calibration |
对比分析不同频率对应三路阵元的均值,可以看出,在频率相同时,经处理修正得到的阵元输出均值有较好的一致性,细微差别可能源自不同阵元自身性能存在差异;同时,注意到,在低频时不同角度下测得的阵元输出起伏较小,分析是波长远大于阵元尺寸,结构散射的影响低。上述试验结果及数据分析,可验证所提出方法的准确性和可行性。
00a~05c路阵元处理结果见表2,计算每条模块(00~05)上的三路阵元校准结果的响应起伏,转化为分贝表示,结果见表3。
|
|
表 2 被校声呐单路阵元(00a~05c)输出性能对比 Tab.2 Comparison of output performance of single channel array elements (00a~05c) of calibrated sonar |
|
|
表 3 被校声呐单条模块阵元校准结果统计 Tab.3 Statistics of calibration results for single module array elements of the calibrated sonar |
对比分析表2和表3数据,对应单条模块,在1~10 kHz频率范围内,随着频率的增大,阵元间校准结果趋于一致,响应起伏整体呈现降低趋势,在低频段响应起伏较大,分析有两方面因素影响,首先是偏离声呐阵元谐振点处对应的灵敏响应较低,噪声将对输出结果产生一定影响;其次,声呐自身结构的低频声散射也会产生干扰。
纵向对比不同模块统计结果,05模块的最大起伏为6.5 dB@10.0 kHz,最小为4.1 dB@1.6 kHz,远大于其余5条模块,据此判断05模块中存在性能异常的阵元,进一步分析05a~05c数据,可以看出,在1~10 kHz频率范围内,05a路的输出结果均小于同频下其他路的输出,认定此阵元性能异常,超差过大,剔除该路的值后,再次统计分析,05模块最大起伏为2.0dB@1.25 kHz,平均为0.8 dB,此时与00~04模块表现相同的统计特征,可认为对05a路阵元性能判定正确。
3 结 语针对声呐基阵实船安装后接收性能难以准确获取的问题,本文提出了一种圆柱形基阵阵元灵敏度原位校准方法,从理论和试验上对该方法的可行性和准确性进行分析验证。该方法基于标准水声源,结合圆弧距离修正和循环叠加平均处理算法实现圆柱阵阵元间接收性能的校准,进而获取阵元间灵敏度一致性,通过湖上验证试验表明,本文方法在实际使用上准确可行,采用循环叠加校准方式,并对多次校准结果取能量均值,可以很好的平滑降低自身结构及环境散射对校准的影响;圆弧距离修正法则降低了实际校准过程的操作难度。通过降低每次校准的模块间隔或者增大单次校准覆盖声呐模块数量,可以提高实验的精度。在后续的工作中,将进一步研究采用发射窄带脉冲噪声或调频脉冲来提高校准效率,并在实际声呐安装环境下开展试验。
| [1] |
田坦. 声呐技术[M]. 哈尔滨: 哈尔滨工程大学出版社, 2010.
|
| [2] |
ZHANG Xiaoyong, SHANG Zhenzhen, JI Songxiang, et al. Influence of array elements’ consistency on SNR of hydrophone array[J]. Journal of Measurement and Instrument, 2019, 10(3): 241-245. |
| [3] |
李俊杰. 易地时间延时谱在阵元幅度灵敏度一致性测量中的应用[J]. 声学与电子工程, 2011, 3: 14−17 LI Junjie. The application of time delay spectrum in measuring the consistency of array element amplitude sensitivity [J]. Acoustics and Electronics Engineering, 2019, 10(3): 241−245. |
| [4] |
张雨. 换能器幅相一致性测试系统[D]. 哈尔滨: 哈尔滨工程大学, 2018.
|
| [5] |
王布宏, 王永良, 陈辉. 多径条件下基于加权空间平滑的阵元幅相误差校正[J]. 通信学报, 2004, 25(5): 166-174. WANG Buhong, WANG Yongliang, CHEN Hui. Correction of array element amplitude and phase errors based on weighted space smoothing under multipath conditions[J]. Journal on Communications, 2004, 25(5): 166-174. |
| [6] |
王楠. 基于时空矩阵信息的阵列幅相误差校正方法研究[D]. 西安: 西安电子科技大学, 2009.
|
 2024, Vol. 46
2024, Vol. 46
