2. 兰州理工大学 计算机与通信学院,甘肃 兰州 730050
2. School of Computer and Communication, Lanzhou University of Technology, Lanzhou 730050, China
无人船船队在进行远航作业时,需要承载大量的通信设备与传感器来保证船舶间的目标探测与信息传输。这些设备间的干扰会严重影响船舶目标探测精度和信息传输效率,过多的设备也会缩短船舶续航时间,提高硬件成本[1-2]。光通信具有高带宽、低时延的优势[3],激光雷达的测距精度高、距离远[4],雷达通信一体化技术可以共享硬件资源,从而降低系统的成本和复杂性[5]。因此,将光通信与激光雷达一体化系统应用到远航船队中可以在提高船舶通信性能与雷达性能的同时降低设备成本。
实现雷达通信一体化的关键在于一体化波形的设计。刘冰凡等[6]提出一种采用OFDM-LFM系统的一体化方案,通过调整多输入多输出(Multiple Input Multiple Output,MIMO)每个阵元发射信号的初始频率,实现了雷达通信的一体化,该方案中每个阵元的距离分辨率与传统的OFDM-LFM系统相当,但通信效率略低。赵玉振等[7]提出一种采用空白保护间隔替代循环前缀,防止OFDM-LFM载波间干扰和符号干扰的方法,但会引入额外的系统噪声。王冠等[8]提出一种基于CPM调制的OFDM-LFM雷达通信一体化信号模型,但在CPM调制下该模型的雷达速度分辨率略低。上述方法都在一定程度上平衡了通信与雷达性能,但由于射频领域的频谱资源有限,雷达与通信性能无法同时得到优化,存在一定的局限性。
针对上述问题,设计一种基于OFDM-LFM的船舶激光雷达通信一体化信号系统,在保证雷达速度分辨率的同时保证一体化信号系统的雷达距离分辨率和通信误码性能达到最优。在此基础上,采用比尔-朗伯定律、瑞利散射和菲涅耳公式对水体光学特性进行建模,研究了水面对光的吸收、散射以及水面起伏对光信号的影响。
1 OFDM-LFM一体化系统模型图1为设计的OFDM-LFM的船舶间激光雷达通信一体化系统模型。在系统的发送端,根据数字调制方式对输入的二进制数据分组。为了保证传输信号为单极性实数信号,还需要对调制后的信号进行共轭对称、非对称性限幅光(Asymmetrically Clipped Optical,ACO)以及逆快速傅里叶变换(Inverse Fast Fourier Transform,IFFT)[9]。然后将通信信息加载到LFM信号上作为OFDM的子载波,在添加循环前缀(Cyclic Prefix,CP)后,通过激光二极管(Laser Diode,LD)由船A发送到大气信道中,实现对目标1的探测和与船B间的信息传输。传输信道采用Gamma-Gamma模型[10],同时考虑水面对光的吸收、散射以及水面起伏对光信号的影响。

|
图 1 基于OFDM-LFM的船舶间激光雷达通信一体化系统模型 Fig. 1 Integrated lidar communication system between ships based on OFDM-LFM |
在系统的接收端,船A接收到的信号既是目标1的雷达回波又是船B的通信信息,信号经过光电转换器(Photodetector,PD)后去除循环前缀,然后进行通信信号处理和雷达信号处理。在通信信号处理中,快速傅里叶变换(Fast Fourier Transform,FFT)将OFDM-LFM的子载波从时域变换到频域,各路子载波经过对应的数字解调后输出二进制数据;在雷达信号处理中,OFDM-LFM的每一路子载波都对目标进行了一次探测,为了解决雷达距离分辨率和雷达测距距离之间的矛盾,对每一路目标回波都进行了脉冲压缩,然后提取目标的距离信息和速度信息。
1.1 OFDM-LFM一体化信号模型对LFM信号进行OFDM调制得到OFDM-LFM信号,其数学表达式为:
| $\begin{split} &{s_{\rm OFDM - LFM}}(t) = \\ &\sum\limits_{n = 0}^{{N_c} - 1}\sum\limits_{m = 0}^{{N_s} - 1} {\rm rect}(\frac{{t - (m - 1)T}}{T}){\rm exp}[j2{\text π} ({f_n}t + k{t^2}/2)] 。\end{split}$ | (1) |
式中:
根据式(1),16QAM、QPSK、BPSK以及MSK调制方式下的OFDM-LFM信号模型如表1所示[11 - 13]。
|
|
表 1 不同调制方式下一体化信号模型 Tab.1 Integrated signal models under different modulation formats |
其中:
可以看出,16QAM、QPSK以及BPSK 只是对
针对水面对光的吸收作用,采用比尔-朗伯定律[14](Beer-Lambert Law)进行建模。比尔-朗伯定律描述了光通过透明介质时的光强衰减与介质的吸收系数、光程长度和入射光强度之间的关系,其数学模型如下:
| $ I = \varsigma {I_0} = {I_0}{\rm exp}( - \kappa \iota d) 。$ | (2) |
式中:
针对水面对光的散射作用采用瑞利散射[15](Rayleigh Scattering)理论进行建模。瑞利散射是描述微小颗粒(或分子)对入射光散射的现象的物理原理,它适用于小于入射光波长的颗粒。水中的微小波动、悬浮物、气泡等都可以引起瑞利散射。瑞利散射的数学模型如下:
| $ I(\theta)=\eta {I}_{0}={I}_{0}\left(\frac{2{{\text π}}^{2}}{{\lambda }^{4}}\right){({\rm sin}\theta )}^{2} 。$ | (3) |
式中:
在起伏的水面上,入射角和折射角会因水面的曲率而变化,导致光的反射和折射发生变化,所以针对水面的起伏对光的作用采用菲涅耳公式[16](Fresnel Equations)建模,其表达式为:
| $ I = \xi {I_0} 。$ | (4) |
式中:
1)垂直极化(s极化)
反射系数
| $ {r_s} = \frac{{{n_1}{\rm cos}{\theta _i} - {n_2}{\rm cos}{\theta _t}}}{{{n_1}{\rm cos}{\theta _i} + {n_2}{\rm cos}{\theta _t}}} ,$ | (5) |
| $ {t_s} = \frac{{2{n_1}{\rm cos}{\theta _i}}}{{{n_1}{\rm cos}{\theta _i} + {n_2}{\rm cos}{\theta _t}}}。$ | (6) |
式中:
2)平行极化(p极化)
反射系数
| $ {r_p} = \frac{{{n_1}{\rm cos}{\theta _i} - {n_2}{\rm cos}{\theta _t}}}{{{n_1}{\rm cos}{\theta _i} + {n_2}{\rm cos}{\theta _t}}},$ | (7) |
| $ {t_p} = \frac{{2{n_1}{\rm cos}{\theta _i}}}{{{n_1}{\rm cos}{\theta _i} + {n_2}{\rm cos}{\theta _t}}} 。$ | (8) |
为实现更远的测量距离,雷达需要发射高能量的信号,高能量信号理论上有2种实现方式,一种是峰值较低、时宽较长的信号,另一种是峰值较高、时宽较窄的信号。但由于发射机和馈线系统对峰值功率有严格限制,获取高能量信号仅能通过加大脉冲宽度来实现。另一方面,雷达距离分辨率是雷达分辨2个相邻目标的能力,较好的分辨率通常需要较窄的脉冲宽度,导致雷达测量距离变短。为解决该问题,通过发射时宽较长的信号获得较大的作用距离,再将回波信号压缩为窄脉冲以实现更佳的距离分辨率。
对于OFDM-LFM信号,每一路子载波都是独立的LFM信号,其信号表达式为[17]:
| $ {s_{\rm LFM}}(t) = {\rm rect}(\frac{t}{T}){\rm exp}[j2{\text π} ({f_c}t + k{t^2}/2)] 。$ | (9) |
将上式改写为:
| $ {s_{\rm LFM}}(t) = {S_{\rm LFM}}(t){\rm exp}(j2{\text π} {f_c}t) 。$ | (10) |
其中,
| $ {S_{\rm LFM}}(t) = {\rm rect}\left(\frac{t}{T}\right){\rm exp}(j{\text π} k{t^2})。$ | (11) |
信号
| $ h(t) = {s^*}( - t),$ | (12) |
输出信号
| $ {s_0}(t) = s(t)\cdot h(t),$ | (13) |
最后整理得其包络为:
| $ {S_0}(t) = TS a({\text π} Bt){\rm rect}\left(\frac{t}{{2T}}\right) 。$ | (14) |
当
采用Gamma-Gamma分布模型来描述大气光强起伏,其表达式为[10]:
| $ f({ X}) = \frac{{2{{(\alpha \beta )}^{(\alpha + \beta )/2}}}}{{\varGamma (\alpha )\varGamma (\beta )}}{{ X}^{(\alpha + \beta )/2 - 1}}{{K}_{\alpha - \beta }}(2\sqrt {\alpha \beta { X}} ),{ X} > 0 。$ | (15) |
式中:
| $ \alpha = {\left\{ {{\rm exp}\left[ {\frac{{0.49\sigma _R^2}}{{{{\left( {1 - 1.11\sigma _R^{12/5}} \right)}^{7/6}}}}} \right] - 1} \right\}^{ - 1}} 。$ | (16) |
| $ \beta = {\left\{ {{\rm exp}\left[ {\frac{{0.51\sigma _R^2}}{{{{\left( {1 + 0.69\sigma _R^{12/5}} \right)}^{5/6}}}}} \right] - 1} \right\}^{ - 1}}。$ | (17) |
式中:Rytov方差
通信系统中的误码率定义为[18]:
| $ BE{R_{\rm FSO}} = \int\nolimits_0^\infty {P({S_{\rm NR}}} )f({ X}){\mathrm{d}}{ X} 。$ | (18) |
考虑水面对信号强度的影响:
| $ {{ X}_0} = \varsigma \eta \xi { X}。$ | (19) |
得出误码率:
| $ BE{R_{\rm FSO}} = \int\nolimits_0^\infty {P({S_{\rm NR}}} )f({{ X}_0}){\mathrm{d}}{{ X}_0}。$ | (20) |
式中:
为验证所提一体化信号的通信性能,在3种湍流强度条件下对传统OFDM-CPM-LFM系统和OFDM-LFM雷达通信一体化信号系统的误码率进行仿真,参数设置如表2。
|
|
表 2 仿真参数 Tab.2 Simulation parameters |
由图2可知,当误码率降为10−5时,弱湍流下,传统CPM调制的一体化系统信噪比为11.5 dB ,而16QAM、QPSK、BPSK以及MSK调制的一体化系统信噪比分别为18、11、8 、10 dB。可以看出,采用的4种调制方式中BPSK调制方式的误码性能最好,优于传统CPM调制下的一体化系统3.5 dB,MSK和QPSK次之,16QAM的最差。另外,随着湍流强度的增大,不同调制方式下的一体化系统的误码性能都有所下降,在误码率为10−5时,传统CPM调制下的一体化系统强湍流相比弱湍流和中湍流误码性能分别差3.7 dB和3.5 dB,而BPSK调制分别差3 dB和2.5 dB,MSK分别差3.5dB和3dB,BPSK的变化最小,说明其抗强湍流干扰的能力比CPM调制更好。
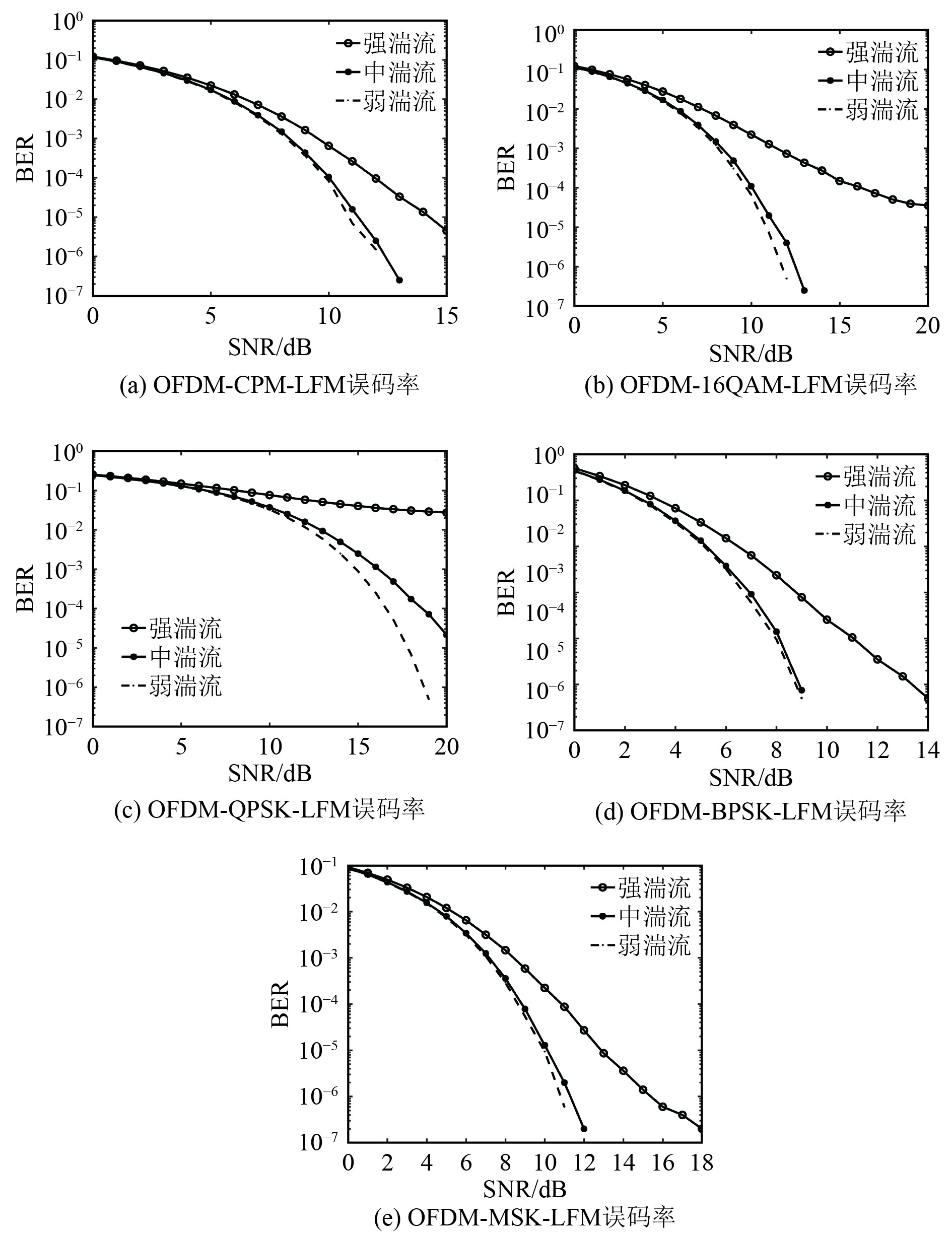
|
图 2 不同调制方式、不同湍流强度下系统误码率 Fig. 2 System ber under different modulation schemes and turbulence intensities |
为验证所提一体化系统的雷达探测性能,进行了雷达目标探测仿真实验,分析了不同调制方式下一体化系统最小可分辨距离和最小可分辨速度。
图3和图4分别为BPSK调制下的一体化系统有无脉冲压缩的最小可分辨距离-速度信息图。可以看出,通过脉冲压缩技术一体化系统的最小可分辨距离从15.6 m降到5.9 m,距离分辨率提升了9.7 m;最小可分辨速度都是
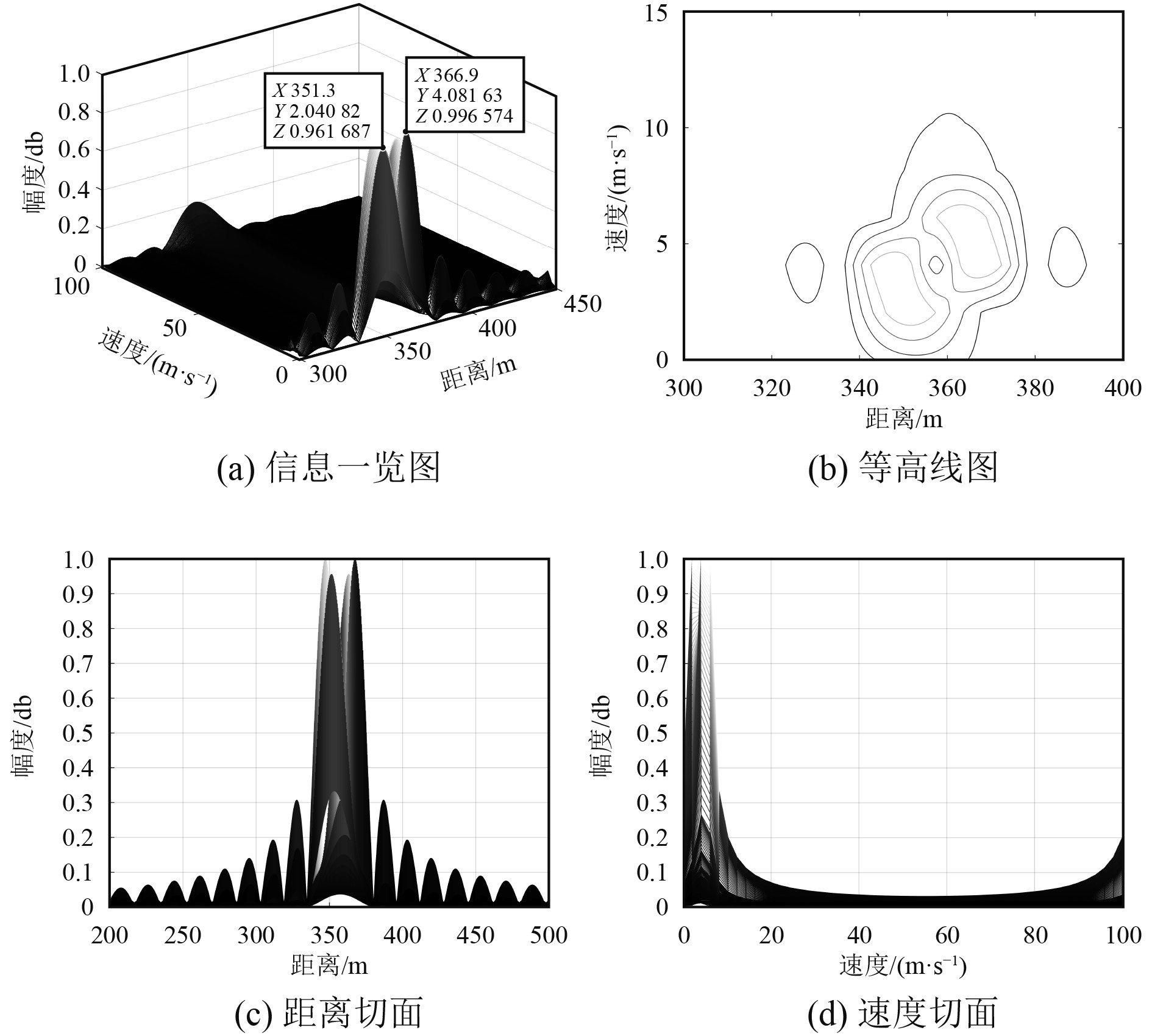
|
图 3 OFDM-BPSK-LFM无脉冲压缩探测 Fig. 3 Detection without pulse compression in OFDM-BPSK-LFM |
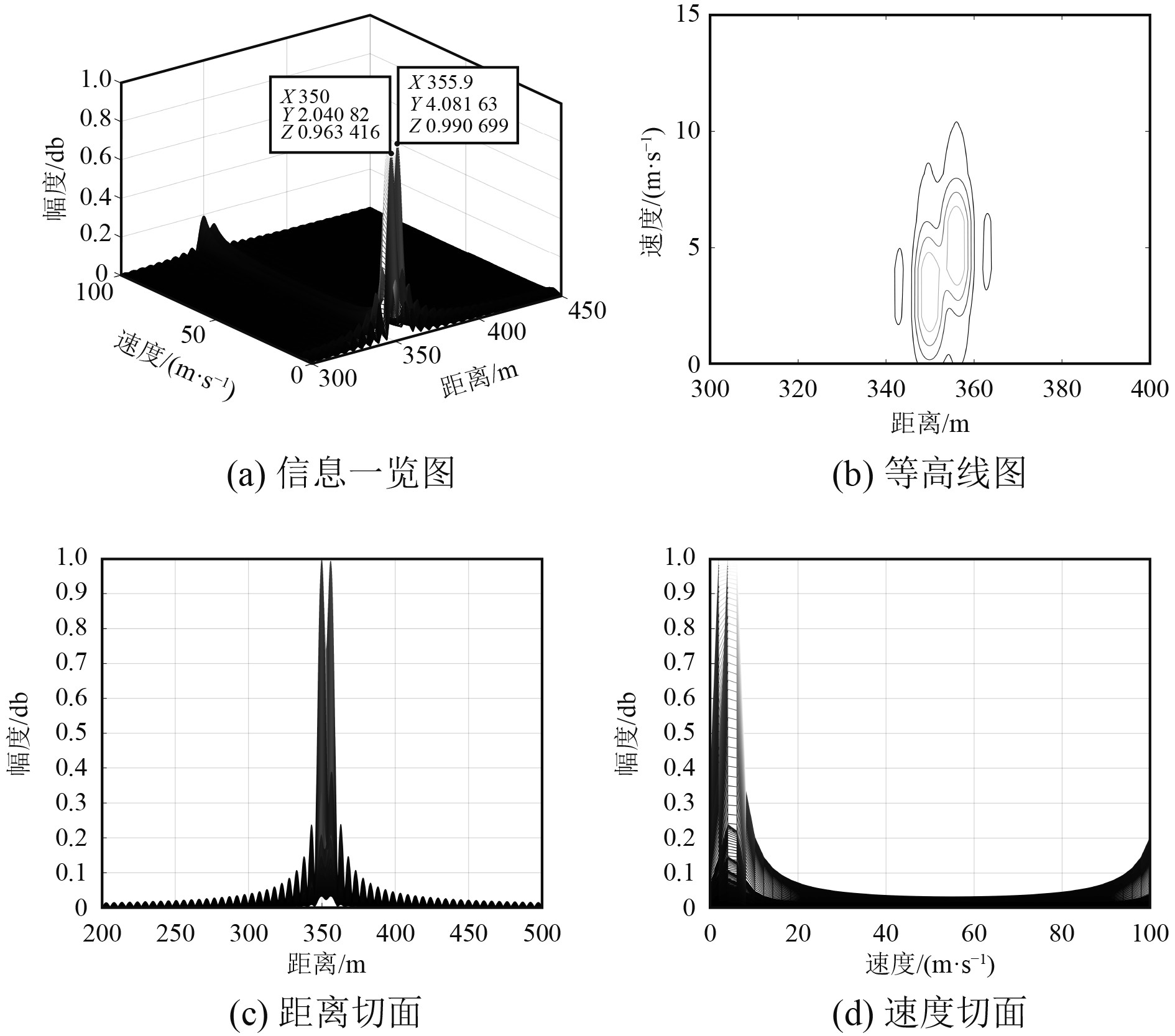
|
图 4 OFDM-BPSK-LFM有脉冲压缩探测 Fig. 4 Detection with pulse compression in OFDM-BPSK-LFM |
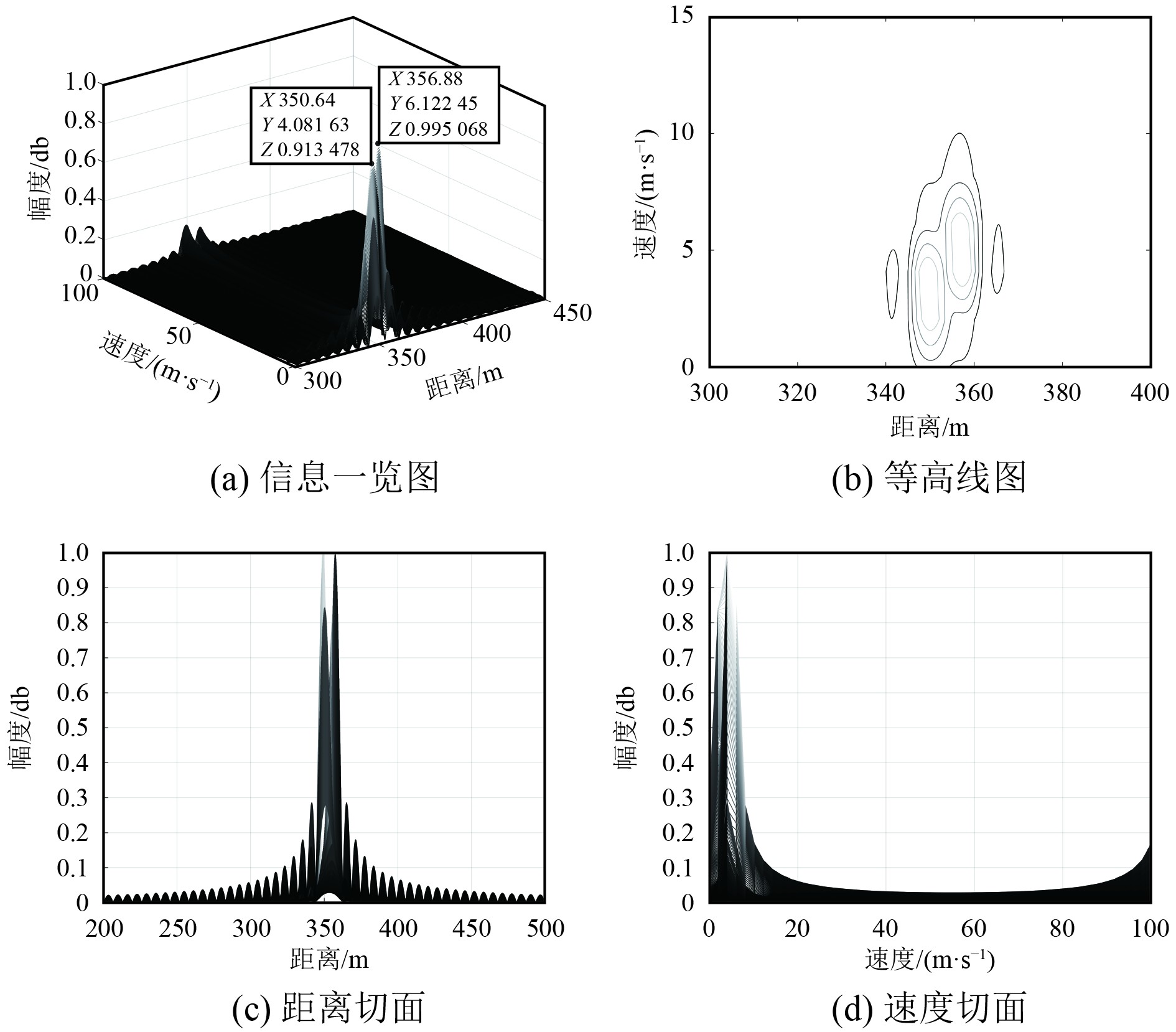
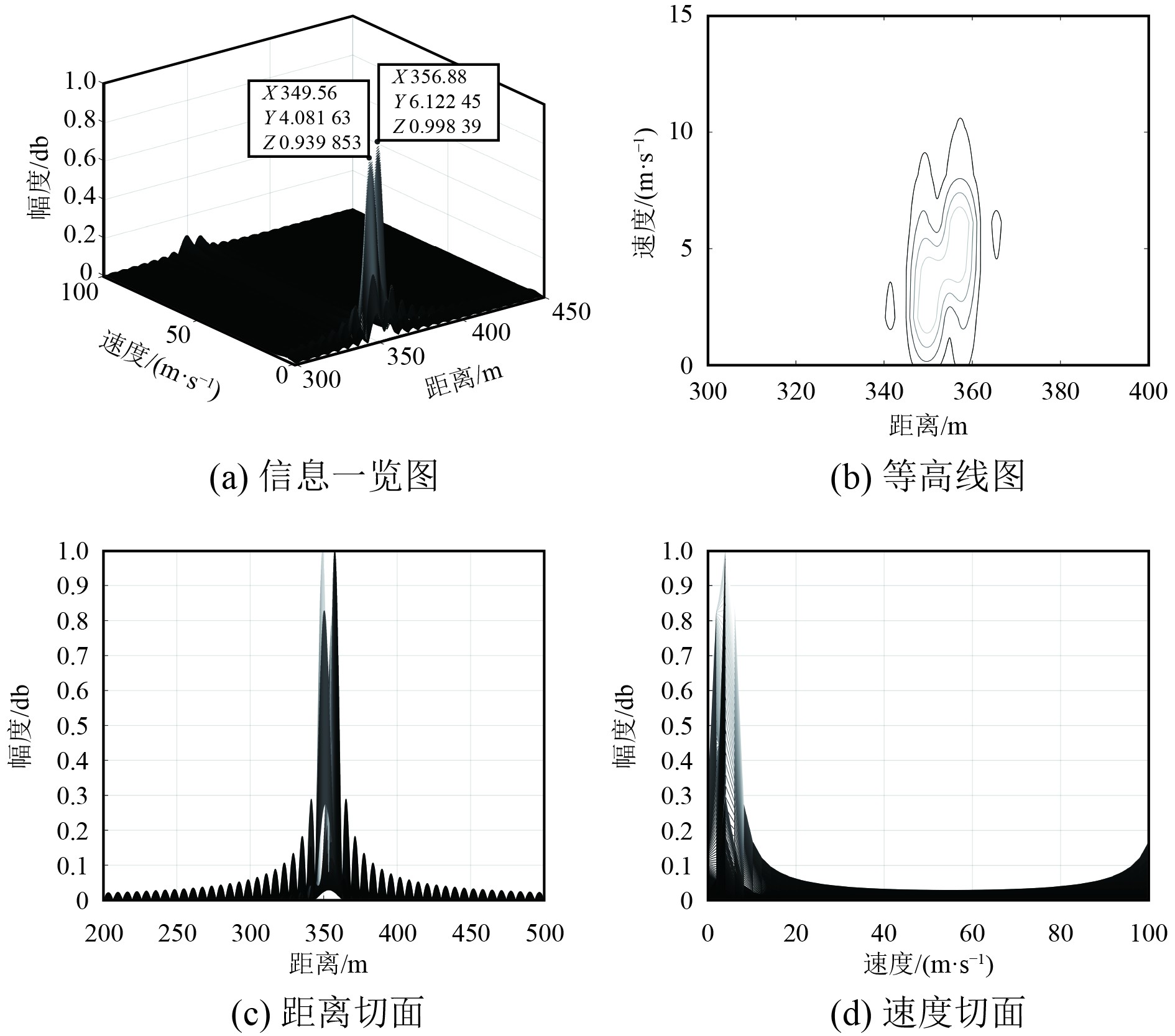
图5~图8分别为CPM、16QAM、QPSK、MSK调制下的一体化系统脉冲压缩后的最小可分辨距离-速度信息图。可知,传统CPM调制下的一体化系统脉冲压缩后的雷达最小可分辨距离和最小可分辨速度分别为6.96 m和
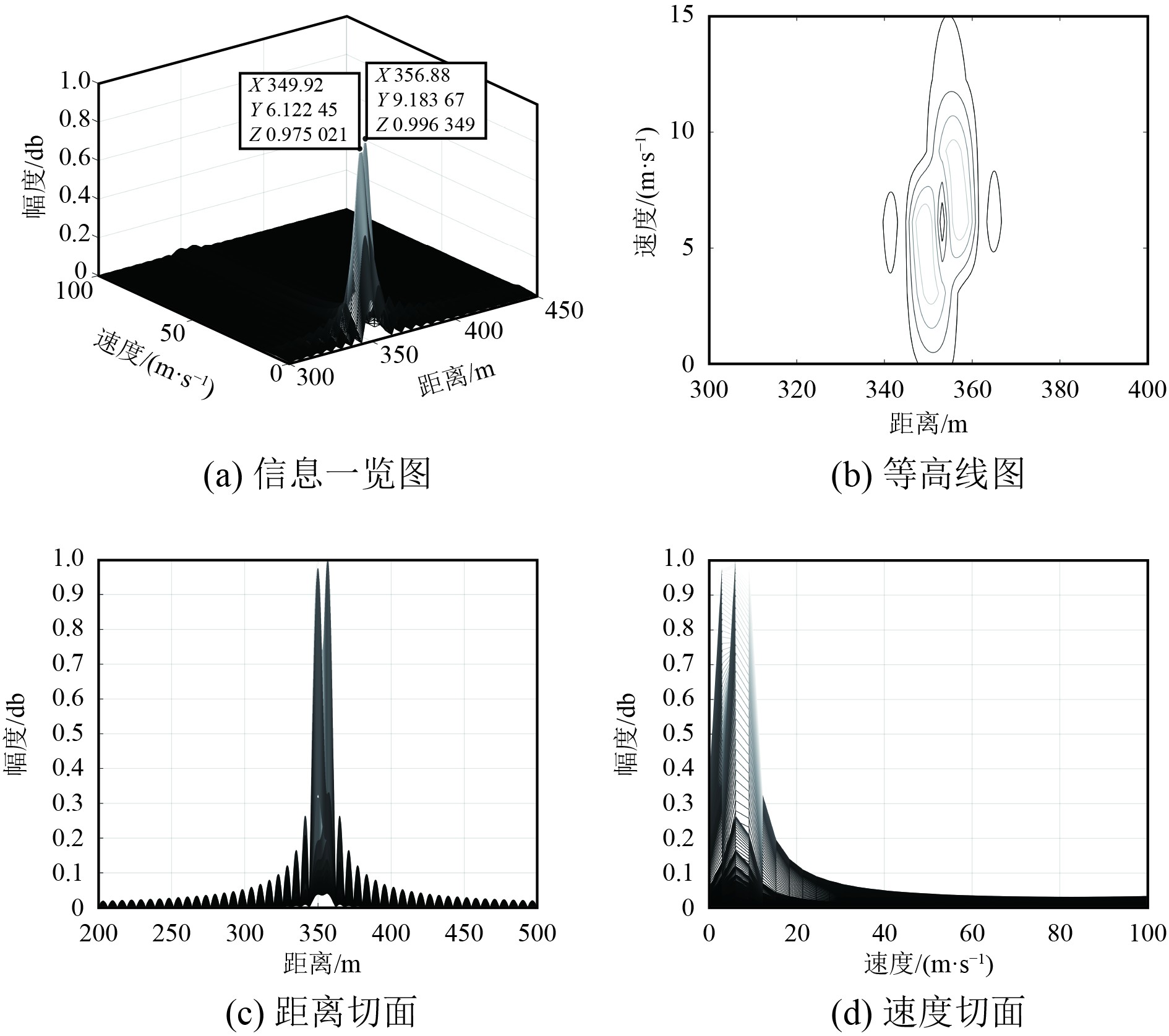
|
图 5 OFDM-CPM-LFM有脉冲压缩探测 Fig. 5 Detection with pulse compression in OFDM-CPM-LFM |
|
图 6 OFDM-16QAM-LFM有脉冲压缩探测 Fig. 6 Detection with pulse compression in OFDM-16QAM-LFM |
|
图 7 OFDM-QPSK-LFM有脉冲压缩探测 Fig. 7 Detection with pulse compression in OFDM-QPSK-LFM |

|
图 8 OFDM-MSK-LFM有脉冲压缩探测 Fig. 8 Detection with pulse compression in OFDM-MSK-LFM. |
针对无人船通信时延大及目标探测精度低的问题,提出OFDM-LFM激光雷达通信一体化信号系统,同时考虑水面对光信号的吸收、散射以及光在水面起伏中的影响,仿真分析了16QAM、QPSK、BPSK以及MSK四种调制方式下的一体化系统的通信性能和雷达性能。最终得出结论:在通信性能方面,BPSK调制下的一体化系统误码率最好,优于传统CPM调制3.5 dB,并且在不同湍流强度下,误码性能变化最小,可靠性最高;在雷达性能方面,BPSK调制下的一体化系统有最佳的距离分辨率5.9 m和速度分辨率
| [1] |
WANG Jia, XIAO Yang, LI Tieshan, et al. A survey of technologies for unmanned merchant ships[J]. IEEE ACCESS, 2020, 8: 224461-224486. DOI:10.1109/ACCESS.2020.3044040 |
| [2] |
冯炜, 崔东华, 夏天冰, 等. 国外无人船集群运用特点分析及其应对启示[J]. 中国舰船研究, 2023, 18(1): 1-12. FENG Wei, CUI Donghua, XIA Tianbing, et al. Analysis of characteristics of foreign unmanned surface vehicle swarm combat application and propo-sed countermeasures[J]. Chinese Journal of Ship Research, 2023, 18(1): 1-12. |
| [3] |
朱全, 刘润琪. 无线光通信技术在海上通信中的应用探讨[J]. 舰船科学技术, 2022, 44(12): 121-125. ZHU Quan, LIU Runqi. Discussion on application of free space opt-ical communication technology in maritime communication[J]. Ship Science and Technology, 2022, 44(12): 121-125. |
| [4] |
庄加兴, 焦侬, 殷非. 毫米波雷达与激光雷达在无人船上的应用[J]. 船舶工程, 2019, 41(11): 79-82. ZHUANG Jiaxing, JIAO Nong, YIN Fei, et al. Application of MMW Radar and LIDAR in MASS[J]. Ship Engineering, 2019, 41(11): 79-82. |
| [5] |
刘凡, 袁伟杰, 原进宏, 等. 雷达通信频谱共享及一体化: 综述与展望[J]. 雷达学报, 2021, 10(3): 467-484. LIU Fan, YUAN Weijie, YUAN Jinhong, et al. Radar-communicatio-n spectrum sharing and integration: Overview and prospect[J]. Journal of Radars, 2021, 10(3): 467-484. DOI:10.12000/JR20113 |
| [6] |
刘冰凡, 陈伯孝. 基于OFDM-LFM信号的MIMO雷达通信一体化信号共享设计研究[J]. 电子与信息学报, 2019, 41(4): 801-808. LIU Bingfan, CHEN Baixiao. Integration of MIMO radar and communication with OFDM-LFM signals[J]. Journal of Electronics & Information Technology, 2019, 41(4): 801-808. |
| [7] |
赵玉振, 陈龙永, 张福博, 等. 一种基于OFDM-chirp的雷达通信一体化波形设计与处理方法[J]. 雷达学报, 2021, 10(3): 453-466. ZHAO Yuzhen, CHEN Longyong, ZHANG Fubo, et al. A newmethod of joint radar and communication waveform design andsignal proce-ssing based on OFDM-chirp[J]. Journal of Radars, 2021, 10(3): 453-466. |
| [8] |
王冠, 康勇, 王金宇, 等. OFDM-CPM-LFM雷达通信一体化信号研究[J]. 微电子学与计算机, 2023, 40(8): 80-86. WANG Guan, KANG Yong, WANG Jinyu, et a1. Research on integrated signal of OFDM-CPM. LFM radar communication[J]. Microelectron-ics& Computer, 2023, 40(8): 80-86. |
| [9] |
JIANG Y, WANG M, ZHU X, et al. Superposition based nonlinearity mitigation for ACO-OFDM optical wireless communications[J]. IEEE Wireless Communications Letters, 2021, 10(3): 469-473. DOI:10.1109/LWC.2020.3034822 |
| [10] |
曹明华, 武鑫, 王惠琴, 等. Gamma-Gamma大气湍流下超奈奎斯特光通信系统性能[J]. 中国激光, 2020, 47(9): 0906003. CAO Minghua, WU Xin, WANG Huiqin, et al. Performance of faster-than-nyquist optical communication system under Gamma-Gamma atmospheric turbulence[J]. Chinese Journal of Lasers, 2020, 47(9): 0906003. DOI:10.3788/CJL202047.0906003 |
| [11] |
曾浩, 吉利霞, 李凤, 等. 16QAM-LFM雷达通信一体化信号设计[J]. 通信学报, 2020, 41(3): 182-189. |
| [12] |
贺占权, 李晓青, 倪远涵. 基于变速率的高吞吐率LFM-BPSK一体化波形[J]. 计算机应用与软件, 2020, 37(5): 114-117,176. |
| [13] |
刘耀文, 饶烜, 朱炳祺. 基于弱目标积累检测的MSK-LFM一体化信号性能分析[J]. 上海航天(中英文), 2022, 39(3): 38-45. |
| [14] |
CASASANTA G, FALCINI F, GARRA R. Beer–Lambert law in photochemist-ry: A new approach[J]. Journal of Photochemistry and Photobiology A: Chemistry, 2022, 432: 114086. DOI:10.1016/j.jphotochem.2022.114086 |
| [15] |
VINOGRADOV A P, SHISHKOV V Y, DORONIN I V, et al. Quantum theory of Rayleigh scattering[J]. Optics Express, 2021, 29(2): 2501-2520. DOI:10.1364/OE.412852 |
| [16] |
XIE Y, SENGUPTA M, HABTE A, et al. The “fresnel equations” for diffu-se radiation on inclined photovoltaic surfaces (FEDIS)[J]. Renewable and Sustainable Energy Reviews, 2022, 161: 112362. DOI:10.1016/j.rser.2022.112362 |
| [17] |
YOUSSEF A, DRIESSEN P F, GEBALI F, et al. On time compression overlap-add technique in linear frequency modulation pulse compression radar systems: design and performance evaluation[J]. IEEE ACCESS, 2017, (5): 27525-27537. DOI:10.1109/ACCESS.2017.2771799 |
| [18] |
贺锋涛, 杜迎, 张建磊, 等. Gamma-gamma海洋各向异性湍流下脉冲位置调制无线光通信的误码率研究[J]. 物理学报, 2019, 68(16): 230-238. |
 2024, Vol. 46
2024, Vol. 46
