移相变压器作为实现多重叠加逆变和多脉波整流技术的重要设备,现阶段主要分为心柱式移相变压器、圆形移相变压器以及直线移相变压器3种类型。同前2种移相变压器相比,直线移相变压器(Linear Phase Shift Transformer,LPST)除了能够实现传统变压器移相叠加的功能外,还具有可任意角度移相、扩展性好、易于模块化等优点[1]。
LPST运行时产生的振动噪声是一个不可忽视的问题,不仅影响周围环境,还会减少设备的使用寿命[2-3]。LPST的电磁振动大小由所受电磁力和本体结构固有频率共同决定[4]。当结构的固有频率与电磁力频率接近且处于能引起共振现象的频率区间时,变压器结构将可能会产生大幅度振动,进而产生较大的噪声。因此需要在LPST设计阶段分析其产生的电磁振动,观察结构的低阶固有振动频率和激励频率是否接近,尽量避免或减少共振现象的产生[5]。
磁致伸缩效应作为一种变压器运行时无法避免的现象,是指铁磁材料在被磁化的过程中其内部随机取向的磁畴发生旋转,逐渐使得各磁畴的取向趋于一致。即从宏观上的表现为铁心沿磁场变化方向伸长或缩短。常规变压器电磁振动的研究最早始于20世纪初期,主要的研究对象为铁心的磁致伸缩效应,研究方法有实验法、解析法和数值法。近年来,国内外海量学者对磁致伸缩效应的研究都集中于磁致伸缩力的测量方法和数值计算领域。另外因磁致伸缩效应产生的电磁振动噪声占比问题,也逐渐成为研究热点。胡静竹等[6]从变压器噪声产生的原理入手,利用仿真软件建立油浸式电力三柱式变压器的有限元模型,并将电磁场与结构力场进行耦合计算,求解出变压器整个结构(铁心、绕组以及紧固件)的振动情况。祝丽花等[7]在“磁-机械”弱耦合模型的基础上,考虑了铁心磁化特性和材料磁致伸缩力的各向异性的影响,实现磁场与机械场的强耦合。通过有限元仿真对变压器铁心磁致伸缩力及其引起的振动位移进行分析计算。钟思翀等[8]较为系统详实地探究了谐波激励下的变压器电磁振动特性和噪声分布。并通过实验测量了不同谐波含量下铁心硅钢片的磁致伸缩特性,并以此探究了通过谐波注入实现变压器有源降噪的可能性。综上所述,磁致伸缩效应对变压器影响的研究多集中于实验测量和简单的数值计算阶段,在建立准确的磁致伸缩力解析计算模型方面仍需探索。
本文对LPST电磁振动噪声的原理进行理论分析,主要探究铁心电磁场与结构场的耦合模型,计算磁致伸缩力产生的电磁振动和噪声。通过COMSOL Multiphysics建立LPST二维仿真模型,分别对模型进行电磁场分析、模态分析、谐响应分析以及噪声分析,得到LPST运行时振动及噪声的分布特点,为其在前期设计阶段实现减振降噪以及后期的优化提供理论支撑。
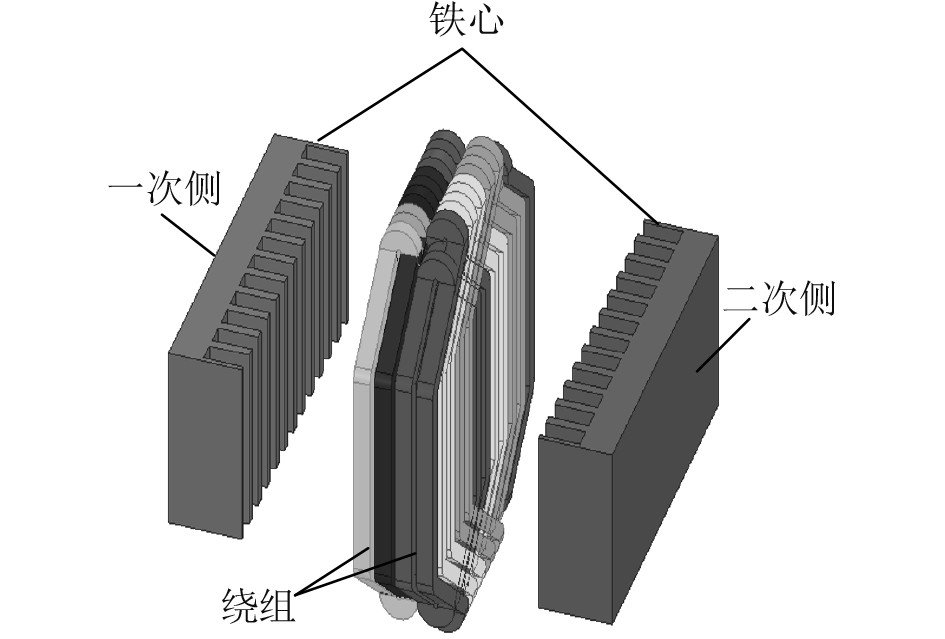
1 LPST的拓扑结构及其原理LPST作为一种新型电能变换设备,其基本原理与直线感应电机类似,结构(见图1)上近似等同于转差率为1的直线感应电机。本文选取一种用于多重叠加逆变系统的双层叠绕组LPST进行分析,具体参数见表1,变压器绕组结构示意图如图2所示。
|
图 1 LPST三维模型 Fig. 1 Three-dimensional model of LPST |
|
|
表 1 LPST参数表 Tab.1 Parameter table of LPST |
|
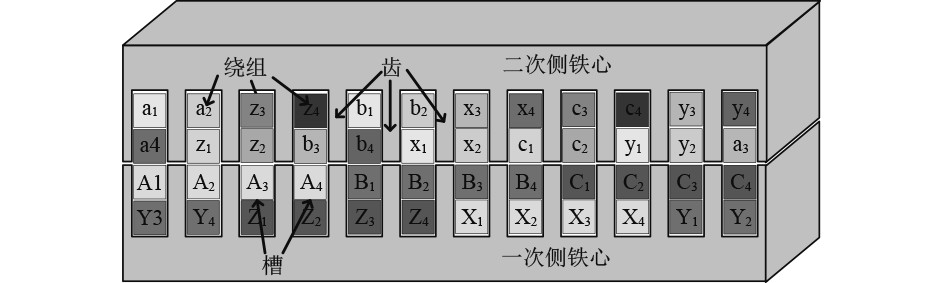
图 2 LPST绕组结构示意图 Fig. 2 Winding structure diagram of LPST |
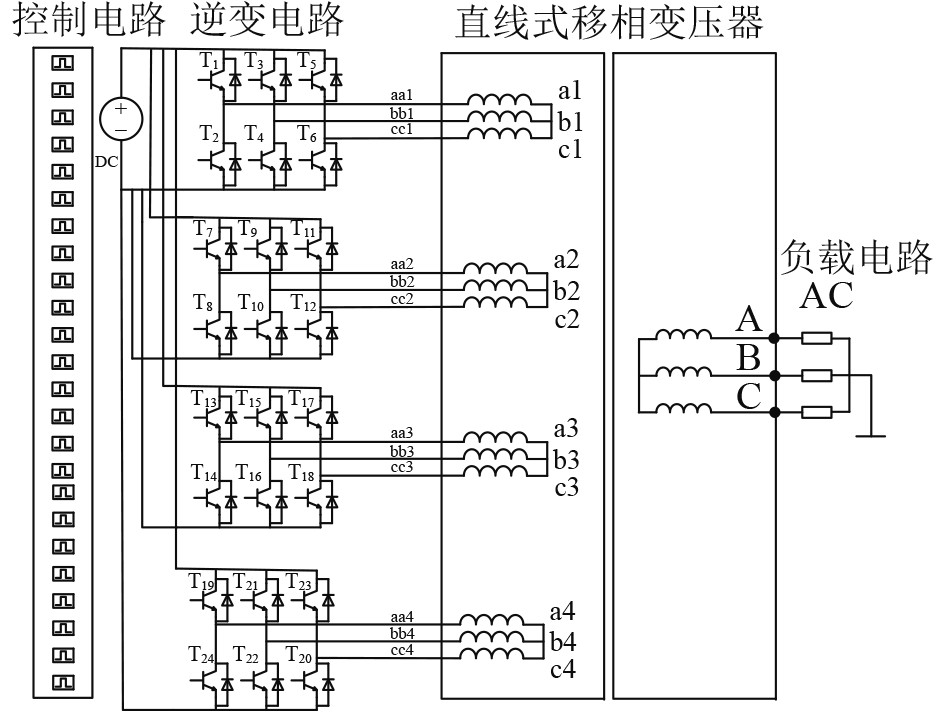
当LPST应用于多重叠加逆变系统时,原边嵌入12组绕组,接4组并联的三相桥式逆变电路,并采用星形联结成4组三相绕组。副边嵌入12组绕组,而后采用星形联结串联成三相,引出3个接线端子,接入负载。系统详细构成如图3所示。
|
图 3 多重叠加逆变系统电路图示意图 Fig. 3 Circuit diagram of multiple superimposed inverter system |
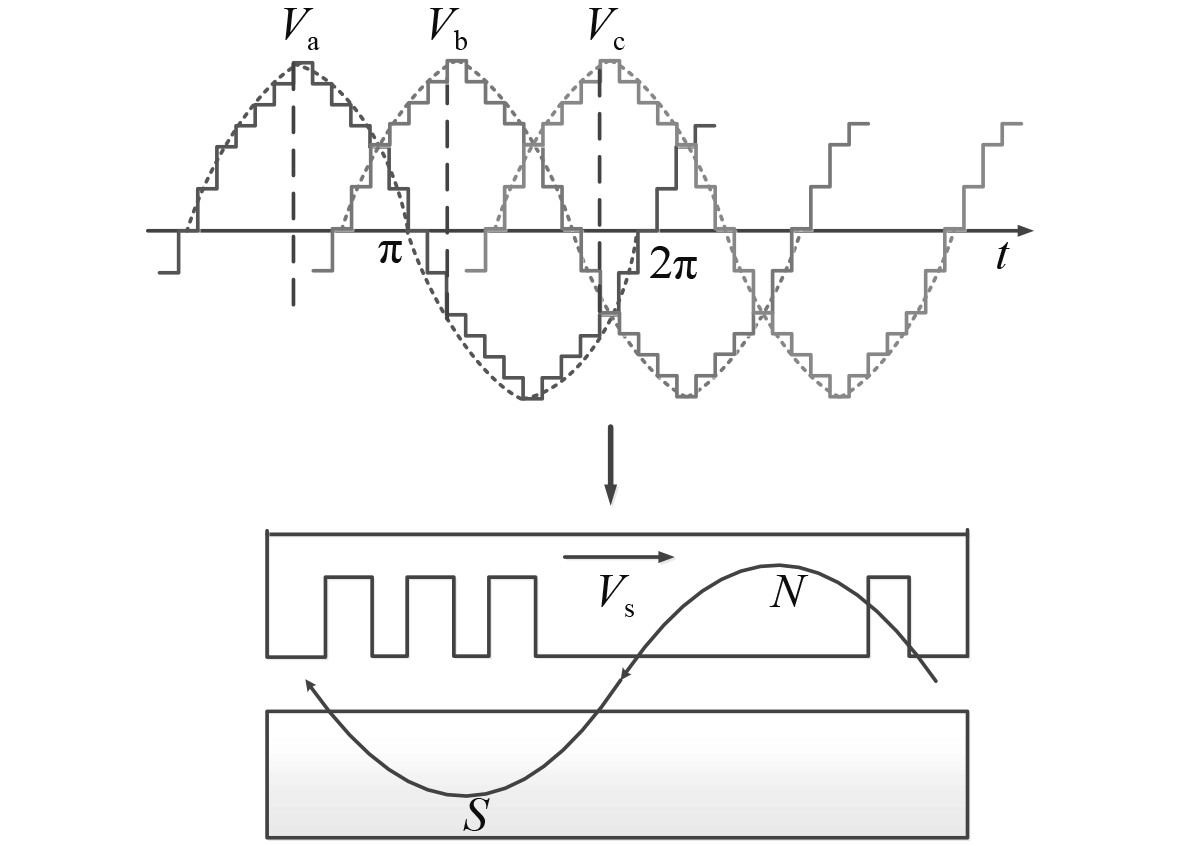
4组逆变电路开始导电的角度依次相差15°,即绕组aa1、aa2、aa3、aa4中的电压波形依次相差15°,绕组bb1、bb2、bb3、bb4中的电压波形依次相差15°,绕组cc1、cc2、cc3、cc4中的电压波形依次相差15°。十二相六脉波交流电经多重叠加后可等效为三相依次滞后120°的24脉波的交流电,高度近似为三相正弦交流电,叠加后的24阶梯波。将合成的三相24阶梯波的交流电输入LPST的一次侧,从而气隙中感应形成一个以固定速度移动的行波磁场,如图4所示。
|
图 4 24阶梯波产生行波磁场示意图 Fig. 4 Diagram of traveling wave magnetic field generated by step wave 24 |
LPST铁心上的电磁场和结构场存在直接耦合关系。变化的磁场引发磁致伸缩效应,进而使LPST铁心产生机械形变,而形变进而导致变压器铁心硅钢片磁导率发生变化,从而影响磁致伸缩力,因此2种场互相影响[9-10],在研究的时候需要同时考虑。
在电磁场中,麦克斯韦方程组是电磁场的基本方程,它描述着电场和磁场之间不可分割的关系。麦克斯韦方程微分形式表示为
| $ \left\{ {\begin{aligned} &\nabla \times {\boldsymbol{H}} = {\boldsymbol{J}} + \displaystyle\frac{{\partial {\boldsymbol{D}}}}{{\partial t}} ,\\ &\nabla \times {\boldsymbol{E}} = - \displaystyle\frac{{\partial{\boldsymbol{B}}}}{{\partial t}} ,\\ &\nabla \cdot {\boldsymbol{D}} = \rho ,\\ &\nabla \cdot {\boldsymbol{B}} = 0 。\end{aligned}} \right. $ | (1) |
其中
| $ {\boldsymbol{D}} = \varepsilon {\boldsymbol{E}},$ | (2) |
| $ {\boldsymbol{B}} = \mu {\boldsymbol{H}} 。$ | (3) |
式中:H为磁场强度;B为磁通密度;E为因电磁感应产生的涡流电场强度;D为电位移;J为传导电流密度;ρ为电荷密度;ε为电容率;σ为电导率;μ为磁导率。
在工频时,位移电流密度
| $ \nabla \times \nabla \times {\boldsymbol{A}} = \mu J。$ | (4) |
在结构场求解域中的方程为
| $ \boldsymbol{T} - {T_i} = \boldsymbol{C}\left( {\boldsymbol{Q} - {Q_i}} \right),$ | (5) |
| $ \rho \frac{{{\partial ^2}\boldsymbol{u}}}{{\partial {t^2}}} - \nabla \cdot \boldsymbol{T} = \boldsymbol{F}\upsilon。$ | (6) |
式中:
磁致伸缩效应可以用线性压磁方程来描述,主要包括应变方程和磁感应方程。虽然铁心硅钢片在应力作用下其材料磁化曲线会发生变化,但由于本文研究的磁致伸缩效应不含外加应力,且假设铁磁材料只在单一轴向上发生形变[12],因此线性压磁方程简化为:
| $ {\varepsilon _{H}} = {\text{d}}\boldsymbol{H} + \frac{\sigma }{{{E_{{H}}}}},$ | (7) |
| $ \boldsymbol{B} = {\mu _\sigma }\boldsymbol{H}。$ | (8) |
式中:
为研究LPST铁心硅钢片因磁致伸缩效应引起的形变,把式(7)和式(8)作为有限元模型中参数的本构关系,则整个“磁-结构”耦合数值模型的强耦合方程可表示为
| $ \boldsymbol{SA{\text{ = }}J} ,$ | (9) |
| $ \boldsymbol{Ku{\text{ = }}F} 。$ | (10) |
式中:
通过上述表达式,可以将LPST铁心因磁致伸缩力产生机械形变与电磁场的变化联系起来,实现电磁场和结构力场的强耦合,为LPST电磁振动的数值计算提供理论基础。
3 LPST电磁振动有限元分析根据上述原理,使用仿真软件COMSOL Multiphysics构建了一个二维LPST多物理场耦合模型,如图5所示。在此模型中,首先要设置磁场模块和固体力学模块的参数;接着需要对模型进行剖分,选择合适的网格尺寸;最后利用磁致伸缩模块实现了磁场与固体力学模块的耦合,就可以求解出LPST铁心的磁场和电磁振动分布,实现瞬态电磁场分析和结构场分析。
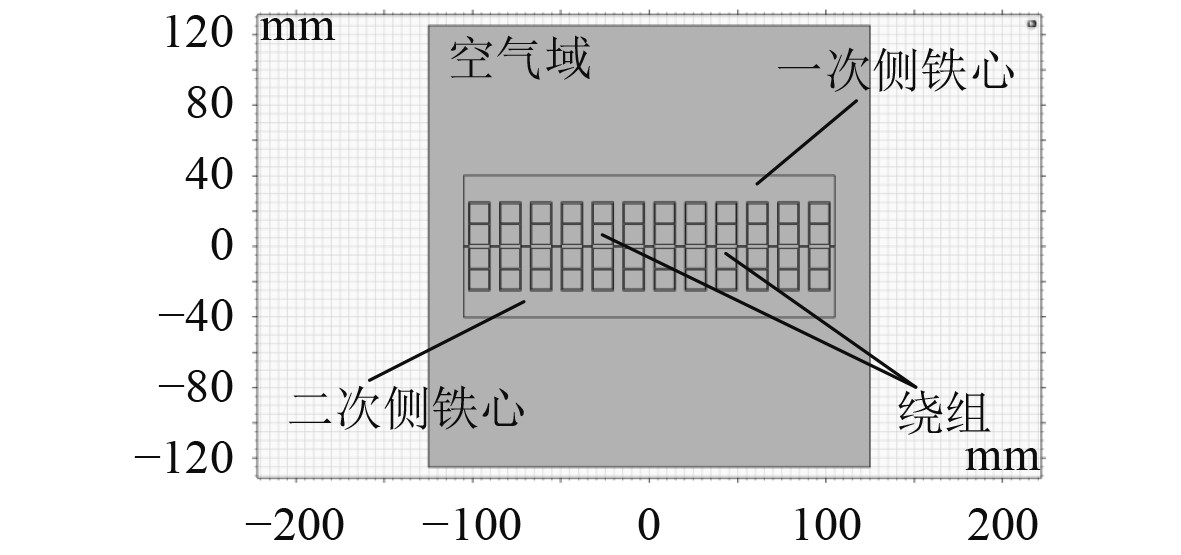
|
图 5 LPST二维模型 Fig. 5 Two-dimensional model of LPST |
在COMSOL搭建LPST二维模型,如图5所示。在磁场模块中设置LPST绕组参数,通过瞬态电磁场分析可以计算出LPST磁场分布情况,如图6所示。
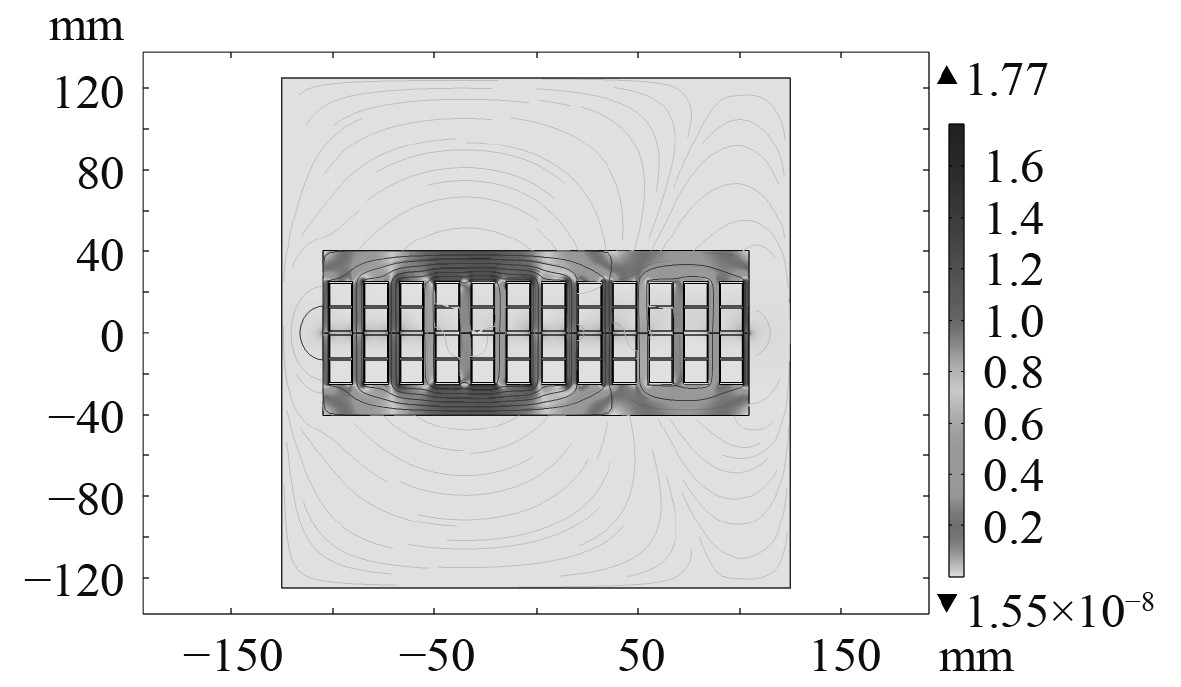
|
图 6 磁通密度分布 Fig. 6 Flux-density distribution |
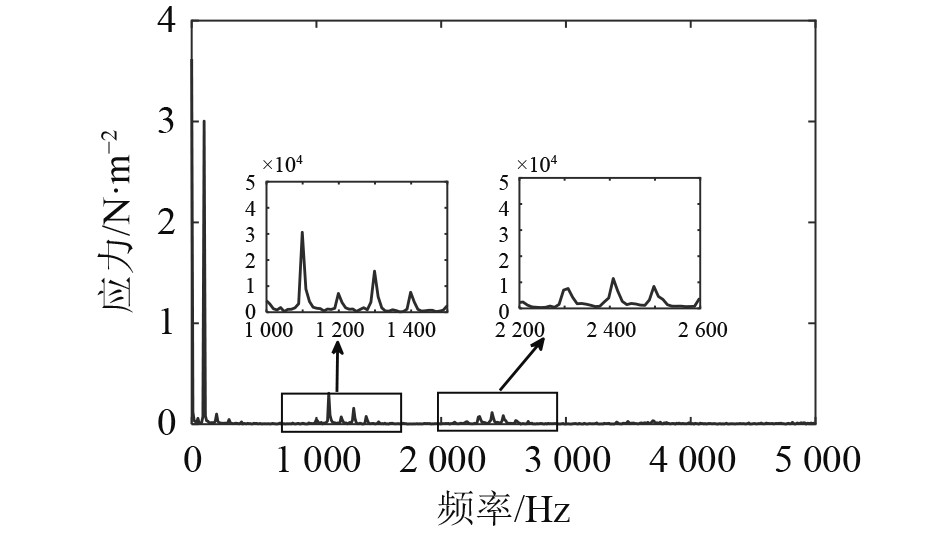
由固体力学和多物理场模块可以得到铁心的应力分布情况如图7所示。应力大小的分布与磁场大小的分布基本一致,在齿根部的值比较突出。取齿根部一点,可以得到该点出应力随时间变化的波形,如图8所示。然后对力波进行FFT变换,得到该点应力的时间频谱。由图9可知,应力在100 Hz处的含量最高,另外在
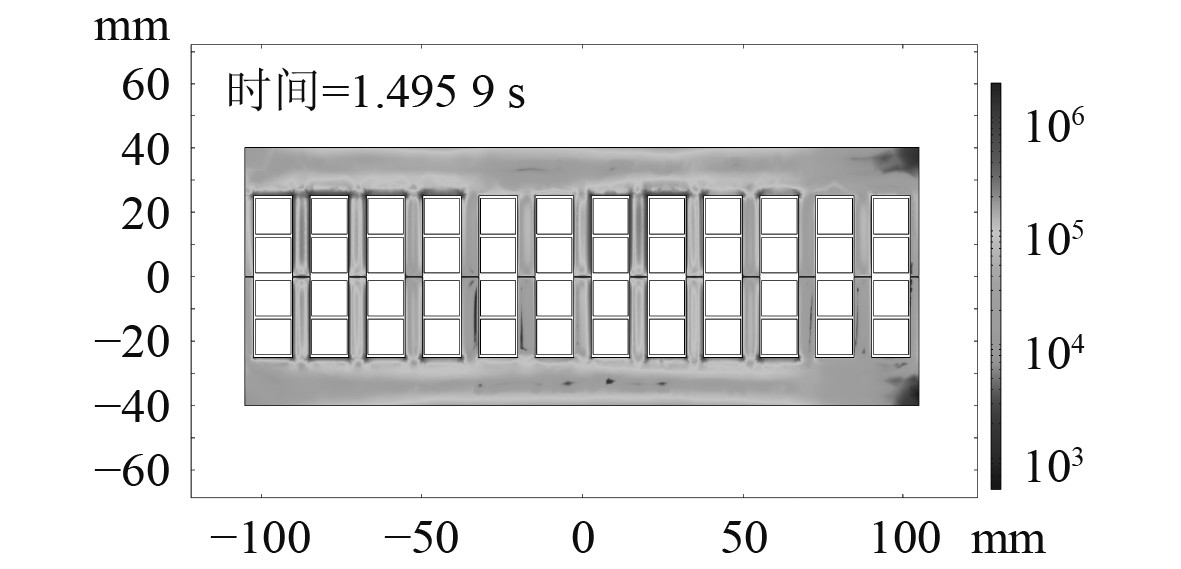
|
图 7 应力分布 Fig. 7 Stress distribution |
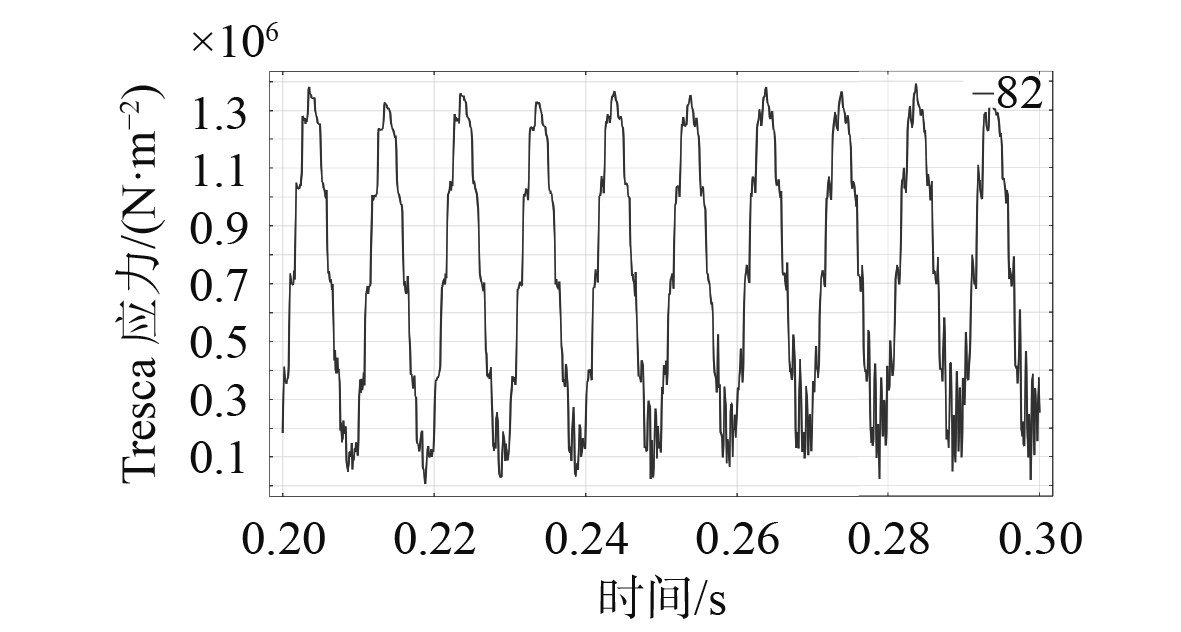
|
图 8 应力随时间变化 Fig. 8 The change of stress with time |
|
图 9 应力频谱 Fig. 9 Spectrum of stress |
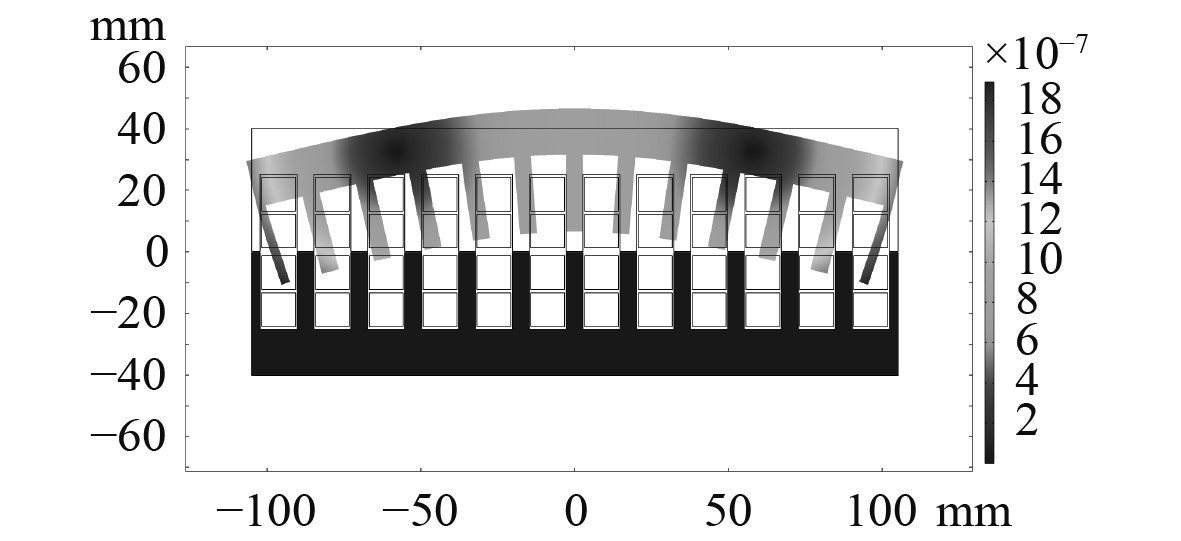
将应力导致的铁心形变量按比例放大后,得到的LPST铁心形变如图10所示,可以看出位移主要集中在齿的部分,齿尖的形变量大于齿根部,方向主要沿气隙方向,且形变大小数量级在10−8 m。

|
图 10 铁心位移分布 Fig. 10 Distribution of core displacement |
接下来需要对铁心部分进行模态分析,求出其固有频率和振型。在自由状态下铁心前六阶非0固有频率如表2所示,且1阶固有频率振型图11所示。此时铁心产生纵向自由度为1的弯曲形变。
|
|
表 2 前六阶非0固有频率 Tab.2 The first six orders of non-zero natural frequencies |
|
图 11
|
在铁心处取一点,其加速度频域响应如图12所示。可以看出,铁心在

|
图 12 加速度频域响应 Fig. 12 The Frequency response of acceleration |
由构建的LPST“磁-结构”耦合模型,可以得到铁心各点磁通密度、应力以及振动加速度等数据,并据此分析了铁心磁场和磁致伸缩振动。这些数值结果为变压器的声场计算提供了重要的数据支撑。为了得到周围空间的噪声数据,在此基础上,需要对模型做进一步拓展,构建LPST“磁-结构-声”多物理场耦合模型。
由文献[13]可知压力声学的基本方程式如下:
| $ \frac{1}{{\rho {c^2}}}\frac{{{\partial ^2}{p_t}}}{{\partial {t^2}}} + \nabla \cdot \left[ { - \frac{1}{\rho }\left( {\nabla {p_t} - {q_d}} \right)} \right] = {Q_m} 。$ | (11) |
式中:
结构场与声场的耦合方程为:
| $ - n \cdot \left[ { - \frac{1}{\rho }\left( {\nabla {p_t} - {q_d}} \right)} \right] = - n \cdot {a_0},$ | (12) |
| $ {p_t} = p + {p_b}。$ | (13) |
式中:
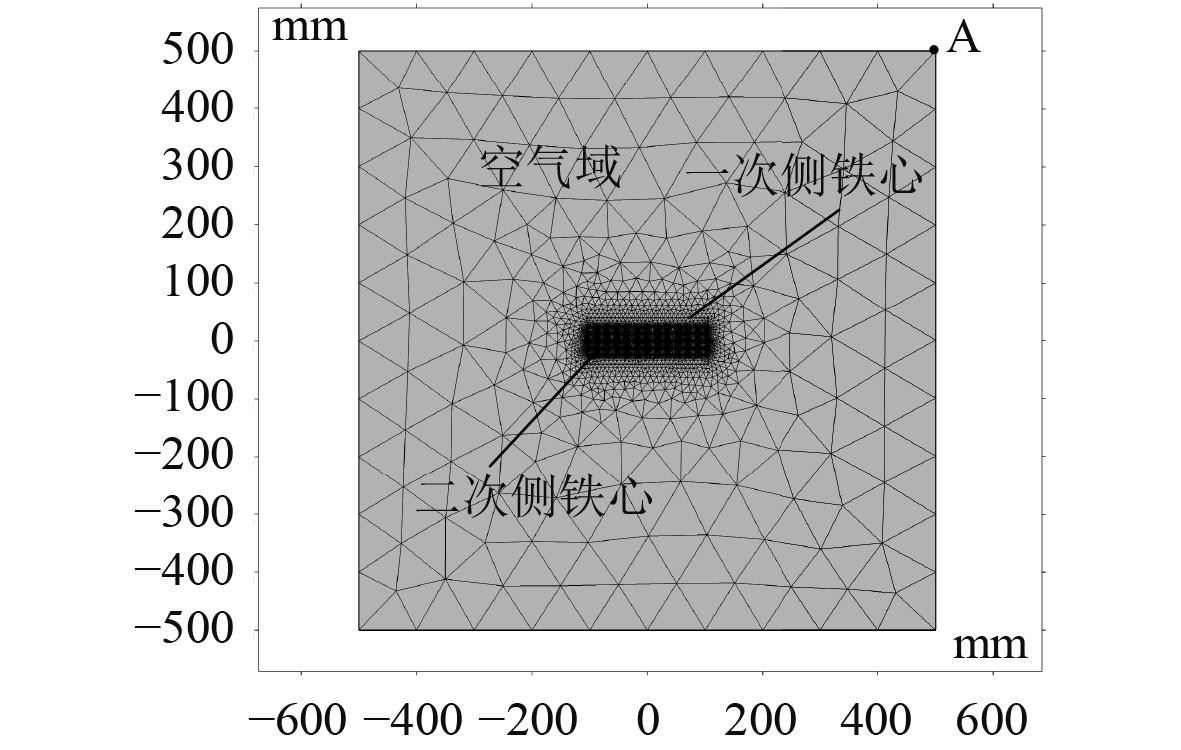
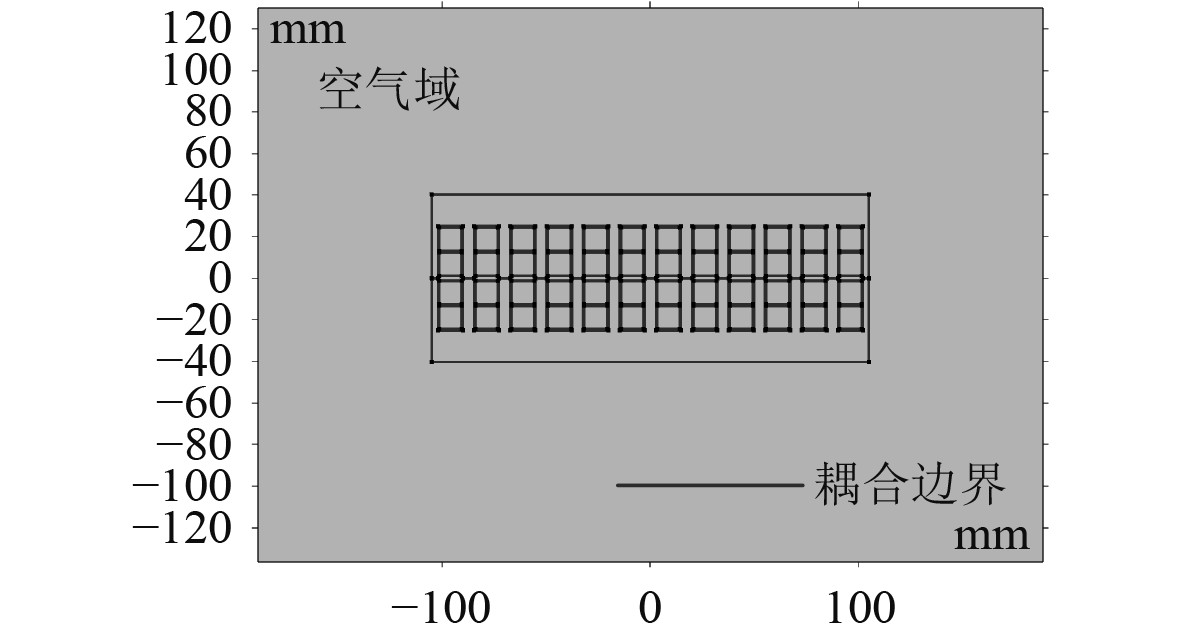
在研究声压场时,首先需要结构场中的LPST模型的空气域范围扩大,使LPST处于一个边长为1 m的正方形空气域内,并对模型进行网格剖分,这里使用的是三角元剖分。得到的声学模型如图13所示。在COMSOL中添加“压力声学,频域”物理场模块,并且设置相应的声学区域(空气域)和边界,最后在多物理场模块中添加 “声-结构边界”,这是结构场中边界的振动加速度参数和声场边界的声压参数耦合的位置,耦合边界如图14所示。
|
图 13 LPST声学分析二维模型 Fig. 13 Two-dimensional sound field analysis model of LPST |
|
图 14 声-结构耦合边界 Fig. 14 Acoustic-structural coupling boundary |
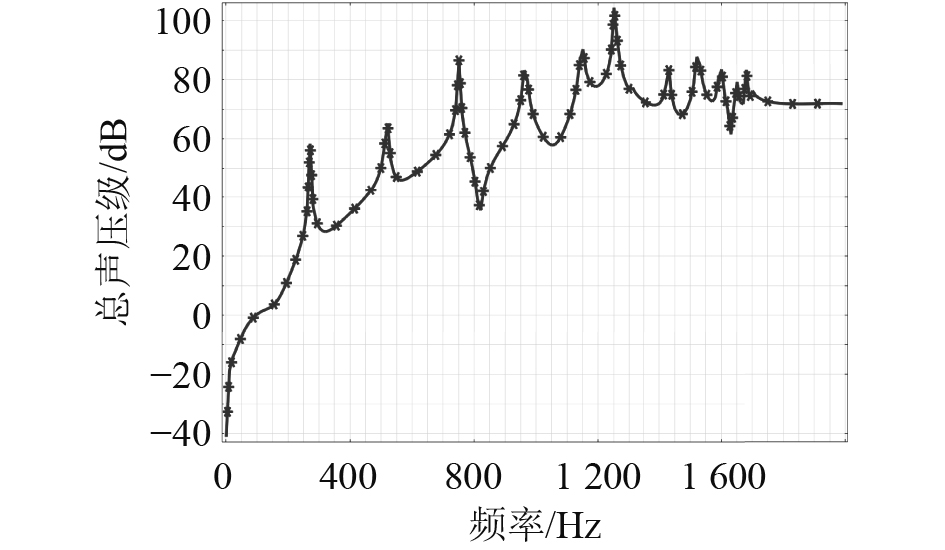
经过COMSOL有限元软件仿真计算后,即可得到空气域内的噪声分布情况。取空气域右上角顶点A,如图15所示,可以得到此处的声压级频域响应曲线。从图中可以看出LPST在A点处的总声压级于
|
图 15 LPST总声压级频域响应 Fig. 15 Frequency response of total sound pressure level |
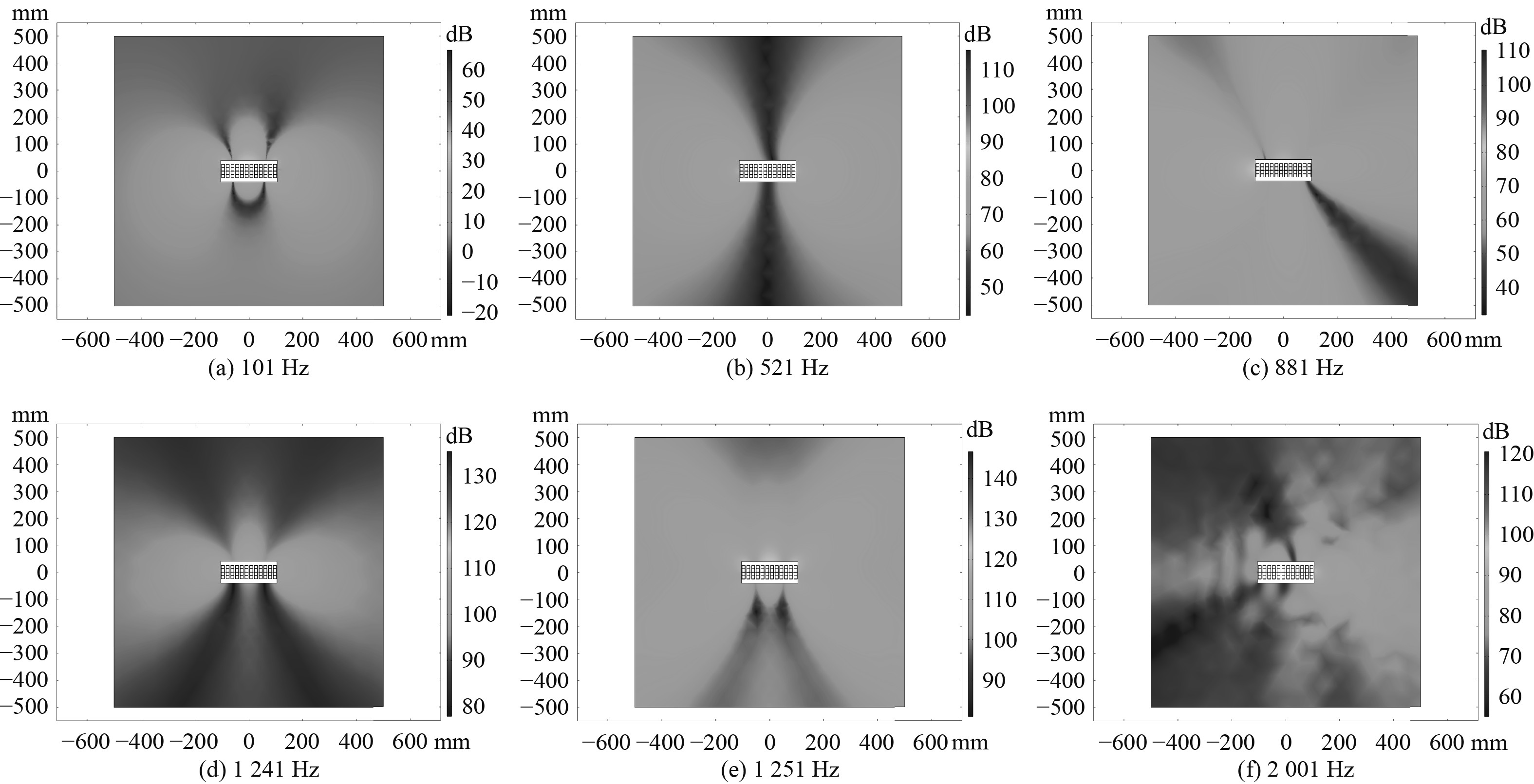
|
图 16 总声压级分布 Fig. 16 Distribution of total sound pressure level |
本文对引起LPST电磁振动的源头之一—磁致伸缩力开展研究。通过理论分析,阐明了LPST铁心“电磁—结构”耦合数值模型中各种参数间的本构关系。接着建立了LPST有限元仿真模型,通过COMSOL Multiphysics平台开展“电磁场−结构−声场”多物理场联合仿真,分析了LPST受磁致伸缩力引起的电磁振动的频率响应,以及周围空间的噪声的分布。研究表明,空载运行状态下的LPST所受磁致伸缩力主要频率为100 Hz,并且会在频率
| [1] |
ZHOU C, ZHAO J, WANG H, et al. Harmonic analysis and cancellation of inverter systems with linear phase-shifting transformer[J]. IEEE Transactions on Electrical and Electronic Engineering, 2023, 18(10): 1617−1625.
|
| [2] |
董兴康. 考虑磁致伸缩的永磁直线电机振动噪声的研究[D]. 沈阳: 沈阳工业大学, 2021.
|
| [3] |
王前超. 基于磁致伸缩等效力计算的变压器电磁振动研究[D]. 天津: 天津工业大学, 2021.
|
| [4] |
KOEN Delaere, WARD Heylen, KAY Hameyer, et al. Local mangetostriction forces for finite element analysis[J]. IEEE Transactions on Magnetics, 2000, 36(5): 3115-3118. DOI:10.1109/20.908703 |
| [5] |
ZHU Lihua, YANG Qingxin, YAN Rongge. Numerical analysis of vibration due to magnetostriction of three phase transformer core[C] //Proceedings of the 6th International Conference on Electromagnetic Field Problems and Applications (ICEF′ 2012), Dalian, China, 2012.
|
| [6] |
胡静竹, 刘涤尘, 廖清芬, 等. 基于有限元法的变压器电磁振动噪声分析[J]. 电工技术学报, 2016, 31(15): 81-88. DOI:10.3969/j.issn.1000-6753.2016.15.010 |
| [7] |
祝丽花, 杨庆新, 闫荣格, 等. 考虑磁致伸缩效应电力变压器振动噪声的研究[J]. 电工技术学报, 2013, 28(14): 1-6+19. DOI:10.3969/j.issn.1000-6753.2013.04.001 |
| [8] |
钟思翀, 祝丽花, 王前超, 等. 电力变压器振动噪声分析及其有源降噪[J]. 电工技术学报, 2022, 37(S1): 11-21. ZHONG Sichong, ZHU Lihua, WANG Cianchao, et al. Electromagnetic vibration of power transformer and active noise reduction[J]. Transactions of China Electrotechnical Society, 2022, 37(S1): 11-21. |
| [9] |
陈传敏, 冯洪达, 郭兆枫, 等. 220kV电力变压器辐射噪声特性仿真分析[J]. 电力学报, 2020, 35(6): 515-521. |
| [10] |
TANZER T, PREGARTNER H, RIEDENBAUER M, et al. Magnetostriction of electrical steel and its relation to the no-load noise of power transformers[J]. IEEE Transactions on Industry Applications, 2018, 54(5): 4306-4314. DOI:10.1109/TIA.2018.2840977 |
| [11] |
ZHANG Pengning, LI Lin, CHENG Zhiguang, et al. Study on vibration of iron core of transformer and reactor based on Maxwell stress and anisotropic magnetostriction[J]. IEEE Transactions on Magnetics, 2019, 55(2): 9400205. |
| [12] |
YAMAGASHIRA M, WAKABAYASHI D, ENOKINOZO M. Vector magnetic properties and 2-D magnetostriction of various electrical steel sheets under rotating flux condition[J]. IEEE Transactions on Magnetics, 2014, 50(4): 6100404. |
| [13] |
祝丽花. 叠片铁心磁致伸缩效应对变压器、交流电机的振动噪声影响研究[D]. 天津: 河北工业大学, 2013.
|
 2024, Vol. 46
2024, Vol. 46
