2. 海军研究院,北京 100161
2. Naval Research Academy, Beijing 100161, China
随着各种海洋爆炸事件的频繁发生,水下爆炸对水工结构的毁伤已成为国际上的研究热点。钢筋混凝土作为各种水工结构的主要构件,其性能直接影响着军事结构和民用设施结构的抗爆能力。因此,研究钢筋混凝土结构在水下爆炸冲击载荷作用下的毁伤特性具有重要意义[1 − 2]。
近年来,国内外学者围绕水下爆炸载荷及其对结构的影响进行了大量研究。在水下爆炸载荷方面,Cole[3]通过对大量水下爆炸研究结果进行分析,总结出了水下爆炸载荷的经验公式。姚熊亮等[4 − 6]对水下爆炸载荷作用下水工结构的动态响应进行数值模拟,并验证了Abaqus声固耦合法计算水下爆炸冲击载荷的准确性。在钢筋混凝土结构毁伤研究方面,爆破试验是研究钢筋混凝土板毁伤失效特征的最有效方法。Kumar等[2,7 − 9]对不同爆炸载荷作用下钢筋混凝土结构的动力响应及损伤特性进行了试验研究。由于水下爆炸试验具有成本高昂、试验条件要求苛刻、可重复性低等特点,数值模拟逐渐成为研究水下爆炸冲击载荷作用下结构毁伤的主要手段。越来越多的学者采用流固耦合、声固耦合等不同数值方法进行水下爆炸数值模拟,得到了很好的仿真结果。
本文以四周固支的钢筋混凝土板为研究对象,基于Abaqus的声固耦合法[10]对其在水下近场爆炸冲击载荷作用下的毁伤特性进行数值模拟,分析了钢筋混凝土板的主要毁伤模式,并通过Kriging模型[11]对钢筋混凝土板的毁伤模式进行预测,为钢筋混凝土结构在水下近场爆炸冲击载荷作用下的毁伤研究提供参考。
1 数值分析 1.1 几何模型钢筋混凝土板数值仿真模型如图1所示,板的尺寸为
|
图 1 钢筋混凝土板水下爆炸数值模型 Fig. 1 Numerical model of underwater explosion of reinforced concrete slabs |
计算过程中炸药爆炸和冲击波传播过程选择Geers-Hunter模型进行数值模拟,内置子程序根据定义的炸药相关参数,计算出不同炸药质量和不同爆距下的水下爆炸冲击波载荷的压力曲线,然后自动计算流场中其他点处的压力分布,这种方法计算速度快,精度高。炸药材料主要参数如表1所示。
|
|
表 1 炸药参数 Tab.1 Explosive parameters |
混凝土材料使用JH-2本构模型描述,该模型充分考虑了材料的大应变率、大变形等特点,可以很好地描述混凝土的动态响应。混凝土材料强度等级选择C30,JH-2材料参数如表2所示。
|
|
表 2 C30混凝土材料参数[12] Tab.2 C30 concrete material parameters |
混凝土板内的钢筋材料采用典型的弹塑性模型模拟,钢筋型号选用HRB400,大部分学者选取钢筋的拉应变作为失效准则,选取的数值有0.1、0.12、0.15、0.18,本文取极限应变为0.15[13],在Abaqus中通过设置单元的失效应变控制单元失效。钢筋材料主要参数如表3所示。
|
|
表 3 钢筋材料参数 Tab.3 Reinforcing steel material parameters |
图2为钢筋混凝土板在水下爆炸冲击波载荷作用下的损伤演变过程,整个钢筋混凝土板经历了弯曲变形和混凝土破碎脱落等形式的损伤过程。炸药在水中起爆 0.1 ms时,混凝土板迎爆面中心最先受到冲击波载荷的作用,随后冲击波逐渐向四周扩散;当10 ms时在四周固支端出现损伤,这是因为板四周固支;当冲击波传播到固支边缘引起的应力集中,导致钢筋混凝土板边缘出现剪切断裂损伤。强压力导致混凝土材料的压缩,在迎爆面板中心形成一个破碎损伤区域,且四周被一些径向和周向裂纹包围。混凝土板背爆面可以观察到十字形裂纹,这是由于反射拉伸波的作用,当冲击波传播到背爆面时,在背爆面反射形成反射拉伸波对底面造成拉伸损伤,混凝土的拉伸应力较小,因此在背爆面形成受拉裂缝。

|
图 2 水下爆炸钢筋混凝土板损伤过程 Fig. 2 Damage process of reinforced concrete slab by underwater explosion |
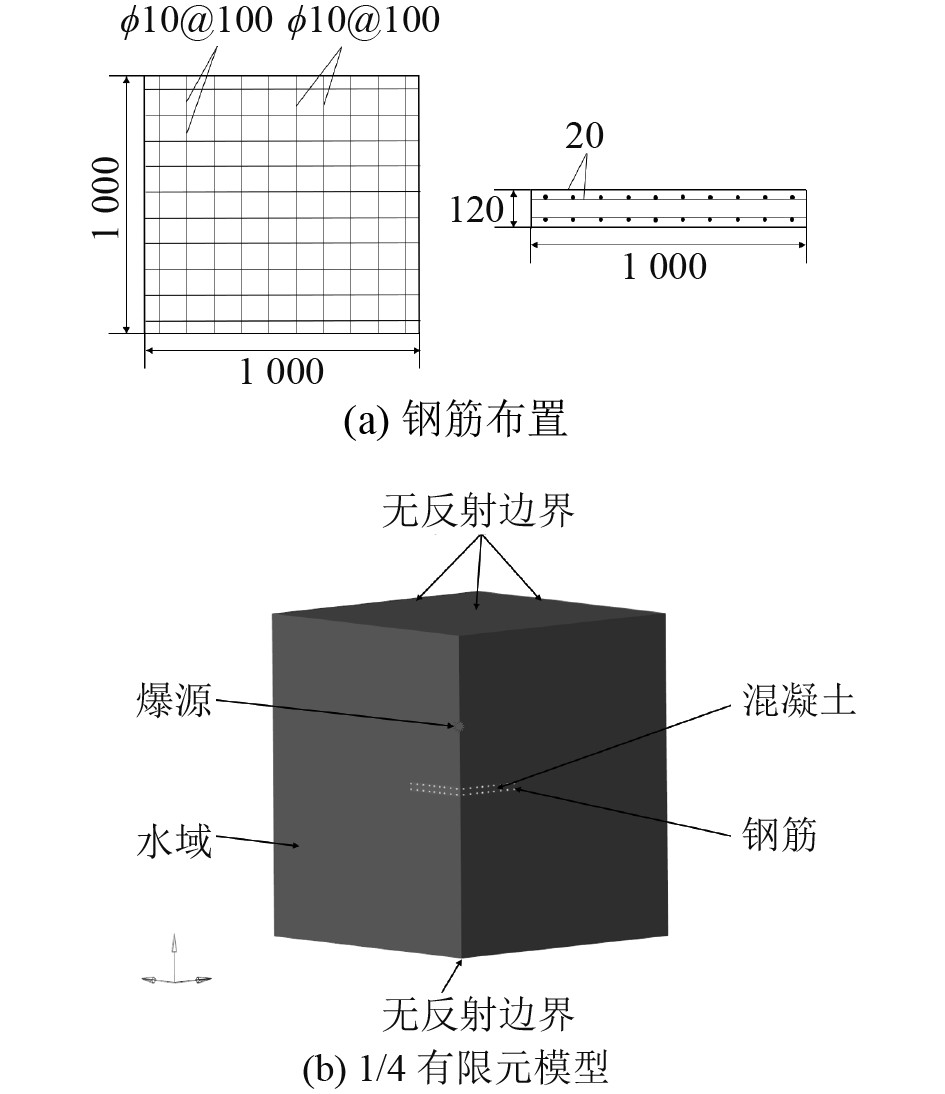
保持其他参数不变,对TNT当量分别为0.1、0.07、0.05 kg时,钢筋混凝土板在水下爆炸作用下毁伤进行分析。对3种条件下板中心的位移时程曲线和速度时程曲线进行对比,如图3所示,最大位移出现在2 ms内,而后,钢筋混凝土板由于惯性和水的作用继续运动。当TNT当量为0.1 kg时,钢筋混凝土板的最大位移为11 mm;当TNT当量为0.07 kg时,板的最大位移为7.29 mm;当TNT当量为0.05kg时,板的最大位移为4.90 mm,随着TNT当量的减小,板的距离逐渐减小。3种TNT当量作用下板的毁伤情况如图4所示 ,当TNT当量为0.1 kg时,板的毁伤最严重,迎爆面出现大量混凝土脱落,整个板面损伤严重,当TNT当量为0.05 kg时,板面损伤较轻,伴有少量破碎。
|
图 3 不同当量板的中心位移时程曲线 Fig. 3 Displacement-time curves of slab center at different equivalents |

|
图 4 不同当量板的损伤云图 Fig. 4 Damage cloud diagrams of the slab at different equivalents |
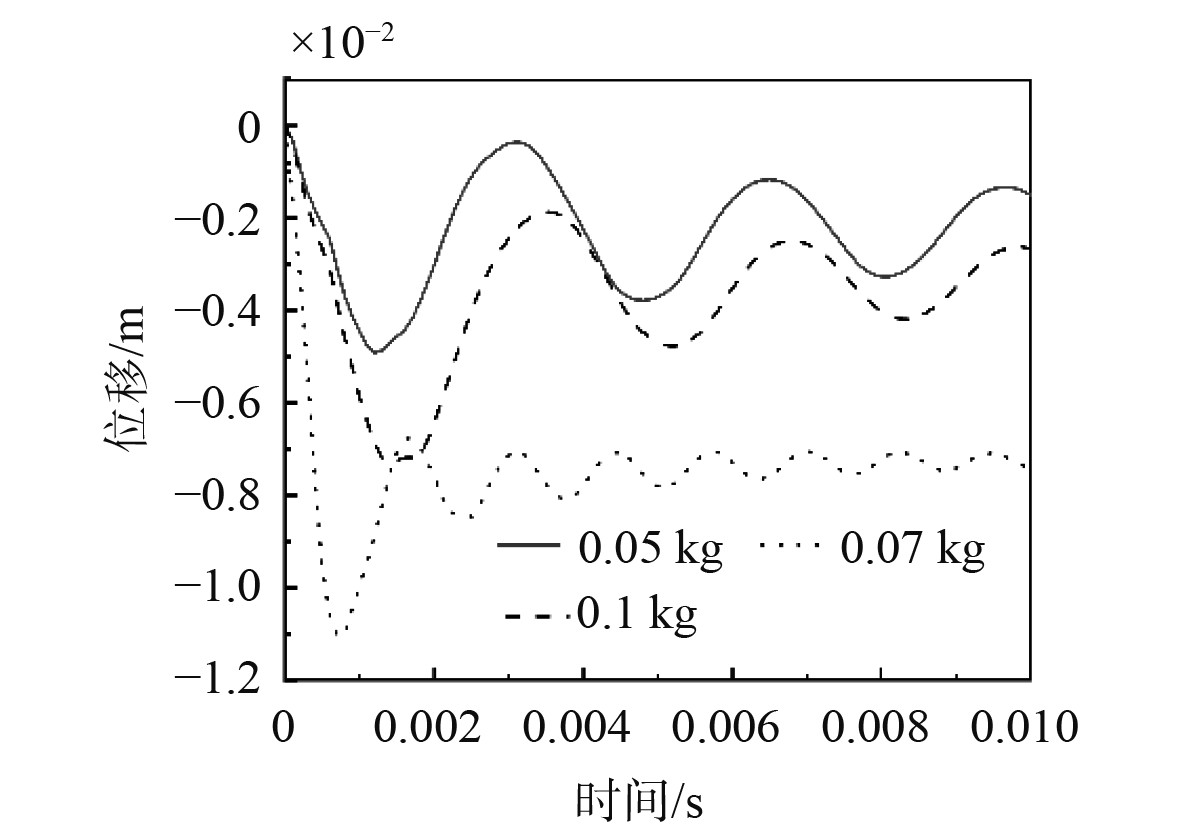
保持其他参数不变,对爆距分别为0.4、0.6、0.8 m时,对于钢筋混凝土板在水下爆炸作用下的毁伤结果进行分析。3种条件下板中心的位移时程曲线如图5所示,当爆距为0.4 m时,钢筋混凝土板的最大位移为11 mm,随着爆距的增加,板的位移逐渐减小;当爆距为0.8 m时,板的最大位移为3.89 mm,3种TNT当量作用下板的毁伤情况如图6所示;当爆距为0.4 m时,板的毁伤最严重,迎爆面中心有大面积混凝土脱落;当爆距为0.8 m时,板面损伤较轻伴有少量破碎且中心损伤区域很小。
|
图 5 不同爆距板的中心位移时程曲线 Fig. 5 Displacement-time curves of slab center at different blast distances |

|
图 6 不同爆距板的损伤云图 Fig. 6 Damage cloud diagrams of the slab at different blast distances |
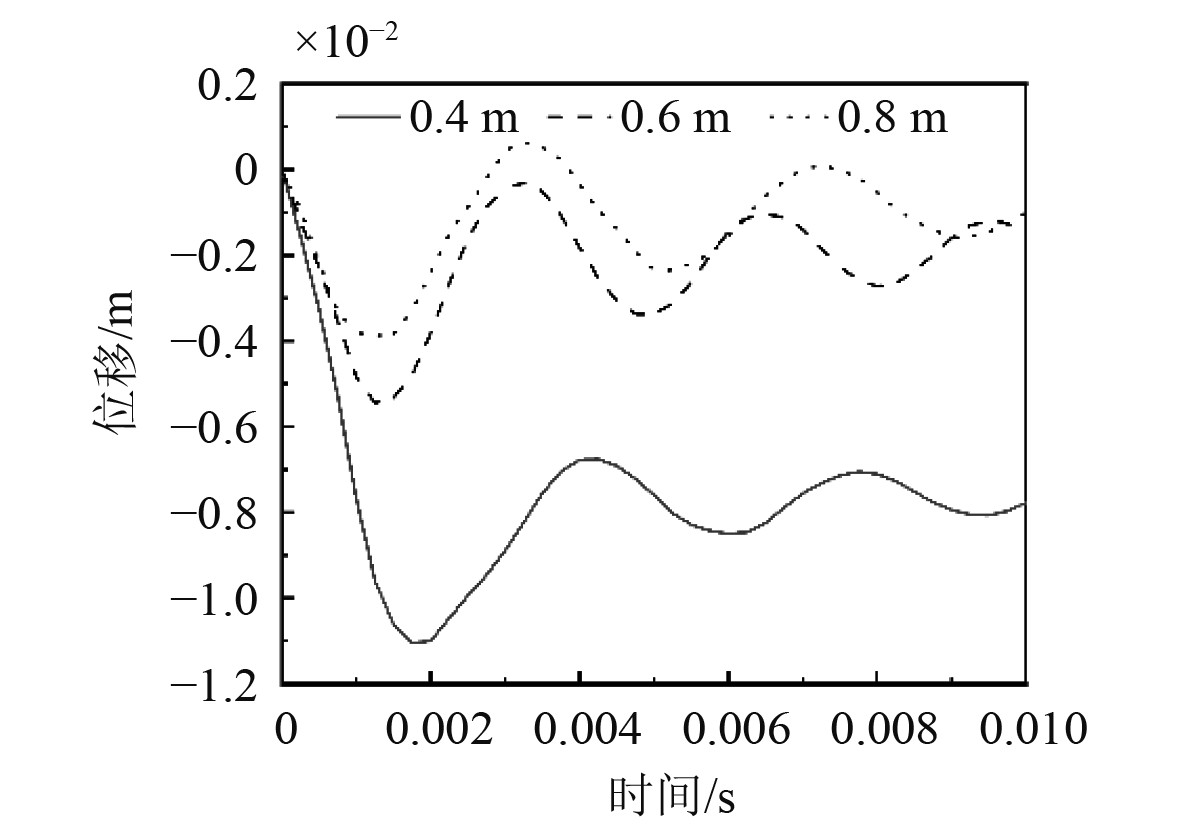
图7为不同板厚在比例距离为0.86的相同工况下位移时程曲线,可以看出,随着板厚度的减小,板中心的位移越来越大,混凝土的损伤情况越来越严重,不同厚度的钢筋混凝土板损伤云图如图8所示,当厚度为0.12 m和0.1 m时,钢筋混凝土板迎爆面中心有圆形破碎,板面布满裂纹。随着板的厚度减小到0.08 m和0.06 m,钢筋混凝土板破碎区几乎消失,板中心弯曲变形严重,基本整体失效。出现上述损伤情况的原因是板厚度越小,混凝土占比减少,整块板的脆性减小,在相同的配筋情况下,塑性就更好。因此较薄的钢筋混凝土板出现了较大的塑性变形。
|
图 7 不同厚度板的中心位移时程曲线 Fig. 7 Displacement-time curves of slab center at different thicknesses |

|
图 8 不同厚度板的损伤云图 Fig. 8 Damage cloud diagrams of the slab at different thicknesses |
根据数值仿真结果,将钢筋混凝土板的毁伤模式主要分为3种,如表4所示。
|
|
表 4 钢筋混凝土板毁伤模式 Tab.4 Damage modes of reinforced concrete slabs |
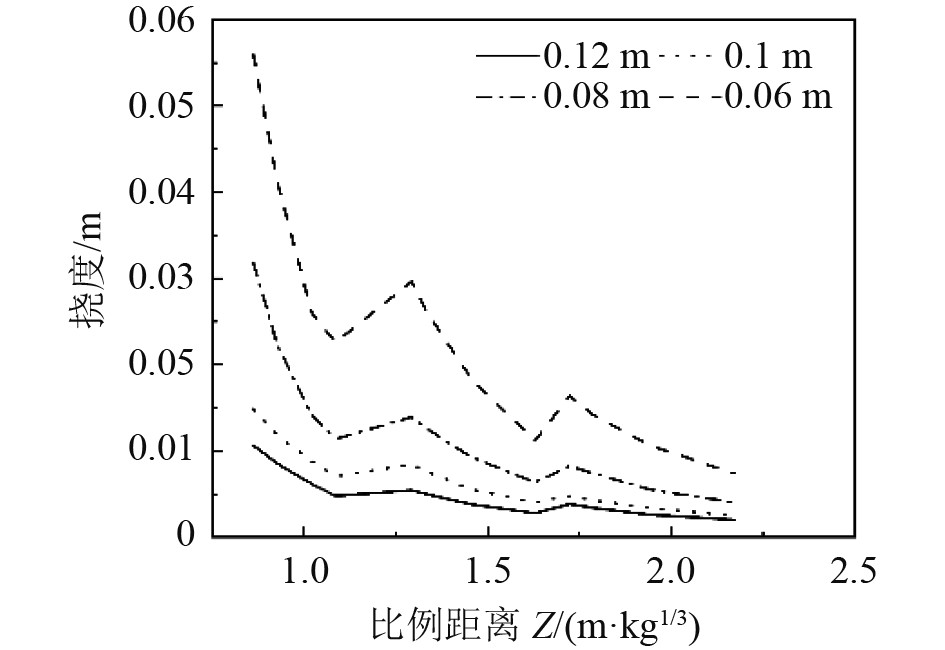
根据仿真结果绘制比例距离-挠度曲线如图9所示,分析毁伤情况,由比例距离-挠度折线图结果可以看出,随着比例距离的增加,钢筋混凝土板的毁伤逐渐严重。当板厚为0.06 m时,板厚度相对较薄,钢筋混凝土板整体塑性较好,可以看到板变形较为明显;当厚度为0.12 m时,板的混凝土含量较高,结构脆性较大。因此易出现板面冲击破碎,混凝土脱落的情况,整体变形不明显。
|
图 9 比例距离-挠度曲线 Fig. 9 Proportional distance-deflection curves |
从折线图中可知,钢筋混凝土板的挠度与比例距离并不是严格的线性关系,无法用比例距离与板挠度关系准确判定板的毁伤状况,进一步分析爆距和当量。由第2节内容可知,在板厚度相同时爆距对结果的影响更大,同一爆距,随着炸药量的增加,板的毁伤情况相差并不是很大,而同一炸药量,随着爆距的增加,板的毁伤越来越小,相差较大。
3.2 结构毁伤模式的预测根据划分的钢筋混凝土板的毁伤模式,采用主要影响板毁伤结果的因素:爆距、当量和板厚作为判定板毁伤模式的主要变量拟合Kriging模型,对钢筋混凝土板的毁伤模型进行预测。预测结果如下:
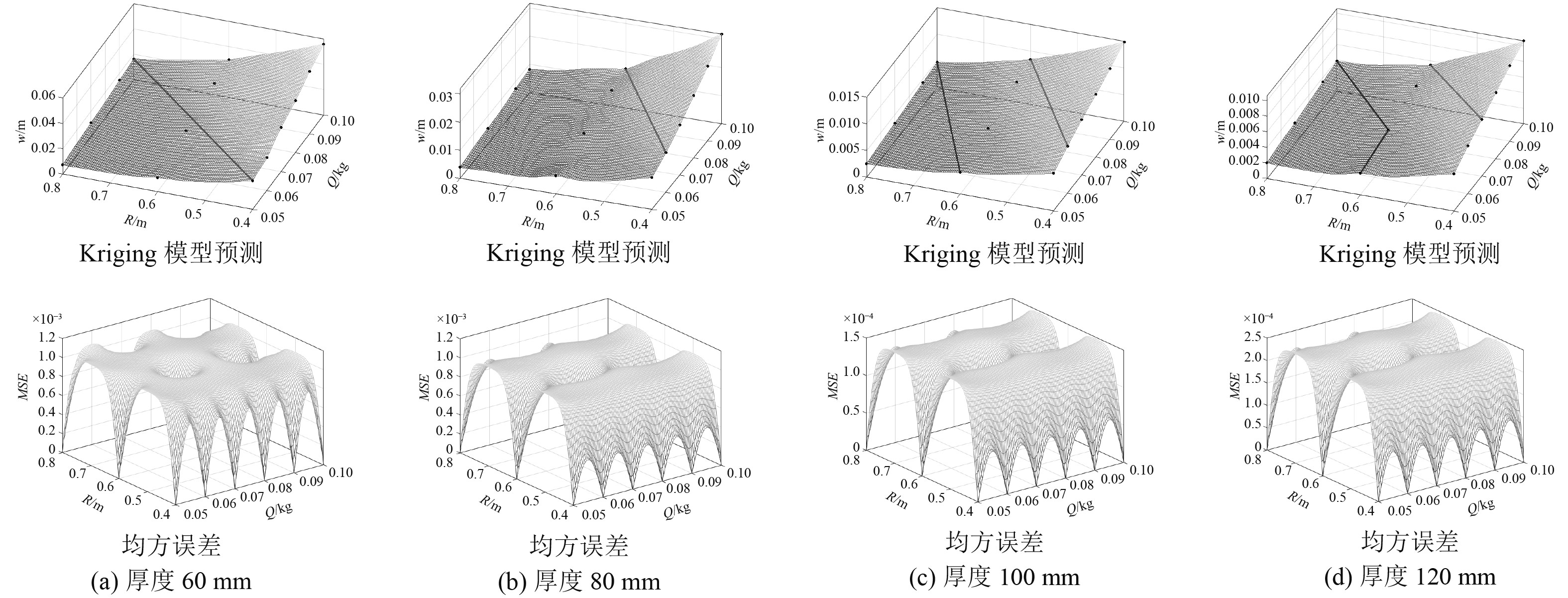
图10为Kriging模型预测结果,不同毁伤模式由一条直线划分,当板的厚度越大时,毁伤模式Ⅰ的范围越大,因此当厚度为0.06 m和0.08 m时,在一定的当量和爆距范围内,毁伤模式Ⅰ基本没有,直线主要区分毁伤模式Ⅱ和毁伤模式Ⅲ。当厚度为0.1 m和0.12 m时,3种毁伤模式都有,在预测图形上,左侧线条是毁伤模式Ⅰ和毁伤模式Ⅱ的分界线,右侧直线是毁伤模式Ⅱ和毁伤模式Ⅲ的分界线。出现上述情况主要原因是板的厚度越厚,脆性越大,变形越小,易出现裂纹损伤。
|
图 10 不同厚度板Kriging预测结果 Fig. 10 Kriging prediction results for slabs with different thicknesses |
根据图10的Kriging的预测结果可以看出,均方误差结果在1.5×10−3以内,反映出 Kriging 模型的期望误差很小,说明构造的 Kriging 模型精度较高,可以进行钢筋混凝土板的毁伤模式预测。
3.3 Kriging预测模型验证随机选取3个不同参数的工况对Kriging模型觉得准确性进行验证,验证结果如表5预测的毁伤模式与仿真结果保持一致,工况1的挠度误差为1.6%,工况2的挠度误差为1.3%,工况3的挠度误差为2.4%,误差都比较小,说明Kriging模型可以很好地预测钢筋混凝土板的毁伤模式和挠度,可以为近场水下爆炸冲击波载荷作用下的钢筋混凝土板毁伤研究提供一定的参考。
|
|
表 5 Kriging预测模型验证 Tab.5 Kriging predictive model validation |
本文基于数值仿真分析方法,研究了水下爆炸冲击波载荷作用下不同厚度的钢筋混凝土板的毁伤模式。运用Abaqus软件,采用声固耦合法对钢筋混凝土板进行了大量的水下爆炸仿真,结果表明:
利用建立的声固耦合数值模拟方法可以很好地模拟水下爆炸冲击波载荷作用下,钢筋混凝土板的毁伤状态。根据仿真结果总结出了钢筋混凝土板在近场小当量水下爆炸冲击波作用下的3种毁伤模式。
在近场水下爆炸冲击波载荷作用下,钢筋混凝土板的毁伤模式与爆距、当量和板厚有关,相对于当量的影响,爆距和板厚度对于结构的毁伤影响更大,采用Kriging模型根据已知的参数可准确预测板的挠度及其毁伤模式。
| [1] |
HAI L, REN X. Computational investigation on damage of reinforced concrete slab subjected to underwater explosion[J]. Ocean Engineering, 2020, 195: 106671. DOI:10.1016/j.oceaneng.2019.106671 |
| [2] |
YANG G, WANG G, LU W, et al. Experimental and numerical study of damage characteristics of RC slabs subjected to air and underwater contact explosions[J]. Marine structures, 2019, 66: 242-257. DOI:10.1016/j.marstruc.2019.04.009 |
| [3] |
COLE R H. Underwater explosion[M]. New Jersey: Princeton University Press, 1948.
|
| [4] |
姚熊亮, 刘东岳, 张阿漫, 等. 潜艇结构水下爆炸动态响应仿真研究[J]. 哈尔滨工程大学学报, 2008, 29(9): 902-906. YAO Xiongliang, LIU Dongyue, ZHANG Aman, et al. Simulating the dynamic response of submarine structures subjected to under water explosions[J]. Journal of Harbin Engineering University, 2008, 29(9): 902-906. DOI:10.3969/j.issn.1006-7043.2008.09.002 |
| [5] |
ZHANG AM, YANG S T, YAO X L. Numerical simulation of the penetration of fuel-filled tank by a high-speed projectile[J]. Journal of Ship Mechanics, 2010, 14(9): 998-1007. |
| [6] |
张艺凡, 宗智, 张文鹏. 水下冲击波作用下结构损伤的数值预报误差分析[J]. 中国舰船研究, 2011, 6(6): 38-44. ZHANG Yifan, ZONG Zhi, ZHANG Wenpeng. Analysis of numerical prediction of structure damages subjected to underwater shock[J]. Chinese Journal of Ship Research, 2011, 6(6): 38-44. DOI:10.3969/j.issn.1673-3185.2011.06.008 |
| [7] |
KUMAR V, KARTIK K V, IQBAL M A. Experimental and numerical investigation of reinforced concrete slabs under blast loading[J]. Engineering Structures, 2020, 206: 110-125. |
| [8] |
闫秋实, 宁素瑜, 王全胜, 等. 近场水中爆炸作用下钢筋混凝土桩破坏模式及损伤评估研究[J]. 混凝土, 2019(7): 32-36. YAN Qiushi, NING Suyu, WANG Quansheng, et al. Damage effect for a typical reinforced concrete pile under the near field explosion in water[J]. Concrete, 2019(7): 32-36. DOI:10.3969/j.issn.1002-3550.2019.07.007 |
| [9] |
ZHAO X, WANG G, LU W, et al. Experimental investigation of RC slabs under air and underwater contact explosions[J]. European Journal of Environmental and Civil Engineering, 2021, 25(1): 190-204. DOI:10.1080/19648189.2018.1528892 |
| [10] |
王鹰宇. ABAQUS分析用户手册[M]. 北京: 机械工程出版社, 2017.
|
| [11] |
ZHANG L, LI X. Thermal-fluid-structure interaction analysis of bladed disk system based on kriging model and hypothetic elastomer method[J]. International Journal of Manufacturing Research, 2017, 12(1): 1. DOI:10.1504/IJMR.2017.085415 |
| [12] |
JOHNSON, G. R. , HOLMQUIST, T. J. An improved computational constitutive model for brittle materials[C]//Proceedings of the Aip Conference. 1994, 309: 981.
|
| [13] |
王强, 宋雪迪, 郝中华, 等. 基于ABAQUS纤维梁单元的钢筋混凝土柱受力破坏全过程数值模拟[J]. 土木工程学报, 2014, 47(12): 16-26,81. WANG Qiang, SONG Xuedi, HAO Zhonghua, et al. Numerical simulation of the whole process of stress damage of reinforced concrete columns based on ABAQUS fiber-beam unit[J]. Journal of Civil Engineering, 2014, 47(12): 16-26,81. |
 2024, Vol. 46
2024, Vol. 46
