2. 大连理工大学 船舶工程学院 工程工业装备结构分析优化与CAE软件全国重点实验室,辽宁大连 116024
2. State Key Laboratory of Structural Analysis, Optimization and CAE Software for Industrial Equipment, School of Naval Architecture Engineering, Dalian University of Technology, Dalian 116024, China
随着全球贸易的不断发展,世界经济紧密联系,集装箱船已经成为海运贸易必不可缺的交通运输工具,正朝着快速化和大型化的方向发展。但随着船舶总长度的不断增加,以及为满足节能减排要求而在建造过程中大量使用高强度钢,使得船体自身振动的固有频率减小,船舶的总纵强度降低。同时集装箱船因其特殊的甲板大开口结构设计特点使得其船体自身可能会发生高频振动,大幅降低了集装箱船的抗扭刚度和抗弯刚度,这些因素共同导致了船体结构的弹性形变与流体耦合的作用效果更加明显。近年来,因水弹性响应所导致的船舶事故时有发生,因此考虑船舶水弹性响应问题尤为重要。
Paik等[1]提出一种基于流固耦合理论来计算船舶的结构载荷的方法,比较了单向和双向耦合方法的数值计算结果和试验结果,发现单向耦合的数值计算结果略大于试验结果,而双向耦合的数值计算结果与试验结果基本一致。Hidars等[2]基于二维和三维的水弹性理论,研究了散货船在规则波中的运动响应和受到的波浪载荷,结果表明波浪引起的垂直弯矩和直接应力在考虑相关惯性矩和截面模量的锯齿状性质的情况下,表现出了较好的总体一致性。Kara[3]基于边界元方法和三维瞬态自由表面格林定理,研究了三维时域的水弹性方法并利用该方法预报了浮体的水弹性响应,提出通过模态分析将流体动力学和结构部分完全耦合以求解流体弹性问题的方法。AKSU等[4]基于二维和三维水弹性理论的对比分析,研究波浪中航行时细长型船体结构的砰击响应,得出细长型船体在二维与三维水弹性理论下的响应计算结果基本一致,但当船体结构不是细长型时,二维理论不再适用而三维理论仍适用的结论。
柳光军[5]利用CFD-FEM双向耦合的数值方法,先后研究了无航速顶浪情况下波长船长比、频率比、波陡以及航速对集装箱船体非线性水弹性响应的影响,得出在船体梁自身固有频率较大时,航速对集装箱船的刚体运动幅值影响较明显而对近船中截面的垂向弯矩影响不明显的结论。陈占阳等[6]分析不同航速与模型分段数量对总弯矩响应中高频和低频成分的影响,认为基于非线性水弹性理论的计算结果与总弯矩吻合更为准确。焦甲龙等[7 − 9]基于近海大尺度船模试验数据,研究真实海况下船舶波浪载荷的短期预报,提出了利用槽型龙骨梁模型来模拟甲板大开口船体的刚度分布以及实际海浪下大尺度模型波浪载荷与砰击载荷的试验技术。杨鹏等[10]使用三维非线性水弹性方法,在时域内研究集装箱船的非线性弹振和颤振响应,发现非线性波浪入射力对集装箱船的垂向弯矩的影响较大。田超等[11]基于模态叠加原理计算集装箱船在波浪中的运动和水弹性响应,并研究船体航速对船舶所受波浪载荷的影响,结果表明随着船体航速的增大,波激振动的峰值也随之增大,并且数值上超过低频共振时的峰值。
本文基于CFD-FEM 单向耦合的方法,研究波浪因素对船体水弹性响应的影响。以KRISO公布的
本文采用商业 CFD 计算软件 Ansys Fluent 进行流场三维数值仿真研究,通过Transient Structure软件计算船体结构的变形响应。
1.1 控制方程本次计算不考虑空气和水的可压缩性,流场的控制方程是湍流平均运动方程-雷诺方程(RANS),雷诺方程和湍流的平均时间运动的连续性方程一起构成了不可压缩湍流平均运动的基本方程[12]。
| $ \rho \left( {\frac{{\partial \overline {{u_i}} }}{{\partial t}} + \frac{{\partial \left( {\overline {{u_i}{u_j}} } \right)}}{{\partial {x_j}}}} \right) = - \frac{{\partial \overline p }}{{\partial {x_i}}} + \mu {\nabla ^2}{u_i} + \frac{\partial }{{\partial {x_j}}}\left( { - \rho \overline {u_i^{'}u_j^{'}} } \right),$ | (1) |
| $ \frac{{\partial \overline {{u_i}} }}{{\partial {x_i}}} = 0。$ | (2) |
式中:u为速度;t为时间;ui为x方向上的速度分量;uj为y方向上的速度分量;ρ为流体的密度;p为压力;μ为动力粘度;
标准的
| $ \rho \frac{{{\mathrm{D}}k}}{{{\mathrm{D}}t}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k} + {G_b} - \rho \varepsilon - {Y_M},$ | (3) |
| $\begin{split} \rho \frac{{{\mathrm{D}}\varepsilon }}{{{\mathrm{D}}t}} =& \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \rho {C_1}{S_\varepsilon } +\\ & {G_{1\varepsilon }}\frac{\varepsilon }{k}{G_{3\varepsilon }}{G_b} - \rho {C_2}\frac{{{\varepsilon ^2}}}{{k + \sqrt {\upsilon \varepsilon } }} ,\end{split}$ | (4) |
| $ {\mu _t} = \rho {C_\mu }\frac{{{k^2}}}{\varepsilon }。$ | (5) |
式中:k为湍流动能;
VOF多相模型用于求解涉及不混溶流体混合物、自由表面和相接触时间的问题。此建模方法假设网格分辨率足以求解相之间的交界面位置和形状,交界面的相分布和位置由相体积分数
| $ {a_i} = \frac{{{V_i}}}{V}。$ | (6) |
式中:
| $ \sum\limits_{i = 1}^N {{a_i} = 1}。$ | (7) |
式中:N 为总相数。相i的分布由相的质量守恒方程控制:
| $ \begin{split} \frac{\partial }{{\partial t}}\int\limits_V {{a_i}{\mathrm{d}}V} + \oint\limits_A {{a_i}v} \cdot {\mathrm{d}}a =& \int\limits_V {\left( {S{a_i} - \frac{{{a_i}}}{{{\rho _i}}}\frac{{{\mathrm{D}}{\rho _i}}}{{{\mathrm{D}}t}}} \right)} {\mathrm{d}}V -\\& \int\limits_V {\frac{1}{{{\rho _i}}}\nabla \cdot } \left( {{a_i}{\rho _i}{v_{{d_i}}}} \right){\mathrm{d}}V 。\end{split}$ | (8) |
式中:a 为表面积矢量;v为混合(质量平均)速度;
有限单元法主要通过弹性力学、几何和物理3种方程完成。
| $ \left\{\begin{gathered} \frac{{{\text{δ}}{\sigma _x}}}{{{\text{δ}} x}} + \frac{{{\text{δ}} {\tau _x}}}{{{\text{δ}} y}} + \frac{{{\text{δ}} {\tau _z}}}{{{\text{δ}} z}} + {q_x} = 0,\\ \frac{{{\text{δ}} {\tau _x}}}{{{\text{δ}} x}} + \frac{{{\text{δ}} {\sigma _y}}}{{{\text{δ}} y}} + \frac{{{\text{δ}}{\tau _y}}}{{{\text{δ}} z}} + {q_y} = 0,\\ \frac{{{\text{δ}} {\tau _x}}}{{{\text{δ}} x}} + \frac{{{\text{δ}} {\tau _y}}}{{{\text{δ}} y}} + \frac{{{\text{δ}} {\tau _z}}}{{{\text{δ}} z}} + {q_z} = 0。\\ \end{gathered}\right. $ | (9) |
几何方程则包含弹性体形变和位移两部分,其公式分别为:
| $ {\varepsilon _x} = \frac{{{\text{δ}} u}}{{{\text{δ}} x}},{\varepsilon _y} = \frac{{{\text{δ}} v}}{{{\text{δ}} y}},{\varepsilon _z} = \frac{{{\text{δ}} w}}{{{\text{δ}} z}} ,$ | (10) |
| $ {\kappa _x} = \frac{{{\text{δ}} u}}{{{\text{δ}} x}} + \frac{{{\text{δ}} v}}{{{\text{δ}} y}}, {\kappa _y} = \frac{{{\text{δ}} w}}{{{\text{δ}} x}} + \frac{{{\text{δ}} v}}{{{\text{δ}} y}}, {\kappa _z} = \frac{{{\text{δ}} u}}{{{\text{δ}} y}} + \frac{{{\text{δ}} v}}{{{\text{δ}} z}}。$ | (11) |
物理方程矩阵为:
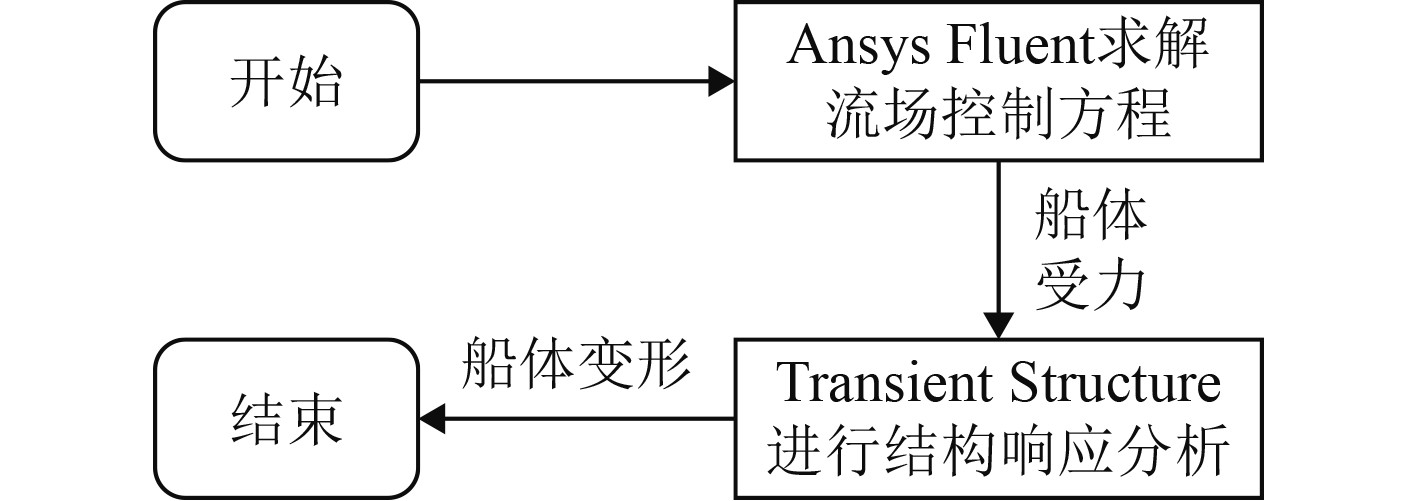
单向耦合指通过Fluent计算流体工况,将耦合面上的压力导入到Structural中,计算结构仿真的应力、应变等参数,但由于变形量不大,不足以影响原先的流场形态,故变形位移不回传给Fluent[15]。既先求解流场,然后将流场计算结果作为载荷施加到结构上求解结构场。单向流固耦合计算如图1所示。
|
图 1 单向流固耦合计算思路图 Fig. 1 Unidirectional fluid-structure coupling calculation diagram |
本文的主要研究对象是韩国船舶与海洋工程研究所(KRISO)公布的 3750-TEU 集装箱船(简称KCS船)[16]。
2.1 KCS船几何模型本文所使用的模型来源于2008年的Simulation Workshop for Ship Maneuvering学术讨论会中韩国船舶与海洋工程研究所提供的几何模型(见图2)。其主要参数如表1所示。

|
图 2 KCS船几何模型 Fig. 2 KCS ship geometry model |
|
|
表 1 KCS船主要参数 Tab.1 Main parameters of KCS ship |
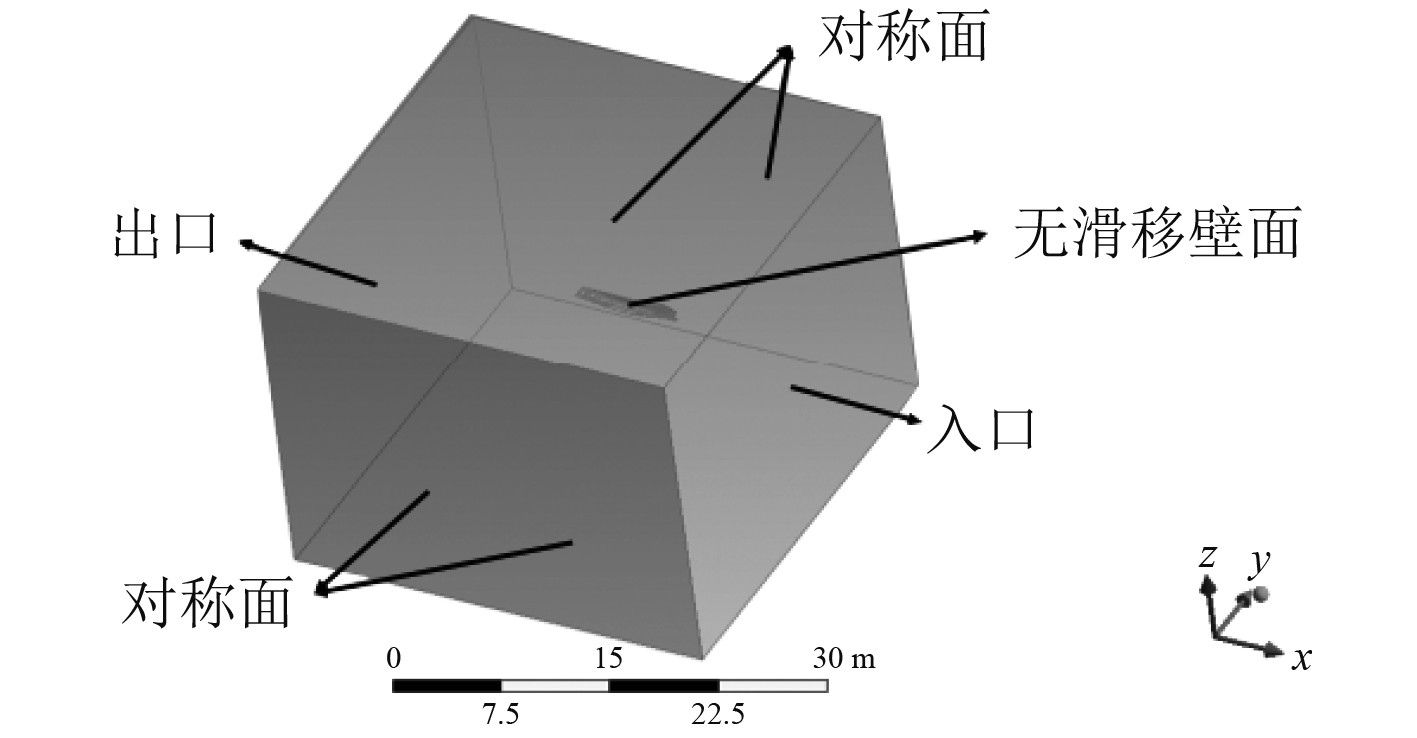
根据相关研究可知,入口距船首1倍船长,出口距船尾2倍船长,左右两侧的对称面距船体2倍船长,顶部距船体1倍船长,底部距船体2倍船长。自由液面设置在船舶水线位置。流场中还需设置5个加密区域,分别是船首加密区、船尾加密区、湍流涡加密区、自由液面加密区以及开尔文波加密区。边界条件的具体设置如图3所示。
|
图 3 边界条件设置图 Fig. 3 Boundary condition setting diagram |
本文选用VOF模型作为多相流模。湍流模型选用Realized k-ε模型,选用标准壁函数模型。入口选用压力入口,并设为波浪入口,给定航速、自由液面位置、水深;出口选用压力出口,给定自由液面位置和水深。压力速度耦合为SIMPLE算法,压力选用PRESTO!格式,动量为二阶迎风格式,体积分数采用HRIC格式,湍流黏度及耗散率均采用一阶迎风格式。
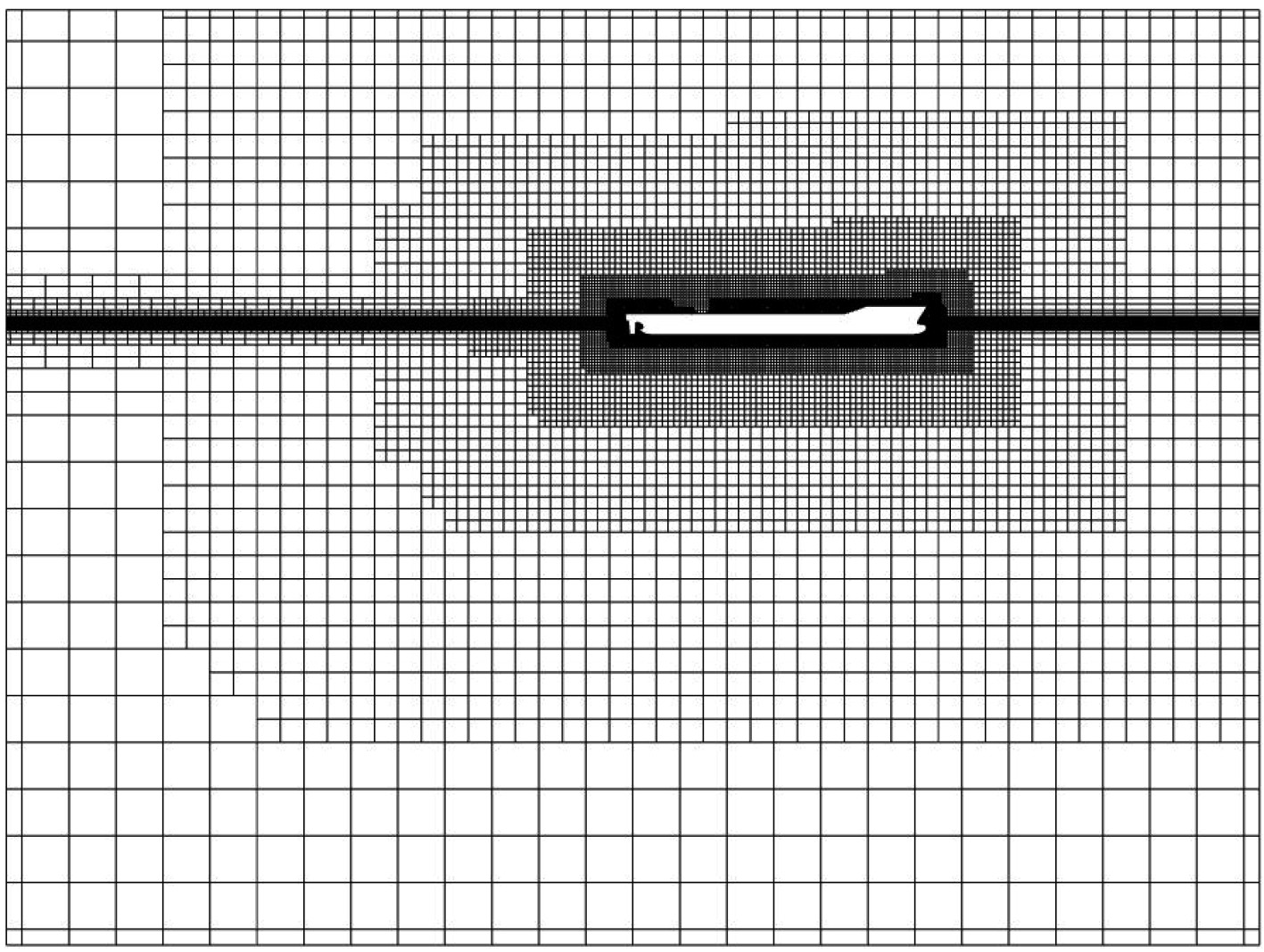
2.2.2 流场网格无关性验证与时间步长无关性验证以KCS船在静水中Fr=0.26时作为验证算例,以粗糙、中等、细密3种网格进行计算,并与韩国船舶与海洋工程研究所(KRISO)公布的实验结果对比,具体数值如表2所示。可以看出,3种网格的均和实验数据较为接近,随着网格数目的增加,阻力计算结果基本收敛,计算结果较为准确。为尽可能减少计算时间,后续的计算均选用中等网格。图4为中等网格中纵剖面网格图。
|
|
表 2 网格无关性验证 Tab.2 Grid independence verification |
|
图 4 中等网格中纵剖面网格图 Fig. 4 Profile grid diagram in medium grid |
在网格无关性验证之后,以中等网格为基础进行时间步长无关性验证,计算结果如表3所示。可以发现,时间步长对计算结果影响较小,后续皆选用0.03时间步长计算。
|
|
表 3 时间步长无关性验证 Tab.3 Time step independence verification |
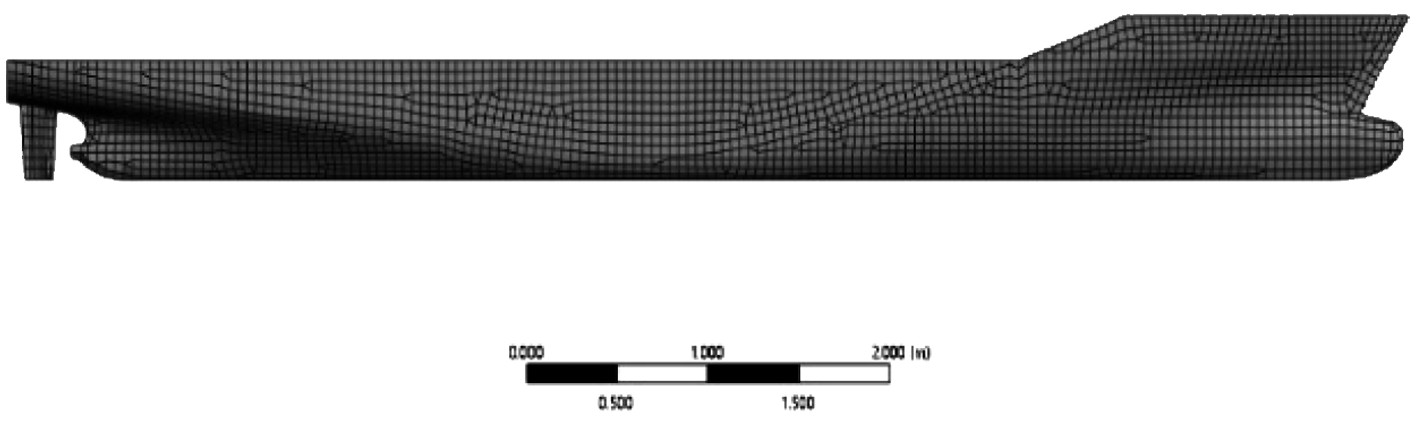
船体有限元网格划分比较困难,尤其是在船尾、船首、舵等大曲率变化区域,因此使用非结构网格。其中船体厚度为0.01m,船体均为壳单元,从首柱至尾柱设置一船体梁用于提供船体的抗弯刚度(见图5)。船体网格划分也采用粗糙、中等、细密3种网格类型(见图6),以Fr=0.26时的静水航行阻力为准。

|
图 5 船体外壳和船体梁几何图 Fig. 5 Hull shell and hull beam geometry |
|
图 6 船体外壳网格图 Fig. 6 Hull shell grid diagram |
本文以静态下的船体结构所受的海水压力为计算要求,探究结构网格无关性,设定船底位移限制(船深方向自由,其他方向锁定)以及船体左右两侧的舷侧板位移限制(船宽方向自由,其他方向锁定)。图7为船体表面静液压力。
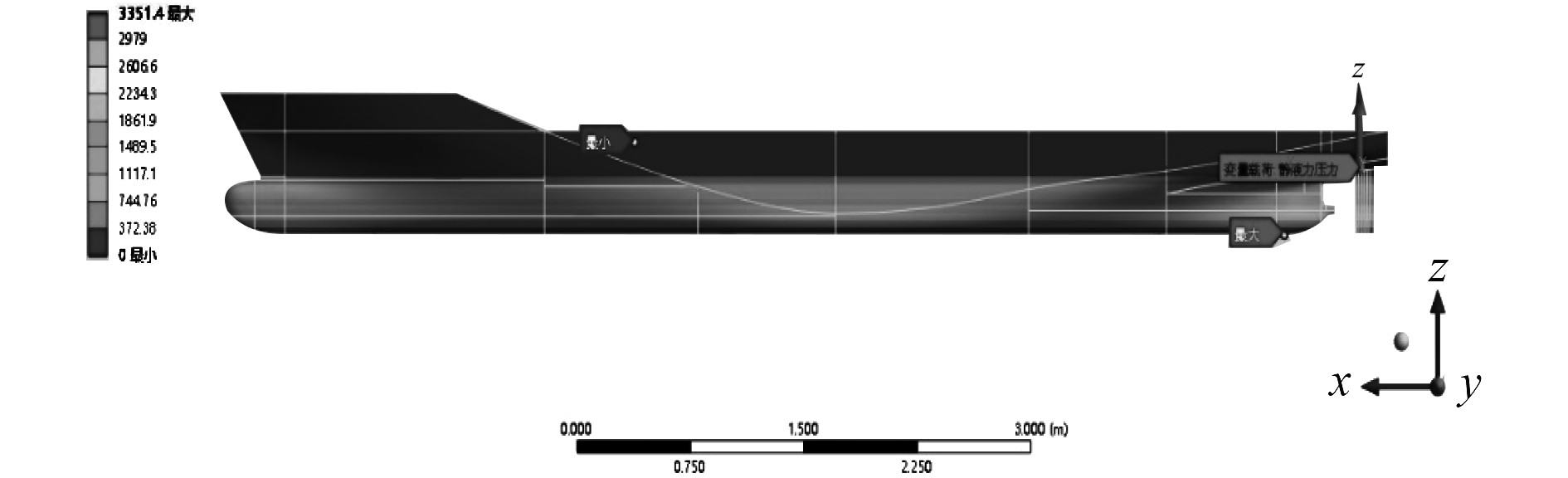
|
图 7 船体表面静液压力 Fig. 7 Hull surface hydrostatic pressure |
由表4可知,根据网格无关性,认为网格3基本收敛,选定网格3为基准作为后续计算中所使用的船体结构网格。
|
|
表 4 船体网格无关性验证 Tab.4 Hull grid independence verification |
为研究不同波浪环境中的Fr=0.26时的船舶阻力情况、流场情况以及船舶水弹性特征情况,通过Fluent软件,将压力入口改为速度入口,以Stokes五阶波浪模拟,共设计5个波浪情况,其波浪的相关数据如表5所示。
|
|
表 5 波浪载荷相关数据 Tab.5 Wave load related data |
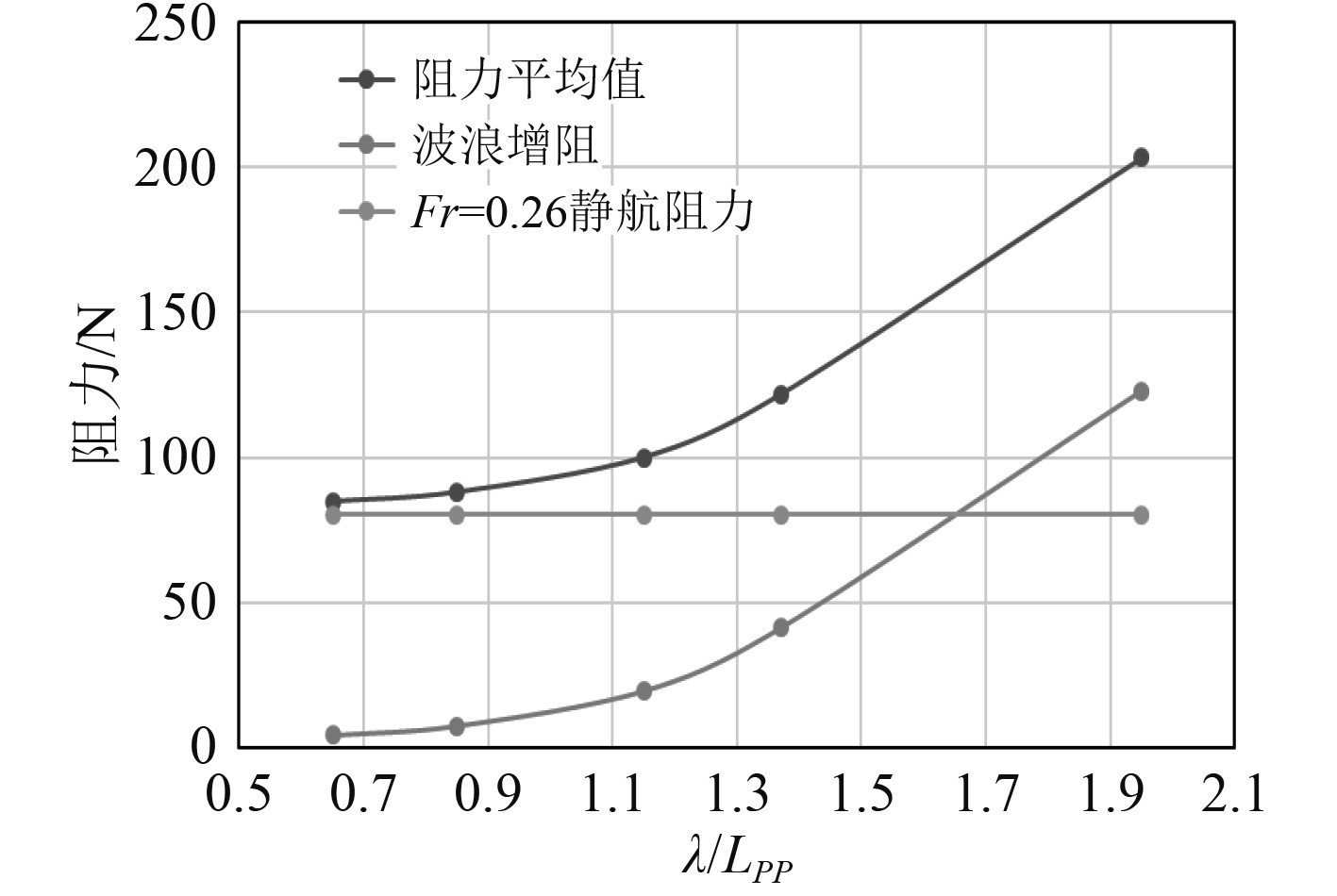
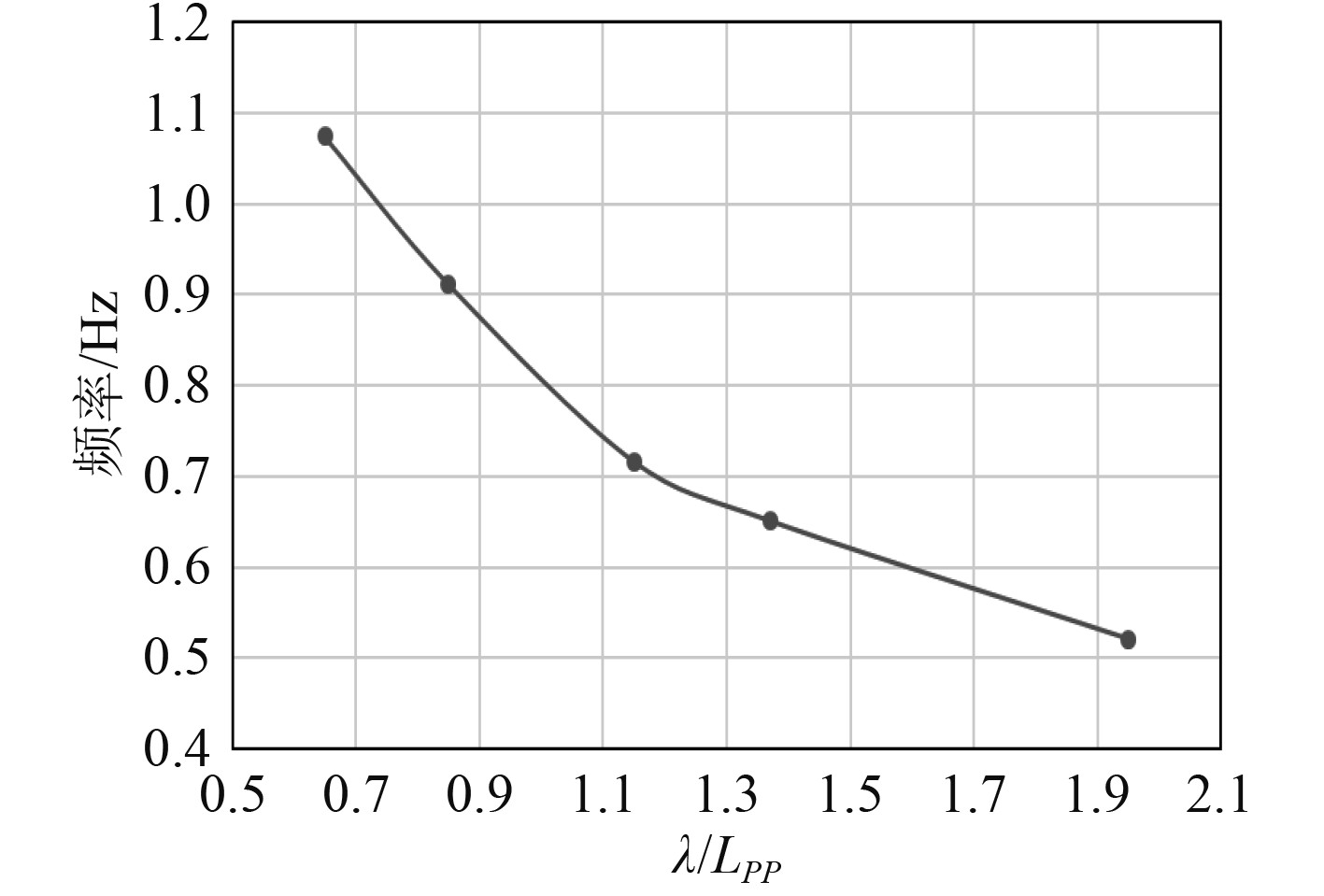
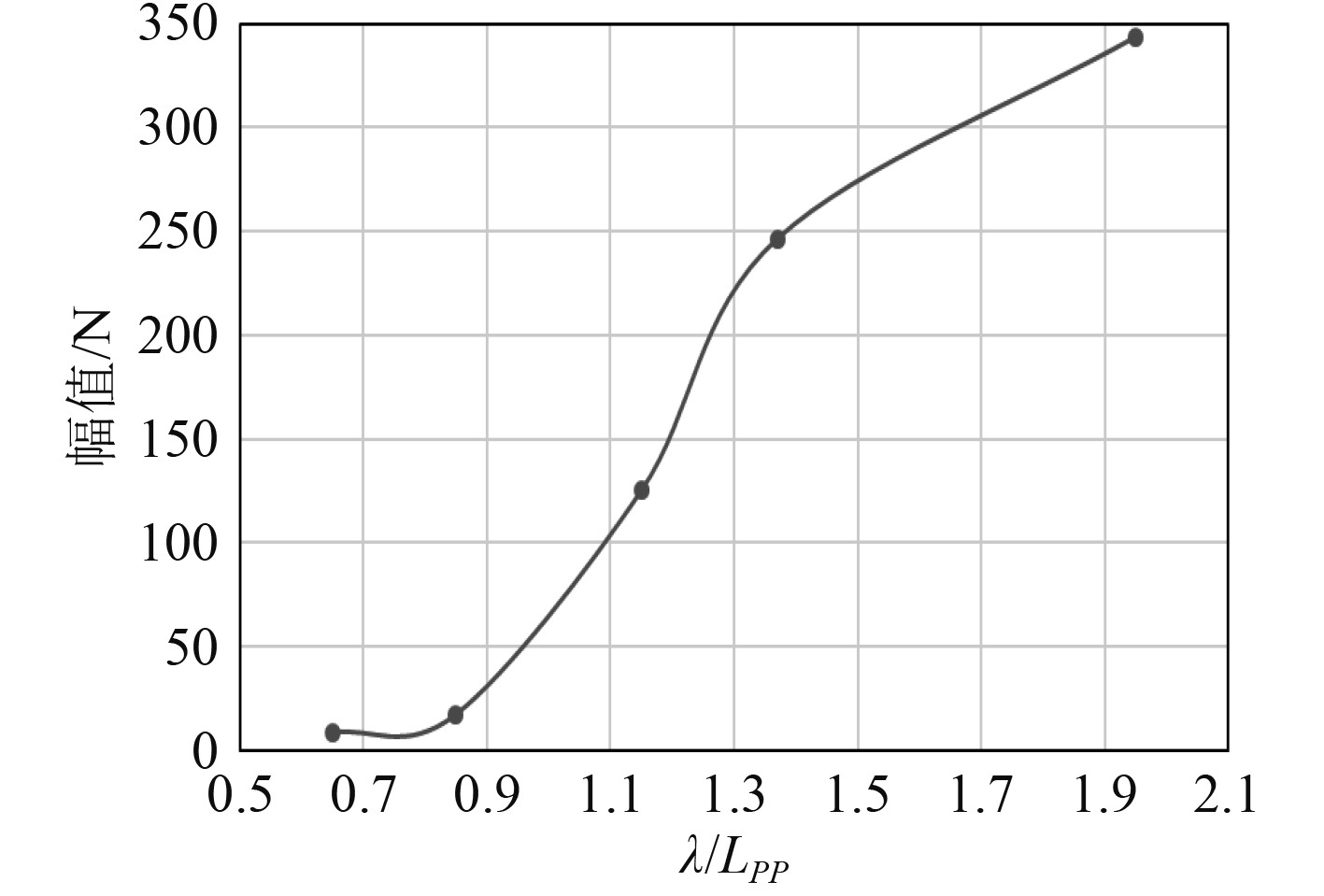
图8为波浪阻力与波长/垂线间长关系图。图9为波浪周期与波长/垂线间长关系图,图10为波浪阻力幅值与波长/垂线间长关系图。可以看出,随着波长垂线间长比的增加,船舶阻力呈上升趋势,频率呈减小趋势,阻力的波动幅值亦呈上升态势。当波长垂线间长比大于1时,阻力和波动幅值快速增加,但频率减小的趋势逐渐放缓。
|
图 8 波浪阻力平均值与波长/垂线间长关系图 Fig. 8 Plot of mean wave resistance and length between wavelength/vertical lines |
|
图 9 2 波浪频率与波长/垂线间长关系图 Fig. 9 2 Graph of the relationship between wave frequency and wavelength/vertical length |
|
图 10 波浪阻力幅值与波长/垂线间长关系图 Fig. 10 Wave resistance amplitude and length relationship between wavelength/vertical |
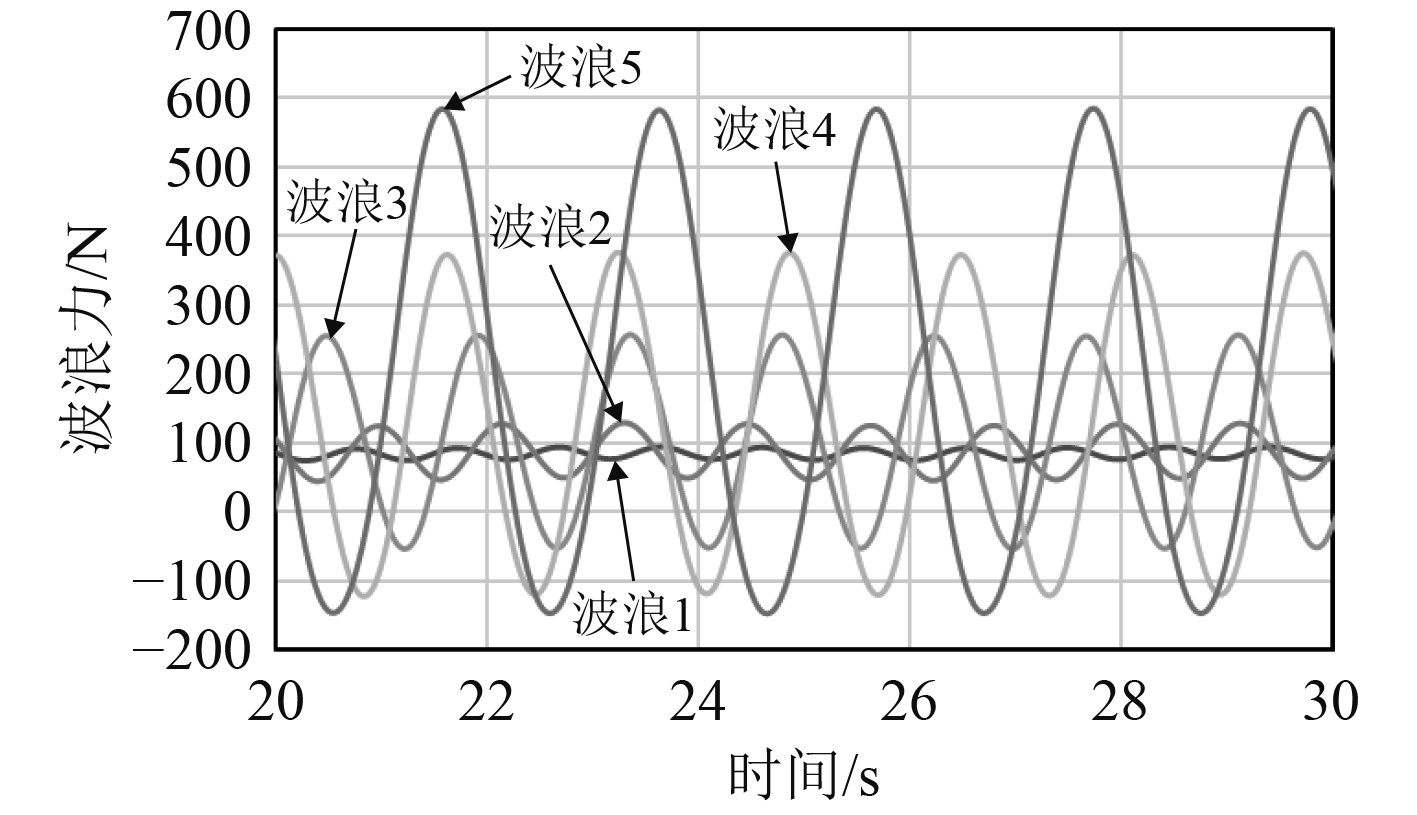
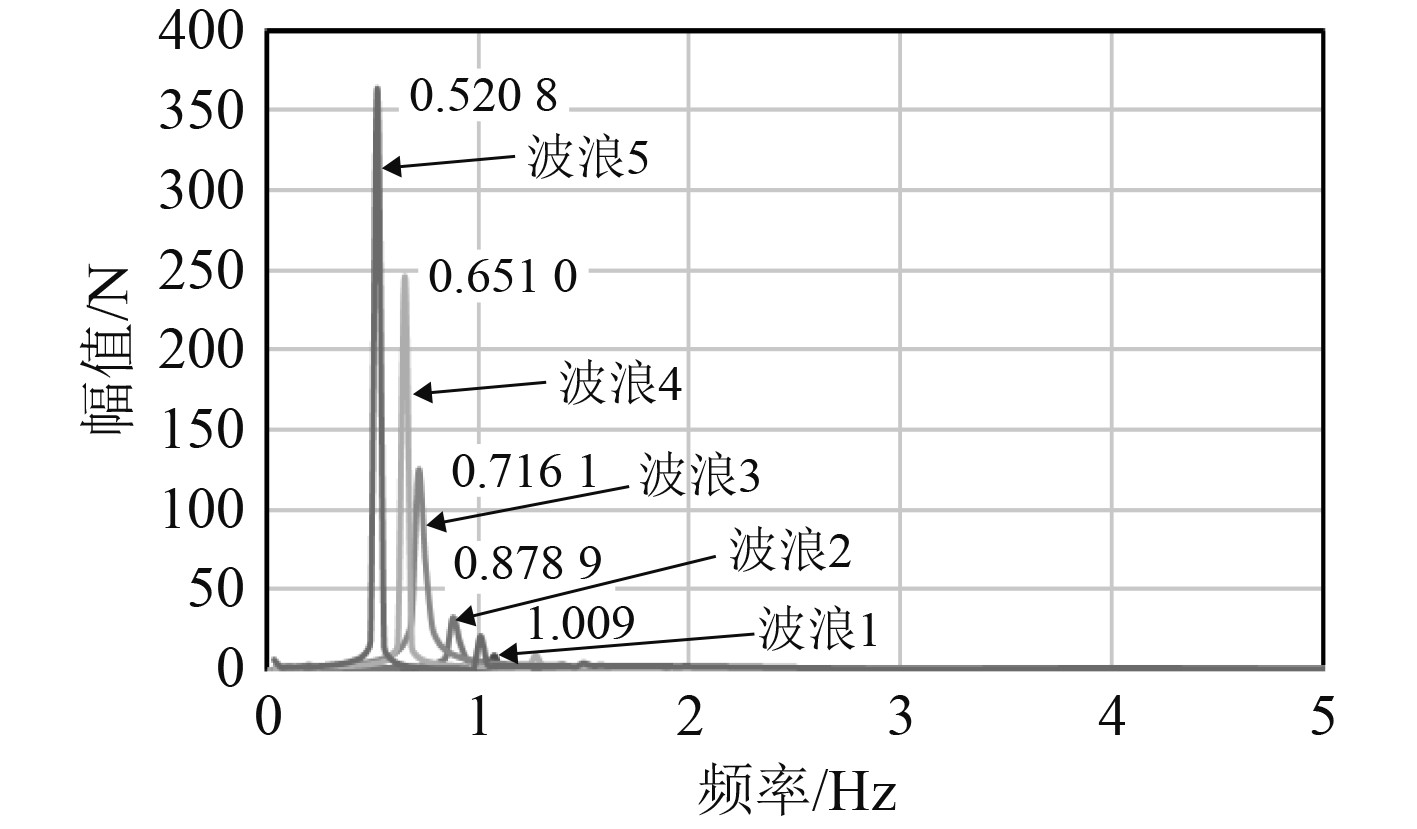
以波浪1的计算结果为例,图11为船舶波浪阻力时间历程曲线,如图所示,船舶阻力波动比较规则,通过傅里叶变换得到图12的幅值-频率图,可以看出其频率为1.074 Hz。
|
图 11 船舶波浪阻力时间历程曲线 Fig. 11 Ship wave resistance time history curve |
|
图 12 船舶波浪阻力频率幅值 Fig. 12 Frequency amplitude of ship wave resistance |
有鉴于波浪的波长波高较小,因此其中纵剖面的密度分布图(见图13)中波浪形态并不明显,船尾处出现小的自由液面波动,远端则恢复平静。图14为船舶水线位置波浪高度图,可以看出,此时船舶尾端出现了开尔文波,可以断定波浪对船舶自航产生的尾流轨迹影响不大。图15为船体表面压力云图。

|
图 13 船中纵剖面密度分布图 Fig. 13 Midship profile density distribution |

|
图 14 船舶水线位置波浪高度图 Fig. 14 Wave height diagram of ship's waterline position |

|
图 15 船体表面压力云图 Fig. 15 Hull surface pressure cloud image |
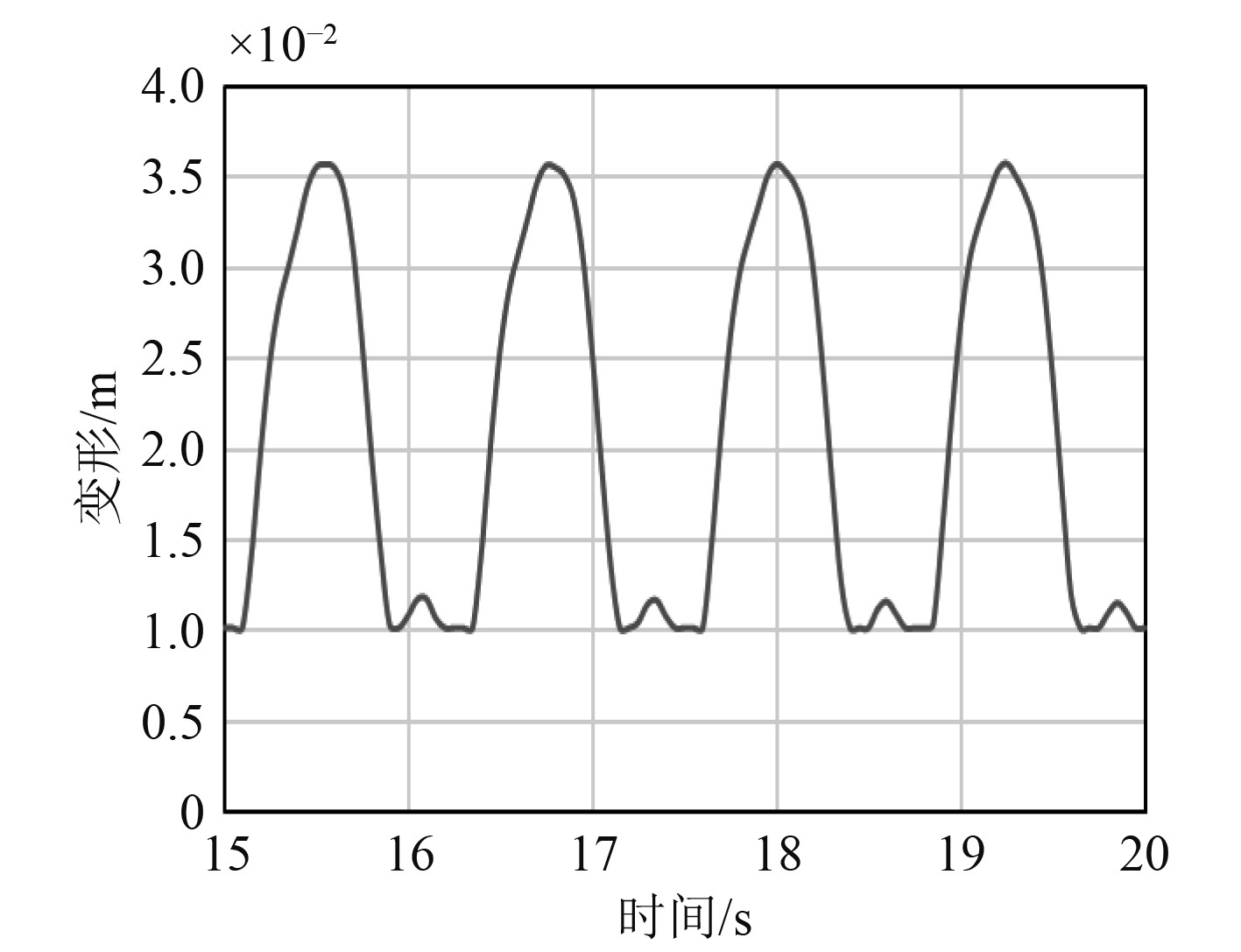
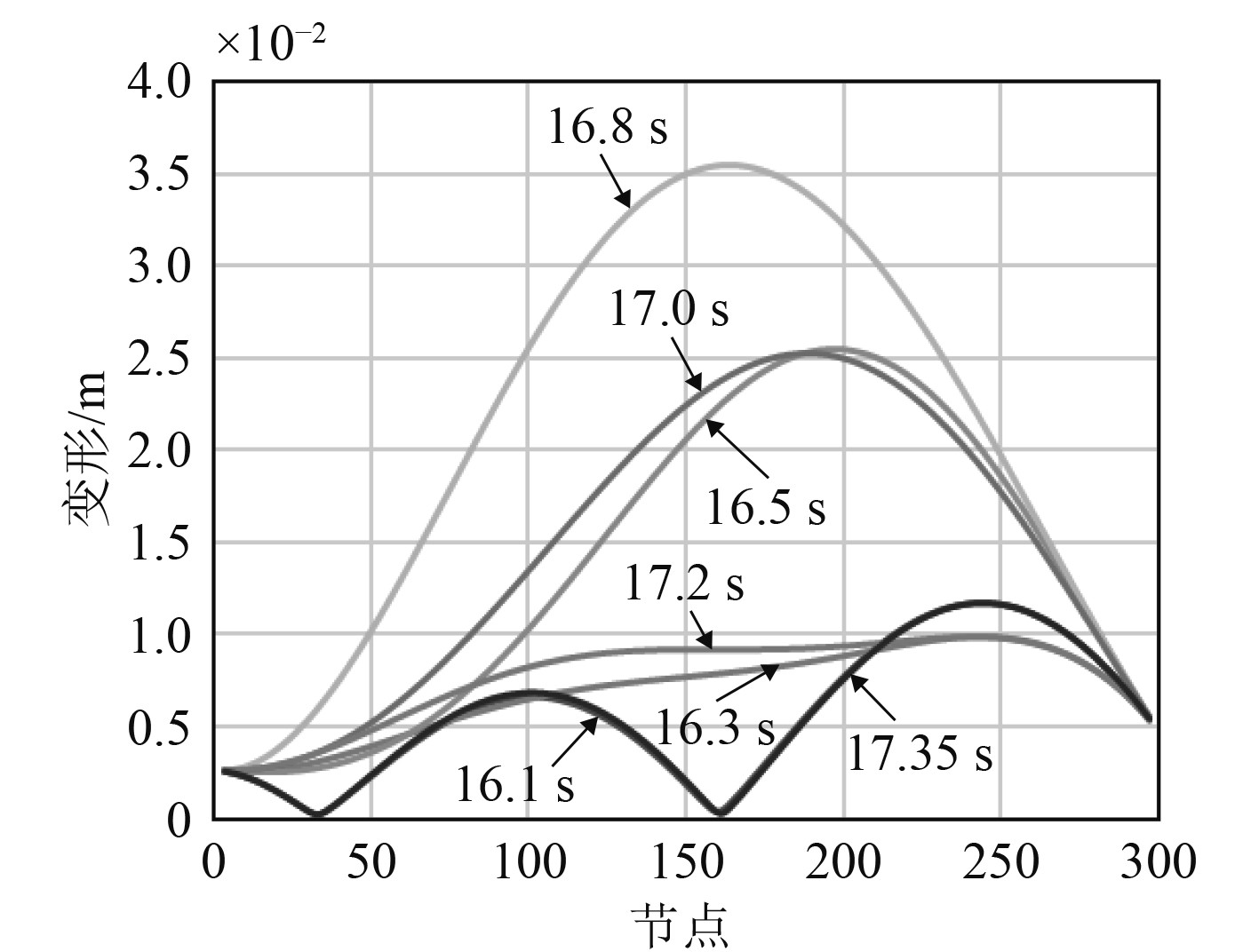
图16为船体梁变形时间历程图,总体上来说其变形幅度较小,并且其变形也呈周期性变化,与其所受到的波动力有关。图17为一个周期时间内的船体梁节点的线形图。可知,其船体梁变形从二阶模态变化为一阶模态,并且有较为规律的周期性。如16.1 s和17.35 s基本重合。
|
图 16 船体梁变形时间历程图 Fig. 16 Deformation time history diagram of hull beam |
|
图 17 船体梁变形各时间线形图 Fig. 17 Time line diagram of hull beam deformation |
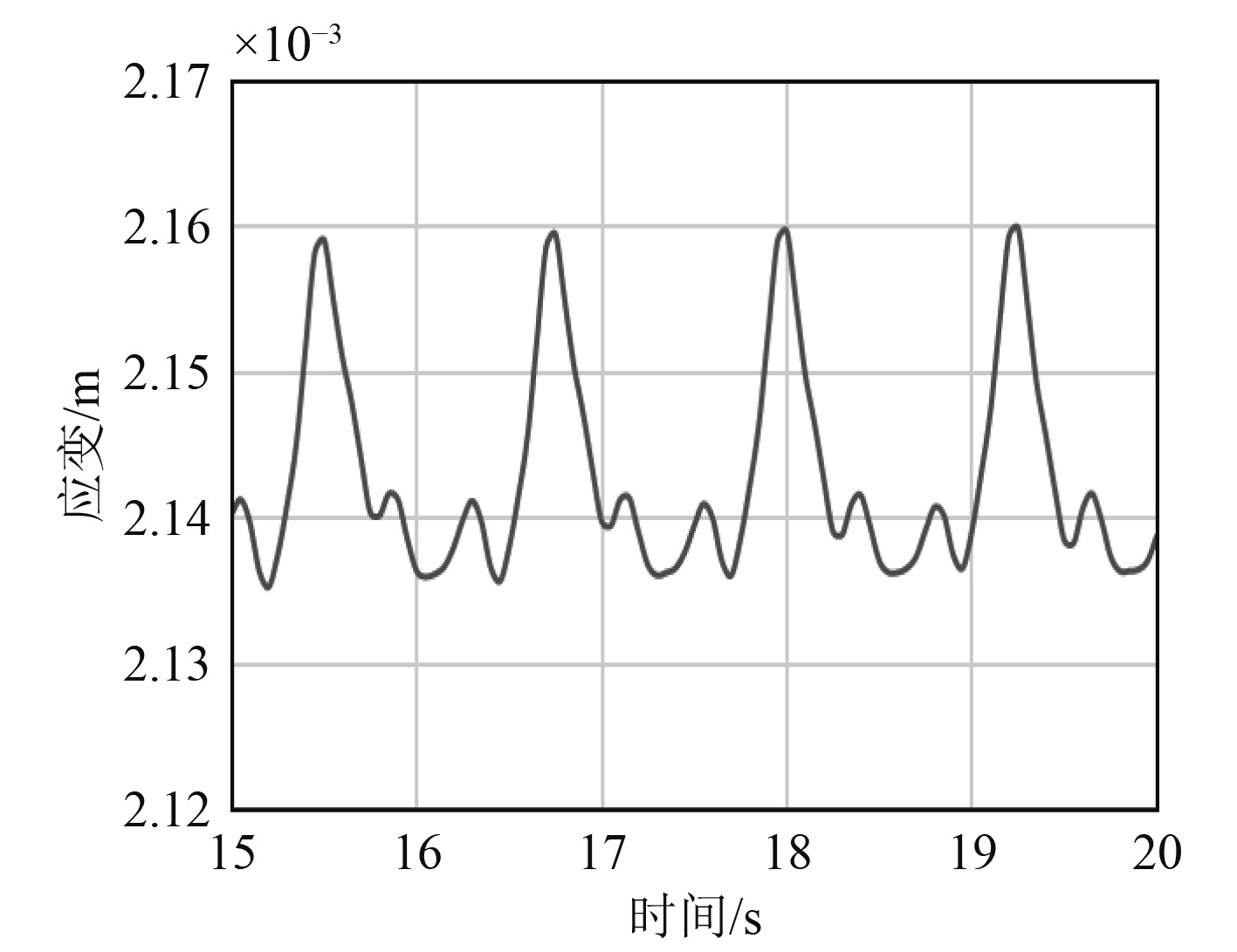
图18和图19分别为船体板材上的应变云图和其时间历程图。可以看出,船体梁的最大变形出现在船中位置,并且随着波动力的状态变化,最大值位置从船尾处向前传递,直至船中,据此推断出该处应该进行加强以防止其疲劳损伤。

|
图 18 船体外壳应变图 Fig. 18 Strain diagram of hull shell |
|
图 19 船体外壳应变时间历程图 Fig. 19 Strain time history diagram of hull shell |
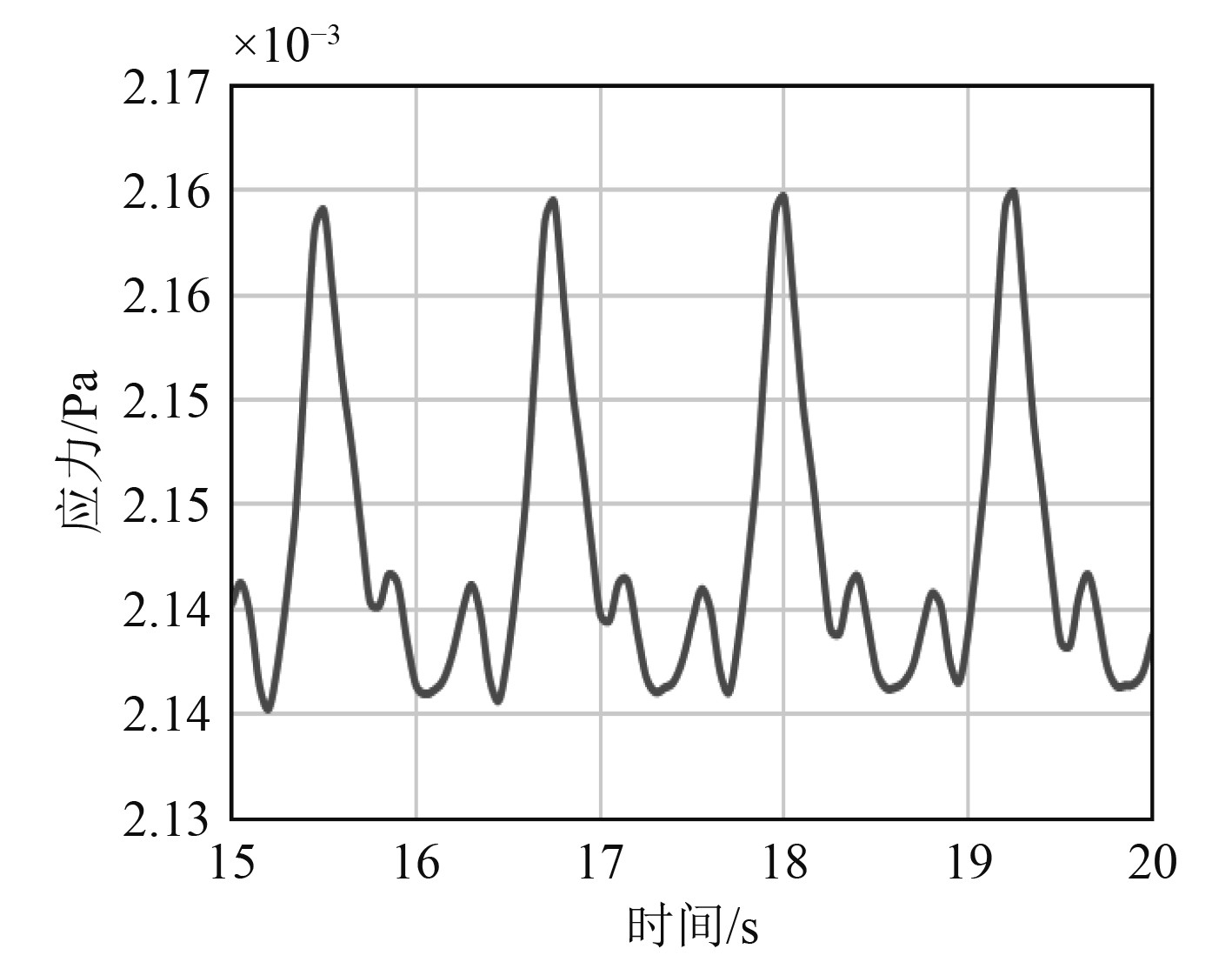
图20和图21为船体板材的应力云图及其时间历程图,应力应变呈线性关系,二者云图和时间历程图基本相同。并且应力应变主要在球鼻艏和船舵以及船底处,最大值点出现在船舵,推断其产生原因,主要是船身产生的尾流叠加波浪的波动力增加了船舵所受的合力,并且船舵迎流面较小,所受压力较大,产生了较高的应力和应变。

|
图 20 船体外壳应力图 Fig. 20 Hull stress diagram |
|
图 21 船体外壳应力时间历程图 Fig. 21 Stress time history diagram of hull shell |
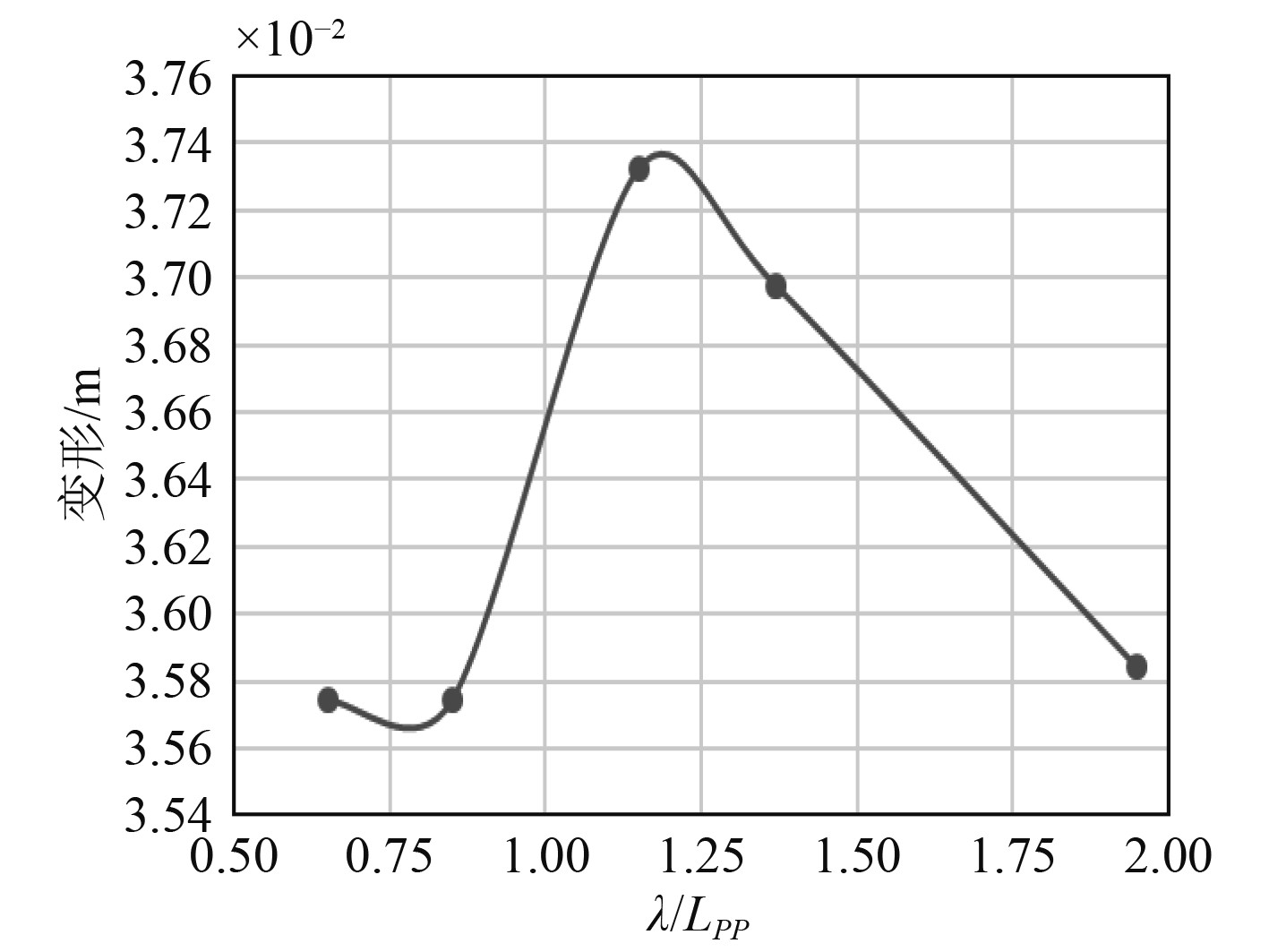
由波浪航行的计算结果可知,KCS船的波浪阻力与波长垂线间长比呈正相关,在波长垂线间长比小于1时阻力缓慢上升;在波长垂线间长比大于1时阻力快速上升。当波长垂线间长比小于1时,可以在船体流场波浪高度图中发现船体兴波以及船后的开尔文波;当波长垂线间长比大于1时,船体兴波不在明显,开尔文波基本消失,波浪对船舶自航性产生极大的影响。另外在船体结构上,鉴于杨氏模量和板厚以及船体梁截面形状等诸多因素的影响,其受波浪影响产生的流体力导致的水弹性特征变化幅度较小,总体上船体梁变形在
|
图 22 船体梁变形与波长垂线间长比关系图 Fig. 22 Relation diagram of length ratio between hull beam deformation and wavelength perpendicular |
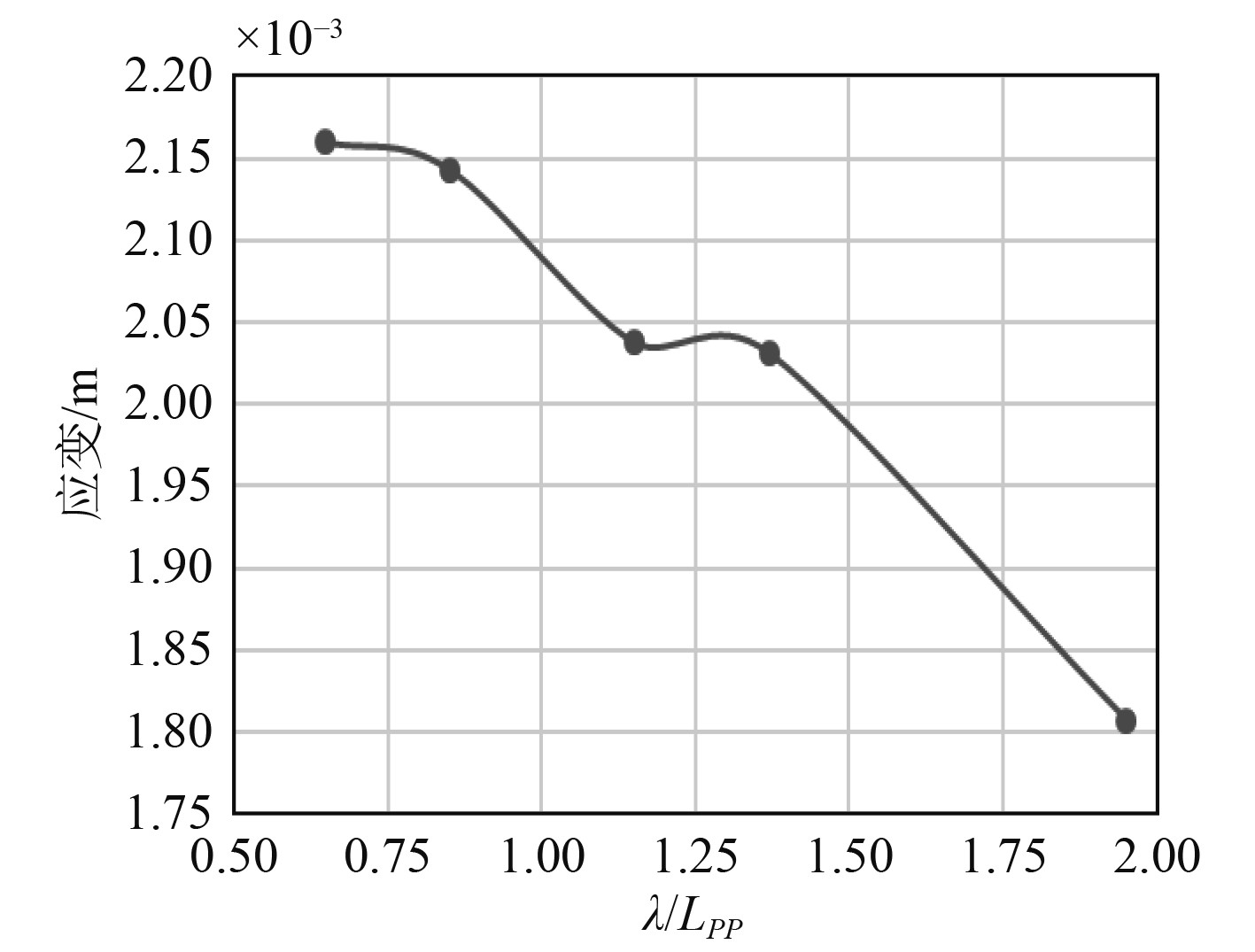
图23和图24是船体外板应变、应力与波长垂线间长比关系图。可知,其整体上呈现下降态势,波长垂线间长比小于1时,其下降较为缓慢,而当波长垂线间长比大于1时其快速下降,最终达到最小值。以此说明,波长对于船舶外板应力应变的影响和对船体梁的影响并不一致,其主要原因在于,船体梁贯穿整个船体,而船舶外板上是分散的“面元”,并未形成一个整体,因此二者走势并不相同。
|
图 23 船体外板应变与波长垂线间长比关系图 Fig. 23 Relation diagram of length ratio between strain of hull plate and wavelength vertical line |

|
图 24 船体外板应力与波长垂线间长比关系图 Fig. 24 Diagram of length ratio relationship between stress of hull plate and wavelength vertical line |
本文主要研究波浪因素对船体水弹性响应的影响,计算了不同波浪情况下的船舶流畅特性和水弹性特性,通过流场分析、结构分析等方法总结了计算结果中波浪载荷对集装箱船水弹性性质的一般影响规律,研究结论如下:
1) KCS船的波浪阻力与波长垂线间长比呈正相关,在波长垂线间长比小于1时阻力缓慢上升;在波长垂线间长比大于1时阻力快速上升。当波长垂线间长比小于1时,可以在船体流场波浪高度图中发现船体兴波以及船后的开尔文波;当波长垂线间长比大于1时,船体兴波不在明显,开尔文波基本消失,波浪对船舶自航性产生极大的影响。
2) 在波长垂线间长比在1附近时,波浪频率恰与船舶固有频率接近,诱发船体共振,导致其船体梁出现大变形,船舶亦会出现相应的中拱现象。
3) 波长对于船舶外板应力应变的影响和对船体梁的影响并不一致,其主要原因在于,船体梁贯穿整个船体,在船舶的总纵强度中占主要地位,而船舶外板上是分散的“面元”,互相拼接并未形成一个整体,因此二者趋势并不相同。
| [1] |
PAIK K, CARRICA P M, LEE D, et al. Strongly coupled fluid–structure interaction method for structural loads on surface ships[J]. Ocean Engineering, 2009, 36(17): 1346−1357.
|
| [2] |
HIRDARIS S E, PRICE W G, TEMAREL P. Two and three-dimensional hydroelastic modelling of a bulker in regular waves[J]. Marine Structures, 2003, 16(8): 627−658.
|
| [3] |
KARA F. Time domain prediction of hydroelasticity of floating bodies[J]. Applied Ocean Research, 2015, 51: 1−13.
|
| [4] |
AKSU S, PRICE W G, TEMAREL P. A comparison of two-dimensional and three-dimensional hydroelasticity theories Including the effect of slamming[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Mechanical Engineering Science, 1991, 205(1): 3−15.
|
| [5] |
柳光军. 基于CFD-FEM双向耦合的船舶非线性水弹性问题研究[D]. 大连:大连理工大学, 2021.
|
| [6] |
陈占阳, 任慧龙, 李辉, 等. 超大型船舶变截面梁分段模型的载荷试验研究[J]. 哈尔滨工程大学学报, 2012, 33(3): 263−268.
|
| [7] |
焦甲龙, 赵玉麟, 张皓, 等. 船舶波浪载荷与砰击载荷的大尺度模型水弹性试验研究[J]. 振动与冲击, 2019, 38(20): 229−236.
|
| [8] |
焦甲龙, 任慧龙, 杨虎, 等. 分段模型波浪载荷试验槽型龙骨梁设计与研究[J]. 振动与冲击, 2015(14): 11−15.
|
| [9] |
焦甲龙. 实际海浪环境中舰船大尺度模型运动与载荷响应试验研究[D]. 哈尔滨:哈尔滨工程大学, 2016.
|
| [10] |
杨鹏, 顾学康, 彭正梁, 等. 6750箱集装箱船非线性波激振动和颤振响应分析[J]. 船舶力学, 2020, 24(2): 221-235. YANG Peng, GU Xuekang, PENG Zhengliang, et al. Study on nonlinear springing and whipping of a 6750 TEU container ship[J]. Journal of Ship Mechanics, 2020, 24(2): 221-235. |
| [11] |
田超, 官腾. THAFTS在大型散货船水弹性响应中的应用[J]. 舰船科学技术, 2018, 40(12): 37-43,48. TIAN Chao, GUAN Teng. Appliction of THAFTS in hydroelastic response of a large bulk carrier[J]. Ship Science and Technology, 2018, 40(12): 37-43,48. |
| [12] |
张亮. 流体力学[M]. 哈尔滨: 哈尔滨工程大学出版社, 2001.
|
| [13] |
袁银梅, 李朝祥. 带钢热镀锌数值模拟[J]. 安徽工程科技学院学报(自然科学版), 2006, 21(4): 27−30.
|
| [14] |
李云, 张栋. 基于有限元分析的船舶结构设计[J]. 舰船科学技术, 2022, 44(6): 40-43. LI Yun, ZHANG Dong. Research on ship structure design based on finite element analysis[J]. Ship Science and Technology, 2022, 44(6): 40-43. |
| [15] |
席雷. 风力机叶片优化设计及气动特性分析研究[D]. 吉林:东北电力大学, 2021.
|
| [16] |
陈科, 赖明雁. 基于CFD数值的模拟船/桨相互干扰流动[J]. 船舶与海洋工程, 2018, 34(2): 5-10. CHEN Ke, LAI Mingyan. CFD Based Numerical Simulation of Ship-Propeller Flow Interaction[J]. Naval Architecture and Ocean Engineering, 2018, 34(2): 5-10. |
 2024, Vol. 46
2024, Vol. 46
