2. 大连海大智船科技有限责任公司,辽宁 大连 116026;
3. 中国船舶及海洋工程设计研究院,上海 200001
2. Dalian Maritime University Smart Ship Limited Company, Dalian 116026, China;
3. Marine Design and Research Institute of China, Shanghai 200001, China
船舶压载水系统作为船舶系统的重要组成之一,通过压载水的吸排实现船舶纵横向平衡的调整,保证船舶处于合适的稳心高度,其安全性能影响船舶的安全航行,重要性不言而喻。但船舶压载水系统的结构分布和运营环境复杂,如相关阀件众多、零件结构错综复杂、各设备分布较散、常规人工巡检盲点较多、频繁工作对相关组件的磨损消耗较快[1]等问题,都对其日常维护和故障排除提出更高要求。一旦发生故障,其故障部位不易查找维修,影响船舶的安全性能和运营效率。因此,为保证船舶的安全运营,降低日常维护的繁琐,提高船舶压载水系统的智能故障诊断精度势在必行。
近年来,随着智能化船舶的发展,机器学习和群智能优化算法成为船舶故障诊断领域的研究热点之一[2]。Jerzy等[3]针对船用柴油机行程提出了一种新的故障诊断方法,其结合极限学习机对每个类别的故障进行二值化处理和训练。Xi等[4]利用振动源自提取和特征可视化方法,建立基于极限学习机的柴油机故障识别网络。王泷德等[4]针对船舶主机监测点多但故障样本少的问题,提出一种使用SMOTE-Tomek构造平衡数据集,再结合改进极限学习机进行船舶主机的故障诊断方法。王忠巍等[6]使用蚁群聚类算法实现数据集特征的横向对比,在柴油机故障样本缺乏的情况下,利用异常性能气缸识别实现了主机的状态检测。Feng等[7]提出一种基于神经网络的大型船舶发动机非确定性环境智能诊断方法,实现了发动机故障的智能诊断。
本文为改善传统麻雀搜索算法容易陷入局部最优的缺陷,结合了自适应权重改进发现者位置公式,实现对个体步长的有效控制,再使用Levy飞行策略充分实现搜索空间的探索,从而达到提升ISSA收敛精度和收敛速度的目的。而后,使用ISSA对ELM的初始参数进行迭代寻优,在此基础上构建基于ISSA-ELM的船舶压载水系统故障诊断模型。最终,将船舶压载水系统的数据集输入ISSA-ELM模型,通过与SSA-ELM、PSO-ELM、GWO-ELM、SVM和ELM模型作对比,进一步证实了所提出的ISSA-ELM模型在船舶压载水系统数据集上具有较好的识别故障性能。
1 基于改进麻雀搜索算法优化极限学习机 1.1 极限学习机Huang等[8]在2004年提出的极限学习机(Extreme Learning Machine,ELM),是在单隐藏层前馈网络(Single-hidden Layer Feedforward Neural Network,SLFN)基础上改进,能够不进行反向学习实现对数据学习和拟合的算法。ELM初始参数生成后,在后续的分类中不再改变数值。通过最小二乘法误差最小化时,仅改变输出权重值,以获得对数据的最充分学习,利用随机映射来拟合输出[8]。
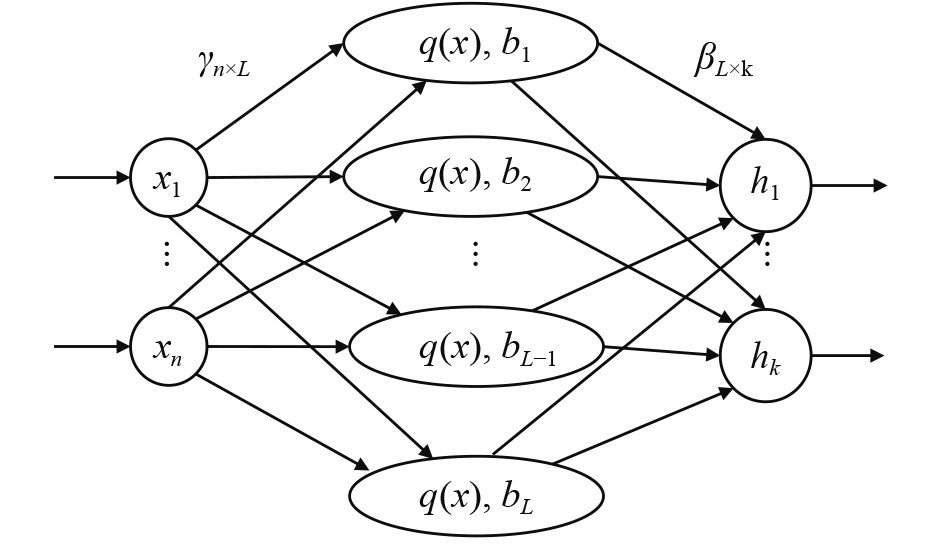
与传统神经网络相比,ELM在对数据进行学习的过程中,神经元不需要对初始参数进行反向迭代调整,因此获得了较好的学习速度和泛化性能[9-10]。如图1所示,ELM结构简洁,数据从输入层输入,通过包含激活函数的隐藏层输入输出层,各层神经元个数依次设为
|
图 1 ELM结构图 Fig. 1 The structure of ELM |
| $ {f_j} = \sum\limits_{j = 1}^L {{\beta _j}q\left( {{\gamma _j} \cdot {x_i} + {b_j}} \right)} 。$ | (1) |
式中:
| $ {p_j} = \sum\limits_{j = 1}^L {{\beta _j}q\left( {{\gamma _j} \cdot {x_i} + {b_j}} \right)} ,$ | (2) |
| $ {\boldsymbol{P}} = {\boldsymbol{H}}\beta 。$ | (3) |
式中:
| $ H{\beta ^*} - T = {{\min}_{\beta}}\left\| {H\beta - T} \right\| 。$ | (4) |
2020年,Xue等[11]提出麻雀搜索算法(Sparrow Search Algorithm, SSA),该算法充分融合麻雀觅食的种群行为,获得了对模型参数更优的迭代寻优性能。在SSA中,麻雀种群被抽象划分为发现者和追随者,并根据麻雀种群不同角色的分工和协作来实现觅食目的。麻雀种群中,担任发现者的麻雀需要找到食物的位置,并向其他的麻雀提供对应方向。追随者则是根据发现者所给出的信息进行觅食。此外,麻雀种群中会抽取10%~20%比例的麻雀作为警戒者,它们负责对觅食区域进行警戒和监视,一旦发现捕食者,警戒者会立刻发出警告,此时麻雀种群飞往新的位置。
发现者的位置更新如下式:
| $ X_{i,j}^{z + 1} = \left\{ \begin{gathered} X_{i,j}^z \cdot \exp \left( {\frac{{ - i}}{{\alpha \cdot {\mathrm{Max}}}}} \right),{\text{ }}{R_2} < ST ,\\ X_{i,j}^z + Q \cdot L,{\text{ }}{R_2} \geqslant ST 。\\ \end{gathered} \right.{\text{ }} $ | (5) |
式中:
追随者的位置更新如下式:
| $ X^{z+1}_{i,j}=\left\{\begin{array}{ll} Q\cdot exp\left(\displaystyle\frac{X^z_{{\mathrm{worst}}}-X^{z}_{i,j}}{i^2}\right), \;\; i > \displaystyle\frac{n}{2},\\ X_B^{z+1}+|X_{i,j}^z- X_B^{z+1}|\cdot L \cdot A^+, \;\; {\mathrm{otherwise}}。\end{array} \right. $ | (6) |
式中:
当麻雀意识到周围环境存在危险时,它们就会出现反捕食行为,即离开当前的位置以躲避天敌,位置更新如下式:
| $ X_{i, j}^{x+I}=\left\{\begin{array}{ll} X_{{bat }}^{z}+\beta\left|X_{i, j}^{z}-X_{{batr }}^{z}\right|, \;\; f_{i}>f_{k},\\ X_{i, j}^{z}+k \displaystyle\frac{\left|X_{i, j}^{z}-X_{ {{\mathrm{worst}} }}^{z}\right|}{\left(f_{i}-f_{ {{\mathrm{worst}}}}\right)+\varepsilon}, \;\; f_{i}=f_{k}。\end{array}\right. $ | (7) |
式中:
传统的麻雀搜索算法存在一定缺陷,如迭代寻优的后期麻雀种群多样性降低,容易陷入局部最优位置等。为了改善上述问题,本文在发现者位置更新公式中进行2处改进:
1)对发现者公式引入自适应加权策略,改进后如下所示。原本SSA中,麻雀个体的步长控制有限,容易跳跃收敛于最优解附近,使得SSA算法不能在全局范围内充分搜索,从而陷入于局部最优,对收敛速度有较大影响。因此在发现者中引入了随迭代次数变化的自适应权重
| $ \omega \left( z \right) = 0.2{\mathrm{cos}} \left( {\frac{{\text π} }{2}\left( {1 - \frac{z}{{{\mathrm{Max}}}}} \right)} \right) ,$ | (8) |
| $ X_{i, j}^{x+r}=\left\{\begin{array}{ll} \omega \cdot X_{i, j}^{z}- exp \left(\displaystyle\frac{-i}{\alpha \cdot {\mathrm{M a x}}}\right), \;\; R_{2}\lt ST ,\\ \omega \cdot X_{i, j}^{z}+Q \cdot L,\;\; R_{2} \geqslant ST,\end{array}\right. $ | (9) |
2)而后为了增强优化算法的全局搜索能力,降低陷入局部最优的可能性,在新发现者公式后再引入Levy飞行策略,Levy飞行服从Levy分布,其运动模式充分发挥了距离跳跃的优越性,在短距离内频繁跳跃,又不缺失偶尔的长距离跳跃交替,使它可以跳出局部最优并扩大麻雀种群的搜索范围[12]。Levy分布比较复杂,通常使用Mantegna算法进行模拟,具体如下:
| $ X_z^{'} = {X_z} + l \oplus levy\left( \lambda \right) ,$ | (10) |
| $ \left\{ \begin{gathered} s = \frac{u}{{{{\left| v \right|}^{1/\gamma }}}} ,\\ \mu~N\left( {0,\sigma _\mu ^2} \right),\\ v~N\left( {0,\sigma _v^2} \right) ,\\ {\sigma _\mu } = {\left\{ {\frac{{\Gamma \left( {1 + \gamma } \right){\mathrm{sin}} \left( {\pi \gamma /2} \right)}}{{\gamma \cdot \Gamma \left[ {\left( {\gamma + 1} \right)/2} \right] \cdot {2^{\left( {\gamma + 1} \right)/2}}}}} \right\}^{\gamma + 1}}。\\ \end{gathered} \right. $ | (11) |
式中:
为了充分验证所提出的ISSA性能,加入麻雀搜索算法、粒子群优化算法[13](Particle Swarm Optimization,PSO)和灰狼优化算法[14](Grey Wolf Optimization Algorithm,GWO)作对比。在基准测试函数上,本文选择在单峰函数Quartic Function i.e. Noise和多峰函数Ackley's Function上验证算法的可靠性。ISSA和SSA中,发现者和追随者的比例按2∶8,预警值 取0.8。PSO算法中,设置参数学习因子均为2[15],惯性权重值为0.9。所有优化算法的种群规模设为30,迭代次数设为
取0.8。PSO算法中,设置参数学习因子均为2[15],惯性权重值为0.9。所有优化算法的种群规模设为30,迭代次数设为
|
|
表 1 对比优化算法在基准测试函数上的测试结果 Tab.1 Test results of comparison optimization algorithms on benchmark testing functions |
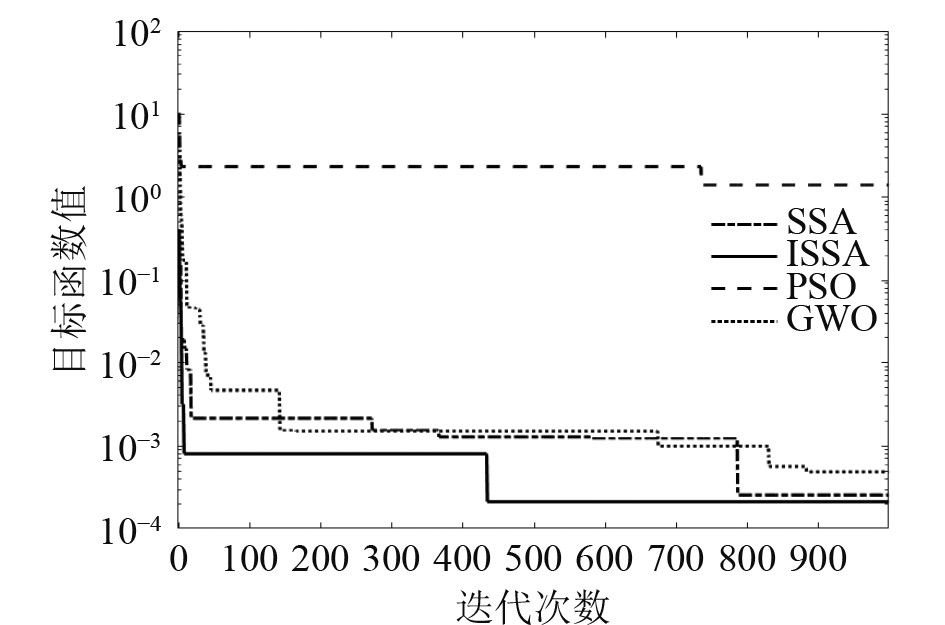
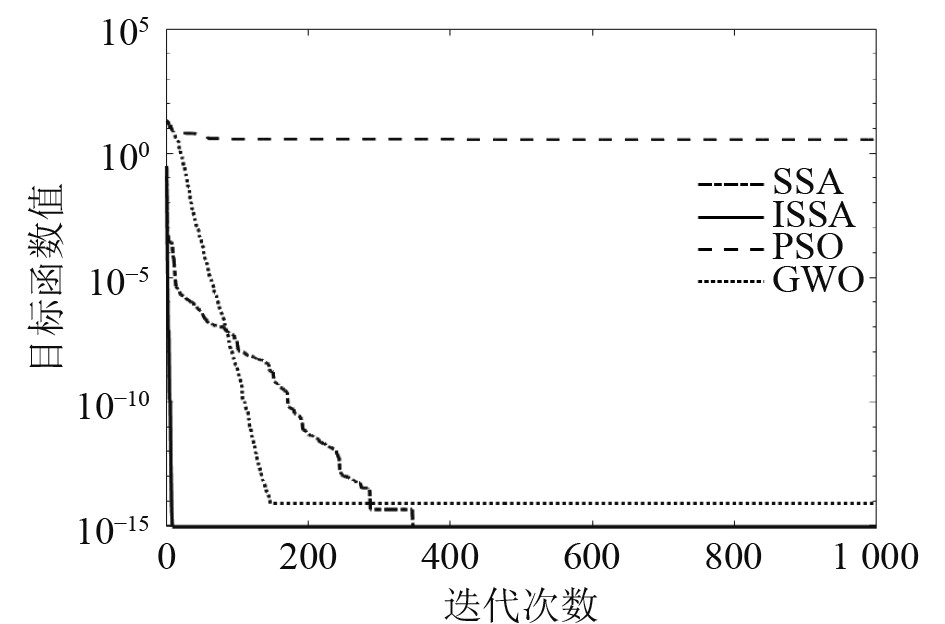
由图2~图3及表1可知,在单峰函数(Quartic Function i.e. Noise)上,ISSA获得的最优解、均值和标准差,数值都比其他3种优化算法更低,具备更优的收敛精度、收敛速度和稳定性,即ISSA在单峰函数具备较好的迭代寻优性能。在多峰函数(Ackley's Function)上,SSA和ISSA都能够获得最小值,但二者的收敛速度有较大区别,ISSA在第30迭代中取得收敛,而SSA却需要在350次左右才能收敛。综上所述,ISSA中引入自适应加权策略和Levy飞行策略进行改进,能够提高算法的稳定性,进一步增强算法的迭代寻优性能。
|
图 2 4种优化算法在单峰函数上的收敛图 Fig. 2 Convergence graph of four optimization algorithms on unimodal functions |
|
图 3 4种优化算法在多峰函数上的收敛图 Fig. 3 Convergence graph of four optimization algorithms on multimodal functions |
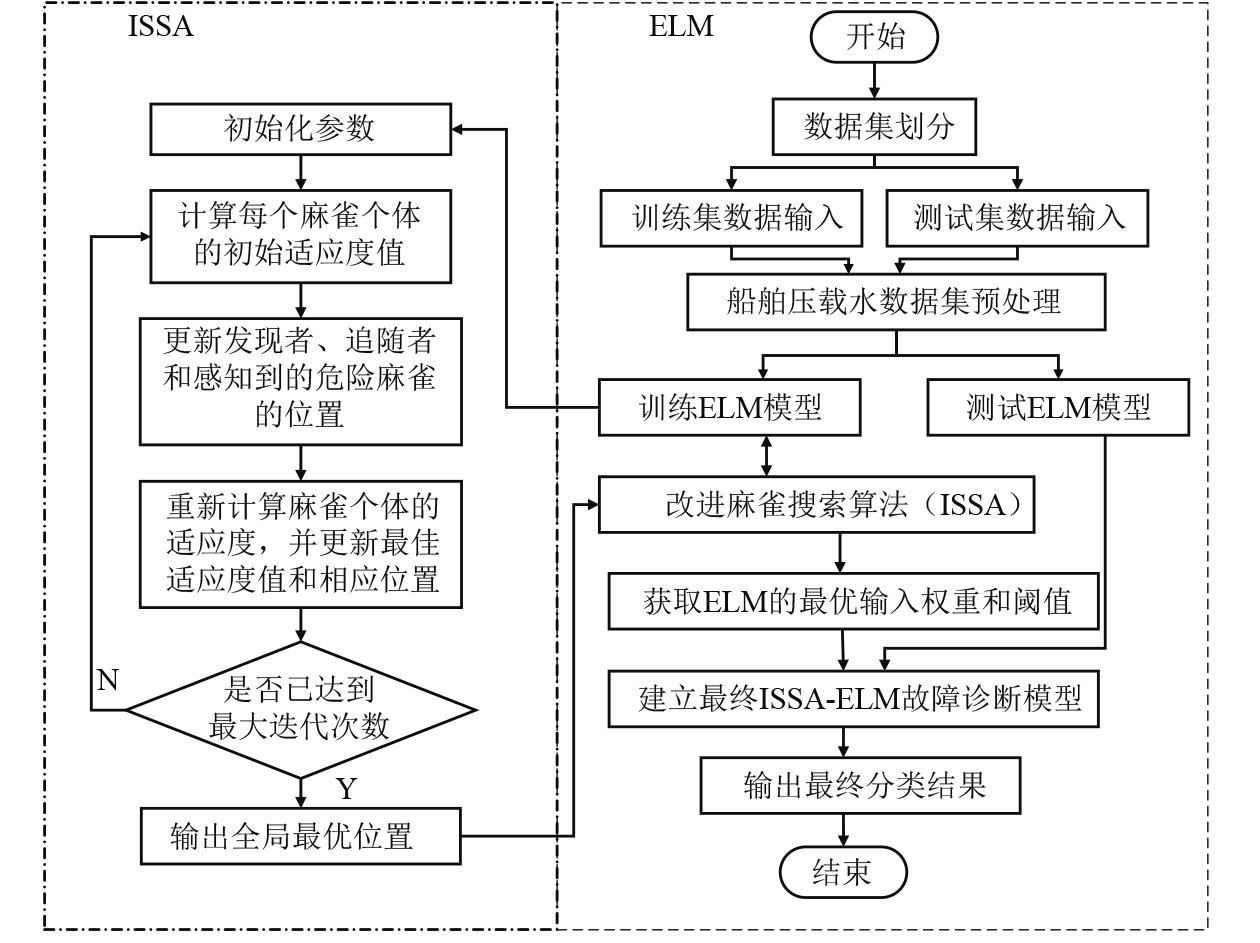
针对船舶压载水系统数据集,使用ISSA对ELM的初始参数迭代寻优,并构建最终的ISSA-ELM故障诊断模型,总体流程如图4所示。
|
图 4 ISSA-ELM故障诊断模型整体流程图 Fig. 4 The overall flowchart of ISSA-ELM model |
1)使用ISSA实现对ELM模型的参数优化。按照7∶3的比例划分训练集和测试集,对数据预处理后,以分类错误率建立ISSA的适应度函数,以获取使用ISSA迭代寻优的最优输入权重和阈值。
2)基于ISSA获得的初始参数构建ELM故障诊断模型,输入测试集以获得最终的故障诊断结果。所提出的ISSA-ELM故障诊断模型,充分发挥ISSA的迭代寻优性能,降低了初始参数对ELM分类准确率的影响,实现了故障诊断精度的提高。
1.5 ISSA的目标函数模型采用分类准确率
| $ Acc = \sum\limits_{j = 1}^m {\left( {\frac{{x_j^z}}{{{x_j}}}} \right)} 。$ | (12) |
式中:
ISSA的适应度函数结合了模型的评价函数,采用分类错误率,即
为了验证所提出ISSA-ELM模型的可靠性,本文将某集装箱船模拟器中的压载水系统作为研究对象,从中提取了5种状态各60组,共300组的样本数据集。5类状态分别为:系统正常运行、海底门滤器脏堵、压载水泵轴瓦磨损、阀门卡阻、和管段泄漏[16]。
每组样本包含1号过滤器的吸入压力、1号过滤器的排出压力、压载泵的吸入压力、压载泵的排出压力、2号过滤器的吸入压力、2号过滤器的排出压力、压载水处理装置的排出压力、12号阀的排出压力、压载泵的流量、压载水处理装置的流量、左舷压载舱的主管流量、右舷压载舱的主管流量和压载泵的电机输出功率,共13个维度特征。样本数据集的顺序被随机打乱,按7∶3的比例划分,抽取210组数据作为训练集,其余则为测试集。
|
|
表 2 船舶压载水系统的数据细节 Tab.2 Details of data for ship ballast water systems |
对所获取的数据集进行预处理,加入随机噪声以提高算法的鲁棒性:
| $ A(i, j)=A(i, j)+m(I)\cdot 0.02 \cdot \left(2{\cdot } { rand }-I\right) 。$ | (13) |
式中:
数据集的预处理为归一化处理,如下式:
| $ x = \frac{{{x_l} - {x_b}}}{{{x_a} - {x_b}}}。$ | (14) |
式中:
本文使用ISSA的迭代寻优性能,解决ELM初始参数随机性影响模型泛化性能[18]的问题。同时,增设SSA-ELM、PSO-ELM和GWO-ELM这3组模型作对比试验,验证所提出的ISSA对ELM初始参数具有较好的迭代寻优性能,以实现故障诊断模型性能的提升。PSO中,设置参数同1.3.2节。每种优化算法独立运行30次,模型结果如图5和表3所示。
|
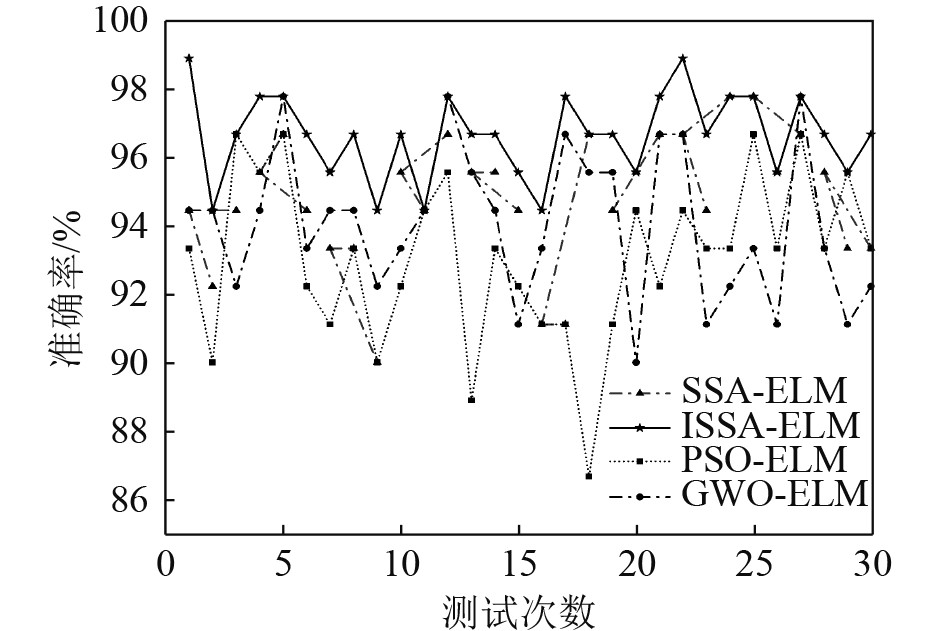
图 5 ISSA-ELM与SSA-ELM、PSO-ELM和GWO-ELM模型对比试验结果 Fig. 5 Comparison test results of ISSA-ELM with SSA-ELM, PSO-ELM, and GWO-ELM models |
|
|
表 3 不同优化算法的故障诊断对比试验结果 Tab.3 Comparative test results of fault diagnosis for different optimization algorithms |
可知,ISSA-ELM模型的平均分类准确率达到96.6%,每次运行平均识别错3组测试样本。SSA-ELM模型的平均分类准确率为94.8%,比ISSA-ELM模型的低1.8%;PSO-ELM模型平均分类准确率为93.1%,比ISSA-ELM模型的低3.5%;GWO-ELM模型平均分类准确率为94.0%,比ISSA-ELM模型的低2.6%。综上所述,本文提出ISSA比其他优化算法在ELM初始参数上的迭代寻优性能更佳,所构建的ISSA-ELM模型能够更好地区分船舶压载水系统的故障,具备更好的故障诊断性能。
2.2.2 不同分类算法的故障诊断对比试验为进一步加强ISSA-ELM模型的性能验证,在船舶压载水系统的数据集上使用SVM、ELM模型作对比。ISSA的核心参数设置同2.2.1节相同,种群规模设为30,最大迭代次数设为50,SVM的惩罚因子和核参数分别设为10和0.01。
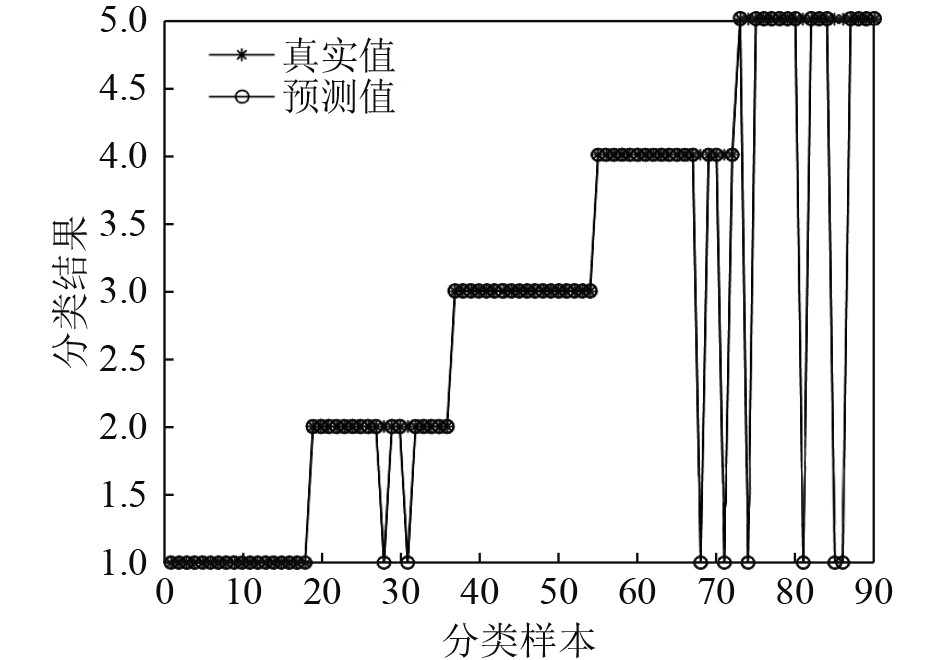
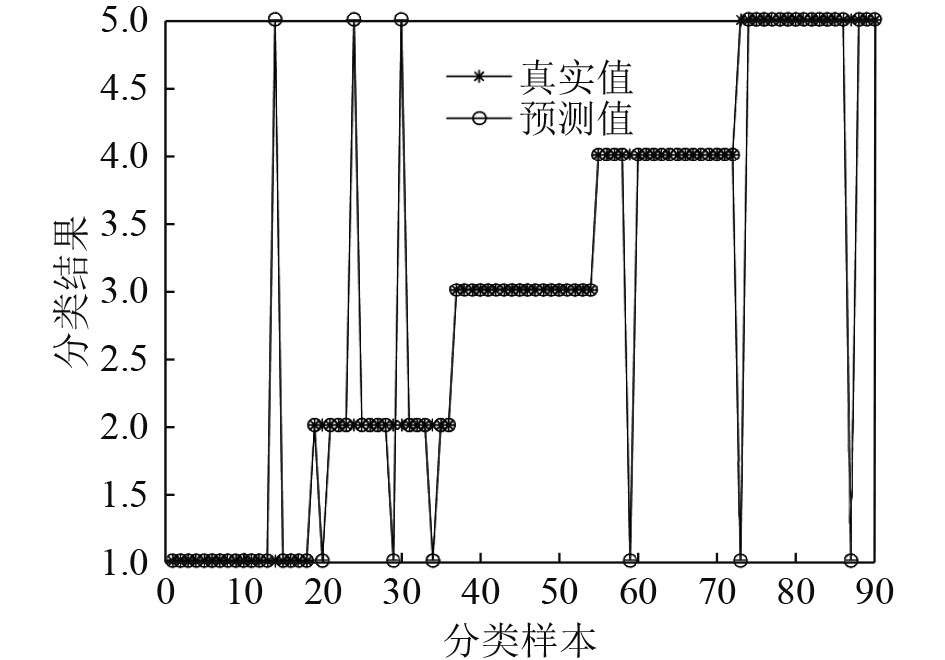
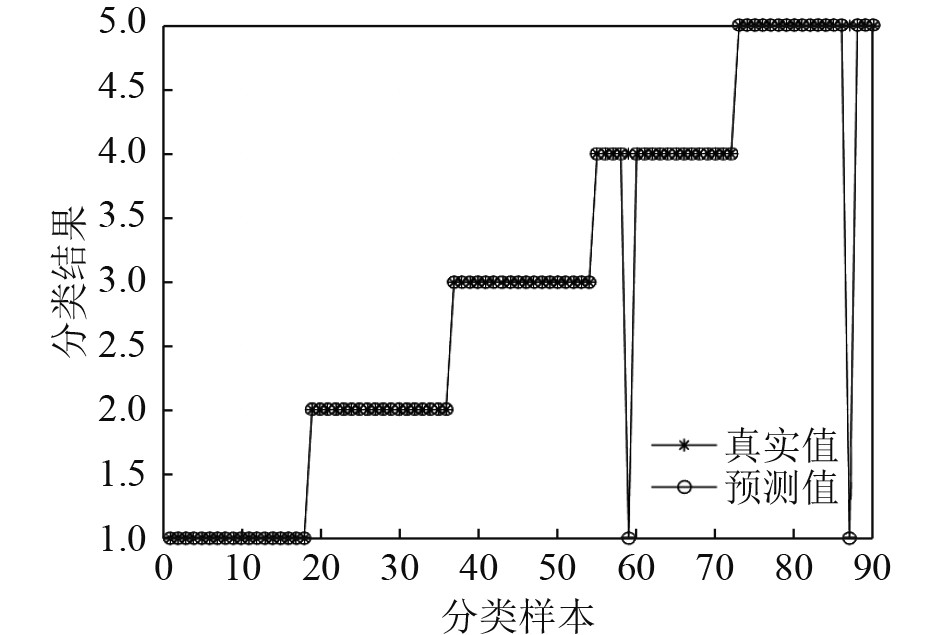
取第1次的故障诊断结果进行展示,如图6~图8所示,图中“○”为预测测试集,“*”为实际测试集,纵坐标“1”、“2”、“3”、“4”、“5”编号为船舶压载水系统的5种状态数据的对应标签。ISSA-ELM模型的分类准确率达到了97.8%,比SVM高出6.7%,比ELM高出7.8%。ISSA-ELM模型仅识别错误2组样本数据,分别是状态“4”和状态“5”数据,而SVM和ELM模型各识别错了8组和9组样本数据。可知,ISSA-ELM模型分类性能更佳。
|
图 6 SVM测试分类结果 Fig. 6 SVM test classification result |
|
图 7 ELM测试分类结果 Fig. 7 ELM test classification result |
|
图 8 ISSA-ELM测试分类结果 Fig. 8 ISSA-ELM test classification result |
其次,为了降低群智能优化算法随机性带来的影响,将3种模型分别运行30次,以平均准确率作为最终评价指标,其输出结果如表4所示。本文所提ISSA-ELM故障诊断模型平均准确率可达96.6%,比SVM高出7.1%,比ELM高出4.5%。综上所述,ISSA-ELM模型的分类能力较强,能够较好地实现对船舶压载水系统的故障诊断。
|
|
表 4 不同模型故障诊断对比试验结果 Tab.4 Comparison test results of fault diagnosis for different models |
1)针对SSA容易陷入局部最优位置等问题,引入自适应加权策略和Levy飞行策略对发现者公式进行改进,得到ISSA算法。
2)在基准测试函数上,将ISSA与SSA、PSO、GWO作对比,验证所提出的ISSA具有较好的收敛精度和迭代寻优性能。
3)在船舶压载水系统数据集上的实验结果表明,与SSA-ELM、PSO-ELM、GWO-ELM、SVM和ELM模型对比,ISSA-ELM故障诊断模型的全局搜索能力更强,具有更好的故障诊断性能。
| [1] |
杨咏, 王晓, 兑红炎, 等. 船舶压载水系统可靠性分析[J]. 舰船科学技术, 2023, 45(12): 35−39. YANG Yong, WANG Xiao, DUI Hong-Yan, et al. Reliability analysis of ship ballast water system[J]. Ship Science and Technology, 2023, 45(12): 35−39. |
| [2] |
石大亮, 张毅然, 湛日景, 等. 基于关联规则分类的船用柴油机故障诊断[J]. 内燃机学报, 2023, 41(4): 369−375.
|
| [3] |
KOWALSKI J, KRAWCZYK B, WOŹNIAK M. Fault diagnosis of marine 4-stroke diesel engines using a one-vs-one extreme learning ensemble[J]. Engineering Applications of Artificial Intelligence, 2017, 57: 134−141.
|
| [4] |
XI W, LI Z, TIAN Z, et al. A feature extraction and visualization method for fault detection of marine diesel engines[J]. Measurement, 2018, 116: 429−437.
|
| [5] |
王泷德, 曹辉, 魏来. 不平衡数据下船舶主机在线故障诊断研究[J]. 中国舰船研究, 2023, 18(5): 269-275. |
| [6] |
王忠巍, 袁志国, 马修真, 等. 一种不依赖特征样本的柴油机故障诊断方法研究[J]. 哈尔滨工程大学学报, 2017, 38(6): 881−886.
|
| [7] |
FENG D, LI Y. Research on intelligent diagnosis method for large-scale ship engine fault in non-deterministic environment[J]. Polish Maritime research, 2017, 24(1): 200-206. |
| [8] |
HUANG G. What are extreme learning machines? Filling the gap between frank rosenblatt’s dream and john von neumann’s puzzle[J]. Cognitive Computation, 2015, 7(3): 263−278.
|
| [9] |
CHENGTIAN O, YAXIAN Q, DONGLIN Z. Adaptive spiral flying sparrow search algorithm[J]. Scientific Programming, 2021(6): 1−16.
|
| [10] |
GUANGBIN H, HONGMING Z, XIAOJIAN D, et al. Extreme learning machine for regression and multiclass classification[J]. IEEE transactions on systems, man, and cybernetics, 2012, 42(2): 513−517.
|
| [11] |
XUE J, SHEN B. A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems Science & Control Engineering, 2020, 8(1): 2144−2158.
|
| [12] |
LI J, AN Q, LEI H, et al. Survey of lévy flight-based metaheuristics for optimization[J]. Mathematics, 2022, 10(15): 27−85.
|
| [13] |
YI L, HUIBING G, YUJIN C, et al. Research on fault prediction of marine diesel engine based on attention-LSTM[J]. Proceedings of the Institution of Mechanical Engineers, 2023, 237(2): 6−13.
|
| [14] |
MENG Y, ZHANG X, LIU Z, et al. Support vector regression ship motion identification modeling based on grey wolf optimizer[C]//中国自动化学会控制理论专业委员会, 2021.
|
| [15] |
尹文哲, 夏虹, 彭彬森, 等. 基于CNN-SVM的核电厂轴承故障诊断方法[J]. 哈尔滨工程大学学报, 2023, 44(3): 410−417.
|
| [16] |
CAO H, ZHANG J, CAO X, et al. Optimized SVM-driven multi-class approach by improved abc to estimating ship systems state[J]. IEEE access, 2020, 8: 206719−206733.
|
| [17] |
王志超, 夏虹, 彭彬森, 等. PSO-LSSVM的核电站破口故障程度评估方法[J]. 哈尔滨工程大学学报, 2021, 42(12): 1748−1753.
|
| [18] |
LIU T, FAN Q, KANG Q, et al. Extreme learning machine based on firefly adaptive flower pollination algorithm optimization[J]. Processes, 2020, 8(12): 15−83.
|
 2024, Vol. 46
2024, Vol. 46
