在船体总纵强度计算中,通常将船体理想化为一变断面的空心薄壁梁,即船体梁,并从整体上进行研究。船体梁在外力作用下沿其纵向铅垂面内会发生弯曲,故需要求得引起船体梁总纵弯曲的剪力、弯矩以及相应的应力,并将它与许用应力相比较以判断船体强度,这是船体总纵强度计算的常规方法。这种方法有较大的近似性,首先它认为横剖面上处于同一高度的构件总纵应力相同,忽略了总纵应力沿船宽方向的变化,其次它不能准确地考虑不连续纵向构件的影响,比如有大开口的舷侧。规范规定强力甲板及其以下所有在0.4L区域内连续的纵向构件的剖面积,均可计入船体梁剖面模数,但如果船舶舷侧有大开口,对总纵强度的影响难以确定,不能用常规梁方法评估船体总纵强度[1],只能凭借设计者的经验进行评估,存在一定的风险。
对于舷侧大开口船舶总纵强度的评估,目前主要采用2种方法,一种是忽略开口以上结构,仅考虑开口以下结构参与总纵进行评估,这种方法效率高但评估结果太保守,可能会大幅增加钢料,一般不采用;另一种是参考船级社规范,通过整船有限元直接计算方法评估船体总纵强度[2-3],但工作量巨大,计算结果的准确性无法保证。朱波[4]对一典型内河邮轮在总纵弯矩作用下的结构响应进行数值仿真模拟,对上层建筑侧壁开口的影响进行了分析。叶旭等[5]采用有限元直接计算方法分析了滚装船上层建筑和主船体连接过渡区域的总纵强度问题,重点关注了首部外板开口处的结构形式。渠基顺等[6]基于中国船级社邮轮规范中的整船直接计算方法对邮轮进行总纵强度评估,对邮轮连续的舷侧开口进行了细网格强度评估。
为高效准确地评估舷侧大开口船舶的总纵强度,本文提出一种舷侧大开口船舶总纵强度的简化评估方法,用此方法评估了实船的总纵强度,并分析了开口对总纵弯曲强度的影响。为具有上述特征船舶的总纵强度评估提供思路和数据参考,对相关区域的结构设计有一定指导作用。
1 舷侧大开口船舶总纵强度的简化评估方法船体梁横剖面固有特性一旦确定,其总纵强度应力水平由船体梁所承受的剪力、弯矩决定,即总纵剪切应力与船体梁剪力是线性关系,总纵弯曲应力与船体梁弯矩是线性关系。以此理论为基础,抛开实际装载工况下动载荷及非结构重量等诸多复杂因素,在整船有限元分析中只考虑最简单的主船体结构重力和静水浮力,当船舶在静水中达到平衡状态时,由于重力与浮力沿船长方向分布不同,会产生垂向剪力,距尾垂线
| $ {Q}_{x}={\int }_{0}^{x}\omega {\mathrm{d}}x-{\int }_{0}^{x}\rho gF{\mathrm{d}}x ,$ | (1) |
| $ {M}_{x}={\int }_{0}^{x}{Q}_{x}{\mathrm{d}}x。$ | (2) |
式中:
根据此剪力
| $ {\tau }^{{'}}=\frac{{Q}_{x}^{{'}}}{{Q}_{x}}\tau \text{,}{\sigma }^{{'}}=\frac{{M}_{x}^{{'}}}{{M}_{x}}\sigma。$ | (3) |
基于如上所述,舷侧大开口船舶总纵强度评估的基本过程如下[7]:
1)在有限元软件里建立主船体结构有限元模型,并得到准确的结构重量分布。
2)按此重量分布通过NAPA软件得到首尾吃水
3)对主船体有限元模型施加重力和静水浮力,静水浮力依据
4)通过有限元计算得到考察点处的剪切应力
5)计算设计剪力
6)若
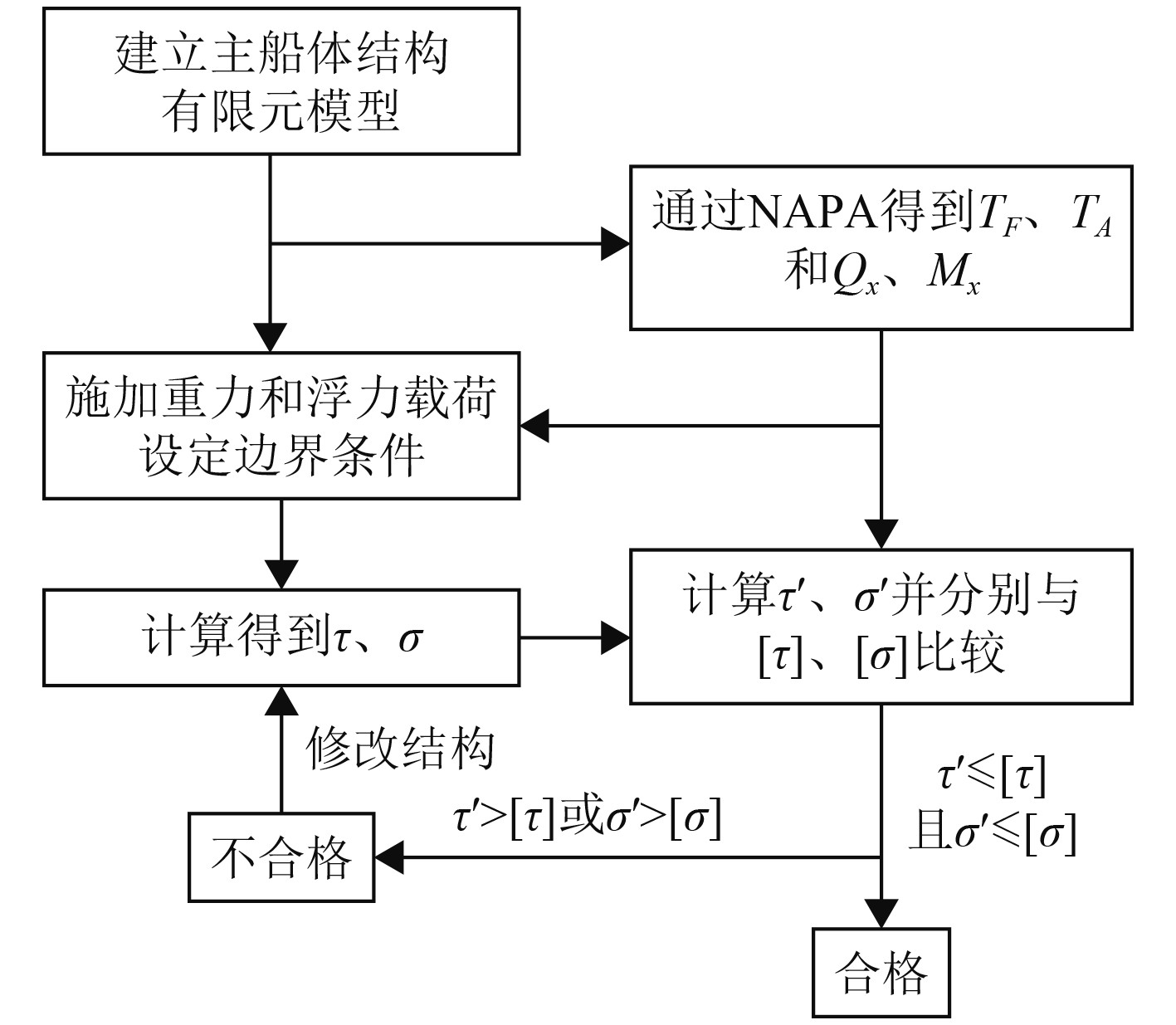
评估流程见图1。
|
图 1 舷侧大开口船舶的总纵强度评估流程 Fig. 1 Longitudinal strength assessment process of ship with large side opening |
以一琼州海峡客滚船为目标船,该船入级中国船级社,具有全贯通的强力旅客甲板,该甲板下方舷侧外板因布置需要有较大的开口。按照上述方法对其舷侧大开口区域的总纵强度进行评估,选取2个典型横剖面,考察船体梁横剖面中和轴附近舷侧外板的剪切强度和旅客甲板的弯曲强度。
2.1 结构有限元模型的建立按常规全船有限元建模规则建立目标船旅客甲板下主船体结构有限元模型,见图2。

|
图 2 主船体结构有限元模型 Fig. 2 Finite element model of main hull structure |
根据NAPA软件得到的艏艉吃水
|
|
表 1 边界约束及其施加位置 Tab.1 Boundary constraint and their application position |
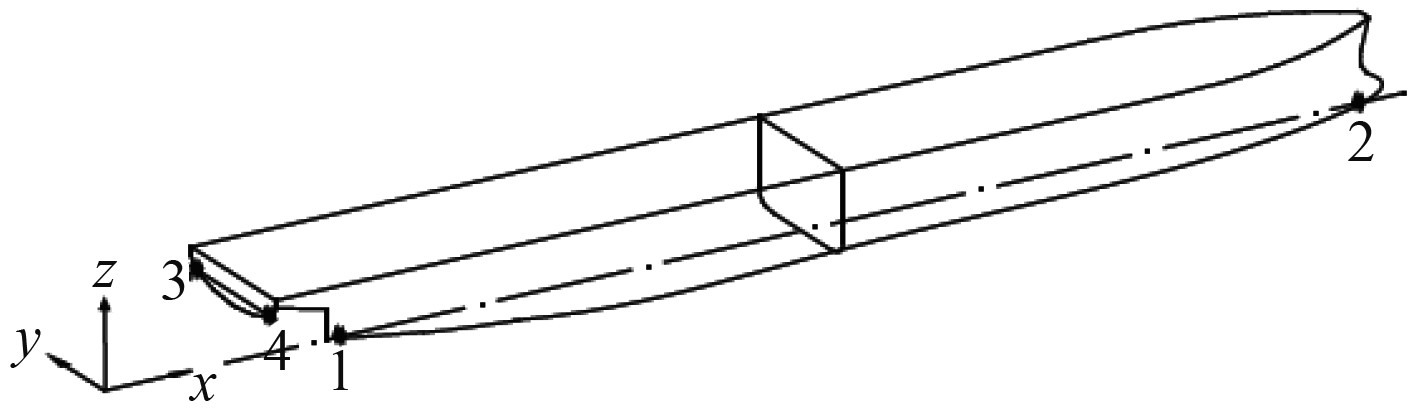
|
图 3 边界条件示意图 Fig. 3 Boundary condition figure |
通过有限元计算,主船体垂向变形及纵向正应力云图见图4和图5,旅客甲板变形云图见图6。以旅客甲板为例,在船长方向,最大纵向正应力出现在船中区域,并向船两端逐渐减小;在船宽方向,纵向正应力是变化的,甲板边板应力水平比中纵高一些,这与常规梁理论略有不同。根据图6可以发现,由于泊松比效应,总纵载荷会导致旅客甲板横向弯曲变形,产生横向压应力,应关注其下方层高和横向屈曲问题[9]。考察点的总纵剪切和弯曲应力结果见表2、和表3。

|
图 4 主船体垂向变形云图 Fig. 4 Vertical deformation figure of main hull |

|
图 5 主船体纵向正应力云图 Fig. 5 Longitudinal normal stress figure of main hull |

|
图 6 旅客甲板变形云图 Fig. 6 Deformation figure of passenger deck |
从计算结果可知,考察点的总纵剪切和弯曲强度满足规范要求,无需进一步处理。另外,本文的舷侧大开口船舶总纵强度的简化评估方法得到了中国船级社的认可,目标船的总纵强度评估也通过了审核。
|
|
表 2 舷侧外板总纵剪切应力计算结果 Tab.2 Calculation result of longitudinal shear stress of side shell |
|
|
表 3 旅客甲板总纵弯曲应力计算结果 Tab.3 Calculation result of longitudinal bending stress of passenger deck |
用有限元法考察旅客甲板下舷侧开口高度分别为0.2H、0.4H、0.6H、0.8H和开口长度分别为0.2L、0.4L、0.6L、0.8L时旅客甲板、上甲板、船底板的总纵弯曲应力,进行开口对总纵弯曲应力的影响分析,L为船长,H为旅客甲板层高。
有限元计算的载荷和边界条件与上述类似,各开口方案下各考察位置总纵弯曲应力计算结果见表4。
|
|
表 4 各开口方案下各考察位置总纵弯曲应力(N/mm2) Tab.4 Longitudinal bending stress at each position under each opening plan |
用常规梁方法计算各考察位置总纵弯曲应力,计算结果见表5。
|
|
表 5 常规梁方法下各考察位置总纵弯曲应力(N/mm2) Tab.5 Longitudinal bending stress at each position under conventional beam method |
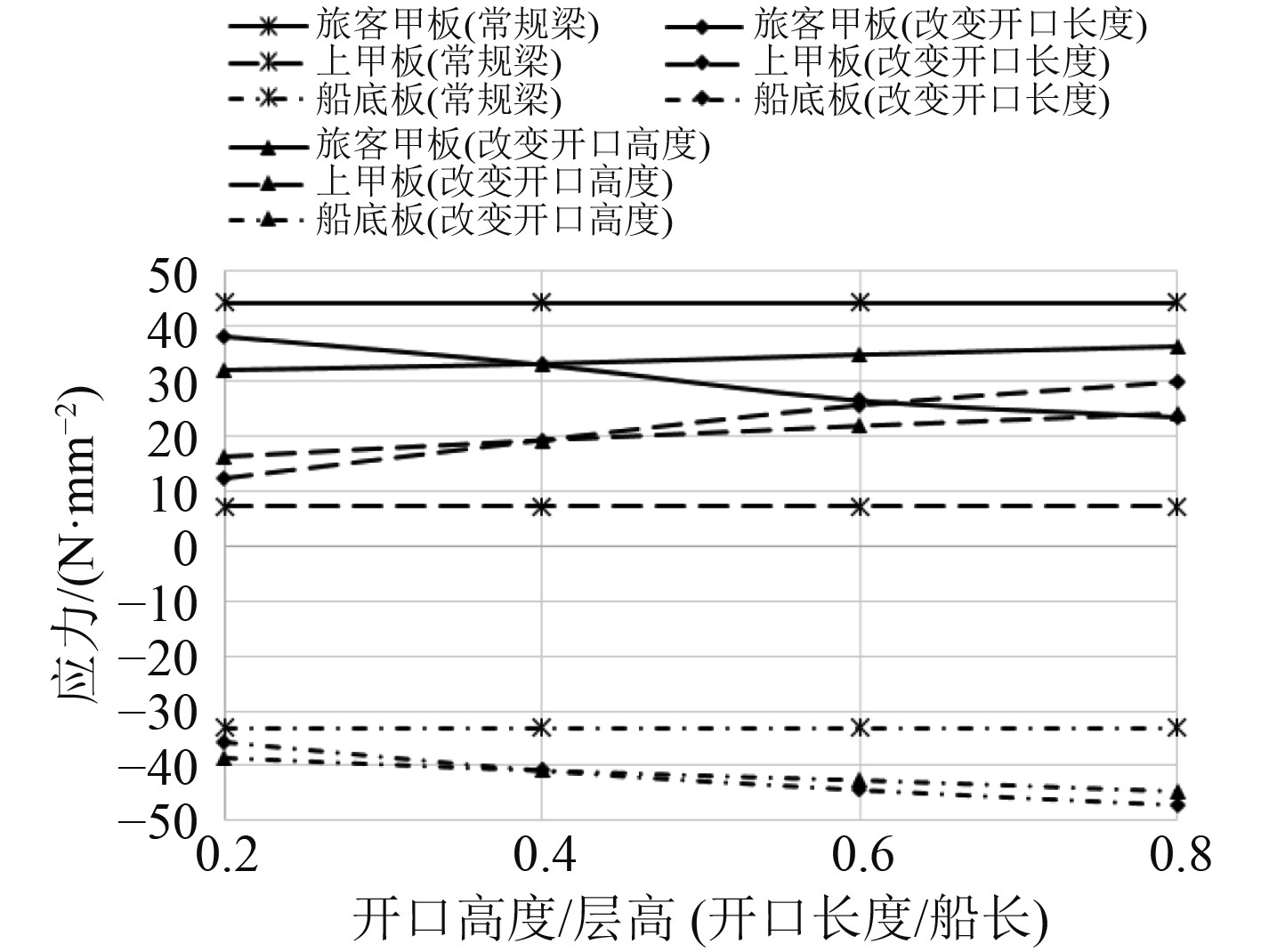
可以看出,当舷侧带有大开口时,有限元计算结果与常规梁差异较大,这说明此时不能用常规梁方法计算船体总纵弯曲应力,图7为总纵弯曲应力随开口大小变化曲线。
|
图 7 总纵弯曲应力随开口大小变化曲线 Fig. 7 Curve of longitudinal bending stress variation with opening size |
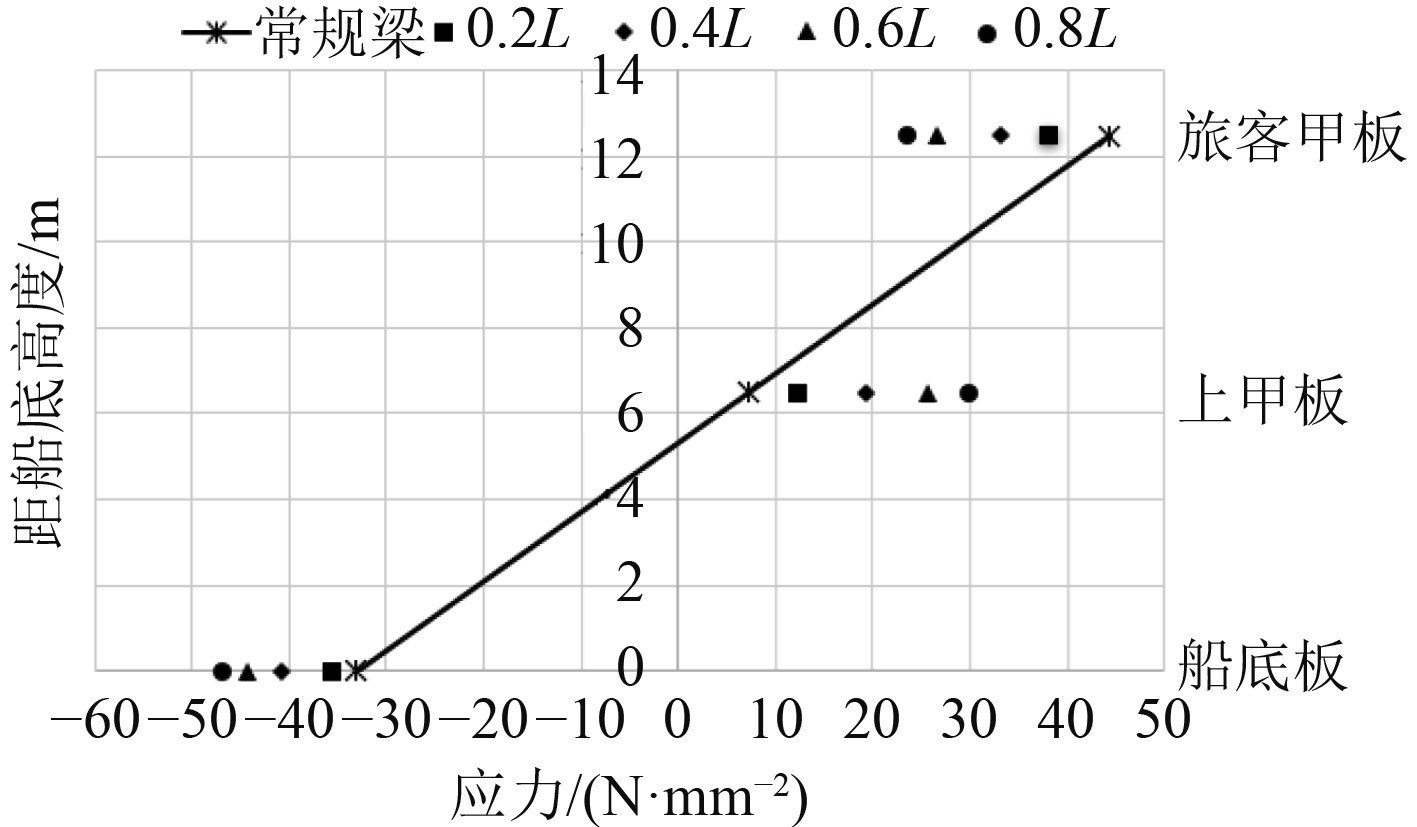
由表4可知,各方案下总纵弯曲应力变化趋势一致。以开口高度0.4H和开口长度0.4L为例考察总纵弯曲应力分布,结果如图8和图9所示。
|
图 8 各开口长度下的总纵弯曲应力分布(开口高度0.4H) Fig. 8 Longitudinal bending stress distribution under each opening length |
|
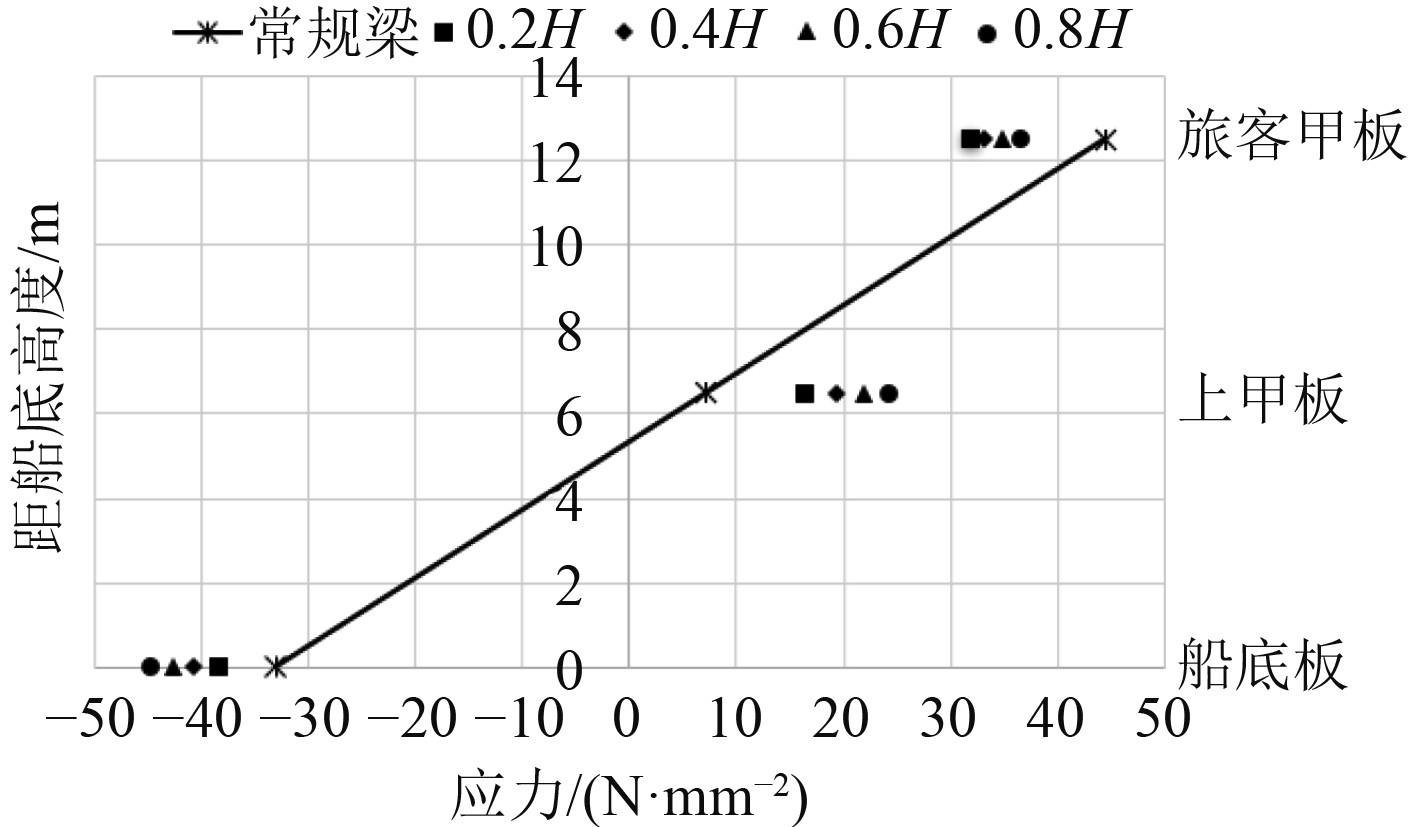
图 9 各开口高度下的总纵弯曲应力分布(开口长度0.4L) Fig. 9 Longitudinal bending stress distribution under each opening height |
可知,开口的长度和高度对总纵弯曲应力的影响均较大,从曲线斜率可以看出开口长度比高度的影响度要高,从曲线走势来看开口的高度、长度与影响程度均呈近似线性关系。因为开口的存在,开口之上的旅客甲板总纵弯曲应力比常规梁应力小,开口之下的上甲板和船底板总纵弯曲应力比常规梁应力大。开口长度越大,开口之上的旅客甲板应力就越低,开口之下的上甲板和船底板应力就越高,均越偏离常规梁应力;开口高度越大,开口之上的旅客甲板总纵弯曲应力就越高,越接近常规梁应力,同时开口之下的上甲板和船底板应力就越高,越偏离常规梁应力。
进一步分析可以发现,对于开口之上的旅客甲板,开口高度和长度对其总纵弯曲应力的影响趋势是相反的,即其应力与开口高度成正比,与开口长度成反比。因为横剖面有效模数越小,旅客甲板总纵弯曲应力越高;开口之上结构参与总纵弯曲的有效度越小,旅客甲板总纵弯曲应力越低。开口高度主导了横剖面有效模数的变化,开口长度主导了开口之上结构参与总纵弯曲有效度的变化,当开口长度不变而高度增加时,有效模数减小对应力的影响更大,因此旅客甲板的应力变高;当开口高度不变而长度增加时,有效度减小对应力的影响更大,因此旅客甲板应力变低。
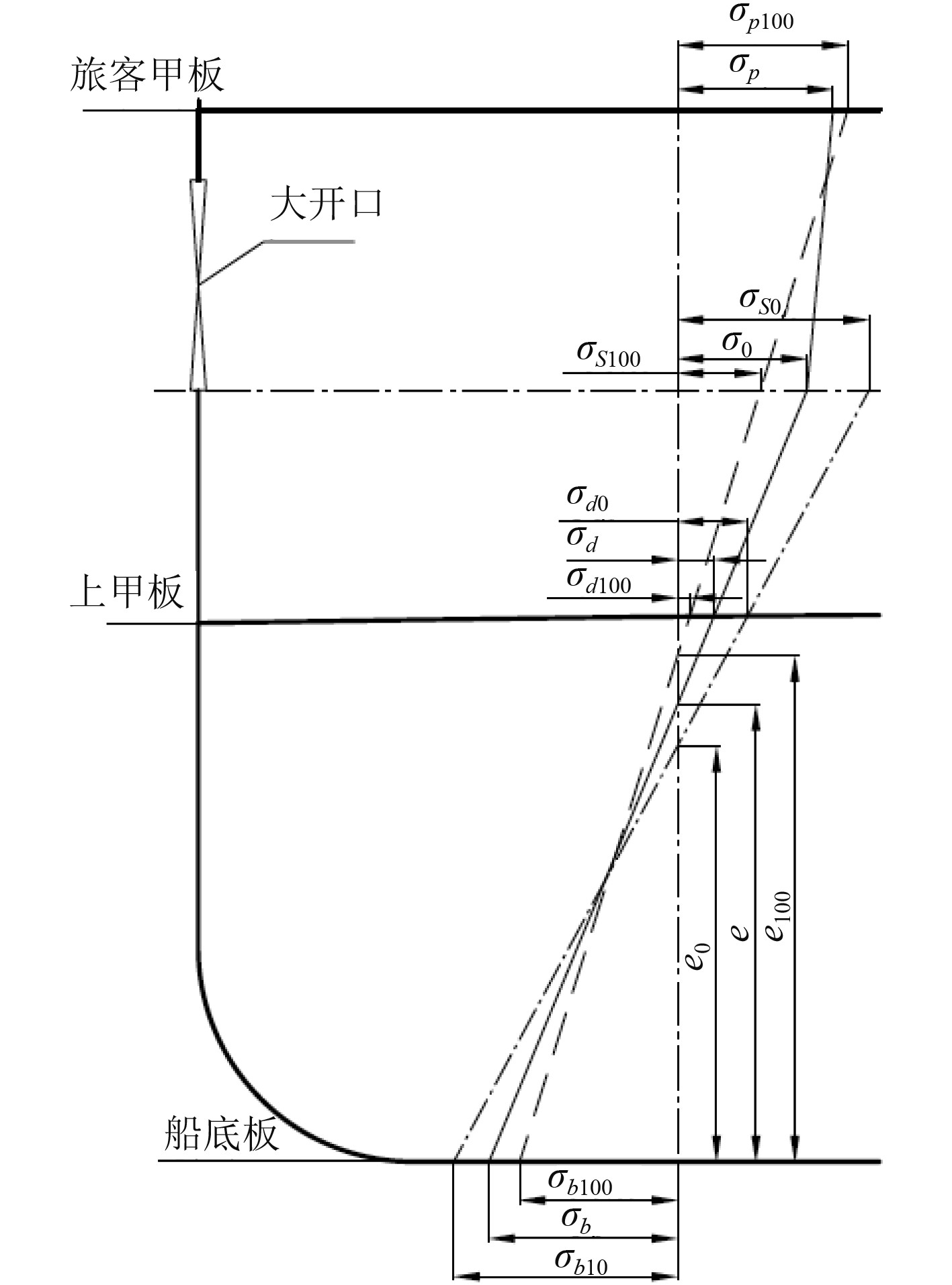
3.2 开口之上结构参与总纵弯曲有效度分析结合有限元计算结果,舷侧大开口下横剖面的总纵弯曲应力见图10,
|
图 10 舷侧大开口下横剖面总纵弯曲应力 Fig. 10 Longitudinal bending stress of cross section under large side opening |
为方便分析,引入开口之上结构参与总纵弯曲的有效系数
| $ \mu =\frac{{\sigma }_{p}}{{\sigma }_{p100}}。$ | (4) |
若开口之上结构完全不参与总纵弯曲,则
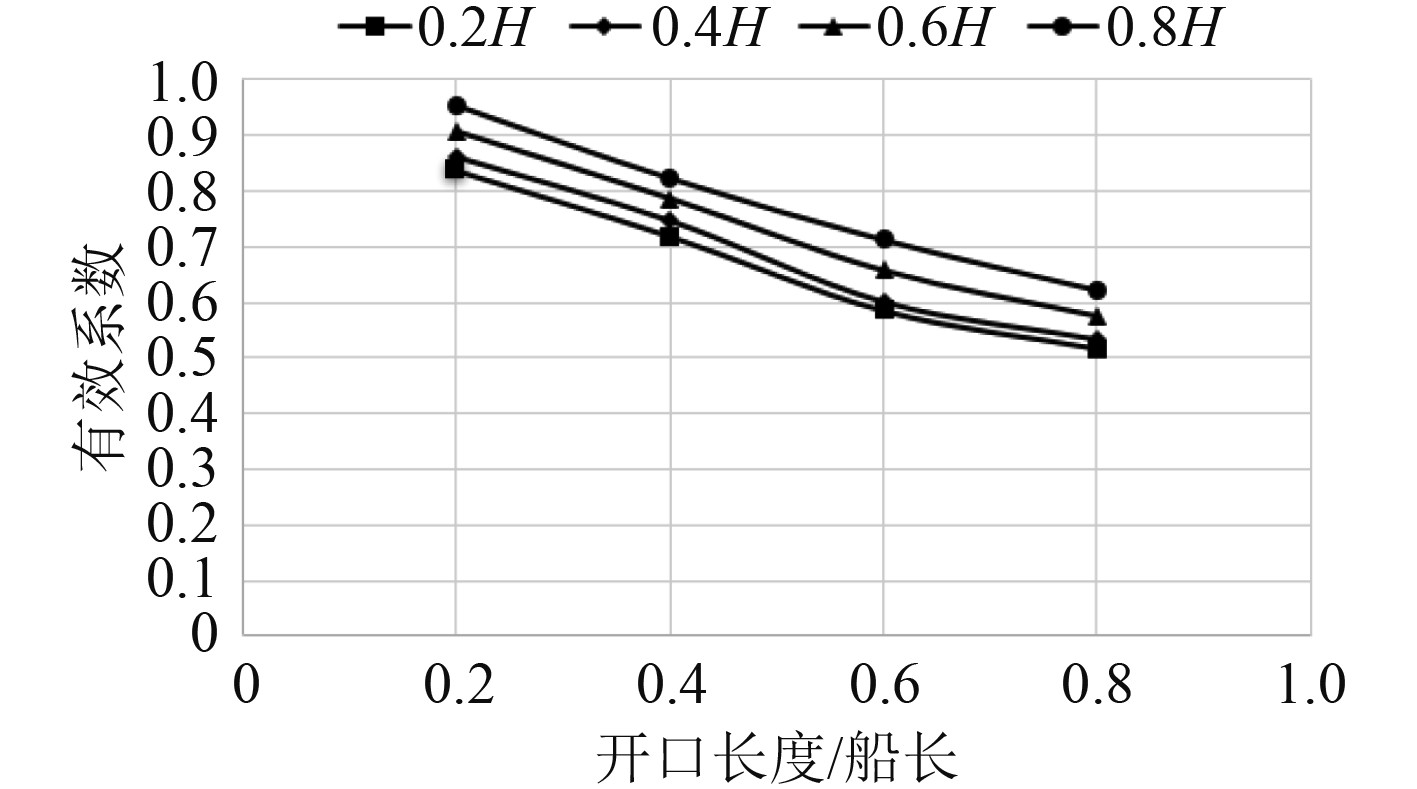
|
图 11 开口之上结构参与总纵弯曲的有效系数曲线 Fig. 11 Effective coefficient curve of structure above opening participating in longitudinal bending |
可知,各开口方案下的有效系数均在0.5~1.0之间。对于舷侧大开口船舶,
1)提出一种舷侧大开口船舶总纵强度的简化评估方法,能高效准确地解决舷侧大开口船舶总纵强度的评估问题,同时弥补现有评估方法的不足,即规避了按照船级社规范通过整船有限元直接计算方法所面临的庞大工作量,如整船模型质量配置、波浪载荷及惯性载荷的计算和施加、整船动平衡调整等,避免了上述每一项工作可能产生的误差,消除了局部载荷产生的影响。
2)舷侧大开口对船舶总纵弯曲的影响较大,不能用常规梁方法计算舷侧大开口船舶的总纵弯曲应力。开口的长度比高度的影响度要高,开口的高度、长度与影响程度均呈近似线性关系。对于开口之上的结构,开口高度和长度对其总纵弯曲应力的影响趋势相反,即其应力与开口高度成正比,与开口长度成反比。
3)各开口方案下开口之上的结构参与总纵弯曲的有效系数均在0.5~1.0之间,对于舷侧大开口船舶,可以根据本文有效系数曲线估算实际的总纵弯曲应力。对于参与总纵弯曲程度较高的上层建筑,其总纵屈服、屈曲问题应引起重视。
| [1] |
郭际, 肖渤舰. 上层建筑(甲板室)参与总纵强度程度分析[J]. 船海工程, 2014, 43(2): 23-26. DOI:10.3963/j.issn.1671-7953.2014.02.007 |
| [2] |
中国船级社. 钢质海船入级规范[S]. 2023.
|
| [3] |
BV. Rules for the Classification of Steel Ships[S]. 2023.
|
| [4] |
朱波. 邮轮上层建筑参与总纵强度有效度研究[D]. 武汉: 武汉理工大学, 2018.
|
| [5] |
叶旭, 赵文斌, 华康, 等. 总纵强度直接计算方法在滚装船上层建筑设计中的应用[J]. 船舶与海洋工程, 2021, 37(2): 30-34. |
| [6] |
渠基顺, 谷家扬, 韦琪, 等. 中型邮轮全船总纵强度评估[J]. 江苏船舶, 2022, 39(5): 13-15. |
| [7] |
张青敏, 吴刚, 邵波, 等. 舷侧大开口船舶总纵剪切强度评估方法[P]. 中国专利: ZL 2020 1 0424327.7, 2023-02-24.
|
| [8] |
中国船级社. 车辆运输船舶船体结构指南[S]. 2011.
|
| [9] |
陆春晖, 师桂杰, 彭文科, 等. 邮轮船体的总纵弯曲强度分析[J]. 船舶与海洋工程, 2019, 35(1): 1-6. |
| [10] |
中国船舶工业集团公司, 中国船舶重工集团公司, 中国造船工程学会. 船舶设计实用手册. 结构分册. 第3版 [M]. 北京: 国防工业出版社, 2013.
|
 2024, Vol. 46
2024, Vol. 46
