2. 天津大学 海洋科学与技术学院,天津 300072
2. School of Marine Science and Technology, Tianjin University, Tianjin 300072, China
海洋环境复杂多变,海风、海浪、海流等环境因素会使海上船舶不停地摇荡,这不但影响船舶正常作业,而且会对船舶和人员的安全造成威胁。如果能够预测船舶状态在未来一段时间内的变化,并利用舭龙骨[1]、减摇鳍[2]等装置施加影响,就能够一定程度上减缓船舶在海洋环境中的摇荡问题。此外,对于搭载仪器设备的船舶,其对于运动姿态稳定性要求更高。高精度的船舶运动姿态预测结果会让船舶运动姿态补偿效果显著提升,进而提升船载仪器的数据质量。
20世纪70−80年代,船舶运动姿态的预测随着卡尔曼滤波技术的应用进入到可研究阶段。随后,国内外研究人员陆续使用卷积法、周期图法、时间序列分析法以及神经网络法,在船舶运动姿态预测方面取得了很多有益成果[3-4]。卷积法利用船舶首前波高和船舶响应核函数进行运算,需知道这2项的准确值是该方法的局限性。Kalman滤波[5]包括预测和校正2个步骤,当水动力参数和环境发生变化时,很难得出船舶的状态方程式,故难以实用化。时间序列分析法利用历史数据来归纳发展规律,通过统计分析来推测发展趋势。由于海浪、潮汐等具有一定的周期性,建立时间序列模型来预测船舶姿态运动具有可行性。经典的时间序列线性预测方法有自回归模型和移动平均模型[6]以及二者结合得到的自回归移动平均模型[7],后者的预测更加精确。
船舶在海面上的运动状态受到包括环境变量和船舶自身变量等多种因素的影响,因此其某一运动自由度的变化是高度非线性的。近几年深度学习越来越成熟,国内外对于船舶运动状态预测的研究方法更多的从卷积法、周期图法等转换为了基于神经网络的预测方法。Yang等[8]通过对船舶运动Matlab模拟数据的训练,构建了一个基于BP神经网络的船舶运动预测模型,实验结果表明,真实值与预测值的变化趋势是一致的。王国栋[9]使用Tensorflow将传统AR分析,RNN模型、LSTM和BLSTM模型对舰船运动姿态预测的实验结果进行了对比分析,实验证明基于LSTM的模型较其他算法具有更高的预测精度。徐国庆等[10]使用基于Attention-LSTM神经网络的船舶航行预测方法,验证了LSTM神经网络在船舶运动状态预测方面上的优越性。王研婷[11]使用CNN和LSTM神经网络相结合的方式对船舶轨迹预测进行建模分析,在相同数据集下该模型具有更低的均方误差损失,预测效果更好。随后又出现了基于CNN和Bi-LSTM的船舶航迹预测[12]和基于CEEMD-POS-MNN的船舶航迹预测[13]等,都得到了比较理想的结果。王余宽等[14]基于滑动窗口LSTM网络针对不同航迹分别进行预测,单点航迹预测的偏离程度很低,整体预测水平优于基础LSTM。
本文在注重原始数据预处理的基础上,构建LSTM网络预测模型完成了对船舶运动姿态的预测和分析。首先,获取无人艇在不同环境下的航行姿态数据,完成包括归一化、滤波、特征选择等环节的数据预处理,研究不同的数据预处理方法对于LSTM网络船舶运动姿态预测精度的影响。以船舶单自由度姿态预测为目标,构建LSTM神经网络模型,将原数据集通过特征选择后得到新数据集,通过仿真手段对比研究基于原数据集以及基于新数据集的LSTM神经网络姿态预测效果。在此基础上,开展数据集切分测试以及三自由度姿态联合预测仿真实验,验证所构建的LSTM网络预测模型对于多自由度姿态预测问题的适用性。
1 基于LSTM的船舶运动姿态方法LSTM神经网络是RNN的一种特殊变体,可以解决RNN所带来的长期依赖问题、梯度消失和梯度爆炸问题,更适用于处理时间序列数据。
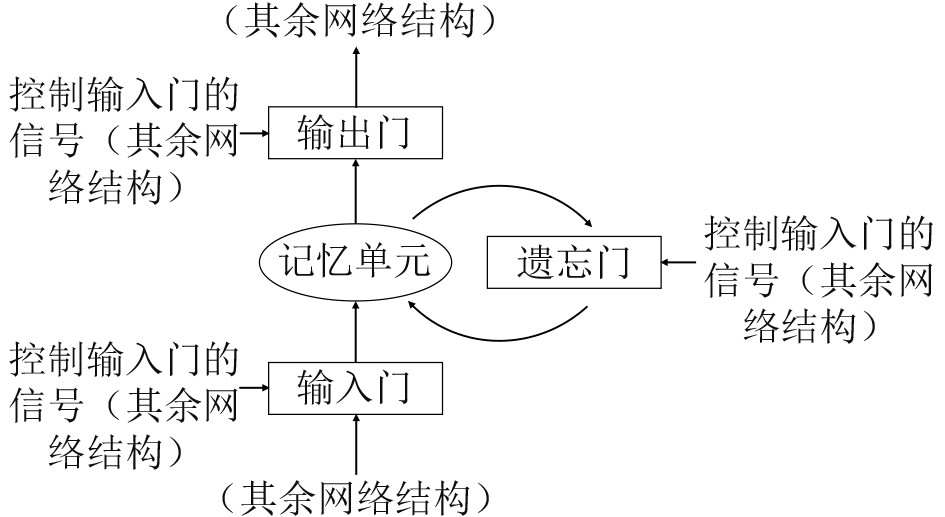
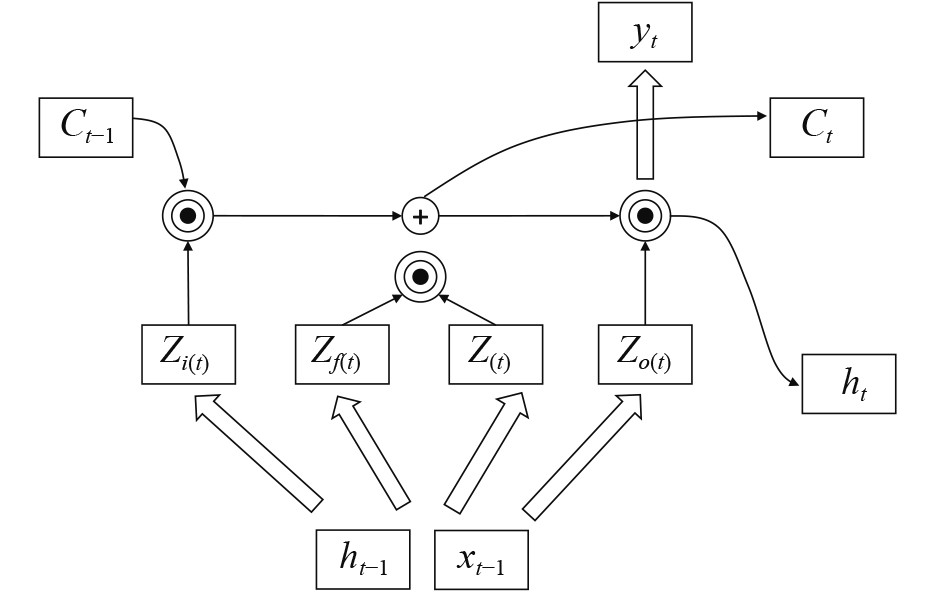
LSTM拥有3个门结构,分别是输入门、输出门和遗忘门,如图1所示,由这3种门来控制每一时刻信息的记忆与遗忘。输入层的信息首先要经过输入门,输入门开启才会有信息传递到记忆单元中;输出门开启时才会有信息从记忆单元传递出去;每一时刻记忆单元里面的信息都面临着是否被遗忘的选择,如果遗忘门开启,那么就会把记忆单元中的信息清除掉。LSTM的内部结构如图2所示。
|
图 1 LSTM门结构 Fig. 1 LSTM gate structure |
|
图 2 LSTM内部结构 Fig. 2 LSTM internal structure |
针对预测船舶运动姿态的问题,LSTM的输入同样是由海洋环境参数和船舶状态参数组成的向量,以时间戳为时间序列特征,与RNN不同的是,图2中的
| $ {Z_{(t)}} = \tanh \left( {\omega \left[ {{x_t},{h_{t - 1}}} \right] + b} \right) ,$ | (1) |
| $ {Z_{i(t)}} = \sigma \left( {{\omega _i}\left[ {{x_t},{h_{t - 1}}} \right] + {b_i}} \right),$ | (2) |
| $ {Z_{f(t)}} = \sigma \left( {{\omega _f}\left[ {{x_t},{h_{t - 1}}} \right] + {b_f}} \right),$ | (3) |
| $ {Z_{o(t)}} = \sigma \left( {{\omega _o}\left[ {{x_t},{h_{t - 1}}} \right] + {b_o}} \right),$ | (4) |
式中:
LSTM神经网络拥有2种记忆,一种是长记忆
| $ {C_t} = {Z_{f(t)}}{C_{t - 1}} + {Z_{i(t)}}{Z_{(t)}},$ | (5) |
| $ {h_t} = {Z_{o(t)}}\tanh \left( {{C_t}} \right) 。$ | (6) |
首先是遗忘阶段,主要是选择性地忘记上一个节点的输入。用计算得到的
本次使用的数据来源于天津大学海洋科学与技术学院,由实验人员操控无人艇在青年湖收集所得,使用的采集软件为Mission Planner,该无人艇搭载了与软件相配套的各类传感器,包括IMU、MAG、AHR2等,如图3所示。经提取筛选,最终获得了AHR2(内含Pitch、Roll、Yaw等3个姿态、经纬度和四元数[15])、IMU(内含3个角速度和加速度)等采集的共计19个参数。数据采集周期为20 ms,总数据量为

|
图 3 船舶姿态数据采集系统 Fig. 3 Ship attitude data acquisition system |
|
|
表 1 无人艇所采集数据的信息 Tab.1 Information about the data collected by the drone |
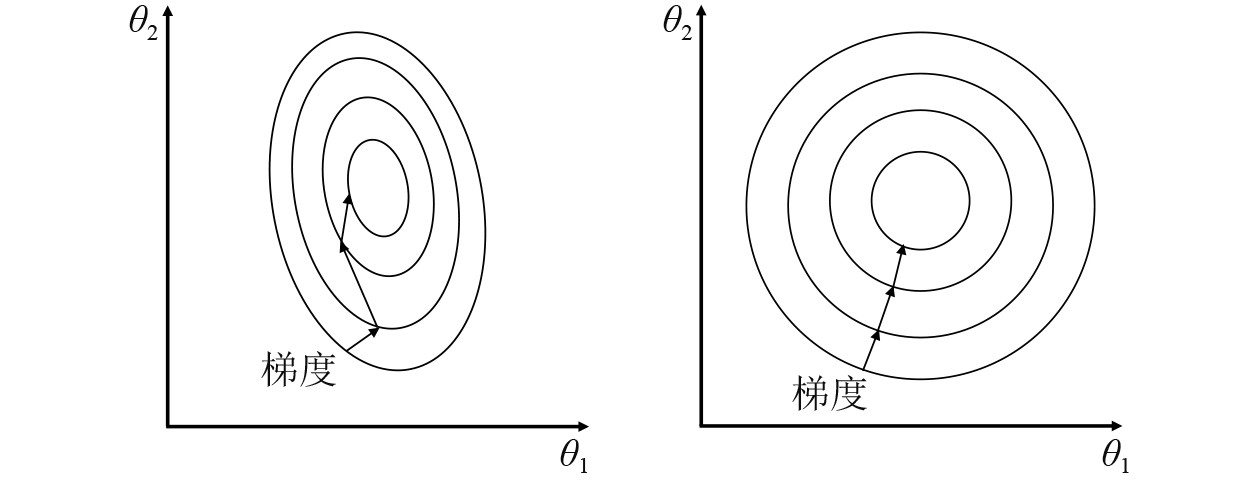
当数据具有多个特征属性且不同特征之间维数不同时,归一化可保证模型学习能力,在一定程度上提高模型精度。对于使用梯度下降法进行优化的模型,如果特征属性的量纲不是统一的,那么在寻求最优解时可以把当前的特征空间视为椭圆形,在每次迭代更新参数的时候,梯度下降的方向会呈现Z字形;在使用归一化方法之后,椭圆形的特征空间会变成近似圆形的空间,且梯度下降的方向一直是朝向圆心的,如图4所示。
|
图 4 归一化对梯度下降的影响 Fig. 4 Effect of normalization on gradient descent |
本文使用max-min归一化法,如式(7)所示。将数据线性地压缩到[0, 1]之间。在完成LSTM预测之后,再通过反归一化,即可得到预测数据的真实值。
| $ x = \frac{{{x_0} - \min }}{{\max - \min }}。$ | (7) |
式中:
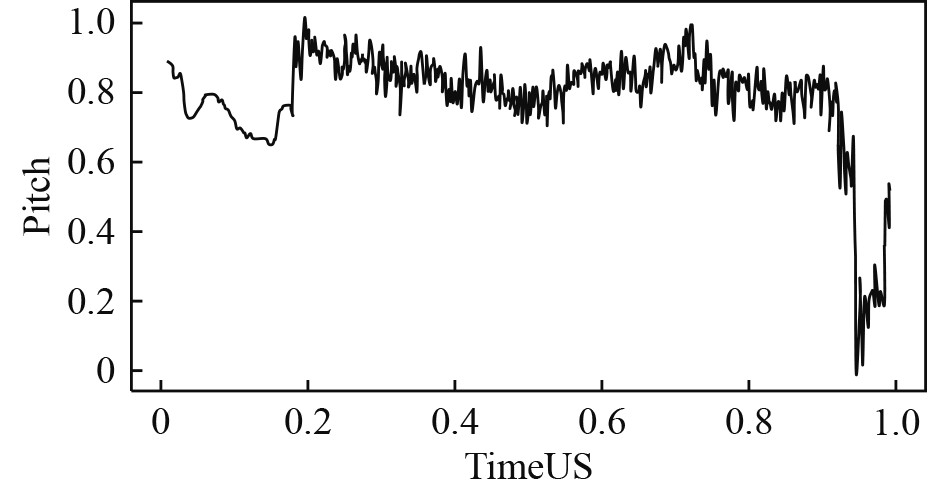
Savitzky-Golay滤波器[16]在1964年由Savitzky和Golay首次提出,这是一种基于时域局部多项式最小二乘拟合的滤波方法,广泛用于数据流平滑化和噪声去除。Python所自带的函数库中拥有该函数,该函数拥有滑窗宽度与拟合多项式阶数2个可调参数。归一化后的纵摇数据(Pitch)如图5所示,经过Savitzky-Golay滤波后的Pitch数据如图6所示,显然Savitzky-Golay滤波法有效去除了数据噪声。
|
图 5 Pitch原数据 Fig. 5 Pitch raw data |
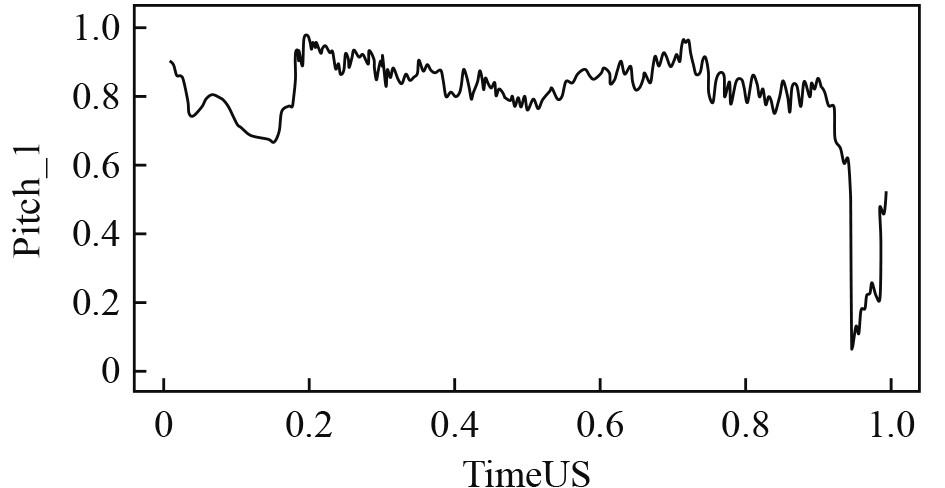
|
图 6 Pitch滤波数据 Fig. 6 Pitch filtering data |
通过计算特征重要性,可以评估作为输入特征对预测目标变量的有用性。特征重要性评估能够选择稳健的特征,减少待提取特征数量,同时还能够提高分类算法泛化能力,在预测建模过程中起着至关重要的作用。一个特征重要性接近于0的变量将不会被选择,特征选择后的数据集可以提高预测模型的效率和精度[17]。
对原数据进行Pitch的特征重要性计算,保留重要特征,把非重要特征所携带的干扰消除掉,以提高预测精度。得到的特征重要性计算结果如图7所示,可见在预测Pitch时,Q2、Q3、TimeUS、Roll、T等5个参数的重要性较高。
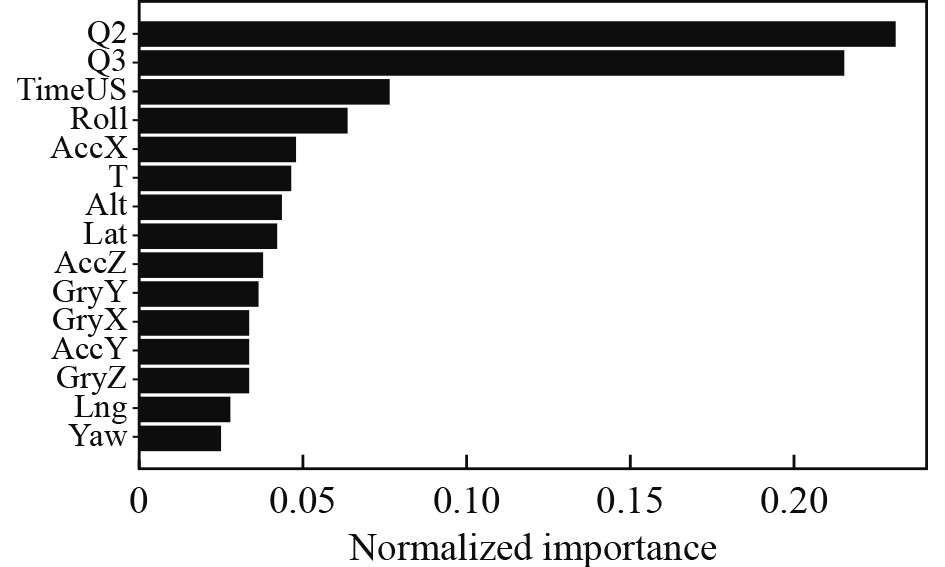
|
图 7 Pitch的特征重要性分析 Fig. 7 Characteristic importance analysis of pitch |
1)RMSE
均方根误差反映了预测值和真实值之间的偏差。如果预测值与真实值相差较大,则RMSE会较大;RMSE越小,代表模型预测准确度越好。其计算公式为:
| $ RMS E = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^n {{{({Y_i} - f({x_i}))}^2}} } $ | (8) |
式中:
2)R-squared
R-squared是衡量模型拟合度的量,取值范围通常为0~1,表示输入变量对输出变量的解释程度。R-squared越接近1,说明模型的拟合程度越高。
3.2 单自由度预测经过筛选处理,采集数据中可供使用的参数除了时间戳和统计时间外共有19个,其中的Roll(横摇)、Pitch(纵摇)、Yaw(首摇)是预测目标参数。以Pitch为例,说明所构建的LSTM神经网络预测模型对船舶运动状态的预测效果。使用除时间戳、统计时间和Pitch自身之外的其余18个参数对Pitch参数进行预测。对LSTM神经网络模型的设置如下:
1)训练集和测试集分别占总数据集的80%和20%;
2)进行批数据处理时每128个数据为一个批数据;
3)序列长度设置为10;
4)神经网络结构为3层LSTM、1层Dropout和1层Dense。
通过LSTM神经网络直接进行预测所得结果如图8所示。
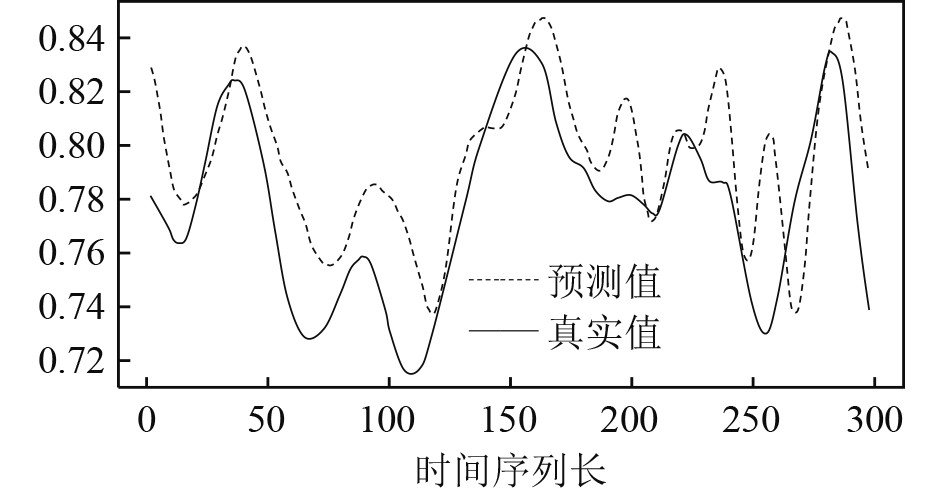
|
图 8 原数据预测结果 Fig. 8 Raw data predicted results |
横轴代表模型向后预测的序列长度,单位间隔20 ms,图中是向后预测了300个单位长度的时间序列,也就是15 s,纵轴代表归一化后的Pitch的真值和预测值的范围。模型预测精度为R-squared=
分别设定阈值为0.02、0.03、0.05、0.07、0.2对原数据进行特征重要性筛选,将筛选后的数据集重新用于预测并与原数据集得到的预测结果作比较。图9是原数据集(以阈值为0表示)和经过各阈值特征筛选后得到的模型预测结果。

|
图 9 预测精度与特征选择阈值的关系 Fig. 9 Relationship between prediction accuracy and feature selection threshold |
可知,R-squared值随着特征筛选阈值的增加呈现出先上升后降低的趋势,R-squared值越接近1说明模型拟合程度就越好,特征筛选阈值设定为0.05时,模型精度达到最高为R-squared=
将原数据与最佳特征选择数据的预测结果进行对比,如图10所示。可以看出,通过特征选择之后的对Pitch未来300个时间序列长度的预测效果明显更加拟合其真实值,说明特征选择方法剔除了无用数据和干扰项,提高了LSTM神经网络模型的预测精度。
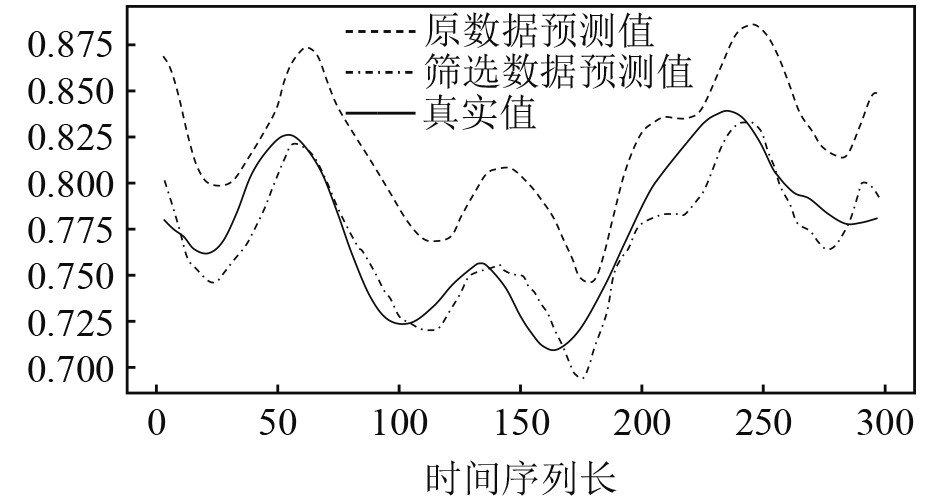
|
图 10 原数据与特征选择数据预测效果对比 Fig. 10 Comparison of prediction effect between raw data and feature selection data |
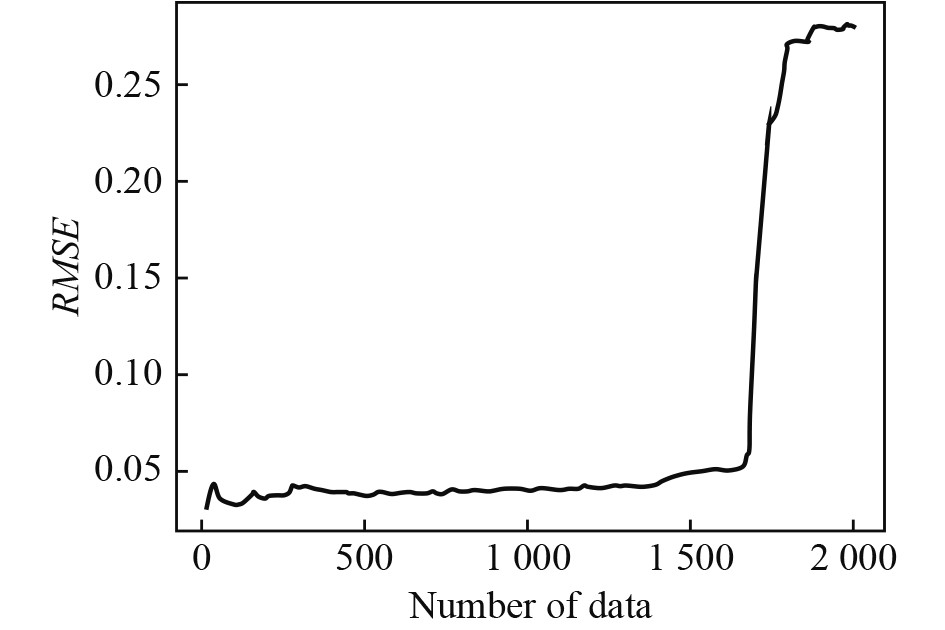
进行三自由度预测时,将预测所用的训练集改为不含Pitch、Roll、Yaw的数据集。使用LSTM神经网络模型同时预测3个自由度的船舶姿态,计算其均方根误差,以20个单位长度的时间序列为间隔,依次计算前20~
|
图 11 RSME与时间序列长度的关系 Fig. 11 Relationship between RSME and time series length |
可以看到,预测的时间序列长度小于
本文采用将LSTM神经网络和特征选择相结合的方法,系统研究了船舶运动状态的预测问题,并认识到在LSTM具有一定预测精度的条件下,通过加入特征选择能够提高LSTM神经网络的预测精度。
在单自由度的船舶姿态预测时,通过特征选择计算特征重要性,确定能够达到最好预测效果的特征,具有不同特征数量的数据集通过LSTM神经网络得到对应的预测结果和精度,对比得到预测精度最好的情况是与特征重要性所给出的特征相吻合。当具有很多低重要性的特征时,预测受到无贡献特征的干扰导致预测结果不好;当有一定贡献的特征被删除时,其所含有的与预测特征之间的隐含信息也不能被神经网络挖掘出来也会导致预测结果的下降。通过特征选择的LSTM神经网络能够把船舶的姿态预测精度提高,证明了本文所进行的研究是可行的。
| [1] |
蒋银, 朱仁传, 缪国平, 等. 三维船体横摇运动数值模拟及舭龙骨阻尼特性研究[J]. 船舶力学, 2020, 24(6): 706-719. JIANG Yin, ZHU Renchuan, MIAO Guoping, et al. Numerical simulation of three-dimensional hull roll motion and study on bilge keel damping characteristics[J]. Journal of Ship Mechanics, 2020, 24(6): 706-719. DOI:10.3969/j.issn.1007-7294.2020.06.002 |
| [2] |
阮光维. 船舶减摇鳍系统的控制方法研究[D]. 大连: 大连海事大学, 2020.
|
| [3] |
张文杰. 基于深度学习的无人艇运动姿态预报[D]. 上海: 上海大学, 2020.
|
| [4] |
谷达京, 施哲源, 陈根良, 等. 基于神经网络的船体运动位姿预测方法[J]. 舰船科学技术, 2022, 44(15): 55-59. GU Dajing, SHI Zheyuan, CHEN Genliang, et al. A method of hull motion posture prediction based on neural network[J]. Ship Science and Technology, 2022, 44(15): 55-59. DOI:10.3404/j.issn.1672-7649.2022.15.012 |
| [5] |
周佳宇, 韩俊庆, 李伟, 等. 基于扩张状态卡尔曼原理的海浪滤波算法[J]. 舰船科学技术, 2023, 45(7): 62-65. ZHOU Jiayu, HAN Junqing, LI Wei, et al. Wave filtering algorithm based on extended state Kalman principle[J]. Ship Science and Technology, 2023, 45(7): 62-65. DOI:10.3404/j.issn.1672-7649.2023.07.013 |
| [6] |
李娜, 郑少智. 平滑转移自回归模型及其应用[J]. 统计与决策, 2018, 34(10): 24-28. LI Na, ZHENG Shaozhi. Smooth transfer autoregressive model and its application[J]. Statistics and Decision, 2018, 34(10): 24-28. |
| [7] |
SHEN C, ZHANG Y, GUO X, et al. Seamless GPS/inertial navigation system based on self-learning square-root cubature Kalman filter [J]. Transactions on Indastrial Electronics, 2020, 68(1): 499–508.
|
| [8] |
GE Yang, QIN Mingjie, NIU Qingtao. Prediction of ship motion attitude based on BP network [C]//2017 29th Chinese Control And Decision Conference (CCDC), 2017: 1596−1600.
|
| [9] |
王国栋. 基于LSTM的舰船运动姿态短期预测及仿真研究[D]. 镇江: 江苏科技大学, 2017.
|
| [10] |
徐国庆, 马建文, 吴晨辉, 等. 基于Attenton-LSTM神经网络的船舶航行预测[J]. 舰船科学技术, 2019, 41(23): 177-180. XU Guoqing, MA Jianwen, WU Chenhui, et al. Ship navigation prediction based on attenton-LSTM neural network[J]. Ship Science and Technology, 2019, 41(23): 177-180. DOI:10.3404/j.issn.1672-7649.2019.12.034 |
| [11] |
王研婷. 基于CNN和LSTM的船舶航迹预测[D]. 大连: 大连海事大学, 2020.
|
| [12] |
刘姗姗, 马社祥, 孟鑫, 等. 基于CNN和Bi-LSTM的船舶航迹预测[J]. 重庆理工大学学报(自然科学), 2020, 34(12): 196-205. LIU Shanshan, MA Shexiang, MENG Xin, et al. Ship track prediction based on CNN and Bi-LSTM[J]. Journal of Chongqing University of Technology (Natural Sciences), 2020, 34(12): 196-205. |
| [13] |
王文标, 董贵平, 汪思源, 等. 基于CEEMD-PSO-MNN的船舶航迹预测[J]. 电子器件, 2021, 44(1): 119-124. WANG Wenbiao, DONG Guiping, WANG Siyuan, et al. Ship track prediction based on CEEMD-PSO-MNN[J]. Electronic Device, 2021, 44(1): 119-124. DOI:10.3969/j.issn.1005-9490.2021.01.023 |
| [14] |
王余宽, 谢新连, 马昊, 等. 基于滑动窗口LSTM网络的船舶航迹预测[J]. 上海海事大学学报, 2022, 43(1): 14-22. WANG Yukuan, XIE Xinlian, MA Hao, et al. Ship track prediction based on sliding window LSTM network[J]. Journal of Shanghai Maritime University, 2022, 43(1): 14-22. |
| [15] |
石宇芃, 马宏军, 陈豹. 基于四元数的四旋翼无人机扩展卡尔曼滤波算法[J]. 控制工程, 2021, 28(11): 2131-2135. SHI Yufan, MA Hongjun, CHEN Bao. Extended Kalman filtering algorithm for four-rotor UAV based on quaternion[J]. Control Engineering, 2021, 28(11): 2131-2135. |
| [16] |
周增光, 唐娉. 基于质量权重的Savitzky-Golay时间序列滤波方法[J]. 遥感技术与应用, 2013, 28(2): 232-239. ZHOU Zengguang, TANG Pin. Savitzky-Golay time series filtering method based on mass weights[J]. Remote Sensing Technology and Application, 2013, 28(2): 232-239. |
| [17] |
OH Sejong. Predictive case-based feature importance and interaction[J]. Information Sciences, 2022, 593.
|
 2024, Vol. 46
2024, Vol. 46
