0 引　言

我国近岛礁自然地理条件非常复杂^{[1 - 3]}，海底地质大多为沙质，水下地形相对平缓，吃水较浅，且水深变化剧烈，船舶吃水靠岸困难^[4]，而箱式平台能很好地解决这一难题。

目前，国内外对平台的水动力性能多集中于未受相邻船舶水动力干扰下的情况。Newman^[5]基于模态展开法研究了铰接双浮体运动响应特性，使得系统自由度大为减少。孙昭晨等^[6] 利用Lagrange方程求解了铰接多浮体在波浪下的运动响应，与实验结果对比，验证了分析方法的有效性。Diamantoulaki^[7]采用Newman的方法研究了入射波频率以及浮体个数对铰接多浮体系统运动响应的影响，研究发现，铰接浮体阵列配置对多体系统运动响应影响显著。Tajali等^[8]应用总模态法探究了不同吃水深度、有无系泊缆索等条件下铰接多浮体系统的运动响应特性，结果表明，浮体的运动响应很大程度上取决于浮体的尺寸和连接件的刚度特性。丁红岩等^[9]研究了四筒型基础平台在静水、顺浪和逆浪中的拖航特性，试验结果表明，平台拖航过程遇到大浪情况下，降低拖航速度是保证结构耐波性和稳性的有效方法。王桂波等^[10]基于线性势流理论，利用模态法在频域内研究了铰接多浮体结构在规则波作用下的运动响应，并以3个铰接的箱型浮体为例，讨论了水深、铰接位置对结构运动响应的影响。Ghafari等^[11]研究了Amirkabir平台和FPSO在里海条件下的耦合水动力特性，数值结果表明，随着平台的靠近，半潜式平台的运动和系泊缆张力的振荡值都会减小。此外，波长的增加会导致半潜式平台的运动加剧。孙建群等^[12]通过水动力模型试验对多模块铰接浮桥在规则波作用下的水动力响应和弯矩分布进行了研究，并基于水动力学理论对浮桥的弯矩和运动响应进行了分析。

国内外对系泊状态和拖曳状态下平台的水动力分析问题已有较为系统的研究，但是对在拖航船水动力干扰下的多模块拼组箱式平台的水动力特性尚无深入认识。拖航船拖航多模块拼组箱式平台时因彼此间的距离较小，水动力作用明显，对于箱式平台的水动力响应产生较大的影响。基于此，本文采用Ansys软件中的AWQA水动力模块，基于三维势流理论，系统开展了拖航船和多模块拼组箱式平台耦合模型在不同波浪周期的规则波工况和不同海况的不规则波工况下的运动、载荷、缆绳张力等响应特性分析。通过对拖航船和多模块拼组箱式平台耦合模型的水动力特性分析，为波浪工况下箱式平台的实际作业提供技术参考。

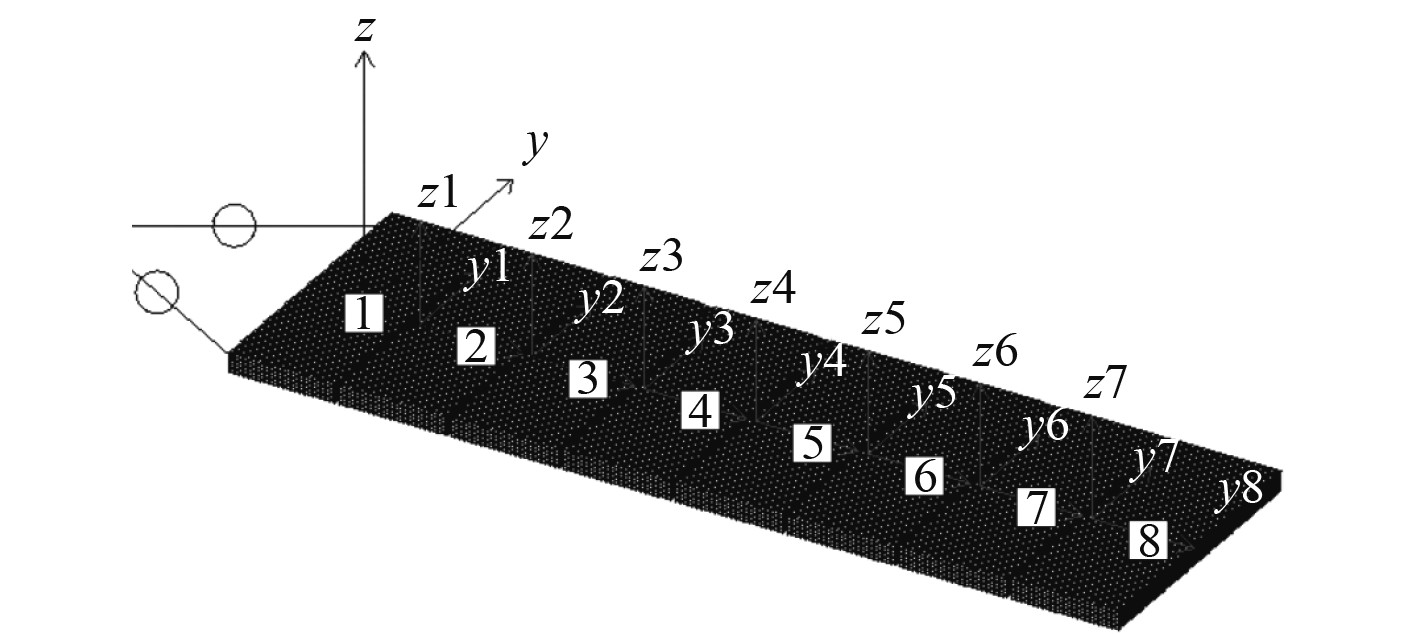
1 模型参数及模拟工况 1.1 箱式平台的模型和参数

建立模型时，先对坐标系进行定义：X轴沿箱式平台纵向延伸，Y轴为箱式平台侧壁方向，Z轴正向为竖直向上，平台系统由8个箱式保障平台组成，从前到后依次为1～8号箱式平台，原点位于1号箱式平台水线面中心。利用Ansys的APDL模块建立单个箱式平台的湿表面模型，导入AQWA后，复制出8个箱式平台，并建立拖航缆绳以及平台间的铰接，在水动力模型通过约束方程来实现平台间的铰接。每个平台上可放置方舱或拖运物资，相邻保障平台间距为0.2 m。水动力分析模型如图1所示，平台主要参数见表1。

1.2 拖航船参数

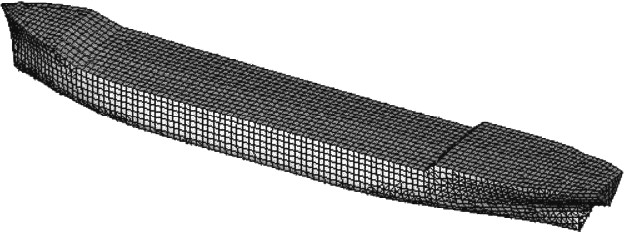
拖航船对采用整体拖运的方式对多模块拼组平台进行拖运，拖曳速度为2.57 m/s。拖航船的水动力分析模型如图2所示，拖航船的主尺度参数见表2。

1.3 缆绳参数

在箱式平台拖曳过程中，拖航船和箱式（第1个）保障平台之间通过2根缆绳相连，每根缆绳长10 m，缆绳与箱式平台成60°。缆绳采用的是纤维牵引绳，缆绳参数见表3。

1.4 连接件参数

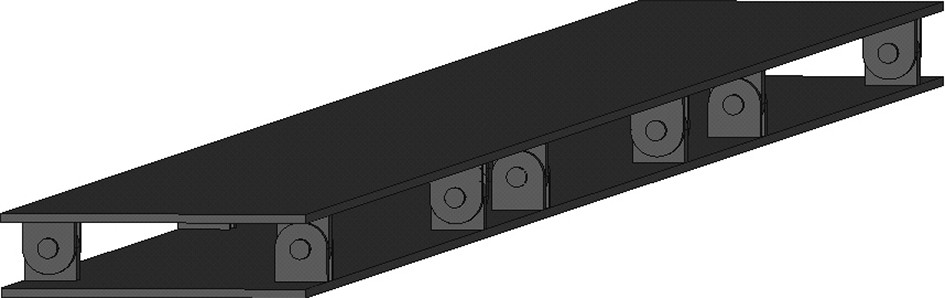
相邻箱式保障平台之间通过铰接连接件相连。每个箱式平台之间的铰接连接件共有6组，每组2个。连接件及其连接相邻箱式平台部分模型三维图如图3所示。铰接连接件采用高强度钢材料，其材料属性见表4。

在水动力软件AWQA中，铰接连接件的铰接刚度、阻尼和摩擦可以针对所有相关的铰接类型来定义。由于关节只允许旋转运动，因此只需要输入旋转刚度、阻尼和摩擦。这些是相对于局部铰接轴定义的。

要定义任何铰接刚度，输入值应具有每弧度的力矩单位。在局部铰接轴上作用在第j个结构上的相应恢复力矩为：

$ {{\boldsymbol{M}}_{js}} = - \left[ {\begin{array}{*{20}{c}} {{k_1}}&0&0 \\ 0&{{k_2}}&0 \\ 0&0&{{k_3}} \end{array}} \right]\left[ {0,{{\boldsymbol{G}}^{\mathrm{T}}}} \right]\left[ {{{\boldsymbol{U}}_j} - {{\boldsymbol{U}}_k}} \right]。$

(1)

式中：$ {k_m} $为沿局部关节轴的相对旋转的刚度系数，是一个3×6矩阵。

将$ {c_m} $表示为沿局部铰接轴的相对旋转的阻尼系数，由作用在该局部轴系统中的第$ j $个结构上的铰接阻尼引起的力矩类似地表示为：

$ {{\boldsymbol{M}}_{jd}} = - \left[ {\begin{array}{*{20}{c}} {{c_1}}&0&0 \\ 0&{{c_2}}&0 \\ 0&0&{{c_3}} \end{array}} \right]\left[ {0,{{\boldsymbol{G}}^{\mathrm{T}}}} \right]\left[ {{{\mathop {\boldsymbol{U}}\limits^. }_j} - {{\mathop {\boldsymbol{U}}\limits^. }_k}} \right]。$

(2)

摩擦可以在时域分析中任意定义，并且始终使用局部右手轴系统$ A{x^{'}}{y^{'}}{z^{'}} $（其中$ {x^{'}} $轴与2个铰接结构的瞬时相对旋转速度方向对齐）。摩擦力矩为：

$ {F_k}{M_f} = \varepsilon \left[ {{f_1} \sqrt {F_{{y^\prime }}^2 + F_{{z^\prime }}^2} + {f_2} \sqrt {M_{{y^\prime }}^2 + M_{{z^\prime }}^2} + {f_3}{F_{{\chi ^\prime }}} + {f_4}} \right]。$

(3)

一旦计算出该摩擦力矩，它将被转换为局部铰接轴、局部结构轴或固定参考轴。

为了计算铰接结构的运动和反作用力，应将式(1)～式(3)中表达的铰接刚度、阻尼和摩擦力矩转换为固定参考轴，然后将其换算为式(4)，即2个连接结构的反作用力和力矩的运动为：

$ \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{K}}_{jj}}}&{{{\boldsymbol{K}}_{jk}}}&{ - {\boldsymbol{H}}_j^{\text{T}}} \\ {{{\boldsymbol{K}}_{kj}}}&{{{\boldsymbol{K}}_{kk}}}&{{\boldsymbol{H}}_k^{\text{T}}} \\ {{{\boldsymbol{H}}_j}}&{ - {{\boldsymbol{H}}_k}}&{\boldsymbol{0}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{U}}_j}} \\ {{{\boldsymbol{U}}_k}} \\ {{{\boldsymbol{R}}_C}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{F}}_j}} \\ {{{\boldsymbol{F}}_k}} \\ 0 \end{array}} \right] 。$

(4)

式中：$ {F_j} $和$ {F_k} $分别为作用在第j个和第k个结构上的力和力矩（不包括反作用力分量）。

1.5 海洋环境条件

多模块拼组箱式平台布置于近岛礁的礁盘区域，考虑海域中风、浪、流的作用。根据典型海况，风速取高出海平面10 m处，平均风速为10 m/s；结合箱式平台布置区域的相关资料，平台附近水域表面流速为0.4 m/s；综合考虑后采用Jonswap谱来拟合设计规则波工况和不规则波工况，风、浪、流的入射角为0°。规则波工况的环境工况参数如表5所示，不规则波工况的环境工况参数如表6所示。

2 计算结果分析 2.1 网格无关性验证

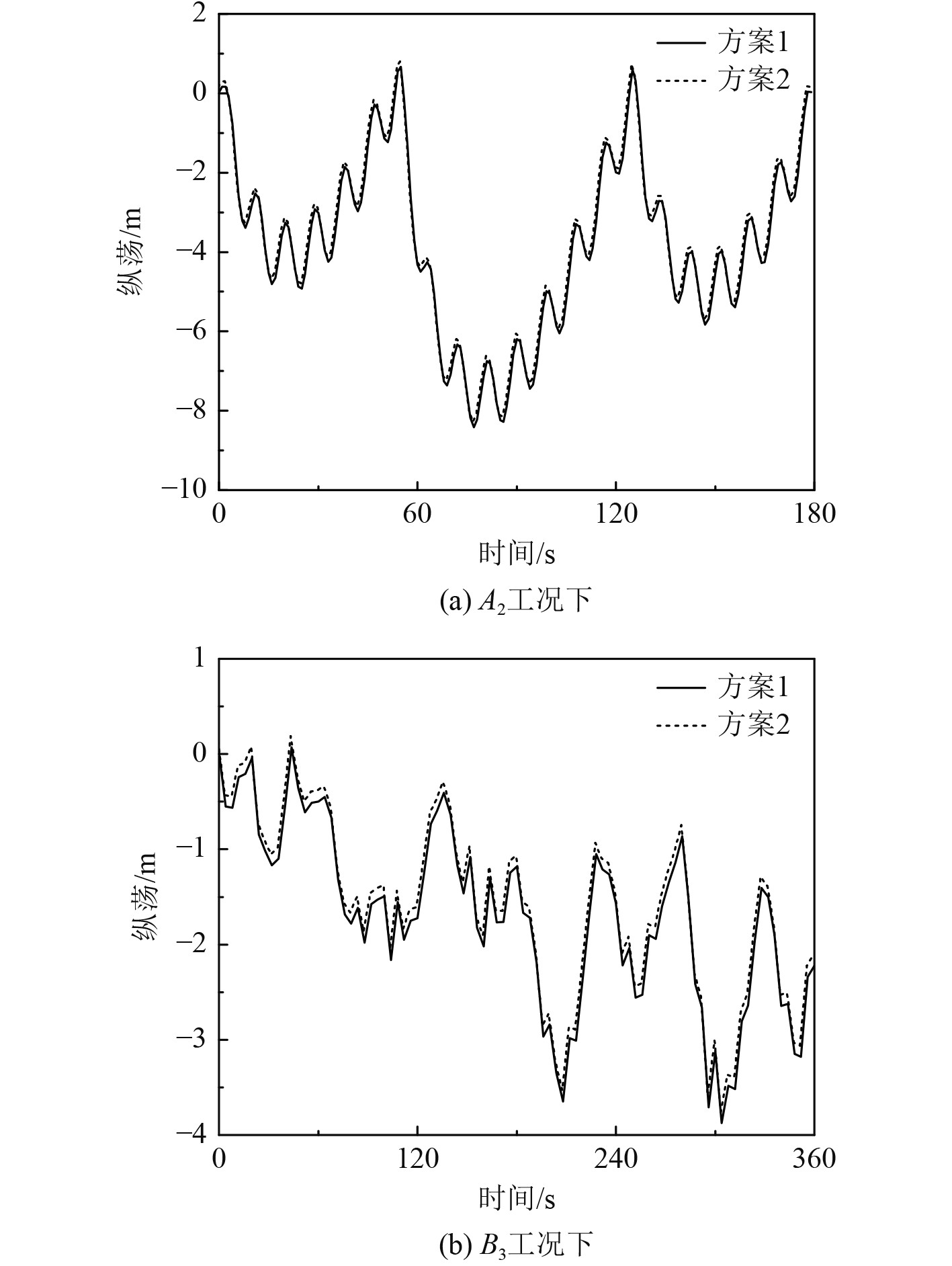
在进行水动力分析之前，为了验证网格的无关性，对拖航船和多模块拼组箱式平台的耦合模型划分为不同密度的网格。方案1是原设定方案，最小网格尺寸为0.1 m的水动力模型；方案2最小网格尺寸为0.05 m的有限元模型。在2种不同网格划分下，选取相同的工况，分别对其进行水动力性能数值分析。由图4可知：2种网格划分下的纵荡运动变化趋势以及具体数值基本一致，满足网格无关性要求。

2.2 箱式平台运动响应计算结果与分析

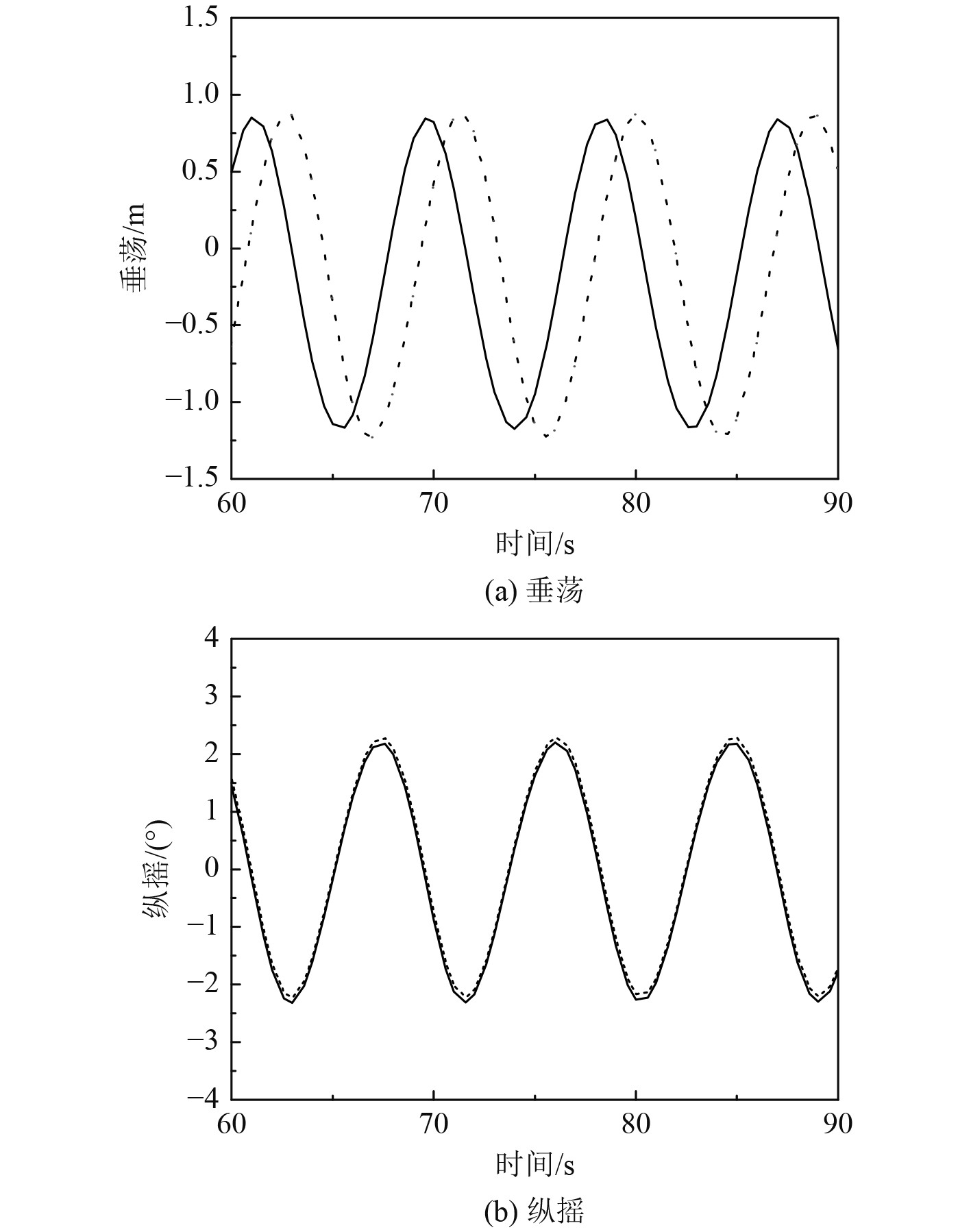
对多模块拼组箱式平台运动响应的计算采用时域方法进行，在规则波和不规则波各3个工况下进行计算，规则波工况计算时长为360 s，不规则波工况计算时长为3600 s。由图5和图6可知：在缆绳拖曳箱式平台的过程中，多模块拼组箱式平台左右两模块运动协调，基本保持一致。

箱式平台最大运动响应统计结果如表7所示。可知：在规则波工况中，平台垂荡运动随波浪周期递增表现往复振荡的特点，当波长周期等于8.00 s时，1号平台垂荡运动响应最为剧烈，垂荡最大值为0.8858 m，当波长周期等于9.00 s时，8号平台垂荡运动响应最为剧烈，垂荡最大值为1.0900 m；平台纵摇运动随波浪周期递增基本表现递减趋势，当波长周期等于8.00 s时，平台运动纵摇响应最为剧烈，1号平台和8号平台纵摇最大值为2.680°。不规则波工况中平台运动响应特性随海洋环境的恶化越发趋于剧烈，即B3工况下，平台运动最为剧烈，其中1号平台垂荡最大值为0.7814 m，纵摇最大值为3.459°；8号平台垂荡最大值为0.7139 m，纵摇最大值为3.460°。1号平台垂荡运动响应最为剧烈，垂荡最大值为0.8858 m，当波长周期等于9.00 s时，8号平台垂荡运动响应最为剧烈，垂荡最大值为1.0900 m；平台纵摇运动随波浪周期递增基本表现递减趋势，当波长周期等于8.00 s时，平台运动纵摇响应最为剧烈，1号平台和8号平台纵摇最大值为2.680°。不规则波工况中平台运动响应特性随海洋环境的恶化越发趋于剧烈，即B₃工况下，平台运动最为剧烈，其中1号平台垂荡最大值为0.7814 m，纵摇最大值为3.459°；8号平台垂荡最大值为0.7139 m，纵摇最大值为3.460°。

2.3 箱式平台缆绳张力计算结果与分析

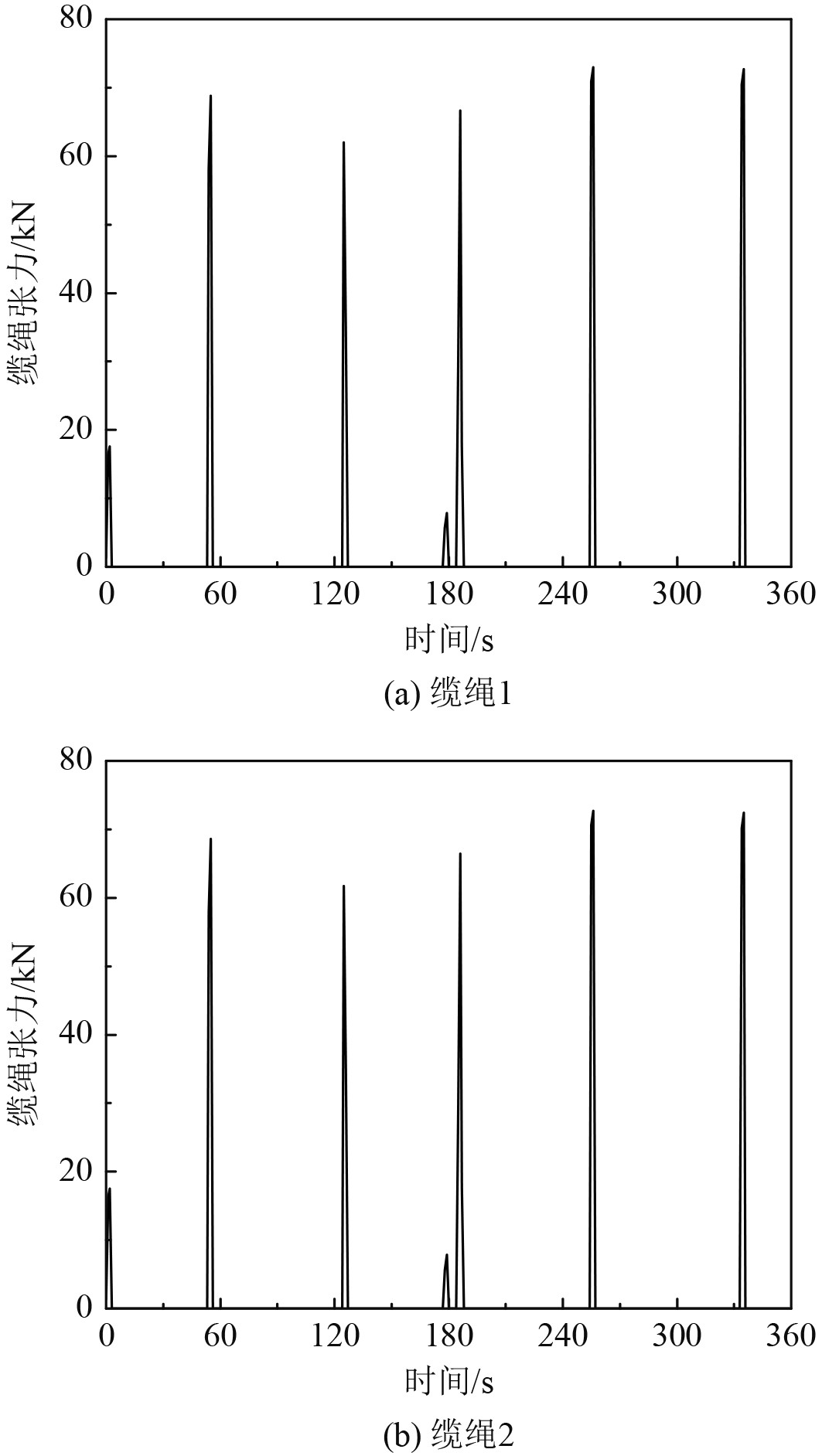
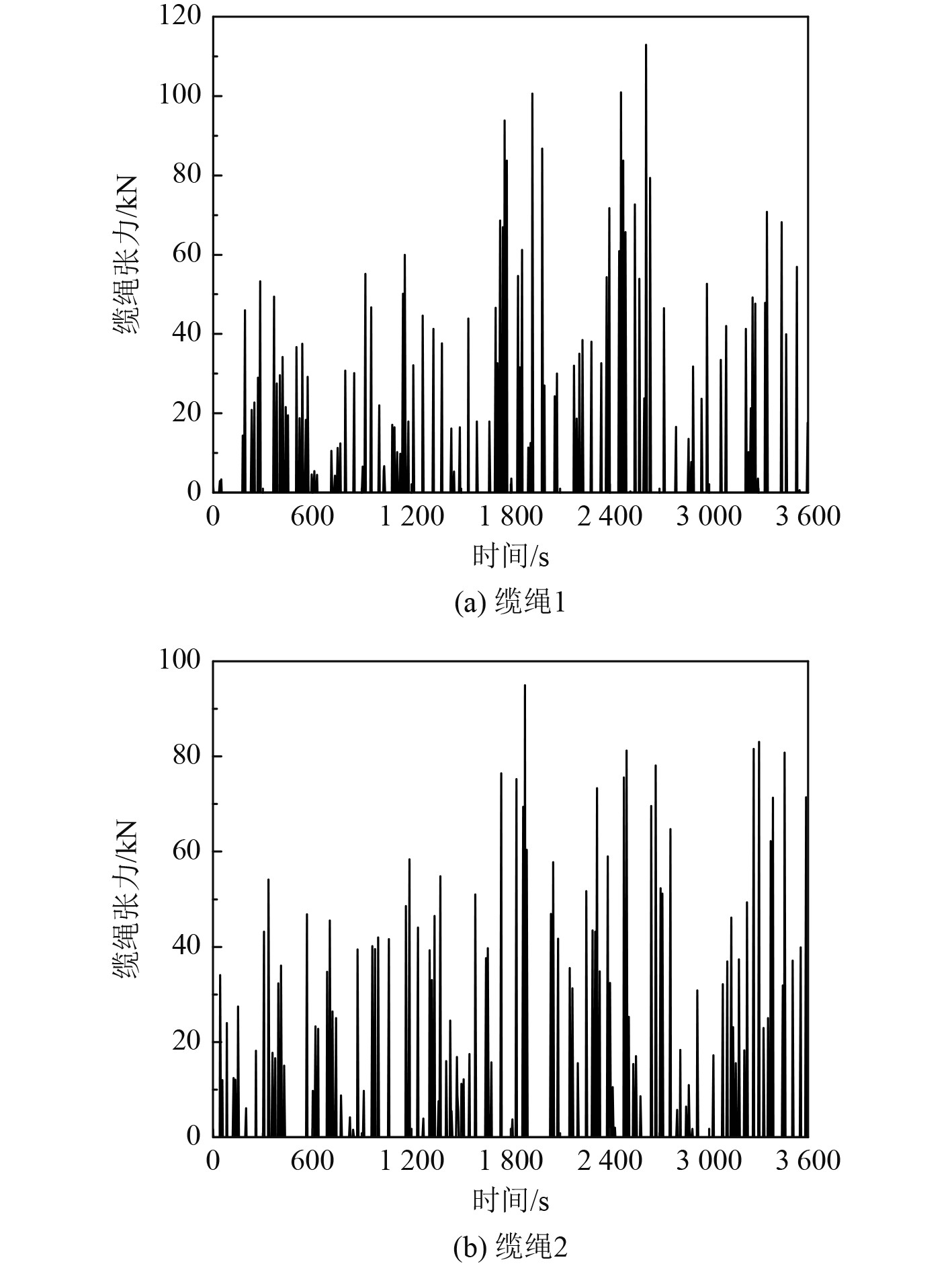
多模块拼组箱式平台的缆绳张力计算分析与平台的运动响应计算同样在时域进行。由图7和图8可知，缆绳1和缆绳2张力变化趋势具有良好的一致性，由于不规则波工况更加复杂，缆绳张力的大小随时间的变化更加频繁。在A₂工况下，箱式平台缆绳1的最大张力为73.0 kN，缆绳2的最大张力为72.7 kN；B₃工况下，箱式平台缆绳1的最大张力为113 kN，缆绳2的最大张力为95 kN。

箱式平台最大缆绳张力统计结果如表8所示。可知：在规则波工况中，单位波幅下，随着周期的增大，拖曳缆绳张力总体表现增大的趋势，缆绳1的最大张力为94.7 kN，缆绳2的最大张力为94.4 kN；在不规则波工况中，拖曳缆绳张力随着海况等级的增加总体表现增大的趋势，缆绳1的最大张力为113 kN，缆绳2的最大张力为95 kN，均小于缆绳的破断强度，满足使用要求。

2.4 中剖面载荷计算结果与分析

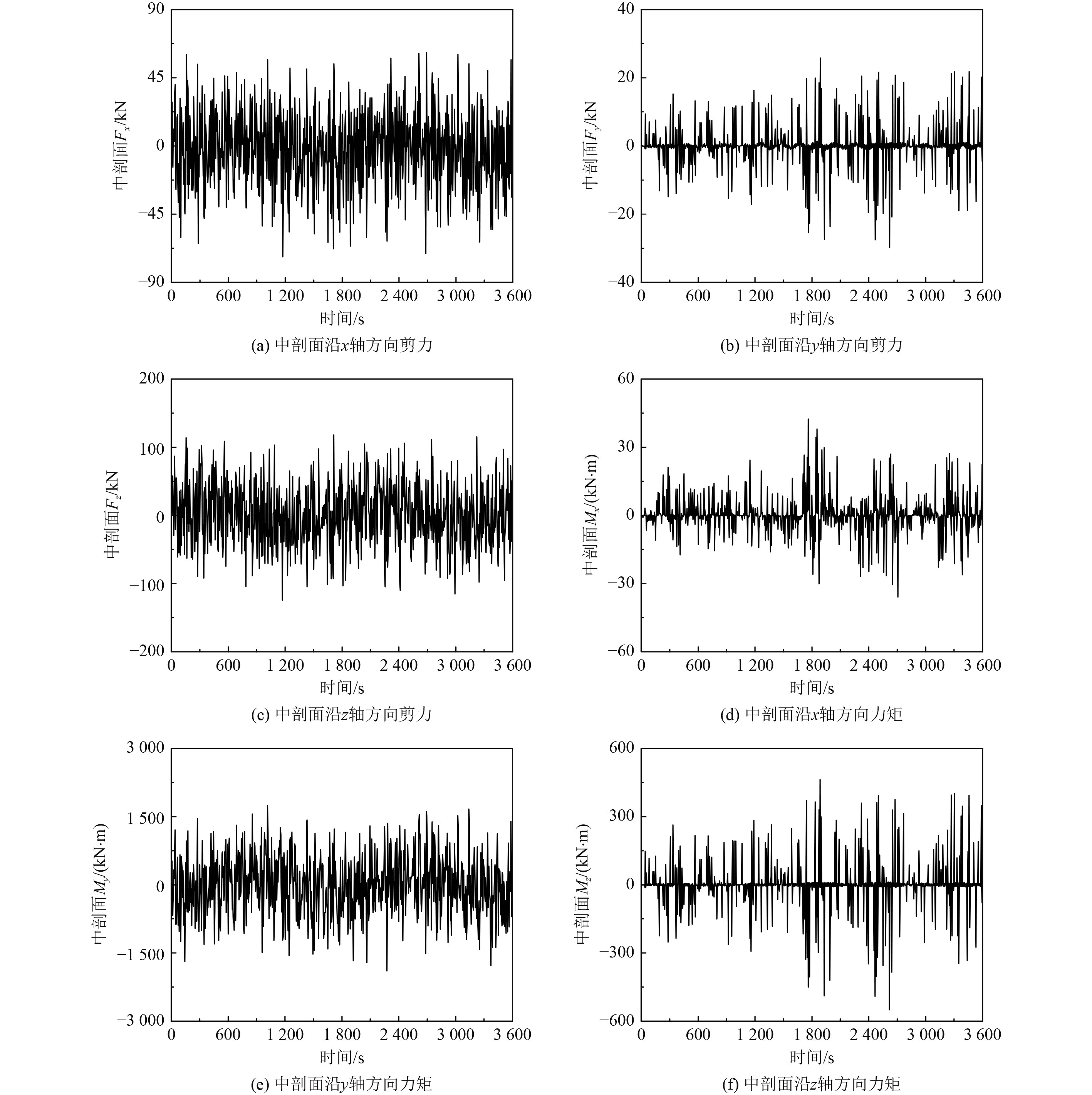
由图9可知，在B₃工况下，中剖面${F_x}$最大值为61.6 kN，中剖面${F_y}$最大值为25.8 kN，中剖面${F_z}$最大值为118 kN，中剖面${M_x}$最大值为42.4 kN·m，中剖面${M_y}$最大值为1750 kN·m，中剖面${M_z}$最大值为463 kN·m。

作业工况下箱式平台最大中剖面载荷统计结果如表9所示。可知：中剖面${F_z}$大于${F_x}$和${F_y}$，${M_y}$大于${M_x}$和${M_z}$。在规则波工况中，单位波幅下，随着周期的增大，中剖面受力和弯矩总体表现下降的趋势，中剖面剪力最大为97.2 kN，弯矩最大为512 kN·m；在不规则波工况中，中剖面受力和弯矩随着波浪等级的增加呈现递增的趋势，中剖面剪力最大为118 kN，弯矩最大为1750 kN·m。

3 结　语

本文针对拖航船和多模块拼组箱式平台的耦合模型，采用Ansys软件中的AQWA 模块，对该平台的水动力性能进行数值模拟。主要结论如下：

1）箱式平台左右两模块运动协调，基本保持一致；

2）在规则波工况中，平台垂荡运动最大值随波浪周期递增表现往复振荡的特点，纵摇运动最大值随波浪周期递增整体呈递减趋势；

3）在规则波工况中，随着周期的增大，拖曳缆绳张力整体呈现增大趋势，中剖面剪力和弯矩整体呈现下降的趋势；不规则波工况中，拖曳缆绳张力，中剖面的剪力和弯矩随着海况等级的增加整体呈现增大的趋势；

4）通过对拖航船水动力干扰下箱式平台的水动力分析，数值结果更加贴合箱式平台的实际工况环境，可为实际作业中拖航作用下箱式平台的水动力特性计算提供基准数据，推动箱式平台设计理论的发展。