螺旋桨激励力是船舶振动的主要激励源之一,挪威船级社对多艘船上层建筑振动问题的研究结果表明[1],在所有振源中,螺旋桨占据了约80%。螺旋桨转动时经水传至船体表面的脉动水压力称为螺旋桨脉动压力[2],其沿船体表面的积分值称为表面力。对于某些船,脉动压力是引起船体尾部和上层建筑振动的主要原因[3],尤其需要注意。目前在设计阶段评估脉动压力主要通过经验公式、数值计算以及模型试验。经验公式是在大量实船和模型试验的基础上,采用理论数值分析和统计回归方法得到的,通常只适用于特定尾型的船舶,其精度较低,有一定的局限性。王蒙蒙[4]提出3种脉动压力的计算模型并预报了某多用途船的脉动压力,并与空泡水池中的实验值进行了比较,结果比较接近。阳涛等[5]采用数值方法对某双尾科船的螺旋桨诱导的脉动压力进行预报,并与试验值进行对比,吻合较好。但由于产生空泡这一物理现象的复杂性,理论预报和数值计算都存在着许多不足之处,最终的预报结果还是需要空泡试验结果来验证,所以在船舶设计中,螺旋桨的空泡试验必不可少,目前这已是一项比较成熟的技术。
将模型试验获得螺旋桨的脉动压力作为船体振动的载荷输入,然后建立全船或部分有限元模型,进而计算船体结构的受迫振动,这是目前常规的船体振动响应求解方法。随着规范对船舶舒适性要求的越来越高,船体振动问题也越来越受到重视,如何合理施加脉动压力,已成为一项重要的研究内容。
陈翔等[6]在散货船上对不同的螺旋桨激励力的施加方法进行比较研究,计算其尾部及上层建筑的强迫振动响应,但采用的脉动压力来源于经验公式,没有考虑脉动压力的不同成分加以施加。殷玉梅[7]、秦升杰等[8]采用CFD计算获得了某船螺旋桨的脉动压力,然后加载在螺旋桨上方一定区域进行频响分析。
综上,目前振动计算考虑的脉动压力一般为总压力值,无论是来源于经验公式或者数值模拟,很少有学者将空泡压力部分单独剥离出来进行施加,究其原因是空泡压力产生的机理比较复杂,数值模拟较为困难。本文介绍一种脉动压力的新型加载方法,根据模型试验结果,考虑了脉动压力中空泡压力和非空泡压力的不同成分和分布规律,通过理论模型分析,求解出由空泡产生的脉动压力部分,然后将空泡引起的压力和非空泡引起的压力,在不同转速下进行线性叠加,得到宽频范围内脉动压力施加的新方法。
1 脉动压力的分布规律国内外众多学者对脉动压力的求解和分布规律已经作了详细的研究,其中有理论和数值预报,也有模型试验,研究结果揭示了脉动压力在船体表面的分布和变化规律,文献[5,8]中描述,螺旋桨最大脉动压力分别发生在桨盘面前方0.1D(D为螺旋桨直径)处以及桨轴心线右侧0.05D 处,然后衰减,即脉动压力是随着船长和船宽非线性变化的一个物理量,这就给在总振动预报中如何加载提出了一个难题,实际工程应用中很难做到如此精确的分布。
脉动压力按照构成又可以分为,无空泡螺旋桨诱导的脉动压力和有空泡螺旋桨诱导的脉动压力[9]。以中国船级社《船上振动控制指南》估算脉动压力的公式为例,介绍脉动压力的构成。
公式如下:
| $ {P_c} = \frac{{{n^2}{D^2}}}{{160}}\frac{{{V_s}\left( {{W_{a\max }} - {W_e}} \right)}}{{\sqrt {{h_a} + 10.4} }}{\left( {\frac{1}{{{d_s}/R}}} \right)^{Kc}},$ | (1) |
| $ {P_0} = \frac{{{n^2}{D^2}}}{{70}}\frac{1}{{{Z_p}^{1.5}}}{\left( {\frac{1}{{{d_s}/R}}} \right)^{{K_0}}},$ | (2) |
| $ P = \sqrt {P_0^2 + P_c^2}。$ | (3) |
式中:ds为从螺旋桨叶片顶部0.9R处到浸入水中的计算表面的距离;P0 为无空泡螺旋桨在船体表面引起的叶片次脉动压力;Pc 为由螺旋桨空泡引起的叶片次脉动压力;P 为螺旋桨的总脉动压力;N为螺旋桨转速,r /min;D为螺旋桨直径;Zp为螺旋桨叶片数目;R为螺旋桨半径;Vs为船速,m/s。其他参数参见指南描述。
从式(1)~式(3),根据目标船型的一些参数,可预报得到螺旋桨脉动压力,不少学者将经验公式获得的脉动压力和模型空泡试验进行对比,其结果表明经验公式预报值与模型试验值会有一定的差异。所以在新船设计阶段,一般都会通过模型试验来获得螺旋桨的脉动压力,作为振动计算的输入参数,这样结果更为准确可靠。试验数据经过处理后,试验报告一般会给出无空泡发生时的脉动压力P0 和总压力P,以及各自对应的相位角,但Pc无法直接通过试验得到,这样显然也无法根据式(1)和式(2)的分布规律来施加载荷,因此确定空泡压力值很有必要。
通过式(1)可知,无空泡螺旋桨在船体表面引起的叶片次脉动压力P0和转速n呈2次方关系,从式(2)可知,空泡螺旋桨在船体表面引起的叶片次脉动压力Pc和转速n呈3次方关系(船速Vs和转速基本是1次线型关系),另外P0和Pc与ds的变化趋势也不同,显然在只有总脉动压力的情况下,无论采用式(1)或式(2)来施加脉动压力都不是一个合理的方法。
2 空泡压力根据Holden[10]分布,空泡螺旋桨脉动压力的叶频分量幅值表述为:
| $ P = \sqrt {P_0^2 + P_c^2 - 2{P_0}{P_c}\cos (180 - \varepsilon )} 。$ | (4) |
式中:
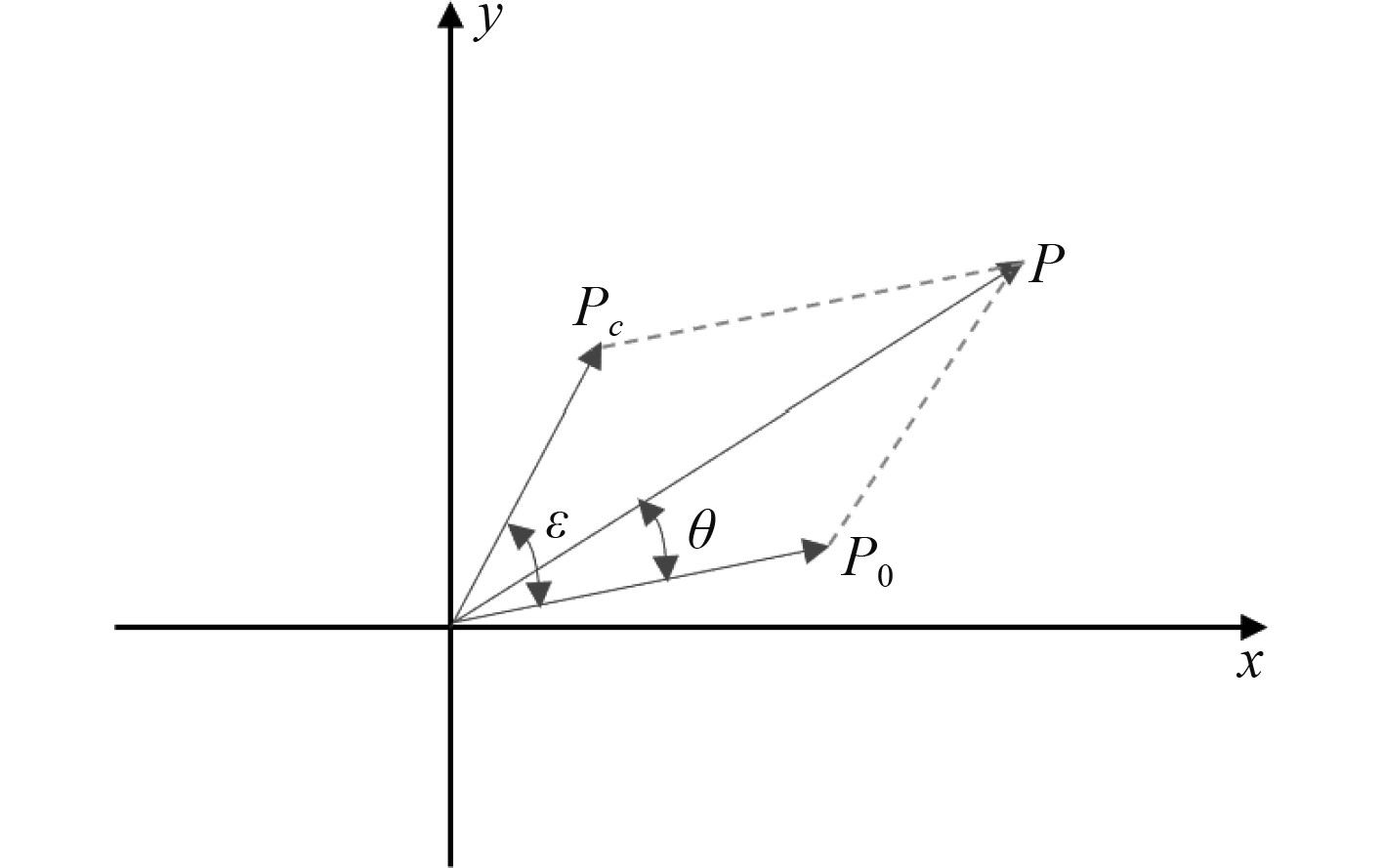
可以看出,总压力P是P0和Pc的矢量和,图形关系如图1所示。
|
图 1 P和P0、Pc的矢量关系图 Fig. 1 Vector diagram of P, P0 and Pc |
观察式(4)可以发现:
当
| $ P = \left| {{P_0} + {P_c}} \right|。$ | (5) |
当
| $ p = \left| {{p_0} - {p_c}} \right|。$ | (6) |
经验公式(3)给出的值介于式(5)和式(6)之间。
根据矢量关系图1,有如下等式:
| $ \frac{P}{{\sin \varepsilon }} = \frac{{{P_c}}}{{\sin \theta }},$ | (7) |
求解式(4)和式(7),得到
| $ {P_c} = \sqrt {{P^2} - {P_0}^2 - 2{P_0}(P\cos \theta - {P_0})} ,$ | (8) |
| $ \cos \varepsilon = \frac{{P\cos \theta - {P_0}}}{{{P_c}}}。$ | (9) |
解析出Pc后,根据式(1)和式(2),即可将P0和Pc施加于船体表面上。
为了获取在宽频范围内的振动响应,在转速为N的情况下,根据脉动压力与转速的相对关系,可以给出如下公式:
| $ {{P} _N} = {P_0}{\left(\frac{N}{{{N_P}}}\right)^2} + {P_c}{\left(\frac{N}{{{N_P}}}\right)^3}。$ | (10) |
式中:
这样就得到了全转速下脉动压力的分布。
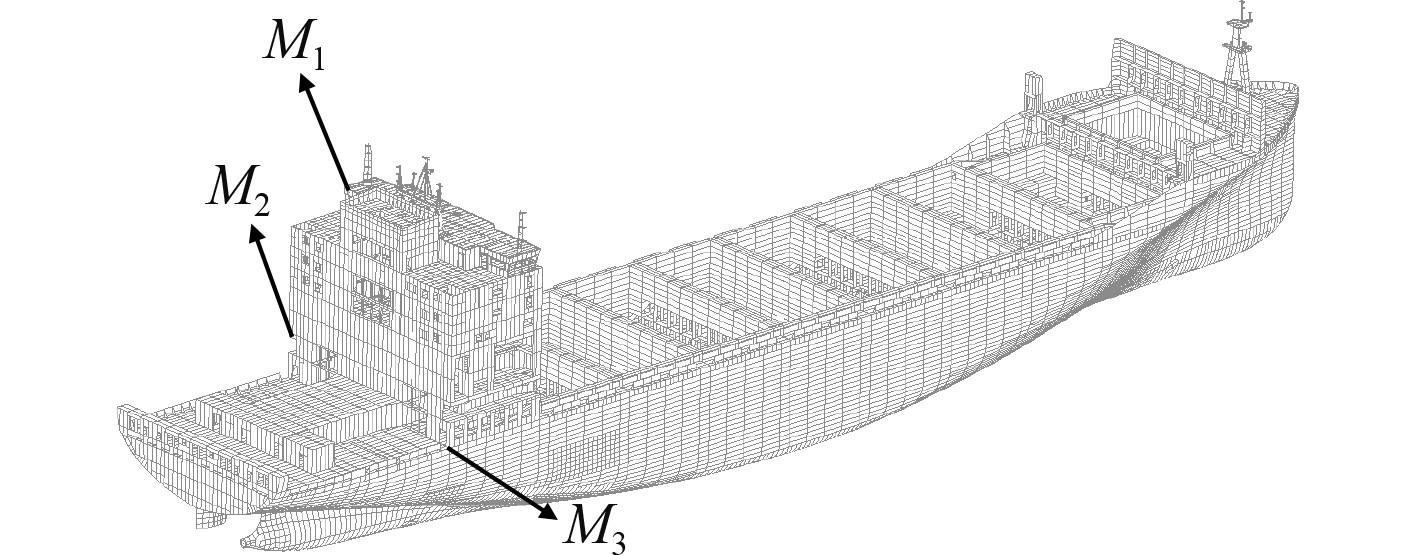
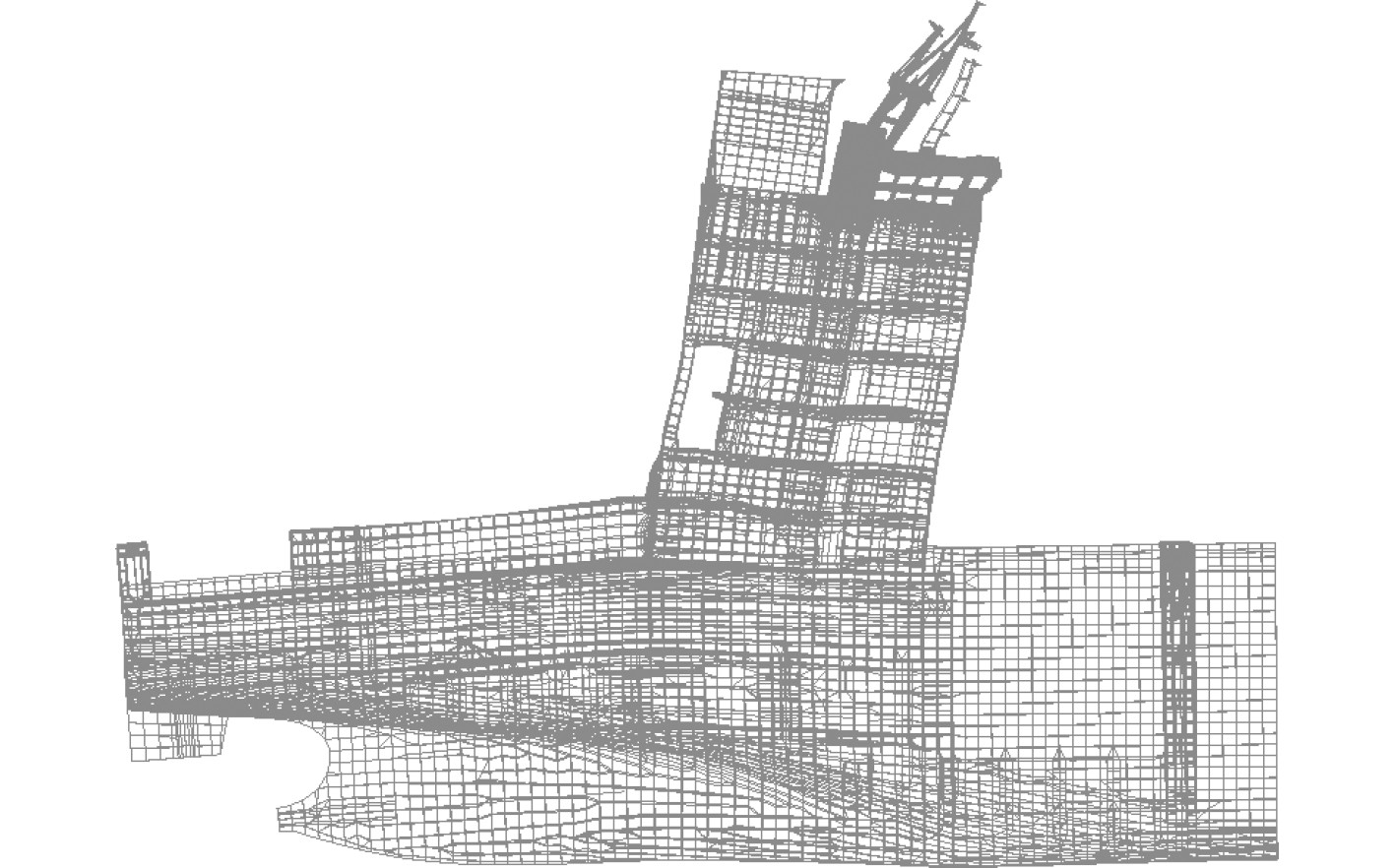
3 计算验证 3.1 脉动压力计算选取某一型集装箱船进行振动分析,采用全船有限元建模,按照装载手册中的质量分布调整相应区域的结构重量,全船振动模型如图2所示。
|
图 2 整船有限元模型 Fig. 2 Finite element model of the whole ship |
集装箱船速度要求较高,通常机舱和尾部区域的线型较瘦,刚性较差,螺旋桨引起的脉动压力易激起尾部和上层建筑的振动,需重点关注脉动压力的影响。
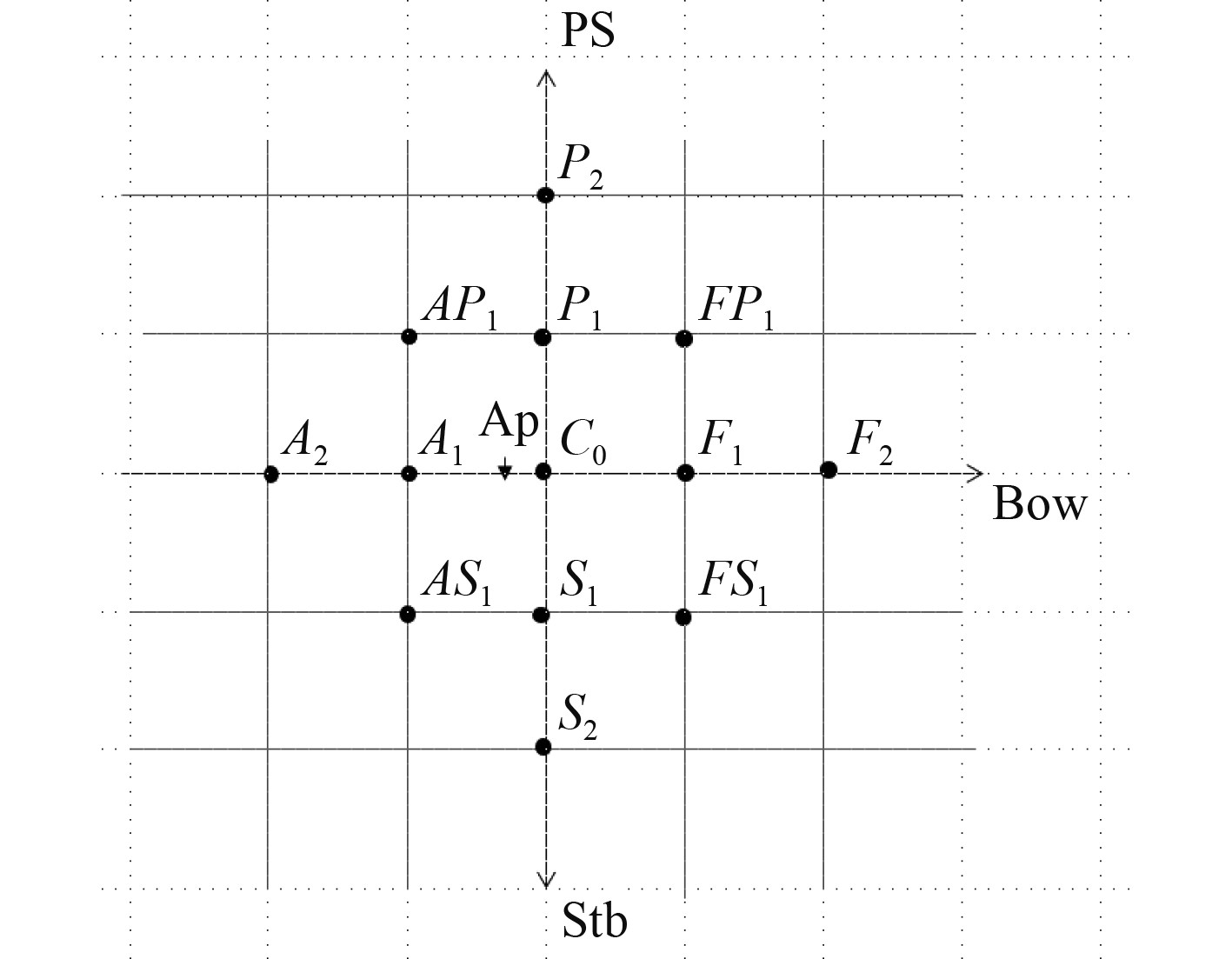
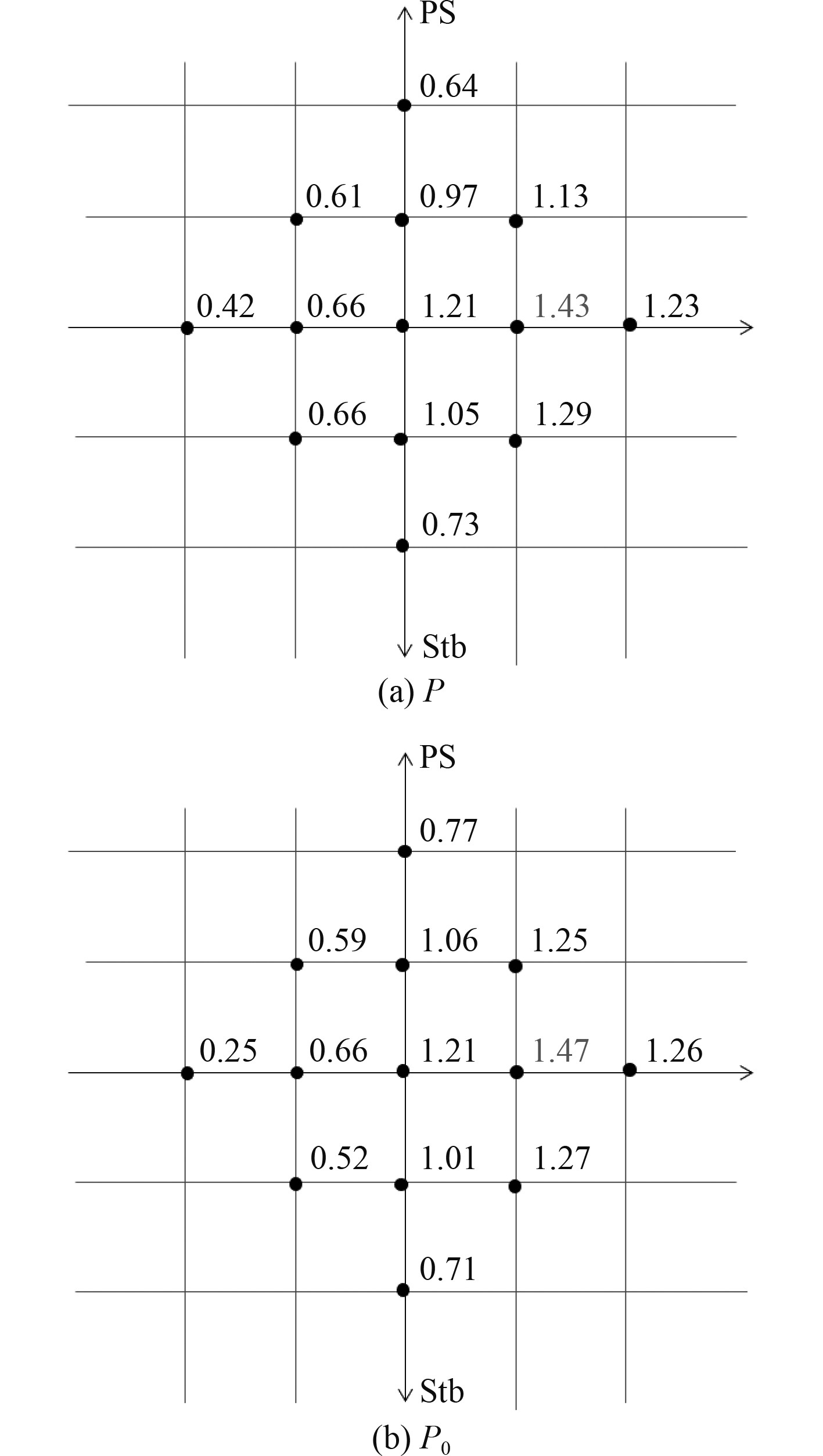
模型报告中给出的脉动压力测点位置如图3所示,测试结果给出了一阶脉动压力P和P0的数值,如图4所示,对应的相位角文中未给出。
|
图 3 脉动压力测点位置 Fig. 3 Location of measurement point for pressure fluctuation |
|
图 4 脉动压力测试值 Fig. 4 Test value of pressure fluctuation |
根据式(8)~式(9),求得空泡脉动压力Pc 以及和P0 的相位差
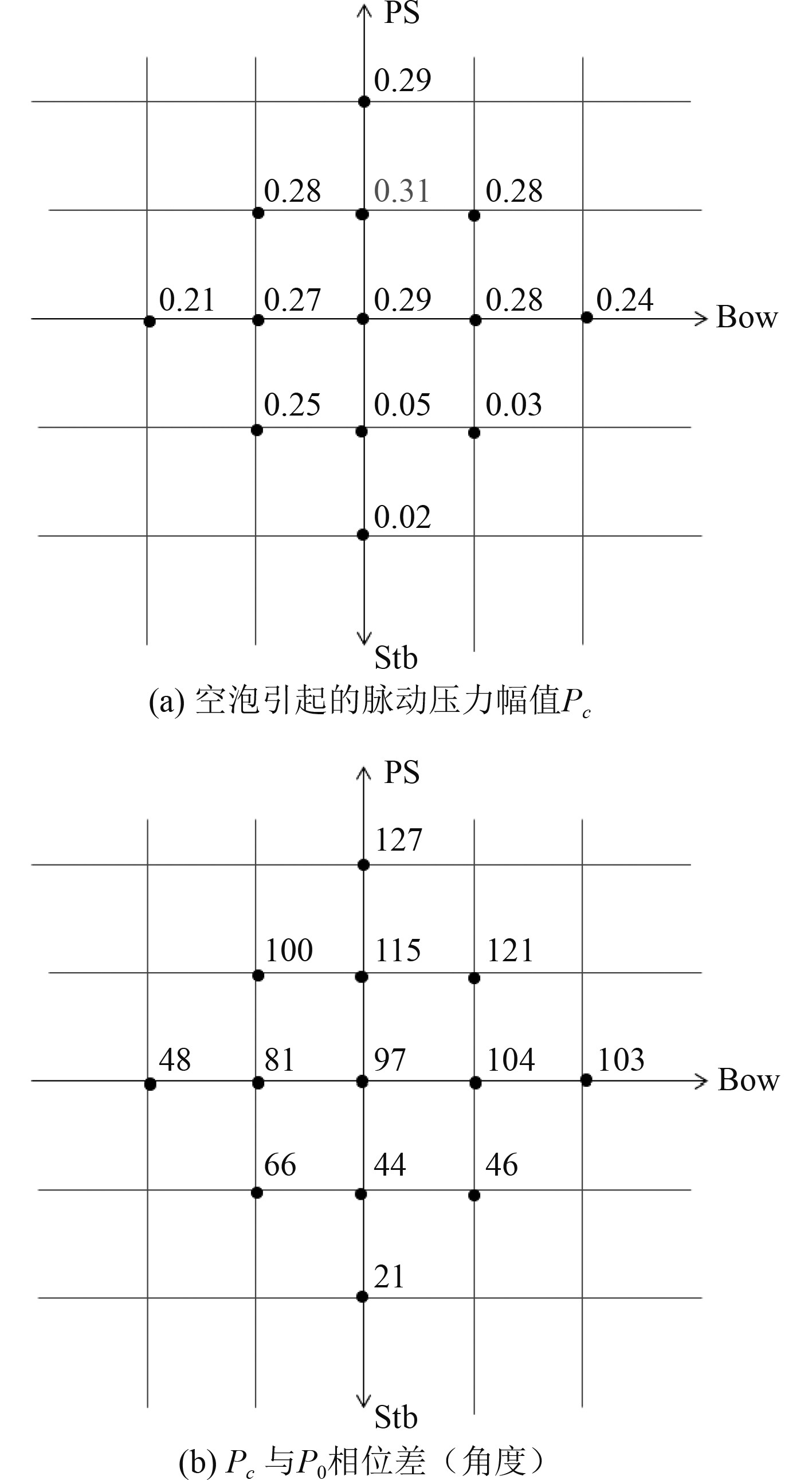
|
图 5 空泡引起的脉动压力幅值与相位差(角度) Fig. 5 Amplitude of pulsating pressure caused by cavitation and phase difference |
由图4可知,螺旋桨脉动压力最大值P和P0均出现在F1点处,F1位于螺旋桨盘面中心点前处,并且右舷脉动压力值要大于左舷值,这与第一节中脉动压力分布规律完全一致。由图5可知,Pc最大值并没有出现在F1点,而是出现在P1点,并且不同测点Pc 与P0相位差别较大,从数值比例上来看,一阶脉动压力Pc在总压力P中占比不大,这是因为螺旋桨一阶脉动压力频率较低,空泡现象不明显,随着频率的增加,Pc在总压力P中占比也相应变大。
3.2 脉动压力施加常规螺旋桨脉动压力的施加,参考文献[6,9],有如下几种方法:
方法1 通过集中力的方法施加在螺旋桨正上方的船体外板上,集中力的大小为:
| $ {F_z} = P{D^2}。$ | (11) |
式中:P为螺旋桨的总脉动压力,可以来源于经验公式、数值仿真或模型试验。
方法2 施加均布载荷,将P均布施加在螺旋桨上方D×D(D为螺旋桨直径)的单元上。
方法3 本文提出的施加方法,根据P0和Pc 值以及式(1)、式(2)压力与距离ds的关系,施加在船体外板上。
按照上述3种方法对本船进行脉动压力的施加,方法1 如图6(a)所示;方法2 如图6(b)所示;方法3如图7所示,P0和Pc分别施加。从图7可知,P0作用范围较小,随着与螺旋桨中线距离的增加,压力值衰减很快。Pc则影响范围较大,在船长和船宽范围内衰减较慢,施加范围从尾部一般到机舱前端壁位置。
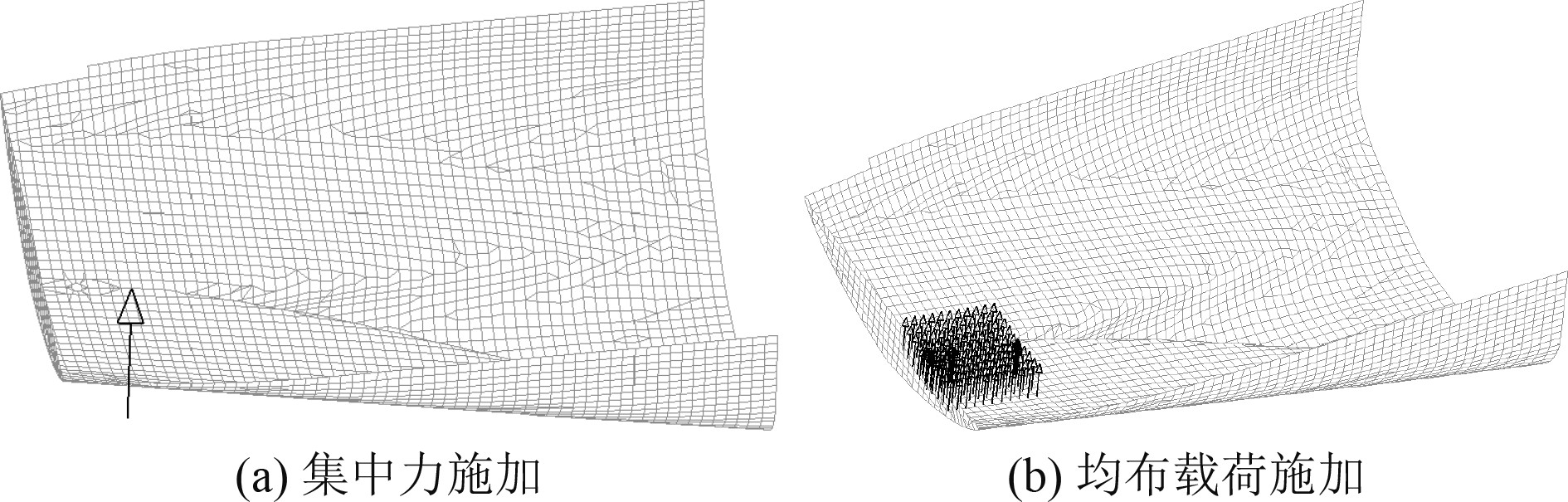
|
图 6 脉动压力施加 Fig. 6 Application method of pressure fluctuation |
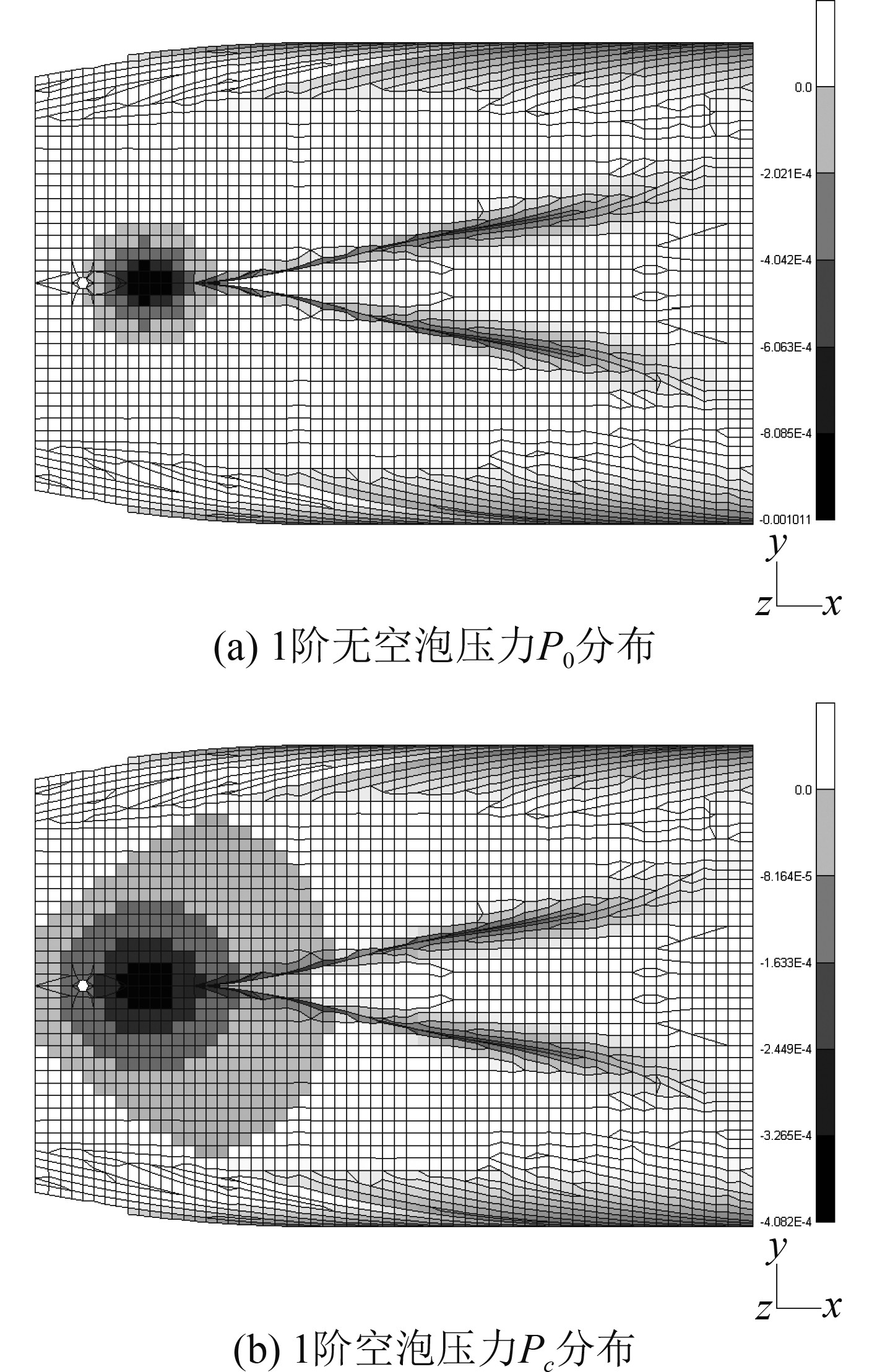
|
图 7 1阶无空泡压力P0与空泡压力Pc分布 Fig. 7 1st pulsation pressure caused by non-cavitation and 1st pulsation pressure caused by cavitation |
将方法3施加的压力在外板上积分,相加后得到总表面压力SF1,根据式(11)计算得到压力值SF2,结果如表1所示。
|
|
表 1 总压力值比较 Tab.1 Comparison of total pressure value |
表1中直接计算的总压力SF1与根据经验公式得到的SF2有较大差别,SF1的结果由空泡试验获得,可以认为结果相对可靠,根据总压力一致性原则,将式(11)修改如下:
| $ F = K\cdot P{D^2} 。$ | (12) |
式中:K为放大系数。由表2可知,K和工况相关。对于本文所分析的集装船来说,满载工况下放大系数为2,压载工况放大系数约为0.6。经过修正后,3种施加方法在外板上的总垂向压力大小一致。
|
|
表 2 不同工况下放大系数 Tab.2 Amplification factor under different operating conditions |
选取上层建筑上3个观测点M1、M2、M3(见图2)作为响应分析目标。
M1为上层建筑驾驶层甲板左后端点;M2为上层建筑第2层甲板左后端点;M3为上层建筑右后端与上甲板交点。
根据式(10)施加全转速下脉动压力,求解全船的振动响应。
在压载和满载工况下,全转速下的速度响应值(3个方向合成值)如图8~图10所示。
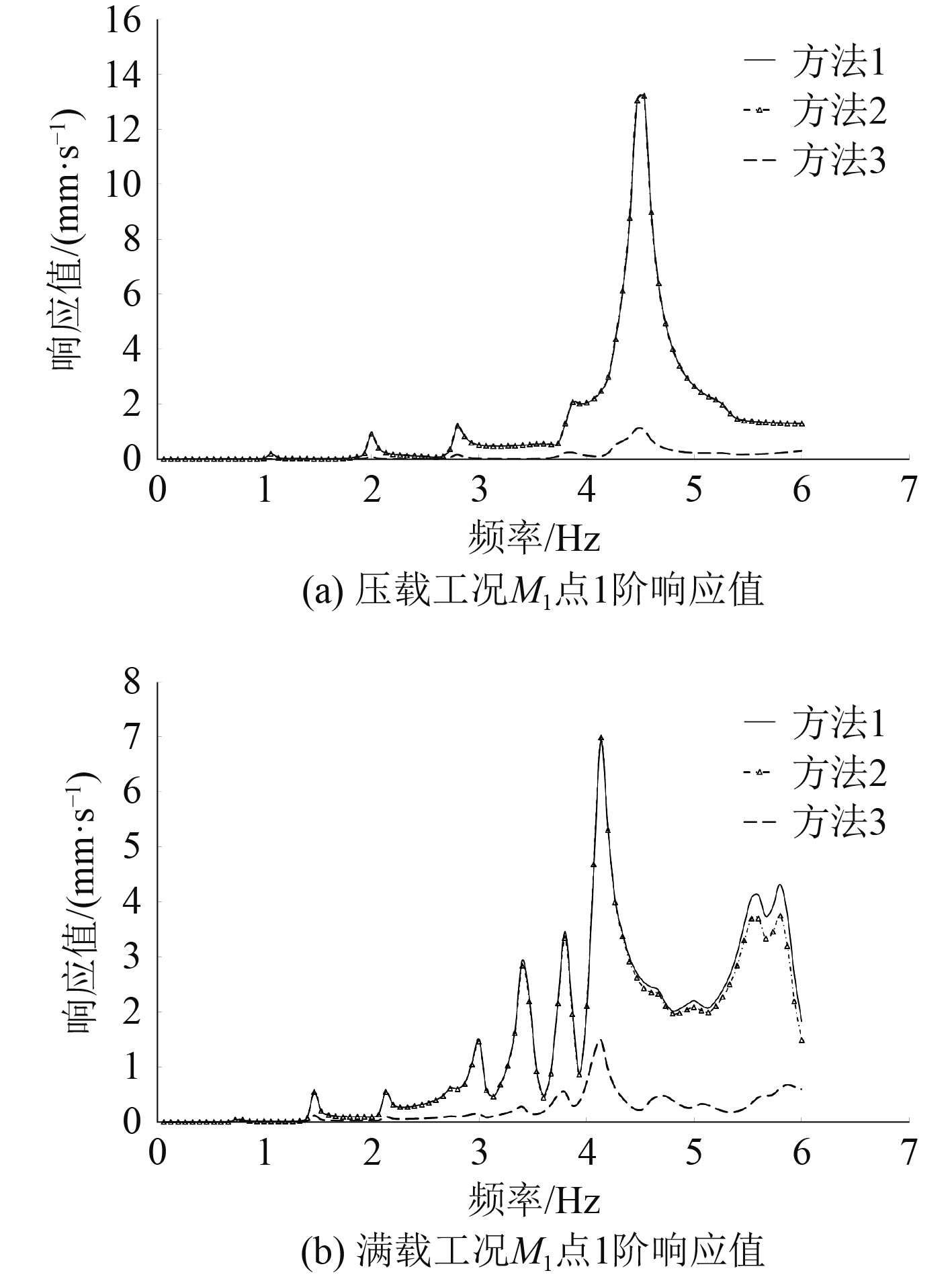
|
图 8 压载工况和满载工况M1点 1阶响应值 Fig. 8 Vibration response value of M1 at ballast condition and full load condition |
|
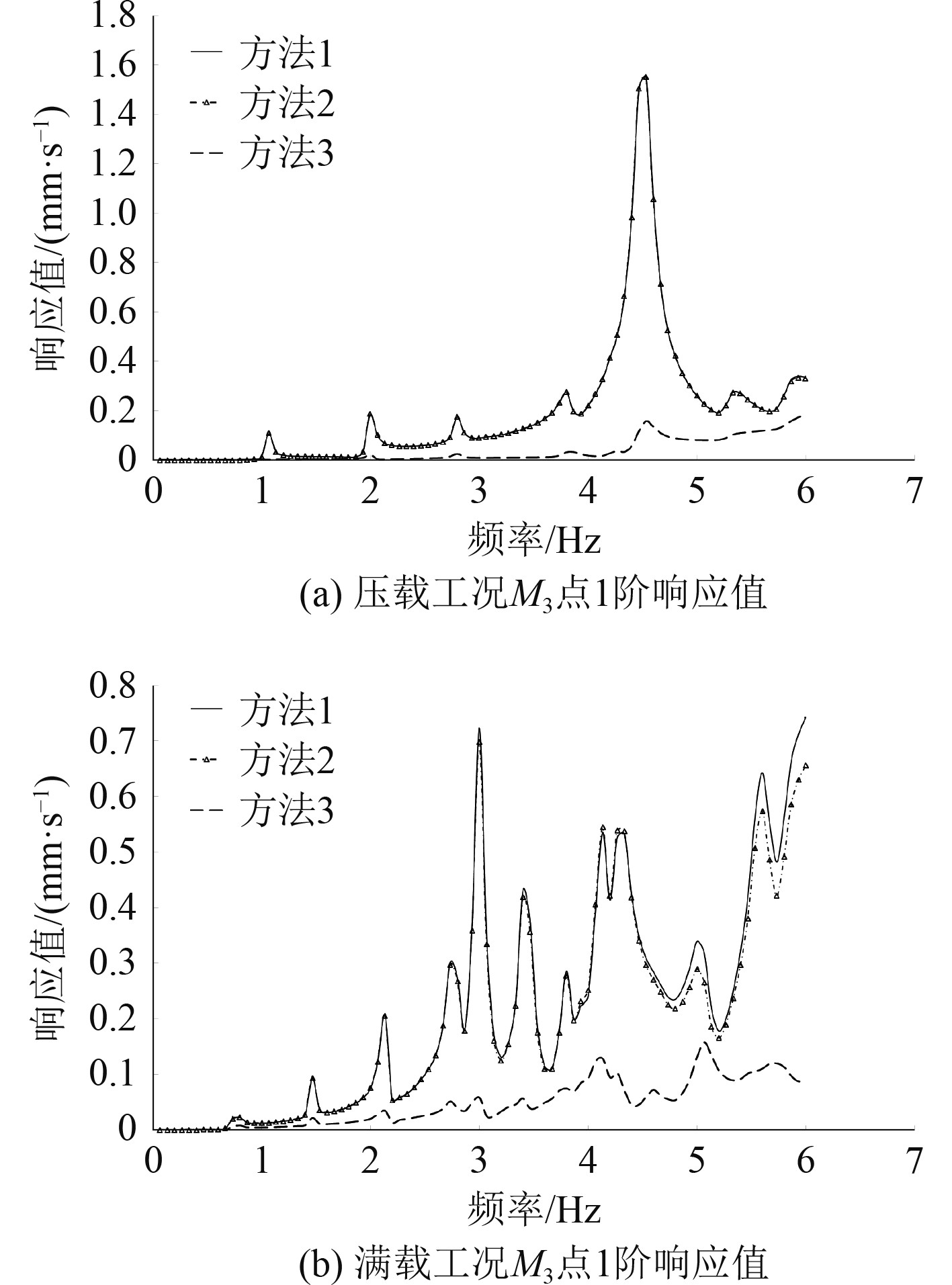
图 10 压载工况和满载工况M3点 1阶响应值值 Fig. 10 Vibration response value of M3 at ballast condition and full load condition |
|
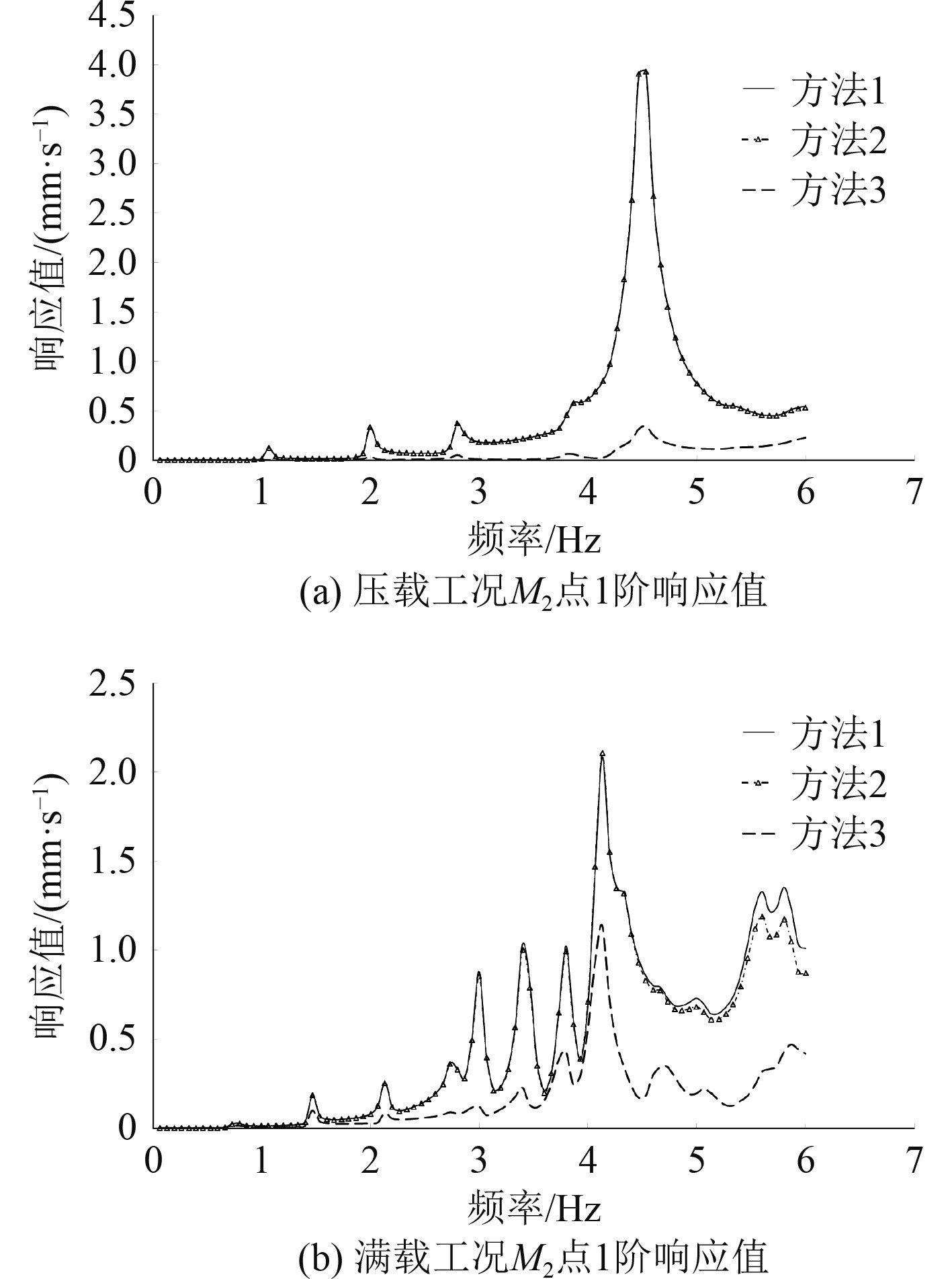
图 9 压载工况和满载工况M2点 1阶响应值 Fig. 9 Vibration response value of M2 at ballast condition and full load condition |
从3种方法计算出的响应数值来看,无论满载还是压载,3种方法计算结果的趋势一致,最大响应值发生的频率位置也相同。对于同一个测点,压载和满载响应趋势不同,这是由压载和满载工况船体本身的固有频率差异导致的。对3个测点而言,方法1和方法2数值非常接近,除了部分满载工况高频部分有细微差别,即在总压力一致的情况下,施加集中力或均匀分布力进行总振动分析,对于船体的响应一致。而方法3和方法1、方法2的结果差别较大,方法3的计算结果也是3种方法中最小的。这是因为方法3从原理上对脉动压力进行分解,分成了无空泡螺旋桨在船体表面引起的叶片脉动压力和空泡引起的叶片脉动压力,虽然保证积分后表面总压力和方法1、方法2一致,但是由于2种压力的作用区域和衰减趋势不同,因此响应值比方法1和方法2要小,这也说明常规施加方法偏保守。
由图8(a)~图10(a)可以看出,压载工况下,在频率为4.5 Hz附近3个目标位置有明显的响应放大,可以判定此频率附近上建产生了共振。分析上层建筑的固有频率以观察是否有共振可能,模态分析结果如图11所示,结果表明上层建筑一阶纵向振动的固有频率在4.5 Hz附近,因此在该频率下,螺旋桨脉动压力会激起上层建筑的纵向共振,以上3种方法都能预报出精确的共振点。以M1点为例,方法1和方法2预报出的响应值在13 mm/s附近,而方法3预报出的响应值在1 mm/s附近,最终实船试航效果反馈,上层建筑在4.5 Hz运行平稳,因此可以说明方法1和方法2虽然振动预报的趋势正确,但具体的响应值有所偏大,这从另外一个角度说明方法3比较合理。
|
图 11 上层建筑纵向振动模态 Fig. 11 Longitudinal vibration mode of superstructure |
本文可以得出以下结论:
1) 螺旋桨的脉动压力P由无空泡螺旋桨在船体表面引起的叶片次脉动压力P0和由螺旋桨空泡引起的叶片次脉动压力Pc构成,P0和Pc存在相位差,总合成压力并不是两者直接相加得到。
2) 通过模型试验报告,根据总压力P和P0以及各自的相位角,根据理论求解,可以得到Pc,Pc的最大值和P不一定出现在同一个位置。
3) 通过实船分析可知,P0影响区域较小,一般为螺旋桨正上方区域,随着距离的增加,衰减很快,Pc作用范围较大,在整个机舱和尾部区域均有影响。
4) 对脉动压力施加的几种方法进行比较,发现常规方法(方法1和方法2)和本文的施加方法(方法3)有所差别,在振动趋势一致的情况下,方法1和方法2要比方法3响应值大,常规施加方法更加保守。
本文的不足之处:
1) Pc值需要从空泡试验报告中进行分解获取,在无空泡试验的情况下,将无法求解得到该值,仍需要借助经验公式或数值分析。
2)对于本文提出的脉动压力施加方法,如何在实船测试中进行单独比对,需要后续做大量工作。
| [1] |
SKAAS K T, RAESTAD A E. The relative importance of ship vibration excitation forces[C]// RINA Symposium on Propeller Induced Ship Vibration. London, 1979.
|
| [2] |
姚熊亮, 张阿漫. 船体振动与噪声[M]. 北京: 国防工业出版社, 2010.
|
| [3] |
林永水, 吴卫国, 翁长俭. 20000t近海散货船有害振动诊断及治理[J]. 武汉理工大学学报(交通科学与工程版), 2015, 39(2): 292-296. |
| [4] |
王蒙蒙. 螺旋桨诱导的船体表面脉动压力预报方法研究[D]. 大连:大连理工大学, 2006.
|
| [5] |
阳涛, 林永水, 吴卫国, 等. 螺旋桨诱导的船体表面脉动压力数值预报[J]. 武汉理工大学学报(交通科学与工程版), 2017, 41(1): 97-103. |
| [6] |
陈翔, 夏利娟, 丁金鸿, 等. 散货船的总振动模态计算和动力响应预报[J]. 舰船科学技术, 2013, 35(3): 115-120. CHEN Xiang, XIA Lijuan, DING Jinhong, et al. The global vibration and dynamic response evaluation of a bulk carrier[J]. Ship Science and Technology, 2013, 35(3): 115-120. DOI:10.3404/j.issn.1672-7649.2013.03.026 |
| [7] |
殷玉梅. 船体振动固有特性及螺旋桨脉动压力预报方法[D]. 大连:大连理工大学, 2015.
|
| [8] |
秦升杰, 吴卫国, 宋慧慧, 等. 螺旋桨脉动压力诱导的船体振动研究[J]. 武汉理工大学学报(交通科学与工程版), 2020, 44(2): 260-264. |
| [9] |
中国船级社. 船上振动控制指南[S]. 北京, 2021.
|
| [10] |
HOLDEN K O. Excitation forces and afterbody vibrations induced by marine propeller blade cavitation [J]. Norwegian Maritime Research, 1979, 7(1):15−26.
|
 2024, Vol. 46
2024, Vol. 46
