受风、浪、流等因素影响,船舶在海上存在大幅度的摇摆及升沉运动,对以大型船舶甲板为起降平台的直升机起降作业产生较大影响,为提高直升机起降的安全性和作业效率,通常将采用基于时间序列的极短期预报技术预测未来一段时间内安全起降时间窗口,为指挥员引导直升机起降提供辅助支持[1]。极短期预报模型需输入多个起降点位置船体运动姿态时间序列值,由于船舶甲板较大,船载惯导装置数量有限且布列位置不能正好位于每个起降点处,所采集的升沉信息与各起降点的升沉差异较大,存在明显杆臂效应,而极短期预报技术是一种仅利用船舶历史运动时历的统计拟合方法,数据的不准确性将对预报模型参数辨识的精度造成很大影响,进而影响预报时长及准确性,因此对各起降点的升沉速度换算变得十分必要[2 − 3]。
本文利用有限传感器实时采集到的横摇、纵摇及升沉速度信息,结合传感器安装点以及起降点的船体坐标,推导出起降点的升沉速度换算方法。结合某型船模型试验数据对升沉速度换算误差进行验证,然后将换算后的升沉速度输入给极短期预报模型,统计预报精度提升程度。研究过程中将船体视为刚性体,所用极短期预报模型为基于时间序列的非线性二阶自适应Volterra级数模型[4]。起降点升沉换算对提高极短期预报精度,补偿杆臂效应影响,提升直升机起降作业效率具有重要意义。
1 三自由度坐标变换理论 1.1 坐标变换理论坐标变换是指一个矢量在2个不同坐标系上分量列阵之间的关系,一般可用变换矩阵表示[7]。
1)平移变换
坐标系
| $ {\left[{x}_{b},{y}_{b},{z}_{b}\right]}^{\rm T}={\left[{x}_{a},{y}_{a},{z}_{a}\right]}^{\rm T}-{\left[{T}_{x},{T}_{y},{T}_{z}\right]}^{\rm T}。$ | (1) |
2)基元旋转变换
| $ {{\boldsymbol{L}}}_{x}\left(\gamma \right)=\left[\begin{array}{ccc}1& 0& 0\\ 0& \mathrm{cos}\gamma & \mathrm{sin}\gamma \\ 0& -\mathrm{sin}\gamma & \mathrm{cos}\gamma \end{array}\right]。$ | (2) |
| $ {{\boldsymbol{L}}}_{y}\left(\varphi \right)=\left[\begin{array}{ccc}\mathrm{cos}\varphi & 0& -\mathrm{sin}\varphi \\ 0& 1& 0\\ \mathrm{sin}\varphi & 0& \mathrm{cos}\varphi \end{array}\right] 。$ | (3) |
| $ {{\boldsymbol{L}}}_{z}\left(\theta \right)=\left[\begin{array}{ccc}\mathrm{cos}\theta & \mathrm{sin}\theta & 0\\ -\mathrm{sin}\theta & \mathrm{cos}\theta & 0\\ 0& 0& 1\end{array}\right]。$ | (4) |
地面坐标系
地面坐标系与船体坐标系之间的关系可以用3个旋转角(艏摇角
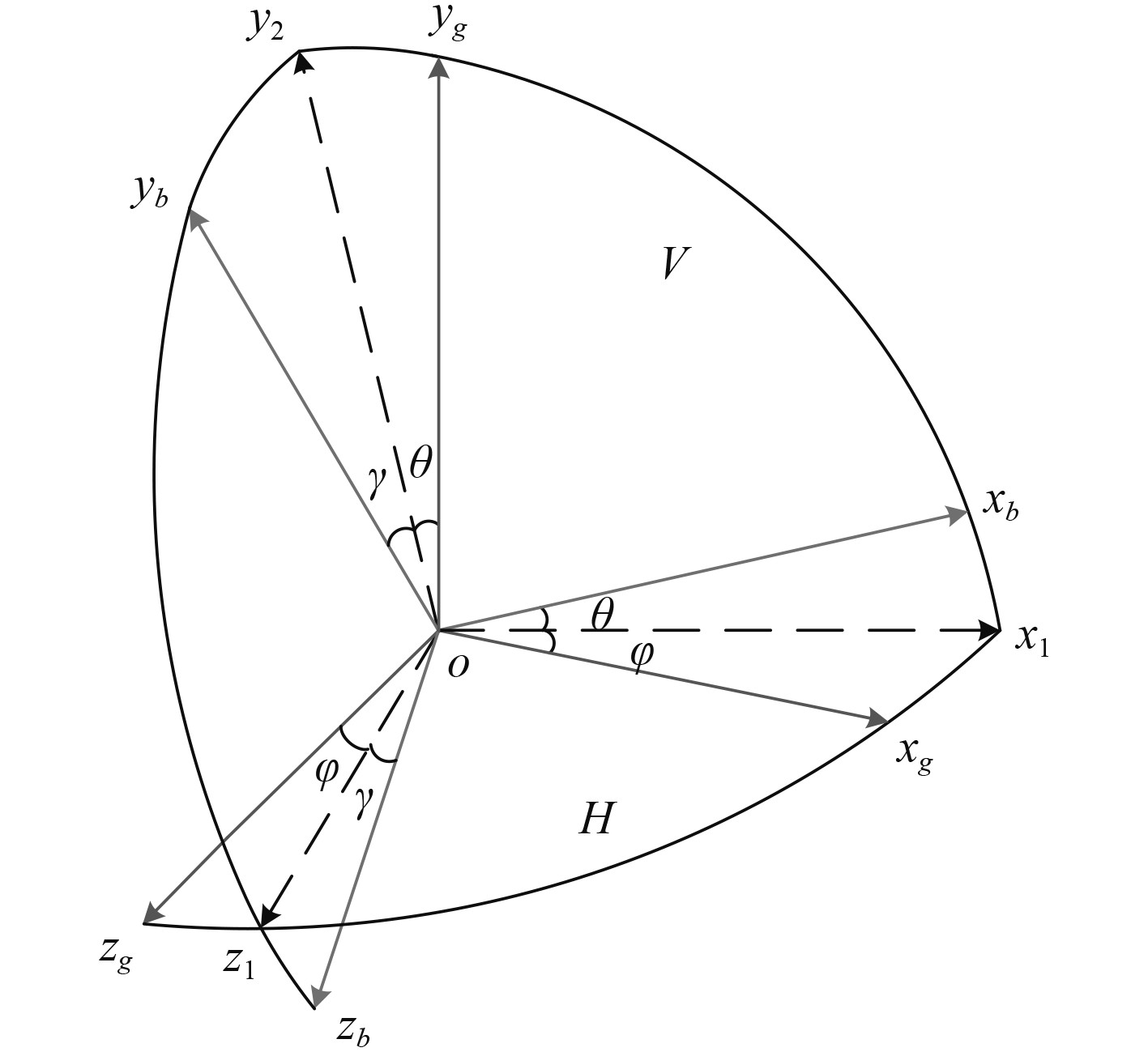
|
图 1 地面坐标系到船体坐标系的变换 Fig. 1 Transformation from ground coordinate system to ship coordinate system |
对应坐标系之间的关系为:
| $ {\left[{x}_{b},{y}_{b},{z}_{b}\right]}^{\rm T}={{{\boldsymbol{L}}}_{x}\left(\gamma \right)\left[{x}_{b},{y}_{2},{z}_{1}\right]}^{\rm T} ,$ | (5) |
| $ {\left[{x}_{b},{y}_{2},{z}_{1}\right]}^{\rm T}={{{\boldsymbol{L}}}_{z}\left(\theta \right)\left[{x}_{1},{y}_{g},{z}_{1}\right]}^{\rm T},$ | (6) |
| $ {\left[{x}_{1},{y}_{g},{z}_{1}\right]}^{\rm T}={{{\boldsymbol{L}}}_{y}\left(\varphi \right)\left[{x}_{g},{y}_{g},{z}_{g}\right]}^{\rm T}。$ | (7) |
代入式(5)~式(7)可得:
| $ {\left[{x}_{b},{y}_{b},{z}_{b}\right]}^{\rm T}={{\boldsymbol{L}}}_{bg}{\left[{x}_{g},{y}_{g},{z}_{g}\right]}^{\rm T}。$ | (8) |
式中:
| $\begin{split} {{\boldsymbol{L}}}_{bg}=&\left[\begin{array}{cc}\mathrm{cos}\theta \mathrm{cos}\phi & \mathrm{sin}\theta \\ -\mathrm{sin}\theta \mathrm{cos}\phi \mathrm{cos}\gamma +\mathrm{sin}\phi \mathrm{sin}\gamma & \mathrm{cos}\theta \mathrm{cos}\gamma \\ \mathrm{sin}\theta \mathrm{cos}\phi \mathrm{sin}\gamma +\mathrm{sin}\phi \mathrm{cos}\gamma & -\mathrm{cos}\theta \mathrm{sin}\gamma \end{array}\right.\\ &\left.\begin{array}{c}-\rm{cos}\theta \rm{sin}\varphi \\ \rm{sin}\theta \rm{sin}\varphi \rm{cos}\gamma +\rm{cos}\varphi \rm{sin}\gamma \\ -\rm{sin}\theta \rm{sin}\varphi \rm{sin}\gamma +\rm{cos}\varphi \rm{cos}\gamma \end{array}\right]。\end{split} $ | (9) |
将式(8)两边求逆,得:
| $ {\left[{x}_{g},{y}_{g},{z}_{g}\right]}^{\rm T}={L}_{bg}^{-1}{\left[{x}_{b},{y}_{b},{z}_{b}\right]}^{\rm T}。$ | (10) |
式中:
| $ {L}_{bg}^{-1}={L}_{bg}^{\rm T}。$ | (11) |
| $ \left[\begin{array}{c}{x}_{g}\\ {y}_{g}\\ {z}_{g}\end{array}\right]={{\boldsymbol{L}}}_{bg}^{-1}\left[\begin{array}{c}{x}_{b}\\ {y}_{b}\\ {z}_{b}\end{array}\right]+\left[\begin{array}{c}{T}_{x}\\ {T}_{y}\\ {T}_{z}\end{array}\right] 。$ | (12) |
结合实际作业需求,以船舶甲板为起降平台的海上直升机起降作业通常受横摇、纵摇及升沉三自由度运动影响较大,研究过程中仅考虑上述3个自由度。设艏摇角
| $ {{\boldsymbol{L}}}_{bg}^{-1}=\left[\begin{array}{ccc}\mathrm{cos}\theta & -\mathrm{sin}\theta \rm{cos}\gamma & \mathrm{sin}\theta \mathrm{sin}\gamma \\ \mathrm{sin}\theta & \mathrm{cos}\theta \rm{cos}\gamma & -\rm{cos}\theta \mathrm{sin}\gamma \\ 0& \mathrm{sin}\gamma & \rm{cos}\gamma \end{array}\right]={{\boldsymbol{L}}}_{bg}^{\rm T}。$ | (13) |
船载惯导装置采集到的横摇角和纵摇角为全船信息,无需进行换算,本文仅对升沉速度进行推导换算。研究过程中假定船体为刚性体,地面坐标系的原点
1)船舶重心的升沉位移
设船载惯导装置位于
| $ \left[ \begin{array}{c}{x}_{g}^{1}\\ {y}_{g}^{1}\\ {z}_{g}^{1} \end{array}\right]=\left[ \begin{array}{ccc}\mathrm{cos}\theta & -\mathrm{sin}\theta \rm{cos}\gamma & \mathrm{sin}\theta \mathrm{sin}\gamma \\ \mathrm{sin}\theta & \mathrm{cos}\theta \rm{cos}\gamma & -\rm{cos}\theta \mathrm{sin}\gamma \\ 0& \mathrm{sin}\gamma & \rm{cos}\gamma \end{array}\right]\left[ \begin{array}{c}{x}_{b}^{1}\\ {y}_{b}^{1}\\ {z}_{b}^{1} \end{array}\right]+\left[ \begin{array}{c}0\\ {T}_{y}\\ 0 \end{array}\right]。$ |
故船舶重心的升沉位移
| ${T}_{y}={y}_{g}^{1}-\left({x}_{b}^{1}\mathrm{sin}\theta +{y}_{b}^{1}\mathrm{cos}\theta \mathrm{cos}\gamma -{z}_{b}^{1}\mathrm{cos}\theta \mathrm{sin}\gamma \right)。$ | (14) |
2)船舶重心的升沉速度
设
| $ \begin{aligned}{v}_{y}=&\frac{{T}_{y2}-{T}_{y1}}{\Delta t}={v}_{yg}^{1}-\Biggr({x}_{b}^{1}\frac{\mathrm{sin}{\theta }_{2}-\mathrm{sin}{\theta }_{1}}{\Delta t}+\\ &{y}_{b}^{1}\frac{\mathrm{cos}{\theta }_{2}\mathrm{cos}{\gamma }_{2}-\mathrm{cos}{\theta }_{1}\mathrm{cos}{\gamma }_{1}}{\Delta t} -\\ &{z}_{b}^{1}\frac{\mathrm{cos}{\theta }_{2}\mathrm{sin}{\gamma }_{2}-\mathrm{cos}{\theta }_{1}\mathrm{sin}{\gamma }_{1}}{\Delta t}\Biggr) 。\end{aligned}$ | (15) |
若时间间隔
| $ \begin{split}{v}_{y}=&\frac{{T}_{y2}-{T}_{y1}}{\Delta t}={v}_{yg}^{1}-\Biggr({x}_{b}^{1}\frac{\mathrm{sin}{\theta }_{2}-\mathrm{sin}{\theta }_{1}}{\Delta t} +\\ &{y}_{b}^{1}\frac{\mathrm{cos}{\theta }_{2}\mathrm{cos}{\gamma }_{2}-\mathrm{cos}{\theta }_{1}\mathrm{cos}{\gamma }_{1}}{\Delta t} -\\ &{z}_{b}^{1}\frac{\mathrm{cos}{\theta }_{2}\mathrm{sin}{\gamma }_{2}-\mathrm{cos}{\theta }_{1}\mathrm{sin}{\gamma }_{1}}{\Delta t}\Biggr)。\end{split}$ | (16) |
式中:
设
| $ \begin{aligned}{v}_{yg}^{L}=&\frac{{y}_{g2}^{L}-{y}_{g1}^{L}}{\Delta t}=\frac{{T}_{y2}-{T}_{y1}}{\Delta t}+\Biggr({x}_{b}^{L}\frac{\mathrm{sin}{\theta }_{2}-\mathrm{sin}{\theta }_{1}}{\Delta t}+\\& {y}_{b}^{L}\frac{\mathrm{cos}{\theta }_{2}\mathrm{cos}{\gamma }_{2}-\mathrm{cos}{\theta }_{1}\mathrm{cos}{\gamma }_{1}}{\Delta t}-\\ &{z}_{b}^{L}\frac{\mathrm{cos}{\theta }_{2}\mathrm{sin}{\gamma }_{2}-\mathrm{cos}{\theta }_{1}\mathrm{sin}{\gamma }_{1}}{\Delta t}\Biggr)。\end{aligned}$ | (17) |
结合式(16)和式(17),最终可推导出
| $ \begin{aligned}[b]{v}_{yg}^{L}=&{v}_{yg}^{1}+\Biggr[\left({x}_{b}^{L}-{x}_{b}^{1}\right)\frac{\mathrm{sin}{\theta }_{2}-\mathrm{sin}{\theta }_{1}}{\Delta t}+ \\ &\left({y}_{b}^{L}-{y}_{b}^{1}\right)\frac{\mathrm{cos}{\theta }_{2}\mathrm{cos}{\gamma }_{2}-\mathrm{cos}{\theta }_{1}\mathrm{cos}{\gamma }_{1}}{\Delta t}-\\ &\left({z}_{b}^{L}-{z}_{b}^{1}\right)\frac{\mathrm{cos}{\theta }_{2}\mathrm{sin}{\gamma }_{2}-\mathrm{cos}{\theta }_{1}\mathrm{sin}{\gamma }_{1}}{\Delta t}\Biggr]。\end{aligned}$ | (18) |
工程实际使用时,式(18)中船舶横摇角度
结合某型船模型试验数据对升沉速度换算误差进行验证,然后将换算后的升沉速度输入给极短期预报模型,计算起降点升沉预报精度提升程度。
3.1 误差计算方式起降点升沉速度换算误差测试采用均方根误差计算方法。设样本个数为
| $ RMSE\left(y,\widehat{y}\right)=\sqrt{\frac{1}{n}{\sum }_{i=0}^{n-1}{\left|{y}_{mean}-\widehat{{y}_{i}}\right|}^{2}}。$ | (19) |
采用某型船模型试验数据进行起降点升沉速度换算验证。试验时选取
|
|
表 1 姿态传感器船体坐标 Tab.1 Ship coordinates of attitude sensors |
选取2组试验数据样本进行测试,每组试验工况条件如表2所示。
|
|
表 2 试验工况条件 Tab.2 Test operating conditions |
根据
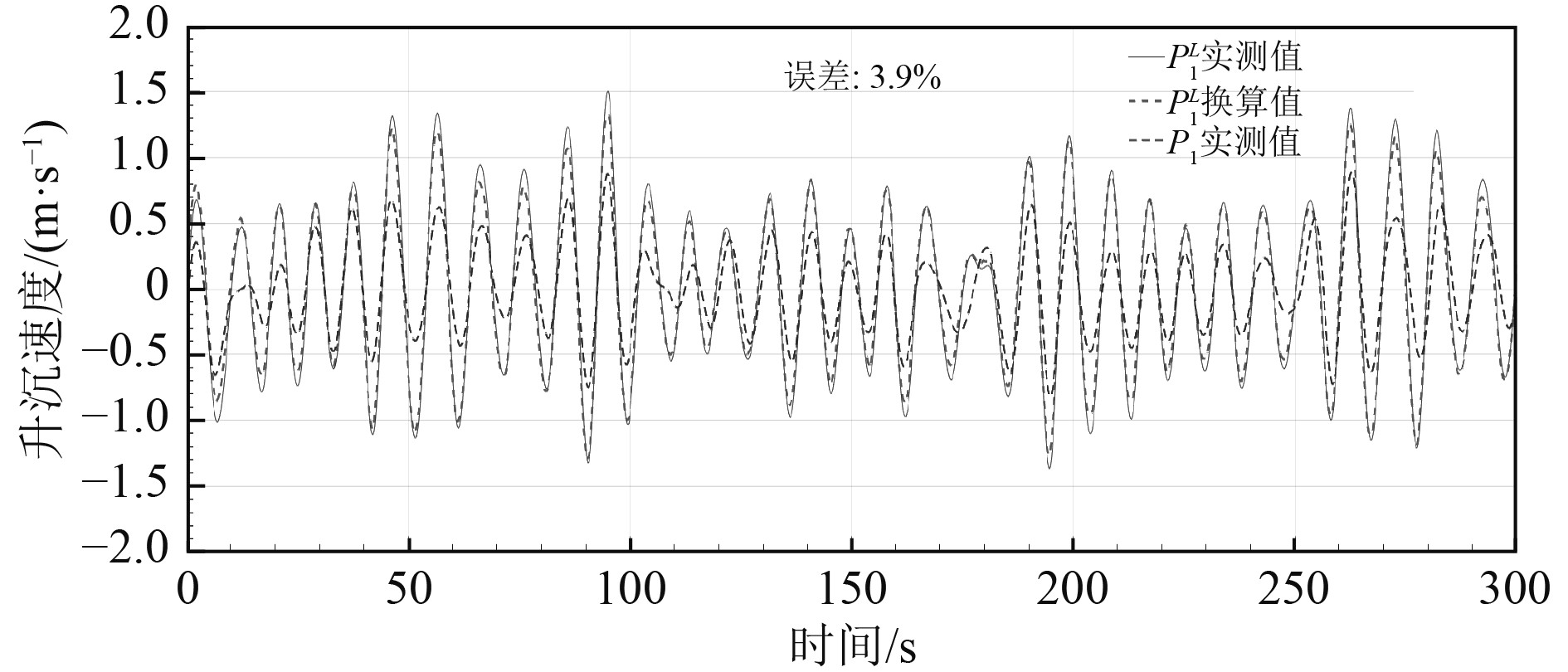
|
图 2 4级海况起降点升沉换算误差测试(工况1) Fig. 2 Test for heave conversion error of landing points at level 4 sea conditions (condition 1) |
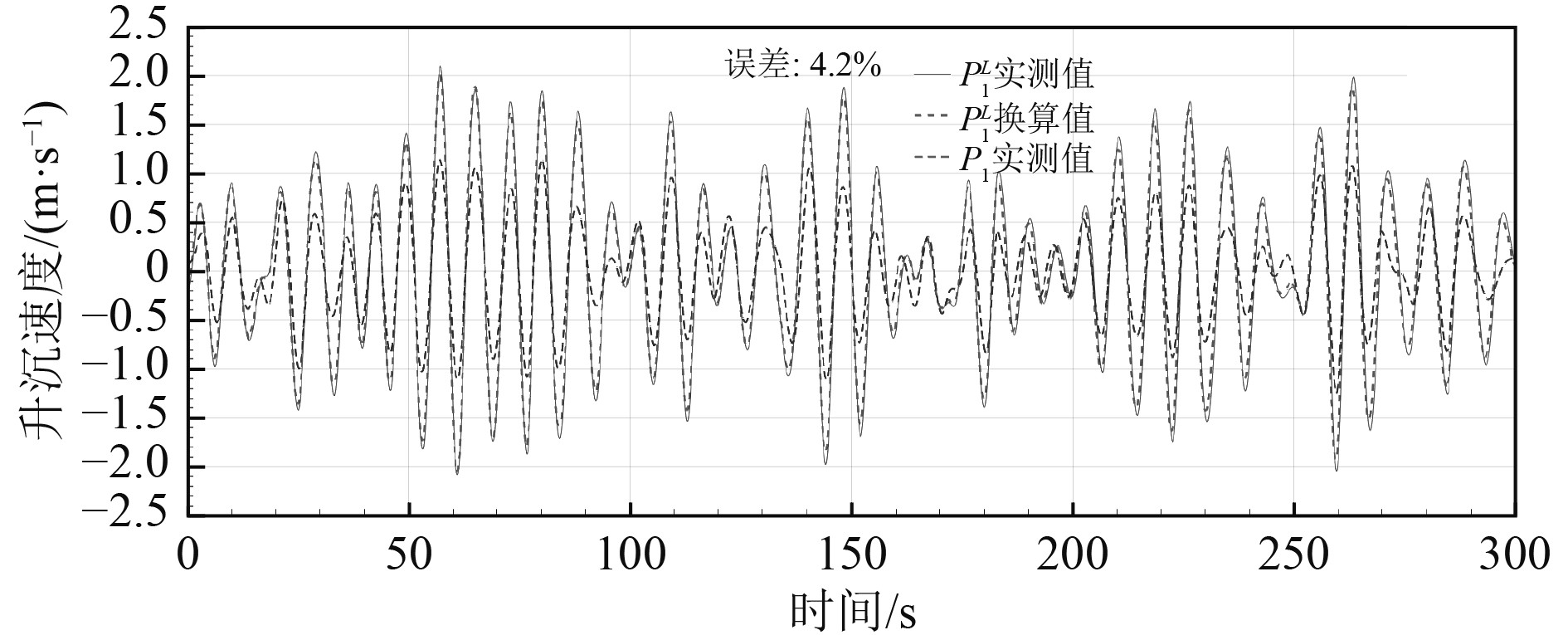
|
图 3 5级海况起降点升沉换算误差测试(工况2) Fig. 3 Test for heave conversion error of landing points at level 5 sea conditions (condition 2) |
图中,“
试验结果表明:在4级和5级海况条件下,任意选取5 min的试验数据进行统计计算,起降点升沉换算误差约为4%,误差较小,对极短期预报结果影响较小,满足工程实际使用需求。实船作业时,可利用本文提出的起降点升沉换算技术,将船载惯导装置采集的升沉速度换算至起降点并输入给极短期预报模型进行升沉预报。
3.4 升沉预报误差测试验证将船载惯导装置采集的升沉速度换算至起降点位置,然后输入给极短期预报模型进行起降点升沉预报,计算升沉预报误差,将该计算结果与未进行升沉换算的预报结果进行比对,验证升沉预报精度是否提升。本文极短期预报模型采用基于时间序列的非线性二阶自适应Volterra级数模型,模型参数采用最小二乘RLS算法进行核估计[5 − 6],模型输入为300个横摇、纵摇及升沉速度历史运动时历,采样间隔为0.5 s,预报时长为10 s每20步。
图4为4级海况,浪向135°、浪高2 m、航速4 kn工况条件下,未进行升沉换算和进行升沉换算的极短期预报情况。图中,“
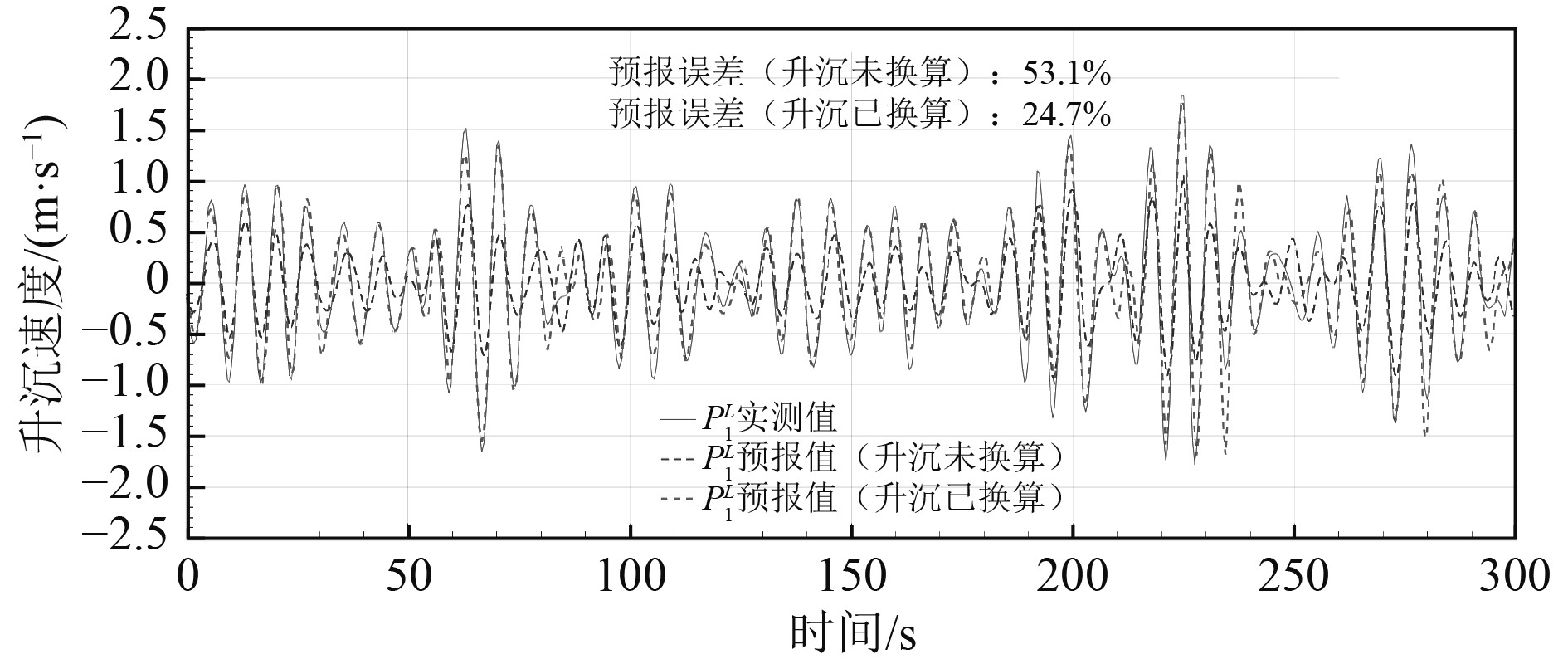
|
图 4 4级海况起降点升沉极短期预报误差测试(工况1) Fig. 4 Test for heave short-term prediction error of landing points at level 4 sea conditions (condition 1) |
可知,4级海况条件下,任意选取5 min数据样本进行统计计算,未进行升沉换算的起降点
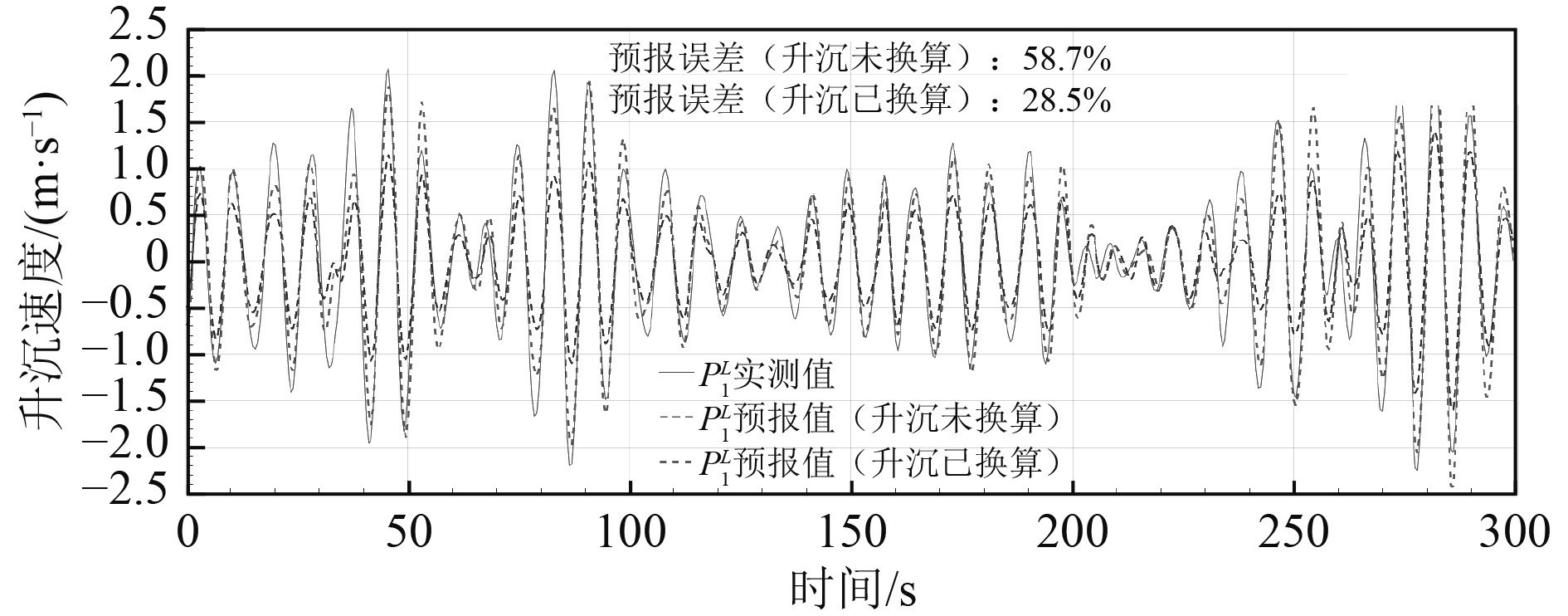
图5为5级海况,浪向180°、浪高3.5 m、航速8 kn工况条件下,未进行升沉换算和进行升沉换算的极短期预报情况。
|
图 5 5级海况起降点升沉极短期预报误差测试(工况2) Fig. 5 Test for heave short-term prediction error of landing points at level 5 sea conditions (condition 2) |
可知,任意选取5 min数据样本进行统计计算。未进行升沉换算的起降点
由表3可知,进行升沉换算后,起降点升沉极短期预报误差减小了约29.3%,预报精度提升显著,能为指挥员引导直升机起降提供更为准确的辅助信息。
|
|
表 3 起降点升沉极短期预报误差统计 Tab.3 Statistics of heave short-term prediction error of landing points |
基于有限点传感器参数的起降点运动姿态换算可以提高船舶运动极短期预报精度,为引导直升机起降提供更为准确的辅助信息。本文利用姿态传感器实时采集的横摇、纵摇及升沉信息,结合传感器及起降点的船体坐标,推导出起降点的升沉速度换算方法,并采用某型船模型试验数据进行测试验证,得出以下结论:
1)对于大型船舶甲板直升机起降作业,船载惯导装置采集的升沉与起降点实际升沉差异较大,需进行升沉换算补偿,消除杆臂效应影响;
2)采用模型试验数据验证,起降点升沉换算误差约为4%,误差较小,满足工程实际使用需求;
3)执行起降点升沉换算,可以使升沉极短期预报精度提升约29.3%,能为指挥员引导直升机起降提供更为准确的辅助指导意见,具有重要军事意义。
| [1] |
刘长德. 基于时间序列的船舶运动建模预报方法研究[D]. 哈尔滨:哈尔滨工程大学, 2009.
|
| [2] |
宋清. 大型舰船甲板运动态势预测方法研究[D]. 南京: 东南大学, 2017.
|
| [3] |
黄礼敏, 段文洋, 韩阳, 等. 船舶运动极短期预报方法综述(英文)[J]. 船舶力学, 2014, 18(12): 1534-1542. HUANG Limin, DUAN Wenyang, HAN Yang, et al. A review of short-term prediction techniques for ship motions in seaway[J]. Journal of Ship Mechanics, 2014, 18(12): 1534-1542. DOI:10.3969/j.issn.1007-7294.2014.12.013 |
| [4] |
翁震平, 顾民, 刘长德. 基于二阶自适应Volterra级数的船舶运动极短期预报研究[J]. 船舶力学, 2010, 14(7): 36-44. WENG Zhenping, GU Min, LIU Changde. Extreme short-term prediction of ship motion based on second-order adaptive volterra series[J]. Journal of Ship Mechanics, 2010, 14(7): 36-44. DOI:10.3969/j.issn.1007-7294.2010.07.005 |
| [5] |
严传续, 孙慧, 张帅. 实船运动与包络的极短期预报分析[J]. 舰船科学技术, 2019, 41(6): 43-47. YAN Chuanxu, SUN Hui, ZHANG Shuai. Research on extremely short-term prediction of real ship motion and envelope[J]. Ship Science and Technology, 2019, 41(6): 43-47. DOI:10.3404/j.issn.1672-7649.2019.06.009 |
| [6] |
彭秀艳, 赵希人, 高奇峰. 船舶姿态运动实时预报算法研究[J]. 系统仿真学报, 2007, 19(2): 267-271. PENG Xiuyan, ZHAO Xiren, GAO Qifeng. Research on real-time prediction algorithm of ship attitude motion[J]. Journal of System Simulation, 2007, 19(2): 267-271. DOI:10.3969/j.issn.1004-731X.2007.02.011 |
| [7] |
赵育善, 师鹏. 航天器飞行动力学建模理论与方法[M]. 北京:北京航空航天大学出版社, 2012.
|
| [8] |
魏晓峰. 舰艇用运动参考单元算法研究[D]. 哈尔滨:哈尔滨工程大学, 2020.
|
 2024, Vol. 46
2024, Vol. 46

