飞机着舰是一个十分复杂而又危险的过程,尤其是最后20 s的下滑道进近,对于飞行员来说无异于一次生死考验。着舰过程中的最大风险是飞机与航母舰尾的相撞。根据着舰安全规定,阻拦索回收状态下舰尾净空不得小于3.05 m,阻拦网回收状态下舰尾净空不得小于2.44 m,这是着舰信号官决定能否回收飞机的依据[1]。因此,舰尾净空是衡量飞机着舰安全性的一个重要指标。
众所周知,飞机在“海面移动漂浮的机场”上着舰。风浪引起航母的纵倾横摇和上下升沉运动会时刻影响着舰尾净空的变化,给准备着舰的飞机造成困难和严重威胁。对美军以往着舰事故的分析表明,25%以上的事故与自然环境有关,而风浪造成的甲板摇荡是最主要的事故原因,导致了其中15%的事故[1]。
由于航母运动对飞机着舰安全有着至关重要的影响,吸引了国内外众多学者对此开展研究。张勇等[2]介绍了美国舰载航空甲板运动准则的方法和形成历史,并详细分析了相关准则数值的确定背景。王可等[3 − 6]对甲板运动的预估进行研究,采用方法或模型有卡尔曼滤波法、粒子滤波法、伏尔特拉级数模型、灰色系统理论(Grey systemtheory)方法、鲁棒学习模型等。在航母运动模型方面,刘喜藏等[7]对几种常见的航母运动模型进行了对比分析,颜世伟等[8 − 10]采用基于功率谱的航母运动模型来模拟不同海况航母甲板运动。
国内外,关于航母运动的研究很多,但缺少关于着舰飞机舰尾净空的研究。考虑到舰尾净空对着舰安全的重要性,本文在建立航母甲板运动模型的基础上,考虑光学助降系统的基本参数和飞机的钩眼距,建立飞机着舰下滑的舰尾净空模型,分析飞机理想着舰下滑时航母运动对舰尾净空的影响,并提出应对舰尾净空不满足着舰要求时的措施,以期为飞机安全着舰提供理论参考。
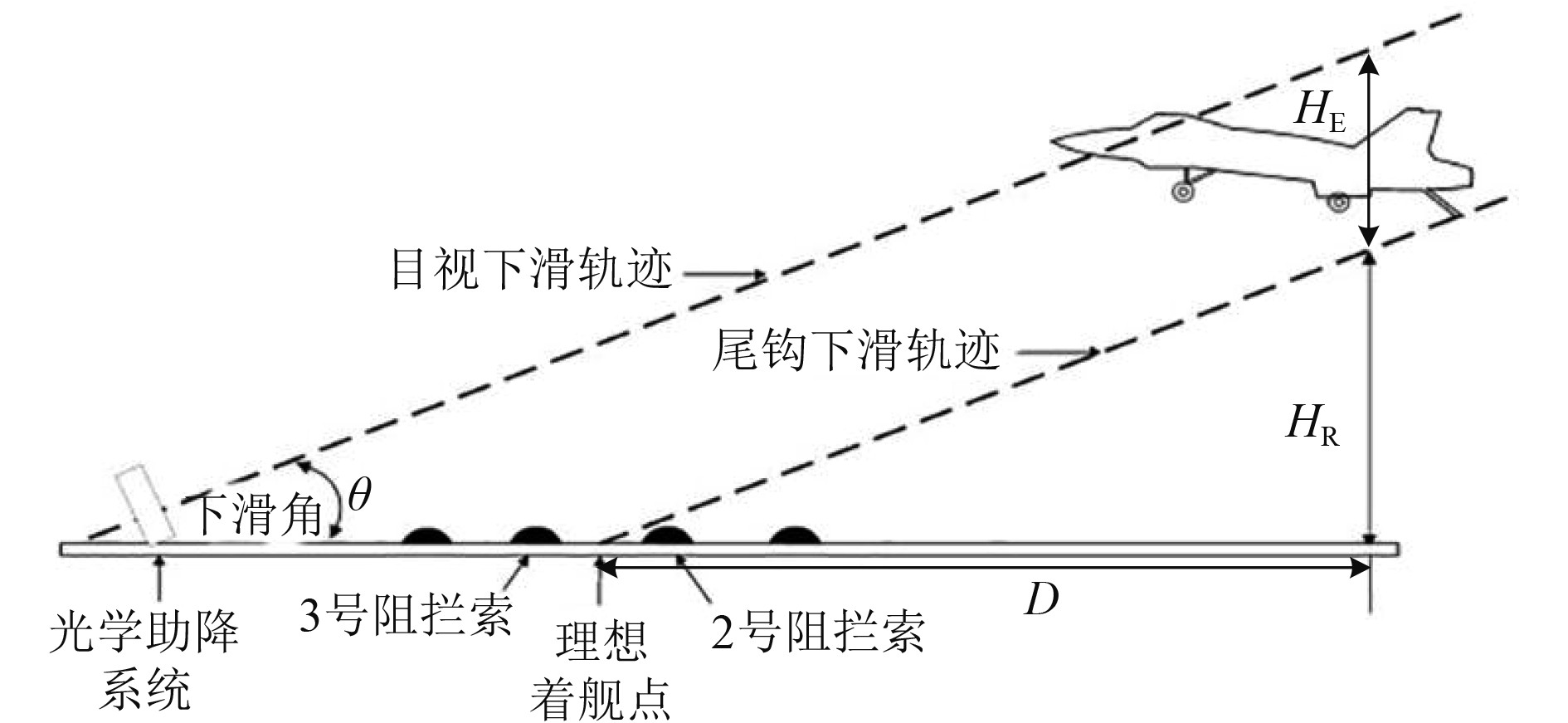
1 问题描述与基本假设飞机着舰时,下滑角度恒定且姿态固定,当飞行员的眼位沿着菲涅尔灯光指示的目视下滑轨迹进近着舰时,飞机的尾钩则沿着与之平行的下滑轨迹触舰,如图1所示。其中,2条下滑轨迹之间的高度差称为钩眼距HE,它由飞机的几何尺寸和下滑姿态确定。
|
图 1 飞机着舰下滑示意图 Fig. 1 Schematic diagram of shipborne aircraft landing |
在图1中,由尾钩下滑轨迹、着舰跑道中心线和过舰尾坡道的铅垂线围成直角三角形,有如下关系:
| $ {{H_R}} = D \times \tan {\theta}。$ | (1) |
式中:HR为舰尾净空,也称为钩坡距,定义为飞机通过航母舰尾上空时尾钩与舰尾坡道的距离;D为着舰点距离,定义为理想着舰点到舰尾坡道的距离;θ为下滑角,定义为尾钩下滑轨迹与甲板平面的夹角。
在甲板处于水平时,D、θ和HR保持不变;而在航母运动时,D、θ和HR则会发生动态变化。所以,利用式(1)只能对舰尾净空进行定量估算,并不能依此直接进行计算。实际上,舰尾净空的大小可由飞机尾钩和航母舰尾坡道在空间的相对位置关系来计算。在不考虑飞行员操纵技术的前提下,飞机过舰尾时的尾钩位置与光学下滑道及采取的稳定模式有关;而航母舰尾坡道主要受到纵摇、横摇和垂荡的影响,会造成垂直方向上的位置偏移。
根据以上对舰尾净空计算的描述,本文在模型建立过程中作出如下基本假设:
1)飞机能够始终沿着理想光学下滑道着舰;
2)只考虑航母纵摇、横摇和垂荡对舰尾净空的影响。
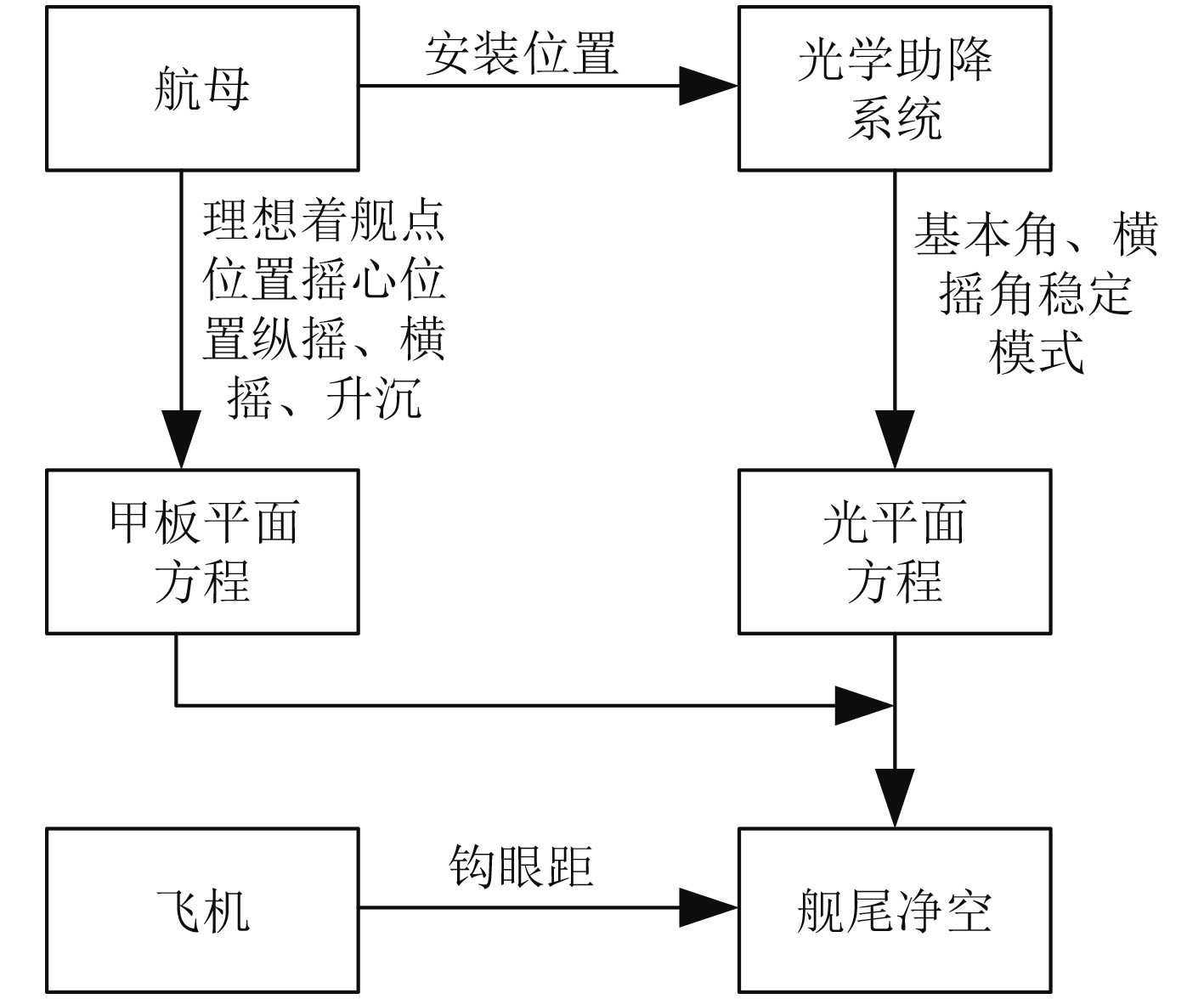
2 舰尾净空模型的建立 2.1 模型建立的基本思路舰尾净空模型的建立,包括:航母甲板运动模型的建立、航母甲板平面方程的计算、光学助降系统理想光平面方程的计算和舰尾净空下滑道的计算等,如图2所示。
|
图 2 舰尾净空的计算流程 Fig. 2 Calculation flow of stern clearance |
具体计算流程如下:
步骤1 建立计算舰尾净空的坐标系;
步骤2 根据航母甲板运动模型输出的横摇角、纵摇角和升沉值,计算当前航母姿态下的甲板平面方程;
步骤3 根据光学助降系统的安装位置及设定参数计算理想光平面方程;
步骤4 根据甲板平面方程和理想光平面方程的空间位置关系并考虑飞机的钩眼距计算出舰尾净空。
2.2 甲板运动模型的建立基于前述分析,在建立航母运动模型时,只需重点分析幅度变化较大且运动频率等级与飞机相匹配的纵摇、横摇和垂荡运动。
大量统计结果表明,充分发展的成熟期海浪是一个高斯分布各态历经的平稳随机过程,而航空母舰的尺寸和重量很大,舰船在一定海况、航向和航速的情况下可以被认为是一个线性定常系统,因此航母运动实际上是一个平稳随机过程。理论研究常将单位白噪声作用在成型滤波器上,得到航母时域运动模型。
文献[3]给出了美国ESSEX航母在航速为8 kn,海浪中心高度为5.18 m情况下的纵摇角θc、横摇角φc和垂荡zc的功率谱密度曲线所对应的成形滤波器:
| $ {\theta _c}(s) = \frac{{0.334\ s}}{{({s^2} + 0.22\ s + 0.303)({s^2} + 0.384\ s + 0.41)}} ,$ | (2) |
| $ {\phi _c}(s) = \frac{{0.238\ s}}{{({s^2} + 0.089\ s + 0.137)({s^2} + 0.12\ s + 0.25)}} ,$ | (3) |
| $ {z_c}(s) = \frac{{0.354\ s(s + 0.04)}}{{({s^2} + 0.16\ s + 0.16)({s^2} + 0.22\ s + 0.302)}} 。$ | (4) |
通过改变白噪声的采样时间,可以同时改变ESSEX航母功率谱航母运动模型的数据周期和幅值,从而建立相应航母在不同海况下的甲板运动模型。
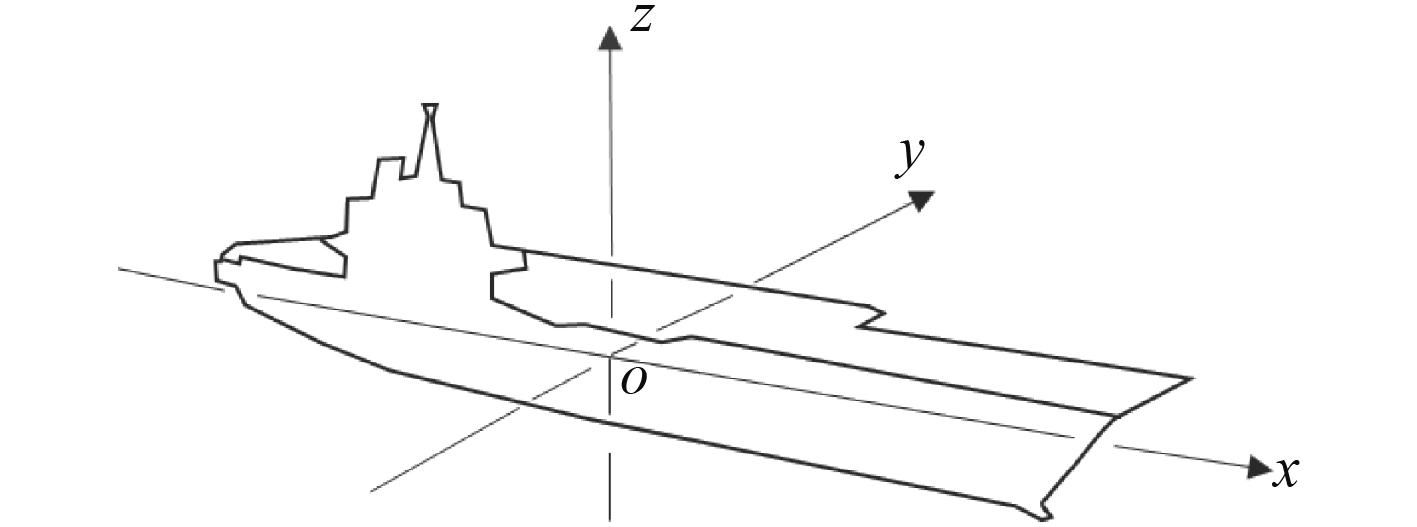
2.3 舰尾净空模型的建立如图3所示,建立航母甲板的惯性坐标系Oxyz(记为S)和舰体随动坐标系Osxsyszs(记为Ss)。
|
图 3 惯性坐标系 Fig. 3 Inertial coordinate system |
坐标系S的原点O位于航母摇心;x轴位于航母中纵剖面内,并与水线面平行,方向指向舰首;y轴与x轴垂直,指向左舷;z轴由右手定则确定。在S系中,设光学助降系统光束发出位置的坐标为M(xM, yM, zM)T。
航母在没有扰动而处于平衡位置时,坐标系Ss与坐标系S重合;航母发生扰动时,Ss系随航母运动,S系在惯性空间中保持静止。在Ss系中,设理想着舰点P的坐标为(xP,S, yP,S, zP,S)T,着舰跑道中心线舰尾端点E坐标为为(xE,S, yE,S, zE,S)T。
根据航母甲板运动模型计算的横摇角φ、纵摇角θ和首摇角ψ,可得Ss系与S系间的坐标变换矩阵T:(这里,舰体的姿态变换顺规按横摇-纵摇-首摇的顺序设定):
| $\boldsymbol{T}=\left[{\begin{array}{*{20}{c}} {\cos \psi \cos \theta }&{\sin \psi \cos \varphi + \cos \psi \sin \theta \sin \varphi }&{\sin \psi \sin \varphi - \cos \psi \sin \theta \cos \varphi } \\ { - \sin \psi \cos \theta }&{\cos \psi \cos \varphi - \sin \psi \sin \theta \sin \varphi }&{\cos \psi \sin \varphi + \sin \psi \sin \theta \cos \varphi } \\ {\sin \theta }&{ - \cos \theta \sin \varphi }&{\cos \theta \cos \varphi } \end{array}} \right] 。$ | (5) |
在S系中,航母处于平衡位置时,甲板的法向量v=(0,0,1)T。根据坐标变换原理,给定航母姿态下,甲板的法向量v′=T·v。理想着舰点P在航母当前姿态下的新位置P′的坐标(xP′, yP′, zP′)T可由下式求得:
| $ \left[ \begin{gathered} {x_{P'}} \\ {y_{P'}} \\ {z_{P'}} \\ \end{gathered} \right] = \boldsymbol{T} \cdot \left[ \begin{gathered} {x_{P,s}} \\ {y_{P,s}} \\ {z_{P,s}} \\ \end{gathered} \right] + \boldsymbol{V} 。$ | (6) |
其中,V为航母摇心位置的平移量,即:
| $ \boldsymbol{V} = \overrightarrow {O{O_S}} 。$ | (7) |
于是可得出当前航母姿态下,甲板所在平面在S系中的方程:
| $ \boldsymbol{v}' \cdot \left[ {\begin{array}{*{20}{c}} {x - {x_{P'}}} \\ {y - {y_{P'}}} \\ {z - {z_{P'}}} \end{array}} \right] = 0 。$ | (8) |
由于光平面在运动过程中,始终经过该点M。当光平面处于初始位置时,设光学助降系统的横摇轴和纵摇轴的方向向量分别为e1、e2。在光平面经过俯仰和滚转运动后,其横摇轴和纵摇轴的方向向量分别变为e′1和e′2,则:
| $ \boldsymbol{e}_{_1}^{'} = \left[ {\begin{array}{*{20}{c}} {\text{cos}}{\alpha} \cdot {\text{cos}}{\gamma} \\ {{\text{cos}}{\alpha} \cdot {\text{sin}}{\gamma}} \\ {-{\text{ sin}}{\alpha} } \end{array}} \right] 。$ | (9) |
| $ \begin{split} {\boldsymbol{e}}_2^{'} = &\overrightarrow {\boldsymbol{OM}} + \cos {\beta} \cdot ({e_2} - \overrightarrow {\boldsymbol{OM}} )+ \\ & (1 - \cos \beta ) \cdot (e_{_1}^{'} \cdot ({e_2} - \overrightarrow {\boldsymbol{OM}} )) \cdot \boldsymbol{e}_{_1}^{'} + \\ & \sin \beta \cdot (e_{_1}^{'} \cdot ({e_2} - \overrightarrow {\boldsymbol{OM}} ))。\end{split} $ | (10) |
式中,γ为着舰跑道与航母纵轴的夹角。
此时,光平面的法向量w=e′1×e′2,于是可得出当前航母姿态下光平面在S系中的方程:
| $ \boldsymbol{w} \cdot\left[\begin{array}{l} x-x_{M} \\ y-y_{M} \\ z-z_{M} \end{array}\right]=0 。$ | (11) |
以上是对于惯性稳定模式下,航母扰动后的光平面方程;线稳定模式下,需要先将点M的竖坐标ZM随着航母的垂荡而变化为ZM+h,其中,h为航母的垂荡量。
在航母当前姿态下,着舰跑道舰尾端点位置E′在S系下的坐标为:
| $ \left[ \begin{gathered} {x_{E'}} \\ {y_{E'}} \\ {z_{E'}} \\ \end{gathered} \right] = \boldsymbol{T} \cdot \left[ \begin{gathered} {x_{E,s}} \\ {y_{E,s}} \\ {z_{E,s}} \\ \end{gathered} \right] + \boldsymbol{V}。$ | (12) |
过E′作铅垂线,与光平面交于点E′′(xE′′,yE′′,zE′′),则显然有:xE′′=xE′,yE′′=yE′,将其带入光平面方程,可解出E′′的竖坐标zE′′,可按下式计算舰尾净空HR:
| $ H_R = {z_{E''}} - {z_{E'}} - H_E 。$ | (13) |
设定舰尾净空仿真分析的基本条件:飞机钩眼距为5.8 m;理想着舰点位于第2、3根阻拦索之间;着舰点距离D=70 m;光学助降系统采用惯性稳定模式,基本角为3.5°,横摇角为0°;海况等级为4级。由式(1)可得甲板处于水平位置时,HR=4.28 m。
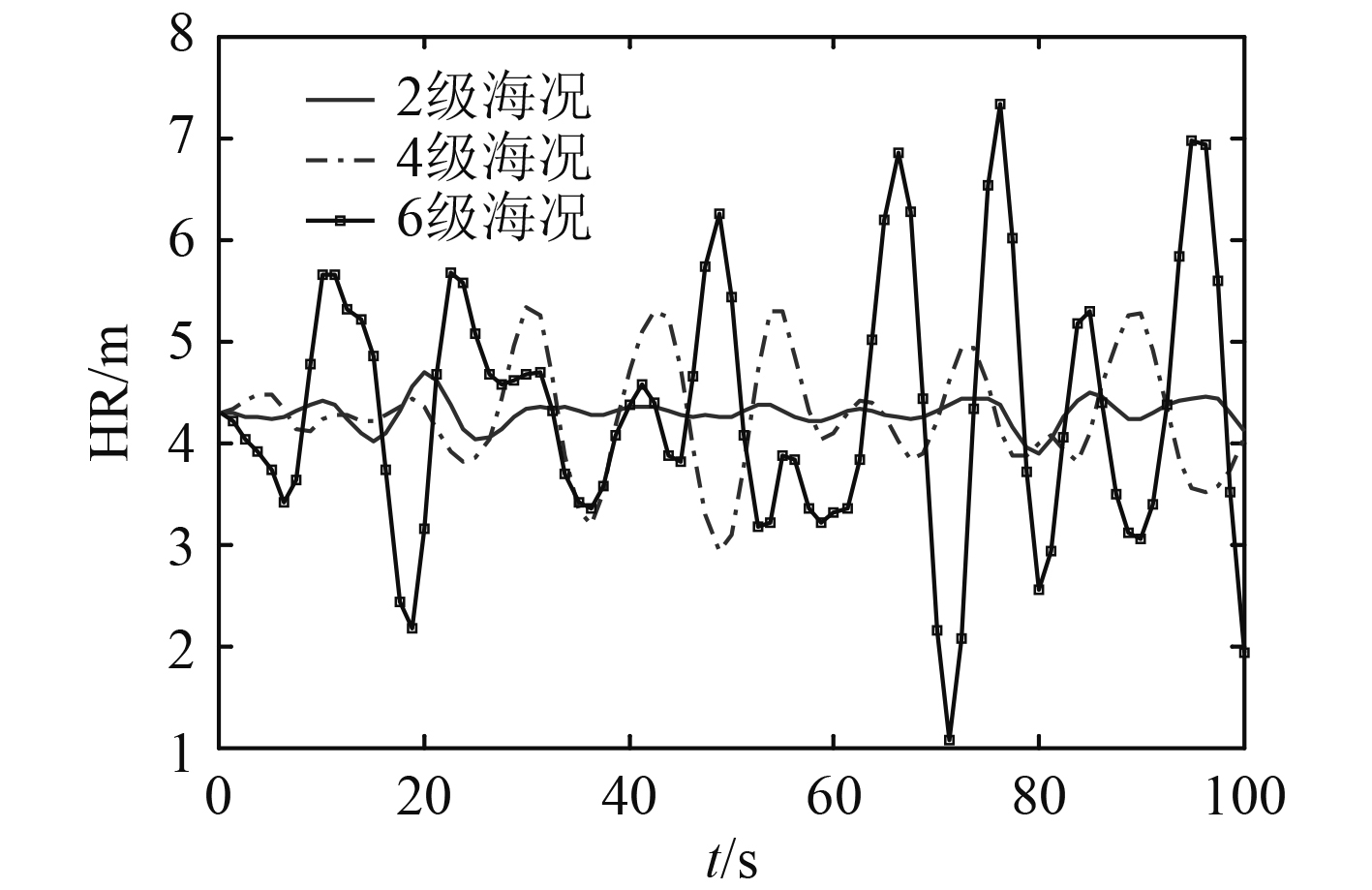
3.1 海况等级的影响在其他基本条件不变的情况下,分析海况等级的影响,海况分别取2级、4级和6级等3种情况,由舰尾净空模型可得不同海况条件下舰尾净空的曲线图,如图4所示。
|
图 4 不同海况下的舰尾净空 Fig. 4 Stern clearance with different sea conditions |
可知,海况等级2级至6级时,由于航母甲板舰尾垂直位移的幅值变化增大,导致舰尾净空的变化也较大,且出现舰尾净空无法满足着舰要求的情况增多,4级海况舰尾净空最小3.1 m,而6级海况舰尾净空最小只有1.1 m。但是总体而言,舰尾净空的变化仍然呈现与甲板运动周期性变化一致的特点,因此在高海况必须回收飞机时,着舰信号官要能提早预测并判断舰尾净空的动态变化,为飞行员选择有利的时机进行着舰。
3.2 稳定模式的影响在其他基本条件不变的情况下,分析稳定模式的影响,分别选择无稳定模式、惯性稳定和线稳定模式等3种情况,由舰尾净空模型可得不同稳定模式下舰尾净空的曲线图,如图5所示。
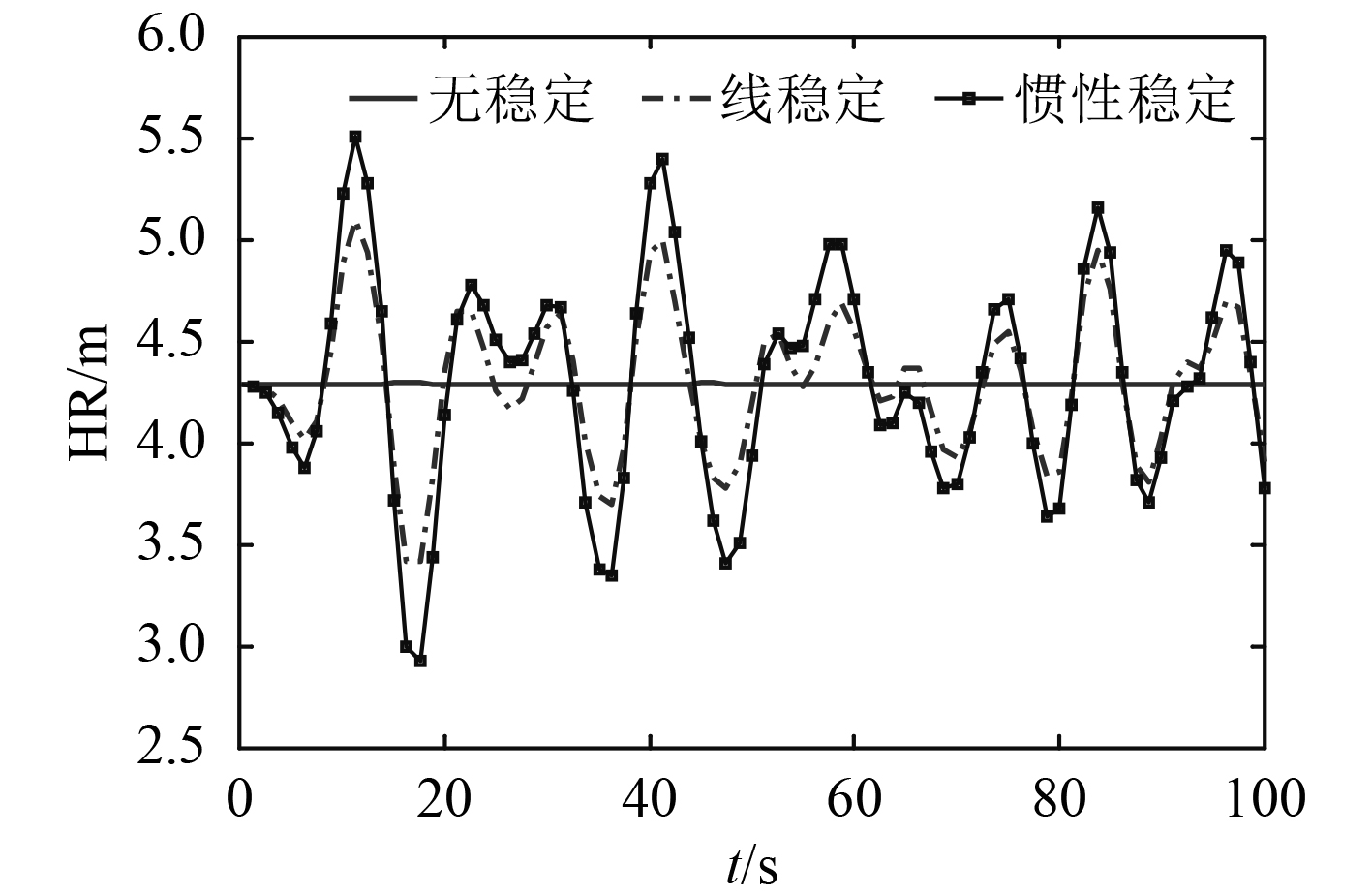
|
图 5 不同稳定模式下的舰尾净空 Fig. 5 Stern clearance with different stability modes |
可知,在相同海况条件下,无稳定模式时光学下滑道跟随甲板运动,不会引起舰尾净空的变化,基本保持在4.28 m不变;而惯性稳定模式和线稳定模式均会引起舰尾净空的变化;由于线稳定模式不补偿垂荡,在相同的海况下惯性稳定模式的舰尾净空变化更大,二者相差最大将近0.5 m。但是惯性稳定模式相对线稳定模式和无稳定模式会最大程度上减少了飞机的机动,减轻了飞行员的操纵负担,对于飞行员跟踪光学下滑道是有利的。
3.3 光学助降系统基本角的影响在其他基本条件不变的情况下,分析光学助降系统基本角的影响,基本角分别取3.25°、3.5°、3.75°和4.0°等4种情况,由舰尾净空模型可得不同基本角的舰尾净空曲线图,如图6所示。
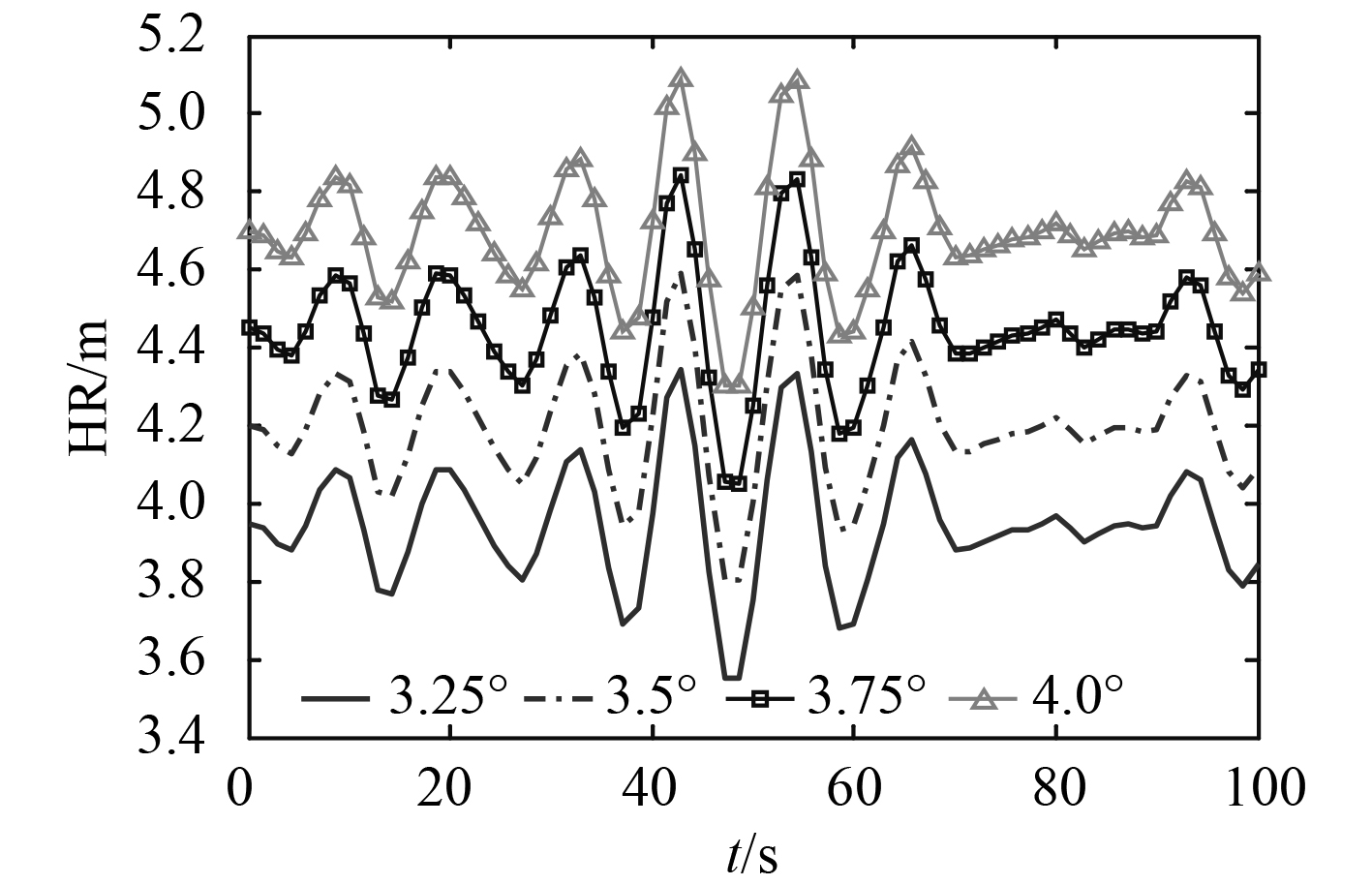
|
图 6 不同基本角的舰尾净空 Fig. 6 Stern clearance with different basic angles |
可知,改变基本角可以改变舰尾净空,基本角改变0.25°,舰尾净空变化大约0.30 m,这与式(1)得出结论是一致的。在海况等级较高出现较多不满足舰尾净空的情况时,着舰信号官可据此来调整,以保证着舰安全。
3.4 光学助降系统横摇角的影响在其他基本条件不变的情况下,分析光学助降系统横摇角的影响,横摇角分别取1°、0°和−1°等3种情况,由舰尾净空模型可得不同横摇角的舰尾净空曲线图,如图7所示。可知,改变横摇角也可以改变舰尾净空,横摇角改变1°,舰尾净空变化大约0.35 m。这是由于改变横摇角可以使得光学下滑道在跑道中心线前后移动,从而使得理想着舰点距离发生变化,从而可以改变舰尾净空。同样,在海况等级较高出现较多不满足舰尾净空的情况时,着舰信号官也可据此来调整,以保证着舰安全。
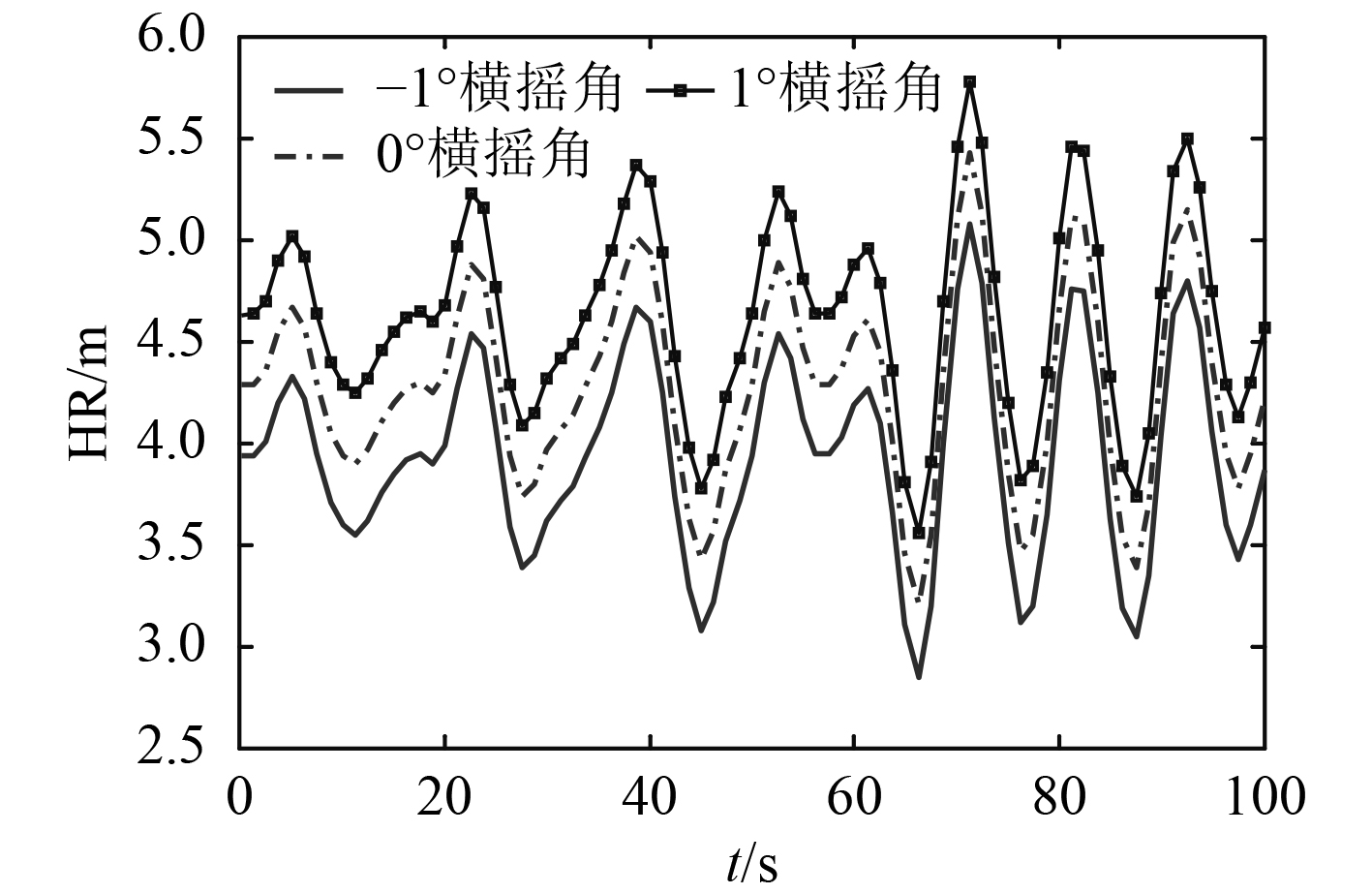
|
图 7 不同横摇角的舰尾净空 Fig. 7 Stern clearance with different roll angles |
因此,在舰尾净空不满足的条件下,着舰信号官通过改变光学助降系统的基本角和横摇角可以实现舰尾净空调整的目的。改变横摇角前移理想着舰点可以实现舰尾净空增加,但是由于此时理想着舰点更靠近最后一道阻拦索,会增加飞机逃逸复飞的概率。而增加基本角理论上对着舰成功率没有影响,但是会增加飞机下降率,由于飞机对下降率有严格的控制要求,所以增加基本角还需要通过更大的回收逆风来补偿,这就对母舰航速提出了相应的要求。当单独采用改变横摇角前移理想着舰点位置或增加基本角的方法都不能达到舰尾净空要求,或虽能达到该要求,但逃逸复飞率过高、无法提供足够的回收逆风时,可同时采用2种方法。
航母经常要回收多种型号的飞机,比如尼米兹号航母要回收F-18、E-2C、C-2等飞机,舰尾净空就需要满足不同机型的要求。为了满足舰尾净空的要求,只要尾钩着舰点位置保持不变,不同机型的舰尾净空就能保持一致。由于不同机型的钩眼距不同,这就使得舰尾处光学下滑道的高度不同,这可通过调整光学助降系统的横摇角来实现。
4 结 语在不同海况条件下,考虑光学助降系统不同下滑道稳定模式、不同光学基本角和不同横摇角的情况,本文建立了飞机着舰下滑的舰尾净空模型,并得出以下结论:
飞机沿理想光学下滑道着舰时,舰尾净空发生变化是海况引起的航母舰尾垂直偏移与光学下滑道稳定模式共同作用的结果,利用该模型可以计算不同海况、不同稳定模式下的舰尾净空。
利用该模型还可以实现舰尾净空的调整,可以利用式(1)来进行估算,1°基本角可以使舰尾净空大约改变
| [1] |
U. S. Navy Landing Signal Officers School. Landing signal officers reference manual[M]. Virginia: Naval Air StationOceana, 1999.
|
| [2] |
张勇, 周益. 美国舰载航空甲板运动准则[J]. 中国舰船研究, 2012, 7(1): 7-11. ZHANG Yong, ZHOU Yi. Deck motion criteria for flight operations aboard USN aircraft carriers[J]. Chinese Journal of Ship Research, 2012, 7(1): 7-11. DOI:10.3969/j.issn.1673-3185.2012.01.002 |
| [3] |
王可, 徐明亮, 李亚飞, 等. 一种面向航空母舰甲板运动状态预估的鲁棒学习模型[J/OL]. 自动化学报: 1−9[2024-08-27]. WANG K, XU M L, LI Y F, et al. A robust learning model for deck motion prediction of aircraft carrier[J/OL]. Acta Automatica Sinica: 1−9[2024-08-27]. |
| [4] |
邢伯阳, 潘峰, 王位, 等. 基于复合地标导航的动平台四旋翼飞行器自主优化降落技术[J]. 航空学报, 2019, 40(6): 214−225. XING B Y, PAN F, WANG W, et al. Moving platform self-optimization landing technology for quad-rotor based on hybrid landmark[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(6): 214−225. |
| [5] |
BHATIA A K, JU J, KUMAR A, et al. Adaptive pre-view control with deck motion compensatio for autonomouscarrier landing of an aircraft[J]. International Journal of AdaptiveControl Signal Processing, 2021, 35(5): 769−785.
|
| [6] |
ZHEN Ziyang, JIANG Shuoying, MA Kun. Automatic carrier land-ing control for unmanned aerial vehicles based on preview con-trol and particle filtering[J]. Aerospace Science and Technology, 2018, 81: 99−107.
|
| [7] |
刘喜藏, 林皓, 张玲. 航母在不同海况下的运动仿真研究[C]// 2020中国航空工业技术装备工程协会年会论文集, 2020. LIU Xicang, LIN Hao, ZHANG Ling. Simulation of carrier motion in different sea-states[C]// Proceedings of the 2020 Annual Meeting of China Aviation Industry Technical Equipment Engineering Association, 2020. |
| [8] |
颜世伟, 郝佳, 李海旭. 基于航母运动的舰载机自动着舰落点分布研究[J]. 舰船科学技术, 2021, 43(21): 173-178. YAN Shiwei, HAO Jia, LI Haixu. Research on distribution of carrier aircraft landing point with the movement of aircraft carrier[J]. Ship Science and Technology, 2021, 43(21): 173-178. |
| [9] |
许东松, 刘星宇, 王立新. 航母运动对舰载飞机着舰安全性的影响[J]. 北京航空航天大学学报, 2011, 37(3): 289-294. XU Dongsong, LIU Xingyu, WANG Lixin. Influence of carrier motion on landing safety for carrier-based airplanes[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(3): 289-294. |
| [10] |
MISRA G, GAO T Y, BAI X L. Modeling and simulation of UAV carrier landing [C]// AIAA Scitech 2019 Forum, 2019.
|
 2024, Vol. 46
2024, Vol. 46
