海洋交通环境中,多船舶之间的相互通信对于确保航行安全、提高运输效率至关重要。复杂多变的海洋环境,容易导致通信信号之间存在相互干扰,不仅会影响船舶通信质量,增加数据传输的误码率,还可能对船舶的航行安全构成威胁[1-2]。
余文曌等[3]研究了船舶精细抗干扰控制方法,引入动态面控制技术和鲁棒自适应项方法,实现船舶通信干扰控制,但其适应性有限。在极端恶劣的海况下,带宽、功率等通信资源受到影响,从而降低通信系统的整体效率。董秀娟等[4]研究用于复杂环境的多径电子通信信号抗干扰方法,但是该方法在深海、极地等极端或复杂的通信环境中,实施难度较大。且受信号强度、干扰源类型、信道条件等因素影响,即使采用了抗干扰措施,也无法完全消除干扰对通信的影响。赵辰乾等[5]研究有色噪声下的GNSS空时抗干扰算法,通过联合空域和时域信息,在多个维度上抑制干扰信号,特别是在面对多径干扰和有色噪声时,其抗干扰性能优越。但是在有色噪声环境下,空时抗干扰算法的性能会显著下降,导致信号失真和误差增大。针对以上方法在通信抗干扰中存在的问题,设计基于径向基函数的多船舶相互通信信号干扰消除方法。利用RBF神经网络的非线性逼近能力,对接收到的船舶通信信号进行实时处理,消除干扰成分。
1 多船舶相互通信信号干扰消除方法 1.1 多船舶相互通信信道模型构建对多船舶通信信号传输的信道进行建模,提取多船舶通信信号的频率、幅度等特征参数。将多船舶相互通信的信道模型中包含的通信特征参数,作为RBF神经网络的输入,用于后续的干扰消除处理。采用海洋岸基信道模型实现多船舶的相互通信。设置岸边基站以及海洋中的船舶分别作为信道模型的发射机以及接收机[6]。ht与hr分别为发射机与接收机的天线高度,he与S分别为海上蒸发波导层高度以及路径传输损耗,f与
| $ {S_1} = 20{\log _{10}}\left( f \right) + 20{\log _{10}}\left( l \right)。$ | (1) |
2-ray模型路径损耗如下:
| $ {S_2} = - {\log _{10}}\left\{ {{{\left( {\frac{\lambda }{{4{\text{π}} l}}} \right)}^2}{{\left[ {2\sin \left( {\frac{{2{\text{π}} {h_t}{h_r}}}{{\lambda l}}} \right)} \right]}^2}} \right\}。$ | (2) |
设多船舶相互通信时,存在水平均匀蒸发管层[6]。he表示蒸发波导层高度,获取3-ray模型路径损耗如下:
| $ \begin{gathered} {S_3} = - 10{\log _{10}}\left\{ {{{\left( {\frac{\lambda }{{4{\text{π}} l}}} \right)}^2}} \right. \left. {{ {\left[ {1 + 2\sin \left( {\frac{{2{\text{π}} \left( {{h_e} - {h_t}} \right)\left( {{h_e} - {h_r}} \right)}}{{\lambda l}}} \right)} \right]}^2}} \right\}。\end{gathered} $ | (3) |
利用以上过程,构建多船舶相互通信的信道模型,模拟多船舶相互通信的实际运行情况,确定多船舶通信信号的频率、幅度等特征参数。
1.2 基于聚类算法的径向基神经网络将多船舶通信信号的特征参数作为径向基神经网络的输入。径向基神经网络的输出,能够逼近无干扰时的理想通信信号,从而实现干扰的消除。由输入层、隐含层以及输出层组成径向基神经网络。
| $ {h_i}\left( x \right) = \exp \left( { - \frac{{{{\left\| {x - {\varphi _i}} \right\|}^2}}}{{2\sigma _i^2}}} \right)。$ | (4) |
式中:
输出层节点
| $ {y_k}\left( x \right) = \sum\limits_{i = 1}^m {{w_k}} {h_i}\left( x \right) + {\varepsilon _k}。$ | (5) |
式中:wk与εk分别为隐含层与输出层的连接权重以及输出层的节点偏差;
径向基神经网络中,隐含层节点中心以及基函数宽度,决定了消除通信信号干扰时的收敛速度。选取聚类算法确定径向基神经网络的参数,设置聚类中心μi,作为径向基函数的中心向量。径向基函数宽度的表达式如下:
| $ {\sigma _i} = \frac{{{d_{\max }}}}{{\sqrt {2m} }}。$ | (6) |
式中,dmax表示各径向基函数中心的最大距离。
选取最小二乘法,获取径向基神经网络的权值参数,将式(5)转化为矩阵形式如下:
| $ Y = Hw。$ | (7) |
式中,
利用
| $ w = H'Y。$ | (8) |
利用以上过程获取径向基函数的中心参数以及宽度参数。径向基神经网络训练过程中,仅需要获取隐含层输出矩阵的伪逆,即可利用式(8)获取隐含层及其对应权重。
1.3 基于梯度学习方法的径向基神经网络学习引入遗忘因子,利用梯度学习方法对径向基神经网络训练。通过最小化目标函数的方式,调节隐含层神经元数量及权值。定义径向基神经网络学习的目标函数如下:
| $ \min E = \frac{1}{2}\sum\limits_{i = 1}^m {\xi e_i^2}。$ | (9) |
式中,ζ与ei分别为遗忘因子以及误差信号。
多船舶相互通信误差信号ei的表达式如下:
| $ {e_i} = {y_i} - \sum\limits_{i = 1}^m {{w_i}{\varphi _i}\left( {{x_i}} \right)}。$ | (10) |
利用径向基函数,更新多船舶相互通信信号特征数据中心μi梯度的表达式如下:
| $ \nabla {\mu _i} = \frac{{2{w_i}}}{{\sigma _i^2}}{\varphi _i}\left( {{x_i}} \right)\left( {{x_i} - {\mu _i}} \right)。$ | (11) |
权值梯度wi的更新表达式如下:
| $ \nabla {w_i} = {\varphi _i}\left( x \right)。$ | (12) |
考虑遗忘因子对多船舶相互通信信号干扰消除的影响,使用大量带有干扰的多船舶相互通信的信号样本对RBF神经网络训练,通过调整网络参数优化其信号干扰消除性能。将完成训练的RBF神经网络应用于多船舶通信网络中,实时处理接收的信号,消除其中的干扰成分,恢复出原始通信信号。
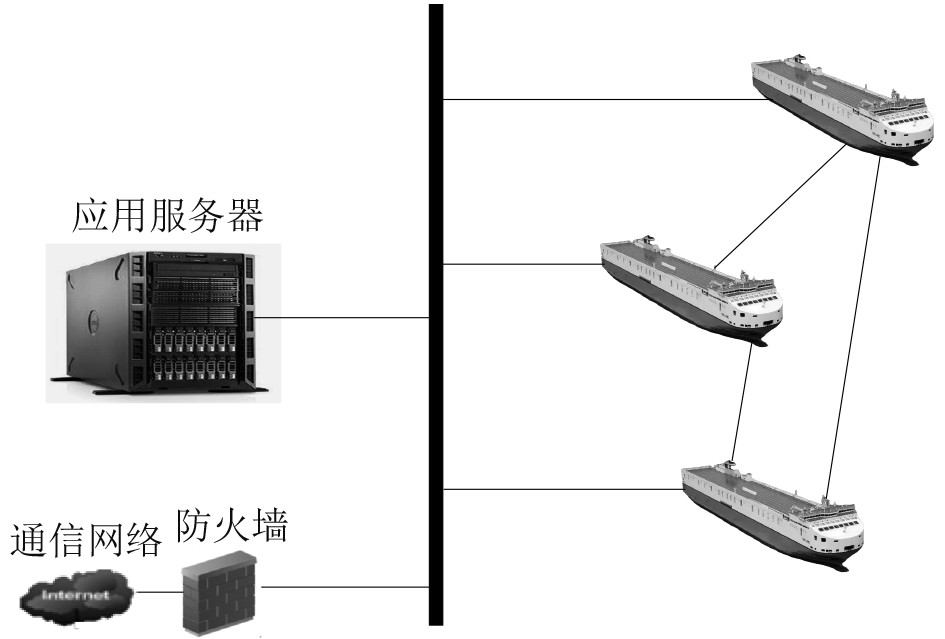
2 实例分析为了验证本文方法消除多船舶相互通信信号干扰的性能,将该方法应用于某海域的多船舶通信网络中。该船舶通信网络的结构图如图1所示。
|
图 1 船舶通信网络结构图 Fig. 1 Structure diagram of ship communication network |
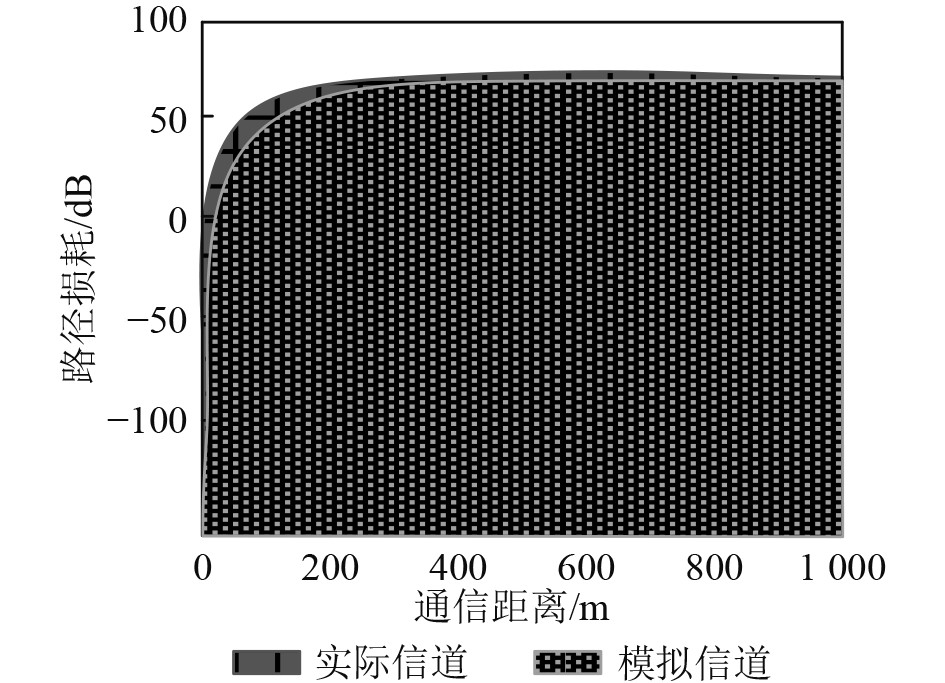
统计采用本文方法构建的船舶通信信道模型的路径损耗,如图2所示。可以看出,采用所构建的信道模型,能够有效模拟船舶通信网络的多船舶相互通信过程中,通信路径的损耗情况。图2的路径损耗拟合曲线,与网络的实际路径损耗曲线极为贴合。结果验证本文方法构建的信道模型,能够有效模拟多船舶相互通信时的信道变换情况,模型的匹配程度较高,拟合精度能够达到预期目标。
|
图 2 通信网络路径损耗 Fig. 2 Communication network path loss |
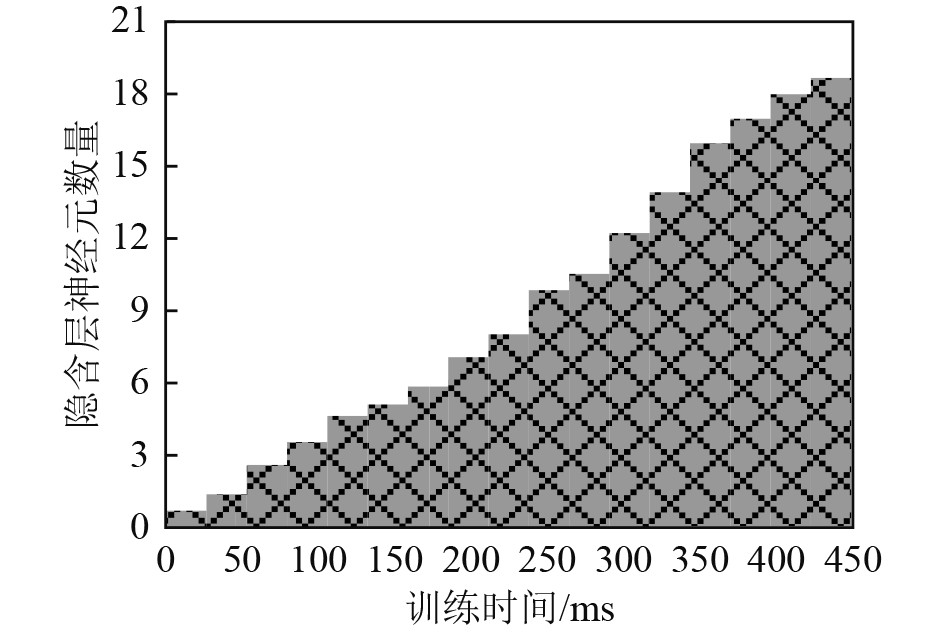
本文方法利用径向基神经网络消除多船舶相互通信信号干扰,统计不同训练时间时,径向基神经网络隐含层节点数量变化,统计结果如图3所示。可以看出,本文方法采用的径向基神经网络学习过程中,隐含层内神经元数量逐渐增加。实验结果验证,采用本文方法消除多船舶相互通信信号干扰,具有较高的自适应调整性能,能够将径向基神经网络调整至最佳状态,提升通信信号干扰消除性能。
|
图 3 隐含层节点数量变化 Fig. 3 Changes in the number of hidden layer nodes |
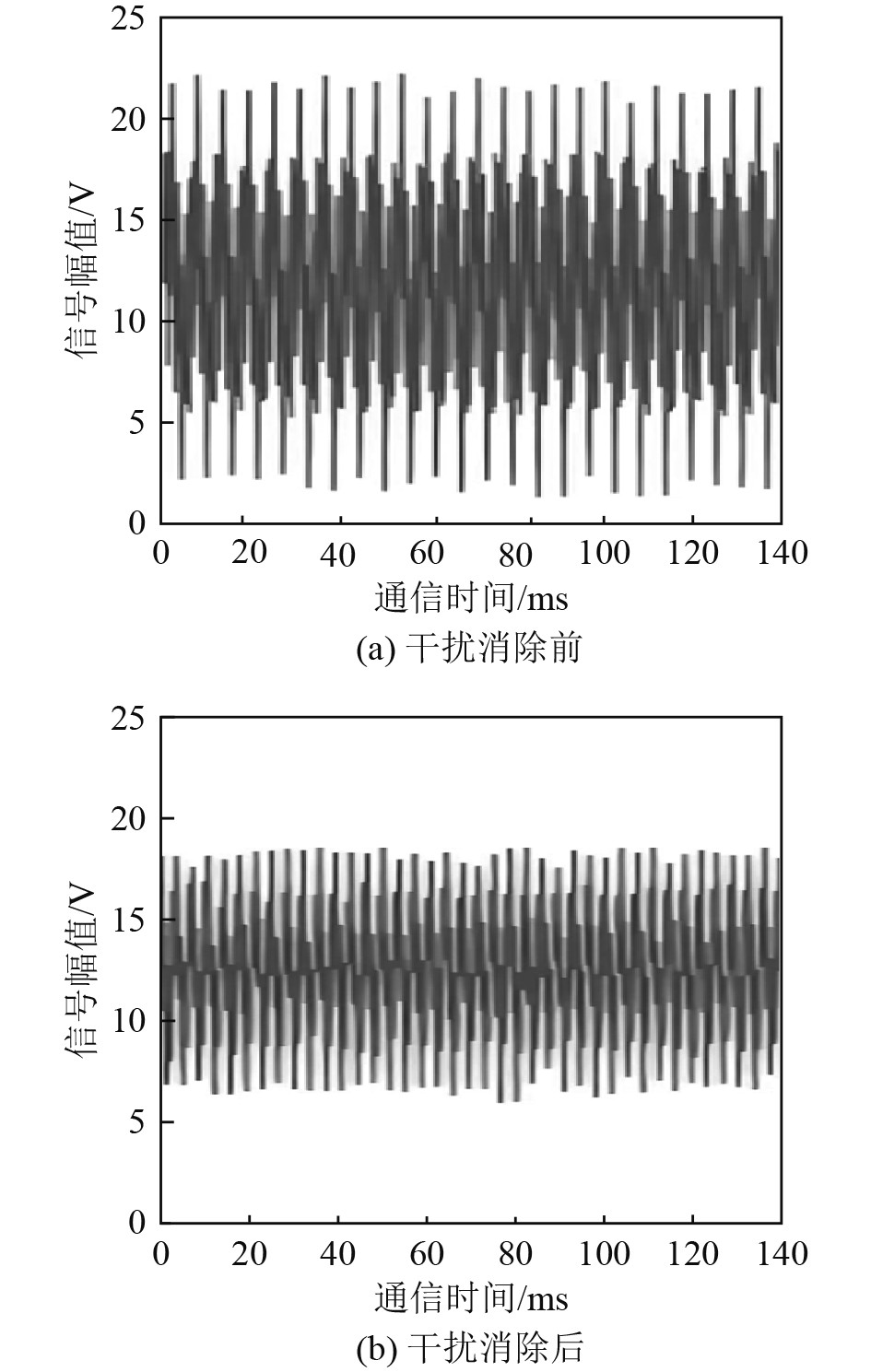
统计采用本文方法进行多船舶相互通信信号干扰消除,干扰消除前后的信号幅值变化,统计结果如图4所示。可以看出,采用本文方法能够有效消除多船舶相互通信时的通信干扰。在复杂多变的海洋环境中,通信信号的稳定性是保障航行安全的重要因素。本文方法通过提高多船舶相互通信信号的抗干扰能力,增强多船舶通信网络的稳定性。
|
图 4 通信信号干扰消除结果 Fig. 4 Communication signal interference elimination results |
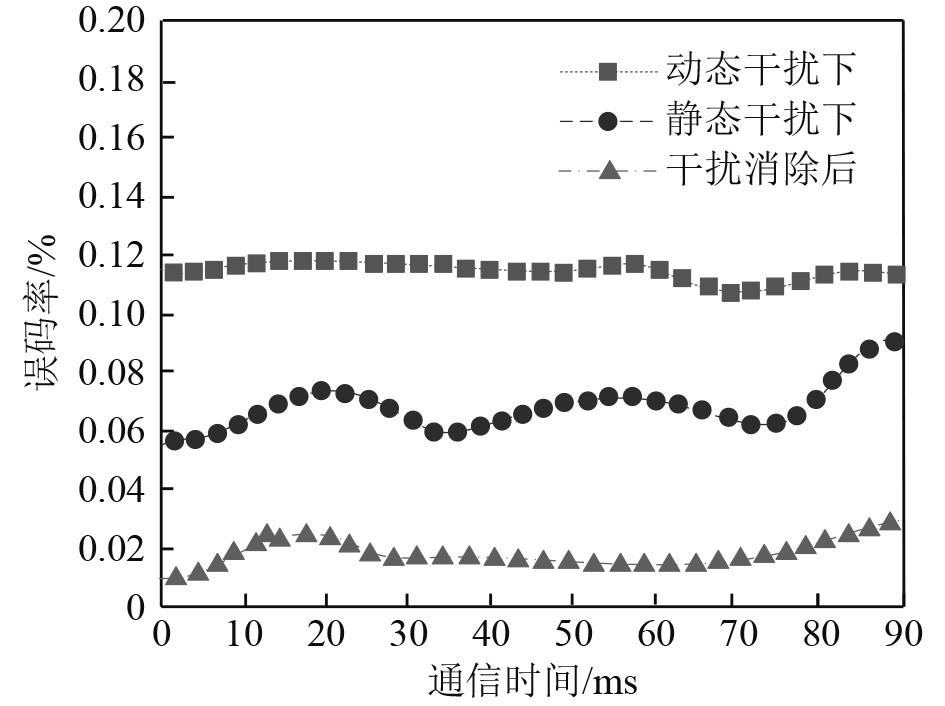
统计采用本文方法消除多船舶相互通信时的通信干扰,通信信道的误码率变化,统计结果如图5所示。可以看出,采用本文方法消除多船舶相互通信时的通信干扰,信道的误码率有了明显地降低。本文方法通过消除通信信号中的干扰成分,提高数据传输准确性和可靠性,降低通信误码率,从而改善多船舶通信网络的整体性能,提升船舶通信网络的通信质量。
|
图 5 信道误码率变化 Fig. 5 Changes in channel error rate |
将RBF神经网络应用于多船舶通信信号干扰消除中,通过实验证明了其有效性。RBF神经网络具有强大的非线性逼近能力,能够准确识别并消除通信信号中的干扰成分,显著提高信号质量。采用该方法后,船舶通信传输的误码率明显降低,通信的可靠性和稳定性得到了增强。该方法对于保障船舶航行安全、提高运输效率具有重要意义。确保了船舶在复杂多变的海洋环境中,能够保持稳定的通信联系。
| [1] |
张国庆, 刘上, 郎雷, 等. 具有速度调节机制的船舶事件触发编队控制[J]. 控制理论与应用, 2022, 39(12): 2377-2384. ZHANG Guoqing, LIU Shang, LANG Lei, et al. Event-triggered formation control for under actuated ships with the speed regulating mechanism[J]. Control Theory & Applications, 2022, 39(12): 2377-2384. |
| [2] |
尚勇志, 赵亮. 基于径向基函数的双体风电运维船型线和片体间距优化[J]. 中国海洋平台, 2022, 37(1): 70-75. SHANG Yongzhi, ZHAO Liang. Optimization of profile and side-hull spacing of wind turbine operation and maintenance catamaran based on radial basis function[J]. China Offshore Platform, 2022, 37(1): 70-75. DOI:10.12226/j.issn.1001-4500.2022.01.20220112 |
| [3] |
余文曌, 陈浩宇, 徐海祥, 等. 面向多源干扰的动力定位船舶精细抗干扰控制[J]. 控制与决策, 2023, 38(7): 2035-2041. YU Wenzhao, CHEN Haoyu, XU Haixiang, et al. Elegant anti-disturbance control of dynamic positioning in the presence of multi-source disturbance[J]. Control and Decision, 2023, 38(7): 2035-2041. |
| [4] |
董秀娟, 兰建平, 梁西银. 用于复杂环境的多径电子通信信号抗干扰仿真[J]. 计算机仿真, 2023, 40(1): 218-222. DONG Xiujuan, LAN Jianping, LIANG Xiyin. Anti-jamming simulation of multi-path electronic communication signals for complex environments[J]. Computer Simulation, 2023, 40(1): 218-222. DOI:10.3969/j.issn.1006-9348.2023.01.040 |
| [5] |
赵辰乾, 刘益辰, 刘欣. 有色噪声下GNSS空时抗干扰算法的性能分析和改进[J]. 电子与信息学报, 2022, 44(4): 1388-1394. ZHAO Chenqian, LIU Yichen, LIU Xin. Effect of colored noise on STAP algorithm for GNSS anti-jamming and algorithm improvement[J]. Journal of Electronics & Information Technology, 2022, 44(4): 1388-1394. DOI:10.11999/JEIT210174 |
| [6] |
闫辉, 周国华. 基于Kalman滤波的船舶磁化干扰系数测量算法[J]. 中国舰船研究, 2022, 17(4): 164-169. YAN Hui, ZHOU Guohua. Measurement of ship's magnetization parameters based on Kalman filtering method[J]. Chinese Journal of Ship Research, 2022, 17(4): 164-169. |
 2024, Vol. 46
2024, Vol. 46
