在人类不断对海洋资源进行探索和开发中,水下图像作为水下信息获取的最有效途径,近年来一直成为人们关注的热点之一。由于清晰的水下图像和视频在各种水下作业中起着重要作用,包括海洋生物学研究、海洋考古学和水下目标检测等。然而,由于光在水下的特定衰减和散射,通过相机传感器的水下图像容易发生退化,通常情况下,光在水下的衰减会导致水下图像发生颜色偏移,而水中悬浮物的各种散射光会使水下图像变得模糊并且对比度降低。水下图像质量的退化会严重影响人眼视觉感知效果以及进一步的科学研究,因此,水下图像增强具有极高的研究价值。
1 相关工作近年来,国内外有大量学者对水下图像增强进行了相关研究,并提出了一系列的方法理论。目前,对于水下图像增强的主要方法分为基于物理模型的方法、基于非物理模型的方法和基于深度学习的方法。例如,Li等[1]提出了一种基于灰度世界理论的颜色校正算法,该算法主要通过蓝绿通道去雾和红通道色彩补偿,然后用自适应曝光图来平衡校正之后图像的整体颜色,但是对于细节恢复不明显。Mishra等[2]对限制对比度自适应直方图均衡(Contrast Limited Adaptive Histogram Equalization,CLAHE)进行改进并应用与水下图像增强,提升了水下图像的对比度,但无法解决色偏问题。He等[3]提出一种暗通道先验算法(Dark Channel Prior,DCP),该算法最初主要用于陆地上图像的去雾,但由于水下图像的退化模糊与陆地上拍摄的有雾图像具有一定的相似性因而将该算法借用到水下图像处理,但在水中由于水对光有选择性的吸收,无法解决水下图像的色偏问题,具有一定局限性。Rrews等[4]建立在DCP的基础上,依据水下光学传播的特性,并假设水下视觉信息的主要来源在于蓝色和绿色通道,提出了一种水下暗通道先验算法(Underwater Dark Channel Prior,UDCP),该算法能够解决水下杂志引起的散光问题,但是对于图像边缘区域处理不够好,容易产生伪影。Ancuti等[5]提出一种基于颜色补偿与白平衡的多尺度融合方法,该方法基于灰色世界假设估计和补偿光源色偏,并利用白平衡水下图与权重图进行多尺度融合,能够有效提高图像全局对比度与边缘清晰度,但色彩补偿使图像整体偏暗,忽视了图像的背景区域,导致图像欠缺真实度。Fu等[6]提出了一种基于Retinex的水下单幅图像增强方法。该方法首先采用快速有效的策略解决偏色问题,使暗区变亮,增强图像的边缘和细节,但迭代优化和多步转换影响了算法的实时性。
而基于深度学习的方法主要依赖于丰富的训练数据和强大的监督学习模型以此来增强图像的视觉效果[7 − 12]。目前,基于生成对抗网络(Generate Adversarial Networks,G-AN)的优势,已经提出了各种基于深度学习的方法,例如WaterCycleGAN[8],WaterGAN[9],UGAN[10]和DenseGAN[11]。基于深度学习的水下图像增强方法取得了很好的效果,但这种方法依赖于丰富的训练数据集。人工合成的水下图像与真实的水下图像之间还存在一定差距,不同水体类型下的水下图像获取比较困难。同时,深度学习方法在不同场景下的泛化能力较差,部分增强不足或过度增强场景的增强效果较差。
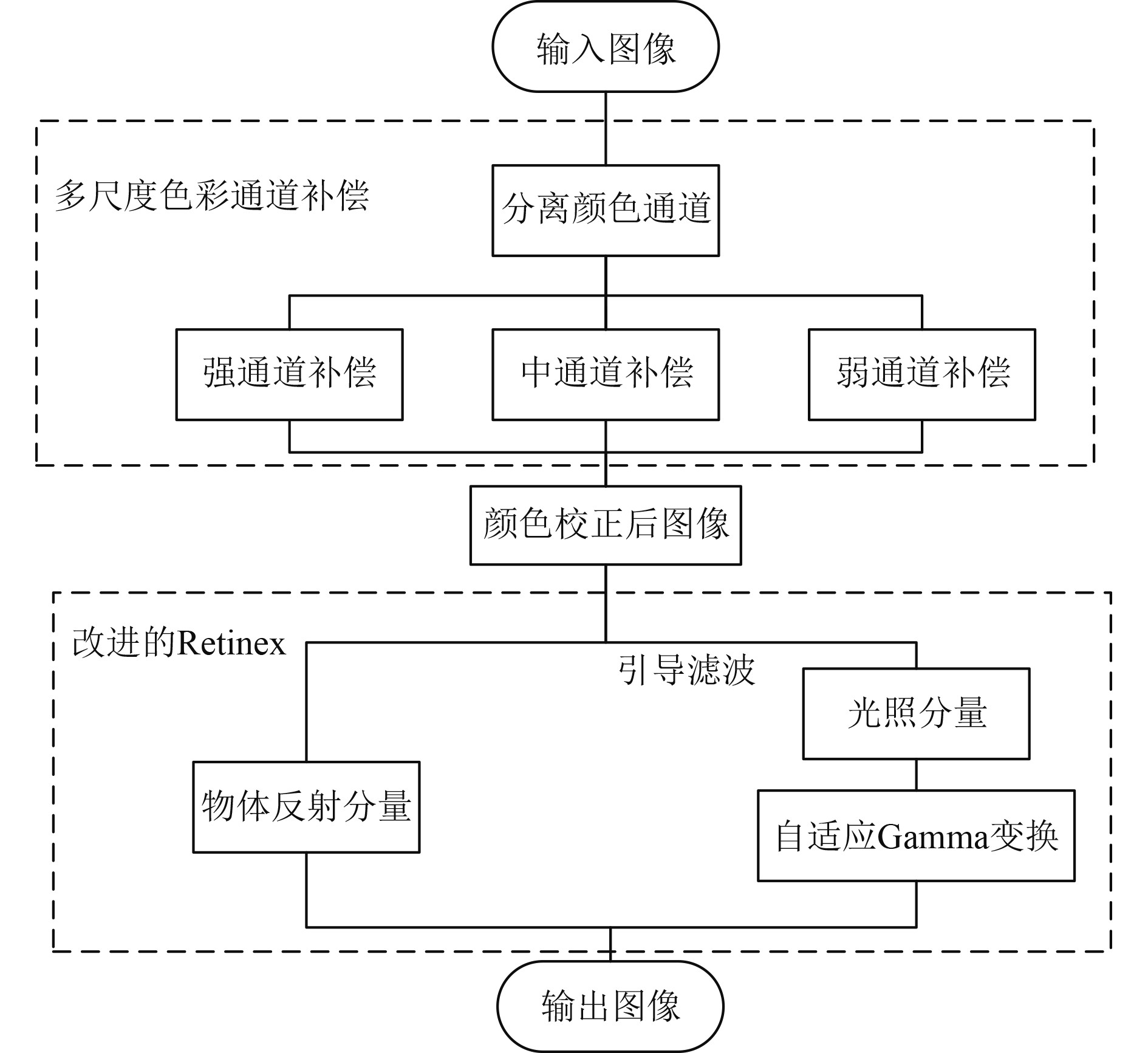
基于以上针对水下图像处理边缘细节不够好、对比度差和色偏严重等问题,本文提出一种融合多尺度的颜色衰减补偿算法,将图像分离为强、中、弱3个通道,依据衰减程度不同的现状依次进行补偿,可以有效校正色偏并防止过度补偿;其次利用改进的多尺度Retinex算法增加图像的对比度,在求取图像的光照分量中利用引导滤波替换高斯滤波,可以快速并有效保持边缘细节,然后利用自适应伽马函数有效校正光照不均匀的区域。整体算法流程图如图1所示。
|
图 1 本文算法流程图 Fig. 1 Algorithm flowchart of this article |
在水下拍摄照片时,由于光在水下传播会发生一定程度衰减的特性,所拍摄的照片会发生不同程度的颜色失真。在浅水区域,红色光衰减的最快,绿色光衰减程度最弱,因此浅水区域的水下图像通常呈现泛绿色,而在深水区域中蓝光衰减最弱,因此深水区中图像通常呈现泛蓝色。对于一张水下图像,首先分别计算出它的R、G、B这3个通道像素的总值,像素总值最大的通道定义为强通道P,像素总值位于中间的通道定义为中通道M,像素值最小的通道则定义为低通道S[13]。对于强通道P,本文使用传统的线性拉伸算法来拉伸强通道,其拉伸过程可表示为:
| $ {P}_{E}(x,y)=\frac{P(x,y)-{P}_{\text{min}}}{{P}_{\text{max}}-{P}_{\text{min}}}\times 255。$ | (1) |
式中:
| $ \begin{gathered} {M}_{E}(x,y)= \, M(x,y)+\left({P}_{\text{ave}}\right(x,y)-{M}_{\text{ave}}(x,y\left)\right)\times\\ (1-M(x,y\left)\right)\times P(x,y)。\end{gathered} $ | (2) |
式中:
| $ \begin{gathered} {S}_{E}(x,y)=\, S(x,y)+\frac{{\sigma }_{P}}{{\sigma }_{S}}\left({P}_{ave}\right(x,y)-{S}_{ave}(x,y\left)\right)\times \\ (1-S(x,y\left)\right)\times P(x,y) 。\end{gathered} $ | (3) |
式中:
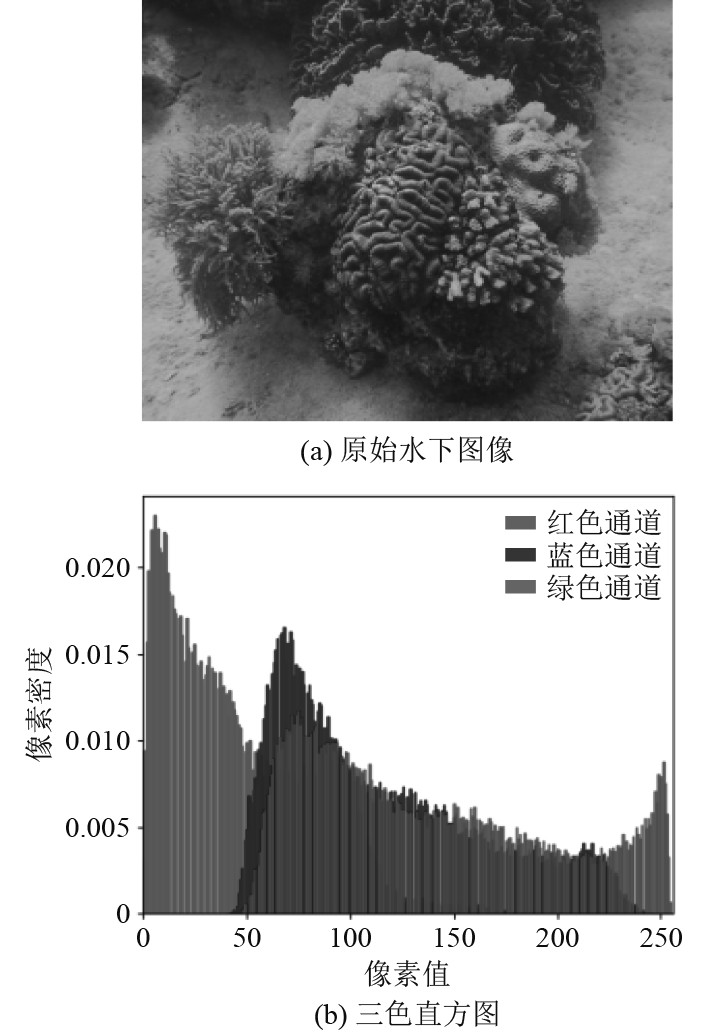
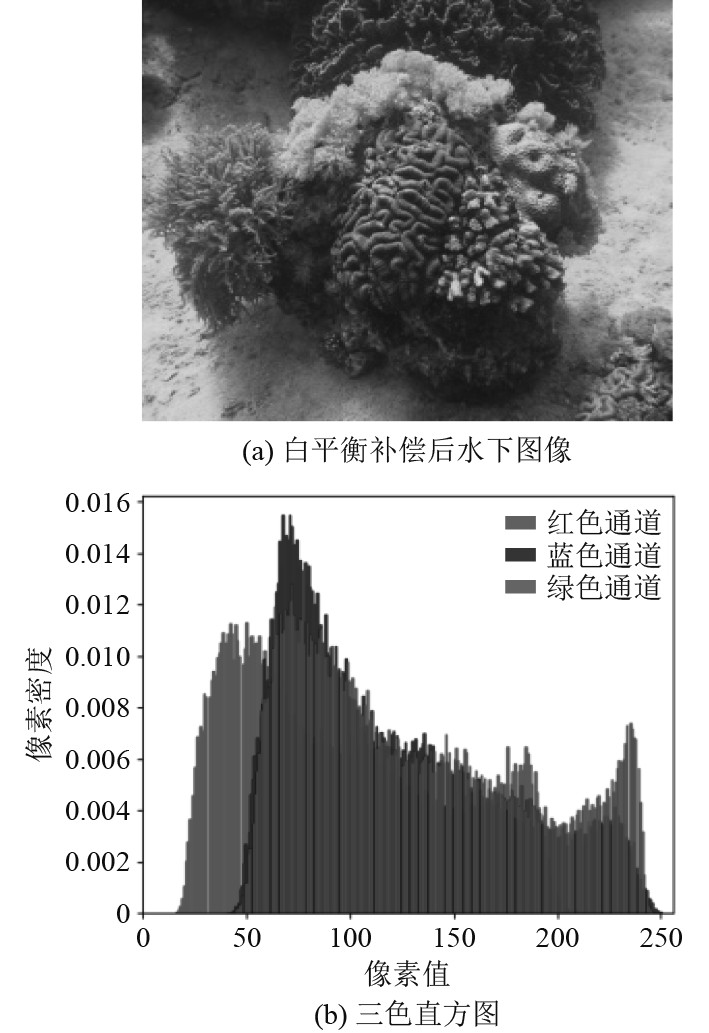
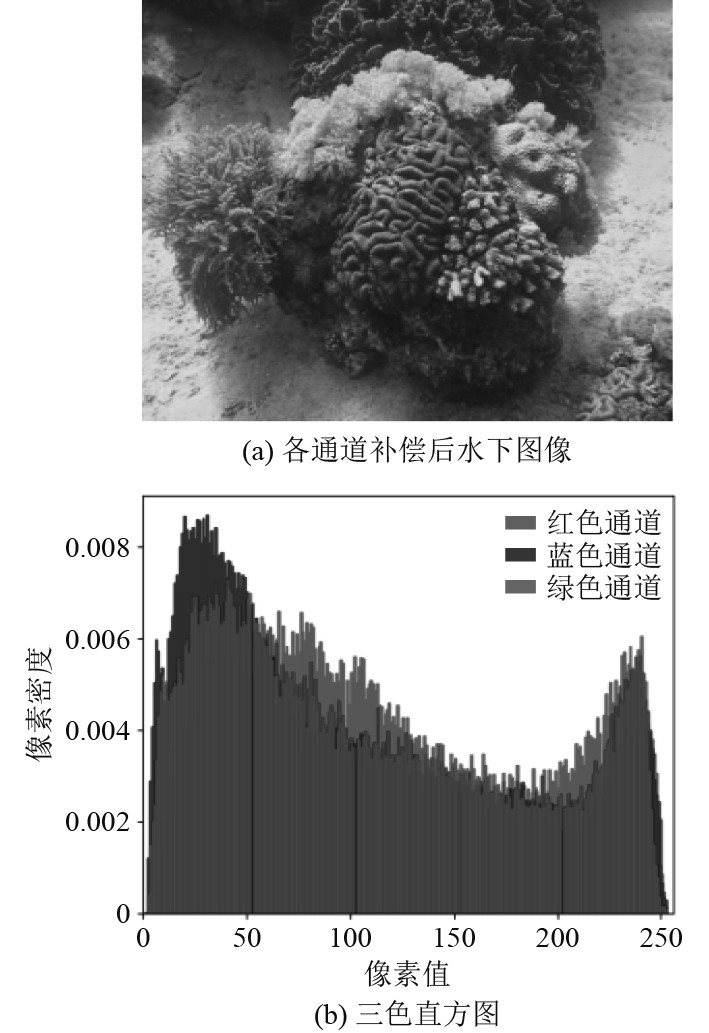
由于对水下不同深度的区域采集照片时,会出现不同程度的色偏,如图2(a)所示,该图像整体呈现绿色,十分影响人的视觉感官;其对应的三色直方图如图2(b)所示,可知它的红通道高频像素值集中在0~100这一区间,而像素值较大的区域被蓝绿通道所占有,且蓝、绿通道像素变化范围对比红通道更广。基于灰度世界理论的白平衡算法改善后的图像如图3(a)所示,该图像整体偏色问题得到了较大改善,从图3(b)的三色直方图来看红通道的变化范围更广,主要集中在 25~200这一区间。经过多尺度颜色这一区间。经过多尺度颜色通道补偿后该水下图像如图4(a)所示,该图像色彩更丰富,能较大还原初始颜色;图3(b)中三通道像素值分布在整个0~255区间,分布更均匀,且每个通道像素密度保持较高的一致性。
|
图 2 水下图像及其三色直方图 Fig. 2 Underwater images and their tricolor histograms |
|
图 3 白平衡补偿后水下图像及其三色直方图 Fig. 3 Underwater image and its tricolor histogram after white balance compensation |
|
图 4 本文方法补偿后水下图像及其三色直方图 Fig. 4 The method proposed in this article compensates for underwater images and their three color histograms |
引导滤波是当前较热门的一种边缘保持滤波器[15],与高斯滤波[16]不同的是,引导滤波用到了局部线性定义的模型,一个复杂的函数可以用多个局部的线性函数来表示。假设一个引导滤波函数的输入与输出在一个二位的窗口内满足线性关系:
| $ {q}_{i}={a}_{k}{I}_{i}+{b}_{k} 。$ | (4) |
式中:
| $ \nabla q=a\nabla I 。$ | (5) |
式中:
| $ {q}_{i}={p}_{i}-{n}_{i} 。$ | (6) |
| $ E({a}_{k},{b}_{k})= \sum _{i\in {\omega }_{k}}\left[{\left({a}_{k}{I}_{i}+{b}_{k}-{p}_{i}\right)}^{2}+\varepsilon {a}_{k}^{2}\right] 。$ | (7) |
式中:
| $ \left\{\begin{aligned} & \frac{\partial E({a}_{k},{b}_{k})}{\partial {a}_{k}}=0,\\ & \frac{\partial E({a}_{k},{b}_{k})}{\partial {b}_{k}}=0。\end{aligned}\right. $ | (8) |
可得结果如下:
| $ \left\{\begin{aligned} & {a}_{k}=\frac{\dfrac{1}{\left|\omega \right|}{\displaystyle\sum} _{i\in {\omega }_{k}}{I}_{i}{p}_{i}-{\mu }_{k}{p}_{k}}{{\sigma }_{k}^{2}+\varepsilon },\\ & {b}_{k}={p}_{k}-{a}_{k}{\mu }_{k}。\end{aligned}\right. $ | (9) |
式中:
| $ \left\{\begin{aligned} & {a}_{k}=\frac{{\sigma }_{k}^{2}}{{\sigma }_{k}^{2}+\varepsilon },\\ & {b}_{k}=(1-{a}_{k}){p}_{k}。\end{aligned}\right. $ | (10) |
在获取图像的照射分量后,依据光照分布特性构造光照不均匀校正函数,对亮度不均匀图像进行校正处理,降低光照过强区域的亮度值,提高光照过低区域的亮度值。本文引用一种基于自适应伽马函数的亮度校正方法[17],利用图像的光照分量的分布特性自适应地调整二维伽马函数的参数,实现提高光照不均匀图像整体质量的目的.对于输入图像
| $ o(x,y)=255{\left(\frac{F(x,y)}{255}\right)}^{\gamma },\gamma ={\left(\frac{1}{2}\right)}^{\frac{m-L(x,y)}{m}} 。$ | (11) |
式中:
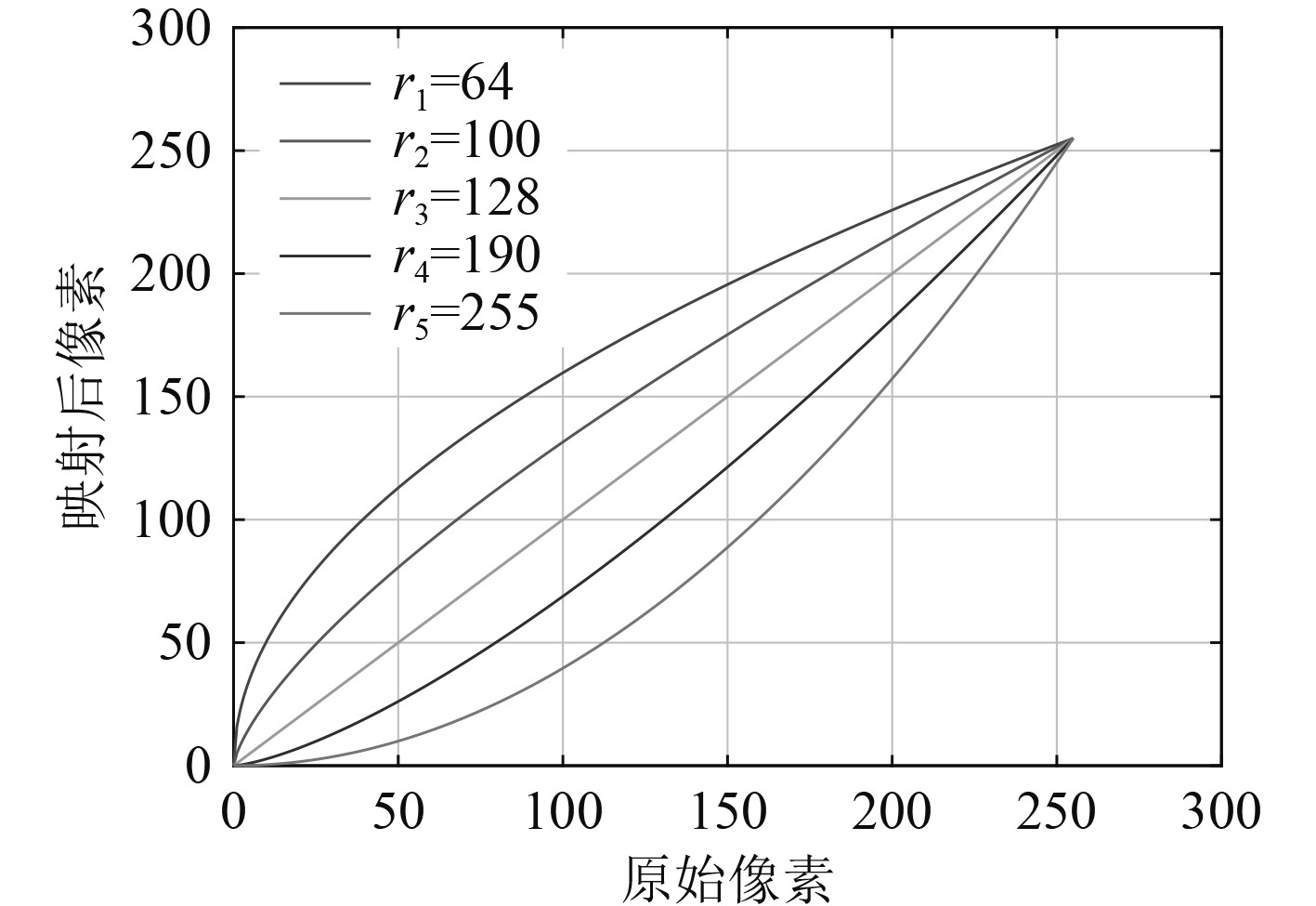
|
图 5 伽马函数曲线 Fig. 5 Gamma function curve |
可知,当
Retinex理论[6]认为人眼所接收到的图像是由入射光的照明分量和物体本身反射的反射分量按像素点乘积的结果:
| $ S(x,y)=L(x,y)\cdot R(x,y)。$ | (12) |
式中:
| $ \text{log}R(x,y)=\text{log}S(x,y)-\text{log}L(x,y) 。$ | (13) |
为了得到照射分量的估计值,单尺度Retinex(Single Scale Retinex,SSR)算法提出照明分量
| $ \text{log}L(x,y)=\text{log}\left[G\right(x,y\left)*S\right(x,y\left)\right]。$ | (14) |
式中:
| $ G(x,y)=K{e}^{-\frac{{x}^{2}+{y}^{2}}{2{\sigma }^{2}}}。$ | (15) |
| $ \iint G(x,y){\text d}x{\text d}y=1 。$ | (16) |
为了保持图像的色彩细节,多尺度Retinex(Multi-Scale Retinex, MSR)被提出,其主要思路在于将原始图像进行通道分离后,将每一个通道进行线性叠加,其主要表达式如下:
| $ \text{log}R(x,y) = \sum_{i = 1}^{k} {\omega }_{k} \left\{\text{log} \left[ S (x,y) \right] - \text{log} \left[ {G}_{i}(x,y) * S (x,y) \right]\right\} 。$ | (17) |
式中:
| $ L(x,y)={f'}(x,y)*S(x,y) 。$ | (18) |
式中:
| $ {L'}(x,y)=255{\left(\frac{S(x,y)}{255}\right)}^{\gamma },\gamma ={\left(\frac{1}{2}\right)}^{\frac{m-L(x,y)}{m}}。$ | (19) |
| $ \left\{\begin{aligned} & r(x,y)=\mathrm{log}R(x,y),\\ & \mathit{log}R(x,y)=\sum _{i=1}^{k}{\omega }_{k}\left\{\mathit{log}\left[S(x,y)\right]-\mathit{log}\left[{L'}(x,y)\right]\right\}。\end{aligned}\right. $ | (20) |
为了验证本文所提方法的有效性,选择来自公开的UIEB数据集中几幅有代表性的水下图像进行验证,这几张图像分别有不同程度的色偏、细节模糊和对比度低等问题,将本文方法与白平衡算法[1]、DCP[4]、改进的单尺度Retinex(Single-Scale Retinex,SSR)[18]、CLAHE[2]和Retinex[13]等方法进行比较,并对实验结果进行主观和客观评价。
3.1 主观评价由图6可知图像1中有大量悬浮物,造成水下成像模糊;图像2、图像3和图像7都有较为严重的色偏现象,导致整张图像偏绿色;图像4较为模糊,图像5和图像6偏蓝色且有伪影现象。经过白平衡算法处理后,虽然整体图像质量上升,色偏得到了较大改善但仍细节不足;DCP算法本质上是用于去雾,但处理水下图像无法解决色偏问题,另外还导致图像整体变阴暗;CLAHE算法能较好平衡三原色之间的变化幅度,但对于偏色严重的水下图像却效果不佳;改进的SSR算法能够对衰减严重的色彩通道有一定的补偿并且能够突出对比度,但部分区域却出现过度补偿或过度突出亮度的现象;Retinex算法虽能够在平衡色彩补偿的基础上最大化还原细节,但整体图像仍较为阴暗,边缘细节不够突出;从实验结果来看,本文方法能够校正水下图像色彩失真的问题,最大化恢复图像原始色彩,并且边缘细节增加明显,去雾效果良好,清晰度和对比度都得到了明显的改善,对比以上几种方法都有明显的优势。
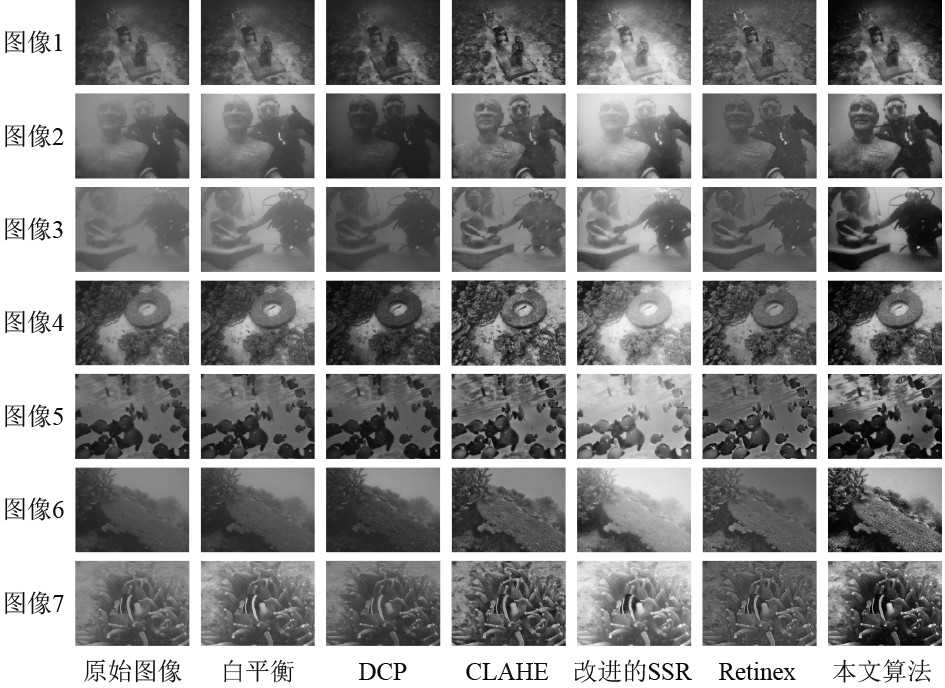
|
图 6 各类算法对比实验结果图 Fig. 6 Comparison experiment results of various algorithms |
为了进一步的验证本文方法的有效性,采用无参考水下彩色图像质量评价UIQM(underwater image quality measures)[19]作为图像质量评价指标,UIQM使用色度、饱和度和对比度这3个独立图像质量度量的线性叠加模型来生成图像质量测量。UIQM的值越高,代表图像质量越好,得到的图像更符合人眼视觉。
| $ UIQM={c}_{1}UICM+{c}_{2}UISM+{c}_{3}UI{C}_{on}M。$ | (21) |
式中:
|
|
表 1 UIQM指标评价结果 Tab.1 Evaluation results of UIQM indicators |
UCIQE(underwater color image qualit-y evaluation metric)是一个综合的评价指标,可以反映图像的整体质量,是由色度、饱和度和亮度对比度的线性组合。通常,较高的UCIQE值表示图像质量较好,UCIQE指数可以描述为[20]:
| $ UCIQE = {c_1} \times {\sigma _c} + {c_2} \times {C_l} + {c_3} \times {\mu _s}。$ | (22) |
式中:
|
|
表 2 UCIQE指标评价结果 Tab.2 Evaluation results of UCIQE indicators |
为了从多个角度对水下图像进行评价,本文还选取信息熵指标作为评价体系,信息熵代表图像的平均信息量,信息熵数值越大,表明图像所含信息量越丰富,其计算公式为:
| $ E=-\sum _{x=0}^{255}P\left(x\right)\mathit{log}P\left(x\right) 。$ | (23) |
式中:x为灰度值;
|
|
表 3 信息熵指标评价结果 Tab.3 Evaluation results of information entropy index |
由于水下环境恶略且复杂多变,在拍摄水下图像时,图像通常具有不同程度的色偏、噪声和细节模糊的问题,对于水下作业形成了严重的阻碍。基于此,本文提出一种基于色彩衰减补偿和改进的多尺度Retinex水下图像增强的方法。首先,针对水下图像出现色偏的问题,将水下图像分为3个通道,并依据总像素值的大小将其归为强、中、弱等3个通道,并对于每个通道进行不同尺度的颜色补偿,该方法能够有效改善水下图像的色偏问题。其次,运用改进的多尺度Retinex算法,在估计图像的光照分量时,用引导滤波替换高斯滤波,能够有效保持图像的边缘细节;最后,经过自适应伽马函数对光照分量进行校正,将亮度值过高或过低的区域进行自适应校正。本文实验使用公开的UIEB数据集进行验证,结果表明,对比目前主流的方法,本文方法能够更有效地改善不同场景下水下图像出现的色偏问题,并且能够同时增加细节和提升对比度,最后得到自然真实的水下图像。
| [1] |
LI Chongyi, QU jichang, PANG Yanwei. Single underwater image restoration by blue-green channels dehazing and red channel correction[C]//2016 IEEE International Conference on Acoustics, Speech and Signal Processing(ICASSP), 2016: 1371−1375.
|
| [2] |
MISHRA A, GUPTA M, SHARMA P. Enhancement of underwater images using improved CLAHE[C]//International Conference on Advanced Computation and Telecommunication(ICACAT), 2018: 1−6.
|
| [3] |
HE K M, SUN J, TANG X O. Single image haze removal using dark channel prior[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(12): 2341-2353. DOI:10.1109/TPAMI.2010.168 |
| [4] |
DREWS J P, NASCIMENTO E, MORAES F, et al. Transmission estimation in underwater single images[C]//IEEE International Conference on Computer Vision Workshops, 2013: 825−83.
|
| [5] |
ANCUTI C O, ANCUTI C, DEVLEESCHOUWER C, et al. Color balance and fusion for underwater image enhancement[J]. IEEE Transactions on Image Processing, 2018, 27(1): 379-393. DOI:10.1109/TIP.2017.2759252 |
| [6] |
FU X, ZHUANG P, HUANG Y, et al. A retinex-based enhancing approach for single underwater image[C]//IEEE international conference on image processing(ICIP), 2014: 4572–4576.
|
| [7] |
REN W, LIU S, MA L, et al. Low-light image enhancement via a deep hybrid network[J]. IEEE Transactions on Image Process, 2019, 28(9): 4364-4375. DOI:10.1109/TIP.2019.2910412 |
| [8] |
LI C, GUO J, GUO C. Emerging from water: underwater image color correction based on weakly supervised color transfer[J]. IEEE Signal Processing Letters, 2018, 25(3): 323–327.
|
| [9] |
LI J, SKINNER KA, EUSTICE RM, et al. WaterGAN: unsupervised generative network to enable real-time color correction of monocular underwater images[J]. IEEE Robot Autom letters, 2017, 3(1): 387–394.
|
| [10] |
FABBRI C, ISLAM MJ, SATTAR J. Enhancing underwater imagery using generative adversarial net-works[C]//IEEE International Conference on Robotics and Automation(ICRA), 2018: 7159–7165.
|
| [11] |
GUO Y, LI H, ZHUANG P. Underwater image enhancement using a multiscale dense generative adversarial network[J]. IEEE Journal of Ocean Engineering, 2019, 45(3): 862-870. |
| [12] |
LI C, GUO C, REN W, et al. An underwater image enhancement benchmark dataset and beyond[J]. IEEE Trans Image Process, 2020, 29(10): 4376-4389. |
| [13] |
田宁, 程莉, 元海文, 等. 基于Retinex模型的水下图像增强方法[J]. 中国科技论文, 2022, 17(11): 1281-1288. DOI:10.3969/j.issn.2095-2783.2022.11.016 |
| [14] |
HO S L, SANG W M, LL K E. Underwater image enhancement using successive color correction and superpixel dark channel prior[J]. Symmetry, 2020, 12(8): 3-5. |
| [15] |
武凌霄, 康家银, 姬云翔. NSST域下基于引导滤波与稀疏表示的红外与可见光图像融合[J]. 红外技术, 2023, 45(9): 915-924. |
| [16] |
WANG M, ZHENG S, LI X, et al. A new image denoising method based on Gaussian filter[C]//IEEE International Conference on Information Science, Electronics and Electrical Engineering, 2014: 163−167.
|
| [17] |
刘志成, 王殿伟, 刘颖, 等. 基于二维伽马函数的光照不均匀图像自适应校正算法[J]. 北京理工大学学报, 2016, 36(02): 191-196+214. |
| [18] |
贾芃, 李博, 赵晓龙. 基于HSI的改进Retinex水下图像增强算法[J]. 实验室研究与探索, 2020, 39(12): 1-4+14. DOI:10.3969/j.issn.1006-7167.2020.12.001 |
| [19] |
PANETTA K, GAO C, AGAIAN S. Human-visual-system-inspired underwater image quality measures[J]. IEEE Journal Oceanic Engineering, 2016, 41(3): 541–551.
|
| [20] |
YANG Miao, ARCOT Sowmya. An underwater color image quality evaluation metric[J]. IEEE transactions on image process, 2015, 21(12): 6062–6071.
|
 2024, Vol. 46
2024, Vol. 46
