0 引　言

自适应波束形成是阵列信号处理中一项重要技术，广泛应用于无线通信、声呐雷达的跟踪和定位等领域^[1]。在阵列准确已知目标信号响应的理想情况下，波束形成可通过调整权系数将大增益主波束对准期望信号方向，同时在指定方向形成零陷^[2]，以达到提高期望信号接收质量和抑制干扰信号的目的。在理论上，自适应波束形成可以最大化输出信干噪比^[3]，因此用输出信号中的期望信号功率与干扰信号加噪声功率之比作为衡量波束形成性能的指标。

在实际雷达侦察、通信侦察等非合作应用环境中，常采用波达方向估计算法求解信号来波方向，由于强干扰信号、角度测量误差等问题存在，期望信号入射方向估计易产生偏差，造成导向矢量失配。此外对高速运动物体进行侦察，采样时间受到严格限制，导致接收信号样本数过低，形成样本协方差矩阵会产生较大误差^[4]。综上，因信号不确定性和接收样本的数量限制会导致导向矢量失配和协方差矩阵估计误差，影响波束形成性能，即表现为波束形成输出信干噪比降低^[5]。

为解决非理想条件下误差造成波束形成性能降低的问题，COX等^[6]提出对角加载算法（Loading Sample Matrix Inversion，LSMI）。LSMI算法将一个缩放后的单位矩阵，按照一定规则加入样本协方差矩阵以降低快拍数据信噪比。但LSMI算法存在对角加载因子固定且加载电平不易确定的问题。张小飞等^[7]提出一种根据协方差矩阵特征结构，自动计算对角加载系数的自适应对角加载算法。殷冰洁^[8]提出基于信号的多普勒信息自适应选择最优对角因子的方法，上述方法经验证均可有效提升信号的抗干扰能力。

此外，基于最小均方误差（Minimum Mean Square Error，MMSE）准则的广义线性组合（General Linear Combination，GLC）算法是一种根据数据协方差矩阵（Sample Covariance Matrix，SCM）调整对角加载系数的自适应波束形成算法。GLC算法能够提升有限快拍条件下阵列波束形成的稳健性^[9]。王杰等^[10]指出，因GLC算法基于数据驱动的理论以计算对角加载水平，所以在快拍数相对于传感器数量较少时，GLC算法可以提升标准Capon波束形成的性能。吕岩等^[11]分析阵元扰动和导向矢量误差对于输出信干噪比的影响，并提出一种结合转换函数的改进GLC算法，在不同信噪比条件下具有比原算法更高的输出信干噪比。但该算法没有考虑来波信号中的随机噪声和相干噪声对波束形成输出性能的影响。

为解决阵列信号处理中因期望信号波达方向估计出现误差和数据协方差矩阵估计误差，导致波束形成输出信干噪比下降的问题，提出一种基于改进广义线性组合的稳健波束形成算法。所提算法首先对接收信号进行降噪预处理，根据降噪处理后的接收信号快拍数不同，构造对角加载系数不同的广义对角加载协方差矩阵。基于期望信号的DOA不确定范围，通过子空间投影和空域积分估计实际来波方向。最后结合改进的协方差矩阵和估计信号导向矢量求解最优波束形成加权系数，实现稳健波束形成。仿真实验可以证明，相比于其他对角加载算法，本算法在来波方向存在误差、阵列协方差矩阵估计不准确的条件下具有较好的输出信干噪比。

1 基于广义线性组合算法的波束形成 1.1 信号模型

假设存在一维M元均匀线阵，在$ k $时刻接收来自方向$ {\theta _{\text{0}}} $和${\theta _i}，i = 1,2, \ldots,P$的远场窄带期望信号和干扰信号，同时满足$ P + 1 \lt M $，则阵列接收数据$ x\left( k \right) $表示为：

$ x\left( k \right) = {x_0}\left( k \right) + {x_i}\left( k \right) + n\left( k \right)。$

(1)

式中：$ {x_0}\left( k \right) = {s_0}\left( k \right)a\left( {{\theta _0}} \right) \in {C^{M \times 1}} $；$ {x_i}\left( k \right) = \sum\limits_{i = 1}^P {s_i}\left( k \right) a\left( {{\theta _i}} \right) \in {C^{M \times 1}} $；$ n\left( k \right) \in {C^{M \times 1}} $分别代表$M \times 1$维期望信号、干扰信号和噪声；$ {s_0}\left( k \right) $和$ {s_i}\left( k \right) $分别为期望信号和干扰信号的波形包络。$ n\left( k \right) $是均值为0，方差为$\sigma _n^2$的高斯白噪声。$ a(\theta ) $为由$\theta $方向入射至M元均匀线阵的导向矢量，记为：

$ a(\theta ) = {\left[ {1,{e^{ - j2{\text π} d\sin \theta /\lambda }}, \cdots ,{e^{ - j2{\text π} d(M - 1)\sin \theta /\lambda }}} \right]^{\text{T}}} 。$

(2)

式中：$\lambda $为信号的波长；$d$为相邻阵元的间距，${\left( {} \right)^{\rm T}}$为转置运算。

波束形成的输出表示为：

$ y(k) = {\omega ^{\rm H}}x(k)。$

(3)

式中：$ \omega = {\left[ {{\omega _1},\;{\omega _2},\; \ldots ,\;{\omega _M}} \right]^{\rm T}} $为波束形成的加权矢量系数。

波束形成的性能可由输出信号的信干噪比SINR（Signal-to-Interference-Plus-Noise Ratio）来衡量，SINR定义为：

$ {\text{SINR}} = \frac{{\sigma _s^2{{\left| {{\omega ^{\text{H}}}a\left( {{\theta _0}} \right)} \right|}^2}}}{{{\omega ^{\text{H}}}{R_{i + n}}\omega }}。$

(4)

式中：$ \sigma _s^2{\text{ = }}E\left\{ {{{\left| {s(k)} \right|}^2}} \right\} $为期望信号的功率；$ \omega $为波束形成器的加权矢量；$ {{\boldsymbol R}_{{\boldsymbol i} + n}} \in {C^{M \times M}} $为干扰信号与噪声信号的联合协方差矩阵，$ {{\boldsymbol R}_{{{\boldsymbol i}} + {{n}}}} = E \{ \left( {{x_i}(k) + n(k)} \right) \left( {x_{\text{i}}}(k) + n(k) \right)^H \} $；$ a\left( {{\theta _0}} \right) $为目标信号方向矢量。

最优波束形成是衡量波束形成算法性能的重要指标，最优波束形成的加权矢量通过最大输出$SINR$准则得到，等价于下式：

$ {\min _\omega }{\omega ^{\rm H}}{{\boldsymbol{R}}_{{\boldsymbol{i}} + {{n}}}}\omega \quad {\text{ subject to }}{\omega ^{\rm H}}{a_0} = 1 。$

(5)

得到理想最优加权矢量为：

$ {\omega _{opt}} = \frac{{{{\boldsymbol R}_{{\boldsymbol i} + n}}^{ - 1}a\left( {{\theta _0}} \right)}}{{{a^{\text{H}}}\left( {{\theta _0}} \right){{\boldsymbol R}_{{\boldsymbol i} + n}}^{ - 1}a\left( {{\theta _0}} \right)}}。$

(6)

实际应用中由于$ {{\boldsymbol R}_{{\boldsymbol i} + n}} $难以直接得到，常用样本协方差矩阵${\widehat {\boldsymbol R}_{\boldsymbol X}}$近似代替$ {{\boldsymbol R}_{{\boldsymbol i} + n}} $，表示为${\widehat {\boldsymbol R}_{\boldsymbol X}} = \frac{1}{K}\sum\limits_{k = 1}^K {\boldsymbol{x}} (k){{\boldsymbol{x}}^{\text{H}}}(k)$，其中K为样本快拍数。

通过最大化SINR的原则求解此时的加权系数$ \omega $，如式(7)所示。

$ {\min _\omega }{\omega ^{\text{H}}}\widehat {\boldsymbol R}\omega {\text{, subject to }}{\omega ^{\text{H}}}a\left( {{\theta _0}} \right) = 1{\text{ }} 。$

(7)

得到阵列加权矢量为：

$ \omega = \frac{{{{\widehat {\boldsymbol R}}_{\boldsymbol X}}^{ - 1}a\left( {{\theta _0}} \right)}}{{{a^{\text{H}}}\left( {{\theta _0}} \right){{\widehat {\boldsymbol R}}_{\boldsymbol X}}^{ - 1}a\left( {{\theta _0}} \right)}} 。$

(8)

1.2 广义线性组合算法的基本原理

GLC算法实际是一种特殊的LSMI算法。传统LSMI算法是基于均匀对角加载思想，阵列加权矢量可表示为:

$ {\omega _{LSMI}} = \frac{{{{\left( {{{\widehat {\boldsymbol R}}_{\boldsymbol X}} + \lambda {\boldsymbol I}} \right)}^{ - 1}}a\left( {{\theta _0}} \right)}}{{{a^{\text{H}}}\left( {{\theta _0}} \right){{\left( {{{\widehat {\boldsymbol R}}_{\boldsymbol X}} + \lambda {\boldsymbol I}} \right)}^{ - 1}}a\left( {{\theta _0}} \right)}}。$

(9)

LSMI算法可以有效提升使采样协方差矩阵的小特征值散布程度降低以提升波束形成稳健性^[12]，但传统对角加载算法的对角加载系数固定且选取困难，GLC算法可以根据协方差矩阵参数自动确定对角加载系数，具体实现理论如下。

GLC算法中理想协方差矩阵的估计矩阵$ \widetilde {\boldsymbol R} $由$ {\widehat {\boldsymbol R}_X} $和单位矩阵的线性组合表示^[13]：

$ \widetilde {\boldsymbol R} = {\widehat {\boldsymbol R}_X} + \alpha /\beta {\boldsymbol{I}} 。$

(10)

参数$\alpha $和$\beta $由最小均方误差准则估计得到。具体求解过程如下：

$ \begin{split} {\min _{\alpha ,\beta }}\left\{ {MMSE\left( {{{\widetilde {\boldsymbol{R}}}_X}} \right)} \right\} = \,&{\min _{\alpha ,\beta }}E\left\{ {{{\left\| {\beta {{\widehat {\boldsymbol{R}}}_X} + \alpha {\boldsymbol{I}} - {{\boldsymbol{R}}_X}} \right\|}^2}} \right\} 。\end{split} $

(11)

设阵列为阵元数为$M$的均匀线性阵列，设置3个中间参数$p、q、l$：

$ p = {tr} \left( {{{\widehat R}_X}} \right)/(M) ，$

(12)

$ q=E\left\{{\Vert {\tilde{{\boldsymbol R}}}_{X}-{{\boldsymbol R}}_{X}\Vert }^{2}\right\}=\frac{1}{{N}^{2}}{\displaystyle \sum _{k=1}^{N}\Vert x(}n){\Vert }^{4}-\frac{1}{N}{\Vert {\widehat{{\boldsymbol R}}}_{X}\Vert }^{2} ，$

(13)

$ l = {\left\| {p{\boldsymbol{I}} - {{\widehat {\boldsymbol{R}}}_X}} \right\|^2} 。$

(14)

最终参数$\alpha $和$\beta $表示为：

$ \beta = 1 - q/l ，$

(15)

$ \alpha = p(1 - \beta ) = pq/l 。$

(16)

设期望信号对应的导向矢量为$ a\left( {{\theta _0}} \right) $，则GLC算法的加权系数为：

$ {\omega _{GLC}} = \frac{{{{\left( {\widehat R + \alpha /\beta {\boldsymbol I}} \right)}^{ - 1}}a\left( {{\theta _0}} \right)}}{{{a^{\text{H}}}\left( {{\theta _0}} \right){{\left( {\widehat R + \alpha /\beta {\boldsymbol I}} \right)}^{ - 1}}a\left( {{\theta _0}} \right)}} 。$

(17)

对应波束形成器输出信干噪比为：

$ {{SINR} _{GLC}} = \frac{{\sigma _0^2{{\left| {\omega _{{\text{GLC}}}^{\text{H}}a({\theta _0})} \right|}^2}}}{{\omega _{{\text{GLC}}}^{\text{H}}{{\boldsymbol R}_{i + n}}{\omega _{{\text{GLC}}}}}} 。$

(18)

2 改进波束形成算法设计 2.1 接收信号的降噪预处理

由式(12)～式(14)可知，参数$p、q、l$的计算过程均用到样本协方差矩阵，协方差矩阵受噪声干扰会影响$DL$系数，因此对接收数据进行降噪处理。采取奇异谱分析（singular spectrum analysis，SSA）方法^[14]实现对接收数据降噪处理，具体步骤如下。

${x_m}$为第$m$个阵元接收长度为$N$的含噪信号，$ {x_m} = {\left[ {{x_m}(0),{x_m}(1), \ldots ,{x_m}(N - 1)} \right]^{\rm T}},(m = 0,1, \ldots ,M) $指定滑动窗口长度为$L$，在满足$L + K = N + 1$，且$L \geqslant K$条件下，将原序列${x_m}$构造成$K$个向量，最终生成$ \mathrm{L}\times \mathrm{K} $$L \times K$维的Hankel矩阵。

$ {{\boldsymbol X}^{(m)}} = \left[ {\begin{array}{*{20}{c}} {{x_m}(0)}&{{x_m}(1)}& \cdots &{{x_m}(K - 1)} \\ {{x_m}(1)}&{{x_m}(2)}& \cdots &{{x_m}(K)} \\ \vdots & \vdots & \vdots & \vdots \\ {{x_m}(L - 1)}&{{x_m}(L)}& \cdots &{{x_m}(N - 1)} \end{array}} \right]。$

(19)

对Hankel$ \mathrm{H}\mathrm{a}\mathrm{n}\mathrm{k}\mathrm{e}\mathrm{l} $矩阵进行分组处理，将矩阵$ {{\boldsymbol{X}}^{(m)}} $表示为信号分量与噪声分量之和，即${{\boldsymbol{X}}^{(m)}} = {\boldsymbol{X}}_{ti}^{(m)} + {\boldsymbol{X}}_n^{(m)}$。为保证分组操作的合适，需要确定有用信号的数量${D_0}$，实现信号与噪声的分离。因此对Hankel矩阵进行奇异值分解

$ {{\boldsymbol{X}}^{(m)}} = \left[ {\begin{array}{*{20}{l}} {{{\boldsymbol{G}}_1}}&{{{\boldsymbol{G}}_2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\Sigma _1}}&{\boldsymbol{0}} \\ {\boldsymbol{0}}&{{\Sigma _2}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{\boldsymbol{P}}_1^{\rm T}} \\ {{\boldsymbol{P}}_2^{\rm T}} \end{array}} \right]。$

(20)

式中：$ {{\boldsymbol G}_1} \in {{\bf{C}}^{L \times {D_0}}} $,$ {{\boldsymbol \Sigma} _1} \in {{\bf{C}}^{{D_0} \times {D_0}}} $,$ {{\boldsymbol P}_1} \in {{\bf{C}}^{K \times {D_0}}} $。

这样，信号分量矩阵可以表示为：

$ {\boldsymbol{X}}_{ti}^{(m)} = {{\boldsymbol G}_1} \cdot {{\boldsymbol \Sigma} _1} \cdot {{\boldsymbol P}_1}^{\rm H}。$

(21)

在得到分离后的信号分量矩阵后，需要将矩阵转化为原长度N的去噪序列。通过对角平均化进行转换。设$ y_{ij}^{(m)} $为矩阵${\boldsymbol{X}}_{ti}^{(m)}$中的一个元素，满足$1 \leqslant i \leqslant L、1 \leqslant j \leqslant K$。则重构得到的去噪序列$ y_{rc}^{^{(m)}} $可通过下式计算获得。

$ {y}_{r{c}_{k}}^{(m)}=\left\{\begin{array}{ll} \dfrac{1}{k}{\displaystyle \sum _{m=1}^{k}{y}_{m,k-m+1}^{(m)}}，1\leqslant k \lt K，\\ \dfrac{1}{K}{\displaystyle \sum _{m=1}^{K}{y}_{m,k-m+1}^{(m)}}，K\leqslant k\leqslant L，\\ \dfrac{1}{N-k+1}{\displaystyle \sum _{m=k-L+1}^{K}{y}_{m,k-m+1}^{(m)}}，L \lt k\leqslant N。\end{array} \right.$

(22)

最终，经重构后的去噪序列表示为$ y_{rc}^{^{(m)}} = \left[ y_{r{c_1}}^{^{(m)}}, \cdots , y_{r{c_k}}^{^{(m)}}, \cdots ,y_{r{c_N}}^{^{(m)}} \right] $。对所有阵元分别进行上述SSA处理，得到降噪后的接收信号：

$ {y_{rc}}(n) = {[y_{rc}^{(0)}(n), \cdots ,y_{rc}^{(M - 1)}(n)]^{\rm T}}。$

(23)

对应生成新的协方差矩阵${R_{yrc}}$。

2.2 GLC算法加载系数改进

GLC算法的对角加载系数表示为：

$ DL = \frac{\alpha }{\beta }=\frac{p}{{l/q - 1}}。$

(24)

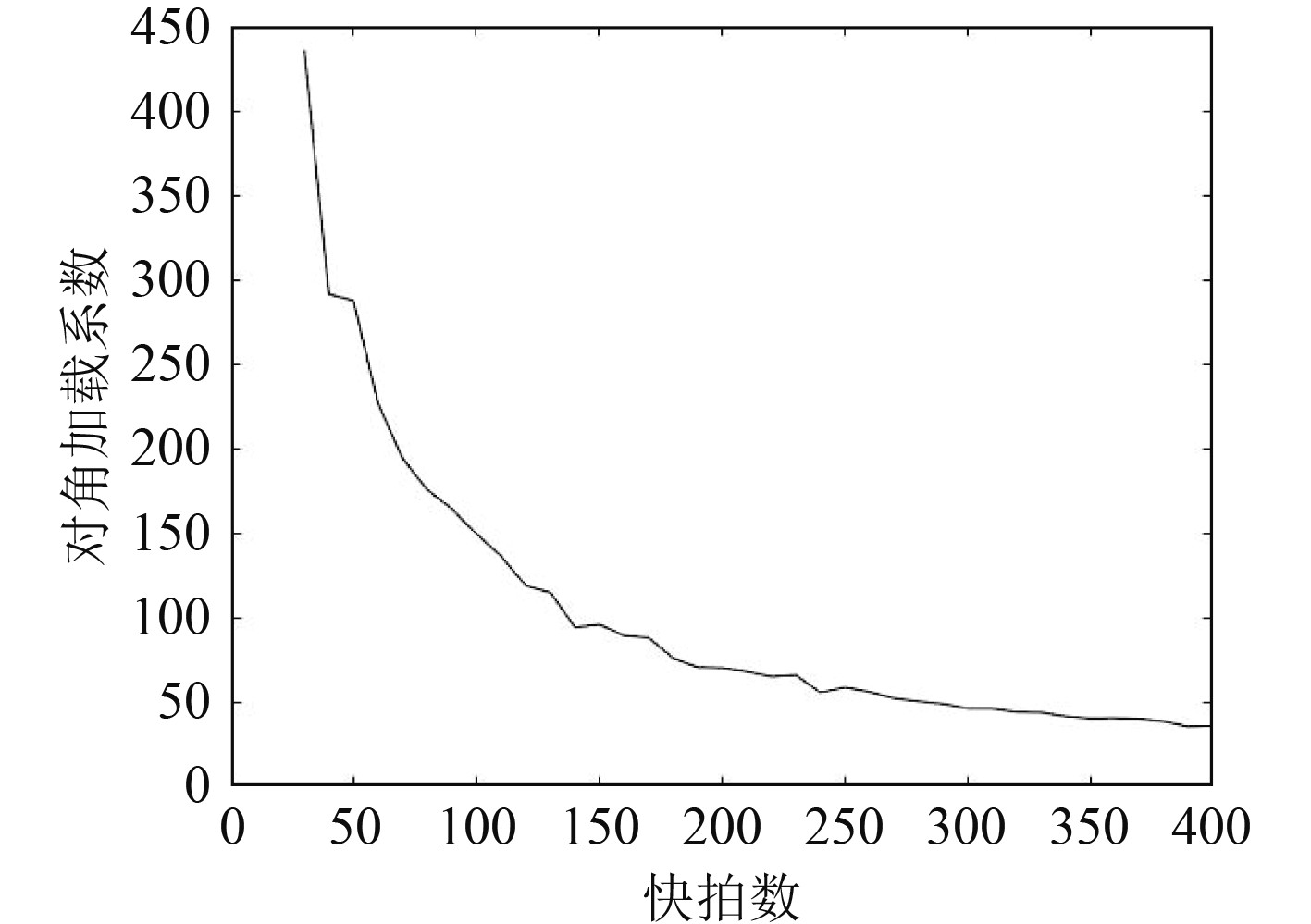
均匀线性阵列接收信号模型，如图1所示。由图2可知，随快拍数增加，$ DL $会逐渐降低，此时GLC算法逐渐趋近为样本协方差矩阵求逆（Sample Matrix Inversion，SMI）算法^[15]。若出现阵列误差或者导向矢量误差，会导致GLC算法的性能下降^[16]，因此需对原GLC算法的系数进行改进。

设$ N_{\text{fix}} $为设定的快拍转换参数，构造转换函数：

$ K(N) = \frac{{{N^t}}}{{1 + \exp ( - 28(N -N_{\text{fix}}))}} + 1。$

(25)

式中：$ N $为当前快拍数，$t \in \left[ {0,1} \right]$为速率调节系数，当快拍数低于参数$N_{\text{fix}} $时，采取式(11)计算对角加载系数，当快拍数大于$ N_{\text{fix}} $时，对系数进行修正：

$ \widehat l = l/K(N) = {\left\| {p{\boldsymbol{I}} - {R_{yrc}}} \right\|^2}/K(N) 。$

(26)

这样得到$ DL $$ DL $系数可以表示为关于快拍参数的分布函数：

$ \widehat {DL} = \left\{ {\begin{array}{*{20}{l}} \displaystyle{\frac{p}{{\widehat l/q - 1}}}，{N < N_{\text{fix}}}，\\ {\dfrac{p}{{\widehat l/q - 1}} \times K(N)}，{N > N_{\text{fix}}} 。\end{array}} \right. $

(27)

2.3 基于半正定规划的导向矢量估计

对角加载系数修正算法可以在接收数据的快拍数变化时，减少样本协方差矩阵与理论协方差矩阵的估计误差。由式(4)可知，当波束指向与实际期望信号入射方向不匹配时，输出信干噪比也会降低^[17]。为减小导向矢量误差造成波束形成性能损失，本节基于导向矢量入射角度范围的先验信息，结合空域积分思路，估计实际入射角度。

导向矢量估计算法唯一使用的先验信息是期望信号到达角和阵列几何的不确定范围。通过引入半正定矩阵$ {\boldsymbol A} = \widehat {a({\theta _0})}{\widehat {a({\theta _0})}^{\rm H}} $，基于扇区先验知识估计期望信号导向矢量的问题可通过公式转化为以下优化问题：

$ \left\{ {\begin{array}{*{20}{l}} {\mathop {\min }\limits_A } \\ {{\text{s}}{\text{.t}}{\text{.}}} \\ {} \\ {} \end{array}} \right.\begin{array}{*{20}{l}} {{{\mathrm{tr}}} \left( {R_{yrc}^{ - 1}A} \right)}，\\ {{{\mathrm{tr}}} (A) = M} ，\\ {{{\mathrm{tr}}} (\widetilde {\boldsymbol{C}}A) \leqslant {\Delta _0}}，\\ {A \geqslant {\boldsymbol{0}}} 。\end{array} $

(28)

式中：$ \widetilde {\boldsymbol{C}} = \int_{\widetilde \Theta } {a(\theta ){a^{\rm H}}(\theta ) {\text{d}}\theta } $，$\widetilde \Theta $为预估到达角范围的补集，$a(\theta )$为预设$\theta $方向的导向矢量。由预设导向矢量，求出不确定集内的补集与导向矢量的乘积最大值，如下式：

$ {\Delta _0} \triangleq {\max _{\theta \in \Theta }}{a^{\rm H}}(\theta )\widetilde {\boldsymbol{C}}a(\theta )。$

(29)

通过凸优化工具箱求解得到最优矩阵$A$，进而求得估计的导向矢量$ \widehat {a({\theta _0})} $。

2.4 改进广义线性组合算法步骤

综合2.1～2.3节的分析推导，本文提出的改进算法总结如下：

1）基于SSA，对接收数据进行信号与噪声的分离,得到去噪后的协方差矩阵${{\boldsymbol R}_{yrc}}$。

2）根据式(12)、式(13)、式(26)计算中间参数$p、q$和$ \widehat l $，并由式(27)求出对角加载系数的修正系数$ \widehat {DL} $。

3）如果存在一定的导向矢量误差，则根据式(20)估计实际导向矢量方向$ \widehat {a({\theta _0})} $。

4）最终根据式(17)计算阵元加权矢量，结束算法。

3 仿真分析 3.1 参数设置

仿真基于16阵元的均匀线性阵列，信号载频为${f_0} = 1\;{\mathrm{GHz}}$，阵元间距为半波长$d = c/(2{f_0})$。阵列噪声是零均值空时高斯白噪声矢量。设入射干扰信号和目标信号均为远场窄带随机信号，且2个干扰信号独立，分别从${\theta _{i{\text{1}}}}{{ = - 20}}^\circ $、${\theta _{i{\text{2}}}}{\text{ = 40}}^\circ $入射到阵列，干噪比分别为20 dB和30 dB。目标信号期望入射方向为${\theta _s}{\text{ = 10}}^\circ $。将所提出的改进广义线性组合波束形成算法与下列波束形成方法进行比较，包括SMI算法，LSMI算法，最差情况性能最优算法^[18]（Worst-Case Optimization，WCPO），GLC算法等，同时理想条件下最优输出信干噪比也展示在仿真结果中。仿真中，WCPO算法的不确定集合的二阶范数设为3。LSMI算法的加载量设为10 dB，期望信号的实际入射角度范围设为${ \varTheta} = [{\theta _s} - 2^\circ ,{\theta _s} + 2^\circ ]$，且进行角度估计时的积分运算采用40个均匀离散点求和代替积分值。转换函数的速率调节系数设为0.2。仿真图中，WORST表示WCPO的输出信干噪比变化趋势，OPT表示理想条件下的最优输出信干噪比曲线。

3.2 导向矢量对输出性能的影响

仿真1:　期望信号入射角度误差对输出SINR影响。

设期望信号的方向误差为$2^\circ $，信噪比为0 dB，快拍数设为400，分别在导向矢量不失配和失配两种条件下，令阵列信号输入SNR从−20～20 dB均匀变化。通过比较不同输入SNR下各算法的输出SINR性能，衡量波束形成算法的性能指标。

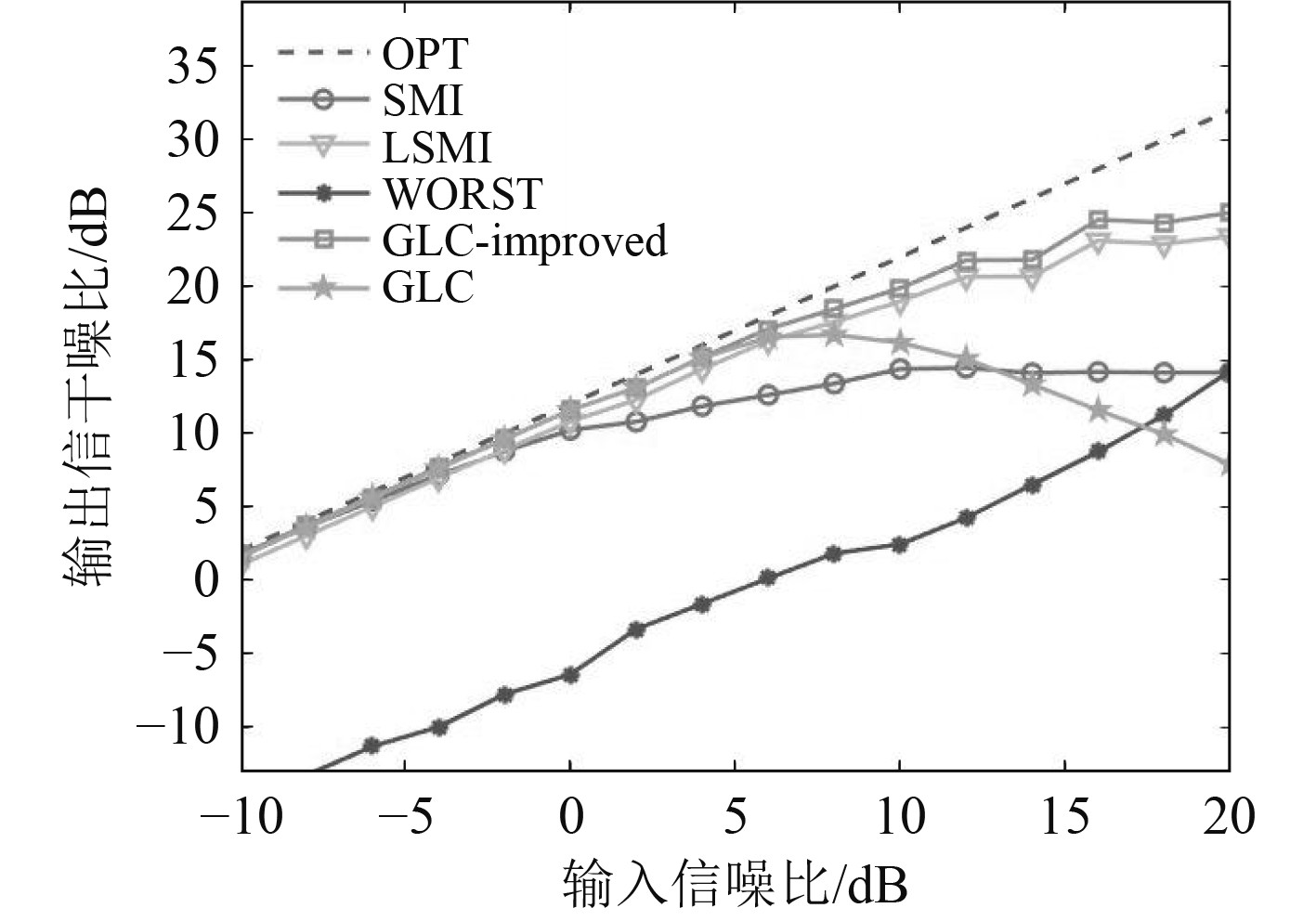
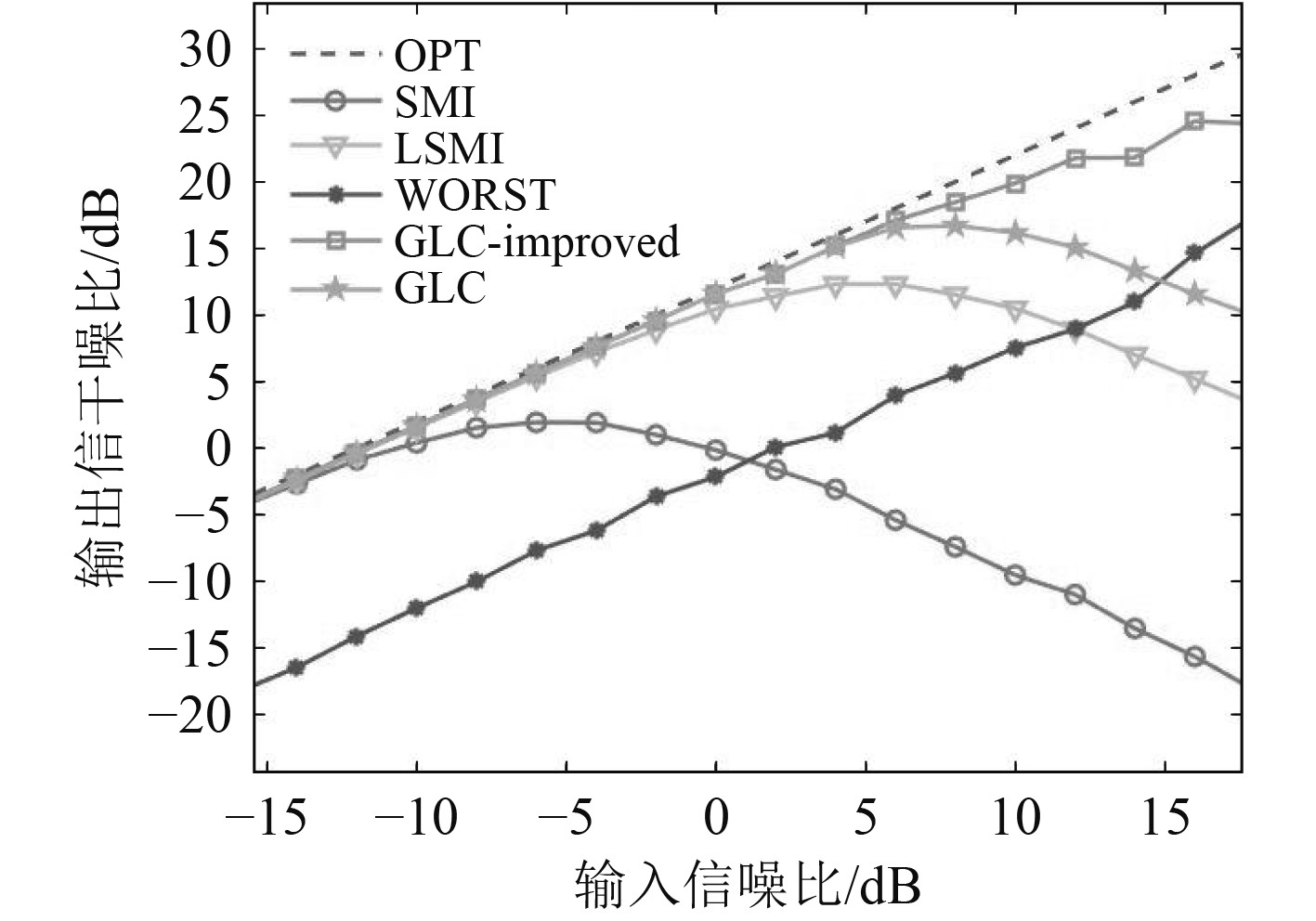
由图3和图4对比可知，当由于入射信号角度估计存在误差，带来导向矢量不失配的情况，随输入信噪比提升，各波束形成算法的输出信干噪比都在增加。导向矢量失配时，由图4输出SINR变化可知SMI、LSMI和GLC算法的性能在高信噪比环境下降低严重，随着输入信噪比的提升，SMI算法的输出信干噪比急剧下降。WCPO算法可以在仿真中保持较好的输出信干噪比，是由于其针对多种失配情况联合建模求解，对导向矢量失配情况具有较好的容忍度。本文提出的改进GLC算法与其他算法进行对比，在导向矢量存在2°误差时，输出信干噪比较高，因此具有较好的抗角度误差性能。

仿真2:　不同误差角度对输出SINR的影响。

固定信噪比为0 dB，期望信号来波方向的角度误差量从−5°～5°均匀变化，观察不同算法的输出SINR。

由图5可以看出，当期望信号来波方向存在较大误差，造成导向矢量失配严重，相比较其他算法随误差角度增大，输出SINR下降严重。本文所提算法的输出SINR与最优输出SINR接近，验证本算法的性能优越性。

3.3 信号快拍数对输出性能的影响

仿真3:　本次仿真实验，固定信噪比为0 dB，快拍数从20～400均匀增加，其余参数设置与仿真1相同。观察各算法的输出SINR与快拍数的关系。

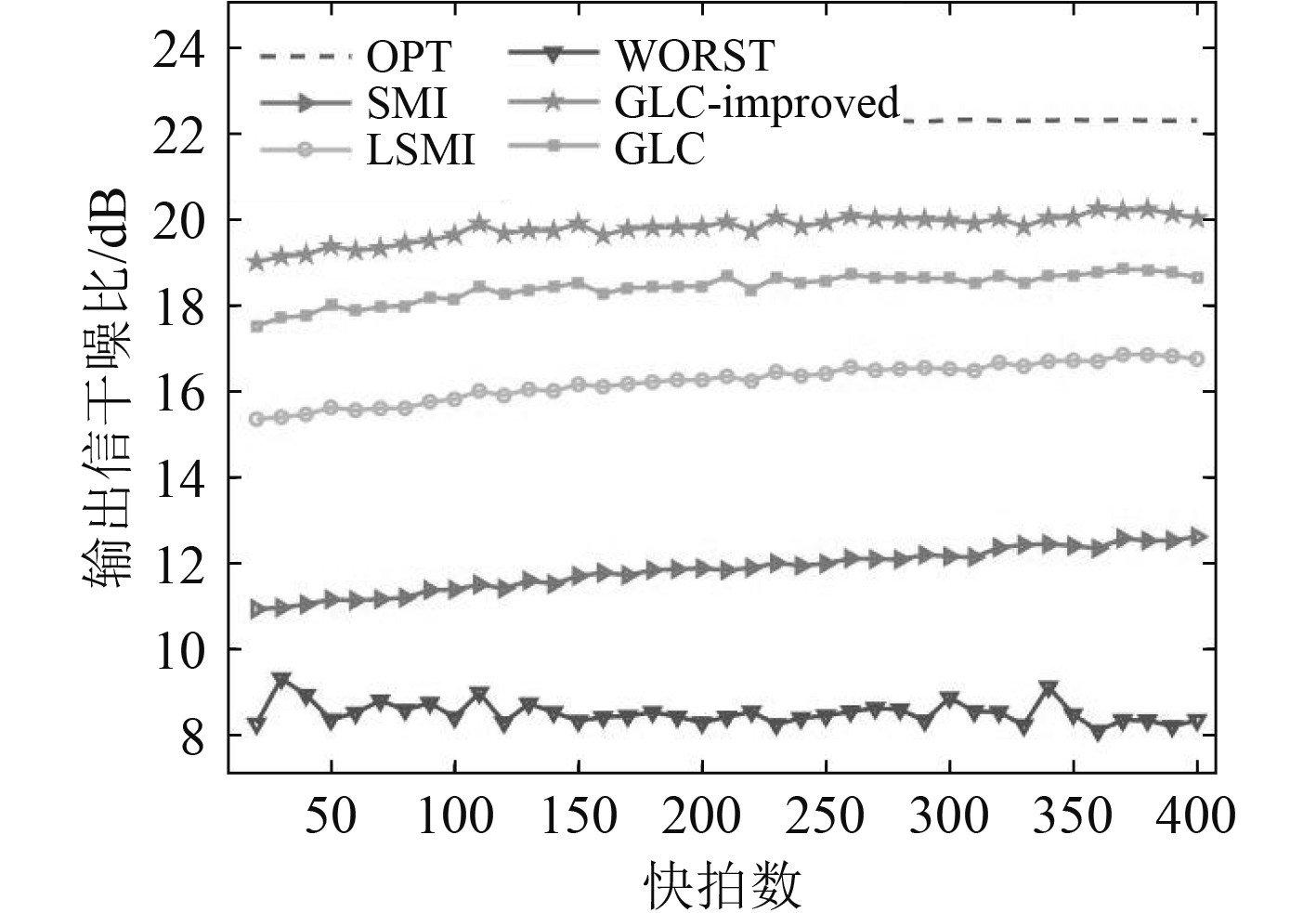
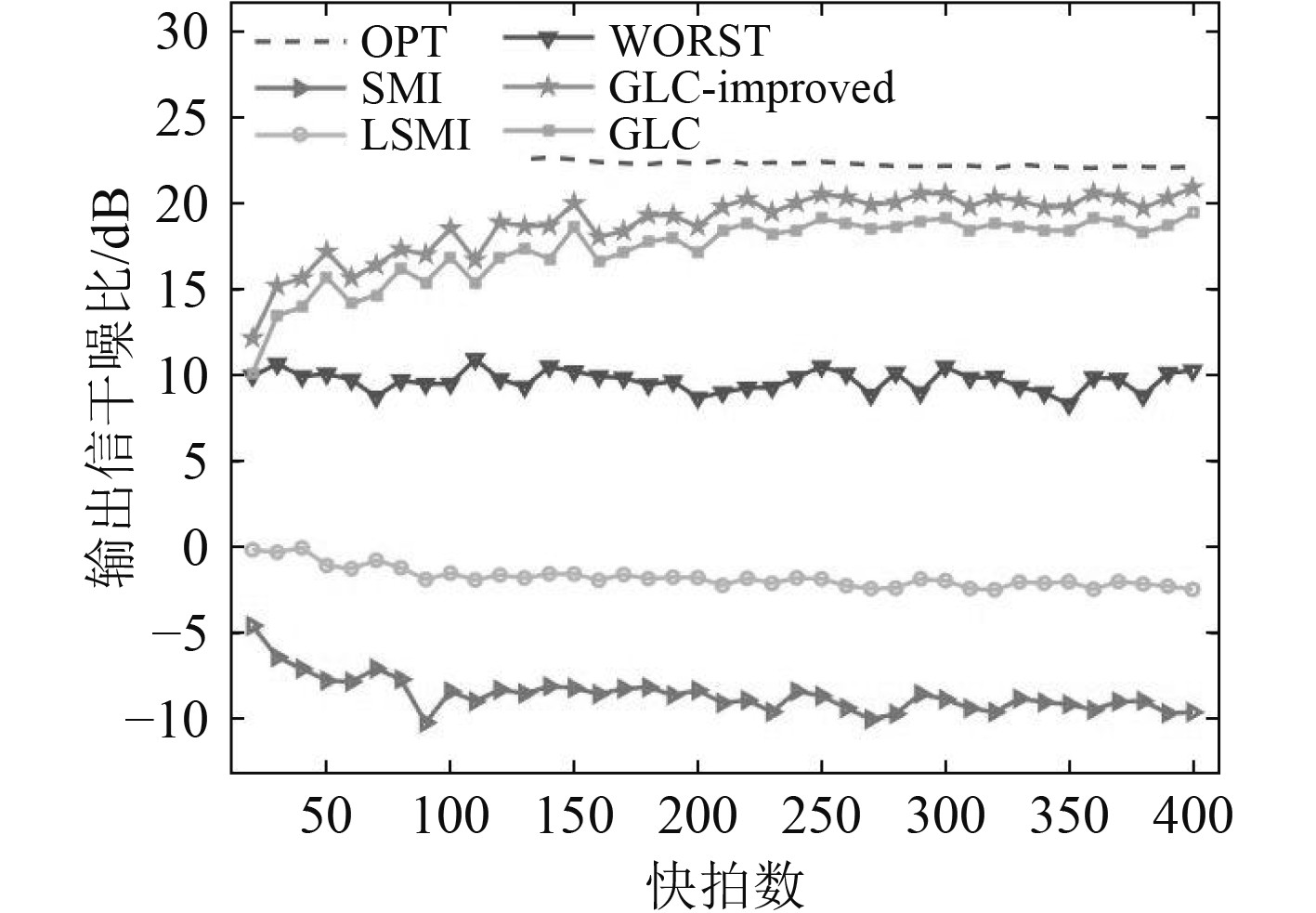
由图6和图7可知，快拍数较低时，各算法的输出信干噪比均较低，这是因为低快拍数下计算生成的样本协方差矩阵与理想协方差矩阵误差较大，影响波束形成输出性能。随着快拍数的增加，本文提出算法在快拍数为100时，输出信干噪比已达到较良好的效果，说明本算法可以在较低快拍数下达到良好的输出SINR，证明算法在低快拍数下的稳健性。将本文提出的改进算法与其它算法进行对比发现在导向矢量匹配和不匹配这2种情况下，输出性能均优于其他算法。

仿真结果证明本文提出的算法可以在较低快拍数条件下，达到较好的输出SINR。

4 结　语

本文提出一种基于改进线性组合的稳健波束形成算法。该算法首先利用对接收数据进行预降噪处理，然后生成随快拍数变化的改进对角加载系数，考虑入射信号实际入射方向与期望方向存在误差，根据期望信号入射角度变化范围进行导向矢量的估计，结合修正后的对角加载系数求出改进后的波束形成加权向量。仿真结果表明，在存在期望信号入射角度误差以及快拍数较低时，本文所提算法输出性能均优于其他对角加载算法，验证了本波束形成算法的稳健性。