0 引　言

动力电路系统作为舰船的“心脏”，其稳定性直接影响舰船的高效运营^[1]。然而，由于舰船动力电路系统结构复杂、工作环境恶劣且长时间运行，故障问题难以避免，且一旦发生故障，通常会对舰船的安全性和经济性造成严重影响。

传统的动力电路故障诊断方法主要依赖于人工经验和技术人员的专业知识，通过观察、试验和测量等手段来判断故障位置和原因。然而，这种方法既耗时，又易受外界因素影响，导致诊断结果的不准确和不及时。此外，随着舰船动力电路系统的不断升级和智能化发展，传统的诊断方法已经难以满足现代舰船故障诊断的需求。因此，研究舰船动力电路故障诊断新方法显得尤为重要。例如，有学者利用核主成分分析（KPCA）与局部线性嵌入（LLE）的联合方式，对电路故障数据进行高效特征提取，以捕捉故障信号的内在规律和关键信息^[2]。通过分数阶与麻雀搜索算法（SSA）的深度融合，对极限学习机（ELM）的权重和阈值进行智能寻优，以优化模型参数，在优化的ELM内输入提取的特征，输出故障诊断结果。虽然ELM具有较好的泛化能力，但经过复杂的前端特征提取和优化过程后，该方法容易出现过拟合现象，特别是在训练数据不足或噪声较多时。夏玲等^[3]根据电路的物理结构、工作原理和运行数据，构建电路数字孪生模型，实时反映电路的运行状态，包括电压、电流、温度等关键参数的变化情况。通过传感器网络将实际电路的运行数据实时传输至数字孪生模型，实现模型与实物的同步更新。通过对比数字孪生模型与实际电路的运行数据，检测两者之间的差异和异常。一旦发现异常，说明电路存在故障。该方法高度依赖于传感器网络的稳定性和准确性。传感器故障或数据误差会导致数字孪生模型与实际电路之间存在差异，影响故障诊断的准确性。刘美容等^[4]利用经验模态分解（EMD）方法分解电路故障信号，得到具有不同频率尺度的本征模态函数（ IMFs）；采用复合多尺度熵（CME）方法计算各IMF在不同时间尺度上的样本熵，捕捉故障信号在不同尺度上的动态特性。通过比较正常状态与故障状态下CME曲线，提取故障特征，并输入支持向量机内，输出故障诊断结果。EMD方法在处理含有噪声的信号时，会出现模态混叠、虚假分量等问题，这会影响后续CME分析和故障特征提取的准确性^[5]。

栈式稀疏自编码器（SSAE）作为一种无监督学习的神经网络结构，专注于学习对故障诊断任务最为关键的特征。概率神经网络（PNN）通过其特殊的网络结构和算法，能够学习和表示复杂的非线性关系。将SSAE提取的特征作为PNN的输入，可以充分利用SSAE在特征提取方面的优势和PNN在分类性能上的优势，不仅提高了特征的质量，还提升了故障诊断的准确性和效率。为此提出了基于神经网络的舰船动力电路故障诊断方法。

1 舰船动力电路故障诊断方法 1.1 基于神经网络的舰船动力电路故障特征提取

舰船动力电路信号受电磁干扰、机械振动与噪声以及环境因素等多种因素的影响会存在噪声和干扰。为此，利用SSAE在舰船动力电路信号内，提取有用的舰船动力电路故障特征，可提升故障特征提取精度，进而提升舰船动力电路故障诊断精度^[6]。AE中包含2个部分，分别是编码器$ Z $与解码器$ D $令舰船动力电路信号为$ X $，作为$ Z $的输入，$ Z $提取的舰船动力电路故障特征是$ X' $，利用$ D $重建$ X' $，得到最终的舰船动力电路故障特征提取结果$ \hat X $。计算过程如下：

$ X' = {f_Z}\left( {{w_Z}X + {b_Z}} \right)，$

(1)

$ \hat X = {f_D}\left( {{w_D}X' + {b_D}} \right)。$

(2)

式中：f_z、f_D为$ Z $与$ D $的激活函数；w_z、b_z为$ Z $的权值与偏置；w_D、b_D为$ D $的权值与偏置。

AE的损失函数为：

$ L\left( {{X_i},{{\hat X}_i}} \right) = \frac{{\displaystyle\sum\limits_{i = 1}^n {\left\| {X_i^2 - \hat X_i^2} \right\|} }}{n}。$

(3)

式中：$ n $、$ i $为舰船动力电路信号样本数量与编号。

在AE内引入稀疏惩罚项得到SAE，SAE的损失函数为：

$ L = L\left( {{X_i},{{\hat X}_i}} \right) + \alpha \sum\limits_{i = 1}^n {\left[ {\beta \log \frac{\beta }{{{\gamma _j}}} + \left( {1 - \beta } \right)\log \frac{{1 - \beta }}{{1 - {\gamma _j}}}} \right]}。$

(4)

式中：β为稀疏性参数；α为正则化系数；γ_j为隐层单元$ j $的平均激活度。γ_j的计算式如下：

$ {\gamma _j} = \frac{{\displaystyle\sum\limits_{i = 1}^n {{\lambda _j}\left( {{X_i}} \right)} }}{n}。$

(5)

式中：$ {\lambda _j}\left( {{X_i}} \right) $为单元$ j $的激活量。

依据式(4)的损失函数$ L $训练SAE网络，令γ_j无限接近β，提升舰船动力电路故障特征提取的稀疏性，减少舰船动力电路故障特征之间的冗余，滤除噪声和干扰。

通过叠加数个SAE，建立SSAE。SSAE内上一层SAE在处理舰船动力电路信号后所提取出的故障特征，会被用作下一层SAE的输入样本，以供进一步的分析和处理。按照逐层贪婪训练方式，结合$ L $，优化SSAE参数，提取到有用的舰船动力电路故障特征$ \tilde X $。

1.2 基于神经网络的电路故障诊断

随着舰船动力电路系统的不断升级和改进，新的故障类型可能会不断出现。PNN具备在线学习的能力，能够不断接收新的故障样本并更新其模型，以适应新的故障类型。这使得PNN在应对未来可能出现的未知故障时具有更强的适应性和可扩展性。为此，在PNN中输入SSAE提取的故障特征样本，输出舰船动力电路故障诊断结果，提升故障诊断精度。PNN共包含4层，分别为输入层O₁、模式层O₂、求和层O₃与输出层O₄，利用PNN进行舰船动力电路故障诊断的具体步骤如下：

步骤1　在O₁中输入提取的有用舰船动力电路故障特征样本$ \tilde X $。O₁只负责接收SSAE发送的$ \tilde X $，并传输至O₂。

步骤2　O₂负责存储$ \tilde X $的模式信息。O₂内各单元都与一个特定的$ {\tilde X_i} $相关联，用于存储$ {\tilde X_i} $的特征向量。当新的舰船动力电路故障特征进入网络时，O₂会计算输入与每个存储模式的相似度，存储这些新故障的模式信息，这样PNN就能够诊断新的故障类型。O₂的输出结果为：

$ {\mu _{j'i}}\left( {{{\tilde X}_i}} \right) = \frac{{{e^{ - \frac{{{{\left( {{{\tilde X}_i} - {r_{j'i}}} \right)}^{{\text{T}}}}\left( {{{\tilde X}_i} - {r_{j'i}}} \right)}}{{2{\delta ^2}}}}}}}{{{{\left( {2{\text π} } \right)}^{\frac{t}{2}}}{\delta ^t}}}。$

(6)

式中：T为转置符号；$ \delta $为平滑系数；$ t $为$ \tilde X $的维度；$ {r_{j'l}} $为第$ l $个舰船动力电路故障类别的第$ j' $个隐中心矢量；$ {\mu _{j'l}}\left( {{{\tilde X}_i}} \right) $为$ {\tilde X_i} $属于第$ l $个舰船动力电路故障类别的初步概率估计值。

步骤3　O₃负责对O₂中相同模式的输出$ {\mu _{j'i}}\left( {{{\tilde X}_i}} \right) $进行加权求和。当新的舰船动力电路故障类型出现时，如果O₂已包含了足够相似的模式信息，O₃就能通过调整权重来适应这种新的舰船动力电路故障类型，使得PNN在应对未来可能出现的未知故障时具有更强的适应性。O₃的输出为：

$ {q_{j'}}\left( {{{\tilde X}_i}} \right) = \frac{{\displaystyle\sum\limits_{i = 1}^{{N_l}} {{\mu _{j'i}}\left( {{{\tilde X}_i}} \right)} }}{{{N_l}}}。$

(7)

式中：$ {N_l} $为第$ l $个舰船动力电路故障类别的故障特征样本数量；$ {q_{j'}}\left( {{{\tilde X}_i}} \right) $为$ \tilde X $属于第$ l $个舰船动力电路故障类别的后验概率。

步骤4　O₄按照贝叶斯决策规则，选取最大$ {q_{j'}}\left( {\tilde X} \right) $对应的故障类别，作为最终的舰船动力电路故障诊断结果，如下：

$ Y\left( {{{\tilde X}_i}} \right) = \arg \max \left\{ {{q_{j'}}\left( {{{\tilde X}_i}} \right)} \right\}。$

(8)

1.3 舰船动力电路故障诊断的神经网络结构优化

通过K-means算法，确定PNN网络的隐中心矢量数量$ M $，优化PNN网络结构，提升舰船动力电路故障诊断精度。利用K-means算法确定$ M $的具体步骤如下：

步骤1　随机选择η个初始聚类中心$ C $。

步骤2　求解提取的全部有用舰船动力电路故障特征样本$ {\tilde X_i} $和第$ k $个初始聚类中心C_k间的距离d_ik。

步骤3　按照最小d_ik的原则，分类全部有用舰船动力电路故障特征样本。

步骤4　更新C_k。

步骤5　当C_k不再发生改变时，则结束算法，输出最终的聚类结果，聚类数量即$ M $。否则，返回步骤2。

在式(6)中代入$ M $，优化O₂，进而完成PNN网络结构的优化。

2 结果与分析

以某舰船动力系统为研究对象，参数见表1。利用本文方法对该舰船动力系统的电路进行故障诊断，增强舰船动力系统运行的稳定性与可靠性。在实验中设置开路故障、接地故障、短路故障、电源故障与元件故障为已知故障类型，设计缺陷故障与材料老化故障为未知故障类型。

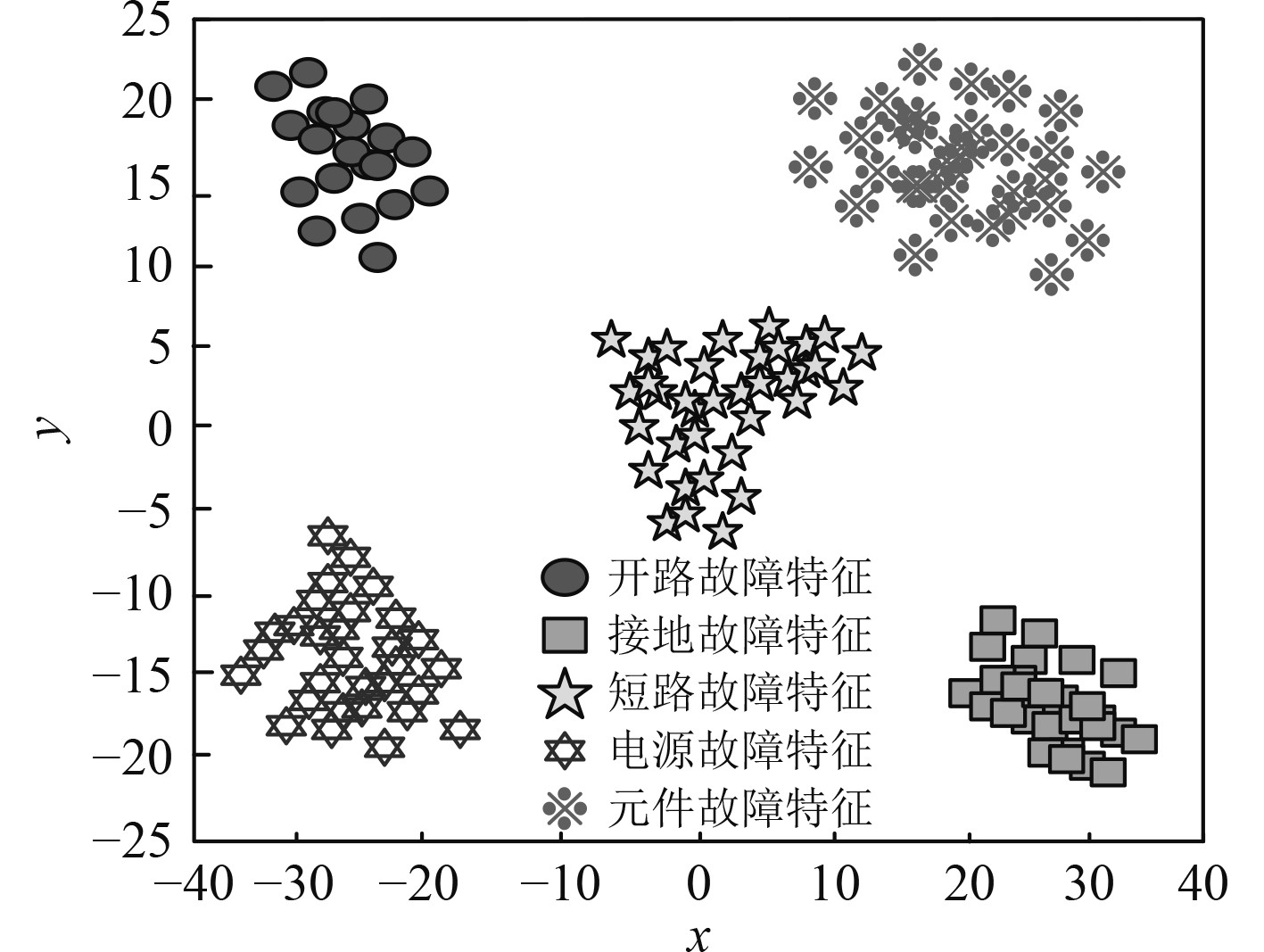
将本文方法提取的故障特征输入至T-SNE方法内，提取故障特征映射至二维空间内，并绘制散点图，以已知的5种故障类型为例，结果如图1所示。可以看出，本文方法可有效在舰船动力电路内，提取舰船动力电路故障特征，且不同类型的故障特征之间，没有任何的重叠区域，具有较优的区分效果，说明本文方法可有效滤除舰船动力电路信号内的噪声与干扰，提升舰船动力电路故障特征提取效果。

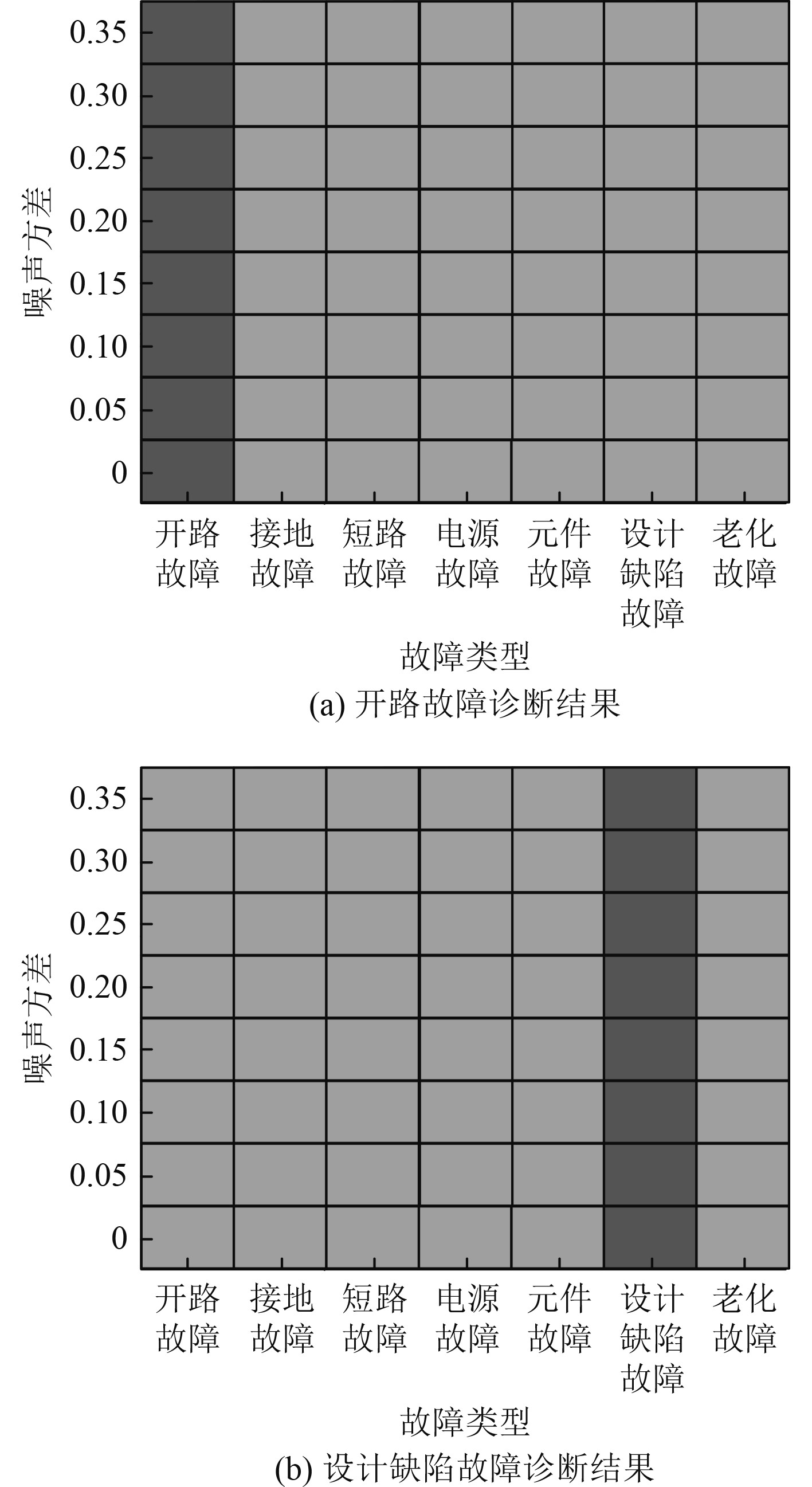
在不同噪声强度的运行环境下，本文方法的舰船动力电路故障诊断结果如图2所示。图中，深色矩形框代表该舰船动力电路信号存在对应的故障，其他矩形框代表该舰船动力电路信号不存在对应的故障。从图2(a)中可以看出，在不同噪声强度下，本文方法的故障诊断结果均为开路故障，与实际故障类型一致，说明对于已知故障类型，本文方法可精准诊断舰船动力电路故障。从图2(b)中可以看出，在不同噪声强度下，本文方法的故障诊断结果均为设计缺陷故障，与实际故障类型一致，说明对于未知故障类型，本文方法也可完成精准诊断。

3 结　语

神经网络以其强大的自学习和模式识别能力，在舰船动力电路故障诊断中表现出高效性和准确性。通过对大量故障数据的训练，神经网络能够自动提取故障特征，实现故障的快速诊断。为此，研究基于神经网络的舰船动力电路故障诊断方法，在不同工况和环境下，均可精准完成故障诊断。