2. 江苏新时代造船有限公司船研所,江苏 泰州 225300
2. Institute of Shipbuilding Research, Jiangsu New Times Shipbuilding Co., Taizhou 225300, China
风能作为一种可再生清洁能源,越来越受到世界的关注,这也带动了风机行业取得了巨大的发展进步。相较与陆地风电场,海上风电场有着不占空间、风能密度大等优势,截止到2022年底,我国已完成风电装机量达到3.42×108 kW[1]。根据我国地理位置和地质条件,在过去的几十年时间中,风电开发的主要方向主要集中在近海海上风电场。但随着近年来近海风电资源的日趋饱和,海上风电从近海走向深远海已经成为目前海上风电发展的主流趋势[2]。
与近海风电场采用的固定式风机不同,远海风电场浮式风机的定位主要依赖于系泊系统,因此系泊安全对远海场的浮式风机而言至关重要。统计挪威海域发生的15起海上风机安全事故,发现系泊疲劳失效占到了1/3[3]。同时,海洋平台系泊安全事故报告显示浮式平台每年系泊缆疲劳失效概率为
系泊疲劳主要是由浮式风机运动引起的低频系泊张力产生,浮式风机的系泊系统疲劳评估问题国内外专家学者进行了一定的研究。桑松等[5]基于线性累积损伤理论的S-N曲线法对5MW-Spar型浮式风机平台系缆进行了张力计算和疲劳寿命预测,分析了我国南海海域风/浪随机变化对系泊缆张力的影响。邓露等[6]建立了浮式风机在海洋环境下的耦合模型,针对OC4-DeepCwind和OC3-Hywind风机进行了时域疲劳计算,揭示了风浪夹角变化对浮式风机系泊疲劳的影响。Zhao等[7]提出利用环境等值线方法来计算浮式风机极端设计荷载,将系泊缆断裂、疲劳和浮体慢漂等多种失效模式串连成一个系统,并基于此多失效模型进行了浮式风机系泊疲劳可靠性分析。Barrors等[8]考虑系泊链轴向载荷和面外弯曲产生的轴向应力,提出了一种计算关键链节热点处应力的解析方法,并以此为基础,利用S-N曲线法计算系泊缆的疲劳寿命。该方法首创的考虑到系泊链的工作角度及各链环的连接角度对应力值的影响,并通过系泊-导缆系统的数值结果验证了该解析法的有效性。除此之外,基于断裂力学的系泊疲劳评估方法也越来越受到关注。Gao等[9]研究了断裂力学法对浮式海上风力机系泊疲劳寿命计算的适用性,将断裂力学方法与传统S-N曲线法和T-N曲线法结果进行比较,通过引入安全系数统一的3种方法,揭示了载荷加载顺序、应力集中系数、初始裂纹形状和尺寸等因素对断裂力学法预测系泊缆疲劳寿命的影响。
目前有关风场湍流强度对系泊疲劳影响的研究尚不完善。本文以NREL设计的5MW风机和OC4-DeepCwind半潜式平台[10]为对象,考虑到多种环境载荷作用,建立一种气动-水动-系泊全耦合计算模型,并基于海洋结构物时域分析法获取系泊缆的在不同分析工况下的张力时历。利用改进四峰雨流计算法统计系泊链张力水平,基于累积损伤理论的T-N曲线计算出浮式风机系泊缆在不同工况下的总疲劳损伤及各海况下的短期疲劳损伤,研究了气动载荷及风场湍流强度对系泊疲劳的影响。
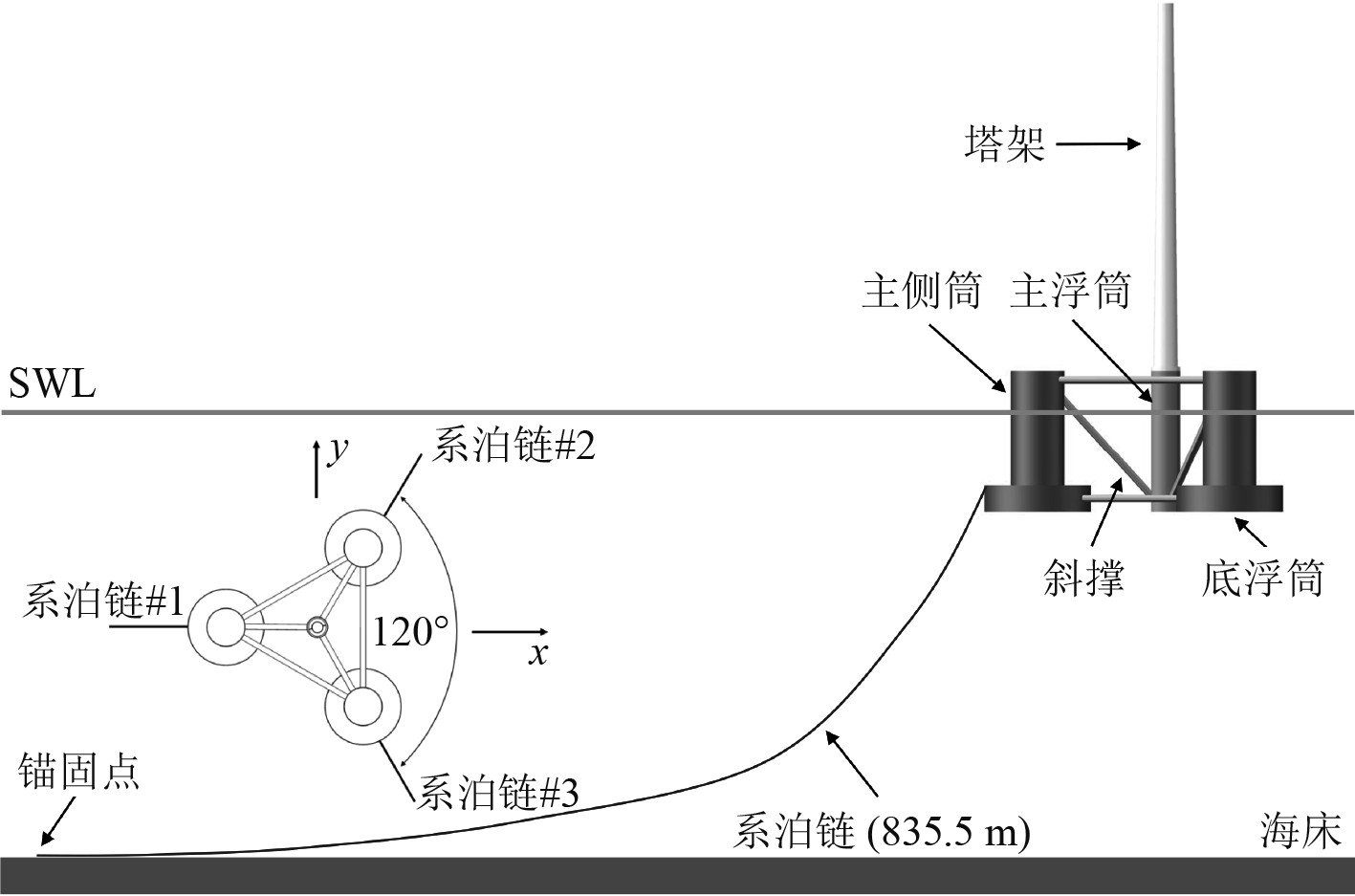
1 环境载荷计算 1.1 浮式风力机平台结构参数及系泊系统本文以NREL设计的5 MW海上浮式风机为研究对象,该风机组浮式基础共设有3根系泊锚链,采用多点悬链式系泊的方式进行定位,浮式风机结构及系泊示意见图1,风力机和平台主要参数见表1。
|
图 1 浮式风机结构及系泊示意图 Fig. 1 Schematic diagram of floating turbine structure and mooring |
|
|
表 1 风力机及平台主要参数 Tab.1 Main scale of the wind turbines and platforms |
远海工作的浮式风机受复杂风载荷的作用,其载荷主要由两大部分组成。一是由风机叶轮旋转引起的气动载荷,二是持续性风作用在风机基础结构上的环境风载荷。
风机气动载荷基于叶素-动量理论[11]计算得到。首先根据叶片单元理论,在叶轮环形平面叶素与叶片根部距离为r处取dr宽度的环形微元,此微元的推力和扭矩如下式:
| $ {\rm d}T = B\frac{1}{2}\rho {v^2}_{all}({C_l}\cos \varphi + {C_d}\sin \varphi )c{\rm d}r ,$ | (1) |
| $ {\rm d}Q = B\frac{1}{2}\rho {v^2}_{all}({C_l}\sin \varphi - {C_d}\cos \varphi )cr{\rm d}r 。$ | (2) |
其中:B为风机叶片的数量;φ为局部流入角;Cl为升力系数;Cd为阻力系数。
再基于动量理论将叶轮诱导速度与上式的推力和扭矩联系起来,即
| $ {\rm d}T = 4{\text π} r\rho {U^2}_\infty (1 - a)a{\rm d}r ,$ | (3) |
| $ {\rm d}Q = 4{\text π} {r^3}\rho {U_\infty }(1 - a)b{\rm d}r。$ | (4) |
式中:
对于作用在风机基础结构上的外部环境风载荷可以表示为:
| $ F(z,t) = 0.5{C_d}\rho A{u^2}(z,t) 。$ | (5) |
式中:A为迎风面积,m2;u(z,t)不同高度下的瞬时速度。
1.3 水动力载荷计算与单桩式风机统一使用Morrison方程计算波浪载荷不同,由于文章的浮式风机平台各结构间尺寸差异较大,故对主浮筒、侧浮筒和底浮筒采用三维势流理论进行求解,而对于尺寸较小的横撑及斜撑采用Morrison方程[12]进行计算,结构单位长度上的波浪力如下式:
| $ {\rm d}F{\text{ = }}\frac{1}{2}{C_D}\rho Du\left| u \right|{\rm d}z + {C_M}\rho A\frac{{{\rm d}u}}{{{\rm d}t}}{\rm d}z 。$ | (6) |
式中:ρ为海水密度;u为垂直于构件轴线的速度分量;A为结构的投影面积;CD和CM分别为曳力系数和惯性力系数。
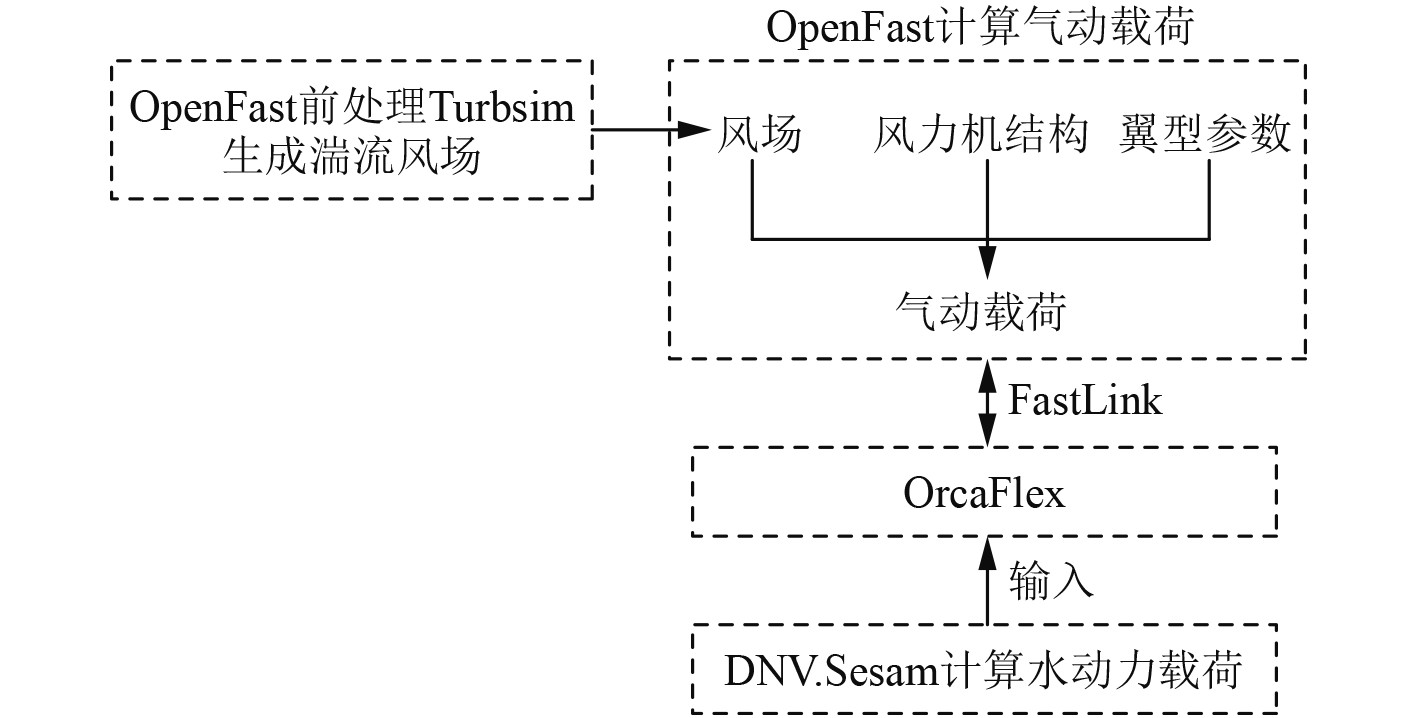
2 计算模型及系泊链张力时历计算 2.1 全耦合分析过程浮式平台整个耦合计算过程利用OpenFast-DNV.Sesam-OrcaFlex三者联合完成,OpenFast为时域气弹耦合程序,DNV.Sesam为水动力计算软件,OrcaFlex为系泊计算软件。通过前处理程序Turbsim生成风场,风谱选择Kaimal谱[13],利用OpenFast软件读取风场信息,计算出浮式风机的气动载荷。通过FastLink将Fast计算出的气动载荷及浮式平台运动响应传递给OrcaFlex软件。通过Sesam/Genie模块建立水动力计算模型,波浪谱选用JONSWAP谱[14],利用Sesam/HydroD模块计算水动力系数,包括一阶波浪幅频RAO、波浪二阶差频力传递函数等水动力参数,并将数据输入OrcaFlex软件。在Oracflex进行参数化建模,利用集中质量法模拟浮式风机系泊缆的系泊载荷。气动-水动-系泊全耦合计算模型见图2。
|
图 2 气动-水动-系泊全耦合计算模型 Fig. 2 A fully coupled aerodynamic-hydrodynamic-mooring calculation model |
海况散布图基于南海某海域,考虑到算力条件,将长期海况等效为7个典型短期海况,具体参数见表2。同时,为了后期研究气动载荷及不同湍流风强度(I)对系泊缆疲劳损伤的影响,具体分析工况见表3。
|
|
表 2 典型短期海况参数 Tab.2 The parameter of typical short-term sea conditions |
|
|
表 3 分析工况 Tab.3 Analyzing working conditions |
基于有限元法建立系泊缆线模型,结合2.2节的短期海况和分析工况,通过Orcaflex软件进行系泊锚链张力的时历计算。根据文献[6]研究结果,当共线风浪时系泊缆张力会出现最大值,故文中计算取风浪夹角0°作为载荷工况,不再讨论其他风浪夹角情况。计算时长设置为
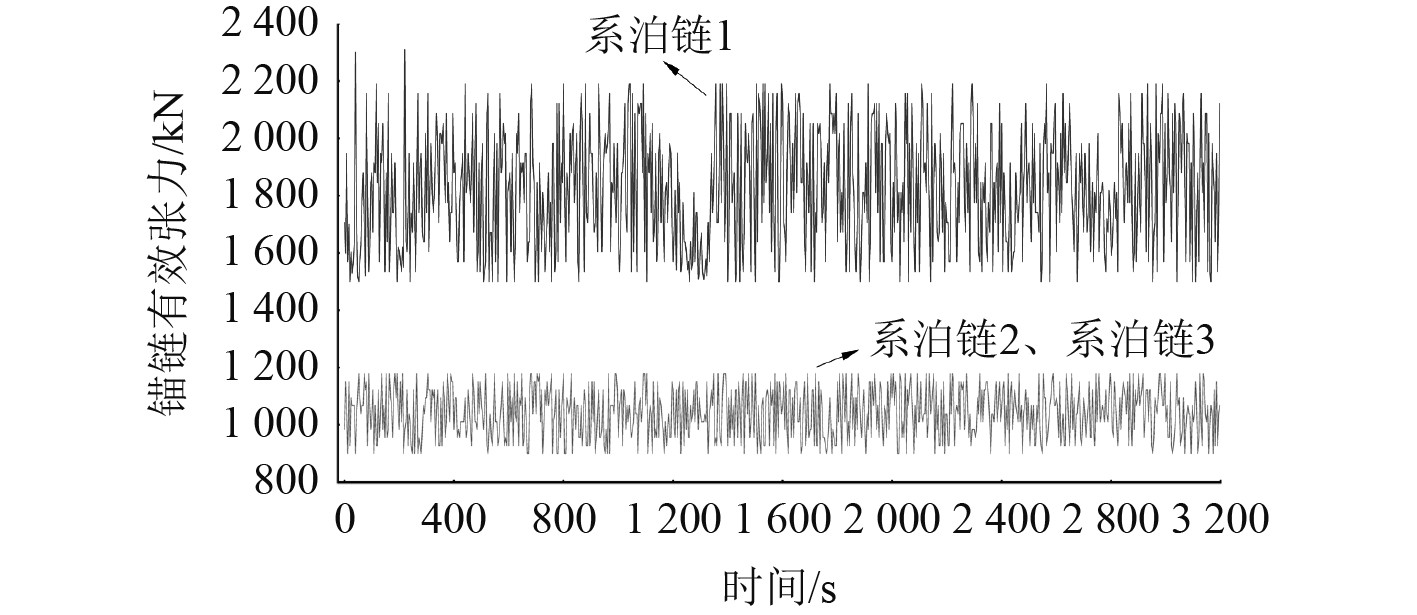
|
图 3 3根系泊链在短期海况4、分析工况1下的张力-时力曲线 Fig. 3 Tension history curves of three mooring chains in short-term sea state 4 and analyzed working condition 1 |
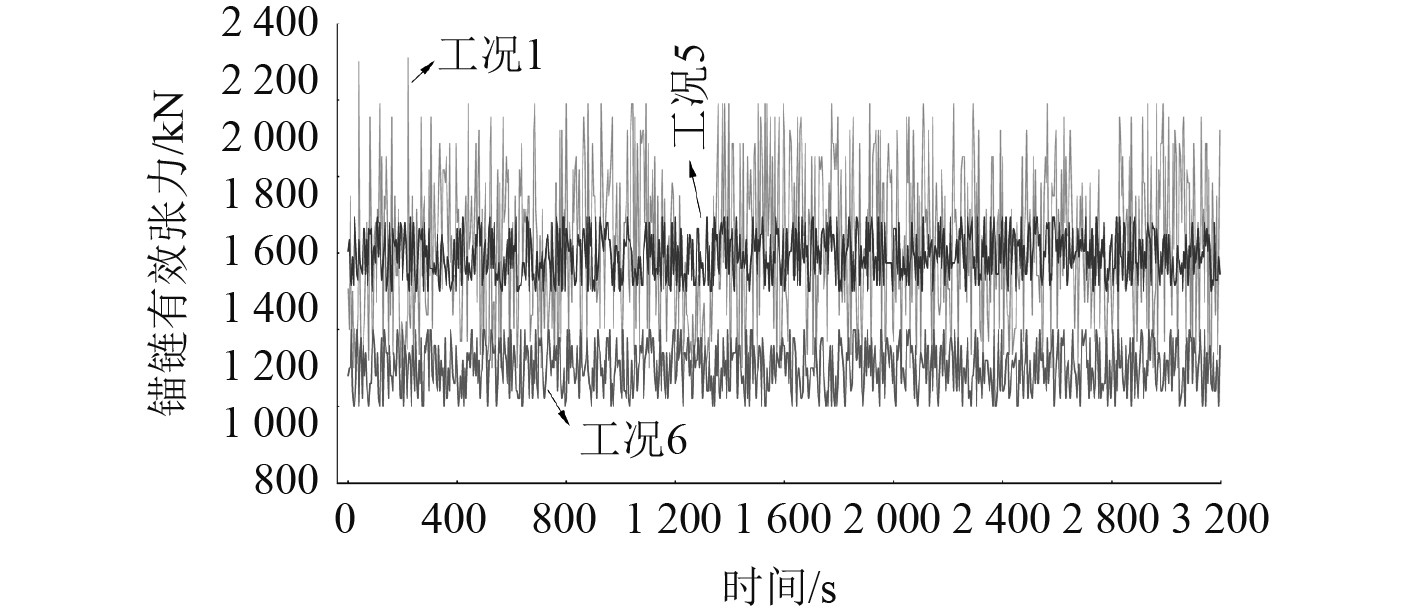
|
图 4 系泊链1在短期海况4时不同分析工况下的张力-时历曲线 Fig. 4 Tension time history of mooring chain 1 under different analyzed working conditions at short-term sea state 4 |
与S-N曲线考虑应力范围不同,T-N曲线考虑的是张力范围,故对于系泊系统更多的使用T-N曲线来进行疲劳损伤计算。T-N曲线给出系泊链发生疲劳破坏时受力循环次数N与张力范围T的关系,如下式:
| $ N{R^M} = K 。$ | (7) |
其中:
通过统计方法得到不同计算工况下的系泊链的张力水平,结合Palmgren-Miner累积损伤准则得到系泊链在j海况下的疲劳累积损伤度Dj:
| $ {D_j} = {p_j}\frac{{3.15576 \times {{10}^7}}}{{{t_j}}}\sum\limits_i {\frac{{{n_{ji}}}}{{{N_i}}}} 。$ | (8) |
式中:Pj为海况j发生的概率;tj为在海况j下的张力时间历程;nji为海况j下的张力范围i的循环次数;Ni为T-N曲线对应张力范围i处的失效循环次数。
3.2 疲劳损伤计算结果及湍流风场影响研究可以看出,要计算系泊缆的疲劳损伤度首先需要统计得到系泊链的张力水平,这里利用改进四峰雨流计数法[16]对第二章计算得到张力-时历进行统计分析。之后基于线性累积损伤理论的T-N曲线法对3根系泊缆在不同分析工况下的损伤度进行计算,各系泊链的总疲劳损伤计算结果见表4。
|
|
表 4 不同分析工况下的系泊链总疲劳损伤度 Tab.4 Total fatigue damage of mooring chains under different analyzed working conditions |
考虑气动载荷影响(工况1~工况5)的疲劳损伤结果,对比仅考虑波浪载荷(工况6)的疲劳损伤结果,可以发现3根系泊缆的疲劳损伤平均增加了241.7%,这说明进行浮式风机疲劳评估时不能忽略气动载荷的影响。真实海洋环境风为湍流风,若将风场视为稳态风场(对比工况5和工况1~工况4),系泊疲劳评估结果偏危险。
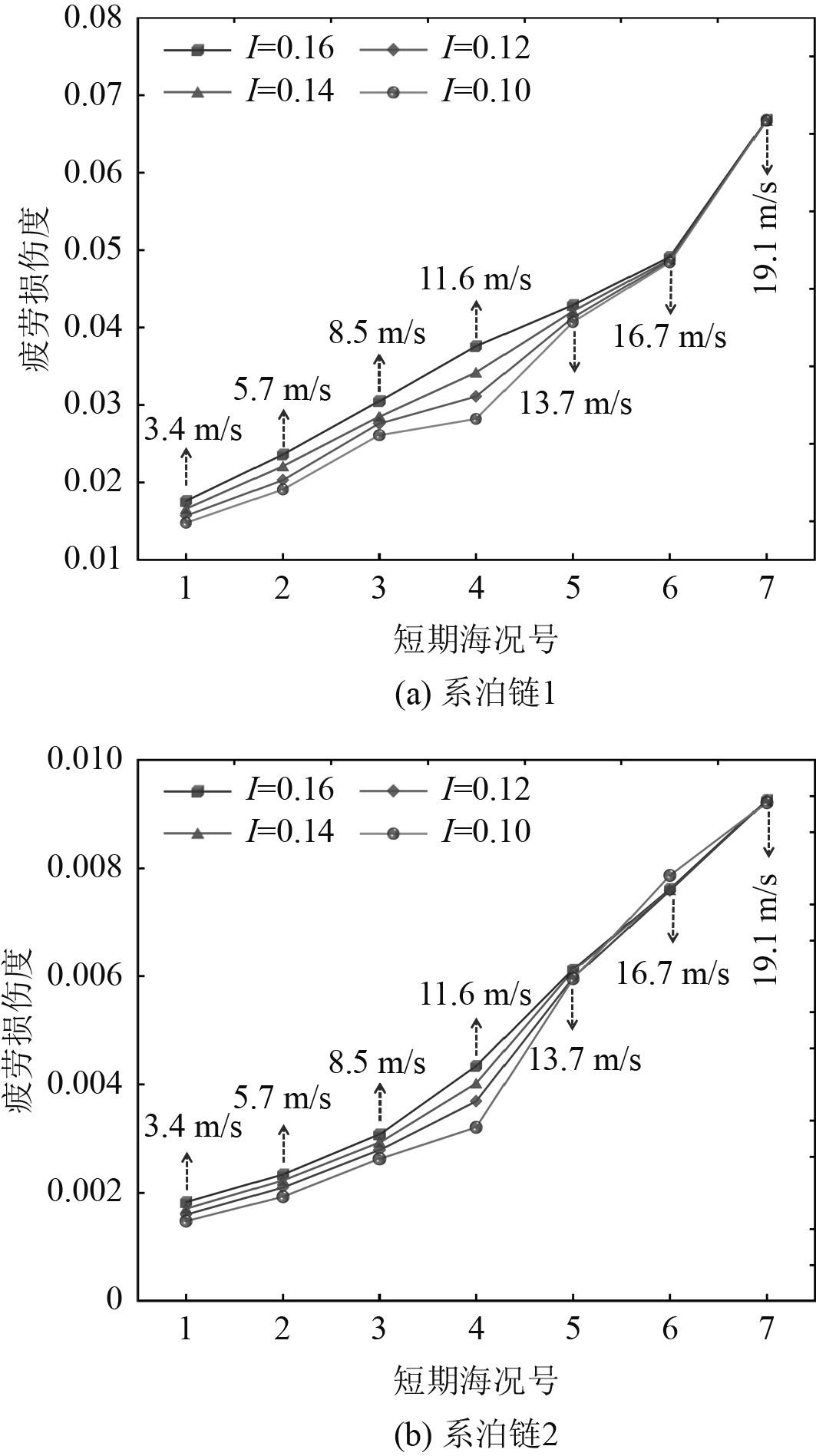
根据IEC规范,风场的湍流强度是定义风机等级的重要参数之一,而有关风场湍流强度对于浮式风机系泊疲劳的影响研究目前较少,故下面进行详细分析。图5为系泊链1和系泊链2(系泊链3和系泊链2结果基本一致,文中不再列出)在不同海况下的短期疲劳损伤计算结果。
|
图 5 系泊链1和系泊链2在不同海况下的短期疲劳损伤结果 Fig. 5 Short-term fatigue damage of mooring chain 1 and chain 2 under different sea conditions |
从图5系泊链不同海况下的短期疲劳损伤结果可以看出,风场湍流强度对系泊疲劳的影响与海况的风速有关,当短期海况风速在额定风速以下时,湍流强度与系泊缆疲劳损伤呈正相关关系,湍流强度越大,系泊缆的系泊疲劳损伤越大,且当短期海况风速接近额定风速时,系泊疲劳损伤受湍流强度影响最大。当短期海况风速大于额定风速时,风场湍流强度对系泊疲劳损伤的影响较小,以文中的海况5−海况7为例,其因湍流强度改变而引起系泊疲劳损伤平均波动率仅为0.87%(系泊链1)和0.93%(系泊链2)。
4 结 语本文建立了一种多场耦合作用下的浮式风力机平台系泊系统疲劳损伤评估方法并揭示了风场湍流强度对风力机平台系泊系统疲劳的影响规律。由系泊缆的疲劳损伤计算结果可以发现,气动载荷会对系泊链产生较大的疲劳损伤,系泊分析时必须考虑气动模型。采用湍流风计算气动载荷时,当短期海况风速在额定风速以下时,湍流强度与系泊缆疲劳损伤呈正相关,且这种影响关系在短期海况风速接近额定风速时达到最大。而短期海况风速超过额定风速时,风场湍流强度对平台系泊疲劳影响很小。本文结论可为类似平台的系泊系统疲劳分析提供一定的参考和依据。
| [1] |
陶建根, 陈怡, 黄博远. 海上风电发展现状与趋势分析[J]. 能源工程, 2023, 43(4): 1-9. |
| [2] |
温斌荣, 田新亮, 李占伟, 等. 大型漂浮式风电装备耦合动力学研究: 历史、进展与挑战[J]. 力学进展, 2022, 52(4): 731-808. |
| [3] |
KVITRUD A. Lessons learned from norwegian mooring line failures 2010–2013[C]//ASME International Conference on Ocean. American Society of Mechanical Engineers, 2014. DOI:10.1115/OMAE2014-23095.
|
| [4] |
FONTAINE E, KILNER A, CARRA C, et al. Industry Survey of Past Failures, Pre-emptive Replacements and Reported Degradations for Mooring Systems of Floating Production Units[C]//Offshore Technology Conference. BioMed Central Ltd, 2014. DOI:10.4043/25273-MS.
|
| [5] |
盛景, 桑松, 曹爱霞, 等. SPAR型浮式风力机涡激特性研究及系缆疲劳评估[J]. 太阳能学报, 2019, 40(10): 2979-2985. |
| [6] |
邓露, 吴松熊, 钟文杰, 等. 风浪夹角变化对海上浮式风机系泊的影响[J]. 土木工程与管理学报, 2018, 35(1): 1-6. DOI:10.3969/j.issn.2095-0985.2018.01.001 |
| [7] |
GUANHUA Z, YULIANG Z, SHENG D. System reliability analysis of mooring system for floating offshore wind turbine based on environmental contour approach[J]. Ocean Engineering, 2023, 285(P2): 115157. |
| [8] |
OLIVEIRA D L B, AGUIAR F H, SILVA R N, et al. Fatigue life estimate of metallic chain links of mooring systems assuming out of plane bending: From constant amplitude to random loading[J]. Ocean Engineering, 2023, 288(P2): 116139. |
| [9] |
XIFENG G, XIAOYONG L, XUTIAN X, et al. Fracture mechanics-based mooring system fatigue analysis for a spar-based floating offshore wind turbine[J]. Ocean Engineering, 2021, 223: 108618. DOI:10.1016/j.oceaneng.2021.108618 |
| [10] |
ROBERTSON A, JONKMAN J, MASCIOLA M, et al. Definition of the semisubmersible floating system for phase II of OC4[R]. United States: National Renewable Energy Laboratory(NREL), 2014.
|
| [11] |
HANSEN M O L, SØRENSEN J N, VOUTSINAS S, et al. State of the art in wind turbine aerodynamics and aeroelasticity[J]. Progress in Aerospace ences, 2006, 42(4): 285-330. DOI:10.1016/j.paerosci.2006.10.002 |
| [12] |
刘贵杰, 王清扬, 田晓洁, 等. 海洋结构物小尺度桩柱的水动力系数研究与进展[J]. 中国海洋大学学报(自然科学版), 2020, 50(1): 136-144. |
| [13] |
COMMISSION I E. Design requirements for offshore wind turbine: IEC 61400-3[S]. Geneva: The International Electrotechnical Commission, 2009: 144.
|
| [14] |
MATTIA O M, MELISA M. A global evaluation of the JONSWAP spectra suitability on coastal areas[J]. Ocean Engineering, 2022, 266(P2): 112756. |
| [15] |
SHU H, YAO A, MA K T, et al. API RP 2SK 4th Edition-An Updated Stationkeeping Standard for the Global Offshore Environment[C]//Offshore Technology Conference. 2018. DOI: 10.4043/29024-MS.
|
| [16] |
周陈炎, 张佳宁, 孟巧, 等. 基于改进四峰谷值雨流计数法的船舶疲劳强度评估[J]. 船海工程, 2022, 51(6): 42-46+52. DOI:10.3963/j.issn.1671-7953.2022.06.009 |
 2024, Vol. 46
2024, Vol. 46
