2. 天津瀚海蓝帆海洋科技有限公司,天津 300300;
3. 天津市深远海智能移动勘测装备研发重点实验室,天津 300300
2. Tianjin Hanhai-lanfan Marine Technology Co., Ltd., Tianjin 300300, China;
3. Tianjin Key Laboratory of Deep-sea Intelligent Mobile Survey Equipment, Tianjin 300300, China
水下机器人(ROV)一直以来都在水底环境勘测、水下作业救援活动中发挥着重要作用。ROV在水中的运动具有强非线性,强耦合性的特点,并且会不可避免地受到外界不确定性因素的干扰,这使得提高ROV在运动时的位姿控制稳定性一直都是近些年来行业内研究的重点。国内外众多学者对ROV的姿态控制、轨迹跟踪、深度控制等内容先后进行了许多基于控制策略的研究。
自抗扰控制(ADRC)技术是韩京清研究员在对经典调节理论与现代控制理论两方面的内在思想不断进行深入思考的过程中,借鉴现代控制理论在分析系统结构性质方面的成果,在经典控制理论思想精华的基础上逐步构建,并于1999年正式提出来的[1 - 2]。
自抗扰技术理论自提出之后,在理论与应用层面均取得了一定进展,Wu等[3]将神经网络与自抗扰控制技术相结合应用于AUV姿态控制,满足了系统对姿态高精度的要求;Liu等[4]利用自抗扰技术跟踪水下航行器的俯仰角,进而实现了航行器的深度控制;Wu等[5]提出了一种PSO-ADRC算法解决了自抗扰参数的自整定问题;Shan等和Wang等[6 - 7]将模糊控制与自抗扰控制技术相结合以实现对目标的高精度跟踪;Shi等和Nahri等[8 - 9]分别对时滞系统以及控制系统的时滞问题进行了研究,利用预测的扩张状态观测器改善了控制系统性能;彭毓卿[10]将自抗扰控制应用于船舶的路径跟踪问题,结果展示出了对轨迹跟踪的稳定性。以上文献在研究ADRC整体性能时并没有对扩张状态观测器本身与非线性函数的关系展开深入的讨论研究。非线性函数与扩张状态观测器之间的关系决定了系统输出的稳定性。消除非线性函数引起的误差突变,是提高ADRC控制性能的关键。
受上述研究启发,为提高ROV在状态响应过程中的位姿控制能力,利用双曲正切函数在原点附近具有良好的平滑性特点,采用多项式拟合的方法构建sfal函数,解决了原fal函数在分段处不够平滑的问题,使其更符合“小误差大增益,大误差小增益”的特性。并基于sfal函数构建出新型ADRC控制器,用以降低系统响应过程中的超调量。
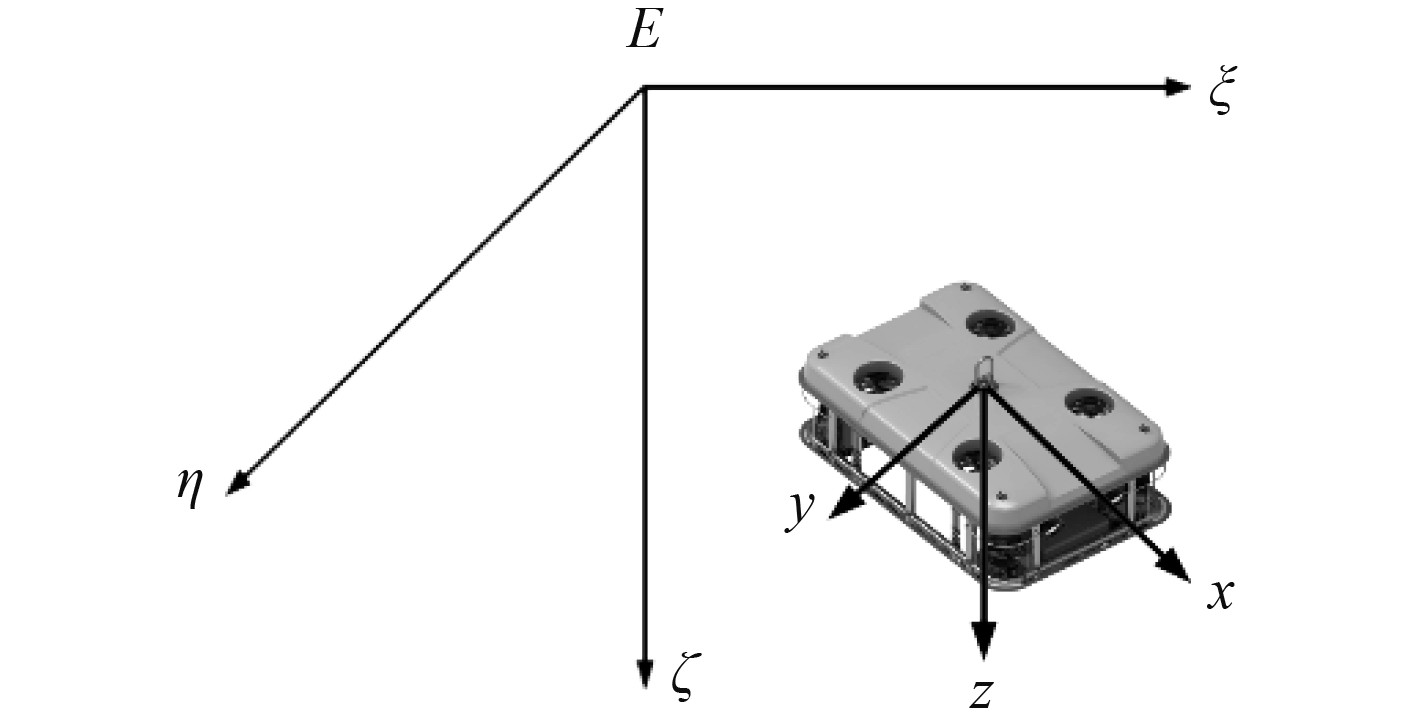
1 ROV数学模型 1.1 ROV运动学模型本文的研究对象为实验小组搭建的ROV,为方便进一步对ROV进行研究,在以下前提下对ROV进行数学分析:1)假设ROV为刚体,质量体积不随时间变化;2)忽略地球自转对ROV运动的影响。建立如图1所示的地面坐标系
|
图 1 地面坐标系与载体坐标系 Fig. 1 Ground coordinate system and carrier coordinate system |
ROV系统的运动学方程如下式:
| $ {{{\boldsymbol{\dot \eta}} = {\boldsymbol J}}}({\mathbf{{\boldsymbol{\eta}} }}){\mathbf{{\boldsymbol{\nu}} }} 。$ | (1) |
式中:
| $ {\boldsymbol{J}}({\mathbf{{\boldsymbol{\eta}} }}){\mathbf{ = }}\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{J}}_1}{{\boldsymbol{\eta }}_1}}&{{{\boldsymbol{0}}_{3 \times 3}}} \\ {{{\boldsymbol{0}}_{3 \times 3}}}&{{{\boldsymbol{J}}_2}{{\boldsymbol{\eta }}_2}} \end{array}} \right] ,$ | (2) |
| $ {{\boldsymbol{J}}_{\mathbf{1}}}({{\boldsymbol{\eta }}_{\mathbf{1}}}) = \left[ {\begin{array}{*{20}{c}} {\cos \varphi \cos \theta }&{{{\boldsymbol{J}}_{12}}}&{{{\boldsymbol{J}}_{13}}} \\ {\sin \varphi \cos \theta }&{{{\boldsymbol{J}}_{22}}}&{{{\boldsymbol{J}}_{23}}} \\ { - \sin \theta }&{\cos \theta \sin \phi }&{\cos \phi \cos \theta } \end{array}} \right] ,$ | (3) |
| $ \left\{ \begin{gathered} {{\boldsymbol{J}}_{12}} = - \sin \varphi \cos \phi + \cos \varphi \sin \theta \sin \phi,\\ {{\boldsymbol{J}}_{13}} = \sin \varphi \sin \phi + \cos \varphi \cos \phi \sin \theta ,\\ {{\boldsymbol{J}}_{22}} = \cos \varphi \cos \phi + \sin \phi \sin \theta \sin \varphi ,\\ {{\boldsymbol{J}}_{23}} = - \cos \varphi \sin \phi + \sin \theta \sin \varphi \cos \phi。\\ \end{gathered} \right. $ | (4) |
| $ {{\boldsymbol{J}}_2}({{\boldsymbol{\eta }}_2}) = \left[ {\begin{array}{*{20}{c}} 1&{\sin \phi \tan \theta }&{\cos \phi \tan \theta } \\ 0&{\cos \phi }&{ - \sin \phi } \\ 0&{\sin \phi /\cos \theta }&{\cos \phi /\cos \theta } \end{array}} \right]。$ | (5) |
在载体坐标系下,ROV的六自由度动力学方程可以描述为[11]:
| $ {\boldsymbol{M\dot \nu + C}}({\boldsymbol{\nu }}){\boldsymbol{\nu + D}}({\boldsymbol{\nu }}){\boldsymbol{\nu + g}}({\boldsymbol{\eta }}){\boldsymbol{ = \tau }} 。$ | (6) |
式中:
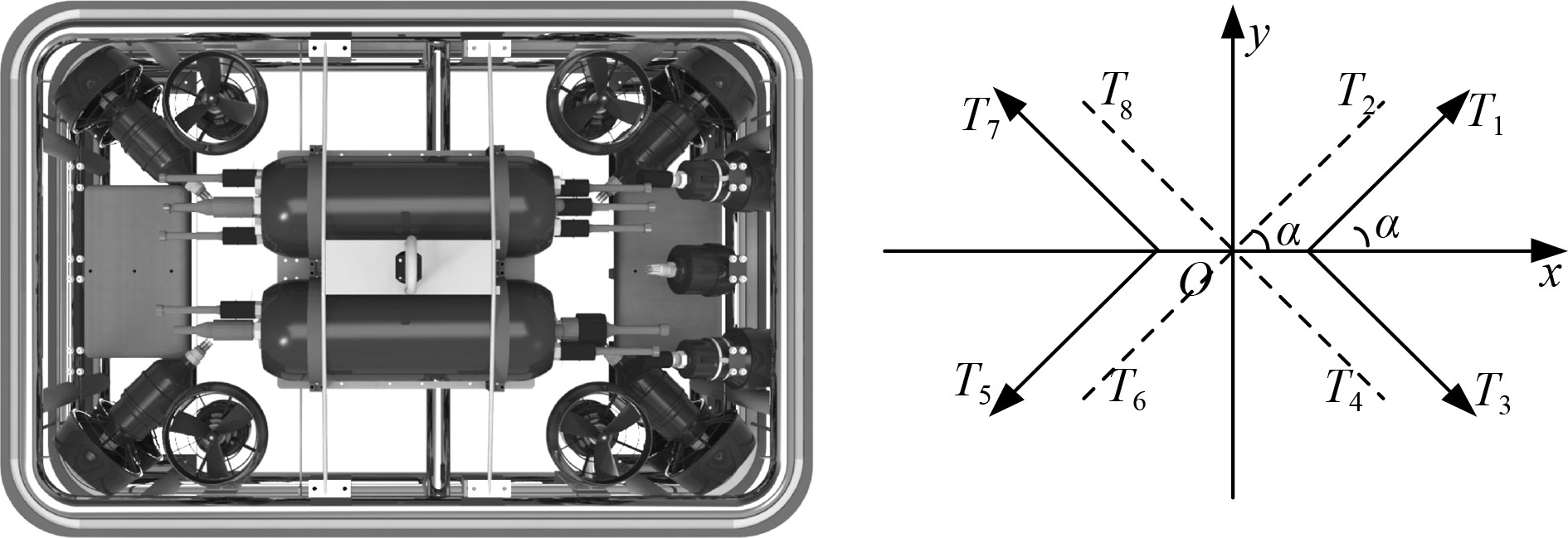
|
图 2 推进器矢量分布图 Fig. 2 Vector distribution diagram of propeller |
将载体坐标系的原点置于ROV的重心,与其对应的上述各矩阵可表示为:
| $ \begin{gathered} M = diag\left[ {m - {X_{{\dot u}}},m - {Y_{{\dot v}}},m - {Z_{{\dot w}}},} \right. \\ \left. {{\text{ }}{I_{\text{x}}} - {K_{{\dot p}}},{I_{\text{y}}} - {K_{{\dot q}}},{I_{\text{z}}} - {K_{{\dot r}}}} \right] 。\\ \end{gathered} $ | (7) |
式中:m为ROV的质量;
| $ {\boldsymbol{C}}({\boldsymbol{\nu }}){\mathbf{ = }}\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{0}}_{3 \times 3}}}&{{{\boldsymbol{C}}_{12}}} \\ {{{\boldsymbol{C}}_{21}}}&{{{\boldsymbol{C}}_{22}}} \end{array}} \right],$ | (8) |
| $ \left\{ \begin{gathered} {{\boldsymbol{C}}_{12}} = \left[ {\begin{array}{*{20}{c}} 0 & {m - {Z_{\dot w}}} & { - (m - {Y_{\dot v}})v} \\ { - (m - {Z_{\dot w}})w} & 0 & {(m - {X_{\dot u}})u } \\ {(m - {Y_{\dot v}})v} & { - (m - {X_{\dot u}})u} & 0 \end{array}} \right] ,\\ {{\boldsymbol{C}}_{21}} = \left[ {\begin{array}{*{20}{c}} 0 & { - (m + {Z_{\dot w}})w} & {(m + {Y_{\dot v}})v} \\ {(m + {Z_{\dot w}})w} & 0 & { - (m + {X_{\dot u}})u } \\ { - (m + {Y_{\dot v}})v} & {(m + {X_{\dot u}})u} & 0 \end{array}} \right] ,\\ {{\boldsymbol{C}}_{22}} = \left[ {\begin{array}{*{20}{c}} 0 & {({I_Z} - {N_{\dot r}})r} & {- ({I_Y} - {M_{\dot q}})q} \\ { - ({I_Z} - {N_{\dot r}})r} & 0 & {({I_X} - {K_{\dot p}})p} \\ {({I_Y} - {M_{\dot q}})q} & { - ({I_X} - {K_{\dot p}})p} & 0 \end{array}} \right] 。\\ \end{gathered} \right. $ | (9) |
| $ {\boldsymbol{g}}({\boldsymbol{\eta }}) = \left[ \begin{gathered} (W - B)\sin \theta \\ - (W - B)\sin \theta \cos \theta \\ - (W - B)\cos \phi \cos \theta \\ B\cos \theta ({z_B}\sin \phi - {y_B}\cos \phi ) \\ B({x_B}\cos \phi \cos \theta - {z_B}\sin \theta ) \\ - B({x_B}\sin \phi \cos \theta + {y_B}\sin \theta ) \\ \end{gathered} \right]。$ | (10) |
式中:W为ROV系统自身的质量;B为ROV在水中所受浮力;
| $ {\boldsymbol{D}}({\boldsymbol{v}}){\mathbf{ = }}{{\boldsymbol{D}}_{\mathbf{L}}}{\mathbf{ + }}{{\boldsymbol{D}}_{\mathbf{Q}}}\left| v \right| ,$ | (11) |
| $ {{\boldsymbol{D}}_L} = diag\left[ {{X_u},{Y_v},{Z_w},{K_p},{P_q},{N_r}} \right],$ | (12) |
| $ {{\boldsymbol{D}}_Q} = diag\left[ {{X_{u\left| u \right|}},{Y_{{\text{v}}\left| v \right|}},{Z_{w\left| w \right|}},{K_{p\left| p \right|}},{M_{q\left| q \right|}},{N_{r\left| r \right|}}} \right]。$ | (13) |
式中:
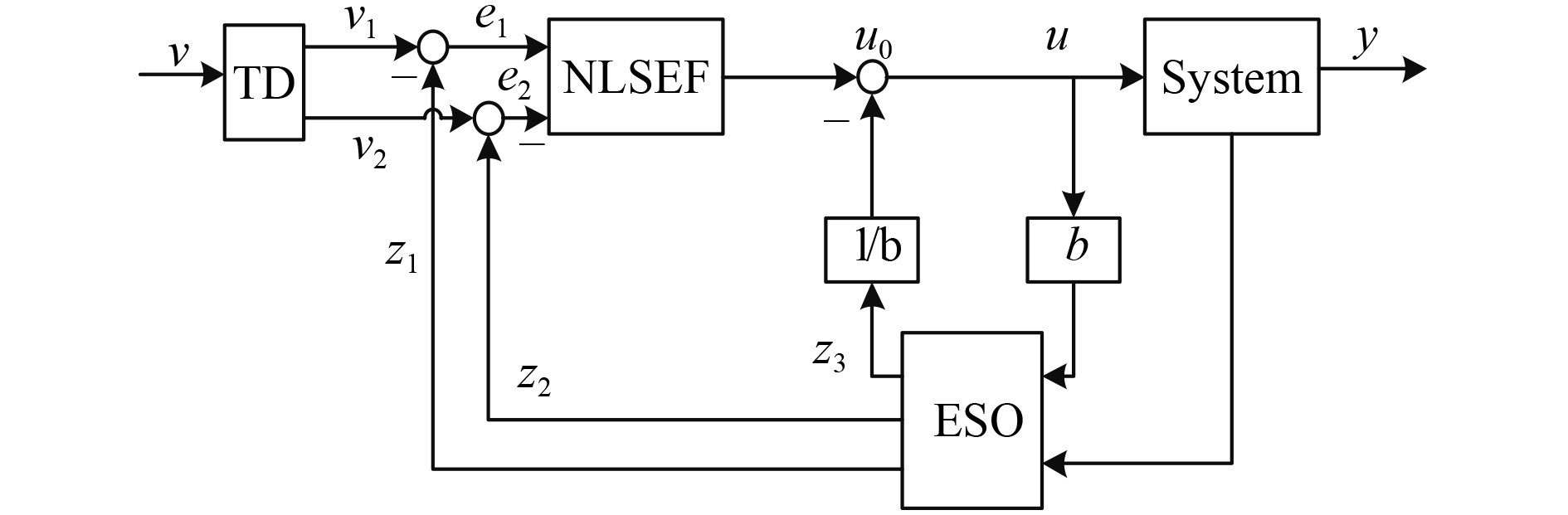
ADRC在扰动估计与整体辨识的基础上,利用控制器产生扰动估计的返回信号进行补偿,做到了扰动的直接整体消减[12]。自抗扰控制器的主要结构由跟踪-微分器(Tracking Differentiator,TD,用于微分信号获取与过渡过程配置)、扩张状态观测器(Extended State Observer,ESO,用于对外界扰动的估计)以及非线性状态误差反馈控制律(Nonlinear State Error Feedback,NLSEF,用于控制器控制量的生成)组成,ADRC基本结构如图3所示。
|
图 3 ADRC基本结构 Fig. 3 The basic structure of ADRC |
1)跟踪-微分器
对系统输入信号
| $ \left\{\begin{gathered}x_1(k+1)=x_1(k)+hx_2(k),\\ \ \ x_2(k+1)=x_2(k)+h\cdot \text{fhan}。\end{gathered}\right. $ | (14) |
式中:
| $ \left\{ \begin{gathered} d = {r_0}h_0^2 ,\\ {a_0} = {h_0}{x_2} ,\\ y = {x_1} + {a_0} ,\\ {a_1} = \sqrt {d(d + 8\left| y \right|)} ,\\ {a_2} = {a_0} + {\rm sign}(y)({a_1} - d)/2 ,\\ {s_y} = [{\rm sign}(y + d) - {\rm sign}(y - d)]/2 ,\\ a = ({a_0} + y - {a_2}){s_y} + {a_2} ,\\ {s_a} = [{\rm sign}(a + d) - {\rm sign}(a - d)]/2 ,\\ {\rm fhan} = - r[a/d - {\rm sign}(a)]{s_a} - {r_0}{\rm sign}(a) 。\\ \end{gathered} \right. $ | (15) |
2)非线性状态误差反馈控制律
基于跟踪-微分器安排过渡过程等手段,生成系统跟踪过程的误差信号与误差微分信号,2种信号通常以非线性组合的方式以得到系统的反馈信号,文章给出一种非线性组合形式如下式:
| $ \left\{ \begin{gathered} {e_1} = {v_1} - {z_1} ,\\ {e_2} = {v_2} - {z_2} ,\\ {u_0} = {\beta _1}{\rm fal}({e_1},{\alpha _1},\delta ) + {\beta _2}{\rm fal}({e_2},{\alpha _2},\delta ) ,\\ u = {u_0} - {z_3}/b 。\\ \end{gathered} \right. $ | (16) |
式中:
| $ {\rm fal}(e,\alpha ,\delta ) = \left\{ \begin{gathered} e/{\delta ^{1 - \alpha }}{\text{, }}\left| e \right| \leqslant \delta,\\ {\left| e \right|^\alpha }{\rm sign}(e),{\text{ }}\left| e \right| \gt \delta 。\end{gathered} \right. $ | (17) |
3)扩张状态观测器
扩张状态观测器的基本思想是将控制系统的总扰动扩张成系统的一个新的状态变量,之后利用系统的输入与输出重构出包含原本系统状态变量与扰动变量的所有状态[13]。其离散形式的一般表达式为:
| $ \left\{ \begin{array}{l} {e_1} = {z_1}(k) - y(k) ,\\ {z_1}(k + 1) = {z_1}(k) + h({z_2}(k) - {\beta _{01}}{e_1}) ,\\ {z_2}(k + 1) = {z_2}(k) + h({z_3}(k) - {\beta _{02}}{\rm fal}({e_1},{\alpha _1},\delta ) + bu) ,\\ {z_3}(k + 1) = {z_3}(k) - h{\beta _{03}}{\rm fal}({e_2},{\alpha _2},\delta ) 。\end{array} \right. $ | (18) |
式中:
非线性函数是自抗扰控制的核心,选取合适的非线性函数是实现ADRC稳定控制效果的前提。在进行非线性函数设计时,应该充分考虑到函数应同时具备以下特征:1)非线性函数在原点附近应收敛到0;2)函数本身应尽可能具备良好的平滑性;3)函数在原点附近应连续可导。
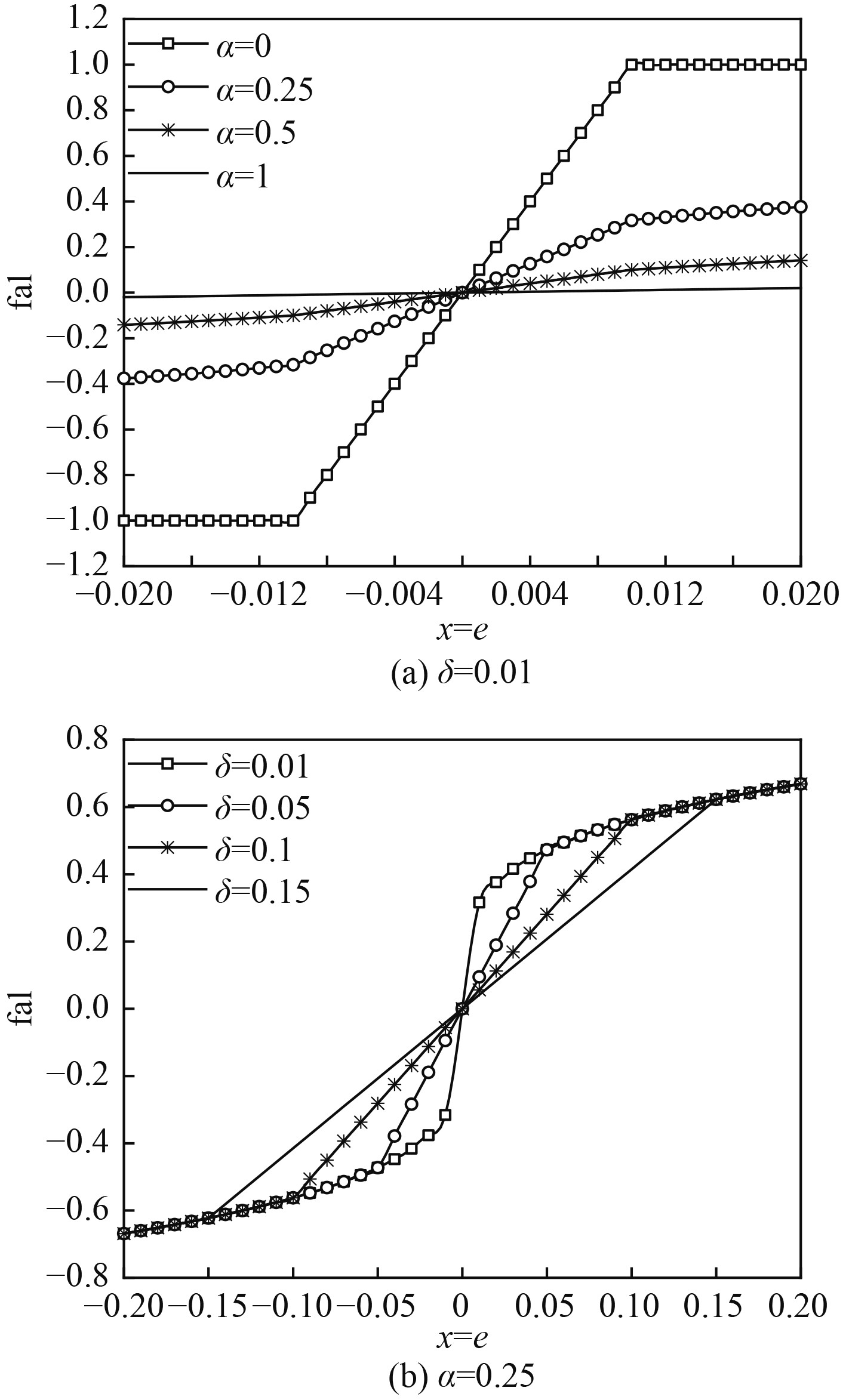
首先结合函数控制参量对fal函数在原点附近性质进行分析。选取
|
图 4 fal函数特性图 Fig. 4 The characteristic diagram of fal function |
根据文献[14 − 15]。提供的思路,这里利用双曲正切函数在原点附近的平滑特征,构建出一种新型的非线性函数sfal,其一般形式如下式:
| $ {\rm sfal} = {k_1}\tanh (e) + {k_2}{\tanh ^2}(e) + {k_3}{\tanh ^3}(e)。$ | (19) |
式中:
| $ \left\{ \begin{gathered} t = \tanh (\delta ) ,\\ {k_1}t + {k_2}{t^2} + {k_3}{t^3} = {\delta ^\alpha }{\text{, }}e = \delta,\\ - {k_1}t + {k_2}{t^2} - {k_3}{t^3} = - {\delta ^\alpha },{\text{ }}e = - \delta,\\ {k_1} + 2{k_2}t\dot t + 3{k_3}{t^2}\dot t = \alpha {\delta ^{\alpha - 1}},{\text{ }}e = \pm \delta 。\\ \end{gathered} \right. $ | (20) |
求解可得:
| $ \left\{\begin{array}{l}t\text{ }=\mathrm{tanh}(\delta ),\\ {k}_{1}=\dfrac{3{\delta }^{\alpha } \cdot {t}^{3}-3{\delta }^{\alpha }+\alpha \cdot {\delta }^{\alpha -1} \cdot t}{2t \cdot ({t}^{2}-1)},\\ {k}_{2}=0\\ {k}_{3}=\dfrac{-{\delta }^{\alpha } \cdot {t}^{2}-{\delta }^{\alpha }+\alpha \cdot {\delta }^{\alpha -1} \cdot t}{2{t}^{3} \cdot ({t}^{2}-1)}。\end{array} \right.$ | (21) |
综上可得,
| $ {\rm sfal}(e,\alpha ,\delta ) = \left\{ \begin{array}{l} {k_1}\tanh (\delta ) + {k_3}{\tanh ^3}(\delta ),\left| e \right| \leqslant \delta ,\\ {\left| e \right|^\alpha }{\rm sign}(e),{\text{ }}\left| e \right| \gt \delta。\\ \end{array} \right. $ | (22) |
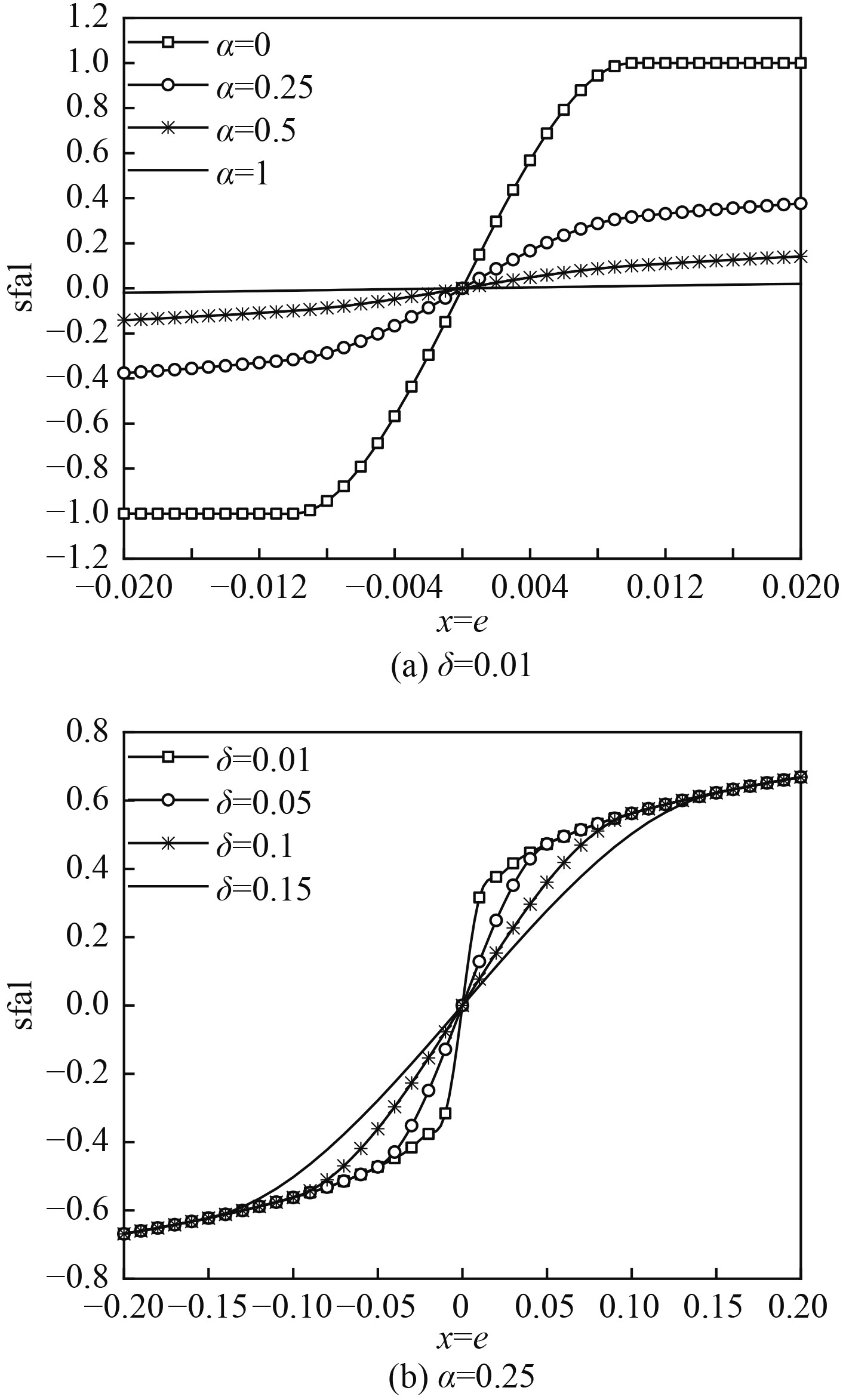
同样选取
|
图 5 sfal函数特性图 Fig. 5 The characteristic diagram of sfal function |
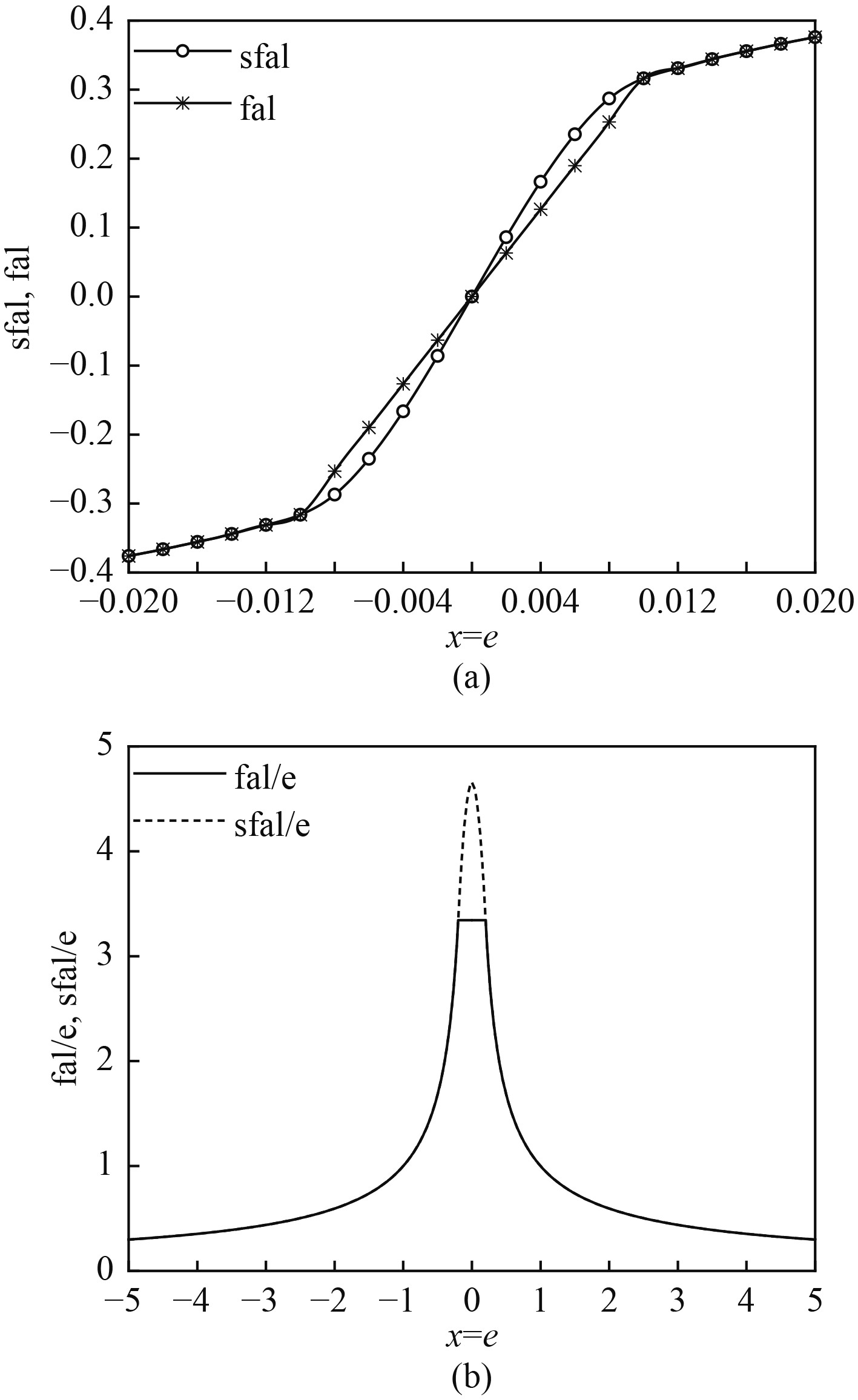
|
图 6 sfal与fal函数响应比较 Fig. 6 Comparison of sfal and fal function responses |
由图6(b)可知,相较于fal函数,sfal函数在原点附近有着更大的增益,同时又避免了增益的突增,从而可以使得系统的控制效果更优。
2.3 函数的稳定性分析基于式(18)构建的扩张状态观测器并由此建立系统的误差系统为:
| $ \left\{ \begin{gathered} {e_1} = {z_1} - {x_1},{e_2} = {z_2} - {x_2} ,\\ {{\dot e}_1} = {e_2} - {\beta _{01}}{e_1} ,\\ {{\dot e}_2} = {e_3} - {\beta _{02}}{\rm sfal}({e_1},{\alpha _1},\delta ) + bu ,\\ {{\dot e}_3} = - {\beta _{03}}{\rm sfal}({e_2},{\alpha _2},\delta ) 。\\ \end{gathered} \right. $ | (23) |
系统新的误差方程为:
| $ \dot e = - {\boldsymbol{A}}({\boldsymbol{e}})e,$ | (24) |
其中,
| $ \left\{ \begin{gathered} {\boldsymbol{A}}({\boldsymbol{e}}) = \left[ {\begin{array}{*{20}{c}} {{\beta _{01}}}&{ - 1}&0 \\ {{\beta _{02}}F}&0&{ - 1} \\ {{\beta _{03}}F}&0&0 \end{array}} \right],\\ F = \frac{{{\rm sfal}({e_1},{\alpha _1},\delta )}}{{{e_1}}} 。\\ \end{gathered} \right. $ | (25) |
引理1 若存在矩阵
| $ {\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} {{d_{11}}}&{{d_{12}}}&{{d_{13}}} \\ { - {d_{12}}}&{{d_{22}}}&{{d_{23}}} \\ { - {d_{13}}}&{ - {d_{23}}}&{{d_{33}}} \end{array}} \right] 。$ | (26) |
并且矩阵D的对角元素为正数,使得矩阵DA(e)为正定矩阵,则式(24)的零解可以看做是Lyapunov渐近稳定的[16]。由式(26)计算可得矩阵DA(e):
| $ {\boldsymbol{DA}}({\boldsymbol{e}}) = \left[ {\begin{array}{*{20}{c}} {{D_{11}}}&{ - {d_{11}}}&{ - {d_{12}}} \\ {{D_{21}}}&{{d_{12}}}&{ - {d_{22}}} \\ {{D_{31}}}&{{d_{13}}}&{{d_{23}}} \end{array}} \right]。$ | (27) |
其中:
| $ \left\{ \begin{gathered} {D_{11}} = {d_{11}}{\beta _{01}} + {d_{12}}{\beta _{02}}F + {d_{13}}{\beta _{03}}F,\\ {D_{21}} = - {d_{12}}{\beta _{01}} + {d_{22}}{\beta _{02}}F + {d_{23}}{\beta _{03}}F,\\ {D_{31}} = - {d_{13}}{\beta _{01}} - {d_{23}}{\beta _{02}}F + {d_{33}}{\beta _{03}}F。\\ \end{gathered} \right. $ | (28) |
为保证矩阵DA(e)为正定对称矩阵,则其需满足以下要求:1)对称元素相等;2)矩阵的顺序主子式均大于零;在此令矩阵元素
| $ {d_{12}} = - \varepsilon {\beta _{01}} + {d_{23}}{\beta _{02}}F - \varepsilon {\beta _{03}}F ,$ | (29) |
| $ {d_{23}} = \frac{{\varepsilon \beta _{01}^2 + \varepsilon {\beta _{01}}{\beta _{03}}F + \varepsilon {\beta _{02}}F + 1}}{{({\beta _{01}}{\beta _{02}} - {\beta _{03}})F}}。$ | (30) |
因为
| $ {D_{11}} \approx {\beta _{01}} + \frac{{\beta _{02}^2F}}{{({\beta _{01}}{\beta _{02}} - {\beta _{03}})}}。$ | (31) |
通过分析易知,
| $ {\beta _{01}}{\beta _{02}} - {\beta _{03}} \gt 0 。$ | (32) |
经验证,当式(32)成立时,矩阵DA(e)顺序主子式均大于0,符合预期要求。式中,
综上条件可知,当条件(32)成立时,可以找到能够满足引理1的矩阵
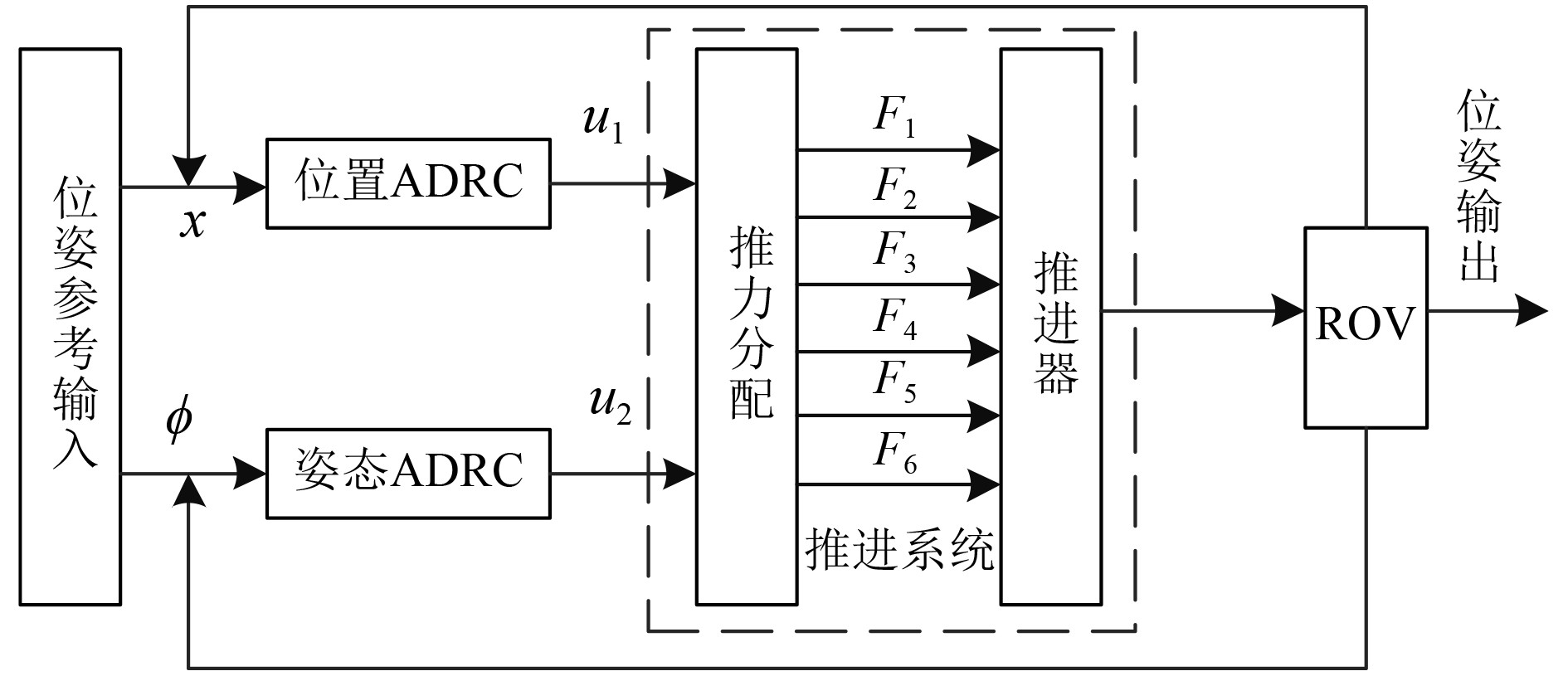
为验证本文中改进型ADRC控制算法在ROV位姿调节中的作用,在Matlab/Simulink中搭建仿真环境,以深度控制与航向控制为例验证改进型ADRC的控制效果,分别针对深度与姿态通道设计仿真实验,并与传统ADRC控制算法以及经典PID算法进行比较,分析改进型ADRC对系统响应的控制性能。ROV控制系统模型如图7所示,ADRC控制器参数如表1所示。
|
图 7 ROV位姿控制系统 Fig. 7 Pose control system of ROV |
|
|
表 1 改进型ADRC仿真参数表 Tab.1 Simulation parameter table of improved ADRC |
给定深度通道期望值为3 m的阶跃信号,航向期望角度为50°阶跃信号,仿真时间设置为10 s,系统完成响应后,在第6 s时加入噪声扰动,对比改进型ADRC、传统ADRC以及PID控制策略的控制能力,仿真结果如图8所示。
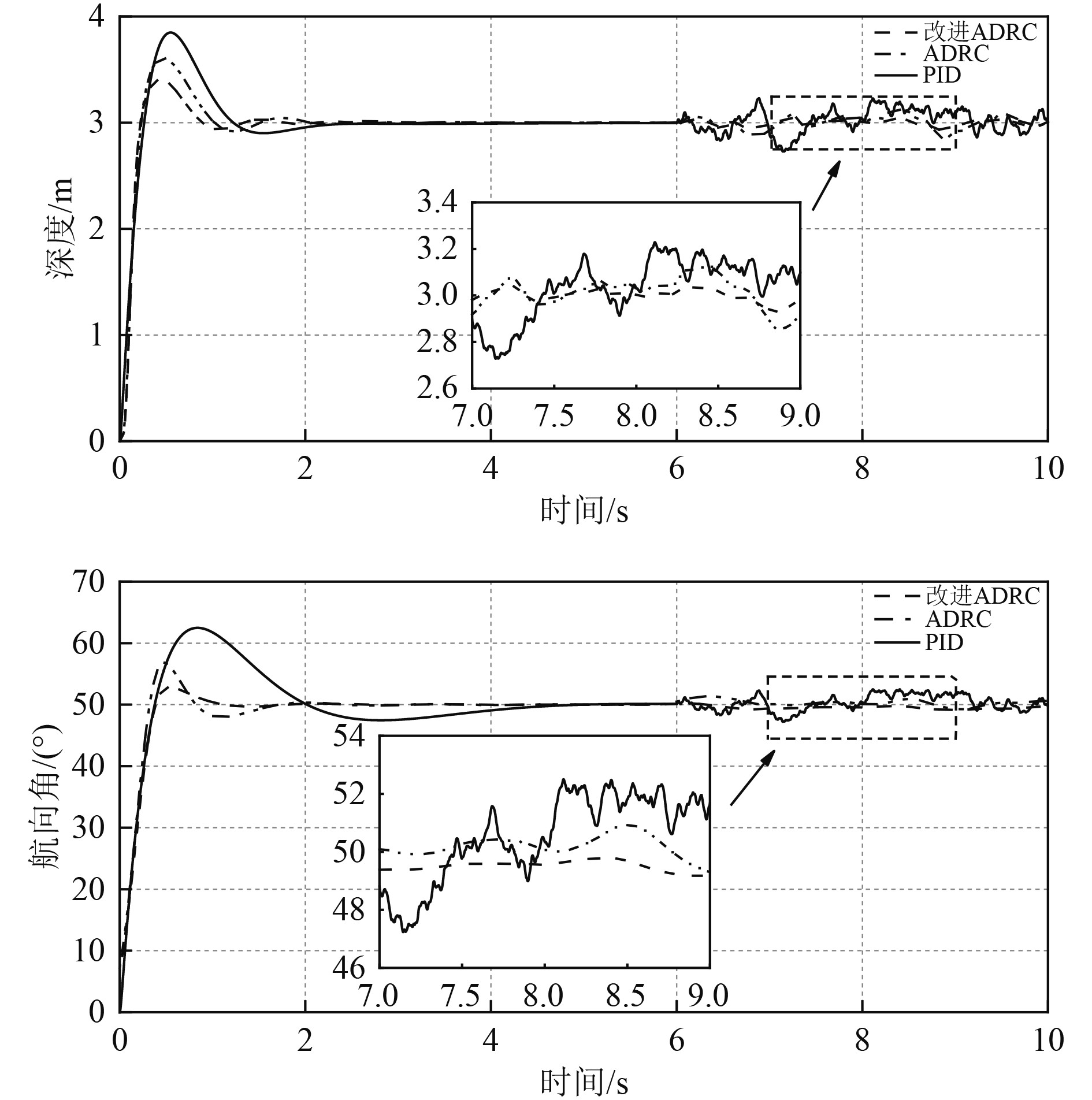
|
图 8 位姿仿真实验 Fig. 8 Pose simulation experiment |
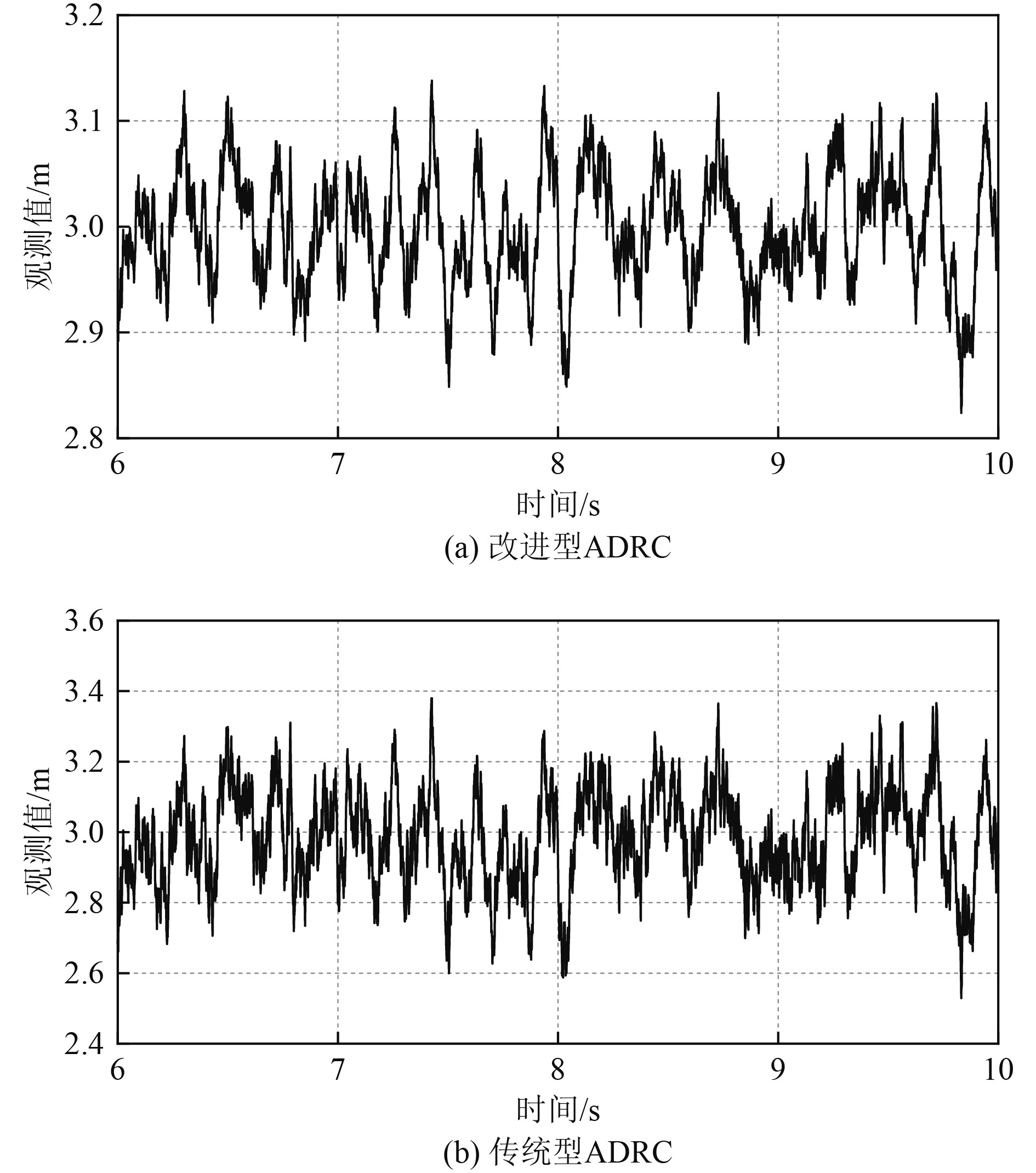
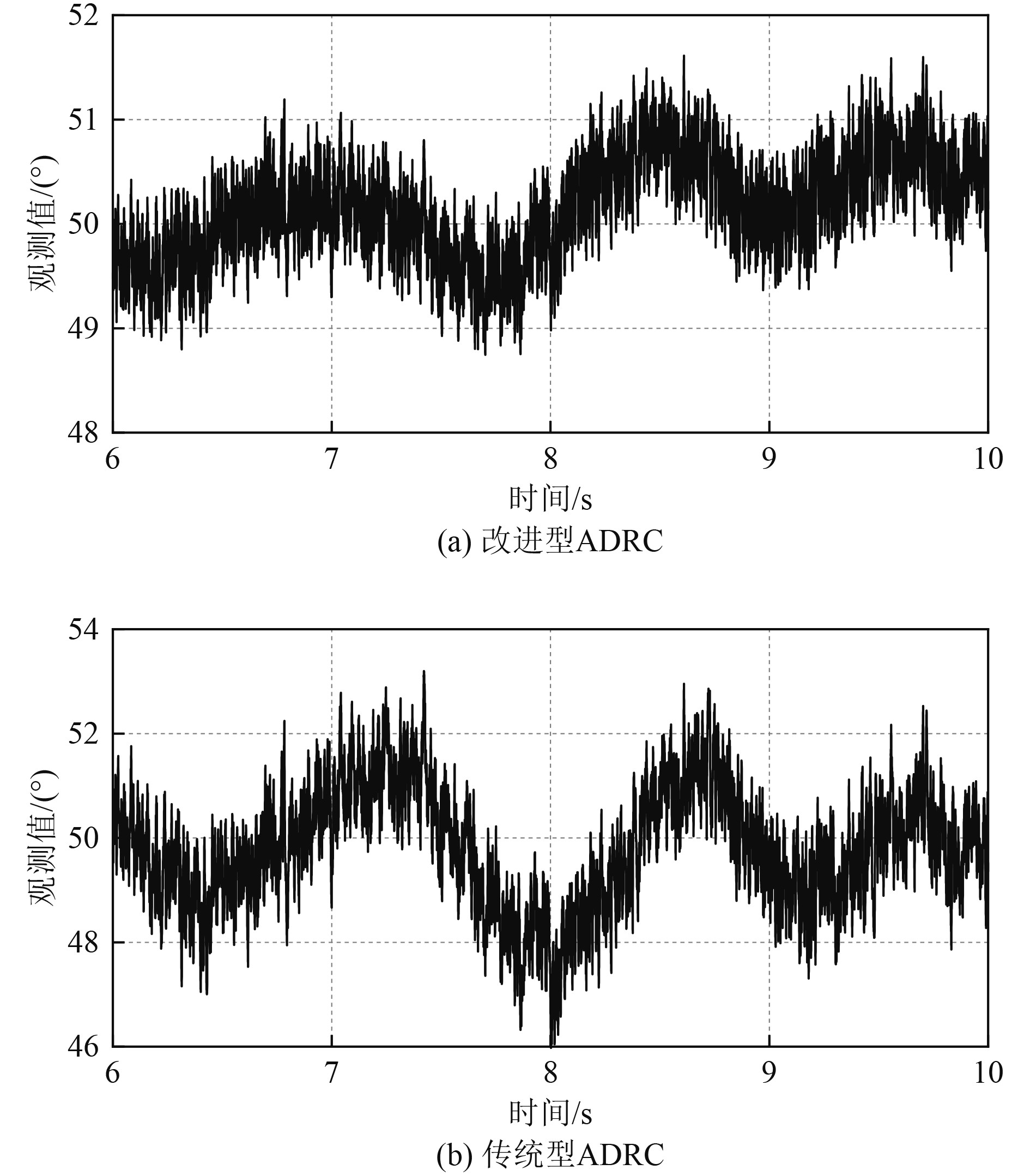
可知,PID控制策略与改进前后的ADRC控制策略均可在系统响应2 s内完成调节过程,但改进型ADRC可以对系统响应过程中超调量起到产生一定的抑制效果,并且在系统受到干扰后保持了较高的稳定性。从扩张状态观测器对位姿状态的观测值层面对比改进前后的观测波动,结果如图9和图10所示,数据对比结果如表2所示,由结果可知改进型ADRC在系统受到干扰时观测值浮动更小,能够保持更高的稳定性。
|
图 9 深度观测值 Fig. 9 Depth observation value |
|
图 10 航向观测值 Fig. 10 Heading observation value |
|
|
表 2 系统稳态误差观测值 Tab.2 System steady-state error observations |
ROV位姿控制系统采用STM32F407单片机为中央处理器,主要完成姿态解算、传感器数据采集、实验数据传输、控制量输出等任务,三维电子罗盘SEC385固连于载体上,该芯片内置三轴磁传感器,姿态测量精度可达到0.1°,深度计测量量程为0~100 m,测量精度可达0.1 m。
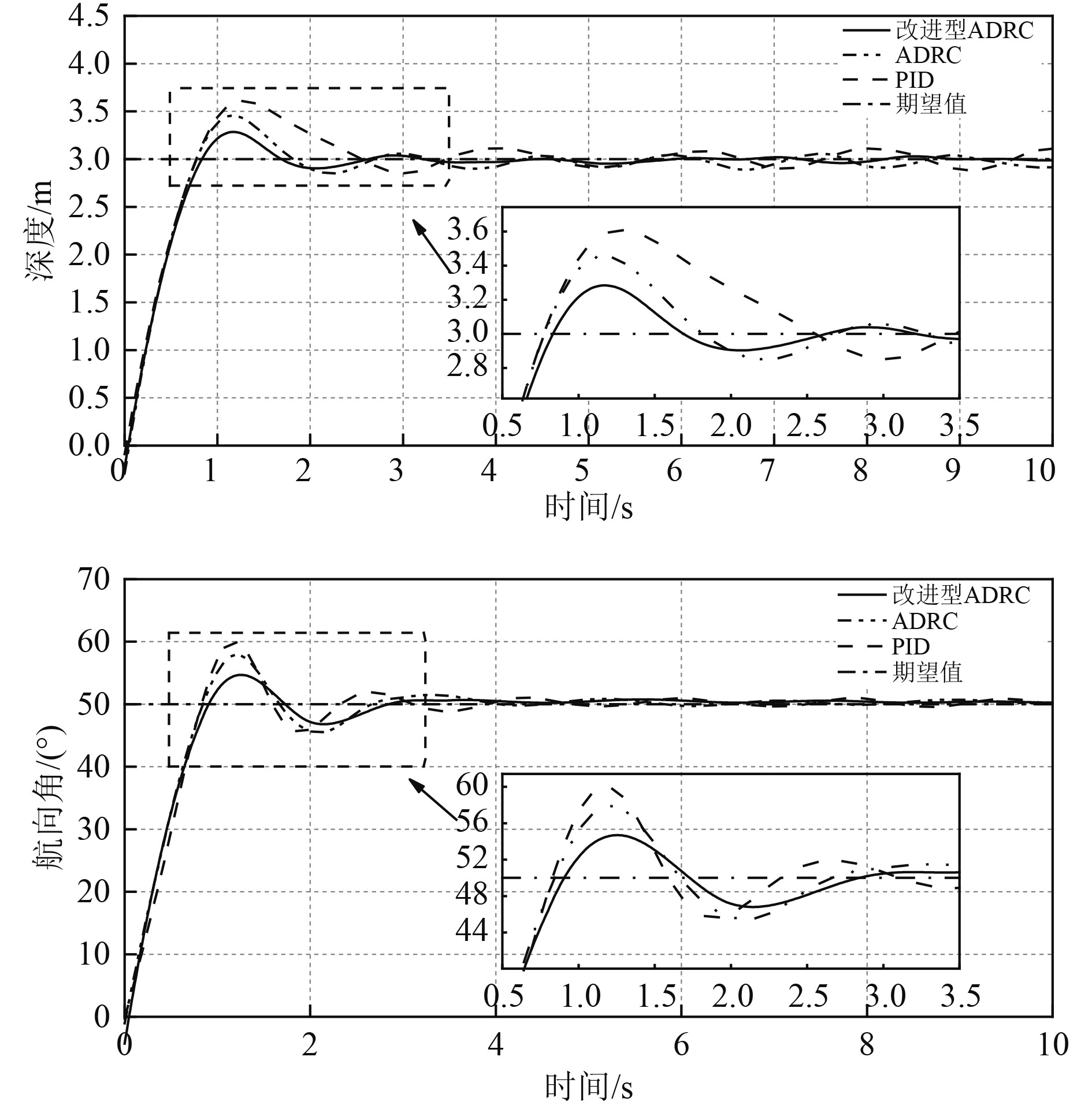
实验选在户外开阔水域中进行湖试,湖中存在自然水流扰动。分别对改进型ADRC与传统ADRC以及PID控制策略进行实验比较,深度值设定为3 m,航向角设定为50°,实验时间设定为10 s,通过岸基显控单元对实验数据进行采集,实验结果如图11所示。
|
图 11 位姿响应实验 Fig. 11 Pose response experiment |
可知,改进型ADRC对系统的超调值产生了明显的抑制效果,采集系统达到稳定状态后的超调最大值进行比较,实验数据如表3所示,通过对比发现,改进型ADRC相较于传统ADRC可降低超调比率30%以上,在一定程度上增强了系统在响应过程中的位姿控制能力。
|
|
表 3 系统超调量数据对比 Tab.3 System overshoot data comparison |
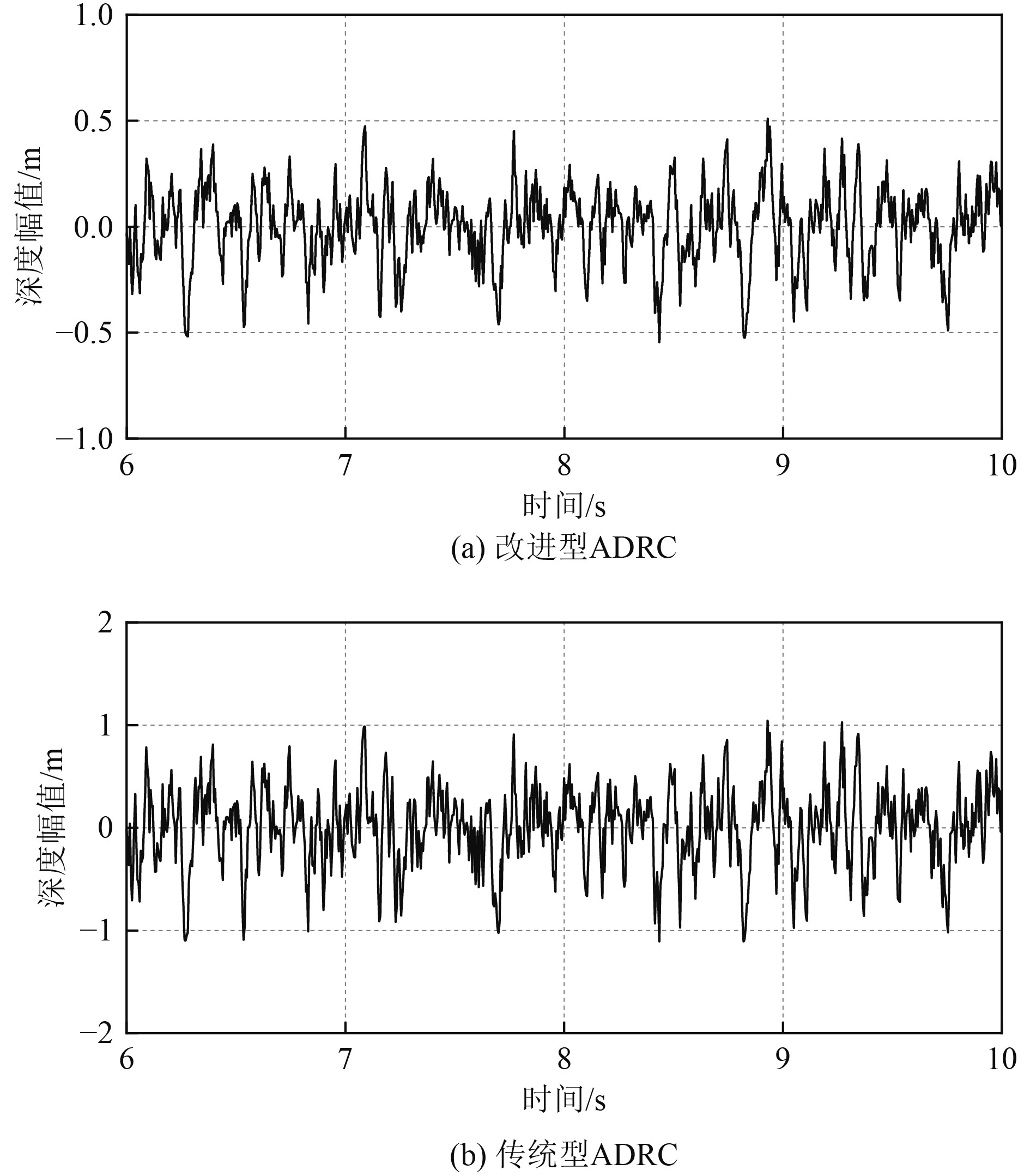
对比ROV的位姿控制通道系统输出幅值,通过控制器输出幅值变化进一步比较改进型ADRC在系统受到扰动时的抗扰能力。对比结果如图12和图13所示。
|
图 12 深度输出幅值 Fig. 12 Amplitude of depth output |
|
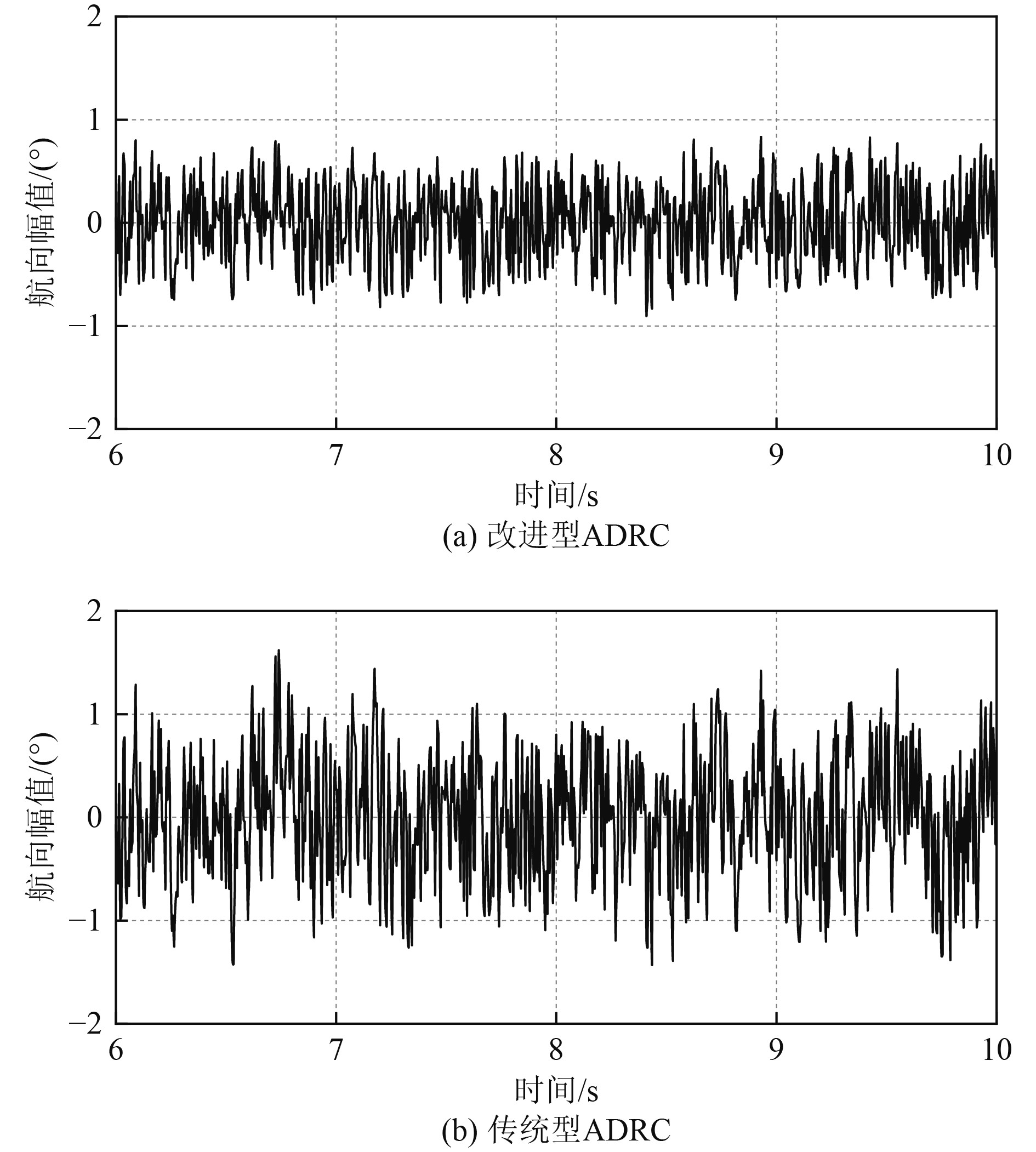
图 13 航向输出幅值 Fig. 13 Amplitude of heading output |
可知,在改进型ADRC控制策略下,ROV的位姿控制输出幅值波动分别为±0.5、±1,而传统ADRC控制策略下ROV位姿系统输出幅值跳变范围位±0.8、±1.5,由此可知改进型ADRC较传统ADRC在抑制外部干扰时能力更强。系统的鲁棒性更高。
4 结 语本文首先针对ROV建立了六自由度的数学模型,并通过分析传统ADRC中fal函数在原点附近拐点处不够平滑,进而引起斜率突变导致扩张状态观测器反馈增益的过大的特点,结合双曲正切函数构建出sfal函数,使得函数在分段处展现出更好的平滑性,并由此设计了改进型ADRC控制器,经过仿真分析与实验验证表明改进型ADRC相比于传统ADRC,在ROV位姿调节过程中可以有效降低系统在响应过程中的超调量,增强系统受到外扰时的稳定性。提高了ROV的位姿控制能力。
| [1] |
韩京清. 自抗扰控制技术——估计补偿不确定因素的控制技术[M]. 北京: 国防工业出版社, 2008.
|
| [2] |
FAREH R, KHADRAOUI S, ABDALLAH M Y, et al. Active disturbance rejection control for robotic systems: Aerview[J]. Mechatronics, 2021, 80: 102671. |
| [3] |
WU Y G, XU H X, JIANG Z B. A modified active disturbance rejection controller based on radial basis function neural network for AUV attitude control[C]//2022 International Conference on Advanced Robotics and Mechatronics (ICARM), Guilin, China: 2022: 962−966.
|
| [4] |
LIU C, XIANG X B, YANG L H, et al. A hierarchical disturbance rejection depth tracking control of undera- ctuated AUV with experimental verifica tion[J]. Ocean Engineering, 2022, 264: 112458. DOI:10.1016/j.oceaneng.2022.112458 |
| [5] |
WU X, JIANG D, YUN J, et al. Attitude stabilization control of autonomous underwater vehicle based on decoupling algorithm and PSO-ADRC[J]. Frontiers in Bioengineering and Biotechnology, 2022, 10: 843020. DOI:10.3389/fbioe.2022.843020 |
| [6] |
SHAN Z, WANG Y, LIU X, et al. Fuzzy automatic disturbance rejection control of quadrotor UAV based on improved whale optimization algorithm[J]. IEEE Access, 2023.
|
| [7] |
WANG X, XU B, GUO Y Y. Fuzzy logic system-based robust adaptive control of AUV with target tracking[J]. International Journal of Fuzzy Systems, 2023, 25(1): 338-346. DOI:10.1007/s40815-022-01356-2 |
| [8] |
SHI S Y, ZENG Z Q, ZHAO C B, et al. Improved active disturbance rejection control (ADRC) with extended state filters[J]. Energies, 2022, 15(16): 5799. DOI:10.3390/en15165799 |
| [9] |
NAHRI S N F, DU S Z, VAN Wyk B J. Predictive extended state observer based active disturbance rejection control for systems with time delay[J]. Machines, 2023, 11(2): 144. DOI:10.3390/machines11020144 |
| [10] |
彭毓卿. 新能源船舶路径跟踪自抗扰控制方法[J]. 舰船科学技术, 2024, 46(2): 161-164. PENG yumin. Research on path tracking active disturbance rejection control method for new energy ships[J]. Ship Science and Technology, 2024, 46(2): 161-164. |
| [11] |
FOSSEN T I. Guidance and control of ocean vehicles[M]. New York: Wiley, 1994.
|
| [12] |
陈增强, 程赟, 孙明玮, 等. 线性自抗扰控制理论及工程应用的若干进展[J]. 信息与控制, 2017, 46(3): 257-266. CHEN zengqiang, CHENG yun, SUN mingwei, et al. Surveys on theory and engineering applications for linear active disturban-ce rejection control[J]. Information and Control, 2017, 46(3): 257-266. |
| [13] |
HU J X, GE Y, ZHOU X, et al. Research on the course control of USV based on improved ADRC[J]. Systems Science & Control Engineering, 2021, 9(1): 44-51. |
| [14] |
于洪国, 康忠健, 陈瑶. 基于双曲正切函数的二阶时变参数扩张状态观测器[J]. 控制理论与应用, 2016, 33(4): 530-534. YU hongguo , KANG zhongjian , CHEN yao. Time-varying para-meter second-order extended state observer based on hyperbolic tangend function[J]. Control Theory and Applications, 2016, 33(4): 530-534. |
| [15] |
鄢化彪, 徐炜宾, 黄绿娥. 基于改进 ADRC 的四旋翼姿态控制器设计[J]. 北京航空航天大学学报, 2022, 49(12): 3283-3292. YAN huabiao, XU weibin, HUANG lve. Design of quadrotor attitude controller based on improved ADRC[J]. Journal of Beijing University of Aeronautics and Astronautics, 2022, 49(12): 3283-3292. |
| [16] |
LOZGACHEV G I. On a method of construction of Lyapunov functions[J]. Automation and remote control, 1998, 59(10): 1365-1369. |
 2024, Vol. 46
2024, Vol. 46
