船型设计是船舶制造的重要环节,通过对船型进行优化设计,有效减小船舶在航行中的阻力,可以直接提高船舶的航行速度。对于需要快速运输货物或乘客的船舶来说尤为重要。船型优化设计还可以有效提高船舶在风浪中的稳定性,最小阻力设计意味着船舶在相同速度下需要更少的动力来克服阻力,因此能够显著降低燃料消耗,减少碳排放[1 − 2]。这对于远洋运输等长时间航行的船舶来说,具有显著的经济效益。因而最小阻力船型设计对于提高船舶性能、降低运营成本、实现环保效益以及推动船舶设计技术发展等方面都具有重要意义。因而未来最小阻力船型的设计理念在船舶设计中将得到更加广泛的应用和推广。
非线性规划(Nonlinear Programming,NLP)是数学优化领域中的一种方法,用于求解具有非线性目标函数或非线性约束条件的优化问题。这类问题通常比线性规划问题更为复杂,因为它们不满足线性规划中目标函数和约束条件都是线性的特性。
船型设计是一种非常典型的非线性目标求解过程,因而使用非线性规划法可以有效解决最小阻力船型设计问题。通过查阅文献可以发现,张宝吉等[3]为了开发具有卓越阻力特性的船舶,采用了非线性规划策略,并且与计算机辅助设计(CAD)技术相结合,对最小阻力船型进行了优化设计研究。将总阻力作为优化目标,以Wigley船型为基础模型,对船体的前端和整体轮廓进行了细致的优化设计工作。王素华等[4]以集装箱船的设计为例,将粘性压力阻力、波浪阻力和平板摩擦阻力作为关键的约束条件,将这些因素整合到船型优化设计流程中,成功实现了显著的优化效果。
本文在既往船型设计优化经验的基础上,将非线性规划法应用于最小阻力的船型优化设计。
1 基于非线性规划法的最小阻力船型设计流程 1.1 兴波阻力计算和分析不同的阻力类型对船舶的影响不同,兴波阻力、摩擦阻力和形状阻力都和船型有关,本文以最小阻力为船型优化设计的最终目标,因而在后续的最小阻力船型设计中,需要对不同类型的阻力进行计算,并在这些约束条件下使得阻力最小。本文以兴波阻力的计算和分析为例进行说明。
兴波阻力修正系数k对船舶的影响与船舶的特定几何形状、操作条件等非常相关。在船型阻力计算中,修正系数与船体的湿表面积、船体形状、航速和水深等因素有关。
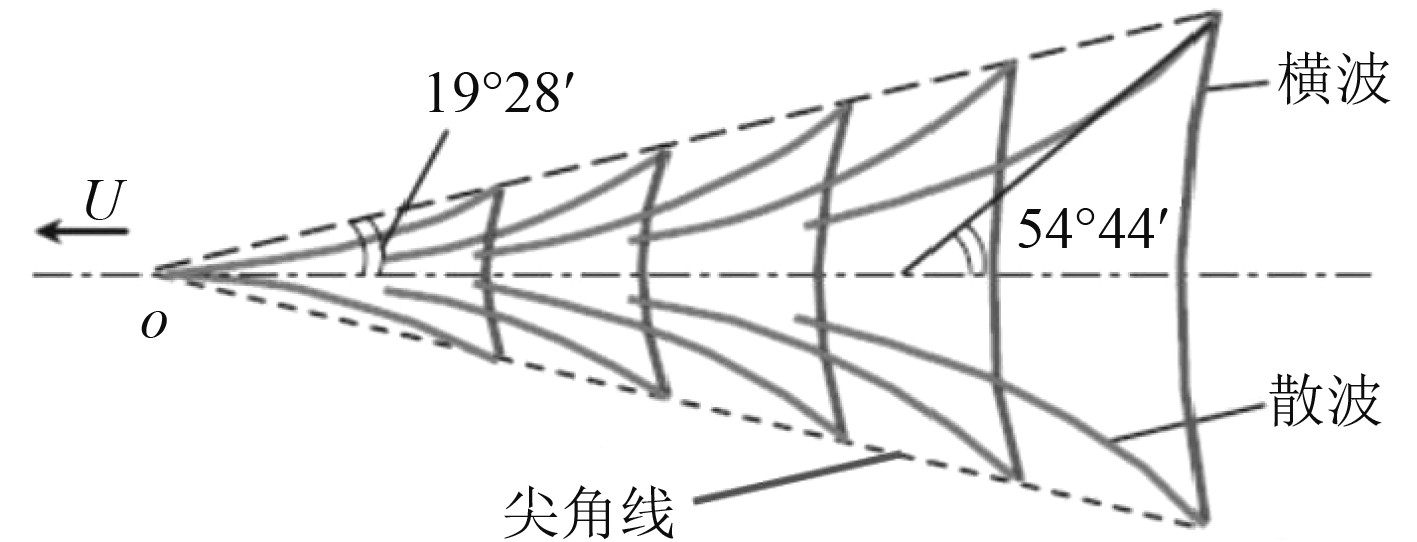
图1为Kelvin波(压力点兴波)理论原理图,船舶在匀速行驶过程中,整个波系分为横波和散波,在船波传播过程中,横波系和散波系相互干涉,并同压力点一起前进。横波系和散波系相交形成尖角。尖角与压力点间的连线称为尖角线,兴波在顶角对应的2×19°28′的扇形范围内。
|
图 1 Kelvin波理论 Fig. 1 Kelvin wave theory |
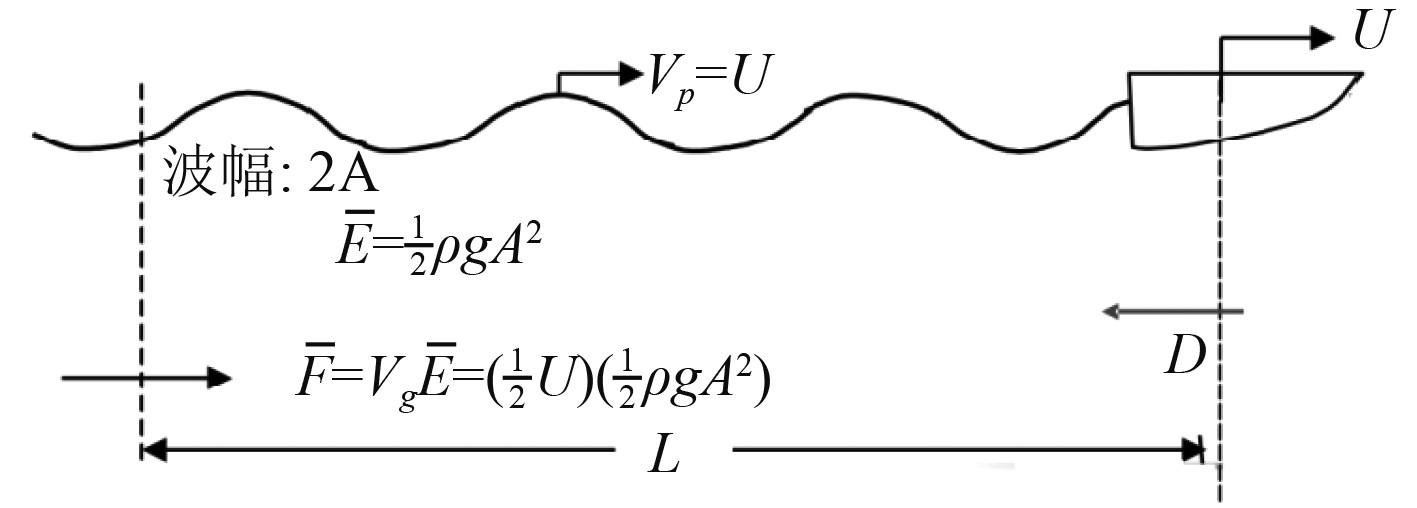
图2为船舶兴波阻力计算模型,假设在船后L处取一与波速方向相垂直的固定平面。设船的兴波阻力为D,船舶航速为U,浪幅为A,单位长度所兴起的波浪能量为E,则船舶兴波阻力为:
|
图 2 兴波阻力计算模型 Fig. 2 Wave resistance calculation model |
| $ D = \frac{1}{2}E = \frac{1}{4}\rho g{A^2} \text{。} $ | (1) |
式中:g为重力加速度;ρ为水的密度;浪幅
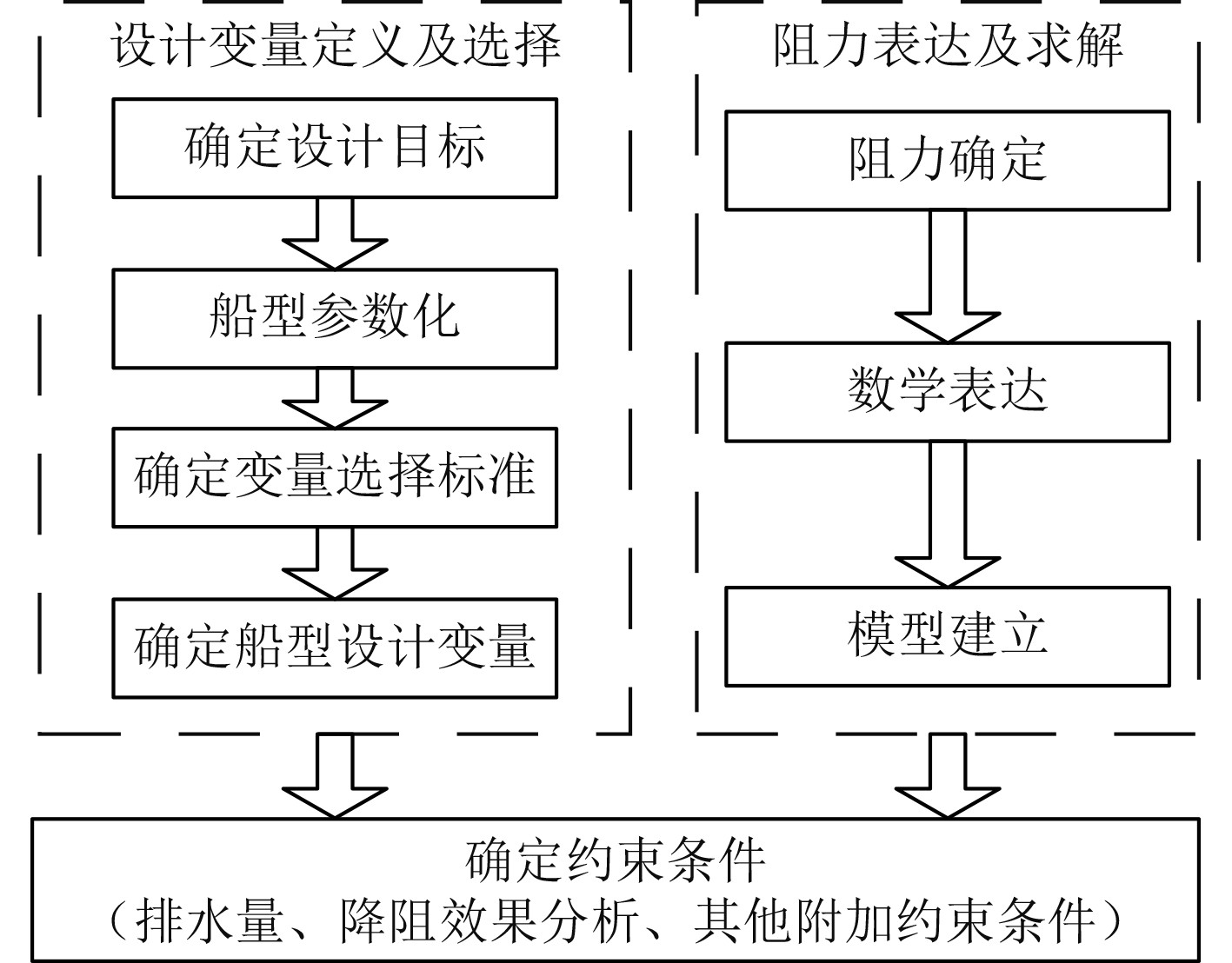
船型设计是船舶设计的重要环节,在船型设计过程中不仅需要考虑到船型在实际航行过程中的阻力问题,同时还要兼顾到经济成本问题,因而船型的设计实际上是一个目标优化问题,在目标优化时需要兼顾考虑多种影响因素[5]。图3为最小阻力船型优化设计的基本流程。
|
图 3 最小阻力船型优化设计流程 Fig. 3 Optimal design flow of minimum resistance ship type |
1)设计变量定义及选择
首先明确设计的主要目标是最小化船体的总阻力,其他目标都是次要目标,在确定目标后需要将船体形状参数化,这些参数包括船体长度L、宽度B、吃水深度T、船体形状参数(如船体截面的曲率、斜率等)。由于最小阻力船型设计几乎涉及到船舶的所有参数,并不是所有的参数都需要选择,有部分参数对最小阻力设计影响极小,因而应当被剔除在外,最终选择的参数需要能够显著影响船体的阻力特性,且具有实际可调性,即在实际船舶设计和制造中可实现调整。设计变量的选择直接影响总阻力的表达和计算,而总阻力的准确表达又是确定有效约束条件的前提。整个优化模型的构建需要综合考虑多方面因素,以确保最终设计的船型既满足性能要求,又具有实际可制造性。
本文选择的参数包括船体截面的形状参数(如圆弧半径、斜率等)、船体线型参数(如前倾角、后倾角、舭线高度等)、船体的体积分布参数(如船体的体积系数、长宽比等)。
2)阻力表达及求解
总阻力由兴波阻力、摩擦阻力和形状阻力组成,兴波阻力Rwave是船体在水中运动时产生的波浪所引起的阻力,k为兴波阻力修正系数。摩擦阻力Rfriction是船体表面与水的摩擦引起的阻力。形状阻力Rshape由船体形状不规则引起的阻力,通常与局部涡流有关[6]。
| $ {R} = k{R_{{\mathrm{wave}}}} + {R_{{\mathrm{friction}}}} + {R_{{\mathrm{shape}}}} \text{。} $ | (2) |
3)确定约束条件
非线性规划法是运筹学中的一个分支,特别适用于处理那些线性模型无法准确描述的复杂系统。在非线性规划法中,通过确定约束条件,可以形成一个全面的优化模型,用于指导船型设计的优化过程,以达到最小阻力的目的,同时满足船舶的实用性和安全性要求。船型最小阻力优化设计的约束条件为:
①排水量约束。保证船舶的排水量作为基本约束条件,即在优化过程中,船舶的排水量变化需保持在特定范围内,变化量范围±0.4%。
②尾部粘性分离影响。在优化设计时,考虑尾部粘性分离的影响,使用简易湍流分离判断式来确定改良船型粘性阻力的变化。
③几何约束。确保船体几何形状的合理性,例如通过控制船体曲面变形的方法(如FFD方法)来实现船体形状的优化,同时保证船体曲面的光顺性。
④多目标优化。确定多个优化目标,总阻力系数最小化和船艉桨盘面处伴流最均匀化,使用多目标优化方法来平衡不同的设计目标。本文为了获得最小阻力,将兴波阻力系数、摩擦阻力系数和形状阻力系数作为优化目标。
为了更好地以最小阻力作为船型设计的优化目标,将遗传算法应用到非线性规划的多目标优化求解中,其具体方法为:选择船体形状的参数化表示方法,使用控制点的坐标来定义船体的几何形状,并在此基础上构建包含目标函数(如阻力系数)和约束条件(排水量、稳定性要求)的数学模型。本文采用二进制编码将设计变量(船体形状参数)编码为遗传算法可以处理的形式,随后随机生成一组船型设计的初始解,作为遗传算法的初始群体,使用数值模拟CFD来评估每个个体(船型设计)的阻力性能作为适应度,再根据适应度从当前群体中选择优秀的个体,以参与下一代的繁殖。最后应用交叉算子在选定的个体间交换遗传信息,产生新的后代船型。由于涉及到多目标优化,因而需要使用罚函数来确保优化过程能够顺利进行,且将以上过程反复迭代,即可实现最小阻力的船型设计。
2 优化结果与分析 2.1 船型优化选择一艘旅游船作为船型优化设计目标,该船具有以下主要尺寸:船长L为80 m,船宽B为30 m,船深d为5.0 m,船体阻塞系数Cb为0.589,航速设定为16 kn,对应的弗劳德数Fn为0.293。在引入约束条件后,对船首进行了优化设计,使其更加贴近实际应用需求,图4为船型尺寸示意图。图5为优化后的前半体横剖线图。

|
图 4 船型尺寸结构 Fig. 4 Ship size structure |

|
图 5 优化后前半体横剖线图 Fig. 5 Optimized transverse profile of the front half body |
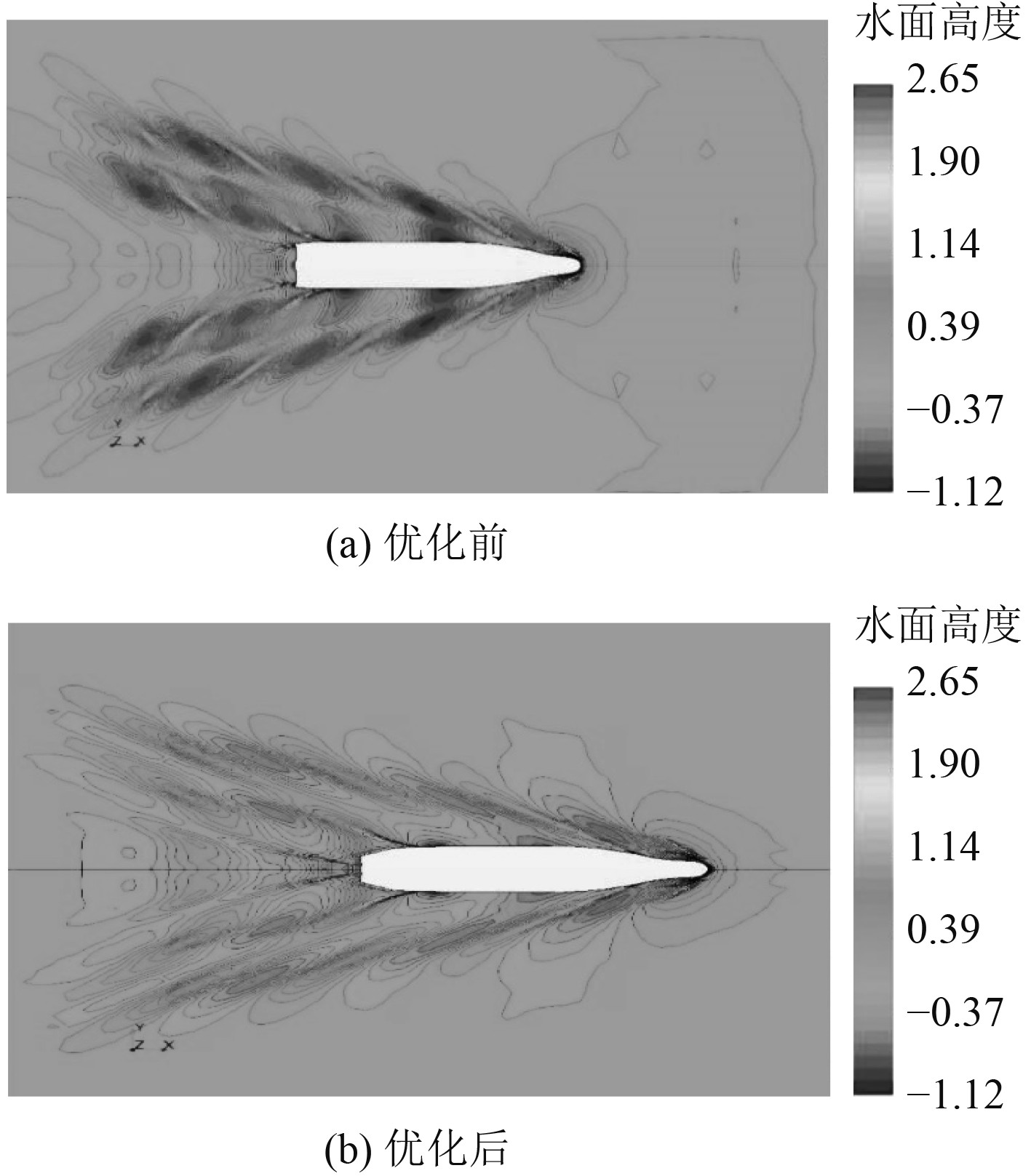
在对船型进行优化后,使用软件对优化前后的兴波阻力进行对比。图6为水面高度优化前后对比效果,通过对水面高度的对比可以发现,在优化后,船舶在行进过程中水面高度明显降低,兴波阻力减小。
|
图 6 水面高度优化前后对比 Fig. 6 Water surface height optimization before and after comparison |
设定船舶船速为10 kn,对使用非线性规划法优化后船型的兴波阻力系数、摩擦阻力系数和形状阻力系数进行仿真计算,并和未优化前进行对比,得到结果如下表1所示。其中优化效率定义为:
|
|
表 1 优化前后阻力系数对比 Tab.1 Comparison of resistance coefficient before and after optimization |
| $ \eta=优化后系数/优化前系数\times 100\text% 。$ | (3) |
可以发现优化后各阻力系数均有不同程度减小,说明船型优化后船舶阻力得到了有效降低,且兴波阻力系数优化效率较高,说明在当前设置条件下优化设计后的船型兴波阻力减少了26.7%。
通过这一系列的优化和计算,可以看出使用非线性规划法优化后的改良船型在阻力性能上的改进,并且通过不同方法的对比分析,验证了优化结果的有效性。
3 结 语船型设计对减小船舶阻力具有非常重要的作用,但是基于最小阻力的船型设计是一个多目标优化的过程,本文提出基于非线性规划法的最小阻力船型设计方案,其结论包括:
1)阐述了船舶兴波阻力计算的原理,分析了基于非线性规划法的最小阻力船型设计流程,并将遗传算法引入到船型设计流程中,通过不断迭代实现最小阻力的船型设计;
2)给出了船型基本结构和优化后的前半体横剖线图,使用仿真软件对优化前后的兴波阻力系数、摩擦阻力系数和形状阻力系数进行计算和对比,结果表明船型优化后船舶阻力得到了有效减少。
| [1] |
恒乙鑫. 不对称片体风电运维船船型设计及阻力耐波性研究[D]. 镇江: 江苏科技大学, 2023.
|
| [2] |
张大朋, 姜淏予, 赵博文, 等. 基于回归分析方法的船舶阻力估算[J]. 舰船科学技术, 2023, 45(18): 25-31. ZHANG Dapeng, JIANG Haoyu, ZHAO Bowen, et al. Ship resistance estimation based on regression analysis method[J]. Naval Science and Technology, 2023, 45(18): 25-31. |
| [3] |
张宝吉, 马坤, 纪卓尚. 基于非线性规划法的最小阻力船型优化设计[J]. 武汉理工大学学报(交通科学与工程版), 2010, 34(2): 358-361. ZHANG Baoji, MA Kun, JI Zhuoshang. Minimum resistance ship type optimization design based on nonlinear programming method[J]. Journal of Wuhan University of Technology (Transportation Science and Engineering Edition), 2010, 34(2): 358-361. |
| [4] |
王素华, 陈建. 非线性规划法的最小阻力船型研究设计[J]. 舰船科学技术, 2019, 41(12): 4-6. WANG Suhua, CHEN Jian. Research on minimum resistance ship type design using nonlinear programming method[J]. Naval Science and Technology, 2019, 41(12): 4-6. |
| [5] |
张萍. 船型参数化设计[D]. 无锡: 江南大学, 2009.
|
| [6] |
崔焰, 卢晓平, 王中, 等. 改进线性兴波阻力帐篷函数法及实船型线优化[J]. 华中科技大学学报(自然科学版), 2011, 39(4): 101-105. CUI Yan, LU Xiaoping, WANG Zhong, et al. Improved linear wave-making resistance tent function method and optimization of actual ship type line[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2011, 39(4): 101-105. |
 2024, Vol. 46
2024, Vol. 46
