2. 武汉理工大学 船海与能源动力工程学院,湖北 武汉 430070
2. School of Naval Architecture, Ocean and Energy Power Engineering, Wuhan University of Technology, Wuhan 430070
船舶的水下辐射噪声不仅会威胁海洋生物和海洋环境,还会影响精密水声设备的正常运行,一直是业界关注的热点问题。按照产生机理可将船舶水下噪声分为机械噪声、螺旋桨噪声和水动力噪声等3种类型[1 − 4]。机械噪声指的是主辅机等主要机械设备的振动通过基座传递到船体,继而通过船体外壳向水中辐射的噪声,主要集中在低频段。螺旋桨噪声包括螺旋桨高速运转时直接向外辐射的噪声和螺旋桨激励力引起的振动向外辐射的噪声,螺旋桨转动时产生的空化噪声是船舶水下噪声谱高频段的主要部分。而水动力噪声主要指船舶航行时水流经过船体表面时船体受到的脉动压力引起的辐射噪声。对于低中速且船体线型经过良好设计的船舶来说,水动力噪声一般较小,可忽略不计。
由于船舶水下辐射噪声源的频率范围广、频谱成分复杂,不同频率下宜采用不同的数值分析方法。本文主要针对由机械设备引起的低频下的船舶水下噪声进行研究。目前低频下水下辐射噪声预报的主流方法包括声学有限元法和声学边界元法。利用有限元法求解船舶结构的振动特性,基于声学有限元法或边界元法离散流场求解水下声场。
如何模拟船舶结构与周围流体介质的耦合作用,一直是船舶水下噪声预报中的重点问题。业界学者通常使用流固耦合法和声固耦合法两种耦合方法来模拟这种耦合作用。
在流固耦合法中,流体被假设为无旋、无粘、不可压缩的理想流体,基于此假设建立流体运动方程。同时,考虑流体作用在结构上的作用力而建立结构的动力学方程。根据流固交界面、自由边界和无限远边界等建立边界条件方程,代入流固耦合系统方程中求解出流固耦合振动。将此耦合振动结果作为边界元法的声学边界条件,求解船舶的水下噪声场。
在声固耦合法中,流体被假设为均匀、无粘、可压缩的理想声学介质,通过声波波动方程模拟声波在流场中传播。同时,将流体中的结构视为弹性体,在流固交界面上联立结构动力学方程和流体域的波动方程,一次性求得耦合系统中的结构位移和流体声场。
杨德庆等[5]、邹春平等[6]、付建等[7]和张波[8]基于声学有限元/边界元法,利用流固耦合法对船舶水下辐射噪声特性进行了预报。崔杰等[9]研究了螺旋桨不同方向轴承力对尾部结构声振特性的影响。目前,针对不同耦合方法对船舶水下辐射噪声预报的影响的研究比较少。杨国栋等[10]基于圆柱壳的自由振动探讨了流固耦合和声固耦合方法的本质,证实了2种耦合模型在求解浸没圆柱壳的低频自振特性上具有一致性。蒋坤等[11]以水下双层圆柱壳为对象,研究了2种耦合方法对水下声辐射计算结果的影响。
本文基于声学边界元法,以实船为研究对象,旨在研究流固耦合法和声固耦合法对船舶低频水下辐射噪声预报的影响。通过对比两种耦合方法下的水下噪声预报结果,为实际工程应用中的耦合方法的选择提出建议。
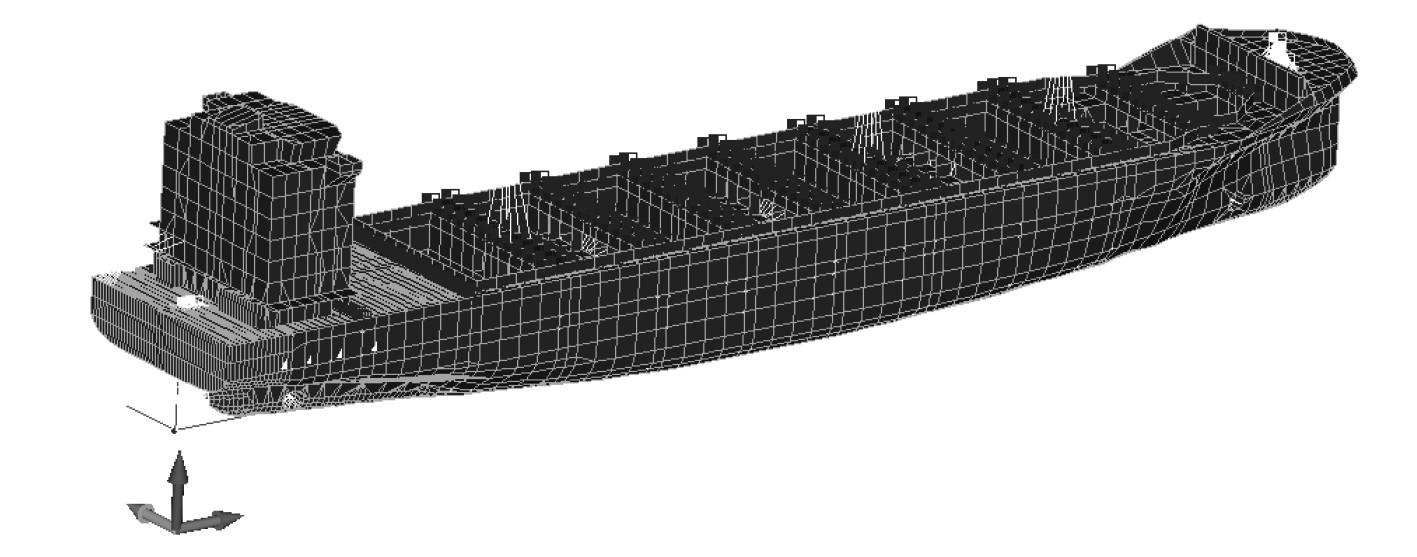
1 分析模型本文以一艘支线型集装箱船为研究对象,基于船舶图纸信息建立全船有限元模型。其中,甲板、舱壁、船体外壳等大型结构用壳单元模拟,甲板、舱壁及外壳等结构上的筋采用梁单元模拟,大型设备、管系、舾装件等采用质量单元模拟,并通过刚性单元与邻近的船体结构连接。根据装载手册进行重量调整,使有限元模型的重量分布与实际装载手册基本一致。最终的有限元模型如图1所示。
|
图 1 全船有限元模型 Fig. 1 Finite element model of the ship |
基于集装箱船的有限元模型,提取船体湿表面网格,导入声学计算软件中,建立边界元模型。外场流体设置为无限深的海水,密度为
本次水下辐射噪声预报的频率范围为10~100 Hz,计算步长为1 Hz。在此频率范围内,有限元网格和边界元网格的单元特征长度均满足最小波长内有4~6个单元的计算精度要求。由于本文主要探索不同耦合方法下的水下辐射噪声预报,为简化问题,现假设激励载荷为单位简谐力,垂直向下作用于主机机脚处。
为有效评估船舶水下辐射噪声,根据集装箱船主尺度,在水下建立长400 m、深200 m的场平面,可通过场平面的声压云图可视化显示水下的声压分布。同时在坐标(−100 m, 0, −200 m)处设置场点获取其声压级结果。最终的边界元模型如图2所示。

|
图 2 声学边界元模型 Fig. 2 Acoustic boundary element model |
在流固耦合法中,需要先计算船舶的耦合响应,为后续的水下辐射噪声计算提供输入数据。本次对比研究中的流固耦合法和声固耦合法的计算均采用模态叠加法,模态阻尼系数均设置为1%。在模态叠加法中,需要对结构模态进行截断。为提高计算效率同时保证计算精度,要选择合适的模态截断频率。本次计算的模态上限频率取分析频率的2倍,即为200 Hz。
计算全船在200 Hz内的湿模态,共有
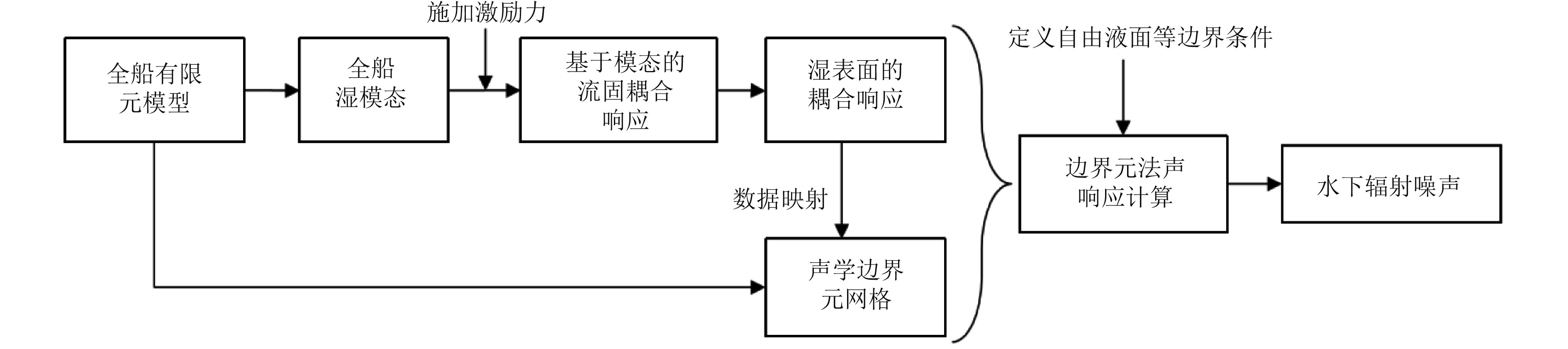
流固耦合法求解水下辐射噪声的流程如图3所示。
|
图 3 水下辐射噪声预报流程图(流固耦合法) Fig. 3 Flow chart of underwater radiated noise prediction (Fluid-structure coupling method) |
基于声固耦合法进行水下辐射噪声的计算,需要先计算200 Hz内的全船干模态,共有
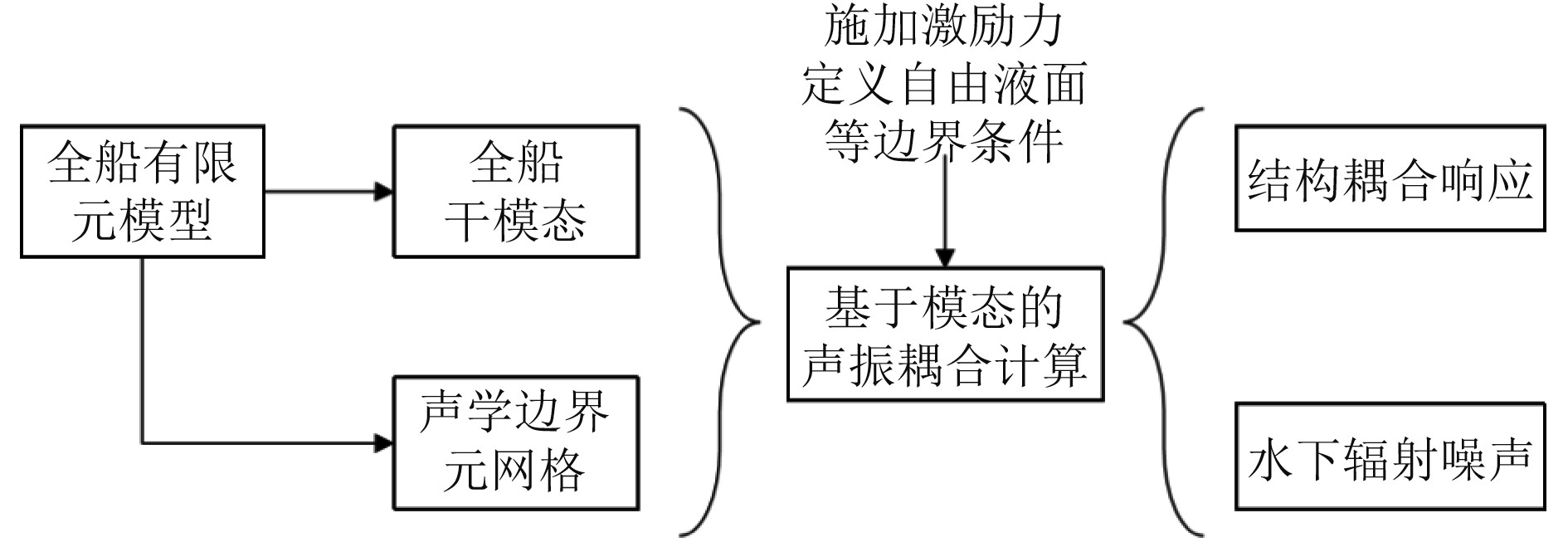
声固耦合法求解水下辐射噪声的流程如图4所示。
|
图 4 水下辐射噪声预报流程图(声固耦合法) Fig. 4 Flow chart of underwater radiated noise prediction (Acoustic-structure coupling method) |
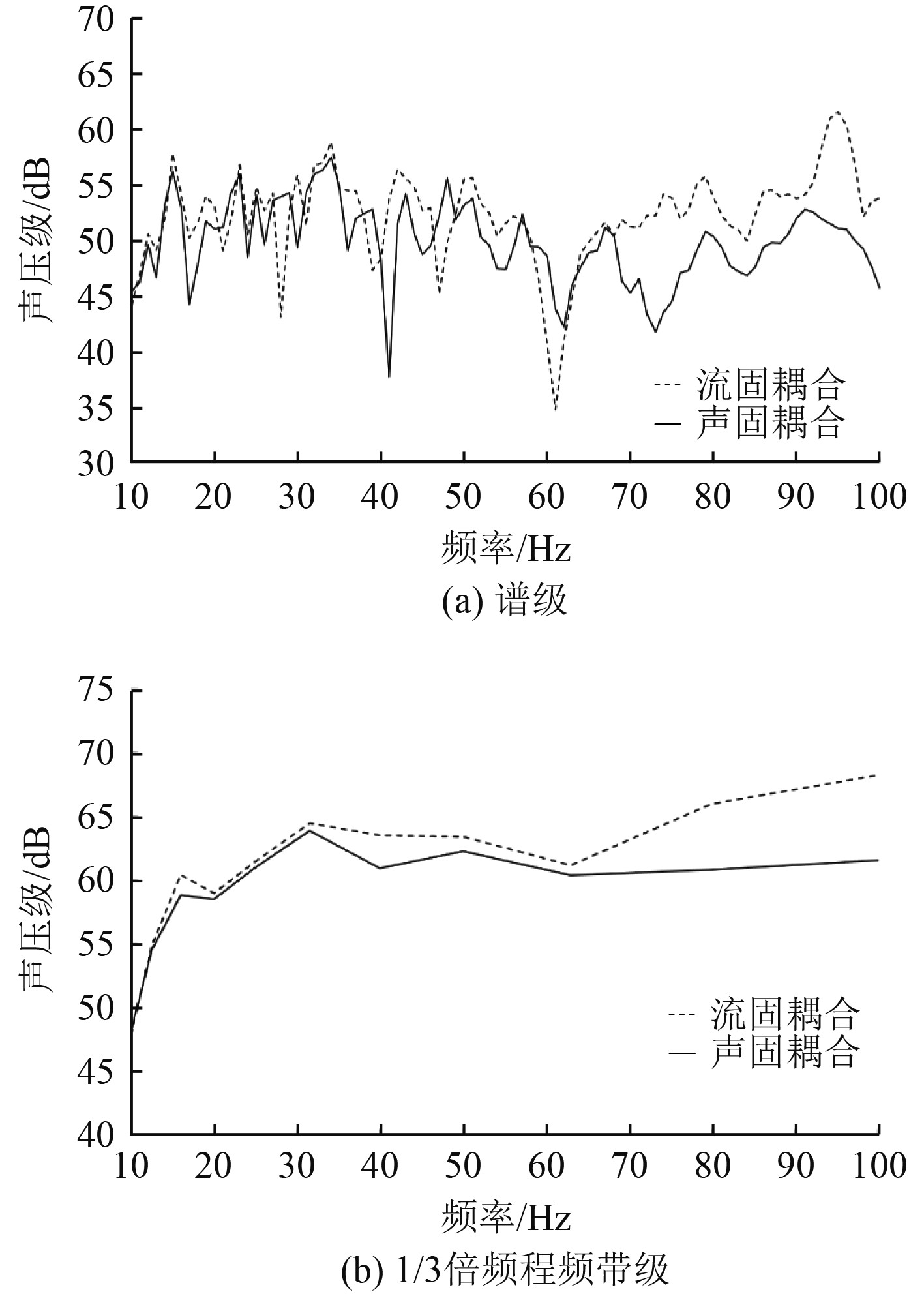
计算得到2种耦合方法下的场点的声压级谱级曲线,步长为1 Hz。根据中国船级社《船舶水下辐射噪声指南》[12],水下辐射噪声的限值为1/3倍频程频带声压级。因此,将本次计算得到的声压级谱级转换为1/3倍频程频带声压级。2种耦合方法下的声压级谱级和1/3倍频程频带级结果如图5所示,水中声压级的参考值为1 μPa。
|
图 5 场点声压级(谱级和1/3倍频程频带级) Fig. 5 Sound pressure level (spectral level and 1/3 octave band level) |
观察图5(a)可得,较低频率下,2种耦合方法下的声压级大小和变化趋势基本一致;随着频率的升高,趋势仍保持相似,但是2种耦合方法的声压级差值变大。较高频率下,流固耦合法的声压级明显大于声固耦合法的声压级。将场点声压级谱级转换为1/3倍频程频带级后,此规律表现的更明显,见图5(b)。在10~31.5 Hz的1/3倍频程内,2种耦合法的场点声压频带级趋势和大小基本一致;31.5~100 Hz的1/3倍频程内,流固耦合法的频带声压级明显大于声固耦合法下的频带声压级。
声压的大小与场点与声源的相对位置有关,而声功率是声源在单位时间内向外辐射的声能量,是一个与位置无关的绝对量。现比较2种耦合方法下的船舶水下辐射声功率级,结果如图6所示。
|
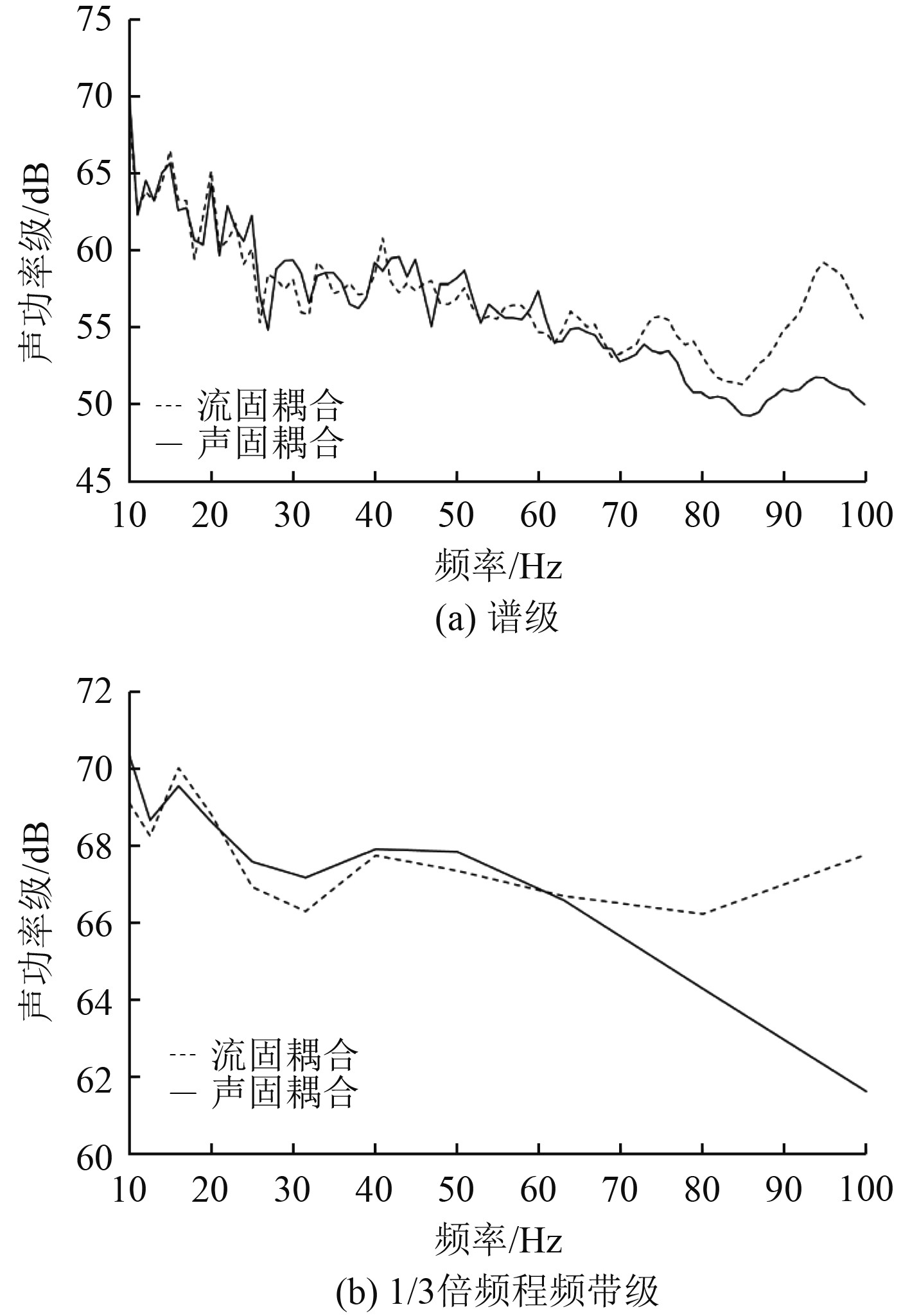
图 6 声功率级(谱级和1/3倍频程频带级) Fig. 6 Sound power level (spectral level and 1/3 octave band level) |
观察可得,船舶的辐射声功率级随着频率的升高而减小,即船舶向水中辐射的能量随着频率的升高而减小。与场点声压级的规律相似,在较低频率下,2种耦合方法的辐射声功率级趋势基本一致,差值不大;随着频率的升高,流固耦合法的辐射声功率级明显大于声固耦合法的辐射声功率级。
现求得2种耦合方法的场点声压级和声功率级的1/3倍频程频带级差值如表1所示。
|
|
表 1 声压级和声功率级的1/3倍频程频带级在两种耦合方法下的差值(流固耦合值-声固耦合值,dB) Tab.1 Differences of 1/3 octave band level of sound pressure and sound power with two coupling methods |
由表可得,大部分频段下流固耦合法的预报结果大于声固耦合法的预报结果。10~100 Hz内,流固耦合法和声固耦合法的声压级总级差值为2.7 dB,辐射声功率级总级差值仅0.1 dB,均小于3 dB,误差满足工程精度要求。10~63 Hz内的预报结果差值均小于3 dB,63~100 Hz内的预报结果差值最大达到6.6 dB。
由图5(a)和图6(a)可得,场点声压级和辐射声功率级均在15 Hz和95 Hz附近处达到了峰值。分别截取两种耦合方法在15 Hz和95 Hz时的场平面声压云图,如图7和图8所示。

|
图 7 2种耦合方法下声压级云图(15 Hz) Fig. 7 Vector image of sound pressure level with two coupling methods (15 Hz) |

|
图 8 2种耦合方法下声压级云图(95 Hz) Fig. 8 Vector image of sound pressure level with two coupling methods (95 Hz) |
观察可得,15 Hz时2种耦合方法的声压级云图基本相似,即此频率下2种耦合方法计算得到的水下声场分布基本相似。95 Hz时2种耦合方法的声压级云图存在明显差异。
综上,2种耦合方法的预报声压级和声功率级结果具有相似的趋势,且流固耦合法的预报结果基本大于声固耦合法的预报结果。在流固耦合理论模型中,流体被假设不可压缩的理想流体,忽略了海水的可压缩性带来的阻尼效应而耗散的能量;而在声固耦合理论模型中,流体被假设为可压缩的声学介质,考虑了此种阻尼效应,这也是流固耦合法的预报结果比声固耦合法的预报结果大的主要原因。频率较低时,阻尼效应不明显,因此2种耦合方法的预报结果相差不大,1/3倍频程频带级差值小于3 dB;随着频率的增加,阻尼效应增强,因此两种耦合方法的预报结果差值增大。
实际流体具有可压缩性,由此可判断声固耦合法更切合实际。因此,在船舶水下辐射噪声预报的实际工程应用中,当频率较低时,由于两种耦合方法的预报结果误差满足工程精度要求(3 dB),可根据实际情况自由选择耦合方法;当频率较高时,使用流固耦合法的预报结果可能会偏高,预报过于保守,建议使用声固耦合法。
3 结 语本文以一艘支线型集装箱船为研究对象,分别基于流固耦合法和声固耦合法进行低频水下辐射噪声预报,分析频段为10~100 Hz。对预报结果进行分析,得出如下结论:
1)2种耦合方法的预报声压级和声功率级谱具有相似的趋势,声压级和声功率的总级差别不大,差值分别为2.7 dB和0.1 dB;且2种耦合方法的水下声压分布在15 Hz时基本相似,在95 Hz时存在明显差异。因此可推测,频率较低时2种耦合方法的水下声压分布基本相似,随着频率的升高,声压分布差异明显。
2)流固耦合法的预报结果基本大于声固耦合法的预报结果,这是因为流固耦合理论中的流体不可压缩的假设忽略了海水的可压缩性引起的阻尼效应。频率较低时(10~63 Hz),阻尼效应不明显,2种耦合方法的预报结果相差不大,1/3倍频程频带声压级和声功率级的差值均小于3 dB;随着频率的升高(63~100 Hz),阻尼效应增强,2种耦合方法的预报结果差值增大,1/3倍频程频带声压级和声功率级的差值最大达到6.6 dB。
3)实际流体具有可压缩性,可定性判断出声固耦合法更切合实际情况。
4)在预报由机械设备引起的船舶水下辐射噪声的实际工程应用中,当频率较低时,由于2种耦合方法的预报结果误差满足工程精度要求(3 dB),可根据实际情况自由选择耦合方法;当频率升高时,使用流固耦合法的预报结果可能会偏高,预报过于保守,建议使用声固耦合法。
| [1] |
童宗鹏, 叶林昌, 倪明杰, 等. 深水物探船水下噪声评估及控制技术[J]. 噪声与振动控制, 2012, 32(2): 79-82. TONG Zongpeng, YE Linchang, NI Mingjie, et al. Evaluation and control of underwater noise of geophysical vessel[J]. Noise and Vibration Control, 2012, 32(2): 79-82. |
| [2] |
夏侯命胜, 李清, 杨德庆. 机械和螺旋桨振动噪声作用下的物探船水下辐射噪声数值预报[J]. 船舶工程, 2019, 41(10): 11-14+65. XIAHOU Mingsheng, LI Qing, YANG Deqing. Underwater noise numerical prediction of seismic survey vessel considering mechanical and propeller vibro-noise[J]. Ship Engineering, 2019, 41(10): 11-14+65. |
| [3] |
李清, 于汉, 杨德庆. 多类振动噪声源下舰船水下噪声的耦合声场计算方法[J]. 上海交通大学学报, 2019, 53(2): 161-169. LI Qing, YU Han, YANG Deqing. Coupled sound field calculating method for ship underwater noise excited by multiple categories of vibration and sound sources[J]. Journal of Shanghai Jiaotong University, 2019, 53(2): 161-169. |
| [4] |
黄嵘, 吴刚. 极地科考破冰船水下辐射噪声分析[J]. 水下无人系统学报, 2020, 28(4): 370-375. HUANG Rong, WU Gang. Analysis of underwater radiated noise of polar icebreaking research vessel[J]. Journal of Unmanned Undersea Systems, 2020, 28(4): 370-375. DOI:10.11993/j.issn.2096-3920.2020.04.003 |
| [5] |
杨德庆, 王德禹, 刘洪林, 等. 某型艇近场噪声和自噪声数值计算[J]. 声学学报, 2003(5): 421-424. YANG Deqing, WANG Deyu, LIU Honglin, et al. Numerieal analysis of acoustic characters in near field and self-noise of ship[J]. ACTA ACUSTICA, 2003(5): 421-424. DOI:10.3321/j.issn:0371-0025.2003.05.007 |
| [6] |
邹春平, 陈端石, 华宏星. 船舶水下辐射噪声特性研究[J]. 船舶力学, 2004(1): 113-124. ZOU Chunping, CHEN Duanshi, HUA Hongxing. Study on characteristics of ship underwater radiation noise[J]. Journal of Ship Mechanics, 2004(1): 113-124. DOI:10.3969/j.issn.1007-7294.2004.01.015 |
| [7] |
付建, 王永生, 丁科, 等. 螺旋桨激振力作用下船体振动及水下辐射噪声研究[J]. 船舶力学, 2015, 19(4): 470-476. FU Jian, WANG Yongsheng, DING Ke, et al. Research on vibration and underwater radiated noise of ship by propeller excitations[J]. Journal of Ship Mechanics, 2015, 19(4): 470-476. DOI:10.3969/j.issn.1007-7294.2015.04.016 |
| [8] |
张波. 船舶水下辐射噪声预报方法与试验研究[D]. 武汉: 武汉理工大学, 2018.
|
| [9] |
崔杰, 高聪, 魏强等. 轴承力作用下船舶尾部声振特性研究[J]. 华中科技大学学报(自然科学版), 2020, 48(2): 126-132. CUI Jie, GAO Cong, WEI Qiang, et al. Study on vibration and acoustic characteristics of ship stern structure by propeller excitations[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2020, 48(2): 126-132. |
| [10] |
杨国栋, 李天匀, 朱翔, 等. 浸没圆柱壳低频自振频率计算中流固与声固耦合模型统一性分析[J]. 中国舰船研究, 2016, 11(4): 87-92. YANG Guodong, LI Tianyun, ZHU Xiang, et al. Unity analysis of the fluid-structure coupling model and the acoustic-structure coupling model in the natural frequency calculation of a submerged cylindrical shell[J]. Chinese Journal of Ship Research, 2016, 11(4): 87-92. DOI:10.3969/j.issn.1673-3185.2016.04.013 |
| [11] |
蒋坤, 向阳, 张波. 不同耦合模式水下结构声辐射计算方法研究[J]. 噪声与振动控制, 2019, 39(3): 11-17+34. JIANG Kun, XIANG Yang, ZHANG Bo, et al. Study on the acoustic radiation calculation method for underwater structures with different coupling modes[J]. Noise and Vibration Control, 2019, 39(3): 11-17+34. DOI:10.3969/j.issn.1006-1355.2019.03.003 |
| [12] |
中国船级社. 船舶水下辐射噪声指南[S]. 2018.
|
 2024, Vol. 46
2024, Vol. 46
