船用阀门作为控制船舶管路内流体压力、流量和流动方向的设备,被广泛应用于船舶管路系统中,由于其内部往往结构复杂、流道多变,容易引发流场压力脉动诱导流噪声,因此是管路系统噪声控制的重点对象。目前,对阀门噪声的研究方法主要包括:理论分析、实验方法以及CFD数值模拟。其中,理论分析通过建立物理方程和数学模型,可以揭示阀门内部流场的本质,Kioni等[1]建立了球阀流场数学模型并编写了瞬态流场数值方法,K.Ito等[2]利用有限差分法对液压锥阀层流流场进行了研究,但理论方法针对越复杂的模型,需要的假设与简化越多,因此不适用于复杂结构阀门分析;实验方法则是通过现场试验测试或实验室检测等手段研究阀门声学特性,吴实等[3]对不同类型的阀门(球阀、蝶阀、闸阀、截止阀)进行了实验研究,探索不同阀体产生涡流和噪声的原因,指出漩涡是阀门产生噪声的重要因素,阀门噪声会随涡流的变化而变化。实验方法虽能直观获取流场数据,但耗时耗力,且对试验环境要求苛刻;伴随计算机技术和计算流体力学的发展,越来越多的学者借助CFD数值模拟进行阀门内流场与声场的可视化预报。张生乐等[4]借助流体力学软件预报了CB855A-DN80等直通截止阀的流阻系数以及管路系统流场、水动力噪声情况;冯卫民等[5]通过数值仿真对不同结构蝶阀的内部流动进行对比分析,获取了各种碟阀的流场特征; 刘华坪等[6]基于动网格和UDF技术,对蝶阀、闸阀、球阀等常用阀门流场进行了动态数值模拟,得到阀门流场随阀门开度的变化规律等一系列结论。
本文选取3类共计6种规格的船用阀门,借助CFD软件Fluent采用数值模拟技术,针对引起阀门水头损失的主要技术参数阀门流阻系数进行研究,并进行了阀门流道的流动数值模拟以及声压级数值预报,掌握了流场、声场分布特征以及流阻系数、声压级随流速的变化规律。
1 基本原理 1.1 流阻系数流阻系数体现了阀门对管路系统造成的压头损失。国家行业标准《阀门流量系数和流阻系数试验方法》(GB/T
| $ \zeta=\frac{2000 \times \Delta p_{v}}{\rho \times v^{2}}。$ | (1) |
式中:
| $ \Delta { {p}}_{ {v}}={p}_{ 入口}-{p}_{出口}。$ | (2) |
本文中的流阻系数均以入口流速为特征速度计算所得。同时由于流速较慢,马赫数低,认为流体是不可压缩的。根据质量守恒与动量守恒定律分别可得流动的控制方程为:
| $ \frac{{\partial \overline {{u_i}} }}{{\partial {x_i}}} = 0,(i = 1,2,3),$ | (3) |
| $\begin{split} \frac{\partial \overline{{u}_{i}}}{\partial t}+\overline{{u}_{j}}\frac{\partial \overline{{u}_{i}}}{\partial {x}_{j}}=&-\frac{1}{\rho }\frac{\partial \overline{p}}{\partial {x}_{i}}+\nu \nabla \cdot \nabla \overline{{u}_{i}}+\\ &\frac{1}{\rho }\frac{\partial \left(-\rho \overline{{u}_{i}{}^{\prime }{u}_{j}{}^{\prime }}\right)}{\partial {x}_{i}},(i、j=1,2,3) 。\end{split}$ | (4) |
式中:u为流体速度;p为压力;
采用无量纲压力均方根表征阀门出流段的流动均匀程度,定义压力平均为
| $ {p_{\rm mean}} = \frac{1}{A}\int_A {p{\text{d}}a} 。$ | (5) |
式中:A为考察截面的面积;p为考察面积某点的压力,da为面积微元。
| $ {p_{\rm rmse}} = \sqrt {\frac{1}{A}\int_A {{{\left( {p - {p_{\rm mean}}} \right)}^2}{\text{d}}a} } 。$ | (6) |
为便于比较不同工况的流场均匀程度,进一步定义无量纲的压力均方根:
| $ C{p_{\rm rmse}} = \frac{{{p_{\rm rmse}}}}{{0.5\rho {v^2}}}。$ | (7) |
式中:ρ为流体密度;v为入口速度。
1.3 大涡模拟模拟非定常流动的方法一般包括:非定常RANS方法、大涡模拟以及直接数值模拟。其中,直接数值模拟计算量大、耗时多,尚难以求解工程问题中复杂的湍流运动;非定常RANS方法针对大尺度漩涡分离流动较有效,但不适合求解含有较小尺度的流动脉动;而大涡模拟既能对大、小尺度漩涡进行模拟,计算工作量又小于直接数值模拟,因此工程中多采用该方法进行流噪声预报。本文采用大涡模拟方法,当计算达到平稳时开始记录数据进行时间平均。压力平均值为:
| $ \overline p = \frac{1}{T}\int_{0}^{\text T} {p{\text{d}}t},$ | (8) |
有效压力为:
| $ {p_e} = \sqrt {\frac{1}{T}\int_0^{\text T} {{{(p - \overline p )}^2}{\text{d}}t} },$ | (9) |
声压级定义为:
| $ SPL = 20\log \frac{{{p_e}}}{{{p_{\rm ref}}}} 。$ | (10) |
海水中参考声压
本文围绕以下6款常见的船用阀门开展研究,如表1所示。
|
|
表 1 各阀门类型及规格信息 Tab.1 Types and specification information of each valve |
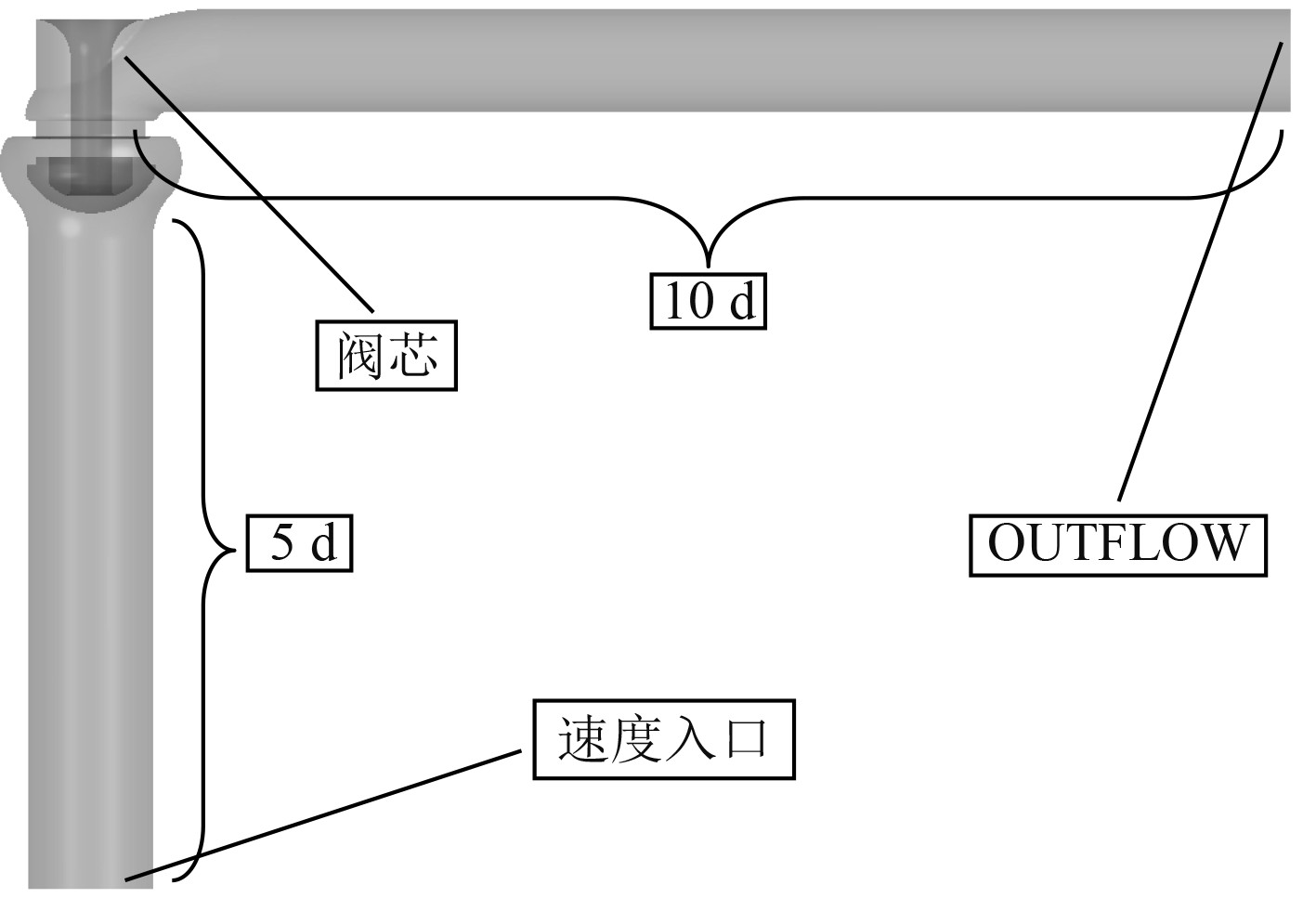
以直角截止阀为例,依据国家行业标准《通用阀门流量系数和流阻系数的试验方法》(JB/T
|
图 1 直角截止阀计算域示意图 Fig. 1 Schematic diagram of calculation domain for right angle globe valve |
其中,边界条件设置如下:
1)流道介质。流体为15 ℃海水,密度为
2)入口条件。采用速度入口边界条件,给定所要求的入口处速度值,流速分别为0.97、1.93、3.09 m/s;
3)出口条件。选用OUTFLOW作为出口边界条件;
4)壁面条件。阀体与阀芯的壁面采用固定壁面,同时在仿真模拟时采用壁面函数的近壁处理方法。
3 仿真分析 3.1 流阻系数流阻计算时采用RANS方法,配合雷诺应力模型,得到各阀门在不同流速下的流阻系数,如表2所示。
|
|
表 2 各阀门流阻系数计算结果 Tab.2 Calculation results of flow resistance coefficients for each valve |
可知,不同阀门类型中,球阀流阻系数远小于其它两类阀门;不同流速下,流阻系数随流速的增加变化不大,最大差值在0.009~0.285之间。
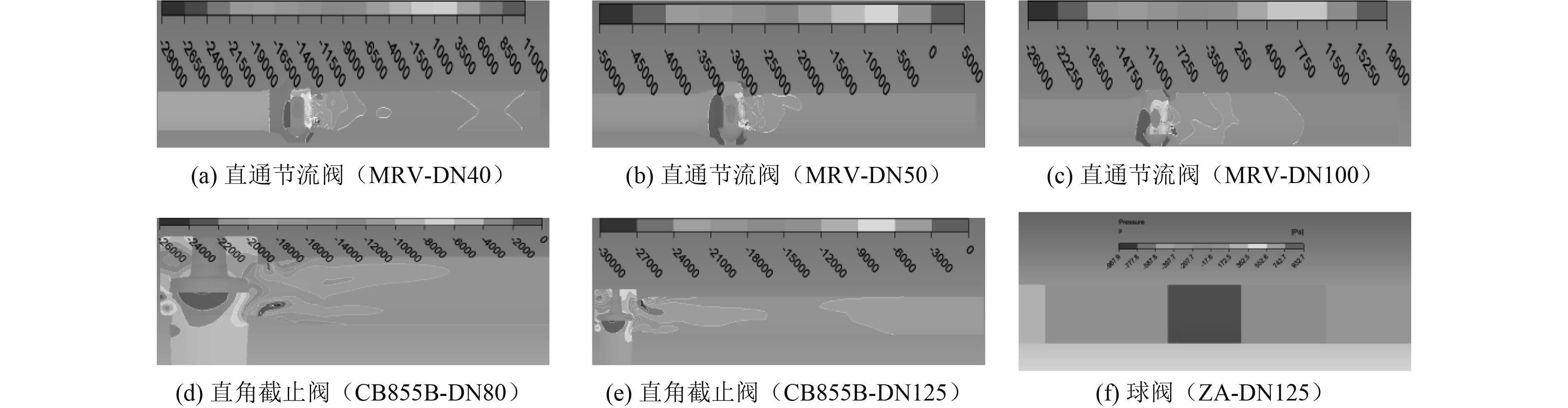
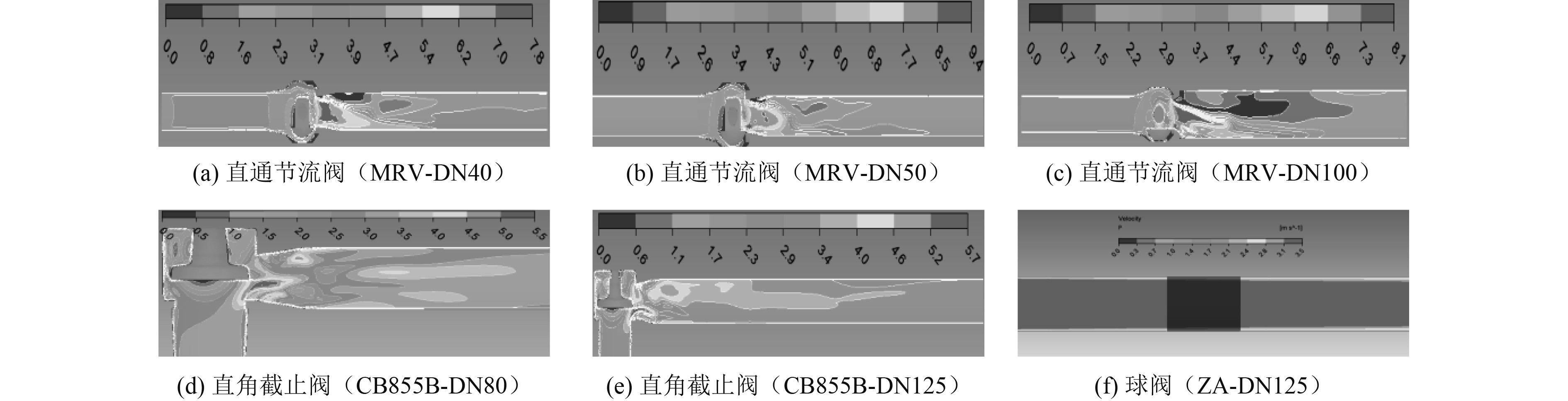
3.2 流场压力与速度计算各阀门流场,得到其流场特征。由于不同流速下各阀门流场压力、速度分布近似,仅提取流速v = 3.09 m/s下各阀门对称面压力分布云图及速度分布云图,分别如图2和图3所示。
|
图 2 各阀门对称面压力分布云图 Fig. 2 Cloud diagram of pressure distribution on the symmetrical surface of each valve |
|
图 3 各阀门对称面速度分布云图 Fig. 3 Cloud diagram of velocity distribution on the symmetrical surface of each valve |
可知,对于直通节流阀,水流至阀芯前端时动能最低,压力能最高,动能向压力能转化;至阀芯后端时动能最高,速度达到最大值;对于直角截止阀,水流至阀芯底部时动能最低,压力能最高,当水流至阀芯下端拐角处时,流通面积迅速减小,压力迅速降低,速度增大并达到最大值;对于球阀,阀芯附近区域流场分布均匀,沿水流流动方向压力与速度梯度较小。
3.3 阀门出流段的流动均匀程度在出口段定义若干剖面:从阀门出口位置向出流管道的出口依次增加1倍阀门直径的距离(共11个剖面),如图4所示。

|
图 4 球阀出口段剖面位置示意图 Fig. 4 Schematic diagram of the cross-sectional position of the outlet section of the ball valve |
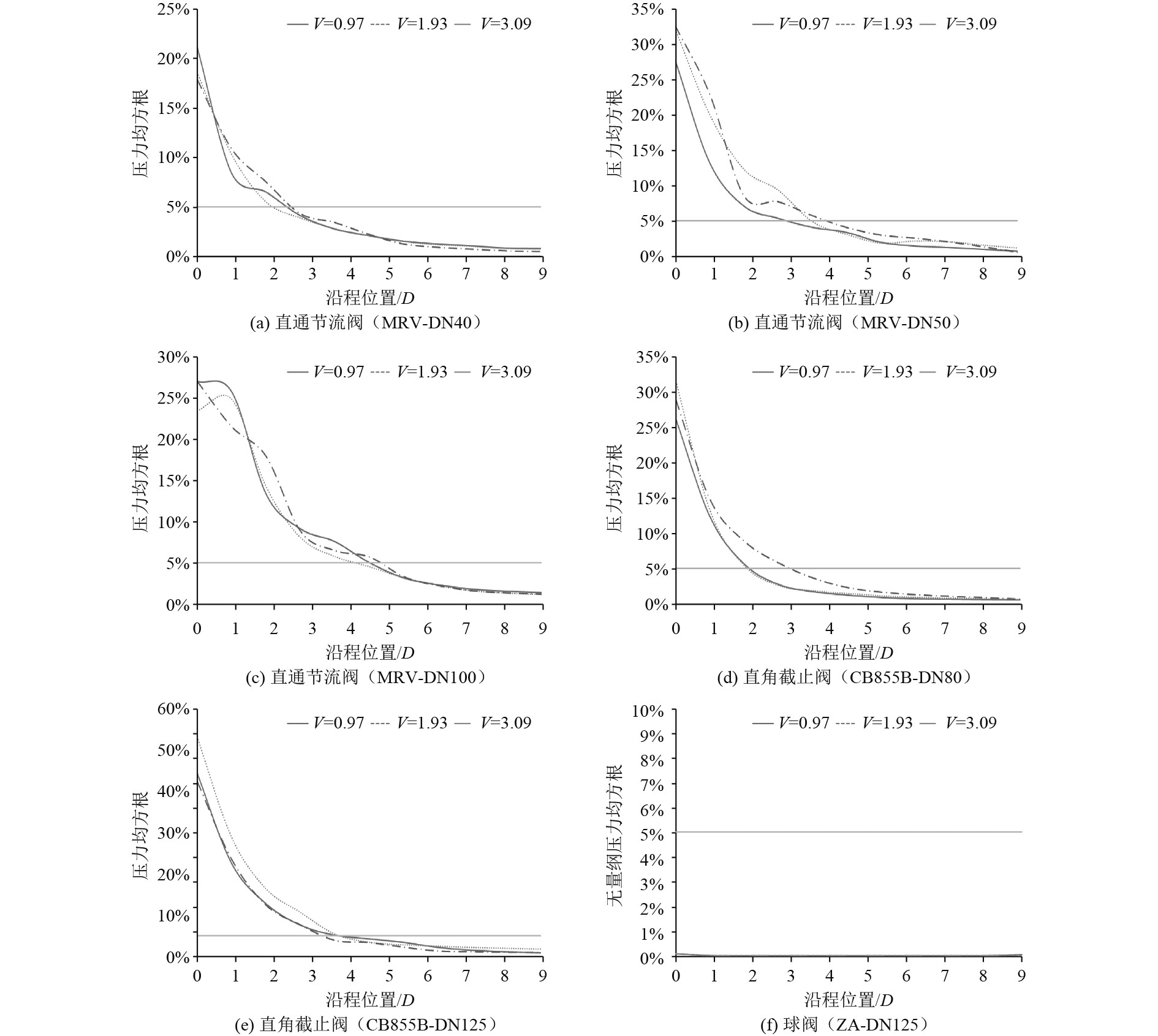
若以衡量剖面压力不均匀分布程度的无量纲压力均方根作为判据,且取阈值5%。计算得到各阀门出口段的无量纲压力均方根沿程变化,如图5所示。
|
图 5 各阀门出口段无量纲压力均方根值沿程变化 Fig. 5 Root mean square value of non dimensional pressure at the outlet section of each valve changes along the path |
可知,若以5%的限界线为标准,对于同类型同规格阀门,一般随着流速的增加,流场稳定时距阀门出口的距离越远;3类阀门中,球阀的流场在阀门出口附近即可认为均匀,原因在于该球阀打开后为纯管流问题,阀门对管内流场无扰动,其他两类阀门在距阀门出口2D~6D之间达到均匀,此时阀门对流场的扰动基本消失,6D后可视作均匀流场。
3.4 噪声声压级采用大涡模拟方法对不同流速下阀门水动力噪声声压级进行预报,进行非定常计算时,时间步长取2×10−4 s,声压级分析取2 s平稳信号进行统计,频率范围0.5~

|
图 6 各阀体内表面声压级分布云图 Fig. 6 Cloud map of surface sound pressure level distribution inside each valve body |
整理不同阀门在不同流速下流噪声声压级计算结果,见表3。
|
|
表 3 各阀门在不同流速下的流噪声声压级计算结果(dB) Tab.3 Calculation Results of Flow Noise Sound Pressure Level for Each Valve at Different Flow Rates (dB) |
综合图4和表3可知,3种流速下,随着流速由0.93 m/s增加至3.09 m/s,6款阀门内部的最大声压级、平均声压级均显著增大,增加幅度△在13.8 dB(ZA-DN125 SPLmax)到39.5 dB(ZA-DN125 SPLmean)之间。阀芯位置的流场受阀芯的阻碍作用,流体的速度和压力急剧变化,速度梯度与压力梯度均较大,声压级最大位置均位于阀体内表面;不同阀门类型中,球阀内部的最大声压级和平均声压级最小,直通节流阀和直角截止阀较大,这是由于这两类阀门相对球阀内部流道复杂,流场脉动更为剧烈。
4 结 语本文研究了不同速度下3类共计6种规格的船用阀门内部的流场与声场,得到以下结论:
1)随着流速的增加,各类阀门的流阻系数变化均不大,在小范围内波动;其中,球阀流阻系数远小于其它两类阀门。
2)球阀全开时对管内流场几乎无扰动,其它两类阀门在距阀门出口2D~6D之间达到均匀,此时阀门对流场的扰动基本消失,6D后可视作均匀流场。
3)随着流速的增加,阀门内部中的最大声压级、平均声压级均显著增大,最大位置均位于阀体内表面处。
| [1] |
KIONI P N. Detailed flow field structure in rapid valve closure[J]. JSME International Journal Series B, 2002, 45(3): 704-11. DOI:10.1299/jsmeb.45.704 |
| [2] |
Ito K, TNKAHASHI K, INOUE K. Pressure distributions and flow force on the body of a poppet valve[C]//. Fluid Power Systems Modeling and Control, New York: John Wiley and Sons, 1991.
|
| [3] |
吴实, 张文平. 阀门流场的数值模拟及流噪声的实验研究[J]. 阀门, 2005, 01: 7-10. |
| [4] |
张生乐, 贾晓丹, 潘国雄, 等. 直通截止阀流场与噪声数值分析[J]. 舰船科学技术, 2016, 38(7): 113-116. |
| [5] |
冯卫民, 肖光宇, 袁波, 等. 基于数值仿真的蝶阀性能对比分析[J]. 排灌机械工程学报, 2010, 28(4): 315-319. |
| [6] |
刘华坪, 陈浮, 马波. 基于动网格与UDF技术的阀门流场数值模拟[J]. 汽轮机技术, 2008, 50(2): 106-108. |
 2024, Vol. 46
2024, Vol. 46
