2. 潍柴动力股份有限公司,山东 潍坊 261061
2. Weichai Power Co., Ltd., Weifang 261061, China
月池是工程船舶中部垂向贯穿船体和甲板的空腔结构,通过月池可将船上的潜水钟下放和回收[1]。由于月池处于开放状态,船舶在航行过程中会受到月池带来的附加阻力,影响航行性能[2]。
近年来,随着CFD技术的发展,相关学者对月池方面的数值模拟进行了研究。姚震球等[3]研究深水钻井船阻力性能及月池优化方案,对无月池方案和2种有月池方案的钻井船进行月池内流场和波高进行计算,并将附加阻力进行对比,分析月池阶梯形状对阻力的影响。李文娟等[4]研究勘探船月池增阻情况,对首月池和双月池方案进行分析,探索其在不同吃水状态下的船舶总阻力情况。程宣恺等[5]研究海工船舶月池形状的影响,分别对月池底部倒圆直径和内壁开孔率进行改变,分析其对总阻力及月池内兴波的影响。采用STAR-CCM+软件进行数值计算,能够有效预报船舶阻力[6]。
目前,有关月池位置变化与阻力关系的研究很少。本文以某一饱和潜水支持船为例,通过CFD仿真手段,研究不同月池位置对船体阻力性能的影响,为工程船舶的月池设计提供参考。
1 船模试验该船为一饱和潜水支持船,首部安装2个侧推,并且在船体中部偏左舷带有月池结构。船体主尺寸见表1。
|
|
表 1 船体主尺寸 Tab.1 Main dimensions of the hull |
船模水池试验在挪威某船舶研究所进行,缩放比例为15.385,对本船设置了傅汝德数FN=0.146~0.260共15个航速的拖拽试验,得到船模总阻力。船模水池试验阻力结果见图1。
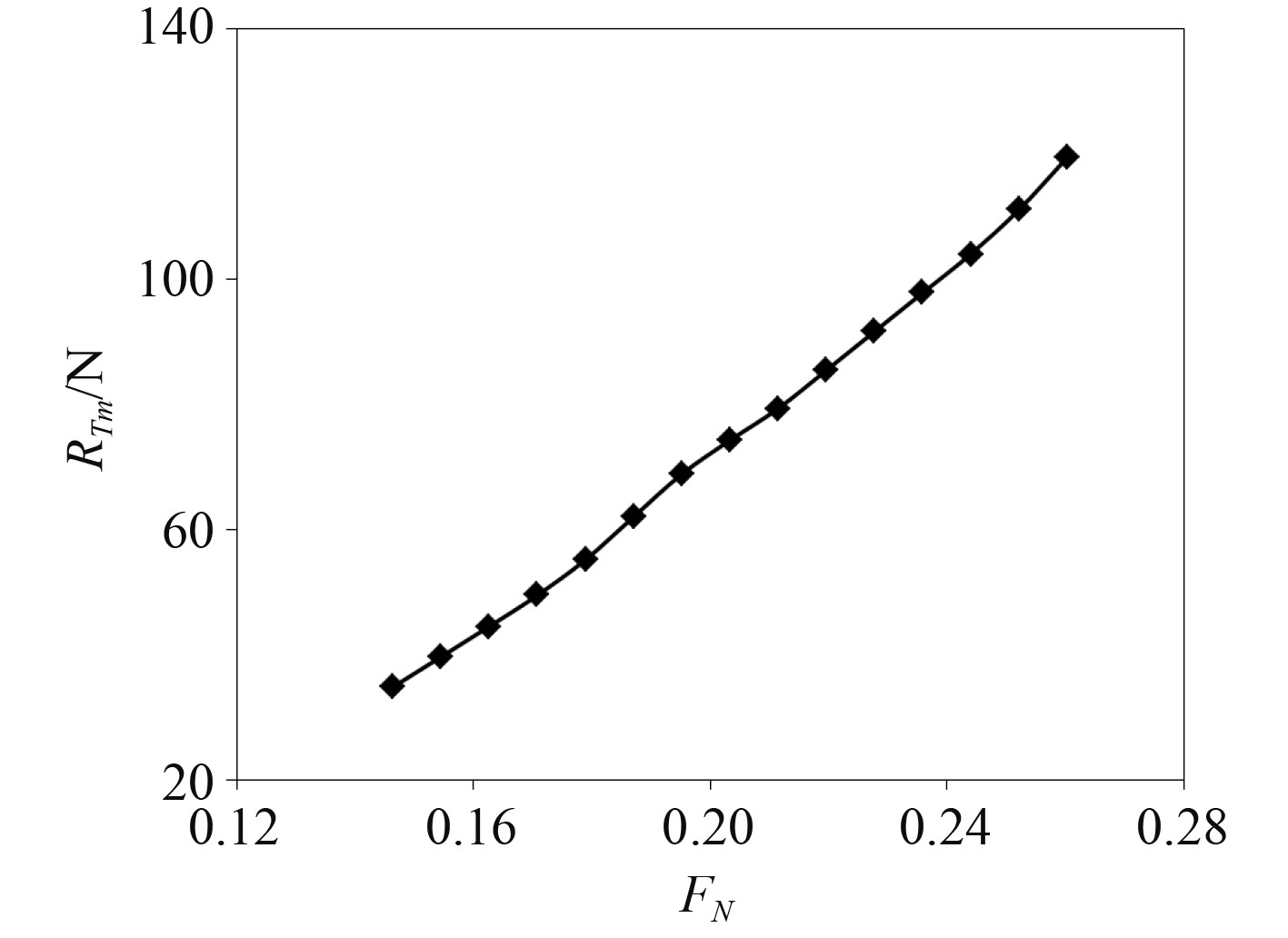
|
图 1 船模水池试验阻力结果 Fig. 1 Resistance result of pool test of ship model |
由于采用三因次换算方法可大大减小尺度效应[7],研究所使用三因次法将船模阻力转换至实船。船模总阻力系数为:
| $ {C}_{Tm}=\frac{{R}_{Tm}}{\displaystyle\frac{{\rho }_{m}}{2}{V}_{m}^{2}{S}_{m}} = {C}_{Fm}\left(1+{k}_{0}\right) + {C}_{Rm} + {C}_{AAm} + {C}_{BDm} 。$ | (1) |
式中:
船模摩擦阻力系数可用1957-ITTC公式计算:
| $ {C}_{Fm}=\frac{0.075}{{\left({\text{log}}{R}_{nm}-2\right)}^{2}} 。$ | (2) |
式中:
则船模剩余阻力系数为:
| $ {C}_{Rm}={C}_{Tm}-\left(1+{k}_{0}\right){C}_{Fm}-{C}_{AAm}-{C}_{BDm}。$ | (3) |
通过船模阻力换算至实船,实船总阻力系数为:
| $ {C}_{Ts} = {C}_{Rm}+\left({C}_{Fs}+ \Delta {C}_{F}\right)\left(1+{k}_{0}\right) + {C}_{A} + {C}_{AAs} + {C}_{BDs}。$ | (4) |
式中:
其中,空气阻力系数和尾封板阻力系数的计算公式分别为:
| $ {C}_{AA}=\frac{{\rho }_{{\mathrm{air}}}{C}_{D}{A}_{T}}{\rho S} ,$ | (5) |
| $ {C}_{BD}=\frac{0.029{\left({{A}_{T}}/S\right)}^{3/2}}{{\left({C}_{F}\right)}^{1/2}}。$ | (6) |
式中:
实船总阻力为:
| $ {R}_{Ts}={C}_{Ts}\frac{{\rho }_{s}}{2}{V}_{S}^{2}{S}_{S} 。$ | (7) |
式中:
换算成有效功率为:
| $ {P}_{E}=\frac{{R}_{Ts}{V}_{s}}{1\ 000}。$ | (8) |
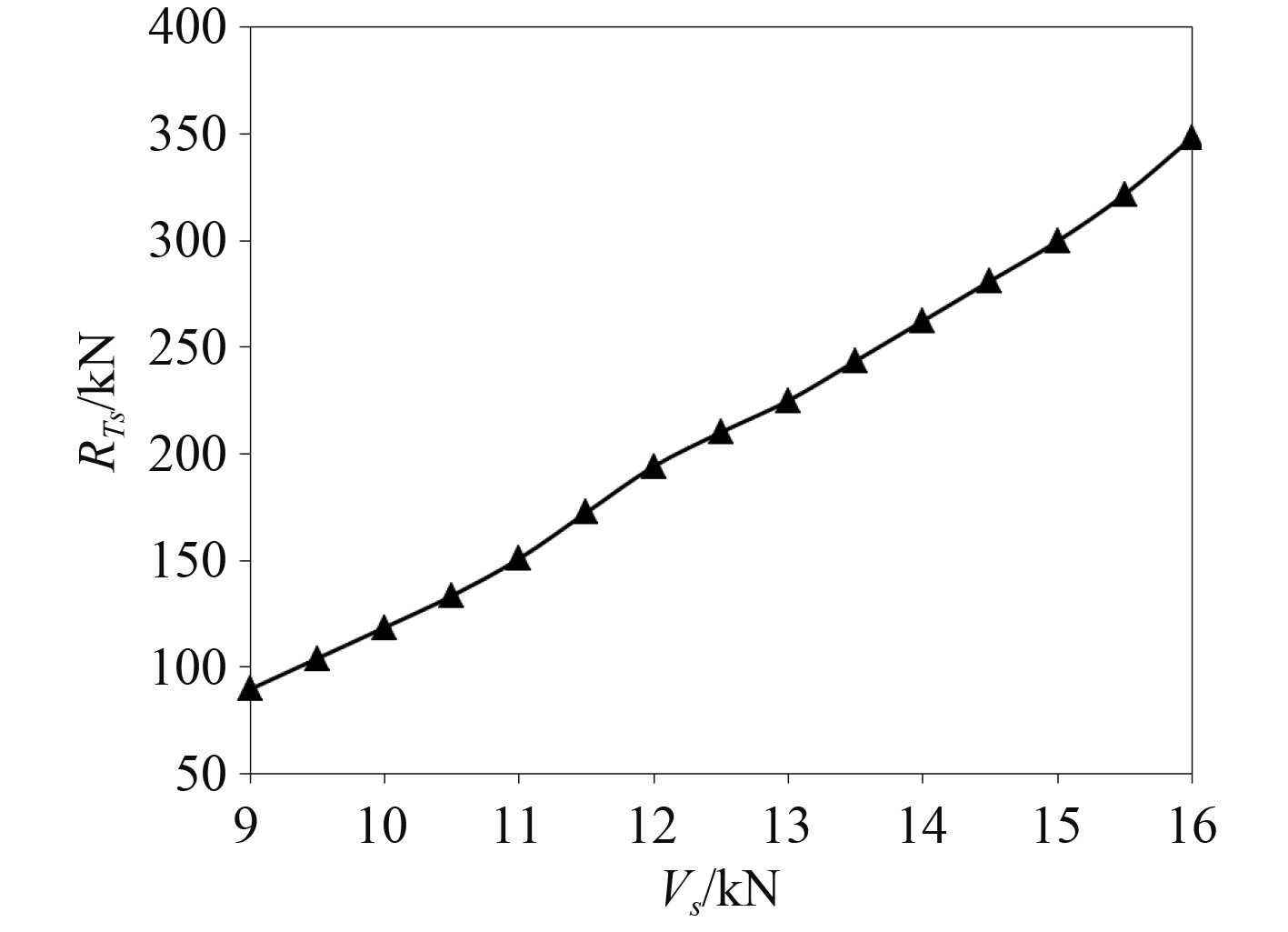
|
图 2 实船总阻力 Fig. 2 Total resistance of ship |
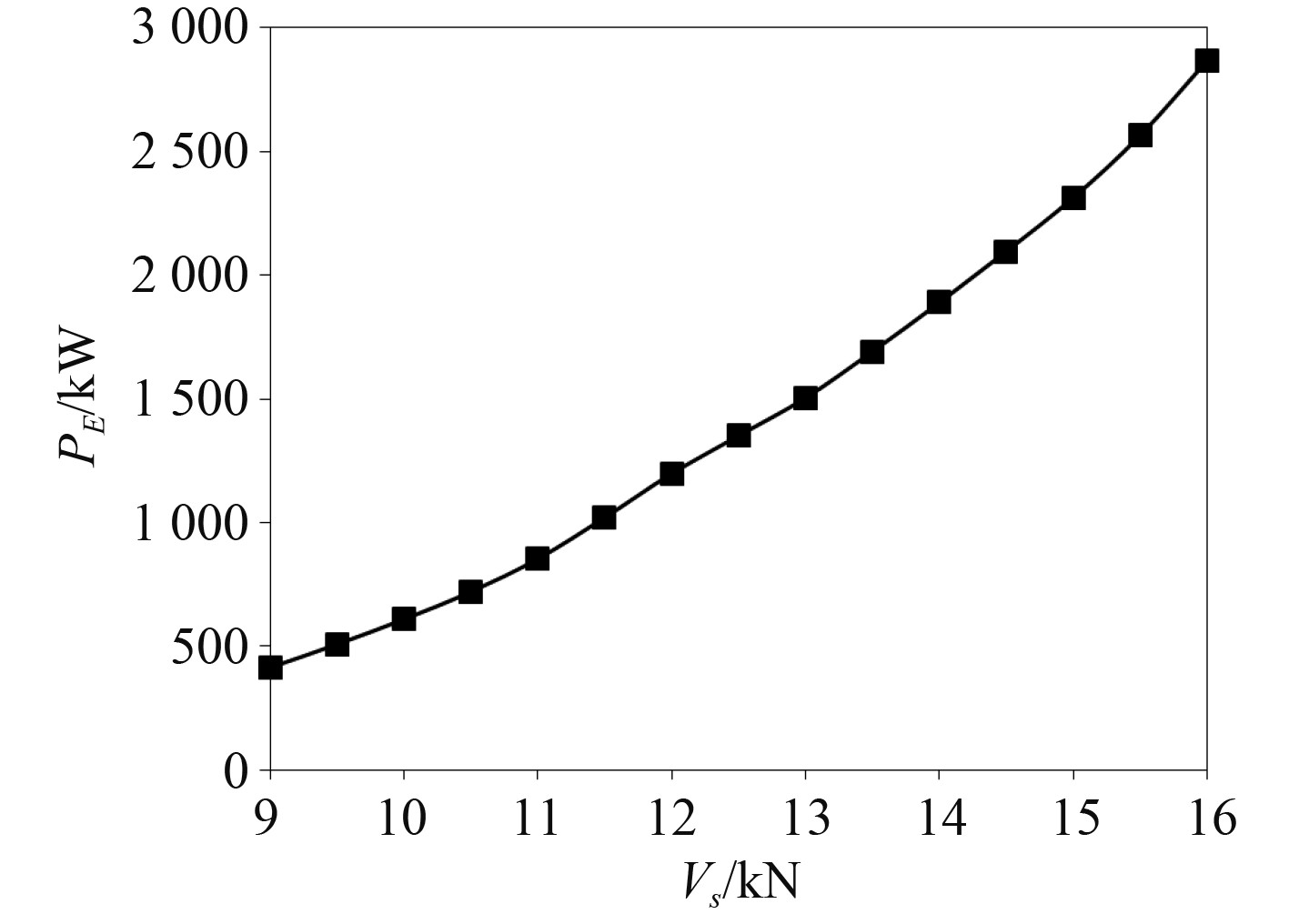
|
图 3 实船有效功率 Fig. 3 Effective power of ship |
采用STAR-CCM+软件,通过RANS法(reynolds average navier-stokes)进行船舶绕流场仿真计算。仿真模型采用与水池模型相同的缩尺比。船模采用壁面函数法处理近壁面的流动,选择

|
图 4 船体模型 Fig. 4 Hull model |
因为船体为非对称结构,所以取整个流场为计算域。为避免兴波在远场边界的反射,船后边界距离船体2.5倍船长,船侧边界距离船体1.5倍船长,船底边界距离船体2倍船长,并在船前、船后与船侧边界设置数值消波阻尼。
2.3 离散网格计算域内主要采用切割体网格。为准确捕捉船体周围的绕流场,在船体近域采用六面体密度盒进行局部加密,在自由面附近采用开尔文波形的密度盒对波高方向的网格进行局部加密。船体表面附近采用棱柱层网格,同时控制最内层棱柱层避免法向高度以满足壁面函数法对y+值的要求[9 − 10]。计算域内的网格总数约236万。
2.4 仿真计算有效性验证对船模进行阻力仿真计算,得到阻力数值并与船模试验结果对比,见图5。
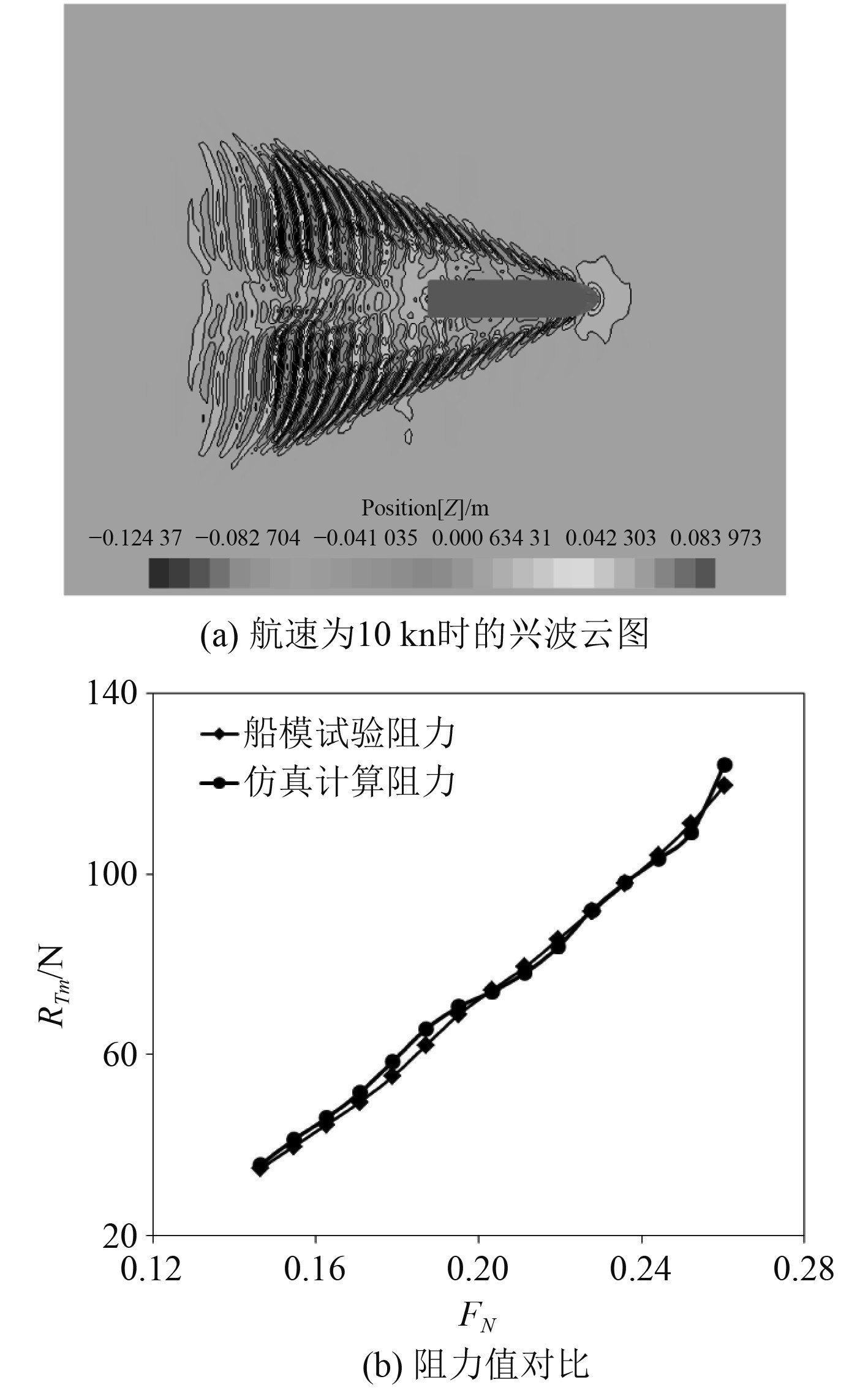
|
图 5 仿真结果与试验结果对比 Fig. 5 Comparison of simulation results with experimental results |
可知,仿真结果与试验结果吻合良好,船模总阻力相对试验数值的误差基本低于5%,说明以该方法进行的绕流场仿真计算是可行的,该数值方法的可行性通过验证。
3 月池位置对船舶阻力性能影响的分析 3.1 月池纵向位置变化对阻力的影响在月池原有位置的基础上,仅改变其纵向距离,共设置5个位置,见图6。
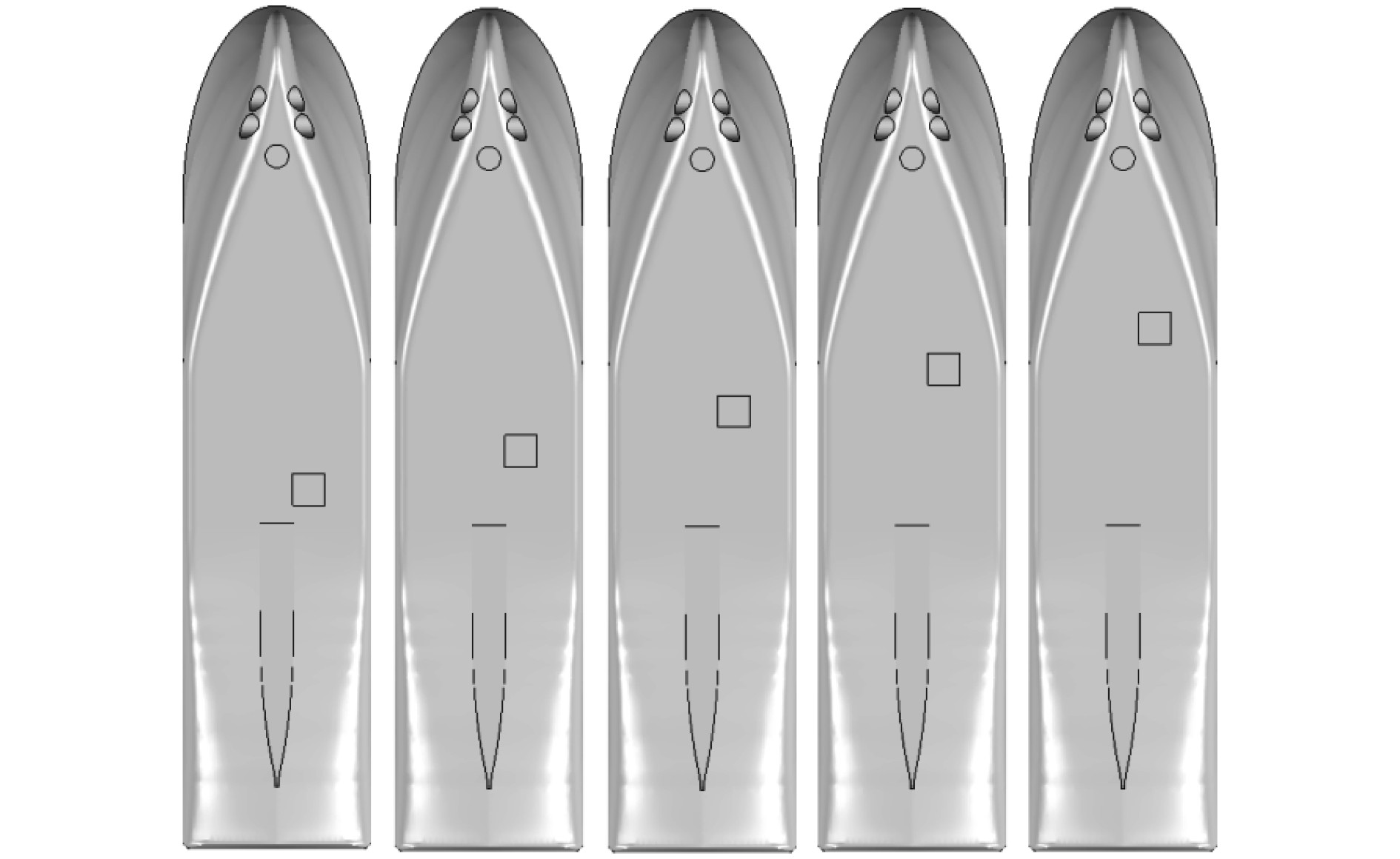
|
图 6 月池纵向位置变化 Fig. 6 Different longitudinal position of moonpool |
分别对10 kn和15 kn的航速进行阻力仿真计算,结果见图7。可知,在较低的10 kn航速下,虽然阻力值有所变化,但平均偏差在1.5%以内,变化不大且无规律;而随着航速的提升,在较高的15 kn航速下,阻力值偏差也在1.5%以内。因此可以得出结论:月池的纵向位置基本不影响其阻力性能。
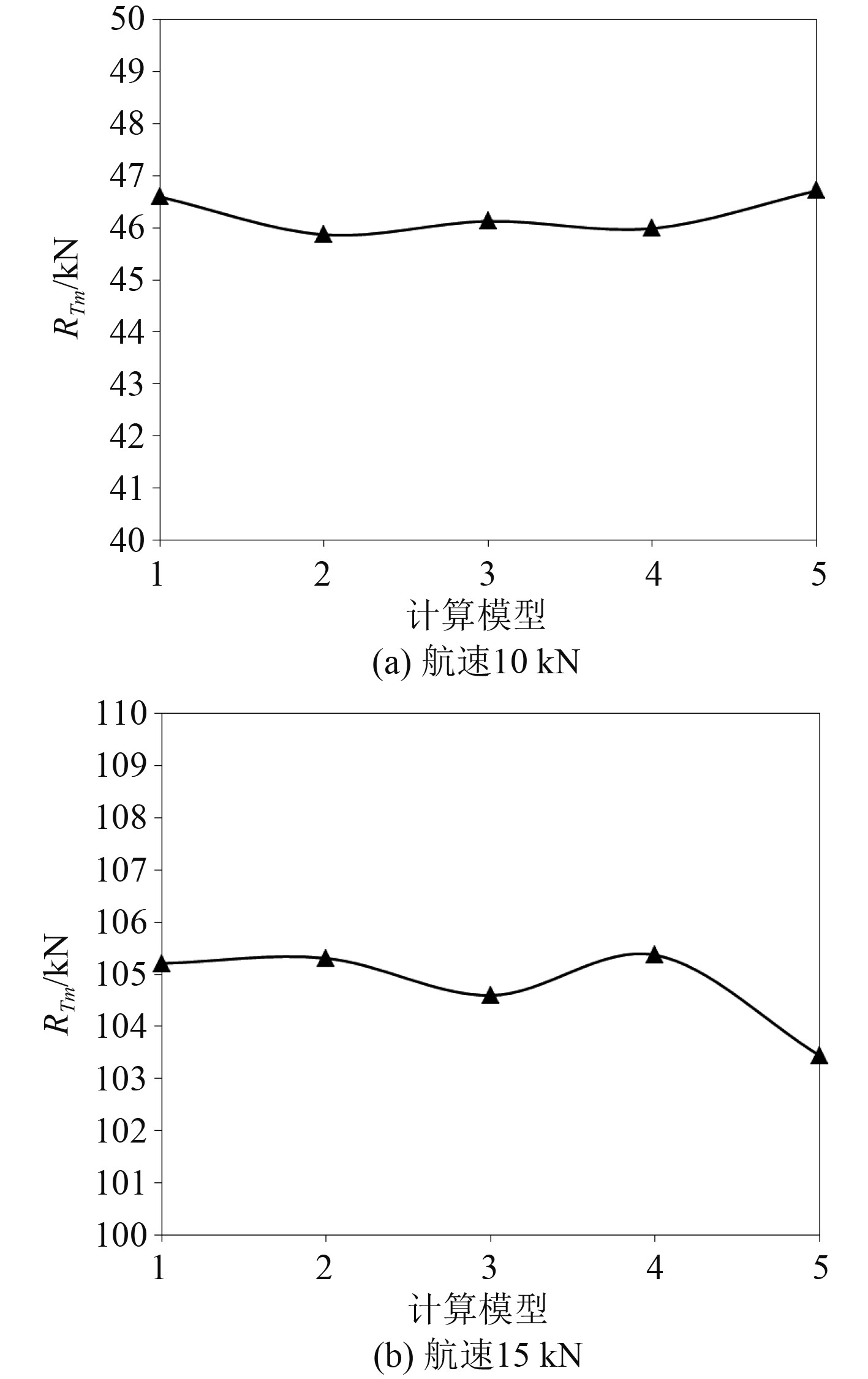
|
图 7 月池纵向位置变化阻力计算 Fig. 7 Resistance calculation of different moonpool longitudinal position |
在月池原有位置的基础上,仅改变其横向距离,共设置5个位置,见图8。

|
图 8 月池横向位置变化 Fig. 8 Different horizontal position of moonpool |
同样分别对10 kn和15 kn的航速进行阻力仿真计算,结果见图9。可知,航速10 kn和15 kn时,阻力值的平均偏差都在1.5%以内,变化同样不大。
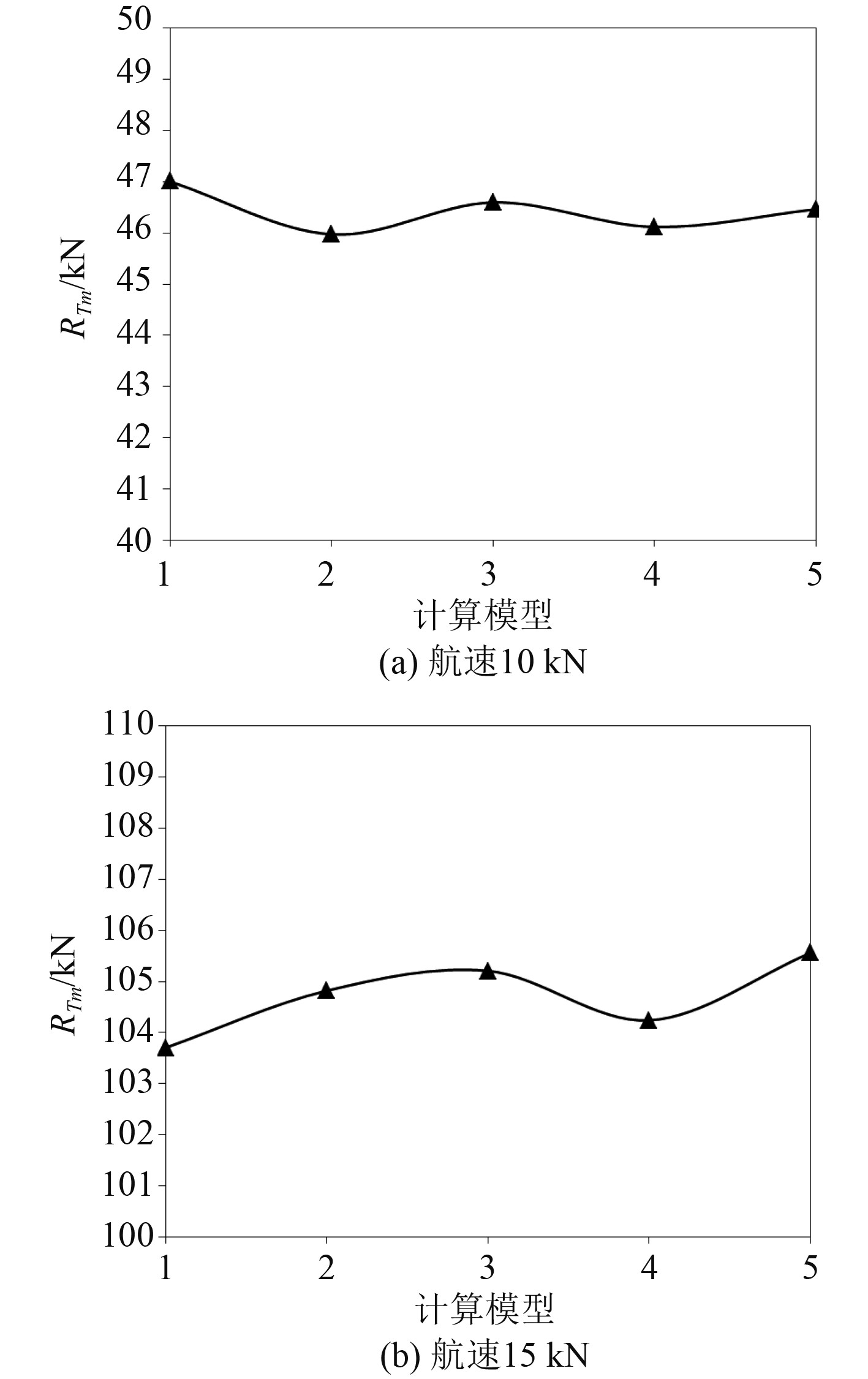
|
图 9 月池横向位置变化阻力计算 Fig. 9 Resistance calculation of different moonpool horizontal position |
在实际船舶设计中,月池的位置涉及到船体设计及机舱布置,进而影响水动力性能及船舶稳性。通过研究月池位置变化对船舶阻力性能的影响,可以综合考虑月池及机舱的布置方案,甚至优化设备选型。
4 结 语1)通过仿真可以较好地预报船舶的阻力,用于水动力计算及推进器设计。
2)在此潜水支持船尺度的基础上,月池位置的变化对船舶阻力性能的影响可忽略不计;其位置的设计可仅考虑船舱内设备的布置情况。
3)本文未考虑月池与船体大小的比值对船舶阻力的影响,后续可以进一步研究分析。
| [1] |
林丰财. 某多功能支持船潜水系统主要设备安装[J]. 广东造船, 2023, 42(4): 69-72. DOI:10.3969/j.issn.2095-6622.2023.04.019 |
| [2] |
詹星宇, 毛筱菲. 船舶月池的阻力与流场特性及其改进型式[J]. 中国舰船研究, 2020, 15(3): 45-53+101. ZHAN Xingyu, MAO Xiaofei. The resistance and flow field characteristics of moonpool and its improvement forms[J]. Chinese Journal of Ship Research, 2020, 15(3): 45-53+101. |
| [3] |
姚震球, 孙硕, 凌宏杰, 等. 不同月池形状对钻井船附加阻力的影响[J]. 造船技术, 2020(2): 7-12. DOI:10.3969/j.issn.1000-3878.2020.02.002 |
| [4] |
李文娟, 陶延武, 羊卫, 等. 大洋勘探船月池阻力特性研究[J]. 舰船科学技术, 2022, 44(19): 32-37. LI Wenjuan, TAO Yanwu, YANG Wei, et al. Research on resistance of moonpool of the ocean exploration ship[J]. Ship Science and Technology, 2022, 44(19): 32-37. DOI:10.3404/j.issn.1672-7649.2022.19.007 |
| [5] |
程宣恺, 周国平, 张雨新, 等. 模型尺度下海工船舶月池对阻力性能影响的数值模拟研究[J]. 船舶力学, 2020, 24(5): 589-598. DOI:10.3969/j.issn.1007-7294.2020.05.004 |
| [6] |
任再美, 孙江龙, 杨云飞. 船舶有效功率预报方法[J]. 舰船科学技术, 2021, 43(3): 141-145. REN Zaimei, SUN Jianglong, YANG Yunfei. Ship effective power forecasting method[J]. Ship Science and Technology, 2021, 43(3): 141-145. |
| [7] |
周健, 姜次平, 盛振邦, 等. 三因次船舶阻力换算方法中确定形状因子的探讨[J]. 中国造船, 1982(4): 1-6. |
| [8] |
王福军. 计算流体动力学分析: CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004.
|
| [9] |
尹晓青, 武璇, 张元浩, 等. 重心纵向位置对滑行艇阻力影响的数值分析[J]. 武汉理工大学学报(交通科学与工程版), 2023, 47(2): 285-289. |
| [10] |
倪崇本. 基于CFD的船舶阻力性能综合研究[D]. 上海: 上海交通大学, 2012.
|
 2024, Vol. 46
2024, Vol. 46
