0 引　言

潜器水下拖曳系统通常是指一种利用拖曳缆将拖曳体连接到潜器的水下能源开发、资源探测工具，拖曳体上安装有各种传感器和通信设备，可以收集海底地质、海洋水文和生态环境等信息，也可以与其他潜器或母船进行数据交换。潜器水下拖曳系统与水面船舶拖曳系统相比具有更高的隐蔽性、灵敏性且不易受风浪等水面环境的影响，因此该拖曳系统更适合在水下进行精密的拖曳作业。对潜器水下拖曳系统操纵运动的研究有助于高效地实现拖曳系统的高精度控制，丰富拖曳系统的操纵控制理论体系，为设计拖曳系统和简化拖曳系统的操纵运动方程提供理论支撑。

Russell等^{[1 − 3]}为了建立拖曳系统操纵性的基本运动模型，通过海上试验和数值模拟的形式对包括圆周回转、直线运动和水平正弦运动在内的水下拖曳系统的操纵运动进行了初步的研究。在研究缆索动力学时，常用的拖曳缆建模方法包括了有限差分法^[3]、集中质量法^{[4 − 6]}、直接积分法^[7]和有限元法^[8]，其中集中质量法的物理意义明确，算法简便，边界条件适应能力强，广泛应用于拖曳系统操纵运动响应的研究中。朱克强等^[9]对拖船做Z型操纵运动时水下拖曳列阵的耦合运动开展了数值计算，并发现在平衡动态过程中采用定值曳力系数即可，对于拖曳缆曲率会发生剧烈变化的场合应该采取变曳力系数进行计算。张锋等^[10]通过凝集参数法模拟了不同回转半径、不同回转速度的回转操纵运动下拖曳体的运动轨迹，得出结论，水面拖曳母船航速越大、回转半径越小则拖曳系统可以较快进入稳态。顾振福等^[11]对变速直航操纵运动下拖曳系统升沉变化的实验值和计算值进行比较，Srivastava等^[12]提出了一种能够预测拖船在变速直航运动时拖曳缆动态行为的数值方法。王志博^{[13 − 14]}针对变速直航操纵运动和回转运动中拖曳系统因受到冲击作用形成的振动响应进行计算，发现拖曳体质量、拖曳缆长度、回转半径等拖曳操纵参数和结构参数对操纵运动中的拖曳系统的冲击效应有显著的影响。ZHANG等^[15] 从不同释放速度和不同深度2个角度，对处于回转运动过程中水下拖曳系统的运动特性和对操纵运动的影响进行了研究，发现拖曳系统的深度和姿态受到拖船转弯动作的影响，转弯半径越小，深度和姿态的变化就越大。李超等^[16]为了有效的控制水下拖曳系统，研究了拖曳速度、翼板攻角、缆长与拖曳缆张力、拖曳定深、展宽之间的影响规律。

为了提高实际工程中选择和设计系统的效率，更准确预报系统的操纵运动响应特性，同时为研究该系统操纵运动数学模型通过基础，因此需要全面的研究不同参数对拖曳系统操纵运动的影响。

1 敏感性分析方法与拖曳系统计算模型

为适应潜器拖曳系统水下运动，本文建立的拖曳系统是一种单拖曳缆配合单拖曳体的形式。包括将潜器的水下六自由度操纵运动以欧拉变换与集中质量法统一。将拖曳体简化为只考虑浮力、重力和水流阻力的质点模型。

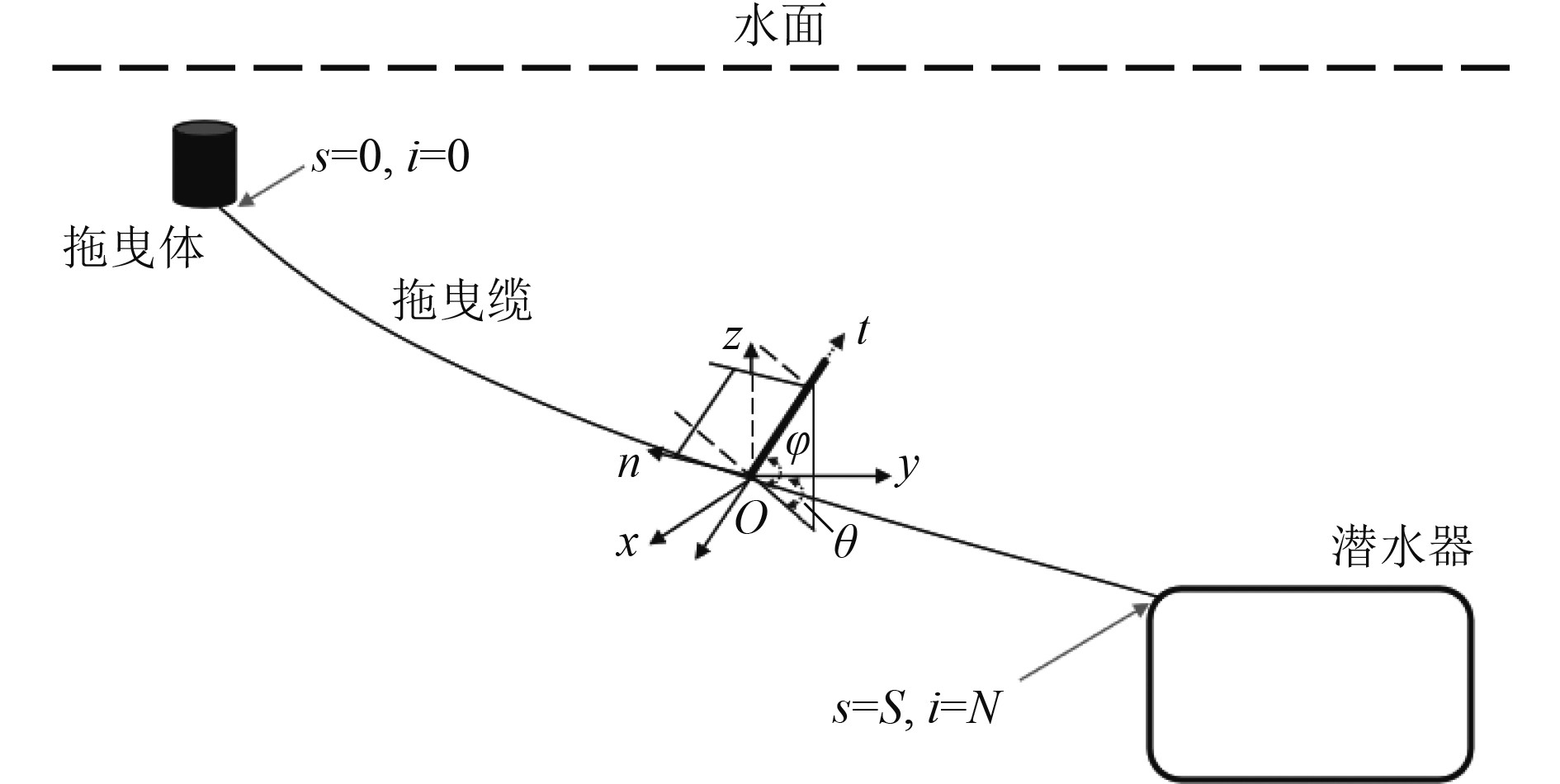
潜器水下拖曳系统示意图如图1所示，拖曳系统包含了潜器、拖曳缆和拖曳体。将缆看成柔性缆，不考虑拖曳缆的弯曲及扭转刚度的影响。潜器所做的运动是一直保持在水面一定深度以下并且为设定静水环境下，拖曳体不上浮到水面，不考虑风、浪、流等因素对拖曳系统的影响。图1中的$ s $表示拖曳缆的坐标，$ S $为拖曳缆的总长度，$ i = 0,s = 0 $是起点，$ (\theta ,\phi ) $为拖曳缆的微元姿态角，方位角θ为缆顺时针偏离y轴角度，$ \phi $为抬升角，这2个角度取决于缆的空间位置。

1.1 敏感性分析方法

进行潜器水下拖曳系统操纵运动敏感性分析是为了确定当不同参数变化时对运动响应产生影响的敏感程度。引入敏感性指数^{[17 − 19]}P来表示这种影响关系的强弱：

$ P = \frac{{(R - {R^ * })/{R^ * }}}{{(H - {H^ * })/{H^ * }}} = \frac{{\Delta R/{R^ * }}}{{\Delta H/{H^ * }}}。$

(1)

式中：R为系统对操纵运动的运动响应参数，如拖曳深度变化范围、拖曳缆张力变化历程等；H为拖曳操纵参数和结构参数，如潜器回转半径、缆长等；上标带有*为基准的运动响应参数、拖曳操纵参数和结构参数；无*上标为变化后的运动响应参数、拖曳操纵参数和结构参数。

可知，敏感性指数P是用来衡量拖曳操纵参数和结构参数发生改变后与运动响应参数之间的关系，P的绝对值越大则表示系统的运动响应对某种参数越敏感，这种参数对运动响应的影响就越重要；反之，P的绝对值越小则这种参数对动响应的影响就越弱；当P = 0时则表示该参数不会对运动响应产生影响。

1.2 坐标系统

因为将系统中的拖曳体简化为只考虑浮力、重力和水流阻力的质点并连接在拖曳缆首端的模型，同时潜器拖曳时运动为定深直线运动和定深回转运动，所以采用2种不同形式的坐标系统来推导水下拖曳系统的动力学模型，即描述潜器运动的惯性坐标系$ O-XYZ $和描述拖曳缆运动的局部坐标系$ O-btn $，其中的转换关系如下式:

$ {[X,Y,Z]^{\text{T}}} = {\boldsymbol{\gamma}}{[b,n,t]^{\text{T}}} ，$

(2)

$ {\boldsymbol{\gamma}} = \left[ {\begin{array}{*{20}{c}} {{\text{cos}}\theta }&{\sin \theta \cos \phi }&{ - \sin \theta \sin \phi } \\ { - \sin \theta }&{\cos \theta \cos \phi }&{ - \cos \theta \sin \phi } \\ 0&{\sin \phi }&{\cos \phi } \end{array}} \right]。$

其中：${\boldsymbol{\gamma}}$为局部坐标系向全局坐标系的转换矩阵。

1.3 控制方程

拖曳缆按照集中质量法离散后建立动力学模型，该方法将拖曳缆从末端至首端离散为N段，即N+1个节点，其中末端$ s = 0 $为第$ i = 0 $个节点，首端$ s = S $为第$ i = N $个节点。对第i个节点应用牛顿第二定律，得拖缆节点的基本运动控制方程，即

$ {{\boldsymbol{M}}_i}{a_i} = \Delta {{\boldsymbol{T}}_i} + {{\boldsymbol{B}}_i} + {{\boldsymbol{G}}_i} + {{\boldsymbol{F}}_{Di}} 。$

(3)

式中：${a_i} = {{\boldsymbol{\ddot x}}_i}$为加速度；$ {{\boldsymbol{M}}_i} $为质量矩阵；$ \Delta {T}_{i}、{B}_{i}、{G}_{i}、{F}_{Di} $为节点$ i $上的所有作用力，分别为拖曳缆张力、浮力、重力以及流体阻力，包括拖缆节点自身的惯性质量及其在水中的附加质量$ {{\boldsymbol{M}}_{a,i}} $, 可分别表示为

$ {{\boldsymbol{M}}_i} = ({\mu _{i - 1/2}}{l_{i - 1/2}} + {\mu _{i + 1/2}}{l_{i + 1/2}}){\boldsymbol{I}}/2 + {{\boldsymbol{M}}_{a,i}}，$

(4)

$ {{\boldsymbol{M}}_{a,i}} = ({{\boldsymbol{M}}_{a,i - 1/2}} + {{\boldsymbol{M}}_{a,i + 1/2}})/2，$

(5)

$ {{\boldsymbol{M}}_a} = \rho l\sigma \left[ {\begin{array}{*{20}{c}} {1 - {{{\mathrm{s}}}^2}\theta {{{\mathrm{c}}}^2}\theta } & { - {\mathrm{c}} \theta {\mathrm{s}} \theta {{{\mathrm{c}}}^2}\phi } & { - {\mathrm{s}} \theta {\mathrm{c}} \phi {\mathrm{s}} \phi } \\ { - {\mathrm{c}} \theta {\mathrm{s}} \theta {{{\mathrm{c}} }^2}\phi } & {1 - {{{\mathrm{c}} }^2}\theta {{{\mathrm{c}} }^2}\phi } & { - {\mathrm{c}} \theta {\mathrm{c}} \phi {\mathrm{s}} \phi } \\ { - {\mathrm{s}} \theta {\mathrm{c}} \phi {\mathrm{s}} \phi } & { - {\mathrm{c}} \theta {\mathrm{c}} \phi {\mathrm{s}} \phi } & {{{{\mathrm{c}} }^2}\phi } \end{array}} \right]。$

(6)

式中：I为3×3的单位矩阵；μ、l、ρ分别为拖曳缆单位长度的质量、节点间长度、横截面积；下标i+1/2为节点$ i $和节点i+1间的物理量；s表示sin（）；c表示cos（）。

1）张力T，通常情况下拖曳缆的应变$ \left|\varepsilon \right|\ll $ 1，可将应力—应变关系弹性化处理，其本构关系可采用胡克定律，即

$ \Delta {{\boldsymbol{T}}_i} = {{\boldsymbol{T}}_{i + 1/2}} - {{\boldsymbol{T}}_{i - 1/2}}，$

(7)

$ {{\boldsymbol{T}}_{i + 1/2}} = E\sigma {\varepsilon _{i + 1/2}}{{\boldsymbol{\tau }}_{i + 1/2}}，$

(8)

$ {\varepsilon _{i + 1/2}} = \sqrt {{{({x_{i + 1}} - {x_i})}^2} + {{({y_{i + 1}} - {y_i})}^2} + {{({z_{i + 1}} - {z_i})}^2}} /{l_{i + 1/2}} - 1。$

(9)

其中：τ为缆长方向上的单位切向量；$ E $为弹性模量。

2）浮力和重力B、G，节点i的浮力和重力可以表示为

$ \begin{split}{{\boldsymbol{B}}_i} +{{\boldsymbol{G}}_i} = & - \rho {\boldsymbol{g}}[({l_{i - 1/2}}{\sigma _{i - 1/2}} + {l_{i + 1/2}}{\sigma _{i + 1/2}}) - \\ &({l_{i - 1/2}}{\mu _{i - 1/2}} + {l_{i + 1/2}}{\mu _{i + 1/2}})]/2。\end{split}$

(10)

式中：g为重力加速度。

3）流体阻力F_Di，将拖曳缆阻力分为切向和法向分别处理，计入缆应变影响后，可以表示为：

$ {{\boldsymbol{F}}_{Di}} = ({{\boldsymbol{F}}_{Di + 1/2}} + {{\boldsymbol{F}}_{Di - 1/2}})/2，$

(11)

$ {{\boldsymbol{F}}_{Di}} \approx - \rho ld\sqrt {1 + \varepsilon } ({C_n}\left| {{v_{n,b}}} \right|{v_{n,b}} + {\text π} {C_t}\left| {{v_t}} \right|{v_t}) 。$

(12)

式中：$v = {\boldsymbol{\dot x}}$为节点的速度向量；d为缆直径；${C_n}$、${C_t}$分别为其法向、切向阻力系数。

对于拖曳体的运动模型参考文献[20]建立，若节点$ i = 0 $处缆悬挂了拖曳体，可将拖曳体看作质点，利用质点运动模型描述拖曳体的运动，根据牛顿第二定律将拖曳体简化成为质点运动写成：

$ {{\boldsymbol{M}}_b}\frac{{{{\text{d}}^2}{{\boldsymbol{{A}}}_s}}}{{{\text{d}}{t^2}}} = {\boldsymbol{S}} 。$

(13)

质量系数矩阵的非零元素为：

$ {{\boldsymbol{M}}_b} = \left[ {\begin{array}{*{20}{c}} {m + {m_{ax}}}&0&0 \\ 0&{m + {m_{ay}}}&0 \\ 0&0&{m + {m_{az}}} \end{array}} \right]，$

(14)

$ {\boldsymbol{S}} = \left[ {\begin{array}{*{20}{c}} {\rho {U^2}{L_x}^2/2} \\ {\rho {U^2}{L_y}^2/2} \\ {\rho {U^2}{L_z}^2/2 + mg - \rho gV} \end{array}} \right]，$

(15)

$ {{\boldsymbol{A}}_S} = {\left[ {{X_b} {Y_b} {Z_b}} \right]^{\text{T}}}。$

(16)

式中：m为拖曳体的质量；m_ax、m_ay、m_az为拖曳体的附加质量；S为作用在拖曳体上的重浮力、惯性力、水流作用、拖曳缆拉力，需要利用来拖曳体的特征长度L_x、L_y、L_z计算水流作用力。

1.4 边界条件与求解方法

拖曳缆$i = 0$处，由于采用的拖曳体尺度相较于整个系统可看作质点，结合式(3)和式(13)此处的边界条件可以写成

$ ({{\boldsymbol{M}}_0} + {{\boldsymbol{M}}_b}){a_0} = {{\boldsymbol{F}}_0} + {\boldsymbol{S}}。$

(17)

其中：下标0表示在节点第$ i = 0 $个节点处。

拖曳缆$i = N$处，此处是拖曳缆和潜器连接的节点，拖曳缆的位移和速度均与潜器保持一致，边界条件可以写成：

$ \left\{ \begin{gathered} {x_N} = {x_s}(t)，\\ {y_N} = {y_s}(t)，\\ {z_N} = {z_s}(t)，\\ \end{gathered} \right. $

(18)

$ \left\{ \begin{gathered} {{\dot x}_N} = {u_s}(t)，\\ {{\dot y}_N} = {v_s}(t)，\\ {{\dot z}_N} = {w_s}(t)。\\ \end{gathered} \right. $

(19)

其中：下标N表示在节点第$i = N$个节点处；x_s、y_s、z_s和u_s、v_s、w_s分别指的是拖曳缆和潜器的节点处关于时间的坐标分量和速度分量。

将式(3)和速度的微分定义$v = {\text{d}}x/{\text{d}}t$联立可以拖曳缆的运动控制方程，即：

$ \left\{ \begin{gathered} \frac{{{\text{d}}{{\dot x}_i}}}{{{\text{d}}t}} = {M_i}^{ - 1} \cdot {F_i}，\\ \frac{{{\text{d}}{x_i}}}{{{\text{d}}t}} = {{\dot x}_i}，\\ \end{gathered} \right. (i = 0, \cdot \cdot \cdot ,N - 1)。$

(20)

将式(20)与边界条件联立，在给定的初值条件下采用四阶龙格库塔方法即可求解出该方程。

2 敏感性系数计算 2.1 基准参数设置

潜器通常需要完成加速、减速、爬升、下潜、回转等水下操纵运动，又以潜器的变速拖曳和回转拖曳更为常见，这2种操纵运动共同的结构参数如表1所示。本文对于直航变速运动选取变速前后深度变化、变速前后拖曳缆末端张力变化作为运动响应参数，选取潜器变速度作为拖曳操纵参数；对于回转拖曳运动选取稳定段深度变化范围（最大深度与最小深度之差）、稳定段拖曳缆末端张力变化范围（最大张力与最小张力之差）作为运动响应参数，选取回转半径作为拖曳操纵参数；选取缆长、拖曳缆法向阻力系数作为2种操纵运动的共同结构参数。

2.2 拖曳系统对操纵运动的响应

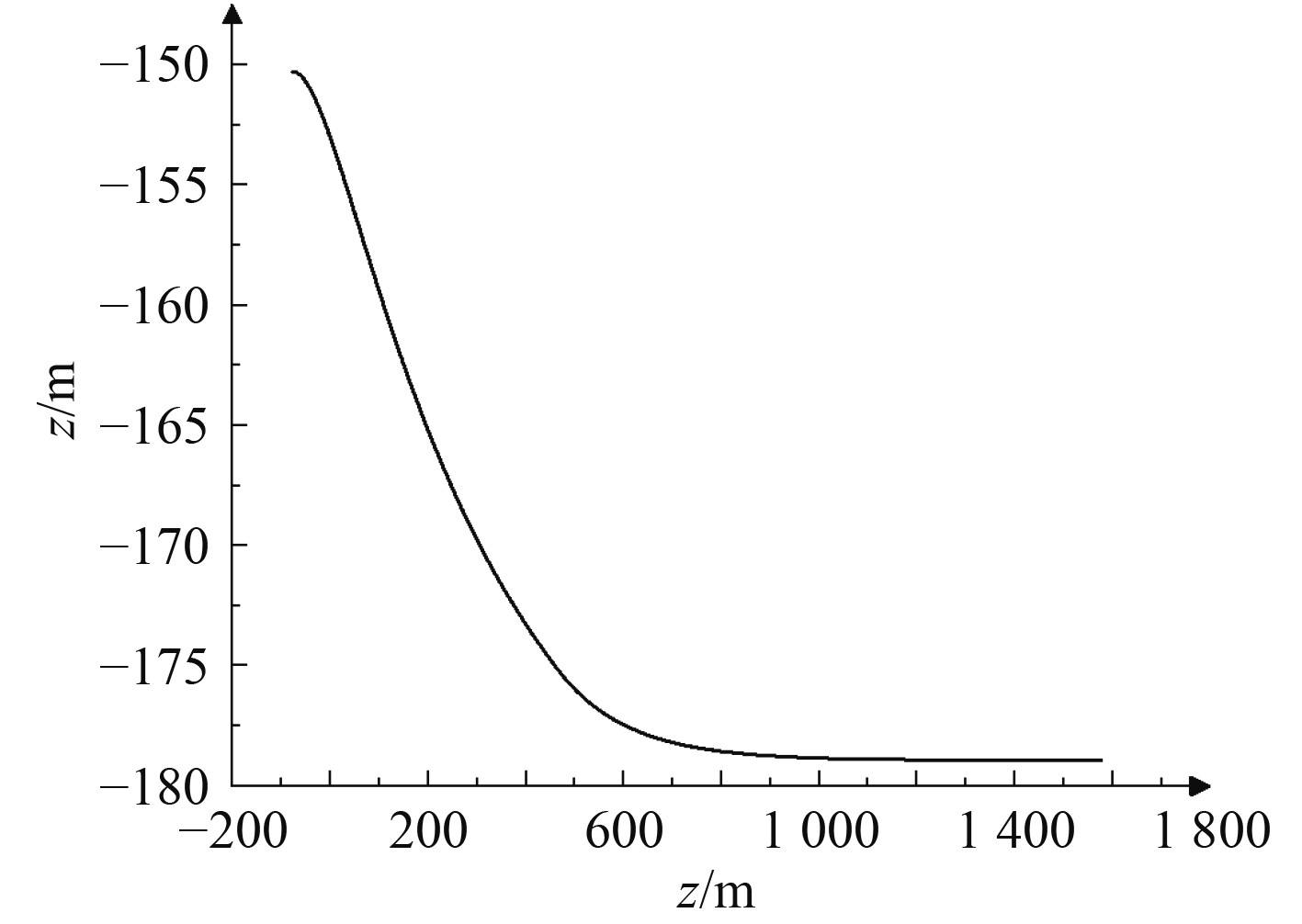
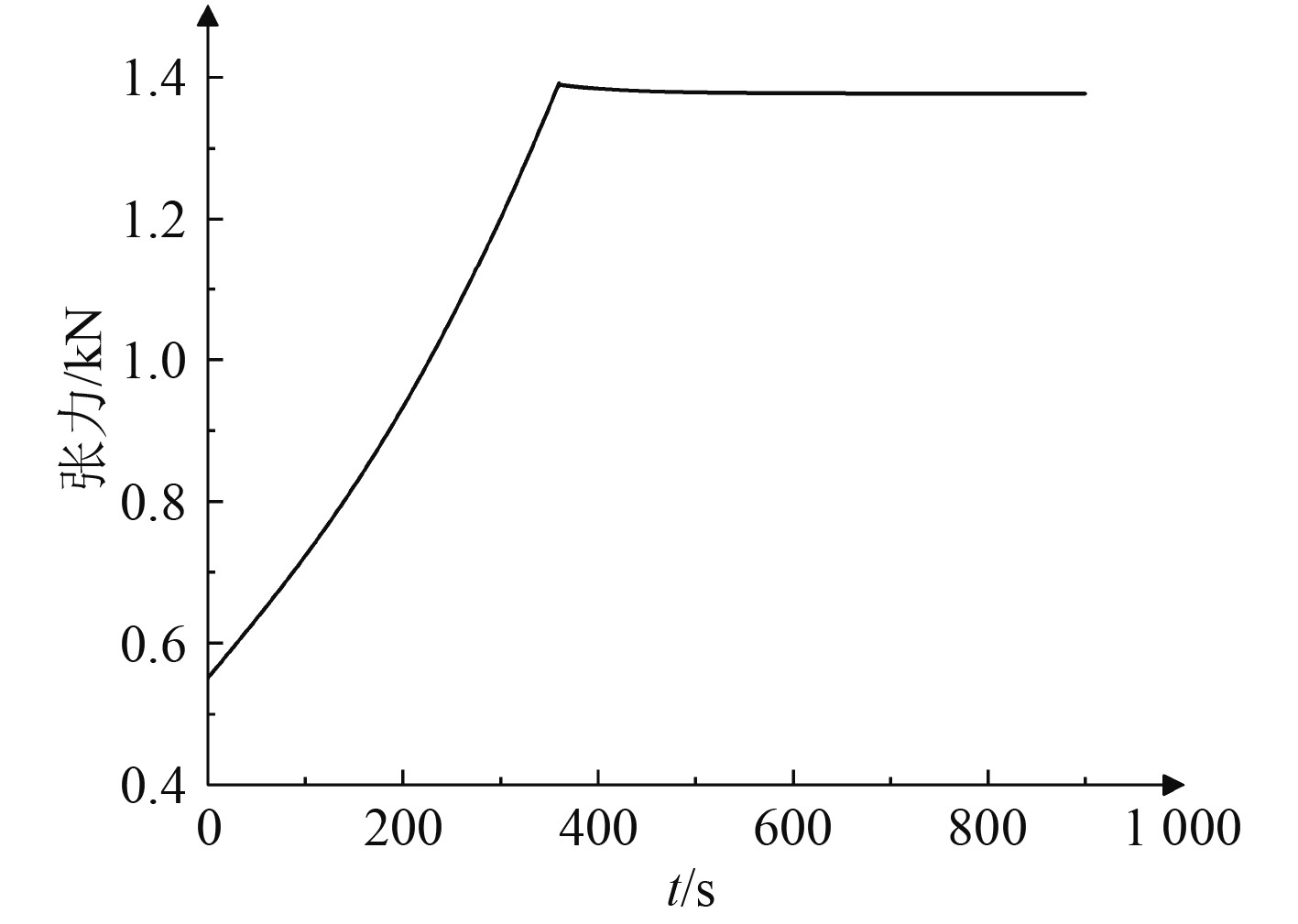
在建立拖曳系统计算模型并求解后，得到了2种操纵运动下拖曳系统的运动轨迹和拖曳缆末端张力变化历程。图2和图3分别为潜器在360 s时间段内由2 kn加速到4 kn时拖曳系统的运动轨迹和拖曳缆末端张力变化，因拖曳体在操纵性中呈现了显著的惯性效应，拖曳系统经过变速时间段从变速前的初始深度逐渐稳定到另一深度，拖曳缆张力随之以线性变化的形式稳到另一值，这种运动响应在潜器做加速运动或加速运动时都会发生，且速度变化的时间段越短、速度变化范围越大响应越剧烈。

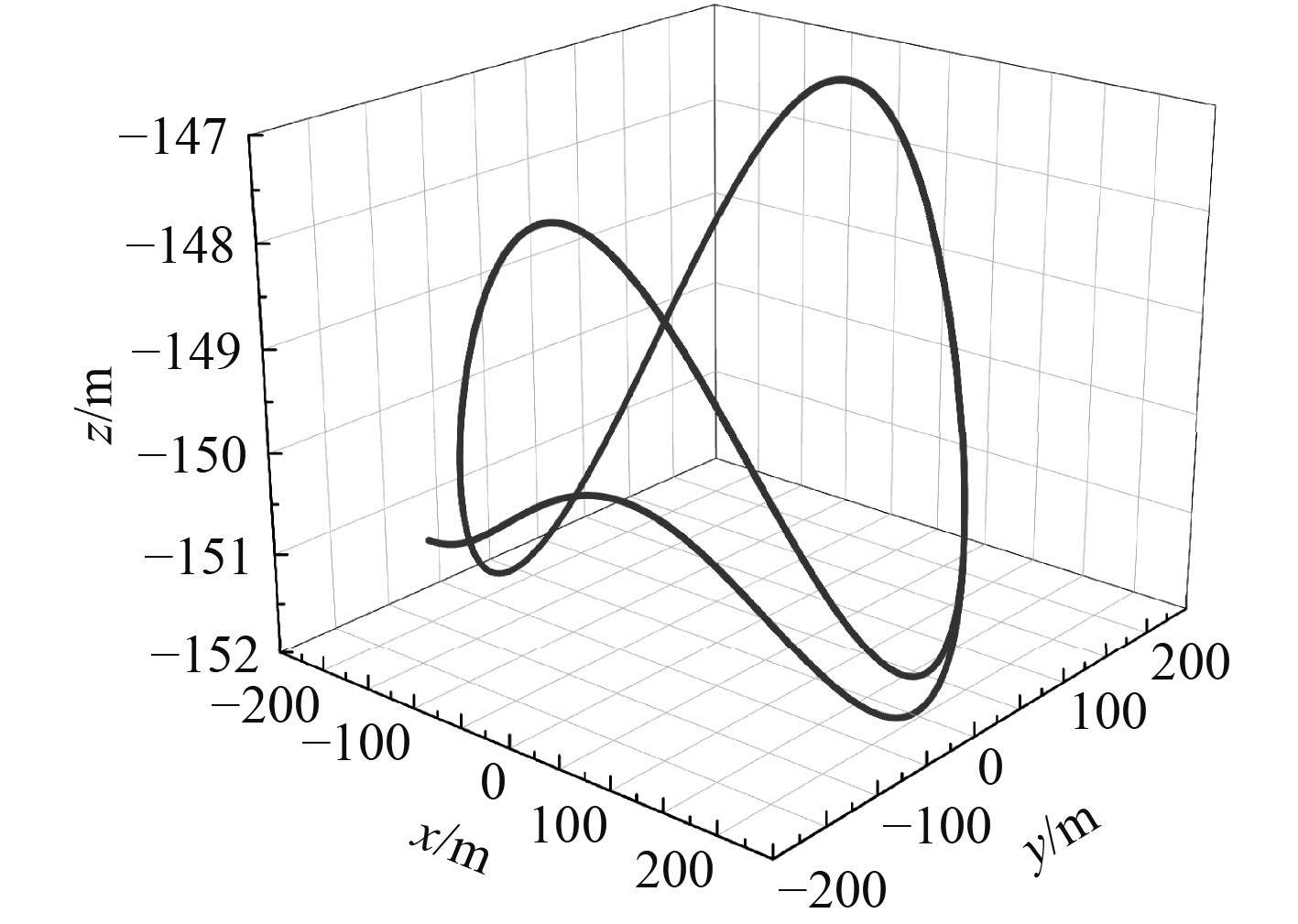
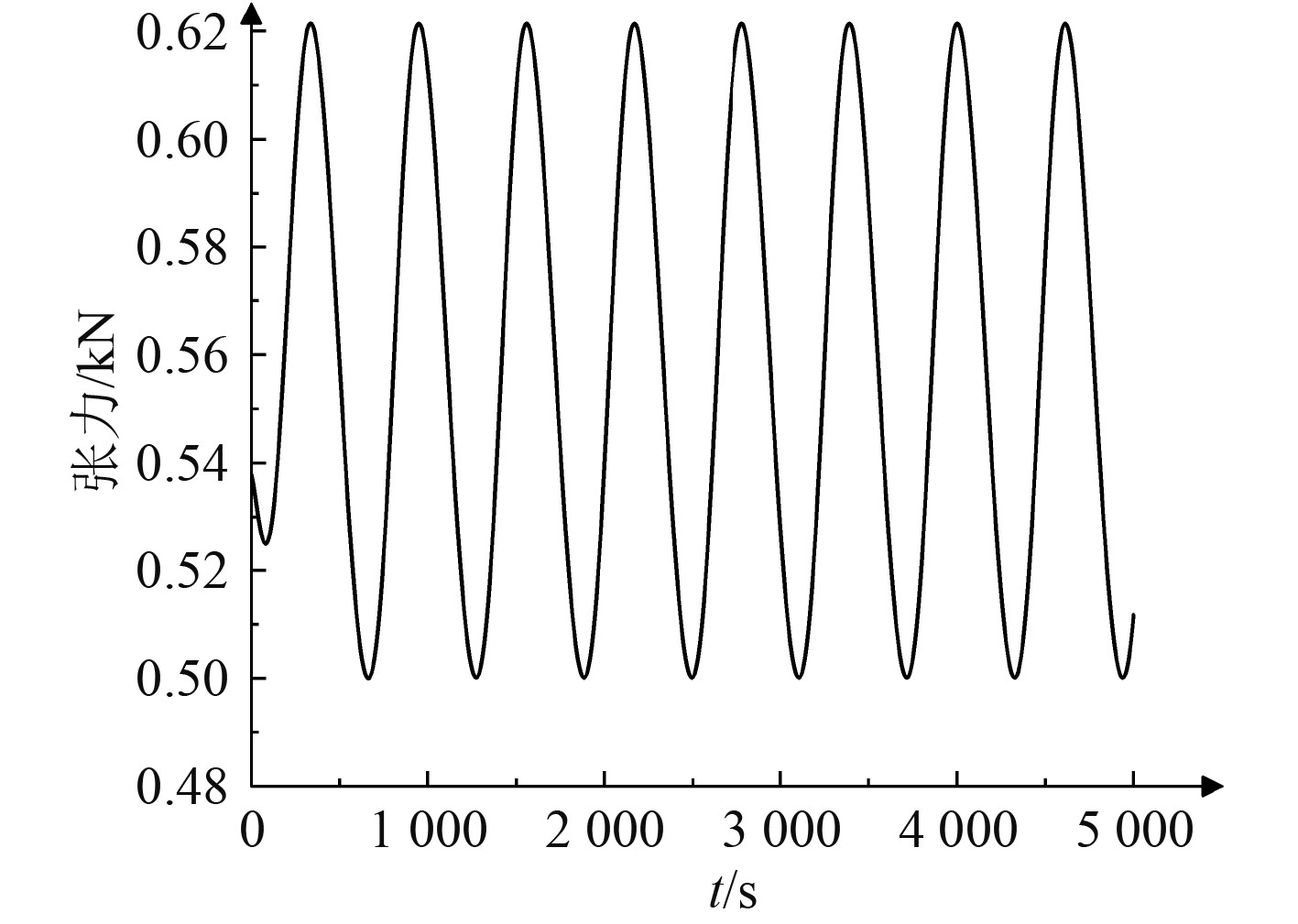
图4和图5分别为潜器在5000 s时间段内以2 kn速度做匀速回转运动时拖曳系统的运动轨迹和拖曳缆末端张力变化。对于一般的潜器水下拖曳系统，因为潜器回转运动时操纵速度有限，且系统本身的惯性很大，系统对潜器操纵运动的响应是一种缓慢的运动。在回转运动中，拖曳系统的运动轨迹和拖曳缆张力变化历程都是先经过一段暂态过程再进入稳定的周期性变化中。

2.3 直航变速运动敏感性系数计算

直航变速运动分成加速和减速2种形式，分别对由2 kn至4、6、8、10 kn作为加速区间、由10 kn至8、6、4、2 kn作为减速区间、速度变化时间为360 s的基准状态，在拖曳操纵参数和结构参数基准值的基础上分别取(−20%、−10%、+10%、+20%)作为该变量展开分析。

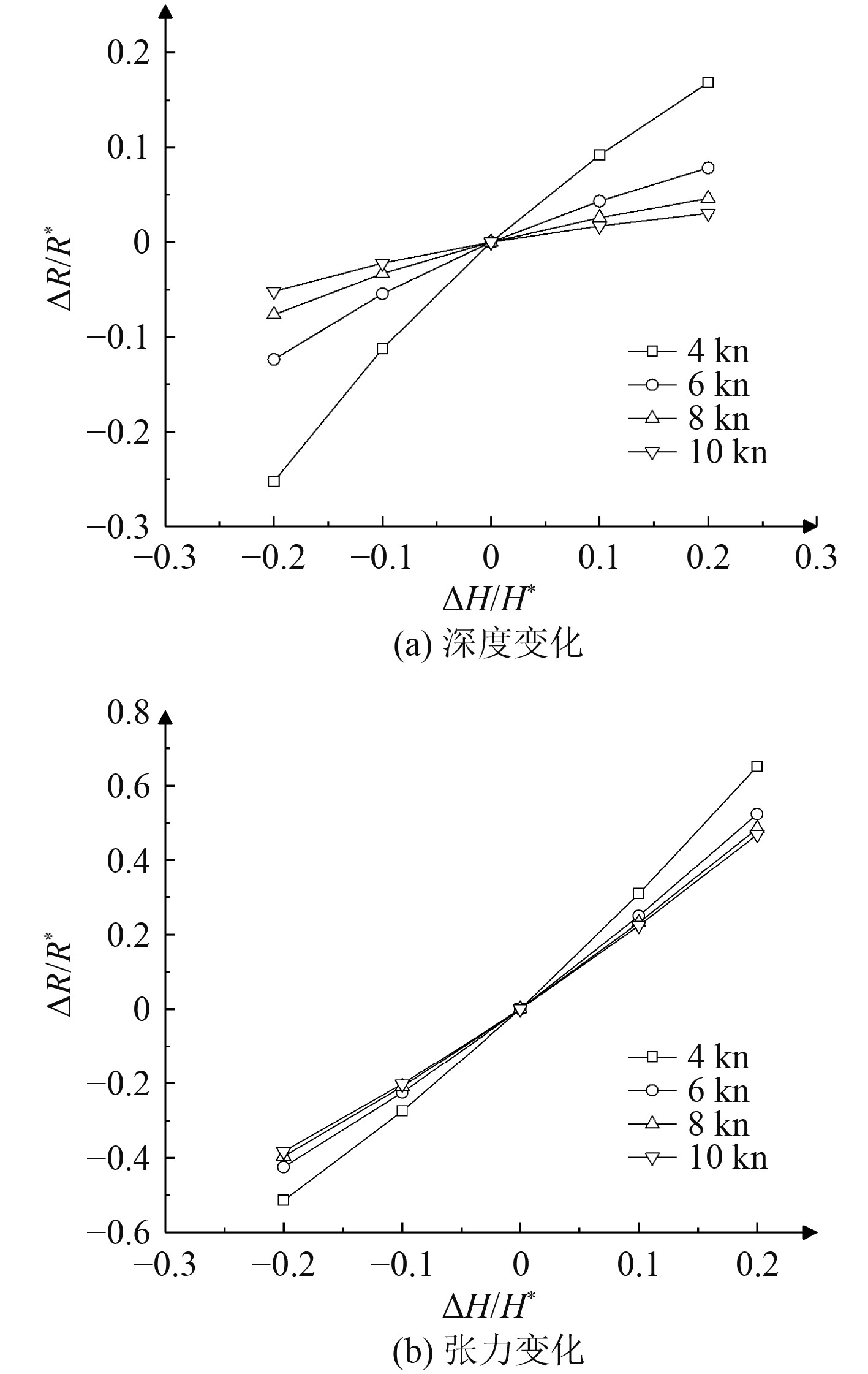
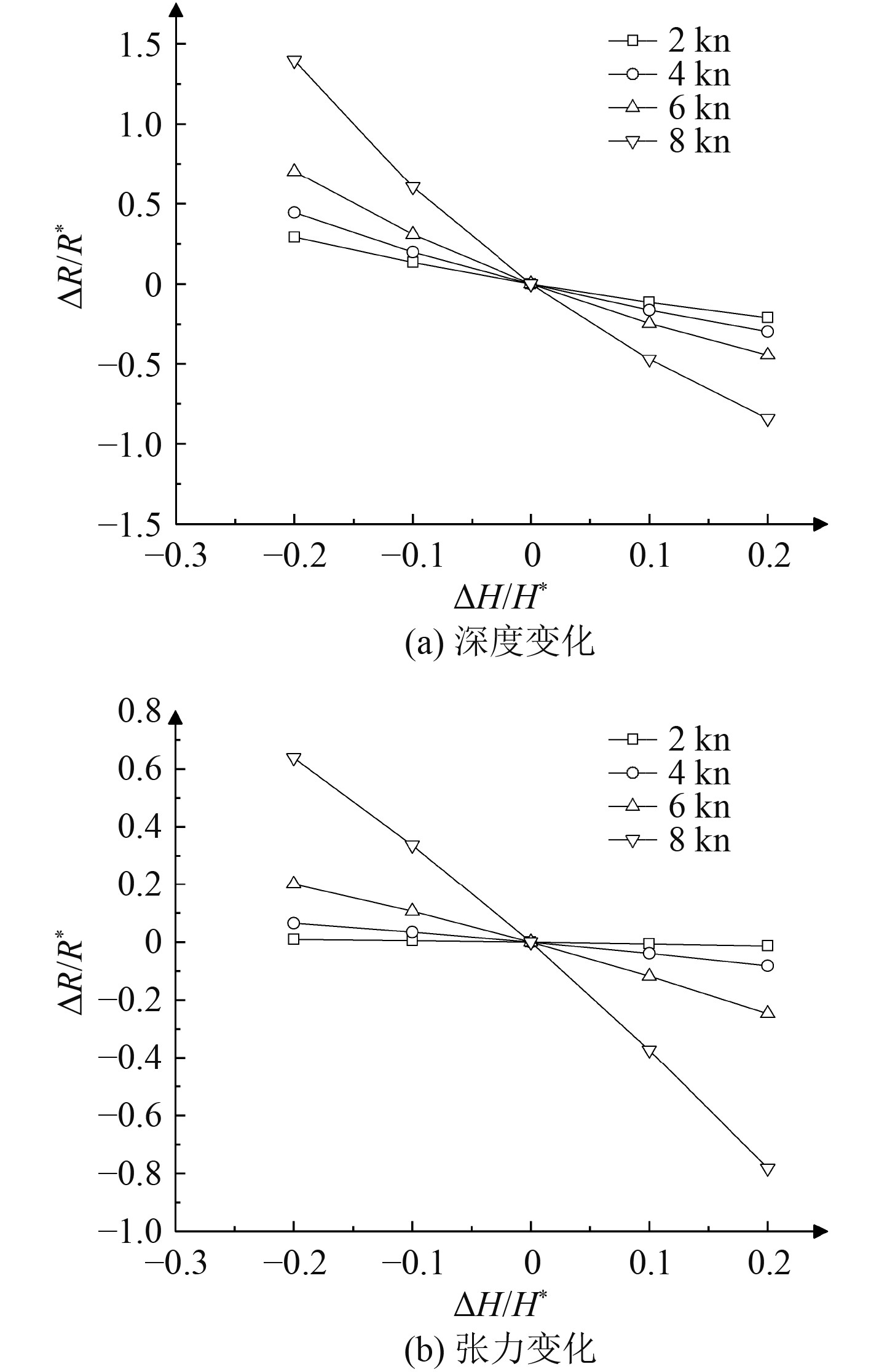
图6和图7所示分别为潜器做加速运动和减速运动时运动响应与潜器变速度的敏感性。其中纵坐标为在不同速度变化区间下运动响应的相对误差值，横坐标为不同速度变化区间的相对误差值，敏感性参数P就是纵坐标与横坐标的比值。对于加速状态的深度变化与张力变化，加速区间为2～4 kn时P的绝对值最大，对于减速状态的深度变化与张力变化，减速速区间为10～8 kn时P的绝对值最大。

为了便于分析，本文对于加速运动和减速运动时运动响应与结构参数之间敏感性指数P关系通过表2呈现。可知，潜器做加速运动或减速运动时各参数之间敏感性指数绝对值趋势是一致，但是减速运动时P的绝对值明显要大于加速运动，潜器做减速运动更容易受到参数的影响。潜器速度变化的敏感性指数的绝对值最大，对深度变化和张力变化的影响最大，其次是拖曳缆长度；而拖曳缆法向阻力系数对于深度变化的影响最小，对张力变化的影响可忽略。因此从敏感性的角度考虑对潜器变速运动中拖曳系统运动响应的调整时，顺序是潜器变速度、拖曳缆长度、拖曳缆法向阻力系数。

2.4 回转运动敏感性系数计算

分别对潜器回转速度2、4、6、8 kn，回转半径200 m为基准状态，在拖曳操纵参数和结构参数基准值的基础上分别取(−20%、−10%、+10%、+20%)作为该变量展开分析。

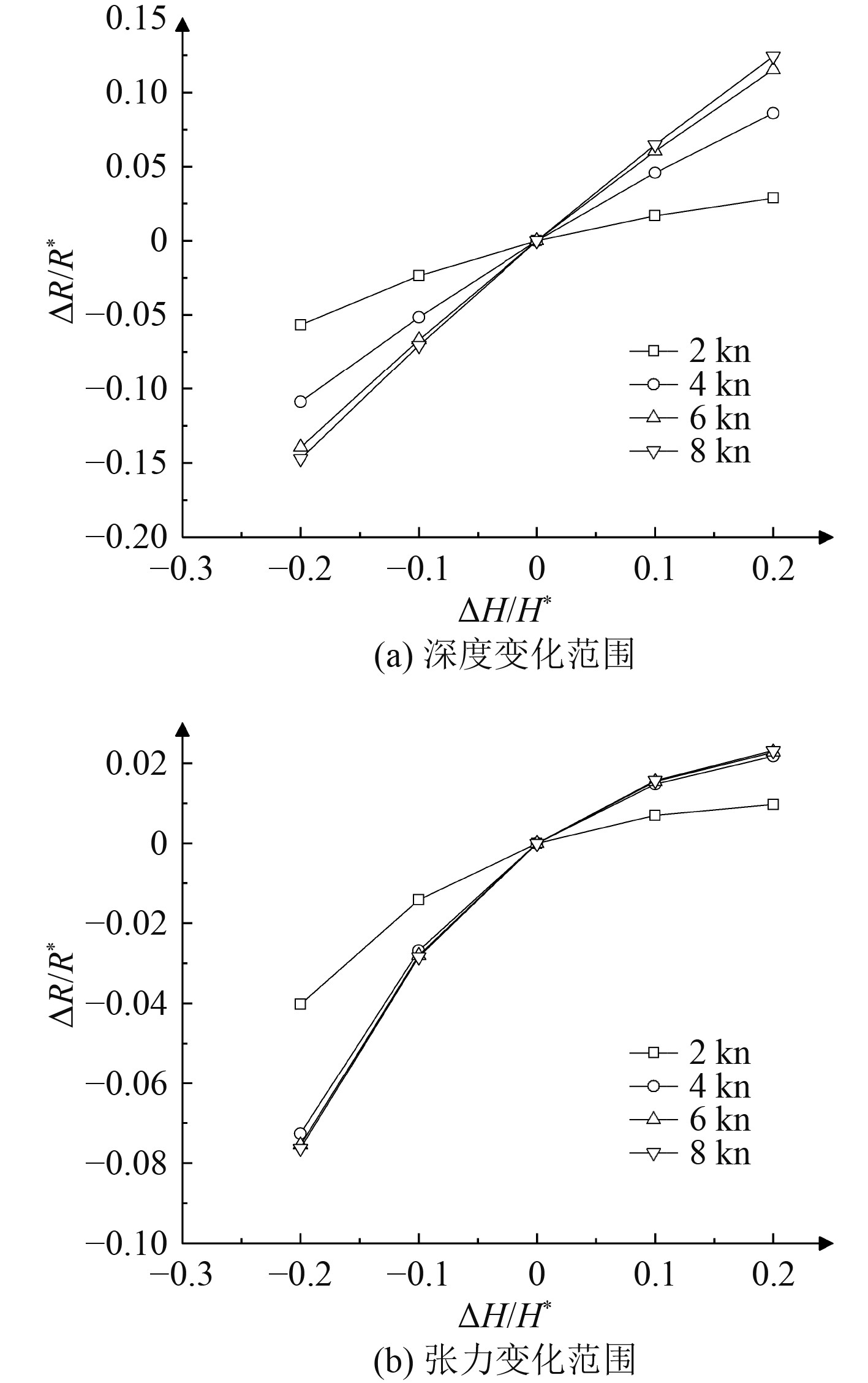
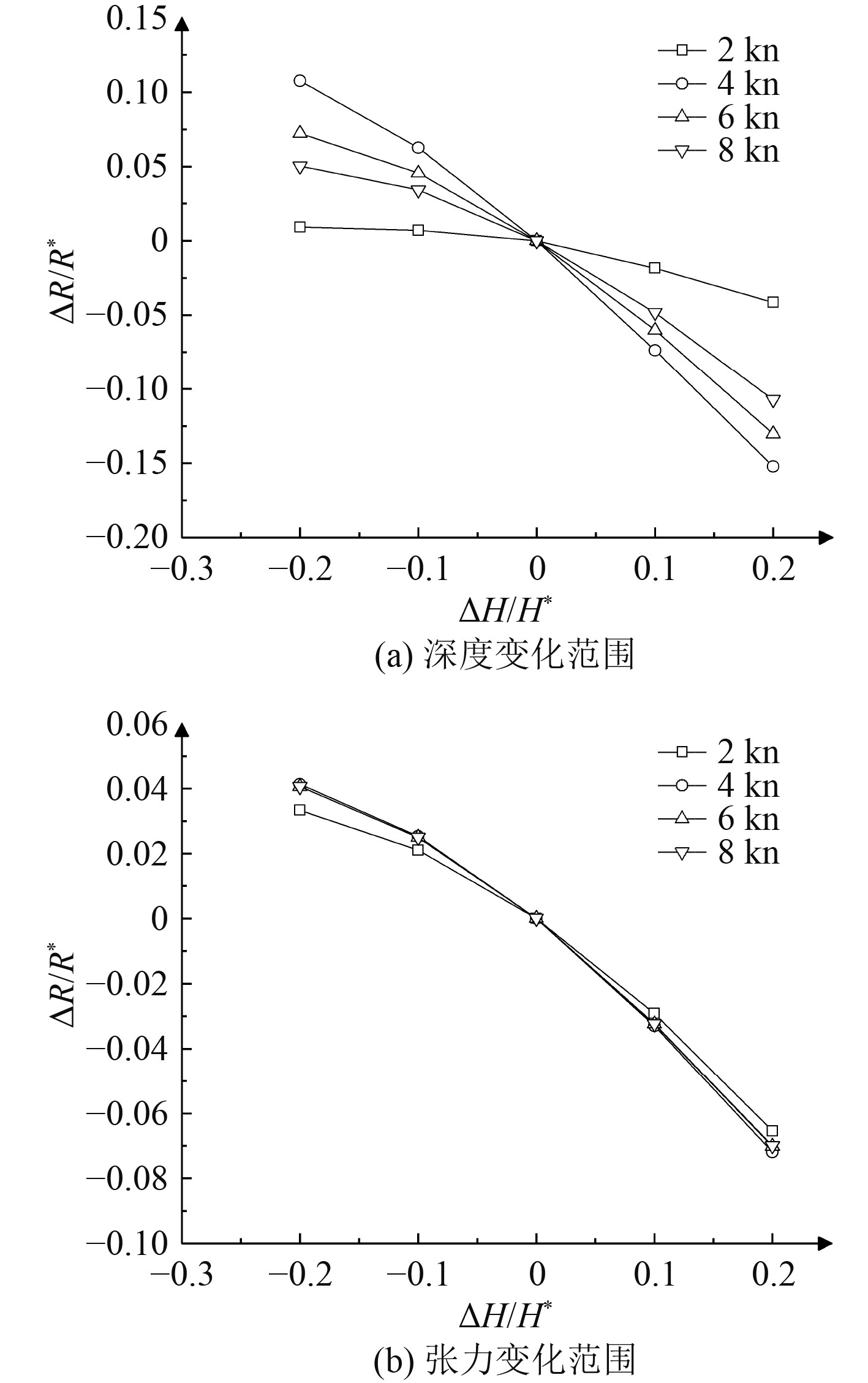
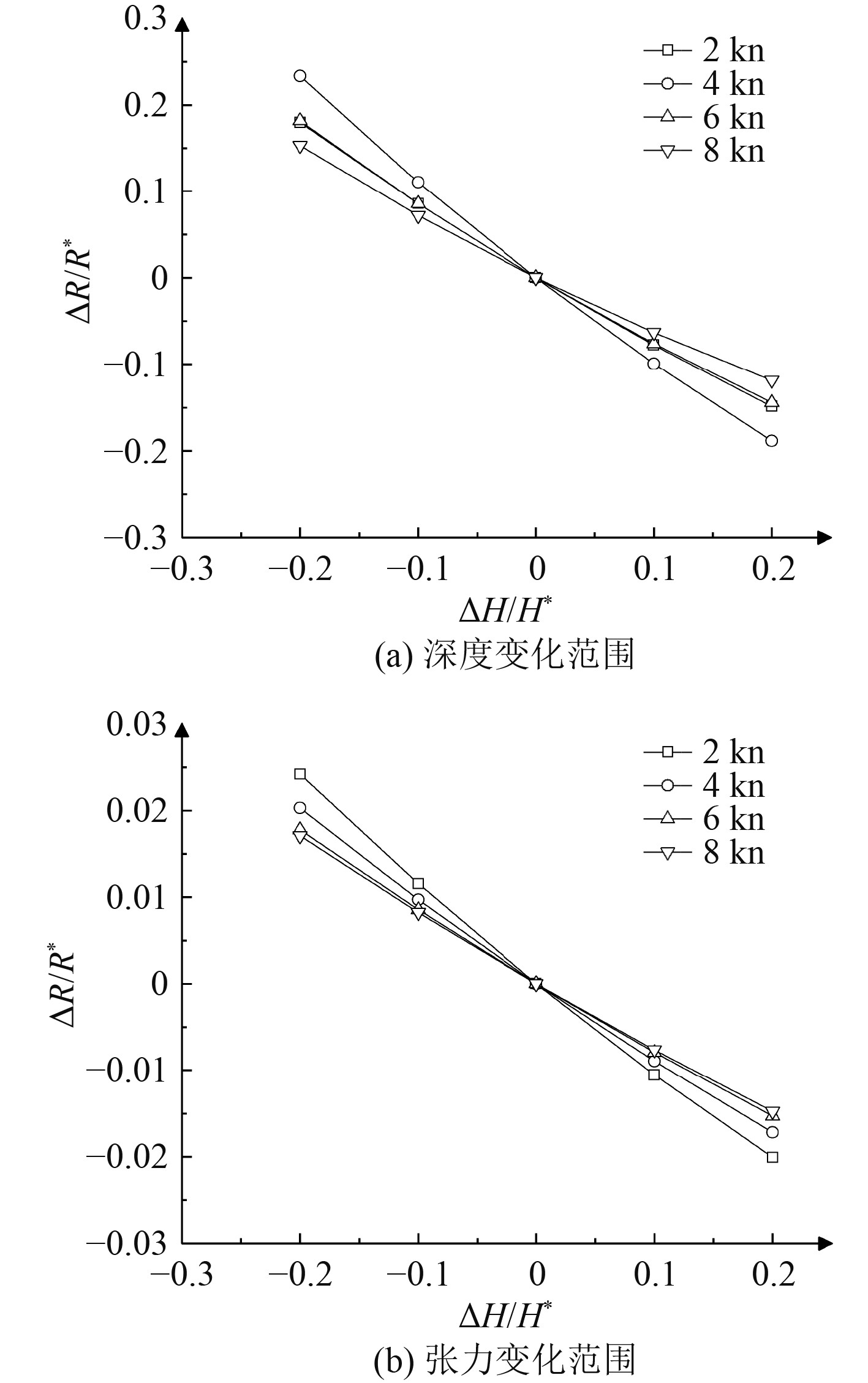
如图8～图10所示，分别为潜器做回转运动时运动响应与潜器变速度的敏感性。其中纵坐标为在拖曳操纵参数或结构参数下运动响应的相对误差值，横坐标为拖曳操纵参数或结构参数的相对误差值，敏感性参数P就是纵坐标与横坐标的比值。对于回转半径，深度变化范围和张力变化范围的敏感性指数P在回转速度为8 kn时最大；对于拖曳缆长度，深度变化范围和张力变化范围的敏感性指数P在回转速度为2 kn时最小，对于拖曳缆法向阻力系数，深度变化范围和张力变化范围的敏感性指数P在回转速度为8 kn时最小。可知不同回转速度会对敏感性指数产生影响，在不同速度下调节拖曳操纵参数和结构参数的效果具有差异性。

如表3所示，回转运动时运动响应系数与结构参数之间敏感性指数P关系。潜器做回转运动时，对于深度变化范围影响最大是拖曳缆法向阻力系数的变化，因为其敏感性指数P的绝对值最大，其次是拖曳缆缆长和回转半径；对于张力变化，回转半径的敏感性指数P的绝对值最大则影响最大，其次是拖曳缆长度和拖曳缆法向阻力系数。因此从敏感性的角度考虑对潜器回转运动中深度变化范围的调整，顺序是拖曳缆法向阻力系数、拖曳缆缆长和回转半径；对潜器回转运动中张力变化范围的调整，回转半径、拖曳缆法向阻力系数和拖曳缆缆长。

3 结　语

1）对于潜器做变速操纵运动，潜器减速时与加速时相比更容易受到参数变化的影响，从敏感性的角度考虑对潜器变速运动中拖曳系统运动响应的调整时，顺序是潜器变速度、拖曳缆长度、拖曳缆法向阻力系数。

2）对于潜器做回转操纵运动，从敏感性的角度考虑对潜器回转运动中深度变化范围的调整，顺序是拖曳缆法向阻力系数、拖曳缆缆长和回转半径；对潜器回转运动中张力变化范围的调整，回转半径、拖曳缆法向阻力系数和拖曳缆缆长。