0 引　言

船舶作为重要的交通运输工具，依靠船舶运输的国际贸易量目前已达到80％，如何实现船舶航运业经济高效化、节能绿色化是大家关注并亟待解决的重要问题。自2008年以来，国际海事组织IMO提出了新船能效设计指数（EEDI） 的概念并强制实施，船舶行业承担了重要的节能减排任务。为了实现船舶的节能减排，通过型线优化来减少船体在波浪中的阻力是重要路径之一。在Gerritsma等^[1]的方法中，船舶在无波浪条件的水中航行产生的波浪称作定常兴波，而在有波浪条件的海况中航行所产生的波浪就称作非定常兴波，这是船舶产生波浪增阻的一个重要因素。同时考虑到静水中的阻力优化变形趋势往往与波浪增阻的优化变形趋势不一致，因此在考虑船舶在波浪中的阻力性能优化问题中应该将兴波阻力与波浪增阻结合起来。

如今船体型线越来越多地基于数值模拟，并结合各类变形技术、近似模型和优化算法进行优化。刘鑫旺等^[2]基于优化设计软件OPTShip-SJTU和势流求解器NMShip-SJTU，以某豪华邮轮为原始船型，通过自由变形方法，对船首、水线、船尾等位置进行局部变形，对其兴波阻力采用带精英策略的非主导排序遗传算法（NSGA-II）进行优化。Yin等^[3]以S60船的前部为优化对象，结合局部参数映射变形法，采用Rankine源法计算其兴波阻力，对比了非线性规划法、非主导排序遗传算法和粒子群优化算法，发现智能优化算法在船型寻优上具有更好的全局搜索能力。魏斯行等^[4]对某多用途船首尾型线以船舶静水中的阻力性能以及桨盘面伴流不均匀度作为优化目标，采用RBF方法进行变换，利用优化拉丁超立方法设计计算样本，结合SHIPFLOW软件计算水动力性能并引入Kriging近似模型，用NSGA-II优化算法完成整个型线优化流程。冯佰威等^[5]采用径向基函数法（RBF），通过Neumann-Michell理论求解器结合NSGA-II算法以兴波阻力为目标对KCS船进行了优化。王超等^[6]基于iSIGHT优化设计平台和计算流体力学软件SHIPFLOW，以最小兴波阻力为目标，利用融合变换法对某内河集装箱船球鼻首区域进行变形，通过遗传算法与序列二次规划法相结合的混合算法寻优。沈冠之等^[7]基于修正函数法对双燃料散货船的船型进行了优化。其优化思路是先对兴波阻力进行优化，然后在兴波阻力较优的方案上再对总阻力和推进效率的优化。但目前基于势流方法的波浪中阻力性能的优化主要还集中在静水兴波阻力和单独的波浪增阻上。

依据KCS船在顶浪规则波中的实验结果^[8]，为降低其阻力峰值，本文结合RBF变形技术、SHIPFLOW中全非线性的时域边界元方法的水动力性能求解器、Kriging近似模型和多岛遗传算法对KCS船在波浪增阻系数峰值处的1.15倍船长的顶浪规则波中的阻力性能进行了优化，为波浪中的船体阻力优化提供借鉴。

1 船型优化方法 1.1 型线变换技术

利用RBF变形技术^[9]可以在保持典型特征不变的同时通过改变控制点的位移来实现船体曲面变形。控制点的位移$ S\left(x\right) $可以表达为：

$ S\left(x\right)=\sum _{i=1}^{n}{\lambda }_{i}\varphi \left(||\mathit{x}-{\mathit{x}}_{i}||\right)+p\left(\mathit{x}\right)，$

(1)

$ p\left(\mathit{x}\right)={c}_{1}x+{c}_{2}y+{c}_{3}z+{c}_{4}。$

(2)

式中：$ {\mathit{x}}_{i} $为径向基中心点的空间坐标；$ ||\mathit{x}-{\mathit{x}}_{i}||$为到径向基中心点的欧式距离；$ n $为控制点的个数；$ p\left(\mathit{x}\right) $为旋转、比例、剪切和平移变换；$ {\lambda }_{i} $、$ {c}_{i} $为控制点控制船体曲面变形的系数；$ \varphi $为径向基函数。该函数选取为：

$ \varphi \left(r\right)=(1-r{)}^{4}(4r+1)。$

(3)

求解式中$ {\lambda }_{i} $和$ {c}_{i} $的方程如下：

$ \left(\begin{array}{c}\boldsymbol{f}\\ 0\end{array}\right)=\left(\begin{array}{cc}\boldsymbol{M}& \boldsymbol{P}\\ {\boldsymbol{P}}^{\rm T}& 0\end{array}\right)\left(\begin{array}{c}{\boldsymbol \lambda }\\ \boldsymbol{c}\end{array}\right)。$

(4)

式中：$ {\boldsymbol{\lambda}} = [\lambda_1,\lambda_2,\dots,\lambda_n]^{\rm{T}} $；$ {\boldsymbol c} = [c_1,c_2,c_3,c_4]^{\rm{T}} $；$ {\boldsymbol f} = [S\left({\mathit{x}}_{1}\right), S\left({\mathit{x}}_{2}\right),\dots ,S\left({\mathit{x}}_{n}\right){]}^{\rm T} $为各控制点坐标位移变化量。

$ 28{\boldsymbol M}_{j,i}=\varphi \left(||\mathit{x}_{j}-\mathit{x}_{i}||\right)\mathrm{},i,j=\mathrm{1,2},\dots ,n ，$

(5)

$ {\boldsymbol P}=\left[\begin{array}{cc}{\mathit{x}}_{1}& 1\\ {\mathit{x}}_{2}& 1\\ \vdots & \vdots \\ {\mathit{x}}_{n}& 1\end{array}\right] 。$

(6)

将所有控制点的变形的前后坐标代入求解以得到系数$ {\lambda }_{i} $、$ {c}_{i} $。然后将剩余的船体曲面型值点代入控制点位移函数中，即可形成新的曲面。

1.2 水动力性能求解器

在优化流程中为了保证计算效率，使用SHIPFLOW作为水动力性能求解器。其MOTION模块采用全非线性的时域边界元方法^{[10 - 11]}，可用于计算船舶在波浪中的运动。该方法对自由表面和船体的湿表面施加与时间相关的非线性边界条件，求解每个时间步长的边界值问题。其内部三维域上的自由面上的动力学和运动学边界条件为：

$ \left\{\begin{array}{l}\displaystyle\frac{{\rm d}\varphi }{{\rm d}t}=-\displaystyle\frac{1}{2}(\nabla \varphi {)}^{2}-g\eta +\\ \displaystyle\frac{\partial \varphi }{\partial z}\left(\displaystyle\frac{\partial \varphi }{\partial z}-\displaystyle\frac{\partial \varphi }{\partial x}\displaystyle\frac{\partial \eta }{\partial x}-\displaystyle\frac{\partial \varphi }{\partial y}\displaystyle\frac{\partial \eta }{\partial y}\right)-v(x,y)\varphi，\\\displaystyle\frac{{\rm d}\eta }{{\rm d}t}=\displaystyle\frac{\partial \varphi }{\partial z}-\displaystyle\frac{\partial \varphi }{\partial x}\displaystyle\frac{\partial \eta }{\partial x}-\displaystyle\frac{\partial \varphi }{\partial y}\displaystyle\frac{\partial \eta }{\partial y}-v(x,y)\eta。\end{array}\right. $

(7)

式中：$ \varphi $为速度势；$ \eta $为自由表面表达式；$ v(x,y) $为自由表面阻尼因子；用于防止在边界上发生反射。

垂直边界上则需要满足Dirichlet条件或Neumann条件；在物面和下底面的边界条件为Neumann条件，分别为：

$ \left\{\begin{array}{l}\displaystyle\frac{\partial \varphi }{\partial n}={\overrightarrow{V}}_{p}\cdot \overrightarrow{n}，\\ \displaystyle\frac{\partial \varphi }{\partial n}=0 。\end{array}\right. $

(8)

1.3 近似模型

近似模型的构建首先用拉丁超立方采样方法^[12]进行采样，该方法通过采样值来有效反映随机变量在空间中整体分布，能够保证采样点将覆盖所有的采样区域。

在此基础上利用Kriging模型^[13]构建近似模型，对样本外的值进行预测。该模型是对已知样本响应值的线性加权和，对于待测点的响应预测值表达如下：

$ 40\widehat{y}\left(x\right)={\sum }_{i=1}^{n}{w}_{i}{y}_{i}。$

(9)

式中：n为已知样本点的个数；$ {w}_{i} $、$ {y}_{i} $分别为对应样本的加权系数和响应值。

在Kriging模型的构建中需要假定待测点和样本点的响应值满足高斯静态随机过程，在无偏估计的前提下，均方差最小。采用拉格朗日乘子法可以得到方程：

$ \left\{\begin{array}{l}{\displaystyle\sum }_{j=1}^{n}{w}_{j}R({x}_{i},{x}_{j})+\displaystyle\frac{\mu }{2{\sigma }^{2}}=R({x}_{i},x)，\\ {\displaystyle\sum }_{j=1}^{n}{w}_{j}=1。\end{array}\right. $

(10)

式中：$ R({x}_{i},{x}_{j}) $为$ {x}_{i} $和$ {x}_{j} $之间空间相关性的相关函数；$ \mu $为拉格朗日乘子；$ {\sigma }^{2} $为方差。

求解式(10)并将结果代入式(9)即可得到Kriging近似模型待测点的响应预测值函数。

1.4 优化算法

多岛遗传算法^[14]对遗传算法进行了一定的改进。该方法将一个大群体划分为几个称为“岛屿”的子群体，对每个子群体分别进行遗传运算。这些岛屿上的个体会定期迁移到其他岛屿，从而维持了岛屿上的个体多样性。

2 KCS船阻力优化 2.1 优化对象

优化对象为KCS船模，其缩尺比为1∶37.9。表1为实船和缩尺模型船的主尺度。

优化工况为实船的设计航速24 kn和设计吃水10.8 m，船模工况根据缩尺比换算得到。依据KCS船在顶浪规则波中的实验结果^[8]，选取波长船长比为1.15，波高为波长1/60的规则波，以顶浪时摩擦阻力、兴波阻力以及波浪增阻之和最小为优化目标对KCS船体首尾进行优化。RBF变形共取7个可变控制点选取如图1红点所示，分别为船首及后续进流段5个，船尾及去流段2个。

2.2 水动力性能计算

在SHIPFLOW网格尺寸的选取上，在静水工况中使用粗中细3套网格对KCS船的阻力进行计算，结果如表2所示。根据尹含SHIPFLOW的计算结果^[15]，兴波阻力系数为0.312×10⁻³，而万超^[16]得到的计算结果为0.543×10⁻³，因而表2中计算得到的兴波阻力系数在这区间内应当是合理的。在本文的计算中发现相比中网格，使用细网格对计算资源的消耗会明显增加，并且万超提到使用粗网格计算稳定性较差，选择中网格能保证一定的计算稳定性并保持计算效率，因此在后续SHIPFLOW的计算中均采用中网格。

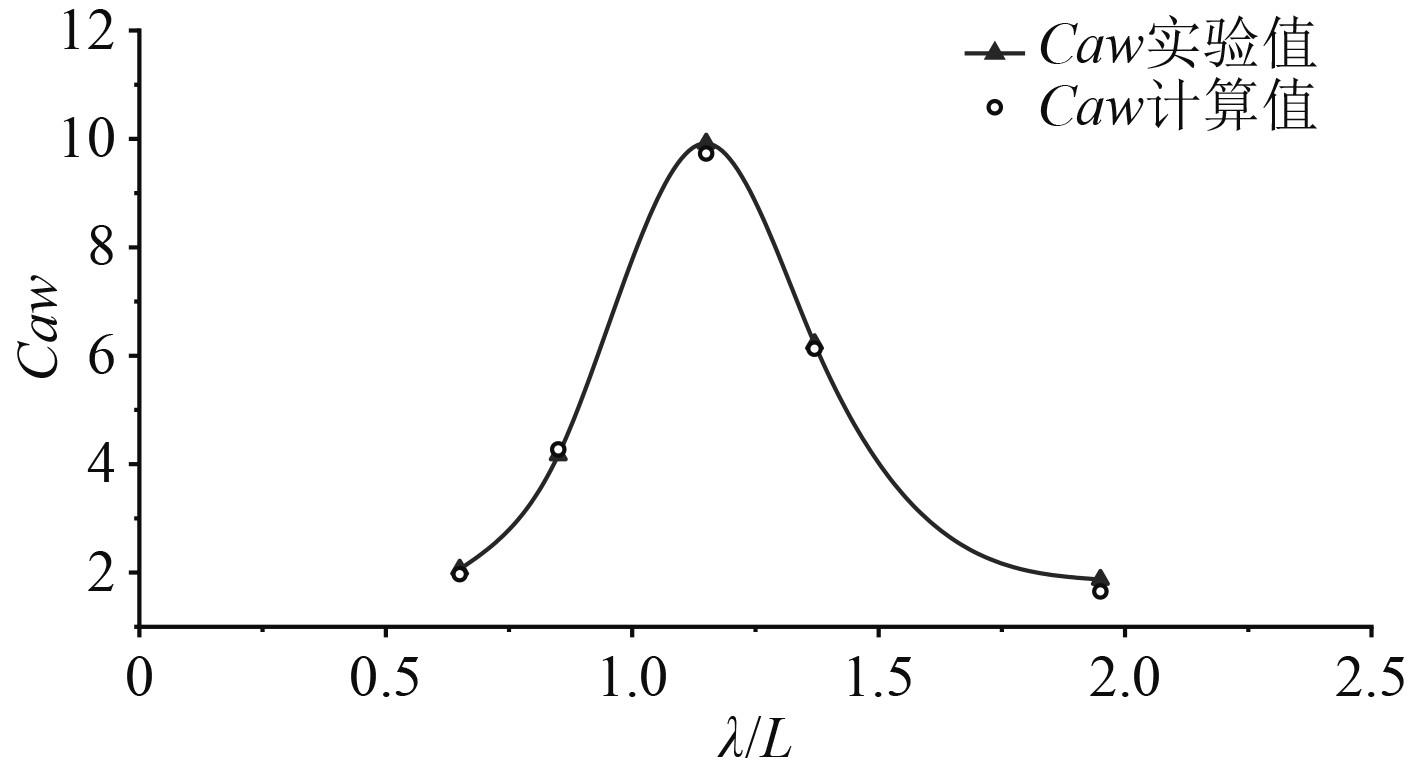
使用SHIPFLOW计算不同波长船长比下的波浪增阻系数，其计算结果如表3和图2所示。可以看到SHIPFLOW的波浪增阻计算结果与实验值^[8]吻合较好。

2.3 结果与分析

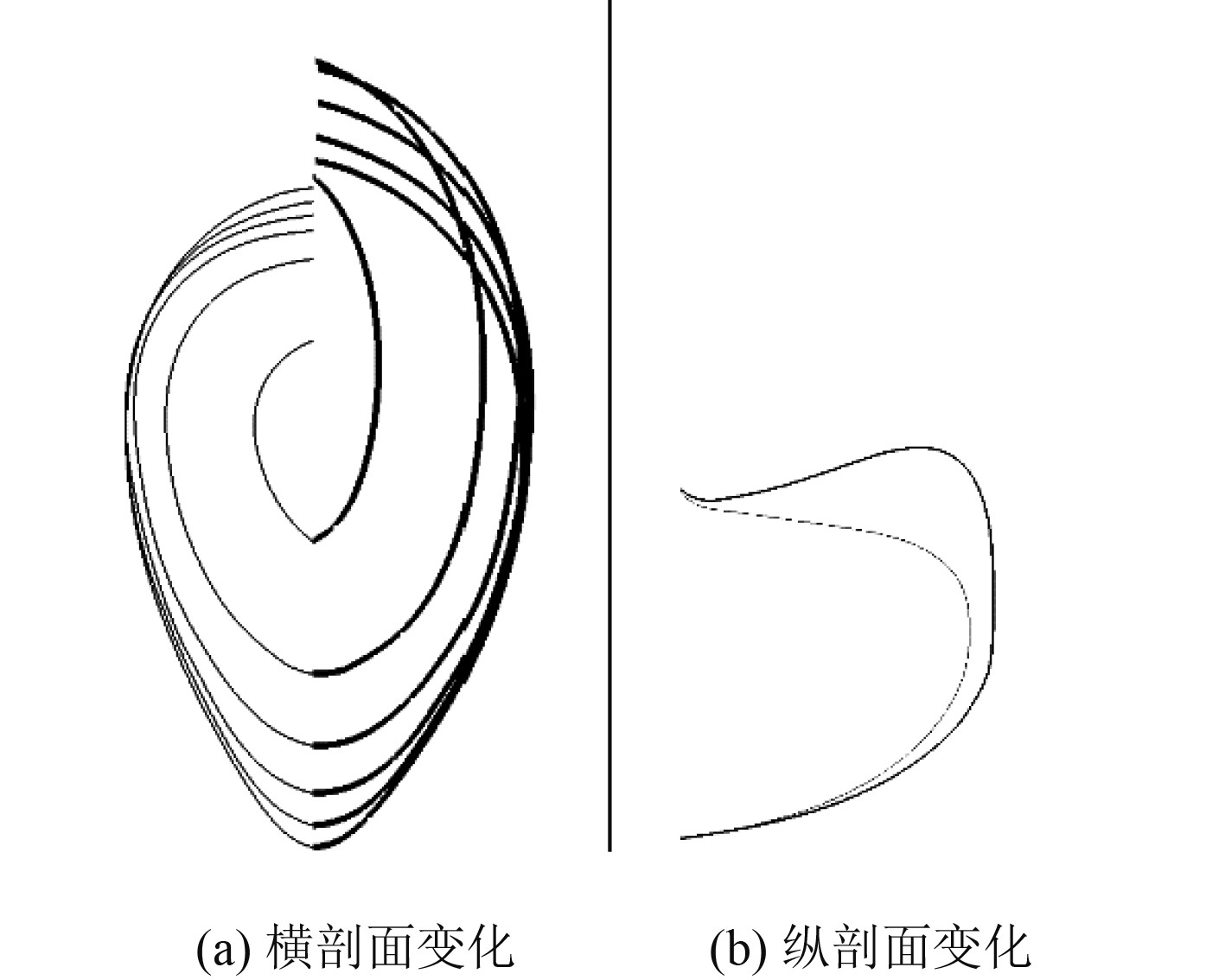
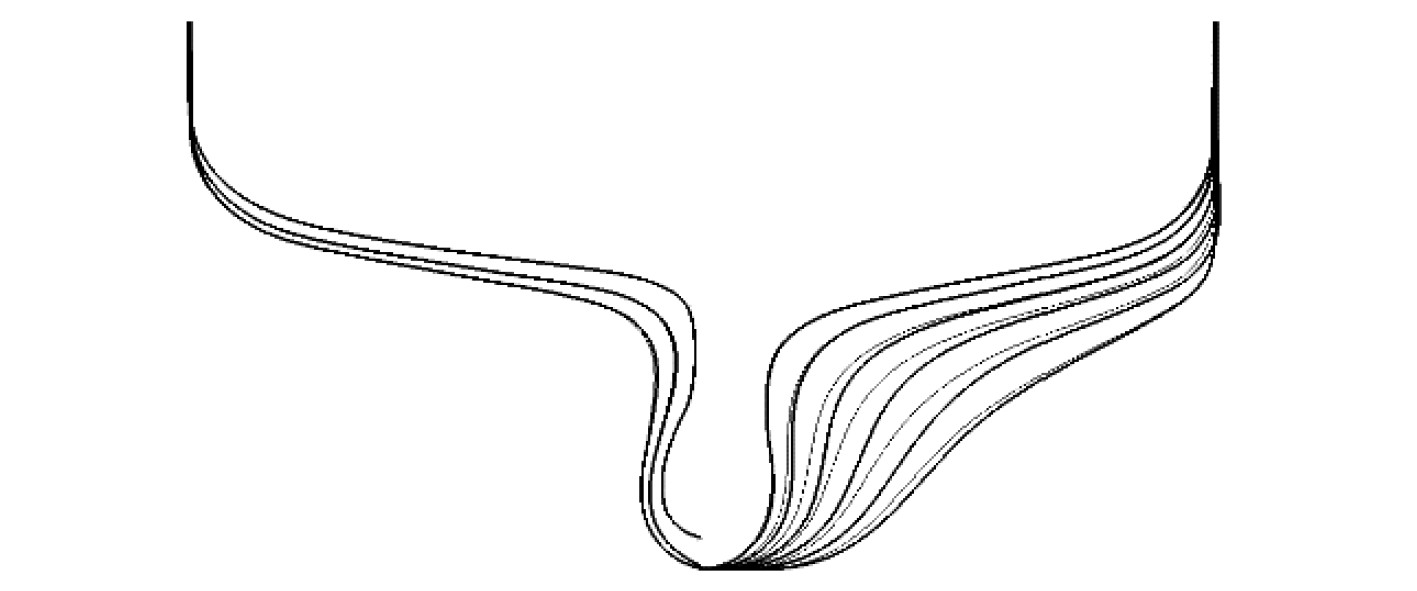
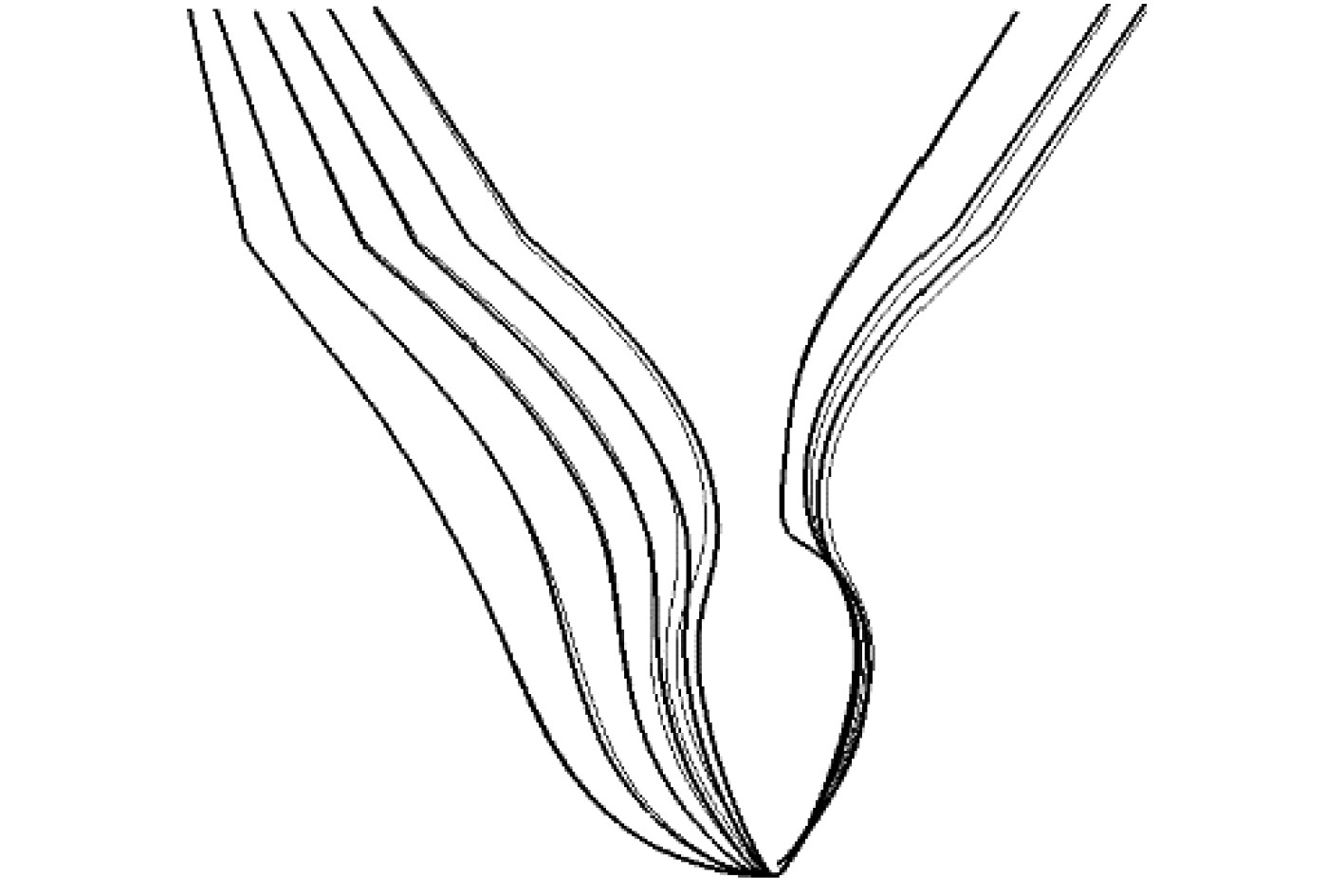
变换后的型线如图3 ～ 图5所示，粗实线为优化后的船体型线，细实线为KCS船的型线。可以看出，球鼻艏长度伸展了8.34%；其横剖面相较原船明显增大，其宽度增加了15.40%；其鼻尖有明显的向上隆起，高度最大增加了32.11%。进流段在靠近球鼻艏有所收窄，如图4所示，2个控制点从前到后分别在船宽方向收缩了1.93%和扩展了0.69%船宽和的船宽。去流段型线变换结果如图5所示，其去流段在离船尾稍远处变得更加丰满，2个控制点分别扩展了2.89%和收缩了0.21%的船宽。

SHIPFLOW的计算结果如表4所示。优化后的船型相比原船型其摩擦阻力增加了0.51%，波浪增阻和兴波阻力之和减少了10.12%，波浪增阻系数减少了15.89%。都换算成阻力后发现波浪增阻减少了6.07 N，表明其阻力优化主要集中在波浪增阻上。在运动幅值上，优化后的船型相比原船型垂荡RAO减小了0.43%，纵摇RAO减小了0.39%。波浪增阻的减少部分归因于垂荡和纵摇RAO的减少。

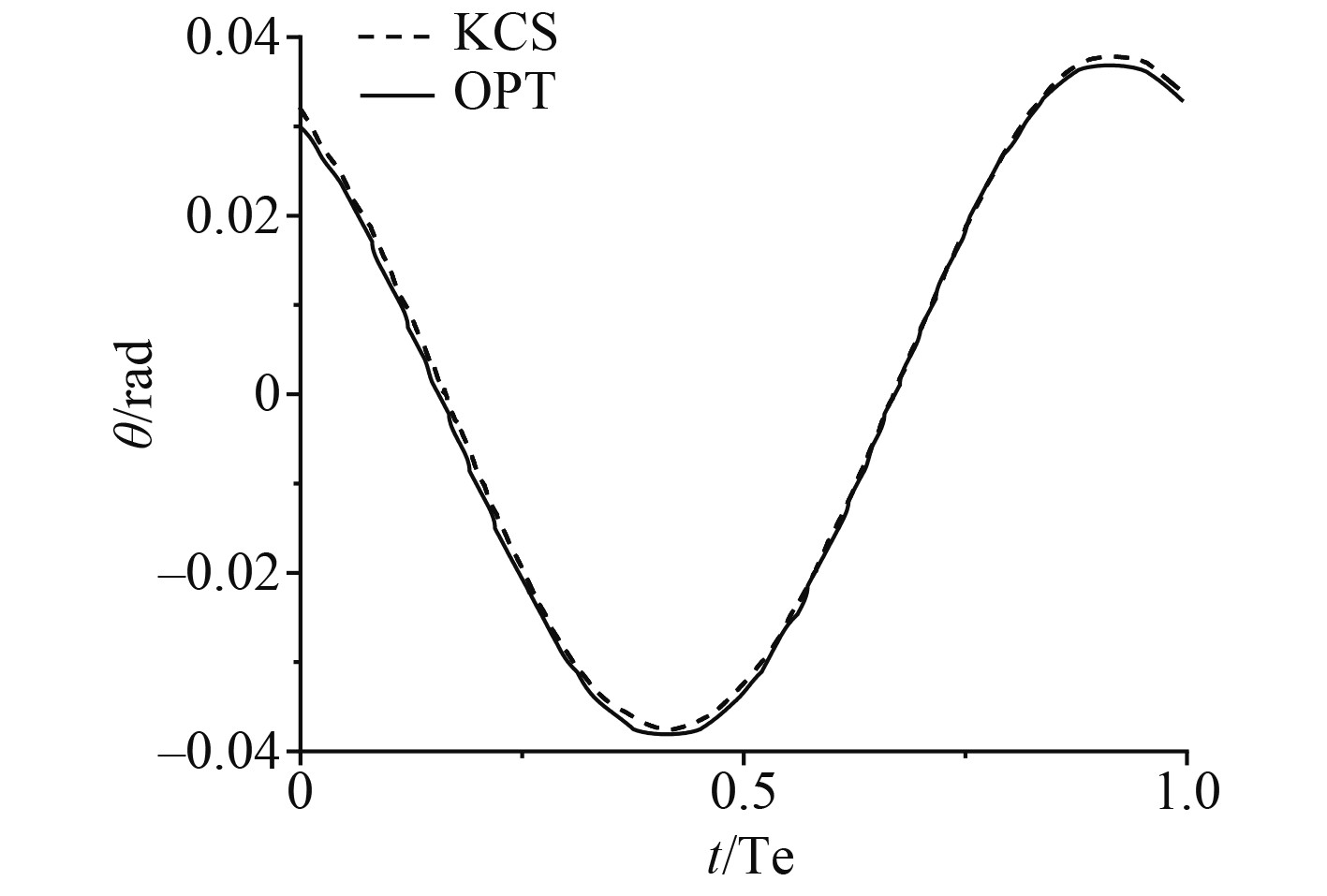
图6和图7为SHIPFLOW计算稳定后的运动时历。可以看到，优化后的船舶相比原船型在运动响应上变化不大，在垂荡的谷值处和纵摇的峰值处有一定的改善。

STAR-CCM+计算采用可实现的$ k-\varepsilon $两层湍流模型，y+值在60及以上。计算结果如表5所示，优化后的船型相比KCS原船静水摩擦阻力增加了0.4%，在波浪中的压阻力减少了7.84%，总阻力减少了4.48%，波浪增阻系数减少了18.08%，这与SHIPFLOW计算得到的趋势相同。图8稳定后的总阻力系数时历也说明了在一个波浪周期内优化后的船型相比KCS原船其总阻力明显减小。

3 结　语

本文以KCS船为研究对象，为降低其在顶浪规则波中的阻力峰值，以摩擦阻力、兴波阻力与波浪增阻之和为优化目标，对KCS船在波长为1.15倍船长的顶浪规则波中的阻力性能进行了优化。利用RBF变形技术对船体型线进行变化，使用SHIPFLOW全非线性的时域边界元方法的水动力性能求解器预报船体的水动力性能。在此基础上结合Kriging近似模型以减少SHIPFLOW数值模拟的次数，并用多岛遗传算法进行优化。SHIPFLOW和STAR-CCM+的计算结果表明优化后的船型相比KCS原船在阻力性能上有所提升，波浪增阻有明显的减少，在顶浪规则波中的阻力性能优化中波浪增阻占主导成分。优化后的船型相比原船型，总阻力减少了4.48%，波浪增阻减少了18.08%。由此可见，结合RBF变形技术、SHIPFLOW中全非线性的时域边界元方法的水动力性能求解器、Kriging近似模型和多岛遗传算法可以得到波浪中阻力性能较优的优化船型。