2. 上海交通大学 机械与动力工程学院,上海 200000
2. School of Mechanical Engineering, Shanghai Jiaotong University, Shanghai 200000, China
水下航行器辐射噪声信号研究涉及领域广泛,它是水声对抗的基础,也是被动式声探测和识别设备的主要信号源。在水声领域的研究过程中需要大量信号样本来进行特性的对比、统计、测试。然而实测水下航行器噪声需要场地,经费,人力物力以及时间成本,且参数不可控,很难获得实验所需要的大量信号数据。因此,水下航行器噪声信号的模拟仿真具有重要的现实意义和作战意义。
目前,对于水下航行器辐射噪声的生成主要方法是分析船舶噪声的功率谱特性,对照实测信号的谱特征,对噪声功率谱进行构造[1]。从水下航行器辐射噪声功率谱中各噪声分量的产生机理出发,将水下航行器噪声信号拆分成线谱,连续谱以及调制谱的仿真[2]。对于连续谱信号,将高斯白噪声通过设计好的FIR滤波器获得符合功率谱形状的连续谱[3-4]。调制谱主要通过demon谱分析获得。何正耀等[5]对信号进行功率谱分析和demon谱分析,研究了舰船辐射噪声功率谱的声学特征。
由于水声信道的作用,信号在从声源到达接收点的过程中经过不同路径传播,从而产生衰减,相位变化以及幅频变化。为了准确获取信号所携带的信息,需要对水声信道的传播特性展开研究。涂峰[6]分析了Bellhop的数学原理,利用Matlab对水声信道的本征路径模型进行了仿真。李庆来[7]基于射线理论对分层非均匀浅海声场进行数值预报。孙博等[8]和丁浩等[9]利用虚源法建立浅海水声信道模型,对于信道的多普勒频移采用的不同的数学模型进行仿真。
为了开发极地地区的丰富资源,近年来,多个国家开展了对极地区域的研究。由于极地地区特殊的水文环境,加上冰面的覆盖,形成了极地特殊的水下声场环境。因此对冰面展开研究是必要的。李贞刚[10]对光滑界面和粗糙界面的冰面不同特性进行了阐述,杨威[11]和明平寿[12]都基于射线理论结合B-T冰水界面模型进行了冰下声传播仿真计算。
本文主要研究水下航行器辐射噪声的建模以及信号经过海洋信道传播后的声学特性。在水下航行器辐射噪声模拟方面,本文采用任意形状频率响应滤波器设计方法,设计FIR滤波器,同时用经验公式模拟调制谱分量以及线谱分量,使仿真获得的噪声信号具有较高逼真度。然后分别利用Bellhop方法和虚源法模拟水声信道传播后的水下航行器辐射噪声,2种方法计算结果基本一致。运用B-T冰水模型计算出冰面反射系数,导入到Bellhop声学工具箱中进行冰下水声信道仿真,开展了辐射噪声信号在冰下水声信道中的传播特性研究。
1 水下航行器辐射噪声特性水下航行器的辐射噪声由螺旋桨噪声、机械噪声以及水动力噪声组成。螺旋桨噪声产生于航行器外,当航速较低时,螺旋桨未发生空化现象,此时机械噪声最高,其次是螺旋桨噪声;当航速较高时,会发生空泡现象,此时螺旋桨噪声就会成为水下航行器噪声的最主要成分。机械噪声在水下航行器噪声的低频段表现为单频线谱,其频率与机械设备的基频和谐频有关。水动力噪声是指水下航行器与周边流体发生相对运动时,流体作用于外壳产生的噪声,随着航速的升高水动力噪声淹没到螺旋桨噪声中。
2 水下航行器辐射噪声及水下信道仿真方法基于上文对水下航行器噪声各噪声成分的分析,将噪声模拟分为对连续谱噪声,线谱噪声以及调制谱噪声的模拟。水下航行器辐射噪声,其时域波形可描述为:
| $ S(t) = [1 + a(t)] \times {g_x}(t) + {g_L}(t)。$ | (1) |
式中:
螺旋桨连续谱噪声的功率谱级在低频段随着频率增加而增加,在高频段以−6 dB/Oct衰减,会在10~
| $ SL = \left\{ \begin{gathered} S{L_0} - {a_1}\lg \left(\frac{{{f_0}}}{f}\right),\quad {f_L} \leqslant f \leqslant {f_0} ,\\ S{L_0},\quad f = {f_0} ,\\ S{L_0} + {a_2}\lg \left(\frac{f}{{{f_0}}}\right),\quad {f_0} \leqslant f \leqslant {f_H} 。\\ \end{gathered} \right. $ | (2) |
式中:
对船舶连续谱噪声进行估计后,调用Matlab的FIR2函数设计任意形状频率响应的FIR滤波器,提取其中的谱峰频率
线谱分量主要集中在低频部分,它是能量集中的体现,具有很高的辨识度。可以采用周期性正弦信号来进行仿真,其数学表达式如下:
| $ {g_L}(t) = \sum\limits_{k = 1}^N {{A_k}\sin \left(2{\text π} {f_k}t + {\varphi _k}\right)}。$ | (3) |
式中:
线谱频率为
水下航行器辐射噪声拥有鲜明的节奏感,这是因为螺旋桨在水中旋转一周,每个叶片产生的噪声对连续信号具有调制作用。使得叶频整数倍上的频谱强度远大于轴频整数倍的频谱强度。这种调制信号可以通过DEMON谱分析提取,目前大多学者认为调制包络是具有随机幅度,相同形状,相同周期的脉冲性随机过程,数学模型为:
| $\begin{split} a(t) =&\sum\limits_{k = 1}^N {{A_1}{e^{ - pk}}\sin (2{\text π} k{f_1}t + {\varphi _1})} +\\ &\sum\limits_{i = 1}^M {{A_2}{e^{ - qi}}\sin (2{\text π} i{f_2}t + {\varphi _2})} 。\end{split}$ | (4) |
式中:
为了研究水声信道对于接收信号产生的干扰以及畸变,本文利用模拟获得的水下航行器辐射噪声与Bellhop模型相结合;首先配置Bellhop的海洋环境参数,设置海水表面为真空,插值方式选择线性插值;水底环境选择为声学半空间,平坦地形;计算信号的输出幅度和到达时间,以及传播路径。声速剖面采用典型深海Munk声速剖面。
同时,为了证明仿真的可靠性,利用文献[9]的虚源法和Xiao模型进行水声信道数值模拟。Xiao模型能反映Rice信道的各种物理性质,其接收信号数学模型为:
| $ r(t) = \sum\limits_{m = 1}^M {{\zeta _m}(t)x(t - {\tau _m})},$ | (5) |
| $ {\zeta _m}(t) = {u_{cm}}(t) + j{u_{sm}}(t) ,$ | (6) |
| ${u_{cm}}(t) =\frac{{{C_m} \left[ {\sqrt K \cos ( 2{\text π} {f_d}t\cos {\theta_m} + {\varphi _m} ) + \displaystyle\frac{1}{{\sqrt N }} \displaystyle\sum\limits_{n = 1}^N {\cos ( 2{\text π} {f_d}t \cos {\alpha _n} + {\varphi _n} )} } \right]}}{{\sqrt {1 + K} }} ,$ | (7) |
| $ {u_{sm}}(t) = \frac{{{C_m}\left[ {\sqrt K \sin (2{\text π} {f_d}t\cos {\theta _m} + {\varphi _m}) + \displaystyle\frac{1}{{\sqrt N }}\displaystyle\sum\limits_{n = 1}^N {\sin (2{\text π} {f_d}t\cos {\alpha _n} + {\varphi _n})} } \right]}}{{\sqrt {1 + K} }} 。$ | (8) |
式中:
虚源法把每一根声线等效为一个虚源所射出的直达声线,接收点处的信号便是这些声线的总和。其中主要分量称为本征声线。各本征声线的衰减系数为:
| $ \left\{ {\begin{array}{*{20}{l}} {{c_{n1}} = \displaystyle\frac{{V_1^nV_{2n1}^n}}{{{R_{n1}}}}} ,\\ {{c_{n2}} = \displaystyle\frac{{V_1^nV_{2n2}^{n + 1}}}{{{R_{n2}}}}},\\ {{c_{n3}} = \displaystyle\frac{{V_1^{n + 1}V_{2n3}^n}}{{{R_{n3}}}}} ,\\ {{c_{n4}} = \displaystyle\frac{{V_1^{n + 1}V_{2n4}^{n + 1}}}{{{R_{n4}}}}} 。\end{array}} \right. $ | (9) |
式中:
| $ \left\{ {\begin{array}{*{20}{l}} {{V_1} = - \sqrt {\displaystyle\frac{{1 + 0.1{{({f_0}/{f_1})}^2}}}{{1 + {{({f_0}/{f_1})}^2}}}} } ,\\ {{V_{2ni}} = \displaystyle\frac{{a\cos {\theta _{ni}} - \sqrt {{b^2} - {{\sin }^2}{\theta _{ni}}} }}{{a\cos {\theta _{ni}} + \sqrt {{b^2} - {{\sin }^2}{\theta _{ni}}} }}} ,\\ {{f_1} = \displaystyle\frac{{378}}{{{w^2}}}} ,\\ {{\theta _{ni}} = \arcsin \displaystyle\frac{{{R_0}}}{{{R_{ni}}}}} 。\end{array}} \right. $ | (10) |
式中:w为风速;a为海底密度与海水密度的比值;b为海水和海底折射率比。
各本征声线的路径长度为:
| $ \left\{ {\begin{array}{*{20}{l}} {{R_{n1}} = \sqrt {{r^2} + {{\left(2nH + z - {z_0}\right)}^2}} } ,\\ {{R_{n2}} = \sqrt {{r^2} + {{(2nH + z + {z_0})}^2}} },\\ {{R_{n3}} = \sqrt {{r^2} + {{[(2n + 2)H - z - {z_0}]}^2}} },\\ {{R_{n4}} = \sqrt {{r^2} + {{[(2n + 2)H - z + {z_0}]}^2}} } 。\end{array}} \right. $ | (11) |
式中:z为声源深度;
冰水界面是研究极地环境声学绕不开的一部分,海冰的大小,形状,分布通常是不规律的。冰水界面分为光滑界面与粗糙界面,粗糙界面呈犬齿状,冰的下表面分布不均匀,也有冰脊的情况。本文通过编写冰面文件导入Bellhop模型,即可对海冰环境下的声传播进行研究。
为了获得不规则海冰的反射系数,Burke和Twersky提出了B-T冰层声反射模型[14]。模型中将冰层下表面看作自由或刚性表面下,随机分布了许多半椭圆凸起。
| $ R = {\left| {\frac{{1 + Z}}{{1 - Z}}} \right|^2} = 1 + 4{Re} \left( {\frac{Z}{{{{\left| {1 - Z} \right|}^2}}}} \right) ,$ | (12) |
| $ Z = \frac{n}{{k\cos {\varphi _0}}}{A_f}。$ | (13) |
式中:n为单位长度内含有半椭圆凸起的平均个数;
半椭圆的长轴表示为
| $\begin{split} Z =& - \frac{n}{{\cos {\varphi _0}}}\Biggr[\frac{{{{\text π} ^2}{k^3}}}{{16}}(2{\xi ^2}{\eta ^2} + {\xi ^2}{(\xi + \eta )^2}{\sin ^2}{\varphi _0}) +\\ & {{i}}\frac{{{\text π} k}}{2}(\xi \eta - \xi (\xi + \eta ){\sin ^2}{\varphi _0})\Biggr] ,\end{split}$ | (14) |
| $\begin{split} Z =& - \frac{{nl}}{{\cos {\varphi _0}}}\left[\cos (\varphi 0 - \gamma ) + \frac{{\tan {\varphi _0}\sin (2kl\sin \gamma \cos {\varphi _0})}}{{2kl}}\right] +\\ &\frac{{n\eta }}{2}{\left(\frac{{{{i}}{\text π} }}{{k\xi \cos {\varphi _0}}}\right)^{1/2}}{e^{ - {{i2k}}\xi {\text{cos}}{\varphi _0}}} 。\\[-10pt] \end{split}$ | (15) |
式中,
| $ \tan \gamma = {\rho ^{ - 2}}\tan {\varphi _0} ,$ | (16) |
| $ {l^2} = {\xi ^2}(1 + {\rho ^4}{\cot ^2}{\varphi _0}){(1 + {\rho ^2}{\cot ^2}{\varphi _0})^{ - 1}}。$ | (17) |
连续谱模拟:由Ross经验公式计算获得式(2)中的各参数,以国外某型号水下航行器公开的参数进行仿真。螺旋桨直径
|
|
表 1 连续谱曲线参数 Tab.1 Continuous spectrum curve parameters |
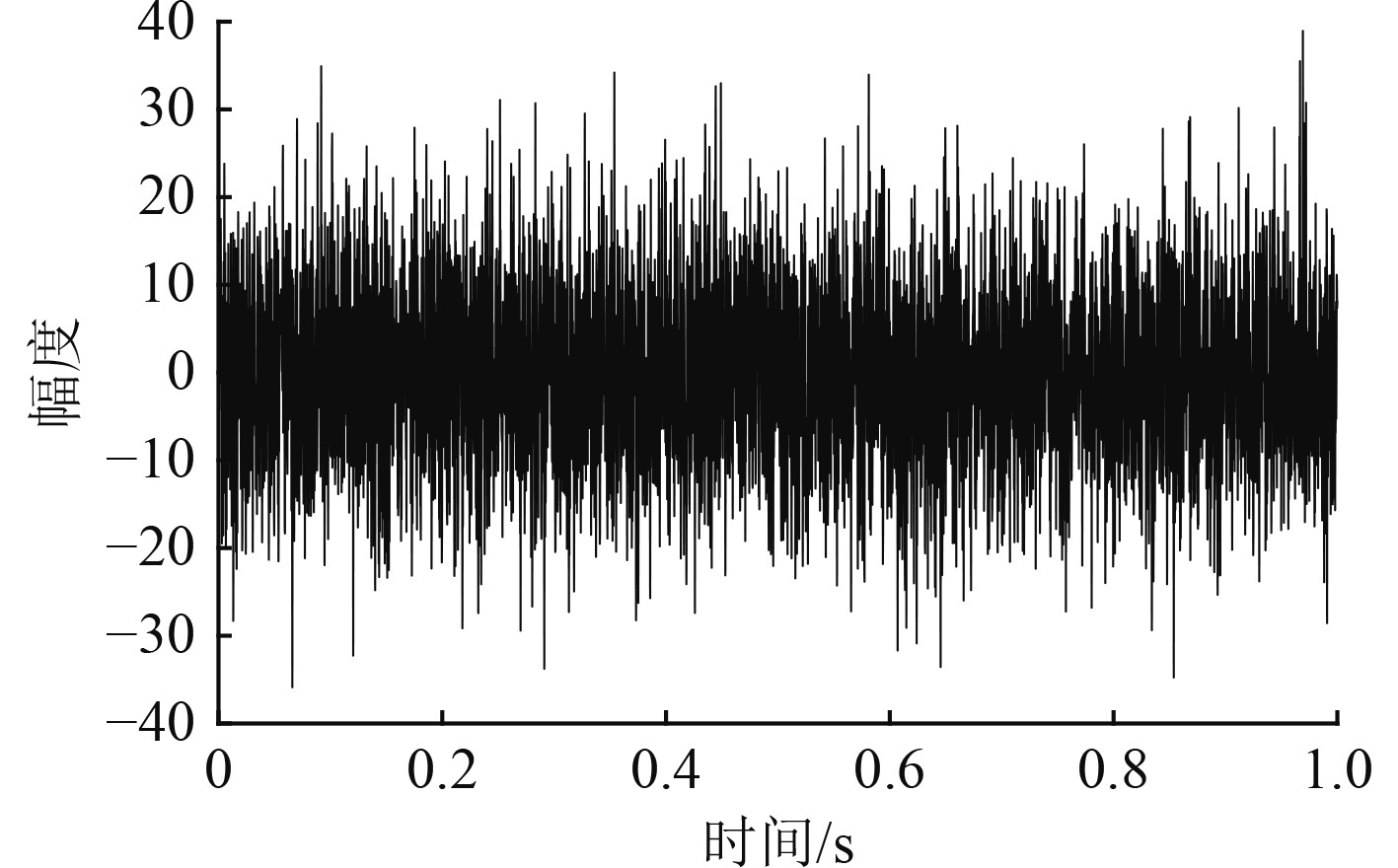
|
图 1 白噪声信号时域谱 Fig. 1 Time domain spectrum of white noise signal |
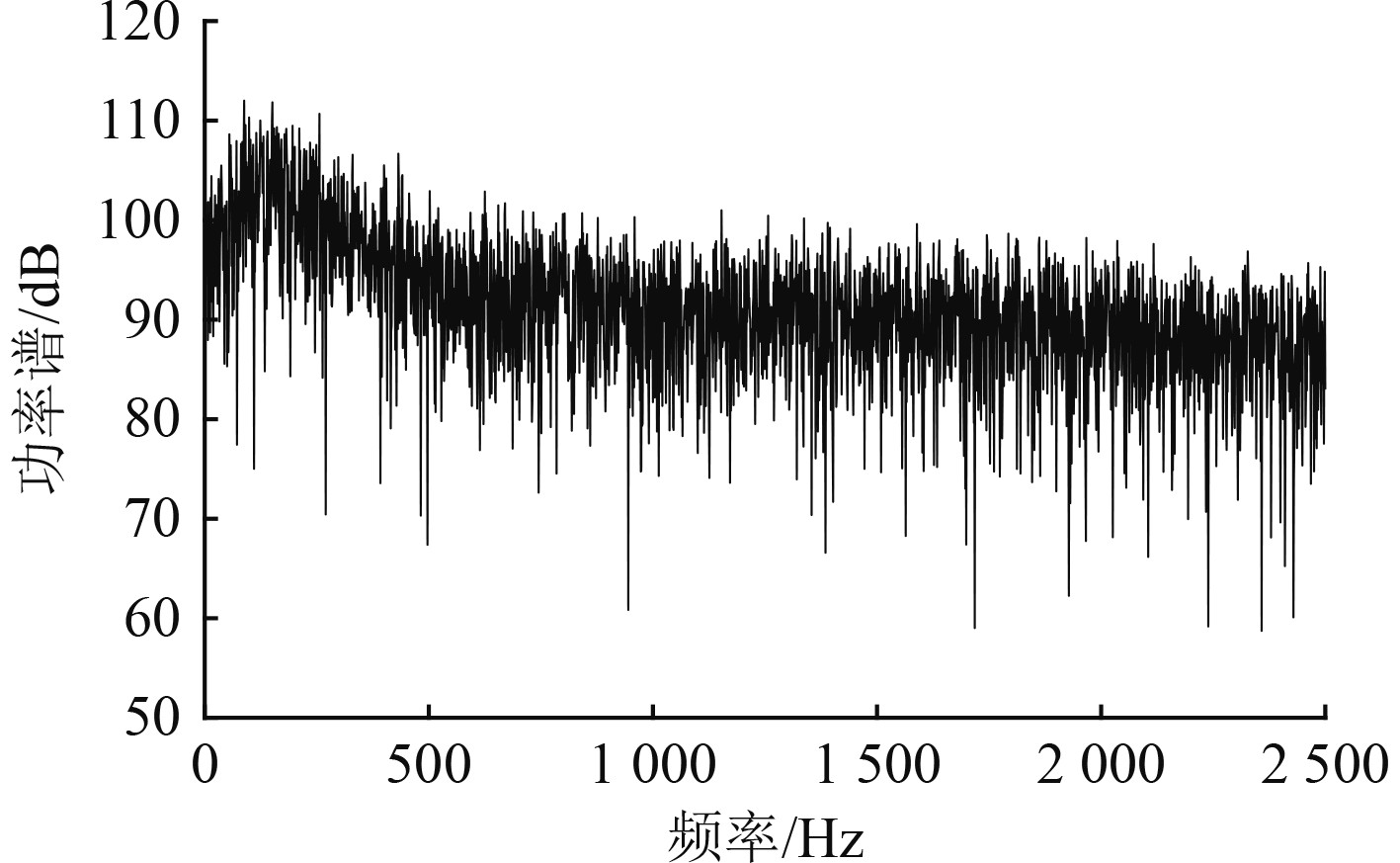
|
图 2 水下航行器噪声连续谱 Fig. 2 Continuous spectrum of underwater vehicle noise |
线谱模拟:本文设定线谱频率为16、32、48、64 Hz,对于随机线谱按照一般情况在
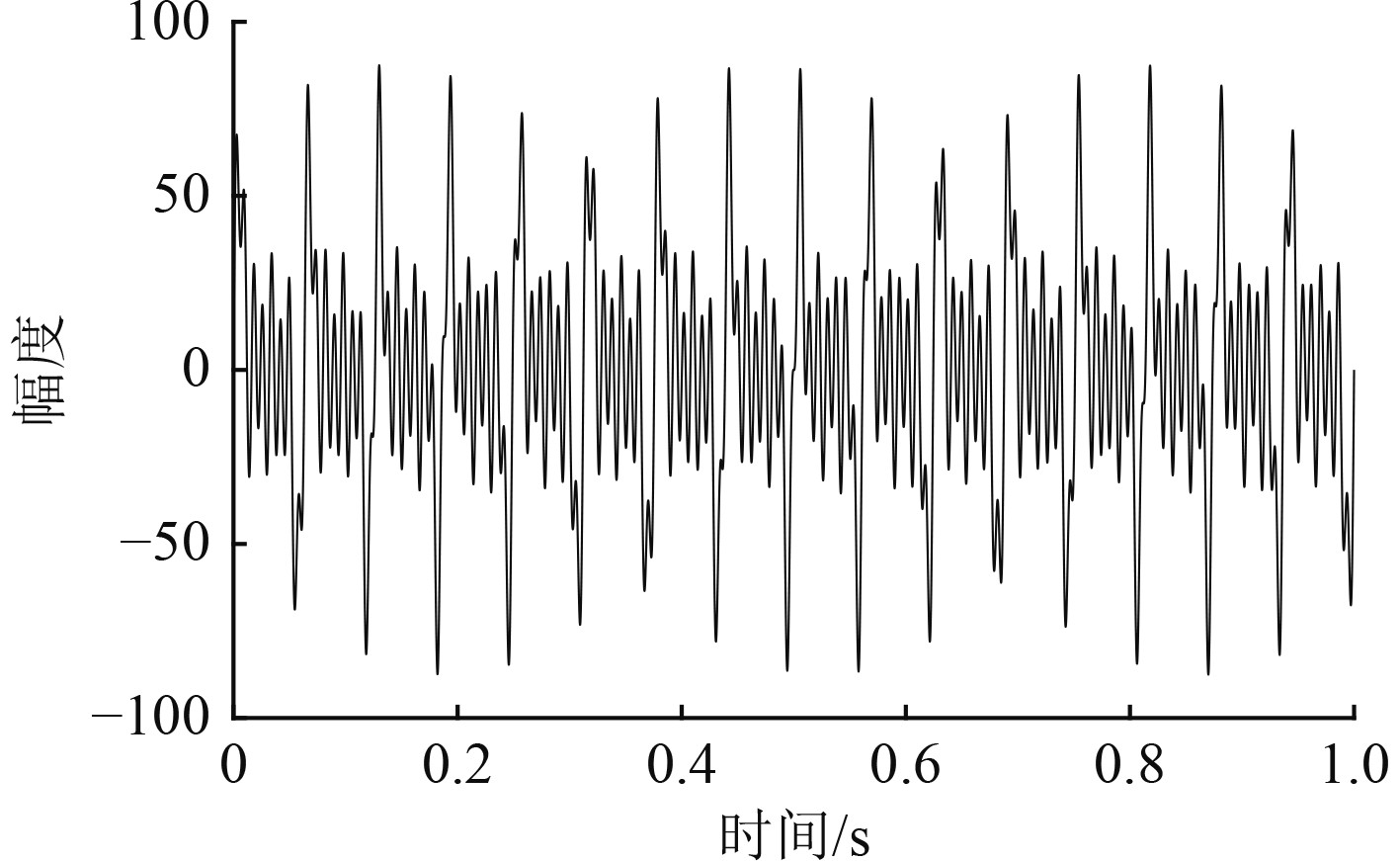
|
图 3 线谱时域信号 Fig. 3 Line spectrum time domain signal |
调制谱模拟:根据轴频及叶频,调制谱选择为4.1、8.2、12.3、28.7 Hz,频域信号如图4所示
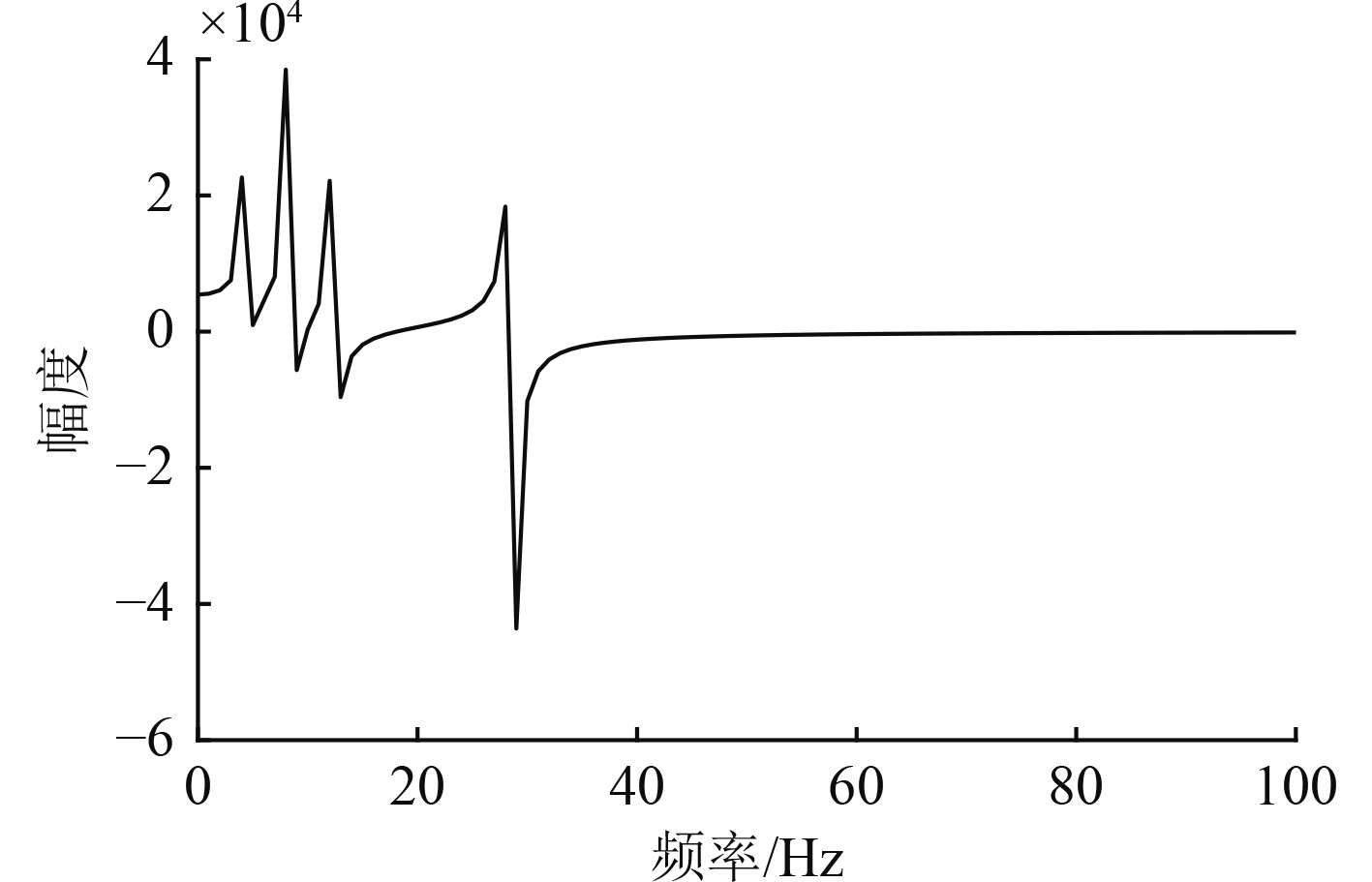
|
图 4 调制谱频域信号 Fig. 4 Modulation spectrum frequency domain signal |
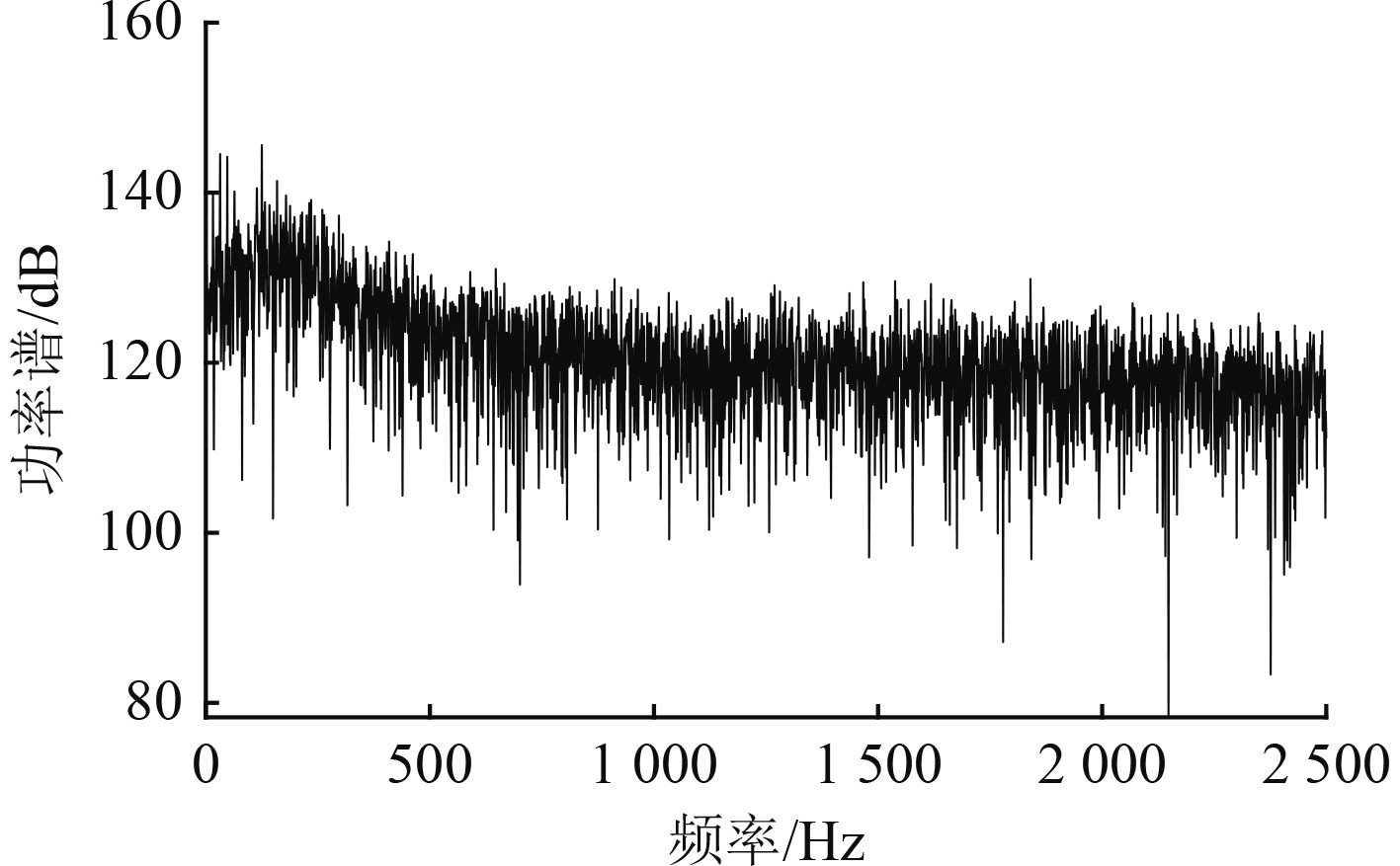
最终利用本节数学模型将3种信号分量整合,获得完整的水下航行器辐射噪声,如图5所示。
|
图 5 水下航行器辐射噪声功率谱 Fig. 5 Power spectrum of radiated noise from underwater vehicles |
水声信道中声传播模拟:对深度为

|
图 6 Bellhop 获得的接收信号功率谱图 Fig. 6 Received signal power spectrum obtained by bellhop |
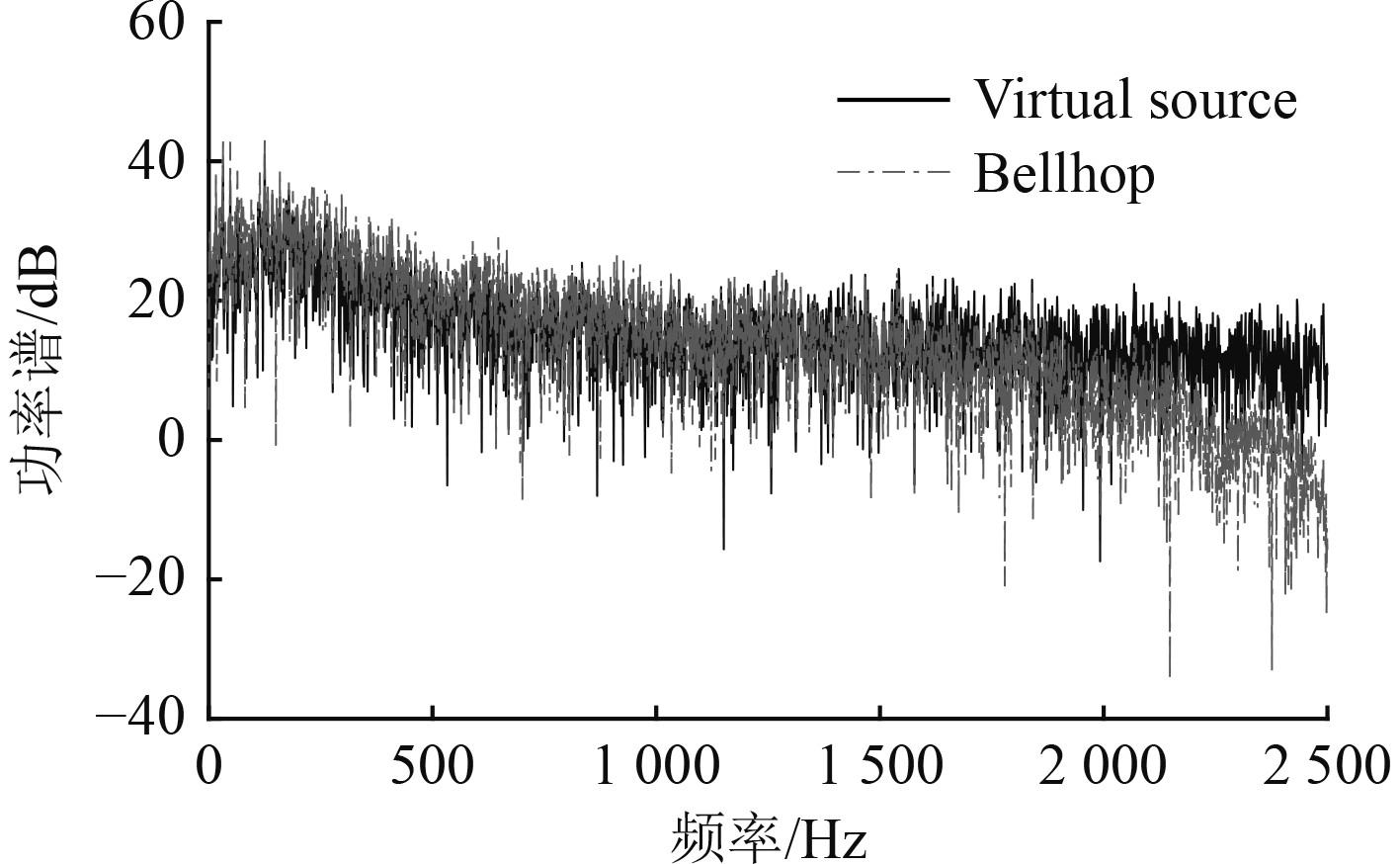
利用基于虚源法的数值计算方法,计算相同海洋环境下的接收信号,与Bellhop的结果进行对比验证,结果如图7所示,从图中可以看出,接收信号衰减后的幅度基本一致,信号谱峰的趋势也一致,在高频段幅值有些许差距,这是因为虚源法模型中无法精准的考虑声速梯度,且其中包含了随机相位,入射角的选取也与Bellhop后台程序有所差异。验证了本文模拟的可靠性。
|
图 7 虚源法与Bellhop法获得接收信号功率谱对比 Fig. 7 Comparison of received signal power spectra obtained by virtual source method and bellhop method |
设冰脊参数为:
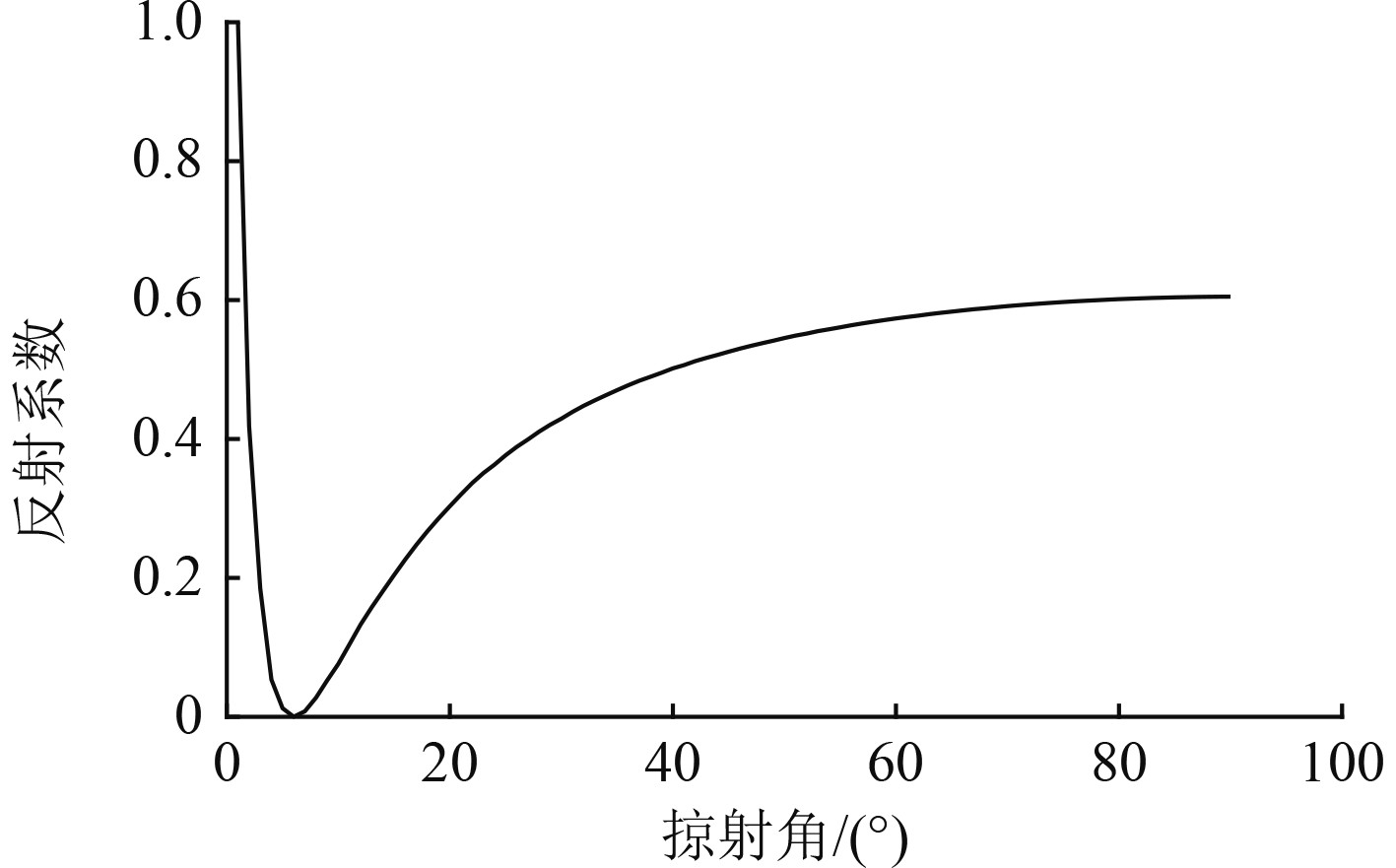
|
图 8 B-T冰水模型下的声反射系数 Fig. 8 Sound reflection coefficient under B-T ice water model |
可知,冰水界面的反射系数在掠射角1°~10°的区间内从1逐渐趋近于0,并在10°~12°之间获得最低值,最终趋近于0.4。
3.3 冰下声信道仿真将3.1节获得的水下航行器辐射噪声信号作为输入信号。分别设置声源深度为60、200和500 m,海深
将3.2节计算获得的反射系数,角度和相位写入到Bellhop中的.trc文件,该文件主要包含了上边界的反射系数。将冰层下表面的半椭圆起伏写入到.ati文件,改变上边界的形状。
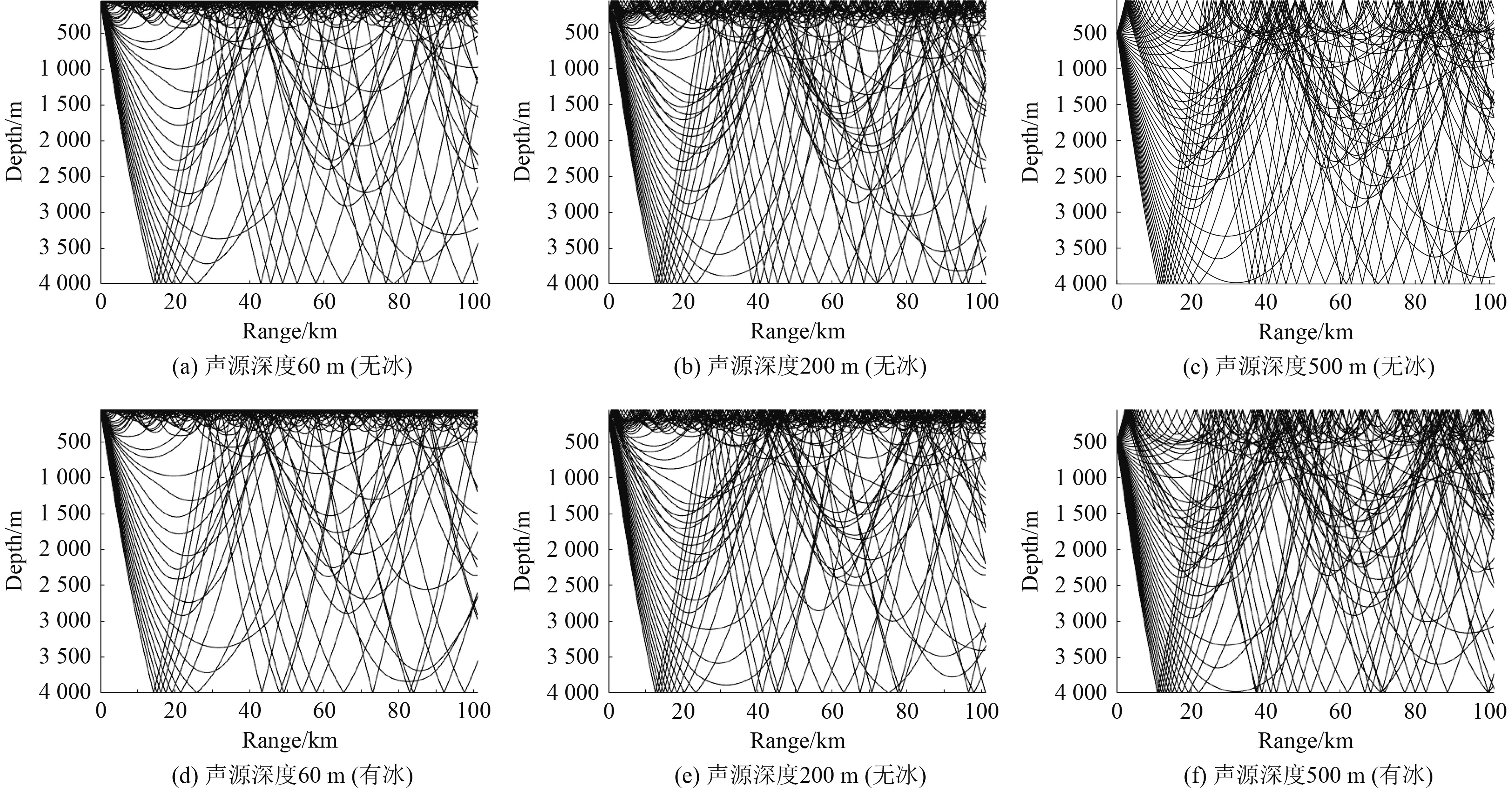
由图9可知,在声源处于同一深度的情况下,有冰界面的声线比无冰界面的声线稀疏。这是由于冰水上边界的存在使声线反射次数增加,传播损失也随之增加,到达远方的声线数量减少。由于极地海域声速剖面整体呈上升趋势,所以声线都向上弯曲。
|
图 9 上边界有冰与无冰的声线轨迹 Fig. 9 Ray tracing with and without ice on the upper boundary |
从图10可以看出,无冰和有冰界面的轮廓几乎一致。无冰界面的声线在深海区域能量较低,而有冰界面中,声线由于不规则冰面的反射,声线能量能够到达深海区域;从水平方向来看,前50 km有冰界面的声传播损失增长较慢,但在后50 km传播损失增长幅度大于无冰界面。观察可知,声源位于500 m时的浅海声传播损失小于声源位于60 m和声源位于200 m时的声传播损失,这是因为随着声源深度的增加,受到冰水上边界的影响减弱。但传播损失的增长幅度更大,在深海处到达100 dB。
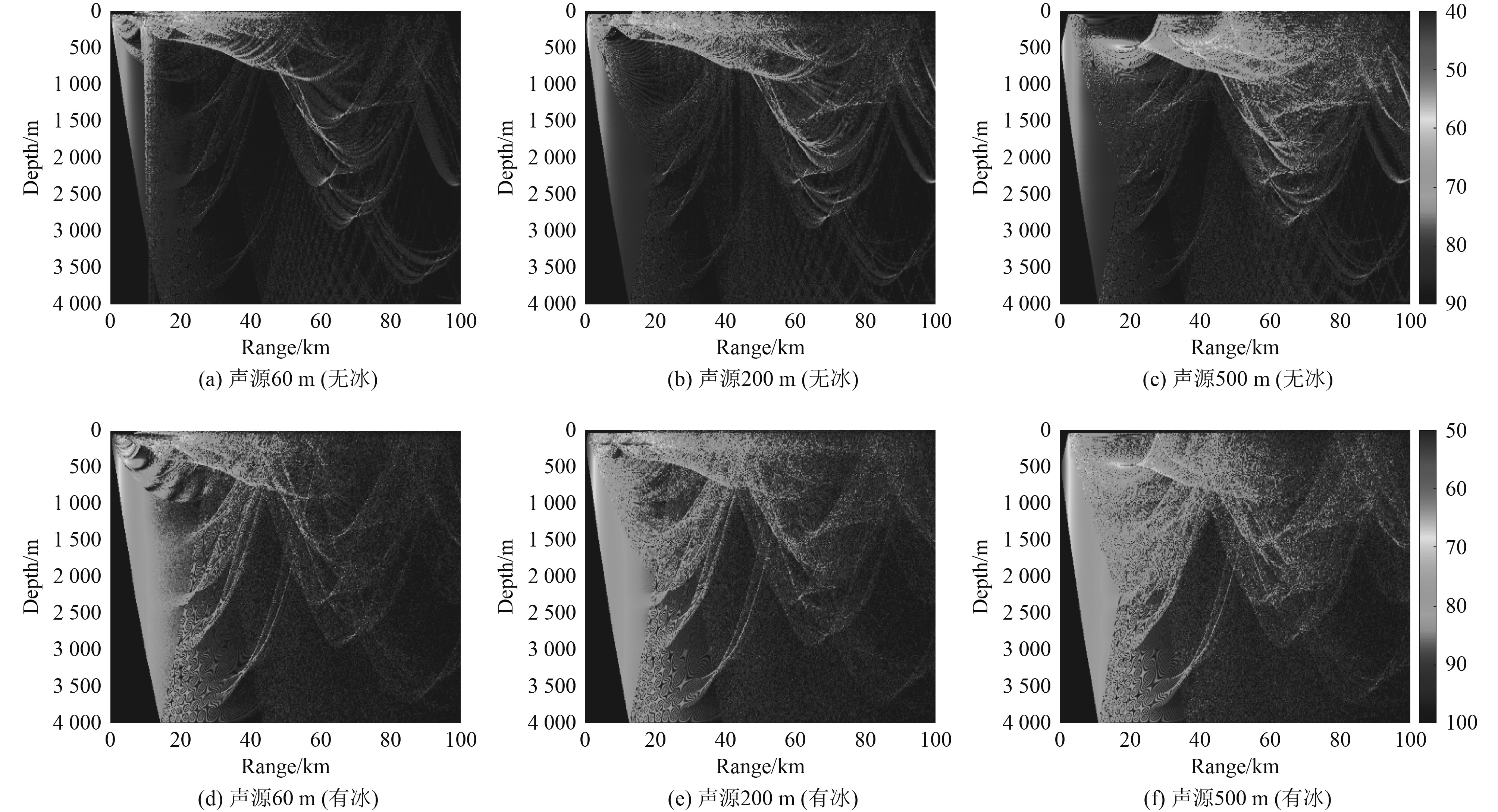
|
图 10 上边界无冰与有冰的传播损失 Fig. 10 Propagation loss in the absence and presence of ice at the upper boundary |
从图11可知,无冰情况下,接收点信号的功率谱集中在20~30 dB,声源深度的变化对接收信号幅度产生了5 dB左右的变化。这与传播轨迹的变化最后到达接收点的声线不同有关。同时,发现有冰界面下,接收点信号功率谱降低20~30 dB,功率谱初始幅度都集中在0 dB,峰值为10 dB。这是因为冰面的存在增加了声线的传播路径和反射次数,到达接收点的声线数量比无冰情况少。

|
图 11 上边界无冰与有冰的接收点信号 Fig. 11 Receiving point signals with or without ice on the upper boundary |
本文首先对水下航行器辐射噪声的连续谱、线谱、调制谱进行建模,之后将模拟获得的辐射噪声信号与Bellhop模型相结合,研究海洋信道对声传播的调制特征。结合B-T冰水模型模拟冰下信道,计算分析了不同声源深度的接收点声信号特性。结果表明:
1)经过海洋信道传播后的接收点信号功率谱与声源处的辐射噪声功率谱趋势一致,幅值根据水平传播距离的变化产生不同程度的降低;
2)由于冰水界面的反射系数较低、声传播损失较大,有冰界面的声线比无冰界面的声线稀疏,导致部分声线在传播途中消失,声线无法远距离传播;
3)由于冰面的不规则界面对声线的多角度反射,声线被散射到海底,使得声能量扩散在海洋空间中;有冰界面下的声传播损失的增长幅度大于无冰界面下声传播损失的增长幅度,在远距离时传播损失能够到达100 dB;
4)经过水平距离为100 km的无冰界面信道传播后,辐射噪声功率谱幅值下降约100 dB,当冰水界面存在时,增加了声线的传播路径和反射次数,功率谱幅值将额外降低20~30 dB。
| [1] |
郑援, 胡成军, 宋汝刚. 船舶航行辐射噪声信号仿真方法研究[J]. 信号处理, 2016, 32(1): 14-20. |
| [2] |
陆越, 李钟. 潜艇辐射噪声模拟及匹配发射技术研究[J]. 声学与电子工程, 2020(3): 39-42. DOI:10.3969/j.issn.2096-2657.2020.03.011 |
| [3] |
向辉平, 罗建, 傅瑞锦. 舰船宽带连续谱噪声的模拟[J]. 声学技术, 2005, 24(3): 140-143. DOI:10.3969/j.issn.1000-3630.2005.03.004 |
| [4] |
XU H, XU H Q, ZHANG B Y. Characteristics modeling and simulation of ship-radiated noise[J]. Advanced Materials Research, 2012, 546: 143-148. |
| [5] |
何正耀, 张翼鹏. 舰船辐射噪声建模及仿真研究[J]. 电声技术, 2005(12): 52-55. DOI:10.3969/j.issn.1002-8684.2005.12.014 |
| [6] |
涂峰. 水声信道的建模与仿真研究[D]. 武汉: 华中科技大学, 2003.
|
| [7] |
李庆来. 基于射线理论的浅海声场数值预报研究[D]. 哈尔滨: 哈尔滨工程大学, 2008.
|
| [8] |
孙博, 程恩, 欧晓丽. 浅海水声信道研究与仿真[J]. 无线通信技术, 2006, 15(3): 11-15,19. DOI:10.3969/j.issn.1003-8329.2006.03.003 |
| [9] |
丁浩, 李伟, 邓鹏, 等. 浅海高频水声信道统计特性分析与仿真[J]. 舰船科学技术, 2021, 43(9): 130-133. DOI:10.3404/j.issn.1672-7649.2021.05.027 |
| [10] |
李贞刚. 冰水界面反射系数的研究[J]. 声学技术, 2004, 23(z1): 87-89. DOI:10.3969/j.issn.1000-3630.2004.z1.029 |
| [11] |
杨威. 极地环境冰下水声传播特性研究[D]. 大连: 大连理工大学, 2021.
|
| [12] |
明平寿. 北极常年冰覆盖下的水下声场建模方法研究[D]. 青岛: 山东科技大学, 2019.
|
| [13] |
钱晓南. 舰船螺旋桨噪声 [M] . 上海: 上海交通大学出版社, 2011: 70-85.
|
| [14] |
朱广平, 殷敬伟, 陈文剑, 等. 北极典型冰下声信道建模及特性[J]. 声学学报, 2017, 42(2): 152−158.
|
 2024, Vol. 46
2024, Vol. 46
